以下の投稿において自然指数関数の正体たる「0を中心に-InfからInfを直線で結ぶ均等尺を1を中心に0からInfを結ぶ直線に射影して現れる対数尺」自体に(等差数列上の)1単位の均等尺を(等比数列上の)ネイピア数単位の対数尺に変換する効能があり、(0±1i)方向へのπ倍のベクトル入力により円形性(Circularity)を取り戻すなる考え方を示しました。
【無限遠点を巡る数理】オイラーの公式と等比数列⑤ネイピア数概念は「1次元の世界」から現れる?
①かつての投稿で(それ自体は数理で直接扱えない観測原点0と観測極限Inf(inity)の間に存在する)自然数集合(Natural Set)=初項(First Term)1/公差(Common Difference)1の等差数列(Arithmetic Sequence=算術数列)Nn(n=1→Inf){a0,an+(n-1)d,…}(ただしa0=初項,d=公差)={1,1+1=2,(1+1)+1=3,…,n}とN次元の直交(Orthogonal)/積(Product)を想定するデカルト座標系(Cartesian Coordinate System) の概念くらいは(最初からプリセットで人間の脳内に存在する)形相(Eidos/Form)と考えても良いかもしれないとした。
【無限遠点を巡る数理】オイラー座標系①自然数/整数概念の再定義。

逆をいえば、それに決して含み得ない、すなわち0を中心に観測極限Inf(inity)が極少値-Infと極大値Infに分割された形で認識される両側無限数列(Both Sides Infinite Sequence)をどう規定するかこそがこの着眼点からの数理の出発点となる。

②最初に質量(Hyle/Prima materia=第一質料)として実存するのは(確率でしか観測結果が得られない)確率密度空間(Probability Density Space)の観測結果集合(Observation Result Set)のみと考えると、まず真っ先に取り組むべきは観測結果を「最大値1,最小値0の振幅」にマッピングし(最大観測値と最小観測値の間に分布する観測結果集合の平均を中心に)確率楕円-1^x(y=(0+1i)を検出する作業という事になる。
【初心者向け】記述統計学と代表値




-
確率楕円-1^x(y=(0+1i)^2x)はN次元の重なりを備え得る。そしてその時の歪曲した輪郭から総称は「円」ではなく「楕円」となった。
【初心者向け】方形描画関数②距離空間(Metric Space)との関係。 -
平均(Mean)は外れ値(Outlier)の影響を受けやすいので誤差関数(ERF=Error Function)や相補誤差関数(ERFC=Complementary Error Function)、さらには「大数弱の法則(WLLN=Weak Law of Large Numbers)」成立を前提に正規分布(Normal Distribution)の考え方が現れたが、(「天才やエリート集団の数理的証明」などに端を発っして近代以降成立した)統計学(Statistics)における帰無仮説(Null Hypothesis)概念はむしろ「有意水準の外れ値(Significance Outliers)」を検出して有効活用しようと考える。
外れ値と判定する方法と、外れ値の除去について
【初心者向け】誤差関数(ERF)と相補誤差関数 (ERFC)。
【初心者向け】正規分布とは何か?
【無限遠点を巡る数理】無限遠点としての正規分布と分散概念の歴史 - かかる「予測の科学(Forecasting Science)」の分野はさらに線形/非線形の回帰分析(Regression Analysis)や機械学習(Machine Learning) の概念へと発展していく。極限として想定する分布も正規分布ばかりではなくなっていく。
回帰分析(単回帰分析)をわかりやすく徹底解説!
【初心者向け】記述統計学と代表値
③どんな方法を用いるにせよ半径1の単位円の定義を確定すると 無限連続等比数列(Infinite Continuous Geometric Progression=無限連続幾何数列)たる1^x(y=(1+0i)と-1^x(y=(0+1i))の接点として整数列(Integer Line)が規定可能となる。ただし後者のピッチは2なので規則正しく離散的な公差(Common Difference)1の等差数列(Arithmetic Sequence=算術数列)を得る為に偶奇一対(Parity Set)で扱う必要が出てくる。
【無限遠点を巡る数理】オイラー座標系②複素等比数列による整数概念の再構築。


- これ以降観測結果集合は(あくまでその結果が有意水準で解離しない事を条件に)演算結果集合(Operation Result Set)にとりあえずその役割を譲る。
- 「偶奇性の発生」ばかりか「ピタゴラスの定理(Pythagorean Theorem)y=±sqrt(1-x^2)が半円しか描けない問題」「緯度経度法において緯度が経度の、三次元極座標系において垂直角θが水平角φの半分で済む問題」「複素数に共役性が存在する問題」全てがこの段階での「無限遠点Infinityの±方向への分割」に関係してくる。
【Rで球面幾何学】「半円しか描けなかった」世界の思い出?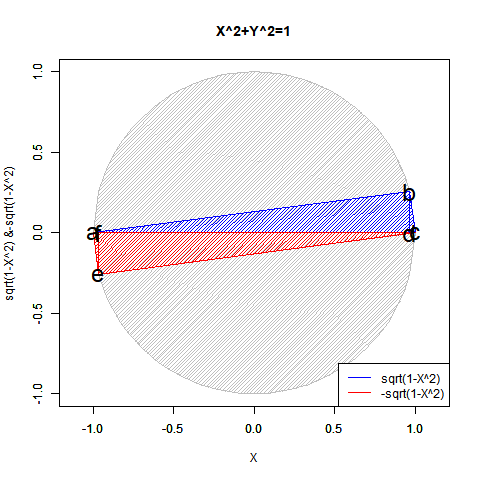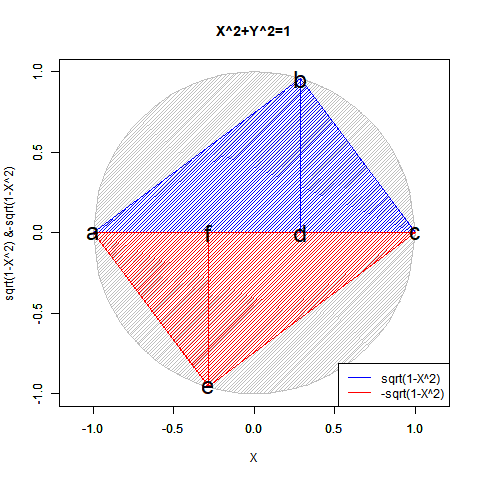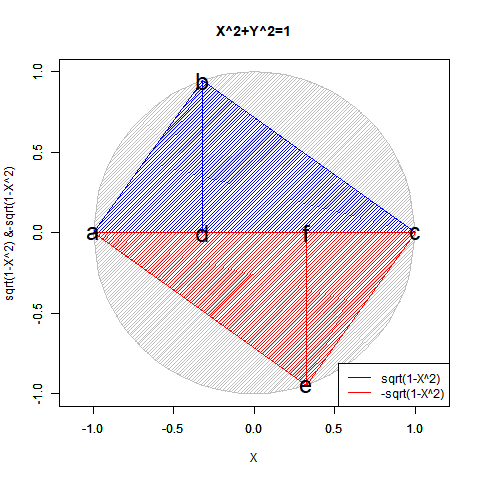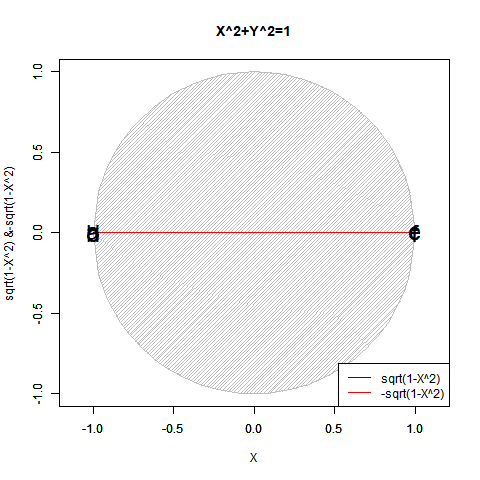
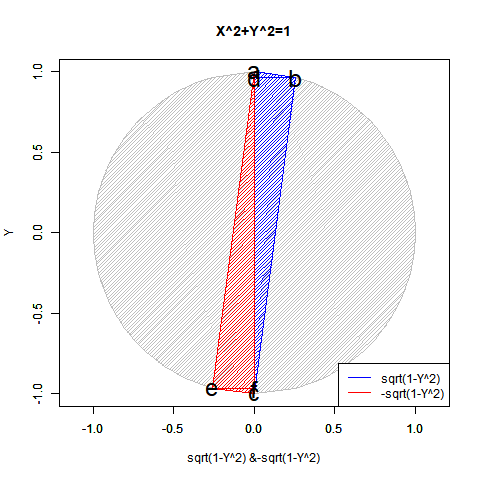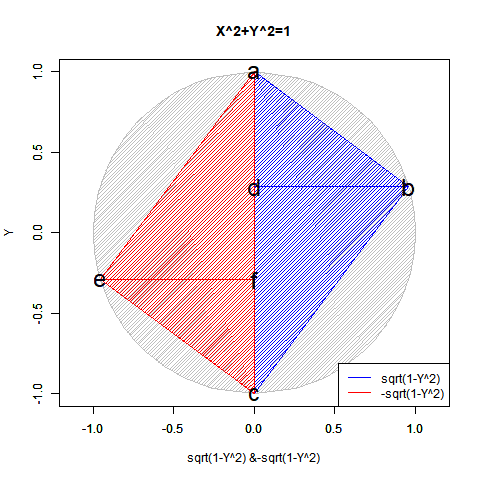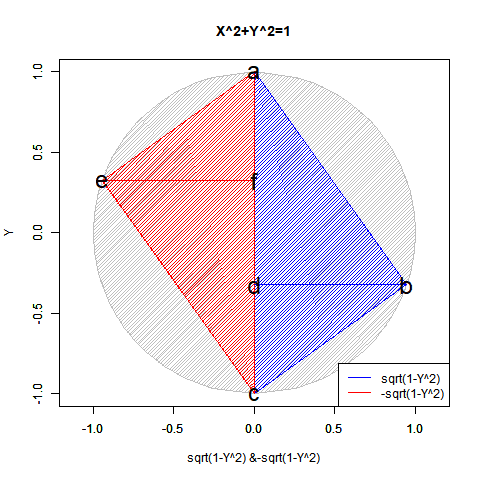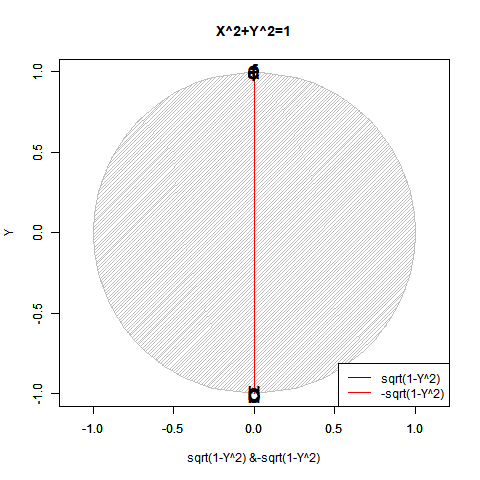
【初心者向け】半径・直径・円周長・円の面積・球の表面積・球の体積の計算上の往復
【初心者向け】複素共役(Complex Conjugate)のアニメーション表示について。
- あるいは「関数-1^xにおける(±1+0i)⇄(0±1i)⇄(∓1+0i)の繰り返しの実数部のみを取り出して周期単位とする事で、交差1の等差数列を得る」とも考えられるが(この場合、定数関数x=0が基準線として通る)、この場合も0を原点とする偶数系(Even System)と-1/1を原点とする奇数系(Odd System)の同時成立は避けられない。いずれにせよこの段階における数理では実数部における添字単位の一次元上の増減のみが重要で(それを導出するのに用いられる)周期単位虚数部の演算は様々な形で想定され、かつ最終的には切り捨てられる。例えば上では円形関数y=-1^xを想定したが、これは方形関数x+y=1に置き換えても構わない。この辺りの「最終的に計算が合っていれば導出過程を問わない」自由度の高さが虚部の虚部たる由縁。要するに補助線といってよい?【初心者向け】方形描画関数①三角関数との関係。


- この考え方を極限まで押し進めたのが「‖x‖=0⇄x=0(演算結果集合の数だけ零元が存在する)」「‖ax‖=|a|‖x‖(スカラー倍演算が成立する)」「‖x‖+‖y‖≧‖x+y‖(三角不等式が成立する)」を三大成立条件とするノルム空間(Norm Space)概念であり、実数の範囲を‖x‖+‖y‖=‖x+y‖から‖x‖+‖y‖≧‖x+y‖に拡張した時(すなわち整数線に垂直する高さの概念を認め、面積の概念が生じる時)初めて距離/計量関数(Distance/Metric Function)操作が統計学上の順位尺度の概念にまで影響を与える展開を迎える(計算の都合上、五問それぞれに20点が割り振られた百点満点のテストの得点配分を「10点/15点/15点/30点/30点」と割り振り直して再集計する場合などに対応?)。この時点ではまだ座標軸{x,y}に立脚するデカルト座標系(Cartesian Coordinate System)そのものが完全成立する訳ではない点に注意。
【初心者向け】方形描画関数②距離空間との関係。
まだまだ途上ですが、こうした展開を(オイラーのφ関数や多面体定理を援用する形で)質量としての素数族2^n概念の導入と捉え、さらに素数族3^n/素数族5^n概念の導入を段階的に考えられないかというのが私が現段階で抱えている構想となります(例えば上掲の場合について単位円定義導入前を2^0段階、導入後を2^1段階と考える)。オイラーやガウスが完成を目指した「近世数学」の実像を明らかにして「現代数学」にどう接続するのか見定める作業、もっと砕いて言うと「高校までに習う数学と大学で習う数学のギャップを埋める作業」と考えています(最近、視野の端に時々コーシーやリーマンの名前が現れる様に…確実に現代数学の世界に近づいてはいる筈だ?)。
ちなみにここまでの概念なら普通に横溢してる様です?
デカルトが扱ったのは、もっとも素直な座標系=直交座標系であった。座標原点という基準点があって、そこからの点の位置の偏りを互いに直交する3方向への成分として表す。この位置を表す3成分=直交座標であるが、その仕組みから、これもあとづけながら、位置ベクトルの成分=座標、と言っても同じことである。これはやがて、一般のベクトルの成分表示につながって行くことになる。
一方で、極座標とかのいわゆる曲線座標というものもある。こちらは、とにかく、点に数を対応させて、点の位置を識別すればよいということで、ある意味、融通無碍、節操のない方法でもある。一方で、自然科学に目を向けると、観測対象があって、その状態を識別するために様々な物理量が使われるのと様子が似ている。様々な物理量を測定することで、扱っている物質の状態を記述するということなので、これも一種の座標と呼んでよかろう。
その背景には、素朴な実在論がある。観測対象が、観測行為とは独立に存在し、実験ないし観測は、それに対して数量を対応させることなので。この意味での「座標系」に、偶然要因による変動を許したものが、確率論でいうところの確率変数に他ならない。
素朴な実在論は、量子論によって否定されることになるのであるが、では、量子論的な座標の概念が確立したかというと、それがなかなか。根源的な問は、とりあえず置いて、道具の使い方にひたすら磨きをかけてきたのが、この100年間の状況である。ただ、非常に面白いところは、直交座標系の背後にある「直交ベクトル空間」をとことん追求したものは、量子論の数学的構造そのものにたどり着くという不思議。
とりあえずオイラーの(Eulerian)φ関数1/2/3/5…と多面体定理(Polyhedral Theorem)V(ertex=頂点)−E(dge=辺)+F(ace=面)=2(計算上の始点にして終点となる一対の対蹠数。二次元上の多面体ではこれをコインの表裏に該当する2とも平面故の0とも換算可能)の関係を調べた以下の投稿では、とりあえず直交の概念に対応するのは素数族2^nと3^n及びその積(Product)2^n3^mのみなる結論に至っています。
【Rで九九】どうして36個の数字しか使われないのか?
【オイラーの多面体定理と正多面体】とある「球面幾何学(Spherical Geometry)」の出発点…
①プラトン立体(Platonic Solid)五種で言うと正四面体(Regular Tetrahedron)、正六面体(Cube=立方体)、正八面体(Regular Octahedron)の範囲で、正六面体は単独、正四面体と正八面体はセットで空間充填(Space-filling)性を備える。


空間充填 - Wikipedia
立方体による空間充填(辺のみ可視化)
正四面体と正八面体による空間充填

また素数族2^n3^mを平面上に全射影した正六角形(Regular Hexagon)は(p-2)q=2p(正p角形の内角をq倍すると2πラジアン/360°になる組み合わせでこの場合p=6/q=3,2π/3=120°)の条件を満たし平面充填(Tessellation)性のみを備える。
平面充填 - Wikipedia

ちなみに平面充填性自体は素数族2^2を平面上に全射影した正方形(Square,p=4/q=4,2π/4=π/2=90°)と素数族3^1を平面上に全射影した正三角形(Equilateral Triangle,p=3/q=6,2π/6=π/3=60°)も備える。どちらも合計4なのは、果たして偶然なのか…




②そして同心円展開上、同構造の再構築を繰り返す(連続同心円を描く)のもまた正方形と正三角形のみなのである。
【オイラーの多面体定理と正多面体】内接円/球面の半径と外接円/球面の半径の狭間
正方形の場合




| Target_size | Target_names | Target_values | |
|---|---|---|---|
| 1 | 2^-1 | 2^-1(2^-0.5r) | 0.5 |
| 2 | 2^-1 | 2^-1d=2^-1*4 | 1 |
| 3 | 2^-1 | 2^-1a1=2^0a0 | sqrt(2)=1.414214 |
| 4 | 2^-1 | 2^-1a1(2^-0.5a0)*4 | 4sqrt(2)=5.656854 |
| 5 | 2^-0.5 | 2^-0.5(2^0r) | sqrt(2)/2=0.7071068 |
| 6 | 2^-0.5 | 2^-0.5d=2^-0.5*4 | sqrt(2)=1.414214 |
| 7 | 2^-0.5 | 2^-0.5a1=2^0a0 | 1 |
| 8 | 2^-0.5 | 2^-1a1(2^0.5a0)*4 | 4 |
| 9 | 2^0 | 2^0(2^-0.5R,2^0.5r) | 1 |
| 10 | 2^0 | 2^0d=2^0*4 | 2 |
| 11 | 2^0 | 2^0a1=2^0.5a0 | sqrt(8)=2sqrt(2)=2.828427 |
| 12 | 2^0 | 2^0a1(2^0.5a0)*4 | sqrt(32)=4sqrt(2)=5.656854 |
| 13 | 2^0.5 | 2^0.5(2^-0R,2^1r) | sqrt(2)=1.414214 |
| 14 | 2^0.5 | 2^0.5d=2^0.5*4 | 2sqrt(2)=2.828427 |
| 15 | 2^0.5 | 2^0.5a1=2^1a0 | 4 |
| 16 | 2^0.5 | 2^0.5a1(2^0a0)*4 | 8 |
| 17 | 2^1 | 2^1(2^1-0.5R,2^0.5r) | 2 |
| Target_size | Target_names | Target_values | |
|---|---|---|---|
| 1 | 3^-1 | 3^-1(3^0r) | 1/2=0.5 |
| 2 | 3^-1 | 3^-1h=3^-1*3 | 3/2=1.5 |
| 3 | 3^-1 | 3^-1a1=3^0a0 | 2*sqrt(1.5)=2.44949 |
| 4 | 3^-1 | 3^-1a1(3^0a0)*3 | 6*sqrt(1.5)=7.348469 |
| 5 | 3^0 | 3^0(3^-1R,3^1r) | 1.0 |
| 6 | 3^0 | 3^0h=3^0*3 | 3.0 |
| 7 | 3^0 | 3^0a1=3^1a0 | 2*sqrt(3)=3.464102 |
| 8 | 3^0 | 3^0a1(3^1a0)*3 | 6*sqrt(3)=10.3923 |
| 9 | 3^1 | 3^1(3^0R) | 3.0 |
通例、多角形にも立体にも数えない二辺形(Bilateral)すなわち均等尺(Even Scale)や対数尺(Logarithmic Scale)や(Cos波やSin波の様な)円状尺(Circular Scale)をポテンシャルとして備える任意の円/球面の対蹠(Antipodes)間における直線的往復(linear Reciprocating Motion)/単振動(Simple Vibration)概念は、(半径1の単位円を生成する)複素数関数-1^x=(0±1i)^2xや(-Inf⇄0⇄Infの範囲の均等尺を0⇄1⇄Infの範囲の対数尺に射影した結果現れる)ネイピア数exp(1)(2.718282)を根とする等比数列、すなわち自然指数関数と自然対数関数の振る舞いに密接に関係してくるが(上に列記した素数族2^n導入に伴う諸現象の原因となるだけで)こうした(-a^xのaが1以上や1以下の場合を想定する)連続同心円展開自体は含まない。

③逆にいえば素数族5^nを要素に含む正十二面体(Regular Dodecahedron)や正二十面体(Regular Icosahedron)は直交の概念から完全に離れ、素数族7^n以上を要素に含む多角形はもはや正多面体を構成しない(辺数が増大するにつれその多角形の内接円と外接円の半径差が0へと収束していくのみ)。後者はある意味無限大Infの頂点数と無限小-Infの辺長によって構成され、全頂点が「中心からの距離が全て均等で」「中心から下ろした垂線と垂直に交わる」性質しか備えない円概念に回帰してしまう様にも見て取れる(なるほど円概念には当初からこういう形で無限大の概念と無限小の概念が内包されているのである!! 文章にまとめる過程で初めて気付いた…)。


④こうして全体像を俯瞰してみると(数理が観測結果集合から演算結果集合に立脚する様になる)1次元未満の空間においては確率演算(Probability Operation)や複素数表現(Complex Expression)が全てであり、実数表現(Real Expression)が可能となる1次元以上の空間においても平面充填条件(p-2)q=2pを満たさない多角形やオイラーの多面体定理V−E+F=2の条件を満たさない多面体などについて記述する上で確率演算や複素数表現が欠かせない。この辺りの実数的安定性(Real Stability)と(確率演算/複素数表現を要する)虚数的不安定性(Imaginal Instability)の交代性はある意味偶奇性(Parity)の本質で(要するに対蹠が通ってデカルト座標系に収まるかどうかが重要。対蹠が通ってない「奇数次元」では、そもそも対蹠の概念が存在しない原始段階を除き、それぞれの対蹠からの対象な展開を一対で扱う事になる。数としての偶数と奇数の関係というより偶関数と奇関数の関係に近いイメージ)、Linuxカーネルのバージョン管理が偶数系を安定バージョン、奇数形を開発バージョンとするのもこの辺りの概念にインスパイアされての事かもしれない。
ちょっぴりLinuxが語れるようになる基礎知識

前者を我々の馴染んだ1次元、2次元、3次元…なる表現に対応させるなら、後者はその間を取って0.5次元、1.5次元、2.5次元と呼ばれる事になるだろう。こうした概念が物理学の世界における量子揺らぎ(Quantum fluctuation)の概念とぴったり重なるかは不明だが、とにかくそれを仮に「数理の量子揺らぎ的側面(Quantum Theory in Mathematical Things)」と呼んでもそれほどの齟齬は生じない様に思える。というか、そう考えると双対性(Duality)や「一対の正四面体から立方体への遷移」「立方体から正十二面体への遷移」といった幾何学のアクロバティックな側面が上手く説明出来る様に感じられるのである。
【オイラーの多面体定理と正多面体】正四面体と正六面体と正八面体の連続性と「テトラパックの思わぬ正体」について。

【オイラーの多面体定理と正多面体】正六面体と正十二面体の間の往復(「屋根掛け法」とは何か?)


こういう形で循環する座標系をとりあえず(主にオイラーの名前を関した定理の積み重ねから導出される事から)オイラー座標系(Eulerian Coordinate System)と呼ぶ事にし、その性質を調べる様になった訳です。正直に打ち明けておくと「ベクトル空間と関数列を巡るバナッハ空間とヒルベルト空間に関する議論」が難し過ぎてついていけないので始めた試みでした。
バナッハ空間とヒルベルト空間
記号‖.‖と線形集合Xで表される関数
‖.‖:X→[0,Inf) (x→‖.‖) (2.1)
に対し以下の条件を考える:
‖x‖=0⇄x=0(2.2)
‖x‖+‖y‖≧‖x+y‖, x,y∈X (三角不等式), (2.3)
‖cx‖=|c|‖x‖, c∈K, x∈X(2.4)①(2.3)と(2.4)を満たす‖.‖をX上の半ノルム (Semi-norm)という。
②(2.2) を満たす半ノルムをX上のノルム(Norm) と言う。
③Xにあるノルム‖.‖を指定した時の組(X,‖.‖)をノルム空間 (Normed Vector Space) という。
既にベクトル=線形空間の概念が生じて以降の議論。とりあえずは‖x‖+‖y‖=‖x+y‖を線形性(Linearity)と定義し、これに±の有向性(Directionality)概念を加えたのがベクトル空間(Vector Space)と考える粗雑な理解でOK?
高校数学における線形性の8つの例
線形性を満たす関数は「原点を通る直線」=一次関数(Linear Function)しか存在しません(y=0を含むy=ax。ただしx=0すなわちy=∞xをこれに含めて良いかについては様々な議論がある)。
統計学上の尺度論と照会するなら半ノルムが「間隔尺度(Interval Scale)」未満(スカラー倍の成立も三角不等式の成立も確信出来ない為、この表現となる)、ノルムが「比例尺度(Proportional Scale)」未満(三角不等式の成立が確信出来ない為、この表現となる)となる様です。三角不等式の成立が確信出来ないのは、この統計量が‖x‖+‖y‖=‖x+y‖となる線形条件しか扱わないからですね。要するにこれが上掲の(等比数列1^xと-1^xの交点として整数列を規定する)素数族2^1空間の概念の出発点となりました。
変数の尺度
提案したのはスタンレー・スティーブンズ(Stanley Smith Stevens)で、1946年サイエンス誌に発表した"On the theory of scales of measurement"なる論文の中で、変数の4つの尺度「名義尺度」「順序尺度」「間隔尺度」「比例尺度」について説明したのが最初とされています。
統計学にはさらに以下の尺度も存在します。
- 「質的変数(Qualitative variable)」と「量的変数(Quantitative variable)」…名義尺度と順序尺度は質的変数に属し、間隔尺度と比例尺度は量的変数に属する。質的変数については「カテゴリー変数(Categorical Variable、カテゴリカル変数とも)」という呼び方もある。
- 「離散変数(Discrete Variable)」と「連続変数(Continuous Variable)」…「離散変数」は飛び飛びの値をとる変数の事で、例えば賽子の出目などを指す。「連続変数」は重さや温度などのように連続した値をとる変数を指す。
①このうち質的辺数に分類される名義尺度については、過去投稿において「全ての観測結果集合の元が共通点を全く持たず(同一次元上に存在せず)かつ有意水準でそれぞれの差異が見出せない状況は(円の半径の距離は全て同じと判断するピタゴラスを援用する形で)ある種の円状/球面状空間を形成する(この段階から如何に脱却するかが統計上の最初の課題となる)」とした。
【無限遠点を巡る数理】オイラーの公式と等比数列②線形性ならぬ円形性について

②また連続変数と離散変数の関係については背景に連続的に存在する確率密度空間(Probability Density Space)を想定し、それに対して離散的にしか取得し得ない観測結果集合(Observation Result Set)と、これを改めて可能な限り連続量として掌握しようとする試行としての演算結果集合(Operation Result Set,表現上数式または規則正しく離散的な添字集合として表される。前者にも離散集合にのみ対応する条件が付与される場合があり、後者も代表値を列記してるだけで連続量を表している場合がある)を対応させる事で統計学上の概念と一般数理上の概念のギャップの発展的解消を試みた。

- ところで賽子の出目自体は1/6が6個の離散均等分布だが、賽子を目の数、すなわち6回振って特定の出目が出ない確率に注目すると(1-1/6)^6=0.334898となり、この考え方を「1/Nの確率の事象をN回試行した場合の確率」と抽象化して極限を求めるとexp(-1)(0.3678794)となる。
【初心者向け】指数・対数関数の発見とそれ以降の発展について。
- この値を公比(Common Ratio)に採用した等比数列は-Inf⇄0⇄Infの範囲の均等尺を0⇄1⇄Infの範囲の対数尺に射影した結果と一致し、さらには「区間分割数Nごとの利率が(1+1/N)倍となる複利式金融商品の全区間を通じての(すなわちN乗した結果としての)最終利率」exp(1)(2.718282)と逆数関係にあって、それぞれを反比例式xy=1のX軸とY軸の目盛に採用すると各目盛が面積1に対応する両対数尺が現れる。
【初心者向け】指数・対数関数の発見とそれ以降の発展について。

- 一方、こうして発見された自然指数関数の添字に複素円関数-1^x=(0+1i)^2xの値をπ/2した結果を与えてもガウス平面(複素数平面)上に円が再現され(オイラーの公式e^θi=cos(θ)+sin(θ)i)、かつ複素関数exp(xi)とexp(-xi)の平均を実数軸(X軸)/虚数軸(Y軸)それぞれについて求めるとCos波とSin波が得られる(ただしその周きは2πではなく2)。
【無限遠点を巡る数理】オイラーの公式と等比数列③Cos波とSin波の正体?
- こうした数理について統計学の分野は原則として踏み込む事なく「利用者」の立場を貫いてきた。かかる従属状態から脱却するには「確率論」だけでなく、それと逆数関係にある「利率論」とでも呼ぶべき分野に踏み込まざるを得なくなる。
【初心者向け】挟み撃ち定理(Squeeze Theorem)による円周率πの近似
- ある意味それが難しいので、全く別方面のMCMC(Markov Chain Monte Carlo methods=マルコフ連鎖モンテカルロ法)アプローチに逃げた側面も?
【初心者向け】「モンテカルロ法」概説
③一方(最後に残された)質的辺数に分類される順序尺度には以下の特徴がある。
- そもそも単一評価次元上の数値比較の結果とも限らないので、最初から根本的に曖昧さを抱える残る尺度ではある(目的意識に対応するプライオリティ付けと密接な関係があり、演算結果集合への持ち込み方に難があるヒューリスティクスな要素を内包する)。
ヒューリスティクス - Wikipedia - さらには距離/軽量関数のパラメーター操作によって順序が入れ替わる可能性がある。
【初心者向け】方形描画関数②距離空間との関係。 - その一方で中央値(Median)による中心検出は、平均による中心検出より外れ値の影響を受けにくいといった長所も備える。
【初心者向け】平均と標準偏差、中央値と平均偏差
こうした統計学上の概念と一般数理との対応づけが今年の出発点となります。もう11ヶ月とちょっとしか残されてませんが…
群概念(Group Concept)からの再出発
基本中の基本、群の定義に立ち返ります。
【初心者向け】群論概念①基本定義
①積もまた集合の要素になっていること。
②結合法則が成り立つこと。
③単位元が存在すること。
④逆元が存在すること。
この定義によって加法整数群(Additive Integer Group)が成立し、添字集合(Indexed Set)として使用可能となる。
こうしてそれまでは等差数列(Arithmetic Sequence=算術数列)で記述する事しか出来なかった自然数(Natural)と整数(Integer)の概念が無事アップデート出来たので、続いて等比数列(Geometric Sequence=幾何数列)An(n=-Inf→0→Inf)={…An^(n-1)…}={1/(a^Inf):=0,…,1/a^2,1/a,a/a=1,a,a^2,…,a^Inf=Inf}概念の乗法群(Multiplicative Group)概念へのアップデートを計ろうと思い立ったのですが…難しくて全然頭に入ってきません。
巡回群について
乗法群 - Wikipedia
ときわ台学代数入門/整数の剰余類の乗法群
剰余類から剰余群へ
むしろ惹かれたのがこっちの話。
微分積分学の基本定理 - Wikipedia
「微分と積分は互いに逆の操作・演算である」。例えばここへの投稿にも良く使ってるテイラー級数(Taylor Series)/マクローリン級数(McLaughlin Series)で用いる高階微積分の反復について考えてみると…
【Rで球面幾何学】オイラーの公式を導出したマクローリン級数の限界?

- 微分や積分の回数が添字の加減算に置き換えられる(単位元も逆元も存在し、結合法則も成りする)。
- (計算しなかった/出来なかった部分は剰余項に追いやる近似システムなので)微分や積分の結果集合に実数および複素数の範囲を超える何かが現れる事はない(おそらく)。
どうやらこういう話になっていく様ですね。
ベクトルと関数のおはなし
フーリエ級数展開
20世紀初頭、微分積分の大域的な議論を線形代数の議論に置き換えて考える方法 が提唱された。関数は関数空間上の点を見なし、基底や内積などの概念を導入して関数をあたかもベクトルのように扱うと非常に便利である。しかし、関数空間は有限次元のベクトル空間ではないので、一般には線形代数の議論を適応する際に困難が生じる。
ややこしいのが以下のジレンマ。
- (-Inf⇄0⇄Infの範囲の均等尺を0⇄1⇄Infの範囲の対数尺に射影した結果現れる)ネイピア数exp(1)(2.718282)や複素円関数-1^x=(0±1i)^2xの演算結果集合や円周率πなどを族とし(πは演算結果として現れる距離に過ぎないので族には含めないのが正しいかもしれない)、自然指数関数exp(xi)、自然対数関数log(xi)、余弦関数Cos(θ)=(exp(xi)+exp(-xi))/2、余弦関数Sin(θ)=(exp(xi)-exp(-xi))/2i、全ての波形をCos波とSin波の合成で近似するフーリエ級数、複素数概念の三次元版たるリーマン面や四元数などの演算結果集合を群規定して下属させる大分類を想定するなら(実際にはもっと細かく分類すべきだが、現時点の私の手には余る)、数学史上、かかる大概念の集大成こそがベクトル空間や線形代数学の概念の大源流だった事となる。
- しかし後になってから(微分積分概念を主力武器に採用した)解析学の立場から、急速に莫大な成果を挙げつつある(配列演算を武器とする)線形代数学の恩恵にあやかろうという動きが出てきた。そもそも基底や内積の概念自体が上掲の大分類に由来する訳だから発想の出発点としては悪くない筈だが、問題はその概念をどうやって一般の関数列にまで適用可能とする形で抽象化するかであった。
とりあえずこっち方面の知識を蓄えるのが「急がば回れ」になりそうな気がしてきました。とりあえずやれるだけやってみる事にしましょう。おっとその前に…
- (10を法とする剰余類{0,1,2,3,4,5,6,7,8,9}を周期単位/桁数だけ入れ子状態にした添字単位にし、小数点下も表せる様にした)十進法(Decimal System)概念は既に導入済みとする。
【初心者向け】N進法(N-ary)とp進数(p-adic)

- また同じ整数集合に(オブジェクト志向言語におけるクラス・メソッドに該当する)複数の群(まだちゃんと規定出来てないが「偶数群/奇数群」に該当する概念の追加も予定されている)が設定されつつあるので(クラス・データに該当する)整数集合を以降は「整数族」と呼ぶ事にする(正直、素数族2^n5^mが規定されるまで待ってはいられない!! そして乗法群が半群としてしか導入出来ない整数環の疑念にあまり無力を感じられなかったのである)。
【初心者向け】群論概念①基本定義
これくらい形相として容認しないと、そもそも計算をコンピューターで走らせられなくなってしまうのです…
冪乗算(Exponentiation)の微積分
この単元は別のトピックとの関連の方が深くなったので以下に切り離しました(2021.2.16)。
冪乗算(Exponentiation)の微積分
連続微分/積分概念の円関数への拡張は難しい?
出来そうな気がしたのですが、試してみたら無理でした。
【初心者向け】半径・直径・円周長・円の面積・球の表面積・球の体積の計算上の往復
# ライブラリ読み込み
library(Ryacas)
# 円周の長さ(2*pi*r)をrで微分すると
# 単位円の円周2*piを返す定関数となる。
> yac("D(r) pi*2*r")
[1] "2*pi"
# 半径rの円の面積(pi*r^2)をrで微分すると
# 円周の長さ(2*pi*r)となる。
> yac("D(r) pi * r^2")
[1] "pi*2*r"
# 逆に円周の長さ(2*pi*r)をrで積分すると
# 半径rの円の面積(pi*r^2)となる?
> yac("Integrate(r) pi * (2 * r)")
[1] "pi*r^2"
# 半径rの球の表面積(4*pi*r^2)をrで微分すると
# 球の円周(2*r*pi)×4となる?
> yac("D(r) r^2 * 4 * pi")
[1] "8*r*pi"
# 球の円周(2*r*pi)×4をrで積分すると
# 半径rの球の表面積(4*pi*r^2)となる?
> yac("Integrate(r) 8 * r * pi")
[1] "4*pi*r^2"
# 半径rの球の体積(4/3*pi*r^3)をrで微分すると
# 球の表面積(4*pi*r^2)となる。
> yac("D(r) 4/3 * pi * r^3")
[1] "r^2*4*pi"
# 逆に球の表面積(4*pi*r^2)をrで積分すると
# 半径rの球の体積(4/3*pi*r^3)となる。
> yac("Integrate(r) r^2 * (4 * pi)")
[1] "(r^3*4*pi)/3"
こういう話もある様なのですが…
球の表面は、図2のように、縦が2r 、横が2πrの長方形に近似することができる。
この長方形の面積は確かに2r×2πr=4πr^2になっている。よって、球の表面を平面にすることができた。しかし、この平面の周の長さは2πr×2+2r×2=4πr+4rとなり、8πrにはならない。しかし、r→r+drとすると、図2のようにπr→π(r+dr)=πr+πdr となるから、面積の増加分はおよそ(2πr×dr)×2+(2r×πdr)×2=8πrdrとなり、8πrが何を意味するかがわかった。
つまり、半径で表面積を表した式を微分した式は、表面積を平面に開いた時の各面の周に関係があるが、その平面の中心から各辺までの距離が違う場合、微小増加分にも増加の倍率を考えなくてはならないので、その式は単純に周の長さにはならず、微小増加の倍率を考えた各辺にできる微小面積の総和になると考えられる。
とりあえず現時点では、何を言ってるのかさっぱり分かりません(2021年.02,21)
①円や直線の主要な幾何学的性質は2階までの微分で決まる(例,接線の
傾き,曲率半径)。
②しかし円と放物線を区別するには少なくとも4階微分までのデータが必要となる(y=±sqrt(1-x^2)=±(1-(x^2)/2)-(x^4)/8+o(x^4))。
③実際、4次の精度まで考慮することにより曲面Sの中に含まれ、与えら
れた点を通る円の数は(球面のような特別な場合を除き)有限個(10個)に制限される。
サイクリッド曲面は3次元空間内の標準的なトーラスに反転をほどこすことによって得られる4次曲面であり,曲率曲線が正円または直線で,各点で互いに直交するという特徴をもつ。
御免なさい。途中で脳がパンクしました。どうやら対称式(Symmetric Polynomial)の概念を用いている様ですが…
【標準】対称式の値 | なかけんの数学ノート
【標準】x+1/xを使った式の値 | なかけんの数学ノート
対称式(Symmetric Polynomial) - Wikipedia
変数を入れ替えても変わらない多項式のことで、任意の対称式は、基本対称式x+yとxyの多項式で書ける。
アルベール・ジラールは、1629年に「代数学の新しい発明」(Invention Nouvelle en l'Algèbre) おいて、n次代数方程式の根と係数の関係を発見した。代数方程式の係数は n個の根の基本対称式と呼ばれる対称式により書かれるというこの関係は、一般の次数の代数方程式の構造を調べるための重要な足掛かりの一つとなった。さらに、ジラールは、これらの関係を用いて虚数の有用性を説いた。
18世紀後半になると、任意の対称式は基本対称式によって書くことができる事が、ウェアリングやヴァンデルモンドらによって示され、ラグランジュによる、代数方程式の根の置換の研究へとつながっていった。
ところで対称式というと、既にこれまでの投稿で扱った一次関数Y=X(Y=-Xで既に対称性が崩れる)についてはどう考えるのでしょう?
【初心者向け】線形関数や絶対値関数


まだまだ数理の世界は奥が深いです。そんな感じで以下続報…



















