【オイラーの多面体定理と正多面体】とある「球面幾何学(Spherical Geometry)」の出発点…

私に思い浮かべられる「数理の世界(Mathematical Things Set)」といえば、せいぜい「加算直積可能な範疇(Countable and Productable Set)」、すなわちとりあえず例外(Exception)を切り捨てて全てが自明の場合(Trivial Case)で説明可能な範囲(Set)を設定(Set)し、その枠内をコンピューター・プログラミングによる表現(Expression)で網羅し尽すといった程度。このアプローチからの実践例の一つが以下という位置付けとなる次第…

オイラーの多面体定理(Euler's Polyhedron Theorem)の援用(Introduce)を受けた正多面体(Regular Polyhedron)の作図=遷移図(Transition Diagram)の制定

正多面体(Regular Polyhedron)が正四面体(Tetrahedron)、正六面体(Cube)、正八面体(Octahedron)、正十二面体（Dodecahedron）、正二十面体(Icosahedron)の５種類しか存在しない事自体の証明は比較的容易です。
正多面体が５種類しかないことの２通りの証明

そしてさらにプログラミング的にオイラーの多面体定理(Euler's Polyhedron Theorem)の概念(Concept)を導入(Introduce)すると、特定の球表面に内接する（すなわち全ての頂点がその球表面上に存在する）これらの図形を任意の原蹠(Portal)から対蹠(Antipodal)に伸ばした立方対角線(Cubic Diagonal)を軸線としてその「断面ごとに現れる多角形の集合」として表現(Expression)可能となるのです。
【初心者向け】「単位円筒」から「単位球面」へ

正四面体(Regular Tetrahedron)

断面数１、頂点分布[1,3]。（特定の辺数が伸びる）頂点と（同数の辺数を備える）面を交換する双対変換操作(Dual Transformation Operation)の結果が同じ正四面体となる自己双対(Self Dual)立体。
【オイラーの多面体定理と正多面体】正四面体(Tetrahedron)と正六面体(Cube)と正八面体(Octahedron)と正二十面体(Icosahedron)の狭間。そして正十二面体（Dodecahedron）との関係について。

• 全体像を俯瞰すると「(外接円上に全ての頂点が存在する)正三角形(Equilateral triangles)２枚の間の補完操作(Completion Operation)によって生じる」という考え方も出来る(とりあえず不可逆的過程と考える)。
  【オイラーの多面体定理と正多面体】正四面体(Tetrahedron)と正六面体(Cube)と正八面体(Octahedron)と正二十面体(Icosahedron)の狭間。そして正十二面体（Dodecahedron）との関係について。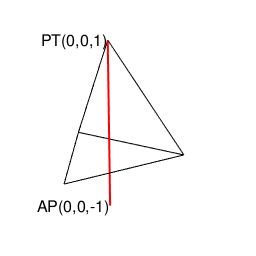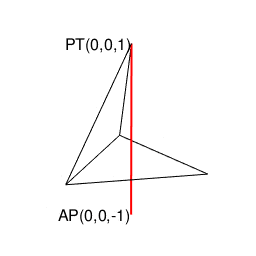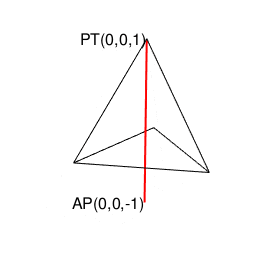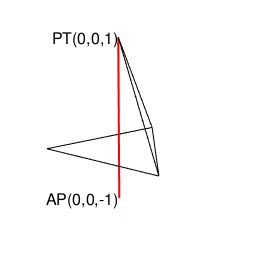
  
• 2回曲がると原蹠に戻る。
• 正多面体唯一の奇数系図形(原蹠と対蹠を結ぶ対角線が１本も存在しない不安定状態)であり、２個１対で顕現(Appearance)すると考えると断面数2、頂点分布[1,3,3,1]。これはパスカルの三角形(二項展開の係数の図式化)４段目の数字であり、正六面体（Cube)のそれと合致する。
  【オイラーの多面体定理と正多面体】正四面体と正六面体と正八面体の連続性と「テトラパックの思わぬ正体」について。
  
• 正八面体（Regular Octahedron)と組み合わせる形で立体充填性を備える。
  【オイラーの多面体定理と正多面体】正四面体と正六面体と正八面体の連続性と「テトラパックの思わぬ正体」について。
  

正六面体（Cube)

断面数2、頂点分布[1,3,3,1]で、これは上掲の様にパスカルの三角形４段目の数字と合致。双対変換操作により正八面体（Regular Octahedron)との間を往復する。(対蹠同士を結ぶ)立方対角線は4本で、それぞれの面に現れる頂点分布[1,2,1]がパスカルの三角形3段目の数字に合致する。
【オイラーの多面体定理と正多面体】正方形における平方対角線(Square diagonal)と立方体における立方対角線(Cubic diagonal)の関係について。

• 上掲の様にこの立体は正十二面体（Regular Dodecahedron）同様「頭蹠と対蹠にそれぞれ正三角形を３枚集めた一対の奇数図形(不安定状態)」から出発してある種の補完操作(Completion Operation)を経て偶数図形(安定状態)に到達した結果とも見て取れる(とりあえず不可逆的過程と考える)。
  【オイラーの多面体定理と正多面体】正四面体(Tetrahedron)と正六面体(Cube)と正八面体(Octahedron)と正二十面体(Icosahedron)の狭間。そして正十二面体（Dodecahedron）との関係について。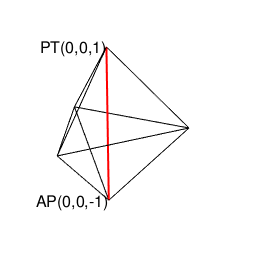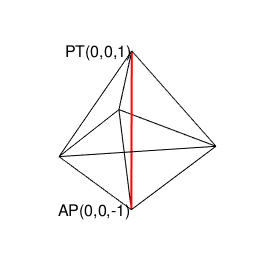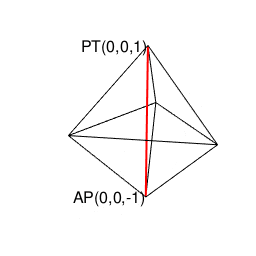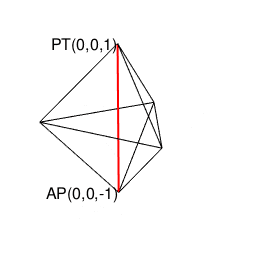
  
• それぞれ立体表面上を(右手の法則・左手の法則的な意味で)左右に1回ずつ直角に曲がると原蹠から対蹠に到達する(5回直角に曲がると原蹠に戻る)。
• 単体で立体充填(Space filling)可能な唯一の正多面体でもある。

正八面体（Regular Octahedron)

断面数1、頂点分布[1,4,1]。双対変換操作により正六面体との間を往復。立方対角線は３本で、それぞれの断面に現れる頂点分布[1,2,1]がパスカルの三角形3段目の数字に合致する。
【オイラーの多面体定理と正多面体】正四面体(Tetrahedron)と正六面体(Cube)と正八面体(Octahedron)と正二十面体(Icosahedron)の狭間。そして正十二面体（Dodecahedron）との関係について。

• この立体は正六面体や正十二面体同様「頭蹠と対蹠にそれぞれ二等辺三角形を３枚あるいは正三角形を4枚集めた一対の奇数図形(不安定状態)」から出発してある種の補完操作(Completion Operation)を経て偶数図形(安定状態)に到達した結果とも見て取れる(とりあえず不可逆的過程と考える)。
  【オイラーの多面体定理と正多面体】正四面体と正六面体と正八面体の連続性と「テトラパックの思わぬ正体」について。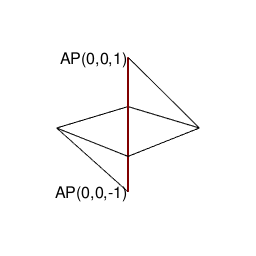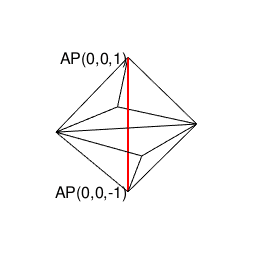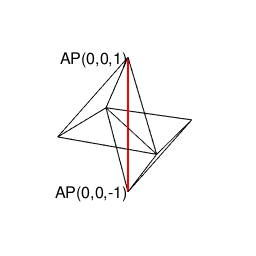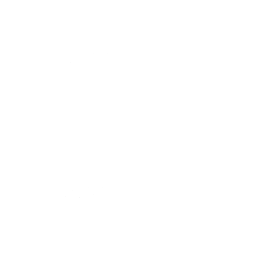
  
• それぞれ立体表面上を直角1回に曲がると原蹠から対蹠に到達する(3回直角に曲がると原蹠に戻る)。
• 正四面体と組み合わせる形で立体充填性を備える。

正十二面体（Regular Dodecahedron）

断面数6、頂点分布[1,3,6,6,3,1]。立方対角線は10本(1+3+6)。双対変換操作により正二十面体(Regular Icosahedron)との間を往復。
【オイラーの多面体定理と正多面体】正12面体(Regular Dodecahedron)の作図について。

• この立体は正六面体同様「頭蹠と対蹠にそれぞれ正三角形を３枚集めた一対の奇数図形(不安定状態)」から出発してある種の補完操作(Completion Operation)を経て偶数図形(安定状態)に到達した結果とも見て取れる(とりあえず不可逆的過程と考える)。
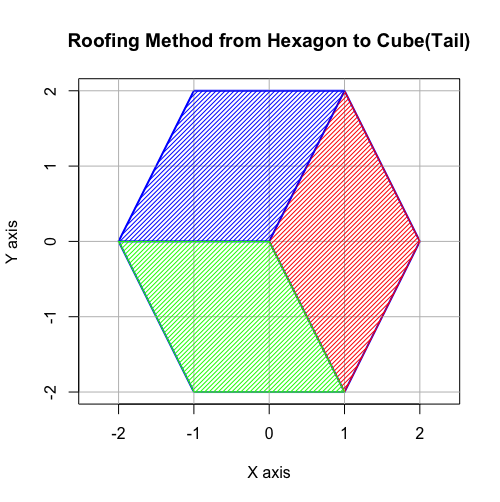
  【オイラーの多面体定理と正多面体】正六面体と正十二面体の間の往復(「屋根掛け法」とは何か？)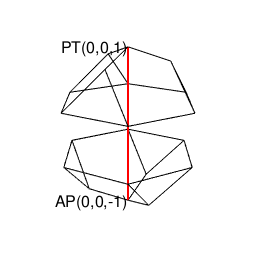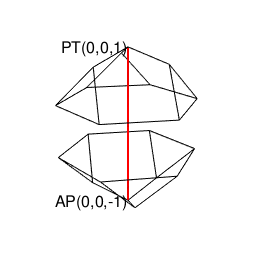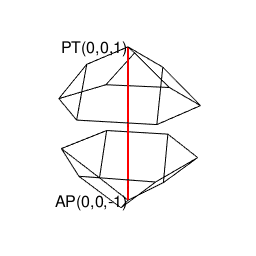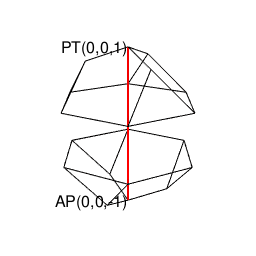
  
  【オイラーの多面体定理と正多面体】正12面体(Regular Dodecahedron)の作図について。
  
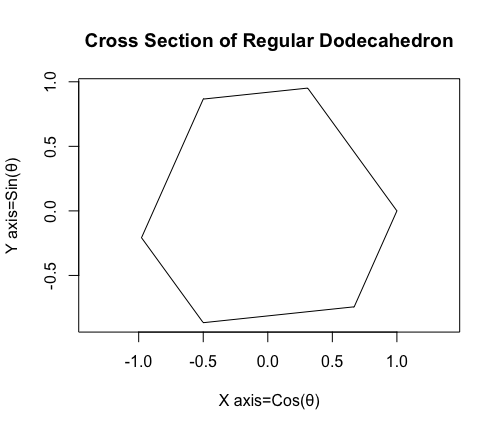
• それぞれ立体表面上を左右に2回ずつ計5回曲がると原蹠から対蹠に最低距離で到達する(11回曲がると原蹠に戻る)。
• 古代ギリシャ時代より「内接する正六面体に屋根掛けした立体」ともイメージされてきた。すなわち正六面体との往復性も備える。
  【オイラーの多面体定理と正多面体】正六面体と正十二面体の間の往復(「屋根掛け法」とは何か？)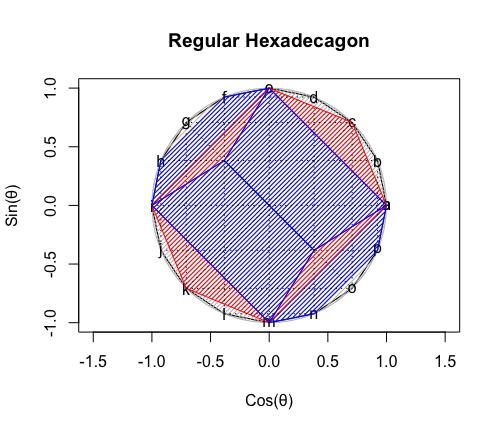
  
  

実は正八面体との往復性も備える。
【オイラーの多面体定理と正多面体】二次元上の多角形と三次元の多面体の往復

正二十面体（Regular Icosahedron）

断面数2、頂点分布[1,5,5,1]。立方対角線は6本(1+5)。双対変換操作により正十二面体との間を往復。
【オイラーの多面体定理と正多面体】正20面体(Regular Icosahedron)の作図について。

• この立体は「頭蹠と対蹠にそれぞれ正三角形を5枚集めた一対の奇数図形(不安定状態)」から出発してある種の補完操作(Completion Operation)を経て偶数図形(安定状態)に到達した結果とも見て取れる(とりあえず不可逆的過程と考える)。
  【オイラーの多面体定理と正多面体】正四面体(Tetrahedron)と正六面体(Cube)と正八面体(Octahedron)と正二十面体(Icosahedron)の狭間。そして正十二面体（Dodecahedron）との関係について。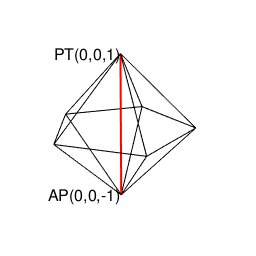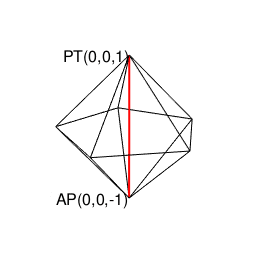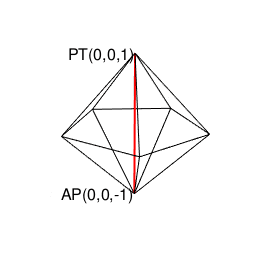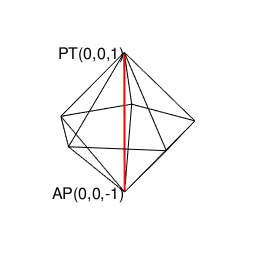
  
• 正六面体同様、それぞれ立体表面上を(右手の法則・左手の法則的な意味で)左右に1回ずつ曲がると原蹠から対蹠に最低距離で到達する(5回直角に曲がると原蹠に戻る)。

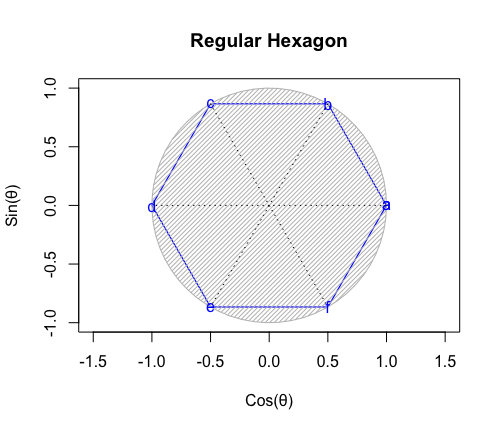
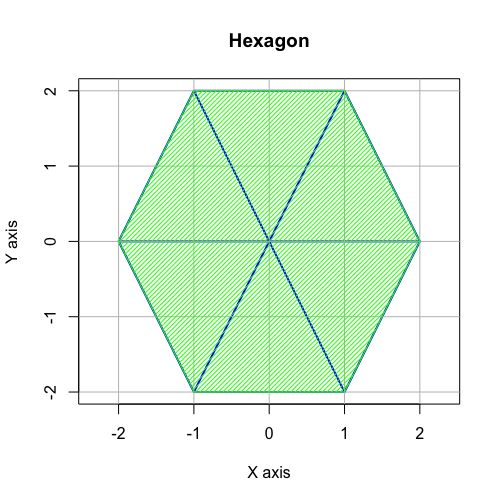
【例外】ただの正六角形(Regular Hexagon)

これまで見てきた様に正多角形は「頭蹠及び対蹠に集めた正三角形の枚数」によって以下の分類が可能である。

• 3枚集めたのが正四面体や正六面体や正十二面体
• 4枚集めたのが正八面体
• 5枚集めたのが正十二面体

この考え方の延長線上において正三角形を6枚集めると「頭蹠座標=対蹠座標となる平面状態」となるが、それはもはや立体ではない。
【オイラーの多面体定理と正多面体】正四面体(Tetrahedron)と正六面体(Cube)と正八面体(Octahedron)と正二十面体(Icosahedron)の狭間。そして正十二面体（Dodecahedron）との関係について。

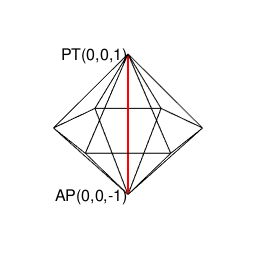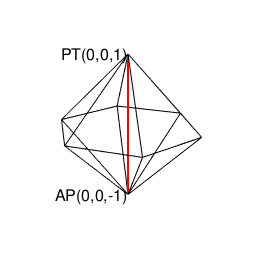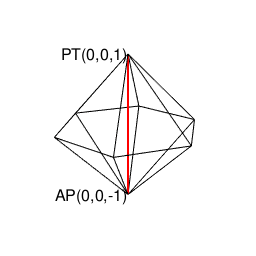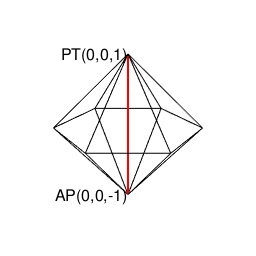
正多角形状態遷移図(Transition Diagram)の解析(Analisis)

それではigraphパッケージを導入して遷移図(有向グラフ)を作成してみましょう。

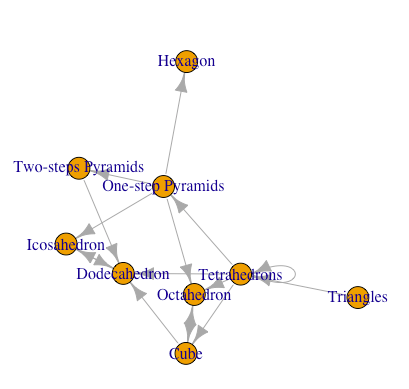
library(igraph)
par(mfrow=c(1,2),mar=c(3,3,3,3))
gd<-graph(c(
"Triangles","Tetrahedrons",
"Tetrahedrons","Tetrahedrons",
"Tetrahedrons","Cube",
"Tetrahedrons","Octahedron",
"Tetrahedrons","Dodecahedron",
"Cube","Octahedron",
"Octahedron","Cube",
"Cube","Dodecahedron",
"Dodecahedron","Icosahedron",
"Icosahedron","Dodecahedron",
"Tetrahedrons","One-step Pyramids",
"One-step Pyramids","Octahedron",
"One-step Pyramids","Two-steps Pyramids",
"Two-steps Pyramids","Dodecahedron",
"One-step Pyramids","Icosahedron",
"One-step Pyramids","Hexagon"
))
plot(gd,layout=layout.fruchterman.reingold,)

#入力されたデータ構造(何かバグってる？)
> str(gd)
List of 10
 $ :List of 1
  ..$ Triangles: 'igraph.vs' Named int 2
  .. ..- attr(*, "names")= chr "Tetrahedrons"
  .. ..- attr(*, "env")=<weakref> 
  .. ..- attr(*, "graph")= chr "fb9143e9-2dd1-44e9-8e62-38ffb5bb47cd"
 $ :List of 1
  ..$ Tetrahedrons: 'igraph.vs' Named int [1:5] 2 3 4 5 7
  .. ..- attr(*, "names")= chr [1:5] "Tetrahedrons" "Cube" "Octahedron" "Dodecahedron" ...
  .. ..- attr(*, "env")=<weakref> 
  .. ..- attr(*, "graph")= chr "fb9143e9-2dd1-44e9-8e62-38ffb5bb47cd"
 $ :List of 1
  ..$ Cube: 'igraph.vs' Named int [1:2] 4 5
  .. ..- attr(*, "names")= chr [1:2] "Octahedron" "Dodecahedron"
  .. ..- attr(*, "env")=<weakref> 
  .. ..- attr(*, "graph")= chr "fb9143e9-2dd1-44e9-8e62-38ffb5bb47cd"
 $ :List of 1
  ..$ Octahedron: 'igraph.vs' Named int 3
  .. ..- attr(*, "names")= chr "Cube"
  .. ..- attr(*, "env")=<weakref> 
  .. ..- attr(*, "graph")= chr "fb9143e9-2dd1-44e9-8e62-38ffb5bb47cd"
 $ :List of 1
  ..$ Dodecahedron: 'igraph.vs' Named int 6
  .. ..- attr(*, "names")= chr "Icosahedron"
  .. ..- attr(*, "env")=<weakref> 
  .. ..- attr(*, "graph")= chr "fb9143e9-2dd1-44e9-8e62-38ffb5bb47cd"
 $ :List of 1
  ..$ Icosahedron: 'igraph.vs' Named int 5
  .. ..- attr(*, "names")= chr "Dodecahedron"
  .. ..- attr(*, "env")=<weakref> 
  .. ..- attr(*, "graph")= chr "fb9143e9-2dd1-44e9-8e62-38ffb5bb47cd"
 $ :List of 1
  ..$ One-step Pyramids: 'igraph.vs' Named int [1:4] 4 6 8 9
  .. ..- attr(*, "names")= chr [1:4] "Octahedron" "Icosahedron" "Two-steps Pyramids" "Hexagon"
  .. ..- attr(*, "env")=<weakref> 
  .. ..- attr(*, "graph")= chr "fb9143e9-2dd1-44e9-8e62-38ffb5bb47cd"
 $ :List of 1
  ..$ Two-steps Pyramids: 'igraph.vs' Named int 5
  .. ..- attr(*, "names")= chr "Dodecahedron"
  .. ..- attr(*, "env")=<weakref> 
  .. ..- attr(*, "graph")= chr "fb9143e9-2dd1-44e9-8e62-38ffb5bb47cd"
 $ :List of 1
  ..$ Hexagon: 'igraph.vs' Named int(0) 
  .. ..- attr(*, "names")= chr(0) 
  .. ..- attr(*, "env")=<weakref> 
  .. ..- attr(*, "graph")= chr "fb9143e9-2dd1-44e9-8e62-38ffb5bb47cd"
 $ : adjacent_vertices(x, i, mode = if (directed) "out" else "all") でエラー: 
  At iterators.c:759 : Cannot create iterator, invalid vertex id, Invalid vertex id

双対変換操作(Dual Transformation Operation)

• 正四面体(Tetrahedrons)同士
• 正六面体(Cube)と正八面体(Octahedron)
• 正十二面体(Dodecahedron)と正二十面体(Icosahedron)

一対の正三角形(Equilateral triangles)からの補完操作(Completion Operation)

• 正四面体(Tetrahedrons)への不可逆的変遷(平面から立体へ)

一対の正四面体(Tetrahedrons)からの補完操作(Completion Operation)

• 正六面体(Cube)への不可逆的変遷。途中で座標がクロスすると考える。
• 正八面体(Octahedron)への不可逆的変遷。途中で四面全てが直角二等辺三角形の状態を経ると考える。
• 正十二面体(Dodecahedron)への不可逆的変遷。途中で一対の二段多角錐(Two-step Pyramids)状態を経ると考える。

一対の一段多角錐(One-step Pyramids)状態を経る補完操作(Completion Operation)

• 四角錐段階を経ての正八面体(Octahedron)への不可逆的変遷。
• 五角錐段階を経ての正二十面体(Icosahedron)への不可逆的変遷。
• 六角錐段階を経ての正六角形(Icosahedron)への不可逆的変遷(立体から平面へ)

正六面体(Cube)からの補完操作(Completion Operation)

• 「屋根掛け法」を経ての正二十面体(Icosahedron)への不可逆的変遷。

一見「何じゃこれは？」という感じですが、実は整数論に基づく交通整理が可能だったりします。考え方の鍵は、さらに「頭蹠と対蹠を結ぶ立方対角線上の往復」を断面数0、頂点分布[1,1](パスカルの三角形2段目の数字に合致)、立方対角線1本の「二辺形(Bilateral)」や三角形(Triangle(s))や正方形(Square(s))や正六角形(Hexagon)の様な非立体(Non 3Dimensional)を図形に加える辺り。
【Rで九九】どうして36個の数字しか使われないのか？

2^n集(Set)

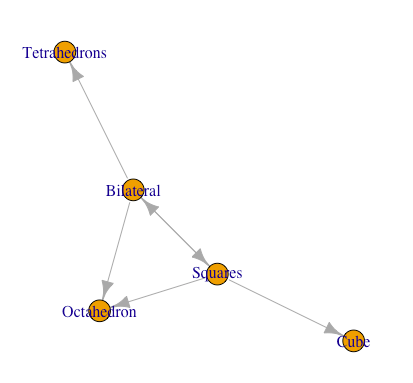
二辺形(Bilateral)と正方形(Squares)が分類される範疇。両者の連続性はちょっと特殊な幾何学的数理によって説明される。
【Rで球面幾何学】何故「正方形」ではCos(θ)+Sin(θ)iが成立するのか？

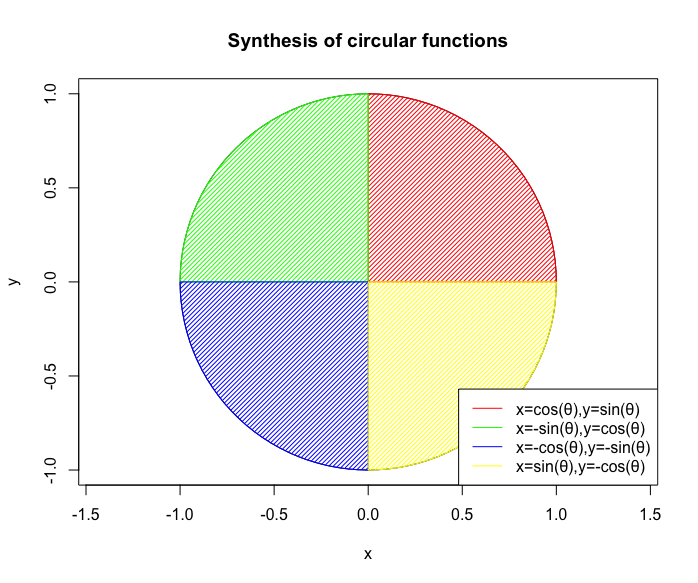
また正方形は自己相似変換により複数と単数の間を往復する。
【Rで球面幾何学】平方眼と立方眼の小宇宙(Square & Cube Grid Set)について。

• (2^n集内での展開)二辺形(Bilateral,面数0/辺数2)と正方形(Tetrahedrons,面数1/辺数4)の間の連続性。
• (3^n集への遷移)二辺形一個(Bilateral,面数0/辺数2)から正四面体二個(Tetrahedrons,面数8(+8)/辺数12(*6))へ。(断面数0→2,立方対角線1→0)。
• (2^n3^m集への遷移)二辺形三個(Bilateral,面数計0,辺数計6)から一個の正八面体(Octahedron,面数8(+8)/辺数12(*2))へ(断面数0→1,立方対角線3→3)。
• (2^n3^m集への遷移)二辺形三個(Bilateral,面数計0,辺数計6)あるいは互いに交差する正方形2個(Squares)に３個目の正方形が補完される(面数計3,辺数計12)形、あるいはある種の「屋根掛け法」によって正八面体一個(Octahedron,面数8(+8)/辺数12(*2))へ(断面数0→1,立方対角線3→3)。
  【オイラーの多面体定理と正多面体】二次元上の多角形と三次元の多面体の往復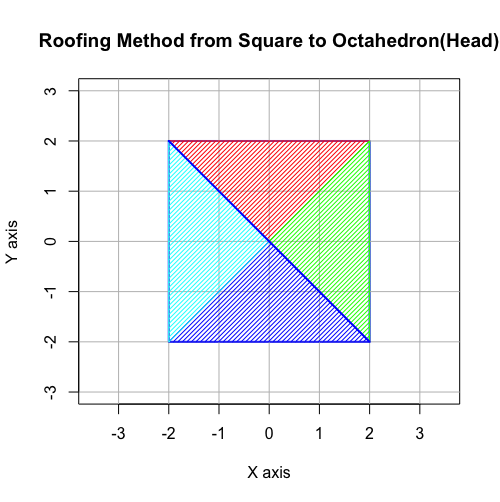
  
  
  
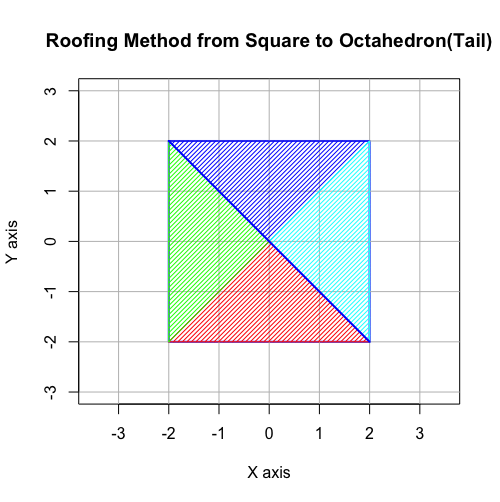
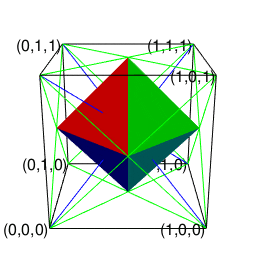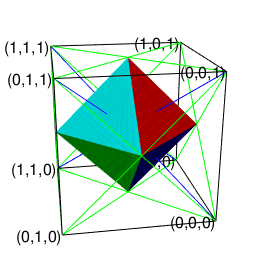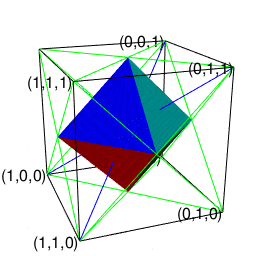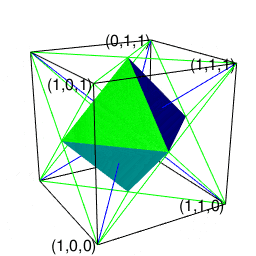
• (2^n3^m集への遷移)「屋根掛け法」により正方形一個から一気に四辺を伸ばして正六面体一個へ。
  【オイラーの多面体定理と正多面体】二次元上の多角形と三次元の多面体の往復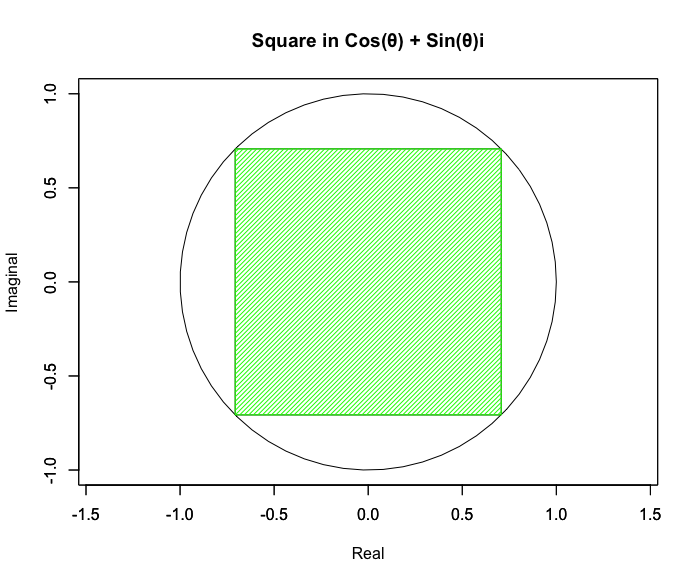
  
  
• (2^n3^m集への遷移)互いに辺を接する正方形2個(Squares)からに３個目の正方形が補完される(面数計3,辺数計12)形で正六面体一個(Octahedron,面数6(*2)/辺数12)へ(断面数0→2,立方対角線0→4)。

library(igraph)
par(mfrow=c(1,2),mar=c(3,3,3,3))
gd<-graph(c(
"Bilateral","Squares",
"Squares","Bilateral",
"Bilateral","Tetrahedrons",
"Bilateral","Octahedron",
"Squares","Octahedron",
"Squares","Cube"
))
plot(gd,layout=layout.fruchterman.reingold)

3^n集(Set)

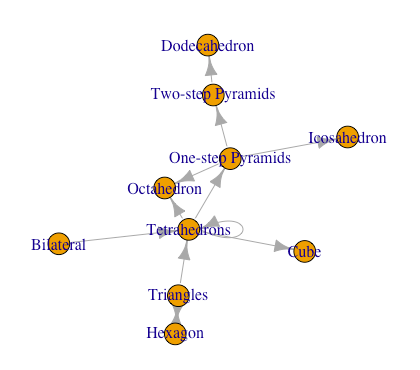
正四面体(Tetrahedrons)と正三角形(Triangles)が分類される範疇。正三角形は自己相似変換により複数と単数の間、さらには双対変換によって正六角形(Hexagon,面数1/辺数6)との間を往復する。
【Rで球面幾何学】平方眼と立方眼の小宇宙(Square & Cube Grid Set)について。

• (平面から立体へ)正三角形二個(Equilateral Triangles,面数計2/辺数計6。)から正四面体一個(Tetrahedrons,面数4(+2)/辺数6(+1-1))へ(断面数0→1,立方対角線0→0)。
• (2^n集からの導入)二辺形一個(Bilateral,面数0/辺数2)から正四面体二個(Tetrahedrons,面数8(+8)/辺数12(*6))へ。(断面数0→2,立方対角線1→0)。
• (3^n集内での展開)正四面体(Tetrahedrons)同士の自己双対(反転。断面数1⇄1,立方対角線0⇄0)
• (2^n3^m集との往復)正三角形(Equilateral Triangle)と正六角形(Hexagon)の間の双対変換。
  【オイラーの多面体定理と正多面体】二次元上の多角形と三次元の多面体の往復
  
  
• (2^n3^m集への遷移)正四面体二個(Tetrahedrons,面数計8/辺数計12)から正六面体一個(Cube,面数6(-2)/辺数12(±0))へ(断面数2→2,立方対角線0→4)。
• (2^n3^m集への遷移)正四面体二個(Tetrahedrons,面数計8/辺数計12)から(各面二等辺三角形段階か四角錐二個段階を経て)正八面体一個(Octahedron,面数8(±0)/辺数12(±0))へ(断面数2→1,立方対角線0→3)。
• (2^n3^m5^l集への遷移)三角錐二個段階を経て正十二面体(Dodecahedron)へ(二段階変遷で断面数2⇄4,立方対角線0⇄10)
• (2^n3^m5^l集への遷移)五角錐二個段階を経て正二十面体(Icosahedron)へ(断面数2→3,立方対角線0→6)

library(igraph)
par(mfrow=c(1,2),mar=c(3,3,3,3))
gd<-graph(c(
"Triangles","Hexagon",
"Hexagon","Triangles",
"Triangles","Tetrahedrons",
"Bilateral","Tetrahedrons",
"Tetrahedrons","Tetrahedrons",
"Tetrahedrons","Cube",
"Tetrahedrons","Octahedron",
"Tetrahedrons","One-step Pyramids",
"One-step Pyramids","Two-step Pyramids",
"Two-step Pyramids","Dodecahedron",
"One-step Pyramids","Octahedron",
"One-step Pyramids","Icosahedron"
))
plot(gd,layout=layout.fruchterman.reingold)

2^m*3^n集(Set)

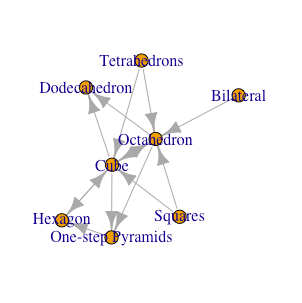
正八面体(Octahedron)と正六面体(Cube)と正六角形(Hexagon)が分類される範疇。

• (2^n集からの導入)二辺形三個(Bilateral,面数計0,辺数計6)から一個の正八面体(Octahedron,面数8(+8)/辺数12(*2))へ(断面数0→1,立方対角線3→3)。
• (2^n集からの導入)「屋根掛け法」により正方形一個から一気に四辺を伸ばすか、正方形2個(Squares)の三枚目補完によって正六面体一個へ。
• (3^n集からの導入)正四面体二個(Tetrahedrons,面数計8/辺数計12)から正六面体一個(Cube,面数6(-2)/辺数12(±0))へ(断面数2→2,立方対角線0→4)。
• (3^n集からの導入)正方形2個(Squares)あるいは正四面体二個(Tetrahedrons,面数計8/辺数計12)から(各面二等辺三角形段階か四角錐二個段階を経て)正八面体一個(Octahedron,面数8(±0)/辺数12(±0))へ(後者の場合は断面数2→1,立方対角線0→3)。
• (2^n3^m集内での展開)正八面体(Octahedron)と正六面体(Cube)の双対操作(断面数1⇄2,立方対角線3⇄4)。
• (2^n3^m集内での展開)「屋根掛け方」を用いての正六角形(Hexagon)と正六面体(Cube)の間の往復。
  【オイラーの多面体定理と正多面体】二次元上の多角形と三次元の多面体の往復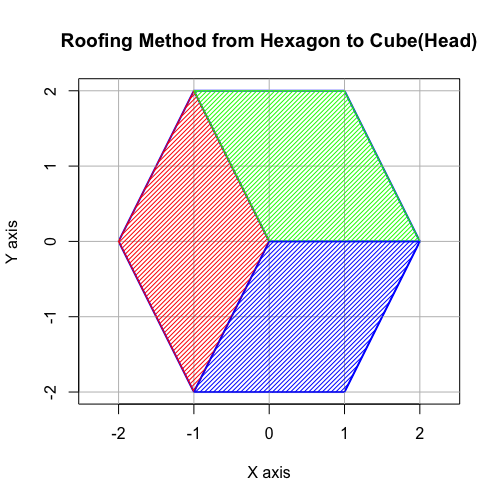
  
  
  
• (立体から平面へ)六角錐二個段階を経て正六角形(Hexagon,面数1/辺数6)へ(辺長0となる事で断面数2→0,立方対角線0→0)
• (2^n3^m5^l集への遷移)正六面体(Cube,面数6/辺数12)に「屋根掛け法」を適用して正十二面体(Dodecahedron,面数12(*4/2)/辺数20)へ(断面数2→4,立方対角線4→10)
• (2^n3^m5^l集への遷移)正八面体(Octahedron)からの変換で正十二面体(Dodecahedron)へ
  【オイラーの多面体定理と正多面体】二次元上の多角形と三次元の多面体の往復

library(igraph)
par(mfrow=c(1,2),mar=c(3,3,3,3))
gd<-graph(c(
"Squares","Octahedron",
"Squares","Cube",
"Bilateral","Octahedron",
"Tetrahedrons","Cube",
"Tetrahedrons","Octahedron",
"Octahedron","Cube",
"Cube","Octahedron",
"Cube","Dodecahedron",
"Cube","Hexagon",
"Hexagon","Cube",
"Octahedron","Dodecahedron",
"Cube","One-step Pyramids",
"Octahedron","One-step Pyramids",
"One-step Pyramids","Hexagon"
))
plot(gd,layout=layout.fruchterman.reingold)

2^n3^m5^l集(Set)

正十二面体(Dodecahedron)と正十二面体(Dodecahedron)が分類される範疇。

• (3^n集からの導入)三角錐二個段階を経て正十二面体(Dodecahedron)へ(二段階変遷で断面数2→4,立方対角線0→10)
• (3^n集からの導入)五角錐二個段階を経て正二十面体(Icosahedron)へ(断面数2→3,立方対角線0→6)
• (2^n3^m集からの導入)正六面体(Cube,面数6/辺数12)や正八面体(Octahedron,面数8/辺数12)に「屋根掛け法」等を適用して正十二面体(Dodecahedron,面数12(*4/2)/辺数20)へ(断面数2→4,立方対角線4→10)
• (2^n3^m5^l集内での展開)正十二面体(Dodecahedron)と正二十面体(Icosahedron)の双対操作(断面数4⇄3,立方対角線10⇄6)。

library(igraph)
par(mfrow=c(1,2),mar=c(3,3,3,3))
gd<-graph(c(
"Tetrahedrons","One-step Pyramids",
"One-step Pyramids","Dodecahedron",
"One-step Pyramids","Icosahedron",
"Cube","Dodecahedron",
"Octahedron","Dodecahedron",
"Dodecahedron","Icosahedron",
"Icosahedron","Dodecahedron"
))
plot(gd,layout=layout.fruchterman.reingold)

そう、まさにこの「量子跳躍めいた離散的遷移過程の全貌」と「平面に始まり平面に終わる感じ」を把握したかったのです。いやはや、まる一ヶ月以上掛かってしまいました。もちろん一応「正多面体の巡回性」そのものについては多くの資料で触れらてる「自明の場合」(とはいえ正八面体と正二十面体の往復については、未だ納得が行ってなくて除外中)な訳ですが…
正六面体群
正多面体群1
正多面体群２
正多面体 くり返しの関係を観察

「オイラーの多面体定理」が示唆する量子飛躍的世界観？

オイラーの多面体定理(Euler's Polyhedron Theorem)

Vertex(頂点数)-Edge(辺数)+Face(面数)=2の条件を満たさない立体は三次元上に存在し得ない。

そう、量子力学的事象同様、「実際に現象が顕現する条件が厳しいだけで、裏では色々な可能性が確率論レベルで進行している」と考えないとこの離散的遷移過程は説明出来ません。数理の世界では有理数や無理数で構成される実数の世界(Integer Number Set)だけでは「数直線の連続性(Number line continuity)」が埋められない局面では躊躇なく虚数(Imaginary Number)の概念を導入して「複素数の世界(Complex Number Set
)」の世界に足を踏み入れますが、実際既にプログラム中では…というお話。

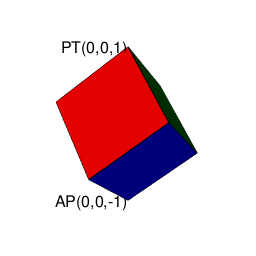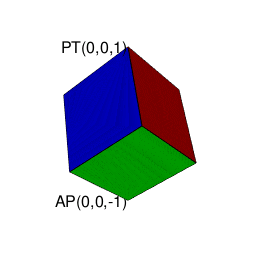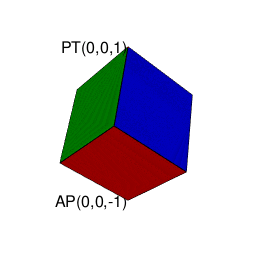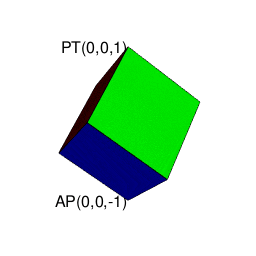
①まずは互いに可換な頭蹠(Portal)と対蹠(Antipordal)を設定し、それを結ぶ軸線を直径=立方対角線とする単位球面(Unit Sphrer)を想定する。するとこれに内接する正多面体の頂点が全て球表面上に含まれる事になり、軸線に沿った「断面」ごとに多角形を描く。こうして求められた頂点の集合を「星座の様に」結ぶとその正多面体が再現される（要するにこれがこれまでの投稿の中で「自明の理」として繰り返し用いられてきたアルゴリズム）。

• 平面上では両者を直接結ぶ軸線を直径とする単位円(Unit Circle)に外接する正多角形がこれに対応し、それが正多角形である場合、ガウスの発見した「１の冪乗定理(Root of Unity Theorem)」を応用したアルゴリズムc0=seq(-pi,pi,length=NoS);cx=cos(c0);cy=sin(c0)(NoS(Number of Sides)=描く多角形の辺数+巡回を完成させる為の1)によって各頂点のX座標とY座標が求められる。実に便利…

②ところで(これまでも繰り返し図示してきた様に)どの頂点間を結ぶ対角線も頭蹠と対蹠が直接結ばない「奇数系図形」は、頭蹠に対応する対蹠あるいは対蹠に対応する頭蹠を面とする一対の形で顕現する(平面上に描画される正多角形だけでなく、正多面体の世界における正四面体もこの条件を満たす)。

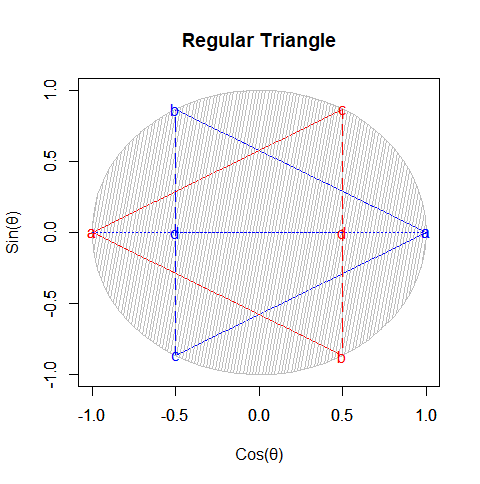
• この概念(Concept)は、マクリーン級数においてCos波が添字(ConceptIndex)が偶数(Even Number)の場合、Sin波が奇数(Odd Number)の場合に割り振られる事、複素平面上においてもCos波がX軸、Sin波がY軸に割り振られる事などとも重なってくる(要するに複素数の基本的特徴なのだけど、それは何故？という話…)。
  【初心者向け】三角関数と指数・対数関数の「巡回性」について。
  【Rで球面幾何学】そもそも複素数Xi（x*(0+1i)）はどう振る舞う？
• そして複素平面/球表面上においては円弧上の2点/球表面上の断面を描く共役複素数(Complex Conjugate)がこれに該当するのである（上で言っている「断面」とはまさにこれの事…）。

そして意外にも、こうした諸概念の大源流を遡ると複式簿記（Double-entry Bookkeeping System）の世界に辿り着くのです。

• 任意の期首と期末を定め、その間の簿記的取引の全てを仕訳帳や総勘定元帳などに記録として残す。すると(不正や誤謬がなければ)借方の合計と貸方の合計が常に一致する。
• これを貸借平均の原理(Principle of Loan Average)資産+費用=負債+純資産+収益といい貸借対照表等式や損益計算書等式の大原則となっている。

ここで重要なのが「あらかじめ期首と期末が設定されるからこそ、期内全ての借方取引と貸方取引の二重性が捕捉可能となる」なる実証科学的思考様式。

• 中世地中海交易圏でアラビア商人が発案し、ルネサンス期のイタリア商人を通じてアラビア数字とセットで欧州に広まったとされている。
• その起爆剤となったのが当時の出版革命で、より具体的に「スムマ（算術・幾何・比及び比例全書,1494年）」の一章として「簿記論」を著したイタリア商人出身の数学者ルカ・パチョリ（1445年頃~1517年）が「複式簿記の父」として崇められていたりする。
• そして医術や占星術を本業としていた数学者カルダノ（1501年〜1576年)が「アルス・マグナ(Ars Magna, 1545年)」の中で三次方程式（Ars Magna, 1545年Cubic Equation）に虚数の概念を導入して解いたのも同じルネサンス期イタリアの出来事だったのである。 さらにオイラーの師匠ベルヌーイ(1667年〜1748年)は自然指数関数e^1=(1-1/N)^N導出を巡る思考実験で「複利発生期間の設定極限」の例えを用いている。そもそも写実絵画や建築分野で「対数尺＝透視図法」の研究が最初に本格化したのも、やはりルネサンス期イタリアではなかったか？
  【初心者向け】指数・対数関数の発見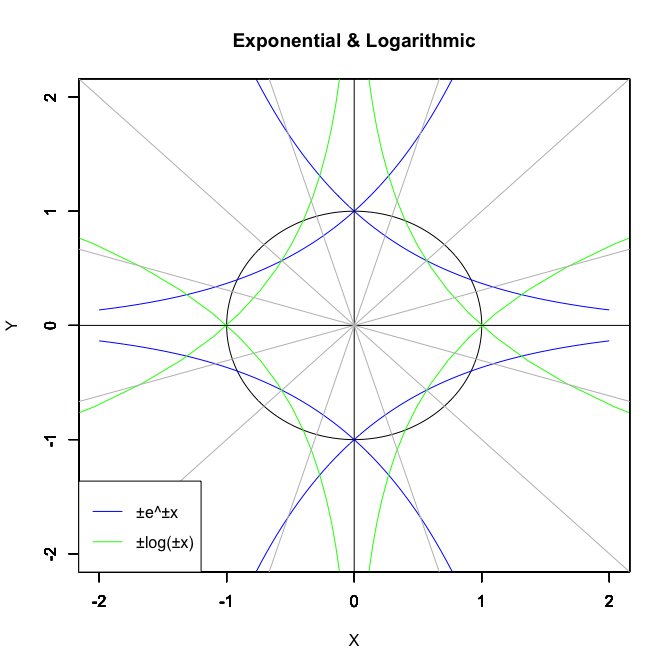
  

もしかして全ては最初から一つだった？　そんな可能性が浮上してきたところで、以下続報…