【初心者向け】「単位円筒」から「単位球面」へ

今回の投稿の出発点はこれ。
【初心者向け】物理学における「単位円筒(Unit Cylinder)」の概念について。

XY軸（円弧）

ZX軸（Cos波）

ZY軸（Sin波）

単位円筒(Unit Cylinder)の概念を単位球面に発展させる為には、まずZ軸の空間化、すなわちX軸やY軸と同様に相応の密度設定が必要となります。

libraly(rgl)
radians<-seq(0,120*pi,length=5000)
f0<-function(x){exp(x*(0+1i))}
Real<-Re(f0(radians))
Imaginal<-Im(f0(radians))
Rtime<-seq(0,2,length=3000)
plot3d(Real,Imaginal,Rtime,type="l",xlim=c(-1,1),ylim=c(-1,1),zlim=c(0,2),xlab="",ylab="",zlab="")

movie3d(spin3d(axis=c(0,0,1),rpm=5),duration=10,fps=25,movie="~/Desktop/unit01") 

そしてこの円筒にピタゴラスの定理に従って曲率を付与するのです。
【初心者向け】ピタゴラスの定理あるいは三平方の定理からの出発

library(rgl)
radians<-seq(0,60*pi,length=3000)
f0<-function(x){exp(x*(0+1i))}
Real<-Re(f0(radians))
Imaginal<-Im(f0(radians))
Rtime<-seq(0,2,length=3000)
#工夫
f1<-function(x){sqrt(1-x^2)}
c0<-seq(-1,1,length=3000)
c1<-f1(c0)
#> plot(c0,c1,type="l",xlim=c(-1,1),ylim=c(0,1))
Real_c<-Real*c1
Imaginal_c<-Imaginal*c1

plot3d(Real_c,Imaginal_c,Rtime,type="l",xlim=c(-1,1),ylim=c(-1,1),zlim=c(0,2),xlab="",ylab="",zlab="")

movie3d(spin3d(axis=c(0,0,1),rpm=5),duration=10,fps=25,movie="~/Desktop/unit03") 

これに「任意の原蹠(Portal)から対蹠(Antipodal)に伸ばした立方対角線(Cubic Diagonal)」なる概念を追加してみます。

library(rgl)

radians<-seq(0,60*pi,length=3000)
f0<-function(x){exp(x*(0+1i))}
Real<-Re(f0(radians))
Imaginal<-Im(f0(radians))
Rtime<-seq(-1,1,length=3000)
#工夫
f1<-function(x){sqrt(1-x^2)}
c0<-seq(-1,1,length=3000)
c1<-f1(c0)
#> plot(c0,c1,type="l",xlim=c(-1,1),ylim=c(0,1))
Real_c<-Real*c1
Imaginal_c<-Imaginal*c1

plot3d(Real_c,Imaginal_c,Rtime,type="l",xlim=c(-1,1),ylim=c(-1,1),zlim=c(-1,1),xlab="",ylab="",zlab="",col=c(200,200,200))

#観測原点**(Observation Origin)
texts3d(0,0,0,texts="OO(0,0,0)",col=rgb(0,0,1),adj=1.0)

#原蹠(PorTal)
portal_i<-0
portal_j<-0
portal_k<-1
portal_text=paste0("PT(",portal_i,",",portal_j,",",portal_k,")")

#原蹠表示
texts3d(portal_i,portal_j,portal_k,texts=portal_text,col=rgb(0,0,1),adj=1.0)

#対蹠(AntiPordal)
antipordal_i<-0
antipordal_j<-0
antipordal_k<--1
antipordal_text=paste0("AP(",antipordal_i,",",antipordal_j,",",antipordal_k,")")

#対蹠表示
texts3d(antipordal_i,antipordal_j,antipordal_k,texts=antipordal_text,col=rgb(0,0,1),adj=1.0)

#立方対角線(Cubic Diagonal)
lines3d(c(portal_i,antipordal_i),c(portal_j,antipordal_j),c(portal_k,antipordal_k),col=rgb(0,0,1),lwd=2)

#アニメーション
movie3d(spin3d(axis=c(0,0,1),rpm=5),duration=10,fps=25,movie="~/Desktop/Sphere001")

さらに赤道円(Equatorial circle)の概念を追加。

library(rgl)
#円描写関数
f0<-function(x){exp(x*(0+1i))}

#無限円(Infinity Circle)
radians0<-seq(0,60*pi,length=60)
Real0<-Re(f0(radians))
Imaginal0<-Im(f0(radians))
Rtime0<-numeric(60)

#無限球面(Infinity Sphere)
radians<-seq(0,60*pi,length=3000)
Real<-Re(f0(radians))
Imaginal<-Im(f0(radians))
Rtime<-seq(-1,1,length=3000)

#工夫
f1<-function(x){sqrt(1-x^2)}
c0<-seq(-1,1,length=3000)
c1<-f1(c0)
#> plot(c0,c1,type="l",xlim=c(-1,1),ylim=c(0,1))
Real_c<-Real*c1
Imaginal_c<-Imaginal*c1

#無限球面(Infinity Sphere)の描画
plot3d(Real_c,Imaginal_c,Rtime,type="l",xlim=c(-1,1),ylim=c(-1,1),zlim=c(-1,1),,xlab="",ylab="",zlab="",col=c(200,200,200))

#無限円(Infinity Circle)の描画
lines3d(Real0,Imaginal0,Rtime0,col=rgb(0,0,1),lwd=2)

#観測原点**(Observation Origin)
texts3d(0,0,0,texts="OO(0,0,0)",col=rgb(0,0,1),adj=1.0)

#原蹠表示
texts3d(portal_i,portal_j,portal_k,texts=portal_text,col=rgb(0,0,1),adj=1.0)

#原蹠(PorTal)
portal_i<-0
portal_j<-0
portal_k<-1
portal_text="AP(0,0,Inf)"

#原蹠表示
texts3d(portal_i,portal_j,portal_k,texts=portal_text,col=rgb(0,0,1),adj=1.0)

#対蹠(AntiPordal)
antipordal_i<-0
antipordal_j<-0
antipordal_k<--1
antipordal_text="AP(0,0,-Inf)"

#対蹠表示
texts3d(antipordal_i,antipordal_j,antipordal_k,texts=antipordal_text,col=rgb(0,0,1),adj=1.0)

#立方対角線(Cubic Diagonal)
lines3d(c(portal_i,antipordal_i),c(portal_j,antipordal_j),c(portal_k,antipordal_k),col=rgb(0,0,1),lwd=2)

#アニメーション
movie3d(spin3d(axis=c(0,0,1),rpm=5),duration=10,fps=25,movie="~/Desktop/Sphere02")

半径(Radius)で考えるとこうです。

library(rgl)

radians<-seq(0,60*pi,length=3000)
f0<-function(x){exp(x*(0+1i))}
Real<-Re(f0(radians))
Imaginal<-Im(f0(radians))
Rtime<-seq(-1,1,length=3000)
#工夫
f1<-function(x){sqrt(1-x^2)}
c0<-seq(-1,1,length=3000)
c1<-f1(c0)
#> plot(c0,c1,type="l",xlim=c(-1,1),ylim=c(0,1))
Real_c<-Real*c1
Imaginal_c<-Imaginal*c1

plot3d(Real_c,Imaginal_c,Rtime,type="l",xlim=c(-1,1),ylim=c(-1,1),zlim=c(-1,1),xlab="",ylab="",zlab="",col=c(200,200,200))

#観測原点**(Observation Origin)
texts3d(0,0,0,texts="OO(0,0,0)",col=rgb(0,0,0),adj=1.0)

#原蹠(PorTal)
portal_i<-0
portal_j<-0
portal_k<-1
portal_text=paste0("Rad(",portal_i,",",portal_j,",",portal_k,")")

#原蹠表示
texts3d(portal_i,portal_j,portal_k,texts=portal_text,col=rgb(0,0,1),adj=1.0)

#立方対角線(Cubic Diagonal)
lines3d(c(portal_i,0),c(portal_j,0),c(portal_k,0),col=rgb(0,0,1),lwd=2)

#アニメーション
movie3d(spin3d(axis=c(0,0,1),rpm=5),duration=10,fps=25,movie="~/Desktop/Sphere01f")

赤道概念の追加。

library(rgl)
f0<-function(x){exp(x*(0+1i))}

#無限円(Infinity Circle)
radians0<-seq(0,2*pi,length=60)
Real0<-Re(f0(radians0))
Imaginal0<-Im(f0(radians0))
Rtime0<-numeric(60)

#無限球面(Infinity Sphere)
Real<-Re(f0(radians))
Imaginal<-Im(f0(radians))
Rtime<-seq(-1,1,length=3000)
#工夫
f1<-function(x){sqrt(1-x^2)}
c0<-seq(-1,1,length=3000)
c1<-f1(c0)
#> plot(c0,c1,type="l",xlim=c(-1,1),ylim=c(0,1))
Real_c<-Real*c1
Imaginal_c<-Imaginal*c1

#無限球面の描画
plot3d(Real_c,Imaginal_c,Rtime,type="l",xlim=c(-1,1),ylim=c(-1,1),zlim=c(-1,1),xlab="",ylab="",zlab="",col=c(200,200,200))

#無限円(Infinity Circle)の描画
lines3d(Real0,Imaginal0,Rtime0,col=rgb(0,1,0),lwd=2)

#観測原点**(Observation Origin)
texts3d(0,0,0,texts="OO(0,0,0)",col=rgb(0,0,0),adj=1.0)

#原蹠(PorTal)
portal_i<-0
portal_j<-0
portal_k<-1
portal_text=paste0("Rad(",portal_i,",",portal_j,",",portal_k,")")

#原蹠表示
texts3d(portal_i,portal_j,portal_k,texts=portal_text,col=rgb(0,0,1),adj=1.0)

#立方対角線(Cubic Diagonal)
lines3d(c(portal_i,0),c(portal_j,0),c(portal_k,0),col=rgb(0,0,1),lwd=2)

#アニメーション
movie3d(spin3d(axis=c(0,0,1),rpm=5),duration=10,fps=25,movie="~/Desktop/Sphere06")

直径(Diameter)で考えるとこうです。

library(rgl)

radians<-seq(0,60*pi,length=3000)
f0<-function(x){exp(x*(0+1i))}
Real<-Re(f0(radians))
Imaginal<-Im(f0(radians))
Rtime<-seq(-1,1,length=3000)
#工夫
f1<-function(x){sqrt(1-x^2)}
c0<-seq(-1,1,length=3000)
c1<-f1(c0)
#> plot(c0,c1,type="l",xlim=c(-1,1),ylim=c(0,1))
Real_c<-Real*c1
Imaginal_c<-Imaginal*c1

plot3d(Real_c,Imaginal_c,Rtime,type="l",xlim=c(-1,1),ylim=c(-1,1),zlim=c(-1,1),xlab="",ylab="",zlab="",col=c(200,200,200))

#観測原点**(Observation Origin)
texts3d(0,0,0,texts="OO(0,0,0)",col=rgb(0,0,0),adj=1.0)

#原蹠(PorTal)
portal_i<-0
portal_j<-0
portal_k<-1
portal_text=paste0("PT(",portal_i,",",portal_j,",",portal_k,")")

#原蹠表示
texts3d(portal_i,portal_j,portal_k,texts=portal_text,col=rgb(0,0,1),adj=1.0)

#対蹠(AntiPordal)
antipordal_i<-0
antipordal_j<-0
antipordal_k<--1
antipordal_text=paste0("AP(",antipordal_i,",",antipordal_j,",",antipordal_k,")")

#対蹠表示
texts3d(antipordal_i,antipordal_j,antipordal_k,texts=antipordal_text,col=rgb(1,0,0),adj=1.0)

#立方対角線(Cubic Diagonal)
lines3d(c(portal_i,0),c(portal_j,0),c(portal_k,0),col=rgb(0,0,1),lwd=2)
lines3d(c(0,antipordal_i),c(0,antipordal_j),c(0,antipordal_k),col=rgb(1,0,0),lwd=2)

#アニメーション
movie3d(spin3d(axis=c(0,0,1),rpm=5),duration=10,fps=25,movie="~/Desktop/Sphere01d")

同じく赤道概念を追加。

library(rgl)
f0<-function(x){exp(x*(0+1i))}

#無限円(Infinity Circle)
radians0<-seq(0,2*pi,length=60)
Real0<-Re(f0(radians0))
Imaginal0<-Im(f0(radians0))
Rtime0<-numeric(60)

#無限球面(Infinity Sphere)
radians<-seq(0,60*pi,length=3000)
Real<-Re(f0(radians))
Imaginal<-Im(f0(radians))
Rtime<-seq(-1,1,length=3000)
#工夫
f1<-function(x){sqrt(1-x^2)}
c0<-seq(-1,1,length=3000)
c1<-f1(c0)
#> plot(c0,c1,type="l",xlim=c(-1,1),ylim=c(0,1))
Real_c<-Real*c1
Imaginal_c<-Imaginal*c1

#無限球面の描画
plot3d(Real_c,Imaginal_c,Rtime,type="l",xlim=c(-1,1),ylim=c(-1,1),zlim=c(-1,1),xlab="",ylab="",zlab="",col=c(200,200,200))

#無限円(Infinity Circle)の描画
lines3d(Real0,Imaginal0,Rtime0,col=rgb(0,1,0),lwd=2)

#観測原点**(Observation Origin)
texts3d(0,0,0,texts="OO(0,0,0)",col=rgb(0,0,0),adj=1.0)

#原蹠(PorTal)
portal_i<-0
portal_j<-0
portal_k<-1
portal_text=paste0("PT(",portal_i,",",portal_j,",",portal_k,")")

#原蹠表示
texts3d(portal_i,portal_j,portal_k,texts=portal_text,col=rgb(0,0,1),adj=1.0)

#対蹠(AntiPordal)
antipordal_i<-0
antipordal_j<-0
antipordal_k<--1
antipordal_text=paste0("AP(",antipordal_i,",",antipordal_j,",",antipordal_k,")")

#対蹠表示
texts3d(antipordal_i,antipordal_j,antipordal_k,texts=antipordal_text,col=rgb(1,0,0),adj=1.0)

#立方対角線(Cubic Diagonal)
lines3d(c(portal_i,0),c(portal_j,0),c(portal_k,0),col=rgb(0,0,1),lwd=2)
lines3d(c(0,antipordal_i),c(0,antipordal_j),c(0,antipordal_k),col=rgb(1,0,0),lwd=2)

#アニメーション
movie3d(spin3d(axis=c(0,0,1),rpm=5),duration=10,fps=25,movie="~/Desktop/Sphere07")

そしてリーマン球面

library(rgl)
f0<-function(x){exp(x*(0+1i))}

#無限円(Infinity Circle)
radians0<-seq(0,2*pi,length=60)
Real0<-Re(f0(radians0))
Imaginal0<-Im(f0(radians0))
Rtime0<-numeric(60)

#無限球面(Infinity Sphere)
radians<-seq(0,60*pi,length=3000)
Real<-Re(f0(radians))
Imaginal<-Im(f0(radians))
Rtime<-seq(-1,1,length=3000)
#工夫
f1<-function(x){sqrt(1-x^2)}
c0<-seq(-1,1,length=3000)
c1<-f1(c0)
#> plot(c0,c1,type="l",xlim=c(-1,1),ylim=c(0,1))
Real_c<-Real*c1
Imaginal_c<-Imaginal*c1

#無限球面の描画
plot3d(Real_c,Imaginal_c,Rtime,type="l",xlim=c(-1,1),ylim=c(-1,1),zlim=c(-1,1),xlab="",ylab="",zlab="",col=c(200,200,200))

#無限円(Infinity Circle)の描画
lines3d(Real0,Imaginal0,Rtime0,col=rgb(0,1,0),lwd=2)

#観測原点**(Observation Origin)
texts3d(0,0,0,texts="OO(0,0,1)",col=rgb(0,0,0),adj=1.0)

#原蹠(PorTal)
portal_i<-0
portal_j<-0
portal_k<-1
portal_text="Inf(inity)"

#原蹠表示
texts3d(portal_i,portal_j,portal_k,texts=portal_text,col=rgb(0,0,1),adj=1.0)

#対蹠(AntiPordal)
antipordal_i<-0
antipordal_j<-0
antipordal_k<--1
antipordal_text="AP(0,0,0)"

#対蹠表示
texts3d(antipordal_i,antipordal_j,antipordal_k,texts=antipordal_text,col=rgb(1,0,0),adj=1.0)

#立方対角線(Cubic Diagonal)
lines3d(c(portal_i,0),c(portal_j,0),c(portal_k,0),col=rgb(0,0,1),lwd=2)
lines3d(c(0,antipordal_i),c(0,antipordal_j),c(0,antipordal_k),col=rgb(1,0,0),lwd=2)

#アニメーション
movie3d(spin3d(axis=c(0,0,1),rpm=5),duration=10,fps=25,movie="~/Desktop/Sphere08")

実は半径rをある種のスカラー(Scalar)として扱い、水平方向の角度φと垂直方向の角度θの組み合わせで球表面上の位置を特定する極座標系(Polar Coordinate System)と完全に重なります。何しろZ軸の値域がX軸とX軸の相関関係と完全に無関係に-1<=cos(θ)<=1と定められていますからね。
極座標系 -Wikipedia-

二次元空間(円弧)におけるデカルト座標系(x,y)と極座標系(r,φ)の相互変換

• 原点(0,0)からの距離r=sqrt(x^2+y^2)
• φ=-(atan2(x,y)-pi/2)
• x=r×cos(φ)
• y=r×sin(φ)

統計言語Rでの検証例

#関数CtoD_2d(半径,角度φ)={x座標,y座標}
CtoD_2d<-function(Rad,Phi)return(c(Rad*cos(Phi),Rad*sin(Phi))) 
#関数DtoC_2d(x座標,y座標)={半径,角度φ}
DtoC_2d<-function(Xax,Yax)return(c(sqrt(Xax^2+Yax^2),-1*(atan2(Xax,Yax)-pi/2))) 

#π=3.14159,π/2=1.5708 
> round(pi, digits = 5)
[1] 3.14159
> round(pi/2, digits = 5)
[1] 1.5708

#半径1の単位円(Unit Circle)

> #0度(0ラジアン)
> round(CtoD_2d(1,0), digits = 5)
[1] 1 0
> round(DtoC_2d(1,0), digits = 5)
[1] 1 0
> #90度(π/2ラジアン)
> round(CtoD_2d(1,pi/2), digits = 5)
[1] 0 1
> round(DtoC_2d(0,1), digits = 5)
[1] 1.0000 1.5708
> #180度(πラジアン)
> round(CtoD_2d(1,pi), digits = 5)
[1] -1  0
> round(DtoC_2d(-1,0), digits = 5)
[1] 1.00000 3.14159
> #270度(3/2πラジアン)
> round(CtoD_2d(1,3/2*pi), digits = 5)
[1]  0 -1
> round(DtoC_2d(0,-1), digits = 5)
[1]  1.0000 -1.5708
> #360度(2πラジアン)
> round(CtoD_2d(1,2*pi), digits = 5)
[1] 1 0
> round(DtoC_2d(1,0), digits = 5)
[1] 1 0

三次元空間(球面)におけるデカルト座標系(x,y,z)の極座標系(r,φ,θ)の相互変換

• 原点(0,0,0)からの距離r=sqrt(x^2+y^2+z^2)
• φ=-(atan2(x,y)-pi/2)
• θ=-(atan2(sqrt(x^2+y^2+z^2),z)-pi/2))
• x=r×sin(θ)cos(φ)
• y=r×sin(θ)sin(φ)
• z=r*cos(θ)

統計言語Rでの検証例

#関数CtoD_3d(半径,角度φ,角度θ)={x座標,y座標,z座標}
CtoD_3d<-function(Rad,Phi,Theta)return(c(Rad*sin(Theta)*cos(Phi),Rad*sin(Theta)*sin(Phi),Rad*cos(Theta))) 
#関数DtoC_3d(x座標,y座標,z座標)={半径,角度φ,角度θ}
DtoC_3d<-function(Xax,Yax,Zax)return(c(sqrt(Rad<-Xax^2+Yax^2+Zax^2),-1*(atan2(Xax,Yax)-pi/2),-1*(atan2(Rad,Zax)-pi/2))) 

#cos(π/4)=cos(-π/4)=0.70711
#-cos(pi/4)=cos(3/4π)=-0.70711
> cos(pi/4)
[1] 0.7071068
> cos(-pi/4)
[1] 0.7071068
> -cos(pi/4)
[1] -0.7071068
> cos(3/4*pi)
[1] -0.7071068

#半径1の単位球面(Unit Sphere)

#角度φ=0の時の角度θの周回
#対蹠なので角度θの値に拠らず座標(0,0,1)を指す。
> round(CtoD_3d(1,0,0), digits = 5)
[1] 0 0 1
> round(CtoD_3d(1,pi/2,0), digits = 5)
[1] 0 0 1
> round(CtoD_3d(1,pi,0), digits = 5)
[1] 0 0 1
> round(CtoD_3d(1,3/2*pi,0), digits = 5)
[1] 0 0 1
> round(CtoD_3d(1,2*pi,0), digits = 5)
[1] 0 0 1
> 
#角度φ=pi/4の時の角度θの周回
#Z座標cos(pi/4)の断面に半径cos(pi/4)の円を描く。
> round(CtoD_3d(1,0,pi/4), digits = 5)
[1] 0.70711 0.00000 0.70711
> round(CtoD_3d(1,pi/2,pi/4), digits = 5)
[1] 0.00000 0.70711 0.70711
> round(CtoD_3d(1,pi,pi/4), digits = 5)
[1] -0.70711  0.00000  0.70711
> round(CtoD_3d(1,3/2*pi,pi/4), digits = 5)
[1]  0.00000 -0.70711  0.70711
> round(CtoD_3d(1,2*pi,pi/4), digits = 5)
[1] 0.70711 0.00000 0.70711
 
#角度φ=pi/2の時の角度θの周回
#Z座標0の断面に半径1の円を描く。
> round(CtoD_3d(1,0,pi/2), digits = 5)
[1] 1 0 0
> round(CtoD_3d(1,pi/2,pi/2), digits = 5)
[1] 0 1 0
> round(CtoD_3d(1,pi,pi/2), digits = 5)
[1] -1  0  0
> round(CtoD_3d(1,3/2*pi,pi/2), digits = 5)
[1]  0 -1  0
> round(CtoD_3d(1,2*pi,pi/2), digits = 5)
[1] 1 0 0
 
#角度φ=3/4πの時の角度θの周回
#Z座標-cos(pi/4)の断面に半径cos(pi/4)の円を描く。
round(CtoD_3d(cos(pi/4),0,cos(pi/4)), digits = 5)

[1]  0.70711  0.00000 -0.70711
> round(CtoD_3d(1,pi/2,pi*3/4), digits = 5)
[1]  0.00000  0.70711 -0.70711
> round(CtoD_3d(1,pi,pi*3/4), digits = 5)
[1] -0.70711  0.00000 -0.70711
> round(CtoD_3d(1,3/2*pi,pi*3/4), digits = 5)
[1]  0.00000 -0.70711 -0.70711
> round(CtoD_3d(1,2*pi,pi*3/4), digits = 5)
[1]  0.70711  0.00000 -0.70711
 
#角度φ=πの時の角度θの周回
#対蹠なので角度θの値に拠らず座標(0,0,-1)を指す。
> round(CtoD_3d(1,0,pi), digits = 5)
[1]  0  0 -1
> round(CtoD_3d(1,pi/2,pi), digits = 5)
[1]  0  0 -1
> round(CtoD_3d(1,pi,pi), digits = 5)
[1]  0  0 -1
> round(CtoD_3d(1,3/2*pi,pi), digits = 5)
[1]  0  0 -1
> round(CtoD_3d(1,2*pi,pi), digits = 5)
[1]  0  0 -1

#関数DtoC_3d(x座標,y座標,z座標)={半径,角度φ,角度θ}
DtoC_3d<-function(Xax,Yax,Zax)return(c(sqrt(Xax^2+Yax^2+Zax^2),-1*(atan2(Xax,Yax)-pi/2),acos(Zax/sqrt(Xax^2+Yax^2+Zax^2)))) 

#座標(0,0,r)は対蹠なので半径r,角度θ=0と定まる。
#実は角度φは定まらない(ある種の極限状態)。
>round(DtoC_3d(0,0,1), digits = 5)
[1] 1.0000 1.5708 0.0000

#Z座標cos(π/4)の断面上では半径r,角度θ=cos(π/4)と定まる。
#角度φは平面上での検出通り。
> round(DtoC_3d(cos(pi/4),0,cos(pi/4)), digits = 5)
[1] 1.0000 0.0000 0.7854
> round(DtoC_3d(0,cos(pi/4),cos(pi/4)), digits = 5)
[1] 1.0000 1.5708 0.7854
> round(DtoC_3d(-cos(pi/4),0,cos(pi/4)), digits = 5)
[1] 1.00000 3.14159 0.78540
> round(DtoC_3d(0,-cos(pi/4),cos(pi/4)), digits = 5)
[1]  1.0000 -1.5708  0.7854

#Z座標0の断面上では半径r,角度θ=π/2と定まる。
#角度φは平面上での検出通り。
> round(DtoC_3d(1,0,0), digits = 5)
[1] 1.0000 0.0000 1.5708
> round(DtoC_3d(0,1,0), digits = 5)
[1] 1.0000 1.5708 1.5708
> round(DtoC_3d(-1,0,0), digits = 5)
[1] 1.00000 3.14159 1.57080
> round(DtoC_3d(0,-1,0), digits = 5)
[1]  1.0000 -1.5708  1.5708
> round(DtoC_3d(0,0,1), digits = 5)

#Z座標-cos(1/4π)の断面上では半径r,角度θ=-cos(1/4π)と定まる。
#角度φは平面上での検出通り。
> pi*3/4
[1] 2.356194
> round(DtoC_3d(cos(pi/4),0,-cos(pi/4)), digits = 5)
[1] 1.00000 0.00000 2.35619
> round(DtoC_3d(0,cos(pi/4),-cos(pi/4)), digits = 5)
[1] 1.00000 1.57080 2.35619
> round(DtoC_3d(-cos(pi/4),0,-cos(pi/4)), digits = 5)
[1] 1.00000 3.14159 2.35619
> round(DtoC_3d(0,cos(pi*3/4),-cos(pi/4)), digits = 5)
[1]  1.00000 -1.57080  2.35619

#座標(0,0,-r)も対蹠なので半径r,角度θ=πと定まる。
#角度φは定まらない(ある種の極限状態)
>round(DtoC_3d(0,0,-1), digits = 5)
[1] 1.00000 1.57080 3.14159

さりげなく水平角φと垂直角θの関係設定に三角関数の加法定理(Trigonometric Addition Formulas)の概念が援用されたりしてます。
【初心者向け】「加法定理の幾何学的証明」に挑戦。

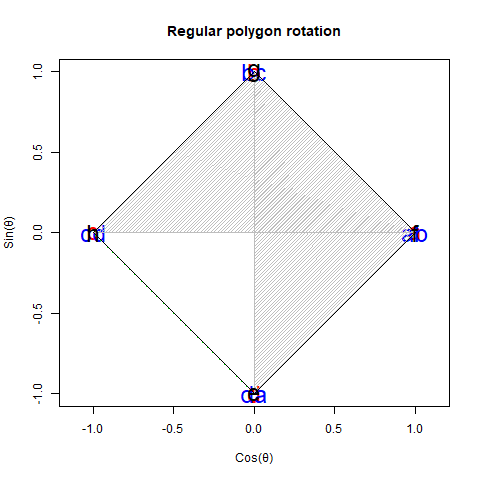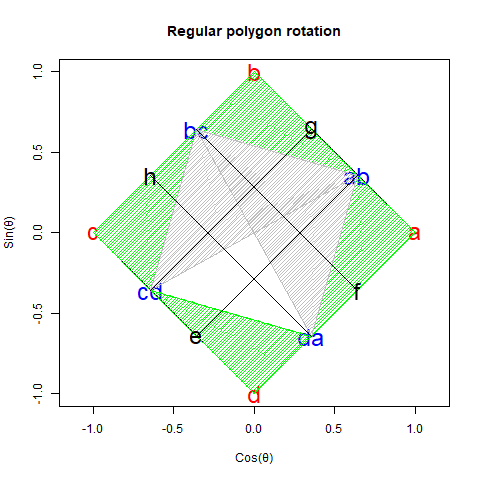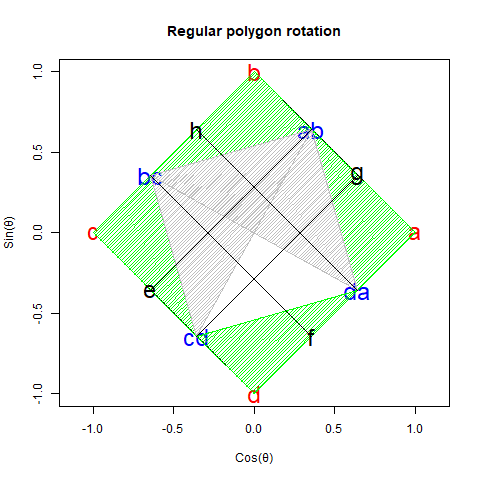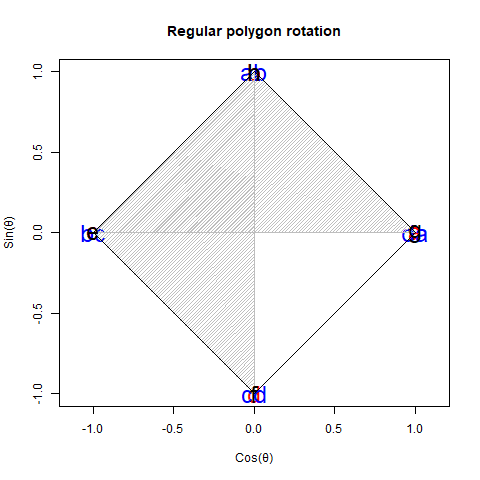
ここでは詳しくは述べませんが、さりげなく「円弧上に位置する原蹠と対蹠の間を1回も曲がらず直線で結ぶ1次元処理」や「円弧上に位置する原蹠と対蹠の間を1回直角に曲がって結ぶ2次元処理」といった次元操作概念もこっそり先取りされています（特に何の説明もなく角度φの範囲が2π、角度θの範囲がπと設定されてる辺り）。
【Rで球面幾何学】ハミルトンの四元数(Hamilton's Quaternion)は何を表しているのか？

①考え方としては「円柱の側面積の求め方を援用して円の表面積を積分する」概念と重なってくる様です。そして、どちらも「メルカトル図法の歪み」問題に直面する展開に…
【初心者向け】半径・直径・円周長・円の面積・球の表面積・球の体積の計算上の往復
メルカトル図法 - Wikipedia


②一方、単位円筒からの発展のさせ方は「単位球面」ばかりとは限りません。
【Rで球面幾何学】「単位円筒」から「トーラス構造」へ

③一応、円筒の場合も試しておきましょう。

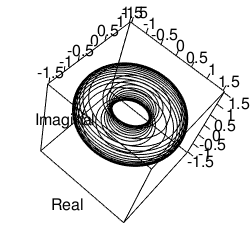
library(rgl)
radians<-seq(0,120*pi,length=5000)
f0<-function(x){exp(x*(0+1i))}
Real<-Re(f0(radians))
Imaginal<-Im(f0(radians))
Rtime<-seq(-1,1,length=3000)
plot3d(Real,Imaginal,Rtime,type="l",xlim=c(-1,1),ylim=c(-1,1),zlim=c(-1,1),col=c(200,200,200))

#無限円(Infinity Circle)の描画
radians0<-seq(0,60*pi,length=60)
Real0<-Re(f0(radians))
Imaginal0<-Im(f0(radians))
Rtime0<-numeric(60)
lines3d(Real0,Imaginal0,Rtime0,col=rgb(1,0,0),lwd=2)

#観測原点**(Observation Origin)
texts3d(0,0,0,texts="OO(0,0,0)",col=rgb(1,0,0),adj=1.0)

#原蹠表示
texts3d(portal_i,portal_j,portal_k,texts=portal_text,col=rgb(1,0,0),adj=1.0)

#原蹠(PorTal)
portal_i<-0
portal_j<-0
portal_k<-1
portal_text="AP(0,0,Inf)"

#原蹠表示
texts3d(portal_i,portal_j,portal_k,texts=portal_text,col=rgb(1,0,0),adj=1.0)

#対蹠(AntiPordal)
antipordal_i<-0
antipordal_j<-0
antipordal_k<--1
antipordal_text="AP(0,0,-Inf)"

#対蹠表示
texts3d(antipordal_i,antipordal_j,antipordal_k,texts=antipordal_text,col=rgb(1,0,0),adj=1.0)

#立方対角線(Cubic Diagonal)
lines3d(c(portal_i,antipordal_i),c(portal_j,antipordal_j),c(portal_k,antipordal_k),col=rgb(1,0,0),lwd=2)

movie3d(spin3d(axis=c(0,0,1),rpm=5),duration=10,fps=25,movie="~/Desktop/test05") 

正方向のみの場合。

library(rgl)
f0<-function(x){exp(x*(0+1i))}

#円筒描画
radians<-seq(0,120*pi,length=5000)
Real<-Re(f0(radians))
Imaginal<-Im(f0(radians))
Rtime<-seq(0,2,length=3000)
plot3d(Real,Imaginal,Rtime,type="l",xlim=c(-1,1),ylim=c(-1,1),zlim=c(0,2),xlab="",ylab="",zlab="",col=c(200,200,200))

#無限円(Infinity Circle)の描画
radians0<-seq(0,2*pi,length=60)
Real0<-Re(f0(radians0))
Imaginal0<-Im(f0(radians0))
Rtime0<-numeric(60)
lines3d(Real0,Imaginal0,Rtime0,col=rgb(0,1,0),lwd=2)
lines3d(Real0,Imaginal0,Rtime0+1,col=rgb(0,1,0),lwd=2)
lines3d(Real0,Imaginal0,Rtime0+2,col=rgb(0,1,0),lwd=2)

#観測原点**(Observation Origin)
texts3d(0,0,0,texts="OO(0,0,0)",col=rgb(0,0,0),adj=1.0)

#座標「1」表示
texts3d(0,0,1,texts="(0,0,1)",col=rgb(0,0,1),adj=1.0)
#座標「2」表示
texts3d(0,0,2,texts="(0,0,2)",col=rgb(0,0,1),adj=1.0)
#数直線(Line)
lines3d(c(0,0),c(0,0),c(0,2),col=rgb(0,0,1),lwd=2)

movie3d(spin3d(axis=c(0,0,1),rpm=5),duration=10,fps=25,movie="~/Desktop/sylinder08") 

負方向のみの場合。

library(rgl)
f0<-function(x){exp(x*(0+1i))}

#円筒描画
radians<-seq(0,120*pi,length=5000)
Real<-Re(f0(radians))
Imaginal<-Im(f0(radians))
Rtime<-seq(-2,0,length=3000)
plot3d(Real,Imaginal,Rtime,type="l",xlim=c(-1,1),ylim=c(-1,1),zlim=c(-2,0),xlab="",ylab="",zlab="",col=c(200,200,200))

#無限円(Infinity Circle)の描画
radians0<-seq(0,2*pi,length=60)
Real0<-Re(f0(radians0))
Imaginal0<-Im(f0(radians0))
Rtime0<-numeric(60)
lines3d(Real0,Imaginal0,Rtime0,col=rgb(0,1,0),lwd=2)
lines3d(Real0,Imaginal0,Rtime0-1,col=rgb(0,1,0),lwd=2)
lines3d(Real0,Imaginal0,Rtime0-2,col=rgb(0,1,0),lwd=2)

#観測原点**(Observation Origin)
texts3d(0,0,0,texts="OO(0,0,0)",col=rgb(0,0,0),adj=1.0)

#座標「1」表示
texts3d(0,0,-1,texts="(0,0,-1)",col=rgb(1,0,0),adj=1.0)
#座標「2」表示
texts3d(0,0,-2,texts="(0,0,-2)",col=rgb(1,0,0),adj=1.0)
#数直線(Line)
lines3d(c(0,0),c(0,0),c(0,-2),col=rgb(1,0,0),lwd=2)

movie3d(spin3d(axis=c(0,0,1),rpm=5),duration=10,fps=25,movie="~/Desktop/sylinder10") 

両表示の場合。

library(rgl)
f0<-function(x){exp(x*(0+1i))}

#円筒描画
radians<-seq(0,120*pi,length=5000)
Real<-Re(f0(radians))
Imaginal<-Im(f0(radians))
Rtime<-seq(-1,1,length=3000)
plot3d(Real,Imaginal,Rtime,type="l",xlim=c(-1,1),ylim=c(-1,1),zlim=c(-1,1),xlab="",ylab="",zlab="",col=c(200,200,200))

#無限円(Infinity Circle)の描画
radians0<-seq(0,2*pi,length=60)
Real0<-Re(f0(radians0))
Imaginal0<-Im(f0(radians0))
Rtime0<-numeric(60)
lines3d(Real0,Imaginal0,Rtime0,col=rgb(0,1,0),lwd=2)
lines3d(Real0,Imaginal0,Rtime0+1,col=rgb(0,1,0),lwd=2)
lines3d(Real0,Imaginal0,Rtime0-1,col=rgb(0,1,0),lwd=2)

#観測原点**(Observation Origin)
texts3d(0,0,0,texts="OO(0,0,0)",col=rgb(0,0,0),adj=1.0)

#座標「1」表示
texts3d(0,0,1,texts="(0,0,1)",col=rgb(0,0,1),adj=1.0)
#座標「2」表示
texts3d(0,0,-1,texts="(0,0,-1)",col=rgb(1,0,0),adj=1.0)
#数直線(Line)
lines3d(c(0,0),c(0,0),c(0,1),col=rgb(0,0,1),lwd=2)
lines3d(c(0,0),c(0,0),c(0,-1),col=rgb(1,0,0),lwd=2)

movie3d(spin3d(axis=c(0,0,1),rpm=5),duration=10,fps=25,movie="~/Desktop/sylinder13") 

④そしてZ軸に対数尺を導入すると「卵形」に。

library(rgl)
#円描写関数
f0<-function(x){exp(x*(0+1i))}

#無限円(Infinity Circle)
radians0<-seq(0,60*pi,length=60)
Real0<-Re(f0(radians))
Imaginal0<-Im(f0(radians))
Rtime0<-exp(numeric(60))

#無限球面(Infinity Sphere)
radians<-seq(0,60*pi,length=3000)
Real<-Re(f0(radians))
Imaginal<-Im(f0(radians))
Rtime<-seq(-1,1,length=3000)
RtimeZ<-exp(Rtime)

#工夫
f1<-function(x){sqrt(1-x^2)}
c0<-seq(-1,1,length=3000)
c1<-f1(c0)
#> plot(c0,c1,type="l",xlim=c(-1,1),ylim=c(0,1))
Real_c<-Real*c1
Imaginal_c<-Imaginal*c1

#無限球面(Infinity Sphere)の描画
plot3d(Real_c,Imaginal_c,RtimeZ,type="l",xlim=c(-1,1),ylim=c(-1,1),zlim=c(exp(-1),exp(1)),col=c(200,200,200))

#無限円(Infinity Circle)の描画
lines3d(Real0,Imaginal0,Rtime0,col=rgb(1,0,0),lwd=2)

#観測原点**(Observation Origin)
texts3d(0,0,exp(0),texts="OO(0,0,exp(0))",col=rgb(1,0,0),adj=1.0)

#原蹠表示
texts3d(portal_i,portal_j,portal_k,texts=portal_text,col=rgb(1,0,0),adj=1.0)

#原蹠(PorTal)
portal_i<-0
portal_j<-0
portal_k<-exp(1)
portal_text="AP(0,0,exp(1)"

#原蹠表示
texts3d(portal_i,portal_j,portal_k,texts=portal_text,col=rgb(1,0,0),adj=1.0)

#対蹠(AntiPordal)
antipordal_i<-0
antipordal_j<-0
antipordal_k<-exp(-1)
antipordal_text="AP(0,0,exp(-1))"

#対蹠表示
texts3d(antipordal_i,antipordal_j,antipordal_k,texts=antipordal_text,col=rgb(1,0,0),adj=1.0)

#立方対角線(Cubic Diagonal)
lines3d(c(portal_i,antipordal_i),c(portal_j,antipordal_j),c(portal_k,antipordal_k),col=rgb(1,0,0),lwd=2)

#アニメーション
movie3d(spin3d(axis=c(0,0,1),rpm=5),duration=10,fps=25,movie="~/Desktop/Sphere09")

以下続報…