- 2020年03月06日 初投稿
- 2020年06月13日 Tex対応
ピタゴラスの定理(Pythagorean theorem)あるいは三平方の定理(Three-square theorem)の証明から出発します。

Three_square_theorem04<-function(x){
c0<-c(0,pi/2,-1*pi,-1*pi/2,0)
c0_cos<-cos(c0)
c0_sin<-sin(c0)
plot(c0_cos,c0_sin,type="l",main="Regular polygon rotation",xlab="Cos(θ)",ylab="Sin(θ)")
text(c0_cos,c0_sin, labels=c("a","b","c","d",""),col=c(rgb(1,0,0),rgb(1,0,0),rgb(1,0,0),rgb(1,0,0),rgb(1,0,0)),cex=c(2,2,2,2,2))
line_scale_01_cos<-seq(cos(c0[1]),cos(c0[2]),length=15)
line_scale_01_sin<-seq(sin(c0[1]),sin(c0[2]),length=15)
line_scale_02_cos<-seq(cos(c0[2]),cos(c0[3]),length=15)
line_scale_02_sin<-seq(sin(c0[2]),sin(c0[3]),length=15)
line_scale_03_cos<-seq(cos(c0[3]),cos(c0[4]),length=15)
line_scale_03_sin<-seq(sin(c0[3]),sin(c0[4]),length=15)
line_scale_04_cos<-seq(cos(c0[4]),cos(c0[1]),length=15)
line_scale_04_sin<-seq(sin(c0[4]),sin(c0[1]),length=15)
text(c(line_scale_01_cos[x],line_scale_02_cos[x],line_scale_03_cos[x],line_scale_04_cos[x]),c(line_scale_01_sin[x],line_scale_02_sin[x],line_scale_03_sin[x],line_scale_04_sin[x]), labels=c("ab","bc","cd","da",""),col=c(rgb(0,0,1),rgb(0,0,1),rgb(0,0,1),rgb(0,0,1),rgb(0,0,1)),cex=c(2,2,2,2,2))
# 塗りつぶし
polygon(c(c0_cos[1],line_scale_04_cos[x],line_scale_01_cos[x],c0_cos[1]), #x
c(c0_sin[1],line_scale_04_sin[x],line_scale_01_sin[x],c0_sin[1]), #y
density=c(30), #塗りつぶす濃度
angle=c(45), #塗りつぶす斜線の角度
col=rgb(0,1,0))
# 塗りつぶし
polygon(c(c0_cos[2],line_scale_01_cos[x],line_scale_02_cos[x],c0_cos[2]),#x
c(c0_sin[2],line_scale_01_sin[x],line_scale_02_sin[x],c0_sin[2]),#y
density=c(30),#塗りつぶす濃度
angle=c(45),#塗りつぶす斜線の角度
col=rgb(0,1,0))
# 塗りつぶし
polygon(c(c0_cos[3],line_scale_02_cos[x],line_scale_03_cos[x],c0_cos[3]),#x
c(c0_sin[3],line_scale_02_sin[x],line_scale_03_sin[x],c0_sin[3]), #y
density=c(30),#塗りつぶす濃度
angle=c(45),#塗りつぶす斜線の角度
col=rgb(0,1,0))
# 塗りつぶし
polygon(c(c0_cos[4],line_scale_03_cos[x],line_scale_04_cos[x],c0_cos[4]),#x
c(c0_sin[4],line_scale_03_sin[x],line_scale_04_sin[x],c0_sin[4]), #y
density=c(30), #塗りつぶす濃度
angle=c(45),#塗りつぶす斜線の角度
col=rgb(0,1,0))
}
# アニメーション
library("animation")
Time_Code=c(1,2,3,4,5,6,7,8,9,10,11,12,13,14,15)
saveGIF({
for (i in Time_Code){
Three_square_theorem04(i)
}
}, interval = 0.1, movie.name = "TEST04.gif")
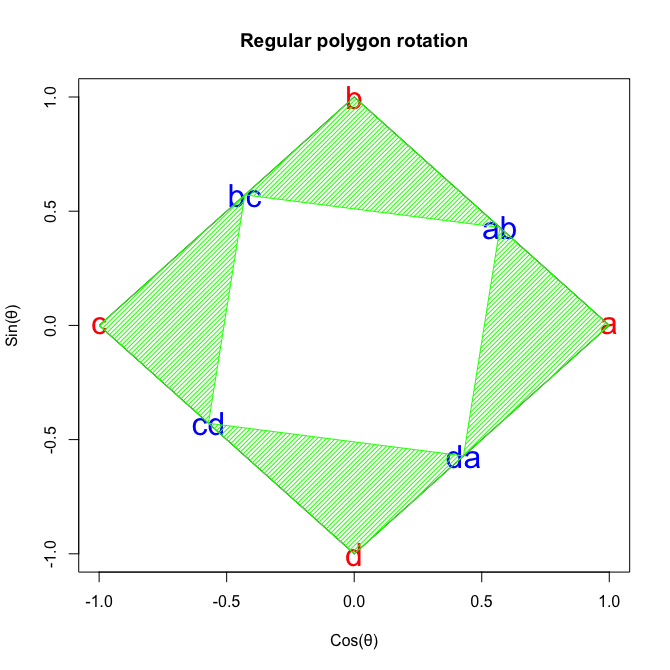
ピタゴラスの定理(三平方の定理)を証明
- 直角三角形を4個集めると正方形が出来る。
- 大きな正方形の面積Sは一辺が{a,ab}={b,bc}={c,cd}={d,da}(Aとする)。かつ{ab,b}+{bc,c}+{cd,c}={da,a}(Bとする)にして{a,ab}+{ab,b}={b,bc}+{bc+b}={c,cd}+{cd,d}={d,da}+{da,a}なのでS=(A+B)^2。
- またSは一辺が{ab,bc}={bc,cd}={cd,da}={da=ab}(Cとする)の正方形とABの直角三角形4つの和でもあるのでS=C^2+41/2A*B。よって$A^2+2AB+B^2=C^2+2AB$。
- これを整理すると$A^2+B^2=C^2$となる。
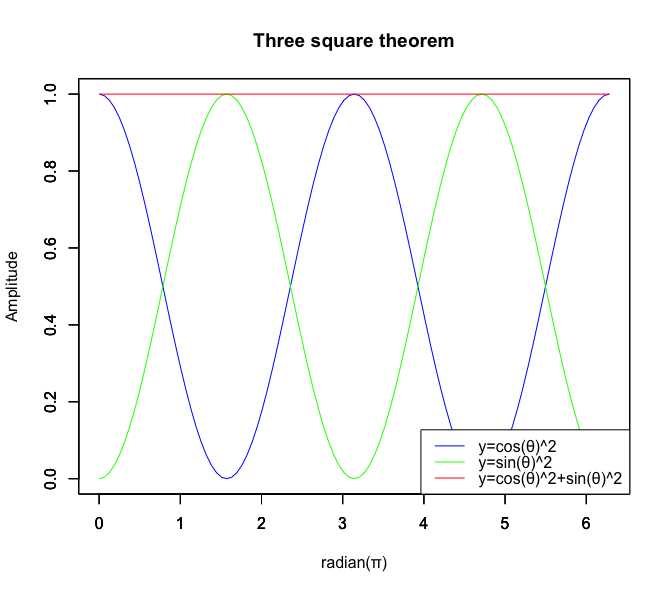
a^2+b^2=c^2からsinθ^2+cosθ^2=1へ
ところで、ここに登場する直角三角形ABCは(プログラム中での扱いを見ても分かる様に)、単位円(Unit Circle=半径1の円弧)上においては「円弧上の任意の点の中心からの距離が全て1となる」事を表す式と重なってくるのです。
【初心者向け】「円そのもの」の近似から派生した角度と経度の概念の起源

- a=cos(θ)
- b=sin(θ)
- c=1
従って同時に任意の角度θに対して以下が成立。
- $cos(θ)^2+sin(θ)^2=1$
f0<-function(x){cos(x)^2}
plot(f0,col=rgb(0,0,1),xlim=c(0,2*pi),ylim=cc(0,1),main="Three square theorem",xlab="radian(π)",ylab="Amplitude")
par(new=T) #上書き
f1<-function(x){sin(x)^2}
plot(f1,col=rgb(0,1,0),xlim=c(0,2*pi),ylim=c(0,1),main="",xlab="",ylab="")
par(new=T) #上書き
f2<-function(x){cos(x)^2+sin(x)^2}
plot(f2,,col=rgb(1,0,0),xlim=c(0,2*pi),ylim=c(0,1),main="",xlab="",ylab="")
legend("bottomright", legend=c("y=cos(θ)^2","y=sin(θ)^2","y=cos(θ)^2+sin(θ)^2"), lty=c(1,1,1), col=c(rgb(0,0,1),rgb(0,1,0),rgb(1,0,0)))
外接/内接多角形が生成する同心円集合
ところで以下の図は正方形における内接円/外接円の半径の推移を示唆してもいるのです。

例えば半径1の単位円に内接する正方形の辺長は$\sqrt{2}$であり、さらにこれに内接する正方形の辺長が最小となるポイントに注目すると…
\cos(\frac{π}{4})=\sin(\frac{π}{4})=\frac{\sqrt{2}}{2}
これはまさに外接/内接正方形の比率連鎖から生じる同心円集合の一部に他なりません。その半径rの推移は以下となり、この比率はそれぞれの外接/内接正方形の辺長/対角線長としても現れてくる形となります。
ここで単位円の半径(Radius)1を$r_0$,単位円に内接する正方形の対角線(Diagonal)2を$d_0$、その辺長(Edge)$\sqrt{2}$を$e_0$と置くと…
r_n,e_n,d_n(n \in \mathbb{Z})=\\
(…,\\
r_{-4},e_{-5},d_{-6}=2^{-2}=\frac{1}{4},\\
r_{-3},e_{-4},d_{-5}=2^{-1.5}=\frac{\sqrt{2}}{4},\\
r_{-2},e_{-3},d_{-4}=2^{^-1}=\frac{1}{2},\\
r_{-1},e_{-2},d_{-3}=2^{0.5}=\frac{\sqrt{2}}{2},\\
r_0,e_{-1},d_{-2}=2^{0}=1,\\
r_1,e_0,d_{-1}=2^{0.5}=\sqrt{2},\\
r_2,e_1,d_0=2^{1}=2,\\
r_3,e_2,d_1=2^{1.5}=2\sqrt{2},\\
r_4,e_3,d_2=2^{2}=4\\
…)
【オイラーの多面体定理と正多面体】内接円/球面の半径と外接円/球面の半径の狭間
| Target_size | Target_names | Target_values | |
|---|---|---|---|
| 1 | 2^-1 | 2^-1(2^-0.5r) | 0.5 |
| 2 | 2^-1 | 2^-1d=2^-1*4 | 1 |
| 3 | 2^-1 | 2^-1a1=2^0a0 | sqrt(2)=1.414214 |
| 4 | 2^-1 | 2^-1a1(2^-0.5a0)*4 | 4sqrt(2)=5.656854 |
| 5 | 2^-0.5 | 2^-0.5(2^0r) | sqrt(2)/2=0.7071068 |
| 6 | 2^-0.5 | 2^-0.5d=2^-0.5*4 | sqrt(2)=1.414214 |
| 7 | 2^-0.5 | 2^-0.5a1=2^0a0 | 1 |
| 8 | 2^-0.5 | 2^-1a1(2^0.5a0)*4 | 4 |
| 9 | 2^0 | 2^0(2^-0.5R,2^0.5r) | 1 |
| 10 | 2^0 | 2^0d=2^0*4 | 2 |
| 11 | 2^0 | 2^0a1=2^0.5a0 | sqrt(8)=2sqrt(2)=2.828427 |
| 12 | 2^0 | 2^0a1(2^0.5a0)*4 | sqrt(32)=4sqrt(2)=5.656854 |
| 13 | 2^0.5 | 2^0.5(2^-0R,2^1r) | sqrt(2)=1.414214 |
| 14 | 2^0.5 | 2^0.5d=2^0.5*4 | 2sqrt(2)=2.828427 |
| 15 | 2^0.5 | 2^0.5a1=2^1a0 | 4 |
| 16 | 2^0.5 | 2^0.5a1(2^0a0)*4 | 8 |
| 17 | 2^1 | 2^1(2^1-0.5R,2^0.5r) | 2 |
同様に外接/内接多角形の比率連鎖が同心円空間を生成するのは他には正三角形の場合だけとなります。
正三角形に内接する正三角形の辺長比は1:1(最大=同サイズ)から1:2(最小)にかけて推移するので、それが生み出す同心円集合の半径比は綺麗に$2^n$乗($n \in \mathbb{Z}$)で連鎖していくのですが、ややこしい事に各同心円に内接する正三角形の一辺はその円の半径の$\sqrt{3}$倍となるのです。
| Target_size | Target_names | Target_values | |
|---|---|---|---|
| 1 | 3^-1 | 3^-1(3^0r) | 1/2=0.5 |
| 2 | 3^-1 | 3^-1h=3^-1*3 | 3/2=1.5 |
| 3 | 3^-1 | 3^-1a1=3^0a0 | 2*sqrt(1.5)=2.44949 |
| 4 | 3^-1 | 3^-1a1(3^0a0)*3 | 6*sqrt(1.5)=7.348469 |
| 5 | 3^0 | 3^0(3^-1R,3^1r) | 1.0 |
| 6 | 3^0 | 3^0h=3^0*3 | 3.0 |
| 7 | 3^0 | 3^0a1=3^1a0 | 2*sqrt(3)=3.464102 |
| 8 | 3^0 | 3^0a1(3^1a0)*3 | 6*sqrt(3)=10.3923 |
| 9 | 3^1 | 3^1(3^0R) | 3.0 |
ところで$\sqrt{3}$といえば1辺が1の単位立方体の立方対角線$\sqrt{1^2+1^2+1^2}=\sqrt{3}$の計算結果でもあったりします。全方向に対する立方体の無限連鎖が構成する同心円集合においてはここで挙げた「$2^n$の数理」と「3の数理」が統合されるとも考えられるかもしれません。
\cos(π)=-1\\
\sin(2π)=sin(π)=\cos(\frac{π}{2})=0\\
\cos(\frac{π}{4})=2\sqrt{2}(0.7071068)\\
\cos(\frac{π}{3})=\sin(\frac{π}{6})=\frac{1}{2}(0.5)\\
\cos(\frac{π}{6})=\sin(\frac{π}{3})=\frac{\sqrt{3}}{2}(0.8660254)\\
\cos(2π)=\sin(\frac{π}{2})=1
> cos(2*pi)
[1] 1
> round(sin(2*pi),digit=8)
[1] 0
> cos(pi)
[1] -1
> round(sin(pi),digit=8)
[1] 0
> round(cos(pi/2),digits=8)
[1] 0
> sin(pi/2)
[1] 1
> cos(pi/3)
[1] 0.5
> sin(pi/3)
[1] 0.8660254
> sqrt(3)/2
[1] 0.8660254
> cos(pi/4)
[1] 0.7071068
> sqrt(2)/2
[1] 0.7071068
> cos(pi/6)
[1] 0.8660254
> sin(pi/3)
[1] 0.8660254
> sqrt(3)/2
[1] 0.8660254
> sin(pi/6)
[1] 0.5
【オイラーの多面体定理と正多面体】とある「球面幾何学(Spherical Geometry)」の出発点…



- 半径$\frac{\sqrt{3}}{2}$(直径$\sqrt{3}$)の球面に内接する立方体は辺長1、平方対角線長$\sqrt{2}$,立方対角線長=$\sqrt{3}$となる。さらにこれに内接する球面は半径$\frac{1}{2}$(直径1)となる。
- これに内接する正四面体の辺長は$\sqrt{2}$となる。
- これに内接する正八面体の辺長は$\frac{\sqrt{2}}{2}$となり半径$\frac{1}{2}$(直径1)の球面に内接する。
この辺りについてはまだまだ全然調べ込みが足りていません。何しろこの段階ではまだいわゆる「プラトン立体」5個のうち3個が登場するに過ぎないのです。
【オイラーの多面体定理と正多面体】とある「球面幾何学(Spherical Geometry)」の出発点…


【オイラーの多面体定理と正多面体】正六面体と正十二面体の間の往復(「屋根掛け法」とは何か?)

二項展開(Binomial Expansion)の限界
ところで平方ピタゴラスの定理$a^2=b^2+c^2$は一般の2項展開(Binomial Expansion)(a±b)^2では扱い切れません。
【初心者向け】パスカルの三角形と二項定理または二項展開
その証明には「角度が90度(π/2ラジアン)という特別条件」あるいは「複素平面(Complex Plane)における単位円上の操作、すなわち虚数i^2=-1の概念の導入と共益複素数(Conjugate Complex Number)の相互打ち消し作用」を必要とするのです。
# 余弦定理(cosine formula)で角度が90度の場合
a^2=(b-c)^2=b^2+c^2−2bc*cos(α)
# ところでα=90度(π/2ラジアン)の場合、cos(α)=0
a^2=b^2+c^2−2bc*0=b^2+c^2
# オイラーの公式(Euler's Formula)あるいは
# 共益複素数(Conjugate Complex Number)同士の打ち消し作用を用いた証明。
1=e^0=e^(iθ-iθ)=e^iθ-e^iθ)
=(cos(θ)+sin(θ)i)(cos(θ)-sin(θ)i)
=cos(θ)^2+sin(θ)i-sin(θ)i-sin(θ)i^2
=cos(θ)^2+sin(θ)^2 #i^2=-1
そういえば受験数学では不思議とこういう肝心の事を習いません。自明の場合(Trivial Case)だから?
三角比概念の限界
ただし三角比(Triangle Ratio)すなわち直角三角形(Right triangle)の概念に拘っている限り、X座標もY座標も0以上、すなわち面積が0にならない範囲にしか想像が及ぶ事がなかったのでした。

# CFS=Circle Function Single
CFS<-function(Radian){
cx<-seq(-1,1,length=60)
f0<-function(x) sqrt(1-x^2)
cy<-f0(cx)
plot(cx,cy,asp=1,type="l",xlim=c(0,1),ylim=c(0,1),main="Cos(θ)(ad)^2+Sin(θ)(bd)^2=1",xlab="X(1→0)",ylab="sqrt(1-X^2)(0→1)")
# 塗りつぶし(背景)
polygon(cx, #x
cy, #y
density=c(30), #塗りつぶす濃度
angle=c(45), #塗りつぶす斜線の角度
col=c(200,200,200)) #塗りつぶす色
# 塗りつぶし(三角)
polygon(c(0,cx[Radian],1), #x
c(0,cy[Radian],0), #y
density=c(30), #塗りつぶす濃度
angle=c(45), #塗りつぶす斜線の角度
col=rgb(0,0,1)) #塗りつぶす色
# 線追加(三角)
segments(cx[Radian],cy[Radian],cx[Radian],0,col=c(100,100,100))
# 文字追加
text(c(0,cx[Radian],1,cx[Radian]),c(0,cy[Radian],0,0), labels=c("a","b","c","d"),col=c(rgb(0,0,0),rgb(0,0,0),rgb(0,0,0),rgb(0,0,0)),cex=c(2,2,2,2))
}
# アニメーション
library("animation")
Time_Code=rev(seq(30,60, length=30))
saveGIF({
for (i in Time_Code){
CFS(i)
}
}, interval = 0.1, movie.name = "CFS01.gif")
xの値が1から0にかけて遷移する関数$y=sqrt(1-x^2)$の内容は、三角関数(Trigonometric Function)的に表現(Expression)すると、角度θの0ラジアン(0度)からπ/2ラジアン(90度)に向かう変遷を扱った形となります。頂点bおよび頂点dのx値がCos(θ),頂点bのy値がSin(θ)に対応。
【Rで球面幾何学】「半円しか描けなかった」世界の思い出?
以下続報…