LoginSignup
0
0
@ochimusha01(yasunori matuki)

【数学溢れ話】【Token】パスカルの三角形と二項定理または二項展開

Last updated at Posted at 2020-03-06
  • 2020年03月06日 Rによる投稿
  • 2021年05月30日 Tex,python追記

吉田武「オイラーの贈物」の「基礎理論(Basic Theory)」における二項定理（binomial theorem）または二項展開 (binomial expansion)の解説はパスカルの三角形(Pascal's triangle)の説明を導入部とします。
20190607050700.png
これ以降の数字列はオンライン整数列大辞典の数列 A003590を参照。
#パスカルの三角形(Pascal's triangle)

二項式(Binomial)の冪の代数的な展開の記述によれば、この定理において冪_(x+y)^n_は_a ^x+b^y+c_の形の項の和に展開できるが、冪指数_b,c_は_b+c=n_を満たす非負整数で、各項の係数(coefficient)_a_はnとbに依存して決まる特定の正整数でなければならない。

パスカルの逆三角形（1,2,1）…ちなみに
$\frac{1}{(a+b)(a-b)}=\frac{1}{a^2-b^2}$

  1. $(a+b)^{-2}=\frac{1}{a^b+2ab+b^2}$
  2. $(a-b)^{-2}=\frac{1}{a^2-2ab+b^2}$

パスカルの逆三角形（1,1）

  1. $(a+b)^{-1}=\frac{1}{a+b}$
  2. $(a-b)^{-1}=\frac{1}{a-b}$

パスカルの三角形（1）…ちなみに
$\frac{a+b}{a-b}=\frac{a+b}{a-b}$

  1. $(a+b)^0=1\frac{a+b}{a+b}$
  2. $(a-b)^0=1\frac{a-b}{a-b}$

パスカルの三角形（1,1）１乗

  1. $(a+b)^1=a+b$
  2. $(a-b)^1=a-b$

パスカルの三角形（1,2,1）２乗…ちなみに
$(a+b)(a-b)=a^2-b^2$。
$5(1+2+1)-2(x±y)^2-2(x+y)(x-y)打消=1$?

  1. $(a+b)^2=a^2+2ab+b^2$
  2. $(a-b)^2=a^2-2ab+b^2$

パスカルの三角形（1,3,3,1）３乗…ちなみに
$(a+b)^2(a-b)=a^3+ab^2-b^2x-a^3b$、
$(a+b)(a-b)^2=a^3-ab^2-a^2y+y^3$。
$8(1+3+3+1)-2(x±y)^2-4(x+y)(x-y)打消=2$？

  1. $(a+b)^3=a^3+3ab^2+3ab^2+b^3$
  2. $(a-b)^3=a^3-3ab^2+3ab^2-b^3$

パスカルの三角形（1,4,6,4,1）４乗…ちなみに
$(x+y)(x-y)^3=x^4-2x^3y+2xy^3-y^4$、
$(x+y)^2(x-y)^2=x^4-2x^2y^2+y^4$、
$(x+y)^3(x-y)=x^4+2x^3y-2xy^3-y^4$。
$16(1,4,6,4,1)-2(x±y)^4-11(x+y)(x-y)打消=3$？

  1. $(a+b)^4=a^4+4a^3b+6a^2b^2+4a+b^3+b^4$
  2. $(a-b)^4=a^4-4a^3b+6a^2b^2-4ab^3+b^4$

パスカルの三角形（1,5,10,10,5,1）５乗…ちなみに
$(x+y)(x-y)^4=x^5-3x^4y+2x^3y^2+2x^2y^3-3xy^4+y^5$、
$(x+y)^2(x-y)^3=x^5-2x^4y+2x+x^3y^2+x^2y^3+x^4y-y^5$、
$(x+y)^3(x-y)^2=x^5-2x^4y-2x^3y^2-2x^2(y^3+xy^4+y^5)$、
$(x+y)^4(x-y)=x^5+3x^4y+2x^3y^2-2x^2y^3-3xy^4-y^5$。$22(1+5+10+10+5+1)-2(x±y)^3-16(x+y)(x-y)打消=4$?

  1. $(x+y)^5=x^5+5x^4y+10x^3y^2+10x^2y^3+5xy^4+y^5$
  2. $(x-y)^5=x^5-5x^4y+10x^3y^2-10x^2y^3+5xy^4-y^5$

パスカルの三角形（1,6,15,20,15,6,1）６乗…ちなみに
$(x+y)(x-y)^5=x^6-4 yx^5+5y^2x^4-5y^4x^2+4y^5x-b^6$、
$(x+y)^2(x-y)^4=x^6-2yx^5-y^2x^4+4y^3x^3-y^4x^2-2y^5x+y^6$、
$(x+y)^3(x-y)^3=x^6-3y^2x^4+3y^4x^2-y^6$、
$(x+y)^4(x-y)^2=x^6+2yx^5-y^2x^4-4y^3x^3-y^4x^2+2y^5x+y^6$、
$(x+y)^5(x-y)=x^6+4yx^5+5y^2x^4-5y^4x^2-4y^5x-y^6$、
$64(1+6+15+20+15+6+1)-2(x±y)^4-53(x+y)(x-y)打消=5？$

1.$(a+b)^6=a^6+6a^5b+15a^4b^2+20a^3b^3+15a^2b^4+6xb^5+y^6$
2.$(a-b)^6=a^6-6a^5b+15a^4b^2-20x^ab^3+15x^2y^4-6xy^5+y^6$

二項式$a^xb^yc$の項の係数aは二項係数、すなわち二項冪$(1+x)^n$の展開における$x^k$の項の係数であり、その値は適切な状況下で$\frac{n!}{k!(n-k)!}$によって与えられる。これら係数をnおよびbを動かして並べることでパスカルの三角形を描くことができる。また組合せ論においても現れ、n-元集合からb個の相異なる元を選ぶ組合せの総数を与える。
【初心者向け】階乗と順列と組み合わせ

Python で実装するパスカルの三角形

#出力例
[1]
[1, 1]
[1, 2, 1]
[1, 3, 3, 1]
[1, 4, 6, 4, 1]
[1, 5, 10, 10, 5, 1]
[1, 6, 15, 20, 15, 6, 1]

ここで興味深いのが、上掲の分析から浮かび上がってくる「符号付パスカルの三角形」

#出力例
[+1]
[+1, -1]
[+1, -2, +1]
[+1, -3, +3, -1]
[+1, -4, +6, -4, +1]
[+1, -5, +10, -10, +5, -1]
[+1, -6, +15, -20, +15, -6, +1]

また、以下の様な特徴も一つ一つ確かめていきたいと思います。

算術三角形の基本

算術三角形には面白い性質がたくさんある。

  • 一番端の列はすべて1である。1つ内側を見れば、自然数が小さい順に並んでいる。その内側は三角数と呼ばれるもので、正三角形の形に点を並べた時の点の総数である。また、1からある数までの和でもなる。その内側は四面体数と呼ばれる数が並ぶ。これもやはり四面体の形に端を並べた時の点の総数である。次の列は五胞体数が並ぶ。五胞体とは四次元図形の一種で、いうなれば四次元版三角形(四次元版四面体でもいい)である。
    三角数 - Wikipedia
    三角数とは，三角数定理，平方数との関係 | 高校数学の美しい物語
    三角錐数 - Wikipedia
    四角錐数 - Wikipedia
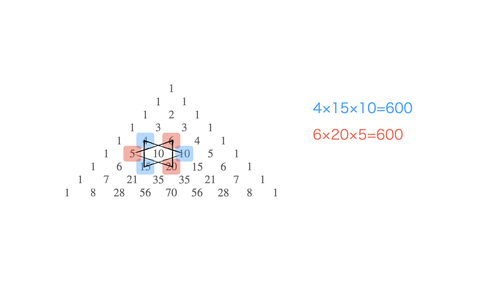
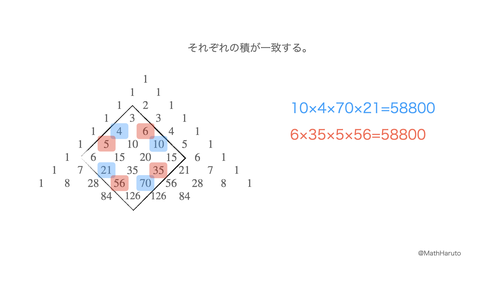
    五胞体数 - Wikipedia
  • 斜めに並んでいる数をたしてゆけば、その答えは最後の数の斜め下に現れることがわかる。例えば、下に太字で表した部分は1+3+6+10=20となっている。そのすぐ右下を見れば1+4+10+20=35である。確かめてみれば、ほかの部分でもそのようになることがわかる。
    image.png

異なるn個のものからr個のものを選ぶときの場合の数は${}_nC_r=\frac{n!}{r!(n-r)!}$であり、例えば、青、赤、黄、白、黒の5色から2色選ぶ方法は[青赤][青黄][青白][青黒][赤黄][赤白][赤黒][黄白][黄黒][白黒]の10通りで${}_5C_2=\frac{5!}{2!3!}=10$通りとなる。

  • 実は、算術三角形の各項はこの組み合わせの数に等しい。例えば、6段目は1, 6, 15, 20, 15, 6, 1となっていて、${}_6C_0=1$,${}_6C_1=6$,${}_6C_2=15$,${}_6C_3=20$,${}_6C_4=15$,${}_6C_5=6$,${}_6C_6=1$である。

なお${}_nC_r$については以下の式が成立する。

{}_{n+1}C_{r+1}={}_nC_{r+1}+{}_nC_r
  • 組み合わせの数のこの性質と算術三角形の作り方はきれいに一致し、端の数がすべて1であることから、算術三角形は下図のようにも書ける。
    image.png

パスカルの三角形の驚くべき対称性
image.png
image.png
パスカルの算術三角形論

ちなみにこれをそのままグラフ化しようとすると大変な事になります。

import networkx as nx

G = nx.DiGraph()
G.add_edge("0C0=1","1C0=1")
G.add_edge("0C0=1","1C1=1")
G.add_edge("1C0=1","2C0=1")
G.add_edge("1C0=1","2C1=2")
G.add_edge("1C1=1","2C1=2")
G.add_edge("1C1=1","2C2=2")
G.add_edge("2C0=1","3C0=1")
G.add_edge("2C0=1","3C1=3")
G.add_edge("2C1=2","3C1=3")
G.add_edge("2C1=2","3C2=3")
G.add_edge("2C2=1","3C2=3")
G.add_edge("2C2=1","3C3=1")
G.add_edge("3C0=1","4C0=1")
G.add_edge("3C0=1","4C1=4")
G.add_edge("3C1=3","4C1=4")
G.add_edge("3C1=3","4C2=6")
G.add_edge("3C2=3","4C2=6")
G.add_edge("3C2=3","4C3=4")
G.add_edge("3C3=3","4C3=4")
G.add_edge("3C3=3","4C4=1")
G.add_edge("4C0=1","5C0=1")
G.add_edge("4C0=1","5C1=5")
G.add_edge("4C1=4","5C1=5")
G.add_edge("4C1=4","5C2=10")
G.add_edge("4C2=6","5C2=10")
G.add_edge("4C2=6","5C3=10")
G.add_edge("4C3=4","5C3=10")
G.add_edge("4C3=4","5C4=5")
G.add_edge("4C4=1","5C4=5")
G.add_edge("4C4=1","5C5=1")
G.add_edge("5C0=1","6C0=1")
G.add_edge("5C0=1","6C1=6")
G.add_edge("5C1=5","6C1=6")
G.add_edge("5C1=5","6C2=15")
G.add_edge("5C2=10","6C2=15")
G.add_edge("5C2=10","6C3=20")
G.add_edge("5C3=10","6C3=20")
G.add_edge("5C3=10","6C4=15")
G.add_edge("5C4=5","6C4=15")
G.add_edge("5C4=5","6C5=6")
G.add_edge("5C5=1","6C5=6")
G.add_edge("5C5=1","6C6=1")

nx.nx_agraph.view_pygraphviz(G, prog='fdp')

tmpfk6h_wsu.png

【Python演算処理】階乗と順列と組み合わせ

import sympy as sp
n,r= sp.symbols('n,r')
comb=sp.binomial(n,r)

Ord=[0,1,2,3,4,5,6]
Num=[[0],[0,1],[0,1,2],[0,1,2,3],[0,1,2,3,4],[0,1,2,3,4,5],[0,1,2,3,4,5,6]]

sp.init_printing()

for ord in Ord:
    for num in Num[ord]:
        print("{}_"+str(ord)+"C_" + str(num)+"=" + str(comb.subs([(n,ord),(r,num)])))

{}_0C_0=1 \\
{}_1C_0=1,
{}_1C_1=1 \\
{}_2C_0=1,
{}_2C_1=2,
{}_2C_2=1 \\
{}_3C_0=1,
{}_3C_1=3,
{}_3C_2=3,
{}_3C_3=1 \\
{}_4C_0=1,
{}_4C_1=4,
{}_4C_2=6,
{}_4C_3=4,
{}_4C_4=1 \\
{}_5C_0=1,
{}_5C_1=5,
{}_5C_2=10,
{}_5C_3=10,
{}_5C_4=5,
{}_5C_5=1 \\
{}_6C_0=1,
{}_6C_1=6,
{}_6C_2=15,
{}_6C_3=20,
{}_6C_4=15,
{}_6C_5=6,
{}_6C_6=1

このグラフ図をどう扱うかも将来の課題の一つです。
Networkxで格子グラフを作ってみよう！(入門的内容)

#Rによる1年前のチャレンジ。

当時は自分のレベルが低くて十分な確認が取れませんでした。一応記録としては残しておきますが、読み飛ばしてしまって結構です。

##乗法公式Ⅰ(中学数学範囲)
$(x+a)(x+b)$と$(ax+b)(cx+d)$、$(a+b)^2$と$(a-b)^2$の解法は本質的に同じですが，両方覚えておいて機械的に計算できる方が若干早いとも。

統計言語Rにおける汎用計算機代数ソフトウェアYacasによる計算例

library(Ryacas)
yacas("Expand((2*x^2+x+3)*(2*x-3))")
expression(4 * x^3 - 4 * x^2 + 3 * x - 9)

pythonのsympyライブラリによる計算例

import sympy as sp
x,a,b= sp.symbols('x,a,b')
a=(2*x**2+x+3)*(2*x-3)
sp.init_printing()
display(a) 
print(sp.latex(a))
display(sp.expand(a))
print(sp.latex(a))
print(sp.latex(a)+"="+sp.latex(sp.expand(a)))

出力

\left(2 x - 3\right) \left(2 x^{2} + x + 3\right)=4 x^{3} - 4 x^{2} + 3 x - 9

##乗法公式Ⅱ(高校数学範囲)
統計言語Rにおける汎用計算機代数ソフトウェアYacasによる計算例

yacas("Expand((x+a)*(x+b))")
expression(x^2 + (a + b) * x + b * a)
yacas("Expand((a+b)*(a-b))")
expression(a^2 - b^2)
yacas("Expand((a+b)^2)")
expression(a^2 + 2 * (b * a) + b^2)
yacas("Expand((a-b)^2)")
expression(a^2 - 2 * (b * a) + b^2)
yacas("Expand((a*x+b)*(c*x+d))")
expression((c * x^2 + d * x) * a + (c * b * x + d * b)

pythonのsympyライブラリによる計算例

import sympy as sp
x,a,b= sp.symbols('x,a,b')
a=(x+a)*(x+b)
sp.init_printing()
display(a) 
print(sp.latex(a))
display(sp.expand(a))
print(sp.latex(a))
print(sp.latex(a)+"="+sp.latex(sp.expand(a)))

出力

\left(a + x\right) \left(b + x\right)=a b + a x + b x + x^{2}

import sympy as sp
x,a,b= sp.symbols('x,a,b')
a=(a+b)*(a-b)
sp.init_printing()
display(a) 
print(sp.latex(a))
display(sp.expand(a))
print(sp.latex(a))
print(sp.latex(a)+"="+sp.latex(sp.expand(a)))

出力

\left(a - b\right) \left(a + b\right)=a^{2} - b^{2}

import sympy as sp
x,a,b= sp.symbols('x,a,b')
a=(a+b)**2
sp.init_printing()
display(a) 
print(sp.latex(a))
display(sp.expand(a))
print(sp.latex(a))
print(sp.latex(a)+"="+sp.latex(sp.expand(a)))

出力

\left(a + b\right)^{2}=a^{2} + 2 a b + b^{2}

import sympy as sp
x,a,b= sp.symbols('x,a,b')
a=(a-b)**2
sp.init_printing()
display(a) 
print(sp.latex(a))
display(sp.expand(a))
print(sp.latex(a))
print(sp.latex(a)+"="+sp.latex(sp.expand(a)))

出力

\left(a - b\right)^{2}=a^{2} - 2 a b + b^{2}

import sympy as sp
x,a,b,c,d= sp.symbols('x,a,b,c,d')
a=(a*x+b)*(c*x+d)
sp.init_printing()
display(a) 
print(sp.latex(a))
display(sp.expand(a))
print(sp.latex(a))
print(sp.latex(a)+"="+sp.latex(sp.expand(a)))

出力

\left(a x + b\right) \left(c x + d\right)=a c x^{2} + a d x + b c x + b d

##大学受験レベルの乗法公式
二項定理で計算してもよいですが，4 乗の展開公式までは一瞬で言えるようにしておいた方がよいとされています。
統計言語Rにおける汎用計算機代数ソフトウェアYacasによる計算例

yacas("Expand((a+b)^3)")
expression(a^3 + 3 * (b * a^2) + 3 * (b^2 * a) + b^3)
yacas("Expand((a−b)^3)")
expression(a^3 - 3 * (b * a^2) + 3 * (b^2 * a) - b^3)
yacas("Expand((a+b)*(a^2-a*b+b^2))")
expression(a^3 + b^3)
yacas("Expand((a-b)*(a^2+a*b+b^2))")
expression(a^3 - b^3)
yacas("Expand((a+b+c)^2)")
expression(a^2 + (2 * b + 2 * c) * a + (b^2 + 2 * (c * b) + c^2))

pythonのsympyライブラリによる計算例

import sympy as sp
x,a,b,c,d= sp.symbols('x,a,b,c,d')
a=(a+b)**3
sp.init_printing()
display(a) 
print(sp.latex(a))
display(sp.expand(a))
print(sp.latex(a))
print(sp.latex(a)+"="+sp.latex(sp.expand(a)))

出力

\left(a + b\right)^{3}=a^{3} + 3 a^{2} b + 3 a b^{2} + b^{3}

import sympy as sp
x,a,b,c,d= sp.symbols('x,a,b,c,d')
a=(a-b)**3
sp.init_printing()
display(a) 
print(sp.latex(a))
display(sp.expand(a))
print(sp.latex(a))
print(sp.latex(a)+"="+sp.latex(sp.expand(a)))

出力

\left(a - b\right)^{3}=a^{3} - 3 a^{2} b + 3 a b^{2} - b^{3}

import sympy as sp
x,a,b,c,d= sp.symbols('x,a,b,c,d')
a=(a+b)*(a**2-a*b+b**2)
sp.init_printing()
display(a) 
print(sp.latex(a))
display(sp.expand(a))
print(sp.latex(a))
print(sp.latex(a)+"="+sp.latex(sp.expand(a)))

出力

\left(a + b\right) \left(a^{2} - a b + b^{2}\right)=a^{3} + b^{3}


import sympy as sp
x,a,b,c,d= sp.symbols('x,a,b,c,d')
a=(a-b)*(a**2+a*b+b**2)
sp.init_printing()
display(a) 
print(sp.latex(a))
display(sp.expand(a))
print(sp.latex(a))
print(sp.latex(a)+"="+sp.latex(sp.expand(a)))

出力

\left(a - b\right) \left(a^{2} + a b + b^{2}\right)=a^{3} - b^{3}

import sympy as sp
x,a,b,c,d= sp.symbols('x,a,b,c,d')
a=(a+b+c)**2
sp.init_printing()
display(a) 
print(sp.latex(a))
display(sp.expand(a))
print(sp.latex(a))
print(sp.latex(a)+"="+sp.latex(sp.expand(a)))

出力

\left(a + b + c\right)^{2}=a^{2} + 2 a b + 2 a c + b^{2} + 2 b c + c^{2}

統計言語Rにおける汎用計算機代数ソフトウェアYacasによる計算例

yacas("Expand((a+b)^4)")
expression(a^4 + 4 * (b * a^3) + 6 * (b^2 * a^2) + 4 * (b^3 * 
a) + b^4)
yacas("Expand((a-b)^4)")
expression(a^4 - 4 * (b * a^3) + 6 * (b^2 * a^2) - 4 * (b^3 * 
a) + b^4)

pythonのsympyライブラリによる計算例

import sympy as sp
x,a,b,c,d= sp.symbols('x,a,b,c,d')
a=(a+b)**4
sp.init_printing()
display(a) 
print(sp.latex(a))
display(sp.expand(a))
print(sp.latex(a))
print(sp.latex(a)+"="+sp.latex(sp.expand(a)))

出力

\left(a + b\right)^{4}=a^{4} + 4 a^{3} b + 6 a^{2} b^{2} + 4 a b^{3} + b^{4}

import sympy as sp
x,a,b,c,d= sp.symbols('x,a,b,c,d')
a=(a-b)**4
sp.init_printing()
display(a) 
print(sp.latex(a))
display(sp.expand(a))
print(sp.latex(a))
print(sp.latex(a)+"="+sp.latex(sp.expand(a)))

出力

\left(a - b\right)^{4}=a^{4} - 4 a^{3} b + 6 a^{2} b^{2} - 4 a b^{3} + b^{4}

##大学数学以上の世界?
逆を言えば、こうした世界において視野外となるのが以下。
統計言語Rにおける汎用計算機代数ソフトウェアYacasによる計算例

yacas("Expand((a+b)^-2)")
expression((a + b)^-2)
#数学的に無意味なので全く解いてくれないパスカルの逆三角形…
#指数規則的に1/(a^2+2*a*b+b^2)では？　
yacas("Expand((a-b)^-2)")
expression((a - b)^-2)
#数学的に無意味なので全く解いてくれないパスカルの逆三角形…
#指数規則的に1/(x^2-2*a*b+b^2)では？
yacas("Expand((a+b)^-1)")
expression((a + b)^-1)
#数学的に無意味なので全く解いてくれないパスカルの逆三角形…
#指数規則的に1/(a+b)では？　
yacas("Expand((a-b)^-1)")
expression((a - b)^-1)
#数学的に無意味なので全く解いてくれないパスカルの逆三角形…
#1/(a-b)では？
yacas("Expand((a+b)^0)")
expression(1)
#(a+b)/(a+b)=1
yacas("Expand((a-b)^0)")
expression(1)
#(a-b)/(a-b)=1
yacas("Expand((a+b)/(a-b))")
expression((a + b)/(a - b))

pythonのsympyライブラリによる計算例

import sympy as sp
x,a,b,c,d= sp.symbols('x,a,b,c,d')
a=(a+b)**-2
sp.init_printing()
display(a) 
print(sp.latex(a))
display(sp.expand(a))
print(sp.latex(a))
print(sp.latex(a)+"="+sp.latex(sp.expand(a)))

出力

\frac{1}{\left(a + b\right)^{2}}=\frac{1}{a^{2} + 2 a b + b^{2}}

import sympy as sp
x,a,b,c,d= sp.symbols('x,a,b,c,d')
a=(a-b)**-2
sp.init_printing()
display(a) 
print(sp.latex(a))
display(sp.expand(a))
print(sp.latex(a))
print(sp.latex(a)+"="+sp.latex(sp.expand(a)))

出力

\frac{1}{\left(a - b\right)^{2}}=\frac{1}{a^{2} - 2 a b + b^{2}}

import sympy as sp
x,a,b,c,d= sp.symbols('x,a,b,c,d')
a=(a+b)**-1
sp.init_printing()
display(a) 
print(sp.latex(a))
display(sp.expand(a))
print(sp.latex(a))
print(sp.latex(a)+"="+sp.latex(sp.expand(a)))

出力

\frac{1}{(a + b)^1}=\frac{1}{a + b}

import sympy as sp
x,a,b,c,d= sp.symbols('x,a,b,c,d')
a=(a+b)**0
sp.init_printing()
display(a) 
print(sp.latex(a))
display(sp.expand(a))
print(sp.latex(a))
print(sp.latex(a)+"="+sp.latex(sp.expand(a)))

出力

1=1

ちなみに参考。
Solve for a d=(a+b)/(a-b) | Mathway
統計言語Rにおける汎用計算機代数ソフトウェアYacasによる計算例

#(a+b)^1=a+b
yacas("Expand((a+b)^1)")
expression(a + b)
#(a-b)^1=a-b
yacas("Expand((a-b)^1)")
expression(a - b)

#二乗レベルにおける(x+y)と(x-y)の混在。係数なし。
yacas("Expand((a+b)*(a-b))")
expression(a^2 - b^2)

#三乗レベルにおける(x+y)と(x-y)の混在。係数(1,1)
yacas("Expand((x+y)^2*(x-y))")
expression(x^3 + x^2*y - x*y^2-y^3)
yacas("Expand((x+y)*(x-y)^2)")
expression(x^3 - y * x^2 - y^2 * x + y^3)

#四乗レベルにおける(x+y)と(x-y)の混在。係数(1,2,2,1)(2,2)
yacas("Expand((a+b)*(a-b)^3)")
expression(a^4 - 2 * (b * a^3) + 2 * (b^3 * a) - b^4)
yacas("Expand((a+b)^2*(a-b)^2)")
expression(a^4 - 2 * (b^2 * a^2) + b^4)
yacas("Expand((a+b)^3*(a-b))")
expression(a^4 + 2 * (b * a^3) - 2 * (b^3 * a) - b^4)

#五乗
yacas("Expand((a+b)^5)")
expression(a^5 + 5 * (b * a^4) + 10 * (b^2 * a^3) + 10 * (b^3 * 
a^2) + 5 * (b^4 * a) + b^5)
yacas("Expand((a-b)^5)")
expression(a^5 - 5 * (b * a^4) + 10 * (b^2 * a^3) - 10 * (b^3 * 
a^2) + 5 * (b^4 * a) - b^5)
#五乗レベルにおける(x+y)と(x-y)の混在。係数（3,2,2,3)(1,2,2,1)
yacas("Expand((a+b)*(a-b)^4)")
expression(a^5 - 3 * (b * a^4) + 2 * (b^2 * a^3) + 2 * (b^3 * 
a^2) - 3 * (b^4 * a) + b^5)
yacas("Expand((a+b)^2*(a-b)^3)")
expression(a^5 - b * a^4 - 2 * (b^2 * a^3) + 2 * (b^3 * a^2) + 
b^4 * a - b^5)
yacas("Expand((a+b)^3*(a-b)^2)")
expression(a^5 + b * a^4 - 2 * (b^2 * a^3) - 2 * (b^3 * a^2) + 
b^4 * a + b^5)
yacas("Expand((a+b)^4*(a-b)^1)")
expression(a^5 + 3 * (b * a^4) + 2 * (b^2 * a^3) - 2 * (b^3 * 
a^2) - 3 * (b^4 * a) - b^5)

#六乗
 yacas("Expand((a+b)^6)")
expression(a^6 + 6 * (b * a^5) + 15 * (b^2 * a^4) + 20 * (b^3 * 
a^3) + 15 * (b^4 * a^2) + 6 * (b^5 * a) + b^6)
yacas("Expand((a-b)^6)")
expression(a^6 - 6 * (b * a^5) + 15 * (b^2 * a^4) - 20 * (b^3 * 
a^3) + 15 * (b^4 * a^2) - 6 * (b^5 * a) + b^6)
#六乗レベルにおける(a+b)と(a-b)の混在。係数（4,5,5,4)(2,4,4,2)(3,3)
yacas("Expand((a+b)*(a-b)^5)")
expression(a^6 - 4 * (b * a^5) + 5 * (b^2 * a^4) - 5 * (b^4 * 
a^2) + 4 * (b^5 * a) - b^6)
yacas("Expand((a+b)^2*(a-b)^4)")
expression(a^6 - 2 * (b * a^5) - b^2 * a^4 + 4 * (b^3 * a^3) - 
b^4 * a^2 - 2 * (b^5 * a) + b^6)
yacas("Expand((a+b)^3*(a-b)^3)")
expression(a^6 - 3 * (b^2 * a^4) + 3 * (b^4 * a^2) - b^6)
yacas("Expand((a+b)^4*(a-b)^2)")
expression(a^6 + 2 * (b * a^5) - b^2 * a^4 - 4 * (b^3 * a^3) - 
b^4 * a^2 + 2 * (b^5 * a) + b^6)
yacas("Expand((a+b)^5*(a-b))")
expression(a^6 + 4 * (b * a^5) + 5 * (b^2 * a^4) - 5 * (b^4 * 
a^2) - 4 * (b^5 * a) - b^6)

#その他の重要公式
yacas("Expand((x+a)*(x+b)*(x+c))")
expression(x^3 + (a + (b + c)) * x^2 + ((b + c) * a + c * b) * 
x + c * b * a)
yacas("Expand((a+b+c)*(a^2+b^2+c^2−a*b−b*c−c*a))")。
#答えがa3+b3+c3−3abcとなる極めて重要な因数分解公式（3つの立方和）
#だがyacasは解かない。
yacas("Expand(a*(b^2-c^2)+b*(c^2-a^2)+c*(a^2-b^2))")
expression((c - b) * a^2 + (b^2 - c^2) * a + (c^2 * b - c * b^2))
#あれ？テストでは(a-b)*(b-c)*(c-a)が答えとして要求されるみたいだけど？

#そして乗法公式
yacas("Expand((a+b)*(b+c)*(c+a))")
expression((b + c) * a^2 + (b^2 + 2 * (c * b) + c^2) * a + (c * 
b^2 + c^2 * b))
yacas("Expand((a+b+c)^3)")
expression(a^3 + (3 * b + 3 * c) * a^2 + (3 * b^2 + 6 * (c * 
b) + 3 * c^2) * a + (b^3 + 3 * (c * b^2) + 3 * (c^2 * b) + 
c^3))

#1年後のPythonによる再チャレンジ。

改めて乗法公式の全体像を俯瞰するにあたって以下のサイトが役立ちました。
乗法公式（式の展開公式）19個まとめ

  • 全体としてパスカルの三角形に関わる$a^2+2ab+b^2$系の数理と因数分解に関わる$a^2+ab+b^2/a^n+b^n$系の数理に大別可能な様に見て取れます。

繰り返し現れる「ほぼ同じ公式」はすべて頻出の形です。それぞれ覚えておくことで機械的に計算することができます（展開のスピードが速くなります）。

この辺りの観点が実践的受験数学では重要となってくる様です。

import sympy as sp
x,a,b,c,d,n= sp.symbols('x,a,b,c,d,n')
y01=(x+a)*(x+b)
y02=(x+a)**2
y03=(x-a)**2
y04=(x-a)*(x+a)
y05=(a*x+b)*(b*x+d)
y06=(a+b)**3
y07=(a-b)**3
y08=(a+b)*(a**2-a*b+b**2)
y09=(a-b)*(a**2+a*b+b**2)
y10=(a+b+c)**2
y11=(a+b)**4
y12=(a-b)**4
y13=(a+b)**n
y14=a**n-b**n
y15=a**n+b**n
y16=(x+a)*(x+b)*(x+c)
y17=(a+b+c)*(a**2+b**2+c**2-a*b-b*c-c*a)
y18=(a+b)*(b+c)*(c+a)
y19=(a+b+c)**3
sp.init_printing()
display(y01) 
display(sp.expand(y01))
print(sp.latex(y01)+"="+sp.latex(sp.expand(y01)))
display(y02) 
display(sp.expand(y02))
print(sp.latex(y02)+"="+sp.latex(sp.expand(y02)))
display(y03) 
display(sp.expand(y03))
print(sp.latex(y03)+"="+sp.latex(sp.expand(y03)))
display(y04) 
display(sp.expand(y04))
print(sp.latex(y04)+"="+sp.latex(sp.expand(y04)))
display(y05) 
display(sp.expand(y05))
print(sp.latex(y05)+"="+sp.latex(sp.expand(y05)))
display(y06) 
display(sp.expand(y06))
print(sp.latex(y06)+"="+sp.latex(sp.expand(y06)))
display(y07) 
display(sp.expand(y07))
print(sp.latex(y07)+"="+sp.latex(sp.expand(y07)))
display(y08) 
display(sp.expand(y08))
print(sp.latex(y08)+"="+sp.latex(sp.expand(y08)))
display(y09) 
display(sp.expand(y09))
print(sp.latex(y09)+"="+sp.latex(sp.expand(y09)))
display(y10) 
display(sp.expand(y10))
print(sp.latex(y10)+"="+sp.latex(sp.expand(y10)))
display(y11) 
display(sp.expand(y11))
print(sp.latex(y11)+"="+sp.latex(sp.expand(y11)))
display(y12) 
display(sp.expand(y12))
print(sp.latex(y12)+"="+sp.latex(sp.expand(y12)))
display(y13) 
display(sp.expand(y13))
print(sp.latex(y13)+"="+sp.latex(sp.expand(y13)))
display(y14) 
display(sp.expand(y14))
print(sp.latex(y14)+"="+sp.latex(sp.expand(y14)))
display(y15) 
display(sp.expand(y15))
print(sp.latex(y15)+"="+sp.latex(sp.expand(y15)))
display(y16) 
display(sp.expand(y16))
print(sp.latex(y16)+"="+sp.latex(sp.expand(y16)))
display(y17) 
display(sp.expand(y17))
print(sp.latex(y17)+"="+sp.latex(sp.expand(y17)))
display(y18) 
display(sp.expand(y18))
print(sp.latex(y18)+"="+sp.latex(sp.expand(y18)))
display(y19) 
display(sp.expand(y19))
print(sp.latex(y19)+"="+sp.latex(sp.expand(y19)))

公式01$(x+a)(x+b)=x^{2}+(a+b)x+ab$

\left(a + x\right) \left(b + x\right)=a b + a x + b x + x^{2}
  • 上掲の「パスパルの三角形」には含まれない形。
  • Sympyはデフォルトでは公式通り整式してくれません。

公式02$(x+a)^2=x^2+2ax+a^2$

\left(a + x\right)^{2}=a^{2} + 2 a x + x^{2}

公式1でa=bとしたものです。

  • Sympyの整式はアルファベット順に遂行されてしまう様です。

公式03$(x+a)^2=x^2-2ax+a^2$

\left(- a + x\right)^{2}=a^{2} - 2 a x + x^{2}

公式2でa→−aとしたものです。

公式04$(x+a)(x−a)=x^2−a^2$

\left(- a + x\right) \left(a + x\right)=- a^{2} + x^{2}
  • 当該サイトでは 「和と差の展開公式」と呼ばれています。
  • ベクトルや複素数式で絶対値(距離)を求める式ですね。

公式05$(ax+b)(cx+d)=acx^2+(ad+bc)x+bd$

\left(a x + b\right) \left(b x + d\right)=a b x^{2} + a d x + b^{2} x + b d

丸覚えというより，分配法則を使って展開してもよいでしょう。式の展開は「それぞれのカッコの中身から1つずつ選んで掛け算、をすべて足し上げる」です。

ここまでが中学数学で習う乗法公式です。

  • Sympyはa,b,cを係数と認識するとこの様に処理する様です。

公式06$(a+b)^3=a^3+3a^2b+3ab^2+b^3$

\left(a + b\right)^{3}=a^{3} + 3 a^{2} b + 3 a b^{2} + b^{3}

重要な公式です。

  • Sympyではこの様にa,b,c系の項のみで表現可能な時はそうするのが吉の様です。

公式07$(a-b)^3=a^3-3a^2b+3ab^2-b^3$

\left(a - b\right)^{3}=a^{3} - 3 a^{2} b + 3 a b^{2} - b^{3}

重要な公式です。

公式08$(a+b)(a^2−ab+b^2)=a^3+b^3$

\left(a + b\right) \left(a^{2} - a b + b^{2}\right)=a^{3} + b^{3}

式を展開する公式というより，右辺を左辺に変形する（因数分解）公式として覚えておくとよいでしょう。

公式09$(a−b)(a^2+ab+b^2)=a^3−b^3$

\left(a - b\right) \left(a^{2} + a b + b^{2}\right)=a^{3} - b^{3}

これも式を展開する公式というより，右辺を左辺に変形する（因数分解）公式として覚えておくとよいでしょう。

ここまでが高校数学の教科書に乗っている公式です。すべての乗法公式は覚えなくても，気合いで（分配法則を使って）1つずつ展開すれば計算はできます。ですが，覚えていたほうが速く解けますし，計算による脳のエネルギー消費を節約することができます。

公式10$(a+b+c)^2=a^2+b^2+c^2+2ab+2bc+2ca$

\left(a + b + c\right)^{2}=a^{2} + 2 a b + 2 a c + b^{2} + 2 b c + c^{2}

これもよく使う公式です。2ab+2bc+2acというようにアルファベット順ではなく，2ab+2bc+2caというように循環するように書く方が美しいです。

ここまで高校数学で習います。覚えておくとよいでしょう。

  • 同じ人間として「美しく表現したい」という気持ちには共感しか感じ得ませんが、残念ながらSympyは人間ではないので、そういう風には整式してくれません。

公式11$(a+b)^4=a^4+4a^3b+6a^2b^2+4ab^3+b^4$

\left(a + b\right)^{4}=a^{4} + 4 a^{3} b + 6 a^{2} b^{2} + 4 a b^{3} + b^{4}

二項定理で計算すればよいのですが，受験生は4乗の展開公式までは一瞬で言えるようにしておいた方がよいでしょう。

公式12$\left(a - b\right)^{4}=a^{4} - 4 a^{3} b + 6 a^{2} b^{2} - 4 a b^{3} + b^{4}$

\left(a - b\right)^{4}=a^{4} - 4 a^{3} b + 6 a^{2} b^{2} - 4 a b^{3} + b^{4}

これも二項定理で計算すればよいのですが，受験生は4乗の展開公式までは一瞬で言えるようにしておいた方がよいでしょう。

公式13n乗の展開公式その1

 (a+b)^n=\displaystyle\sum_{k=0}^{n}{}_n\mathrm{C}_{k}a^kb^{n-k}

有名な二項定理です。
二項定理の意味と２通りの証明

この問題はSympyのexpand関数の手に余ります。

\left(a + b\right)^{n}=\left(a + b\right)^{n}

Sympy関数自体はこの公式をこう扱います。

import sympy as sp
a,b,r= sp.symbols('a,b,r')
k,n=sp.symbols('k,n', integer = True)
org=(a+b)**n
trg=sp.summation(sp.binomial(n,k)*a**(k)*b**(n-k),(k, 0, n) )
sp.init_printing()
display(org) 
display(trg)
print(sp.latex(org)+"="+sp.latex(trg))

\left(a + b\right)^{n}=b^{n} \left(\begin{cases} - a^{n + 1} b^{- n - 1} {\binom{n}{n + 1}} {{}_{2}F_{1}\left(\begin{matrix} 1, 1 \\ n + 2 \end{matrix}\middle| {\frac{a e^{i \pi}}{b}} \right)} + \left(\frac{a}{b} + 1\right)^{n} & \text{for}\: \left(n \leq -1 \wedge \left|{\frac{a}{b}}\right| < 1\right) \vee \left(\left|{\frac{a}{b}}\right| \leq 1 \wedge n > 0\right) \vee \left(n \leq 0 \wedge \left|{\frac{a}{b}}\right| \leq 1 \wedge n > -1 \wedge \frac{a}{b} \neq -1\right) \\\sum_{k=0}^{n} a^{k} b^{- k} {\binom{n}{k}} & \text{otherwise} \end{cases}\right)

例えばN=5と代入すると以下の様に動作します。

import sympy as sp
a,b,r= sp.symbols('a,b,r')
k,n=sp.symbols('k,n', integer = True)
org=(a+b)**n
trg=sp.summation(sp.binomial(n,k)*a**(k)*b**(n-k),(k, 0, n) )
sp.init_printing()
display(org.subs(n,5)) 
display(trg.subs(n,5))
print(sp.latex(org.subs(n,5))+"="+sp.latex(trg.subs(n,5)))

\left(a + b\right)^{5}=b^{5} \left(\begin{cases} \left(\frac{a}{b} + 1\right)^{5} & \text{for}\: \left|{\frac{a}{b}}\right| \leq 1 \\\sum_{k=0}^{5} a^{k} b^{- k} {\binom{5}{k}} & \text{otherwise} \end{cases}\right)

公式14n乗の展開公式その2

(a−b)(a^{n−1}+a^{n−2}b+⋯+ab^{n−2}+b^{n−1})=a^n−b^n

式の展開というよりも因数分解公式として使われることが多いです。
因数分解公式（n乗の差，和）

この問題もSympyのexpand関数の手に余ります。

a^{n} - b^{n}=a^{n} - b^{n}

Sympy関数自体はこの公式をこう扱います。

import sympy as sp
a,b,r= sp.symbols('a,b,r')
k,n=sp.symbols('k,n', integer = True)
org=(a-b)*sp.summation(sp.binomial(n-1,k)*a**(k)*b**(n-k-1),(k, 0, n-1) )
trg=a**n-b**n
sp.init_printing()
display(org) 
display(trg)
print(sp.latex(org)+"="+sp.latex(trg))

\frac{b^{n} \left(a - b\right) \left(\begin{cases} - a^{n} b^{- n} {\binom{n - 1}{n}} {{}_{2}F_{1}\left(\begin{matrix} 1, 1 \\ n + 1 \end{matrix}\middle| {\frac{a e^{i \pi}}{b}} \right)} + \left(\frac{a}{b} + 1\right)^{n - 1} & \text{for}\: \left(n - 1 \leq -1 \wedge \left|{\frac{a}{b}}\right| < 1\right) \vee \left(\left|{\frac{a}{b}}\right| \leq 1 \wedge n - 1 > 0\right) \vee \left(n - 1 \leq 0 \wedge \left|{\frac{a}{b}}\right| \leq 1 \wedge n - 1 > -1 \wedge \frac{a}{b} \neq -1\right) \\\sum_{k=0}^{n - 1} a^{k} b^{- k} {\binom{n - 1}{k}} & \text{otherwise} \end{cases}\right)}{b}=a^{n} - b^{n}

同じくN=5と代入すると以下の様に動作します。

import sympy as sp
a,b,r= sp.symbols('a,b,r')
k,n=sp.symbols('k,n', integer = True)
org=(a-b)*sp.summation(sp.binomial(n-1,k)*a**(k)*b**(n-k-1),(k, 0, n-1) )
trg=a**n-b**n
sp.init_printing()
display(org.subs(n,5)) 
display(trg.subs(n,5))
print(sp.latex(org.subs(n,5))+"="+sp.latex(trg.subs(n,5)))

b^{4} \left(a - b\right) \left(\begin{cases} \left(\frac{a}{b} + 1\right)^{4} & \text{for}\: \left|{\frac{a}{b}}\right| \leq 1 \\\sum_{k=0}^{4} a^{k} b^{- k} {\binom{4}{k}} & \text{otherwise} \end{cases}\right)=a^{5} - b^{5}

公式15n乗の展開公式その3

(a+b)(a^{n−1}-a^{n−2}b+⋯-ab^{n−2}+b^{n−1})=a^n+b^n

この問題も式の展開というよりも因数分解公式として使われることが多いです。
因数分解公式（n乗の差，和）

この問題もSympyのexpand関数の手に余ります。

a^{n} + b^{n}=a^{n} + b^{n}

Sympy関数自体はこの公式をこう扱います。

import sympy as sp
a,b,r= sp.symbols('a,b,r')
k,n=sp.symbols('k,n', integer = True)
org=(a+b)*sp.summation(sp.binomial(n-1,k)*a**(k)*b**(n-k-1),(k, 0, n-1) )
trg=a**n+b**n
sp.init_printing()
display(org) 
display(trg)
print(sp.latex(org)+"="+sp.latex(trg))

\frac{b^{n} \left(a + b\right) \left(\begin{cases} - a^{n} b^{- n} {\binom{n - 1}{n}} {{}_{2}F_{1}\left(\begin{matrix} 1, 1 \\ n + 1 \end{matrix}\middle| {\frac{a e^{i \pi}}{b}} \right)} + \left(\frac{a}{b} + 1\right)^{n - 1} & \text{for}\: \left(n - 1 \leq -1 \wedge \left|{\frac{a}{b}}\right| < 1\right) \vee \left(\left|{\frac{a}{b}}\right| \leq 1 \wedge n - 1 > 0\right) \vee \left(n - 1 \leq 0 \wedge \left|{\frac{a}{b}}\right| \leq 1 \wedge n - 1 > -1 \wedge \frac{a}{b} \neq -1\right) \\\sum_{k=0}^{n - 1} a^{k} b^{- k} {\binom{n - 1}{k}} & \text{otherwise} \end{cases}\right)}{b}=a^{n} + b^{n}

同じくN=5と代入すると以下の様に動作します。

import sympy as sp
a,b,r= sp.symbols('a,b,r')
k,n=sp.symbols('k,n', integer = True)
org=(a+b)*sp.summation(sp.binomial(n-1,k)*a**(k)*b**(n-k-1),(k, 0, n-1) )
trg=a**n+b**n
sp.init_printing()
display(org.subs(n,5)) 
display(trg.subs(n,5))
print(sp.latex(org.subs(n,5))+"="+sp.latex(trg.subs(n,5)))

b^{4} \left(a + b\right) \left(\begin{cases} \left(\frac{a}{b} + 1\right)^{4} & \text{for}\: \left|{\frac{a}{b}}\right| \leq 1 \\\sum_{k=0}^{4} a^{k} b^{- k} {\binom{4}{k}} & \text{otherwise} \end{cases}\right)=a^{5} + b^{5}

公式16$(x+a)(x+b)(x+c)=x^3+(a+b+c)x^2+(ab+bc+ca)x+abc$

\left(a + x\right) \left(b + x\right) \left(c + x\right)=a b c + a b x + a c x + a x^{2} + b c x + b x^{2} + c x^{2} + x^{3}

意味を考えればすぐ導けますが，試験中の脳の省エネのために覚えておいてもよいでしょう。

  • やはりSympyではa,b,c系の変数とx,y,z系の変数の位置がひっくり返ってしまいます。

公式17$(a+b+c)(a^2+b^2+c^2−ab−bc−ca)=a^3+b^3+c^3−3abc$

\left(a + b + c\right) \left(a^{2} - a b - a c + b^{2} - b c + c^{2}\right)=a^{3} - 3 a b c + b^{3} + c^{3}

\left(a + b\right) \left(a + c\right) \left(b + c\right)=a^{2} b + a^{2} c + a b^{2} + 2 a b c + a c^{2} + b^{2} c + b c^{2}

重要な公式です。因数分解公式（3つの立方和）としてもよく出現します。
因数分解公式（3つの立方和）

公式18$(a+b)(b+c)(c+a)=a^2b+ab^2+b^2c+bc^2+c^2a+ca^2+2abc$

式の対称性と係数の和が8になることから瞬時に導けます。展開公式を丸ごと覚えるのではなく，導けるようにしましょう。

  • やはりSympyではa,b,c系の変数とx,y,z系の変数の位置がひっくり返ってしまいます。

公式19$(a+b+c)^3=a^3+b^3+c^3+3(a^2b+ab^2+b^2c+bc^2+c^2a+ca^2)+6abc$

\left(a + b + c\right)^{3}=a^{3} + 3 a^{2} b + 3 a^{2} c + 3 a b^{2} + 6 a b c + 3 a c^{2} + b^{3} + 3 b^{2} c + 3 b c^{2} + c^{3}

やはり同様に式の対称性と多項定理から一瞬で導けます。このように対称式の展開は「対称性，多項定理，係数の和」に注目 して瞬時に行えるようになっておくのが理想です。
対称式の展開は「対称性，多項定理，係数の和」に注目

そして全体としての総論

繰り返しになりますが，乗法公式なんてなくても気合いがあればどんな式も展開できます。だから公式を万一忘れてもビビる必要はありません。しかし，式の展開などのしょうもない部分で脳のエネルギーを無駄に使うと大事なところで集中力が切れてしまうので公式の暗記も大事です。

pythonのsympyライブラリによる計算例

出力…0乗レベルにおける(a+b)と(a-b)の混在。現れる係数

  • (1)
import sympy as sp
x,a,b,c,d= sp.symbols('x,a,b,c,d')
a=(a+b)**0
sp.init_printing()
display(a) 
print(sp.latex(a))
display(sp.expand(a))
print(sp.latex(a))
print(sp.latex(a)+"="+sp.latex(sp.expand(a)))

出力

1=1

出力…一乗レベルにおける(a+b)と(a-b)の混在。現れる係数

  • (1,1)
  • (1,-1)
import sympy as sp
a,b,c,d= sp.symbols('a,b,c,d')
x=(a+b)**1
y=(a-b)**1
sp.init_printing()
display(x) 
display(sp.expand(x))
print(sp.latex(x)+"="+sp.latex(sp.expand(x)))
display(y) 
display(sp.expand(y))
print(sp.latex(y)+"="+sp.latex(sp.expand(y)))

a + b=a + b

a - b=a - b

出力…二乗レベルにおける(a+b)と(a-b)の混在。現れる係数

  • (1,2,1)
  • (1,-2,1)
  • (1,1)
import sympy as sp
x,a,b,c,d= sp.symbols('x,a,b,c,d')
a=(a+b)*(a-b)
sp.init_printing()
display(a) 
print(sp.latex(a))
display(sp.expand(a))
print(sp.latex(a))
print(sp.latex(a)+"="+sp.latex(sp.expand(a)))

\left(a + b\right)^{2}=a^{2} + 2 a b + b^{2}

\left(a - b\right)^{2}=a^{2} - 2 a b + b^{2}

\left(a - b\right) \left(a + b\right)=a^{2} - b^{2}

出力…三乗レベルにおける(a+b)と(a-b)の混在。現れる係数

  • (1,4,6,4,1)
  • (1,-4,6,-4,1)
  • (1,1,-1,-1)
  • (1,-1,-1,1)
import sympy as sp
a,b,c,d= sp.symbols('a,b,c,d')
x=(a+b)**2*(a-b)
y=(a+b)*(a-b)**2
sp.init_printing()
display(x) 
display(sp.expand(x))
print(sp.latex(x)+"="+sp.latex(sp.expand(x)))
display(y) 
display(sp.expand(y))
print(sp.latex(y)+"="+sp.latex(sp.expand(y)))

\left(a - b\right) \left(a + b\right)^{2}=a^{3} + a^{2} b - a b^{2} - b^{3}

\left(a - b\right)^{2} \left(a + b\right)=a^{3} - a^{2} b - a b^{2} + b^{3}

出力…四乗レベルにおける(a+b)と(a-b)の混在。現れる係数

  • (1,4,6,4,1)
  • (1,-4,6,-4,1)
  • (1,-2,2,1)
  • (1,2,-2,1)
  • (1,-2,1)
import sympy as sp
a,b,c,d= sp.symbols('a,b,c,d')
s=(a+b)**4
t=(a-b)**4
x=(a+b)*(a-b)**3
y=(a+b)**2*(a-b)**2
z=(a+b)**3*(a-b)
sp.init_printing()
display(s) 
display(sp.expand(s))
print(sp.latex(s)+"="+sp.latex(sp.expand(s)))
display(t) 
display(sp.expand(t))
print(sp.latex(t)+"="+sp.latex(sp.expand(t)))
display(x) 
display(sp.expand(x))
print(sp.latex(x)+"="+sp.latex(sp.expand(x)))
display(y) 
display(sp.expand(y))
print(sp.latex(y)+"="+sp.latex(sp.expand(y)))
display(z) 
display(sp.expand(z))
print(sp.latex(z)+"="+sp.latex(sp.expand(z)))

\left(a + b\right)^{4}=a^{4} + 4 a^{3} b + 6 a^{2} b^{2} + 4 a b^{3} + b^{4}

\left(a - b\right)^{4}=a^{4} - 4 a^{3} b + 6 a^{2} b^{2} - 4 a b^{3} + b^{4}

\left(a - b\right)^{3} \left(a + b\right)=a^{4} - 2 a^{3} b + 2 a b^{3} - b^{4}

\left(a - b\right)^{2} \left(a + b\right)^{2}=a^{4} - 2 a^{2} b^{2} + b^{4}

\left(a - b\right) \left(a + b\right)^{3}=a^{4} + 2 a^{3} b - 2 a b^{3} - b^{4}

出力…五乗レベルにおける(a+b)と(a-b)の混在。現れる係数

  • (1,5,10,10,5,1)
  • (1,-5,10,-10,5,-1)
  • (1,-3,2,2,-3,1)
  • (1,1,-2,-2,1,1)
  • (1,-1,2,-2,1,-1)
import sympy as sp
a,b,c,d= sp.symbols('a,b,c,d')
s=(a+b)**5
t=(a-b)**5
v=(a+b)*(a-b)**4
x=(a+b)**3*(a-b)**2
y=(a+b)**2*(a-b)**3
z=(a+b)*(a-b)**4
sp.init_printing()
display(s) 
display(sp.expand(s))
print(sp.latex(s)+"="+sp.latex(sp.expand(s)))
display(t) 
display(sp.expand(t))
print(sp.latex(t)+"="+sp.latex(sp.expand(t)))
display(v) 
display(sp.expand(v))
print(sp.latex(v)+"="+sp.latex(sp.expand(v)))
display(x) 
display(sp.expand(x))
print(sp.latex(x)+"="+sp.latex(sp.expand(x)))
display(y) 
display(sp.expand(y))
print(sp.latex(y)+"="+sp.latex(sp.expand(y)))
display(z) 
display(sp.expand(z))
print(sp.latex(z)+"="+sp.latex(sp.expand(z)))

\left(a + b\right)^{5}=a^{5} + 5 a^{4} b + 10 a^{3} b^{2} + 10 a^{2} b^{3} + 5 a b^{4} + b^{5}

\left(a - b\right)^{5}=a^{5} - 5 a^{4} b + 10 a^{3} b^{2} - 10 a^{2} b^{3} + 5 a b^{4} - b^{5}

\left(a - b\right)^{4} \left(a + b\right)=a^{5} - 3 a^{4} b + 2 a^{3} b^{2} + 2 a^{2} b^{3} - 3 a b^{4} + b^{5}

\left(a - b\right)^{2} \left(a + b\right)^{3}=a^{5} + a^{4} b - 2 a^{3} b^{2} - 2 a^{2} b^{3} + a b^{4} + b^{5}

\left(a - b\right)^{3} \left(a + b\right)^{2}=a^{5} - a^{4} b - 2 a^{3} b^{2} + 2 a^{2} b^{3} + a b^{4} - b^{5}

\left(a - b\right)^{4} \left(a + b\right)=a^{5} - 3 a^{4} b + 2 a^{3} b^{2} + 2 a^{2} b^{3} - 3 a b^{4} + b^{5}

六乗レベルにおける(a+b)と(a-b)の混在。現れる係数

  • (1,6,15,20,15,6,1)
  • (1,-6,15,-20,15,-6,1)
  • （1,4,5,-5,-4,-1)
  • （1,-4,5,-5,4,-1)
  • (1,2,-1,-4,1,2,2)
  • (1,-2,-1,4,-1,-2,2)
  • (1,-3,3,-1)
import sympy as sp
a,b,c,d= sp.symbols('a,b,c,d')
s=(a+b)**6
t=(a-b)**6
v=(a+b)**5*(a-b)
w=(a+b)**4*(a-b)**2
x=(a+b)**3*(a-b)**3
y=(a+b)**2*(a-b)**4
z=(a+b)*(a-b)**5
sp.init_printing()
display(s) 
display(sp.expand(s))
print(sp.latex(s)+"="+sp.latex(sp.expand(s)))
display(t) 
display(sp.expand(t))
print(sp.latex(t)+"="+sp.latex(sp.expand(t)))
display(v) 
display(sp.expand(v))
print(sp.latex(v)+"="+sp.latex(sp.expand(v)))
display(w) 
display(sp.expand(w))
print(sp.latex(w)+"="+sp.latex(sp.expand(w)))
display(x) 
display(sp.expand(x))
print(sp.latex(x)+"="+sp.latex(sp.expand(x)))
display(y) 
display(sp.expand(y))
print(sp.latex(y)+"="+sp.latex(sp.expand(y)))
display(z) 
display(sp.expand(z))
print(sp.latex(z)+"="+sp.latex(sp.expand(z)))

\left(a + b\right)^{6}=a^{6} + 6 a^{5} b + 15 a^{4} b^{2} + 20 a^{3} b^{3} + 15 a^{2} b^{4} + 6 a b^{5} + b^{6}

\left(a - b\right)^{6}=a^{6} - 6 a^{5} b + 15 a^{4} b^{2} - 20 a^{3} b^{3} + 15 a^{2} b^{4} - 6 a b^{5} + b^{6}

\left(a - b\right) \left(a + b\right)^{5}=a^{6} + 4 a^{5} b + 5 a^{4} b^{2} - 5 a^{2} b^{4} - 4 a b^{5} - b^{6}

\left(a - b\right)^{2} \left(a + b\right)^{4}=a^{6} + 2 a^{5} b - a^{4} b^{2} - 4 a^{3} b^{3} - a^{2} b^{4} + 2 a b^{5} + b^{6}

\left(a - b\right)^{3} \left(a + b\right)^{3}=a^{6} - 3 a^{4} b^{2} + 3 a^{2} b^{4} - b^{6}

\left(a - b\right)^{4} \left(a + b\right)^{2}=a^{6} - 2 a^{5} b - a^{4} b^{2} + 4 a^{3} b^{3} - a^{2} b^{4} - 2 a b^{5} + b^{6}

\left(a - b\right)^{5} \left(a + b\right)=a^{6} - 4 a^{5} b + 5 a^{4} b^{2} - 5 a^{2} b^{4} + 4 a b^{5} - b^{6}

そんな感じで以下続報…

0
0
0

Register as a new user and use Qiita more conveniently

  1. You get articles that match your needs
  2. You can efficiently read back useful information
  3. You can use dark theme
What you can do with signing up
Sign upLogin
0
0