- (2020.3.6)Rの場合を作成。
- (2021.3.4)以下を参考にpythonの場合を追記。
Pythonで階乗、順列・組み合わせを計算、生成
Pythonで複数のリストの直積(デカルト積)を生成するitertools.product
Pythonでタプルやリストをアンパック(複数の変数に展開して代入)
階乗(factorial)と順列(sequence without repetition)の組み合わせ(combination, choose)こそが組合せ爆発(Combinatorial explosion)なる概念の大源流だったりします。
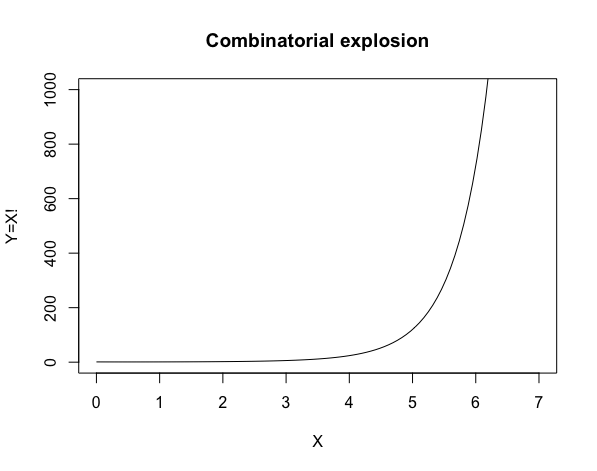
f0<-function(x){factorial(x)}
#グラフのスケール決定
gs_x<-c(0,7)
gs_y<-c(0,1000)
#タイトル定義
Main_title<-c("Combinatorial explosion")
x_title<-c("X")
y_title<-c("Y=X!")
#グラフ描画
plot(f0,xlim=gs_x,ylim=gs_y,type="l", main=Main_title,xlab=x_title,ylab=y_title)
例えばパスカルの三角形(Pascal's triangle)を描く二項定理(binomial theorem)または二項展開(binomial expansion)と縁深かったりします。
【初心者向け】パスカルの三角形と二項定理または二項展開
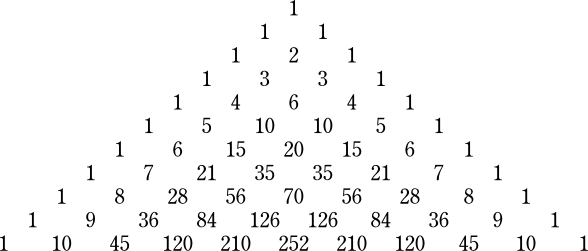
またマクローリン展開(McLaughlin expansion)などでも使われます。
【Rで球面幾何学】オイラーの公式を導出したマクローリン級数

階乗(factorial)
N!。組み合わせの数やポアソン分布など、確率にまつわる様々な場面で登場する数。数学において非負整数nのそれは1からnまでのすべての整数の積と定義されている。ちなみに0!=1。
ガンマ関数・ポリガンマ関数
①整数nについて階乗n!は再帰表現を用いると以下の様に定義される。
n! = \left\{
\begin{array}{ll}
1 & (n = 0) \\
n(n-1)!, & (n < 1)
\end{array}
\right.
②微分に関する「冪の法則」を用いると以下の様に定義される。
n! = \frac{d^n}{dx^n}x^n (n \geq 1)
③nを実部が正となる複素数zにまで拡大定義した連続関数をガンマ関数と呼ぶ。
ガンマ関数 - EMANの統計力学 - EMANの物理学
\Gamma (z)=\int_{0}^{\infty}e^{-t}t^{z-1}dt
④zが整数nであるとき、ガンマ関数と階乗の間には次のような関係がある。
\Gamma (n+1)=n!
⑤zが非整数であっても、Γ(z)は以下の公式によって再帰計算出来る。
\Gamma (z+1)=z \Gamma (z)
⑥また、z=1/2におけるガンマ関数の値を(1)によって計算すると以下となる。
\Gamma (\frac{1}{2} ± 0)= \sqrt{\pi}
⑥すなわち半整数値におけるガンマ関数の値は以下となる。
n次元球の体積 - EMANの統計力学 - EMANの物理学
\Gamma (\frac{1}{2}+n)= \frac{(2n-1)!!}{2^n} \sqrt{\pi}
Rの場合
library(Ryacas)
#統計言語Rでの汎用計算機代数ソフトウェアYacasによる計算例
1*2*3*4*5
[1] 120
yacas("5!")
expression(120)
#Rではガンマ関数を使ってn! = gamma(n+1)と計算する。
#さらに同じ計算をするfactorial(n)も追加された。
n<-5
gamma(n+1)
[1] 120
factorial(n)
[1] 120
#大きな数の階乗を求めようとするとエラーが出る。Rでは階乗を計算するときに、
#Γ函数と呼ばれる函数を用いているのだが、このエラーは、あまりにも数が
#大きすぎて函数の計算範囲を超えていることを示している。
factorial(171)
[1] Inf
警告メッセージ:
factorial(171) で: 'gammafn' 中の値が範囲を超えています
#yacasもほぼ同じ反応だが警告なし。
yacas("171!")
expression(Inf)
#半整数の処理
> gamma(1/2)
[1] 1.772454
> sqrt(pi)
[1] 1.772454
> gamma(1.5)
[1] 0.8862269
> gamma(gamma(1+1)+1)/2*sqrt(pi)
[1] 0.8862269
> f0=function(x) gamma(gamma(2*x-1+1)+1)/(2)^x*sqrt(pi)
> f0(1)
[1] 0.8862269
> gamma(1/2)/2
[1] 0.8862269
pythonの場合
Python の標準ライブラリに含まれるmathモジュールには、zを実数xに限定してガンマ関数を計算する math.gamma() が用意されている。またSciPyパッケージには、「解析接続」とよばれる手法によって全複素数で定義されたガンマ関数を計算するscipy.special.gamma()が用意されている。
math.gamma(x) は正数 x におけるガンマ関数の値を計算する。
# GAMMA_01
import math as m
# Γ(1) = 1!
a = m.gamma(1)
# Γ(4) = 3!
b = m.gamma(4)
# Γ(1.5)
c = m.gamma(171)
print("Γ(1) = {}".format(a))
print("Γ(4) = {}".format(b))
print("Γ(171) = {:.3f}".format(c))
#出力結果
Γ(1) = 1.0
Γ(4) = 6.0
Γ(171) = 7257415615307997787600216093189238323595021061314569179876657528238583563491351147216912252175700986809369474963925369318685576108176561526316564857418094571740407552112273986122786608722724826748926751468485581477832386714387957157022611153528941730324732959325152674587687275857562119239474180415666782208.000
math.gamma(x)による半整数の処理。
# GAMMA_02
import math as m
# Γ(1/2) = √π
a = m.gamma(1/2)
b = m.sqrt(m.pi)
# Γ(1/2+n)=Γ(Γ(2n-1)+1)/2^n*√π
c = m.gamma(1.5)
def f0(x):
return m.gamma(m.gamma((2*x-1)+1)+1)/2**x*m.sqrt(m.pi)
d=f0(1)
e=m.gamma(1/2)/2
print("Γ(0.5) = {:.3f}".format(a))
print("√π = {:.3f}".format(b))
print("Γ(1.5) = {:.3f}".format(c))
print("Γ(Γ((2*1-1)+1)+1)/2^1*√π = {:.3f}".format(d))
print("Γ(1/2)/2 = {:.3f}".format(e))
#出力結果
Γ(0.5) = 1.772
√π = 1.772
Γ(1.5) = 0.886
Γ(Γ((2*1-1)+1)+1)/2^1*√π = 0.886
Γ(1/2)/2 = 0.886
n!に直接対応するのはmath.factorial()関数であるが、こちらは整数の階乗しか求められない。
# Factorial_01
import math as m
# Γ(1) = 1!
a = m.factorial(1)
# Γ(4) = 3!
b = m.factorial(4)
# Γ(4) = 171!
c = m.factorial(171)
print("1! = {}".format(a))
print("4! = {}".format(b))
print("171! = {}".format(c))
#出力結果
1! = 1
4! = 24
171! = 1241018070217667823424840524103103992616605577501693185388951803611996075221691752992751978120487585576464959501670387052809889858690710767331242032218484364310473577889968548278290754541561964852153468318044293239598173696899657235903947616152278558180061176365108428800000000000000000000000000000000000000000
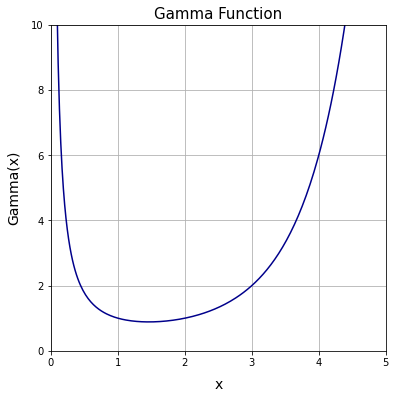
Matplotlib を使って、ガンマ関数をグラフに描いてみる。ただし、NumPyにはガンマ関数を計算する関数が用意されていないので、frompyfunc()を使って、math.gamma()をcに変換しておく。
NumPyの主なユニバーサル関数
# GAMMA_03
import math as m
import numpy as np
import matplotlib.pyplot as plt
# x座標データを作成
x = np.linspace(0.01, 5, 257)
# math.gamma()をユニバーサル化
gamma_u = np.frompyfunc(m.gamma, 1, 1)
# y座標データを作成
y = gamma_u(x)
# ガンマ関数のグラフを描画
fig = plt.figure(figsize = (6, 6))
ax = fig.add_subplot(111)
ax.set_title("Gamma Function", size = 15)
ax.grid()
ax.set_xlim(0, 5)
ax.set_ylim(0, 10)
ax.set_xlabel("x", size = 14, labelpad = 10)
ax.set_ylabel("Gamma(x)", size = 14, labelpad = 10)
ax.plot(x, y, color = "darkblue")
scipy.special.gamma(z)は任意の複素数zを受け取って、ガンマ関数の値を返す。
# # GAMMA_04-1
import numpy as np
from scipy.special import gamma
# [Γ(-2.5) Γ(1) Γ(2+3i)]
a = gamma([-2.5, 1, 2 + 3j])
a = np.round(a, 3)
print(a)
出力結果
[-0.945-0.j 1. +0.j -0.082+0.092j]
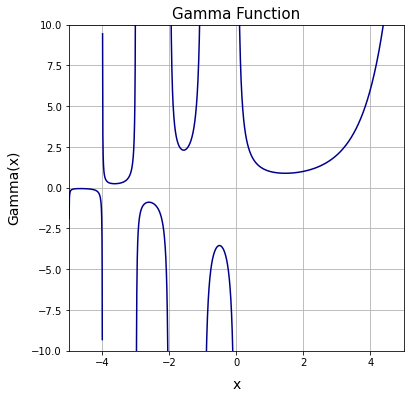
Matplotlib を使って、全実数領域におけるガンマ関数の値をグラフにプロットしてみる。
# GAMMA_04-2
import numpy as np
import matplotlib.pyplot as plt
# x座標データを作成
x = np.linspace(-5, 5, 2251)
# y座標データを作成
y = gamma(x)
# ガンマ関数のグラフを描画
fig = plt.figure(figsize = (6, 6))
ax = fig.add_subplot(111)
ax.set_title("Gamma Function", size = 15)
ax.grid()
ax.set_xlim(-5, 5)
ax.set_ylim(-10, 10)
ax.set_xlabel("x", size = 14, labelpad = 10)
ax.set_ylabel("Gamma(x)", size = 14, labelpad = 10)
ax.plot(x, y, color = "darkblue")
plt.show()
ここで興味深いのがgamma(1)とgamma(2)の返り値は共に1なので勾配0と思いきや中間点gamma(1.5)の値は$\sqrt{\pi}$(0.8862269)で、これが最低値である辺り。
ガンマ関数(階乗の一般化)の定義と性質
そう、Γ関数はガウス積分と表裏一体の関係にあるのです。
\int_{-\infty}^{\infty}e^{-ax^2}dx=\sqrt{\frac{\pi}{a}}(a>0)
a=1と置いた場合
\int_{-\infty}^{\infty}e^{-x^2}dx=\sqrt{\pi}
$\Gamma(\frac{1}{2})=\sqrt{\pi}$の証明。まずは元式。
\int_{0}^{\infty}t^{\frac{1}{2}}e^{-t}dt
ここで$t=u^2$と置く。
\int_{0}^{\infty}u^{-1}e^{-u^2}2udu\\
=2\int_{0}^{\infty}e^{-u^2}du\\
=\sqrt{\pi}
以前から循環照明の様な気がしてるのだけど気のせい?
N次元球の表面積と体積の求め方。
上で触れたガンマ関数の応用例。これも$\sqrt{\pi}$すなわちガウス積分がらみ。
【初心者向け】半径・直径・円周長・円の面積・球の表面積・球の体積の計算上の往復
{\int U(x,y,z)dV=\int_{0}^{2π}\int_{0}^{π}\int_{0}^{1}U(r,θ,φ)r^2\sinθdrdθdφ\\ =\int_{0}^{2π}\int_{0}^{π}\int_{0}^{1}\begin{vmatrix} \frac{∂x}{∂r} & \frac{∂x}{∂θ} & \frac{∂x}{∂φ}\\ \frac{∂y}{∂r} & \frac{∂y}{∂θ} & \frac{∂y}{∂φ}\\ \frac{∂z}{∂r} & \frac{∂z}{∂θ} & \frac{∂z}{∂φ} \end{vmatrix} drdθdφ }
極座標系(r,φ,θ,…)積分範囲の積み重ね方に注目すると以下となってます。
- まずは角度φ=0→2πφ=0→2πの範囲で積分して円周2πrに到達。
- さらに角度θ=0→πθ=0→πの範囲で積分を重ね**球の表面積****$4πr^2$に到達。
- さらに半径r=0→1r=0→1の範囲で積分を重ね球の体積$\frac{4}{3}πr^3$に到達。
垂直角θ(0~πラジアンのπ範囲)を水平角φ(-πラジアン~0~+πラジアンの2π範囲)の半分に取るのが特徴で、地球儀上で緯度(±90度)の概念が経度(±180度)で表されるのも同じ数理に基づきます。
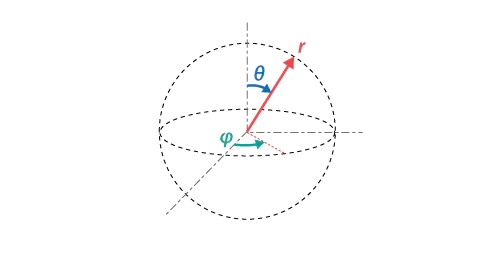
二次元空間(円弧)におけるデカルト座標系(x,y)と極座標系(r,φ)の相互変換
- 原点(0,0)からの距離$r=\sqrt{x^2+y^2}$
- $φ(-π \rightleftharpoons +π)=-(\arctan^2(x,y)-\frac{π}{2})$
- $x=r×\cos(φ)$
- $y=r×\sin(φ)$
三次元空間(球面)におけるデカルト座標系(x,y,z)と極座標系(r,φ,θ)の相互変換
- 原点(0,0,0)からの距離$r=\sqrt{x^2+y^2+z^2}$
- $φ(-π \rightleftharpoons +π)=-(\arctan^2(x,y)-\frac{π}{2})$
- $θ(-\frac{π}{2} \rightleftharpoons +\frac{π}{2})=-(\arctan^2(\sqrt{x^2+y^2+z^2},z)-\frac{π}{2})$
- $x=r×\sin(θ)\cos(φ)$
- $y=r×\sin(θ)\sin(φ)$
- $z=r×\cos(θ)$
Z軸の座標の取り方についてさりげなく単振動系(Simple Vibration System)$Z_n(n=-1 \rightleftharpoons +1)or(n= 0 \rightleftharpoons 2 )$と三角関数系(Trigonometric Function System)を使い分けてますね。
Γ関数を用いた考え方の統合
①まず$C_n$を以下と置く。導出過程は以下。
【Token】半径・直径・円周長・円の面積・球の表面積・球の体積の計算上の往復
c_n = \frac{\pi^{\frac{n}{2}}}{\Gamma(\frac{n}{2}+1)}
②この場合の半径rのn次元球の体積は$c_n r^n$、表面積は$n c_nr^{n−1}$となる。
- 1次元球(n=1)座標系において$C_n=\frac{\pi^{\frac{1}{2}}}{\Gamma(\frac{1}{2}+1)}=2$。従ってその「体積(直径)」は2r。
- 2次元球(n=2)座標系において$C_n=\frac{\pi^{\frac{2}{2}}}{\Gamma(\frac{2}{2}+1)}=\pi$。従ってその「体積(面積)」は$\pi r^2$、「表面積(円周長)」は$2 \pi r$。
- 3次元球(n=3)座標系において$C_n=\frac{\pi^{\frac{3}{2}}}{\Gamma(\frac{3}{2}+1)}=\frac{3}{4} \pi$。従ってその体積は$\frac{3}{4} \pi r^3$、表面積は$4 \pi r^2$。
- 4次元球(n=4)座標系において$C_n=\frac{\pi^{\frac{4}{2}}}{\Gamma(\frac{4}{2}+1)}=\frac{1}{2} \pi^2$。従ってその「体積(?)」は$\frac{1}{2} r^4$、「表面積(?)」は$2 \pi^2 r^3$
なんとスッキリとシンプルこの上なく美しい表現。歴史的に全体像の把握を阻害してきたのは,むしろ人類がそれまで思考の拠り所としてきた「カンブリア爆発期(5億4200万年前から5億3000万年前)に授かった視覚と視覚情報を処理する脊髄の末裔」そのもので、それは四次元以上の空間認識には全く歯が立たないという制約を抱えていたという訳です。
順列(英sequence without repetition、仏arrangement)
$nPr=n!/(n-r)!$。異なるn個の中から異なるr個を取り出して1列に並べる数の事。記号Pで表す。例えば5人(A、B、C、D、E)の中から2人を並べる場合を考えると並べ方は{AB,AC,AD,AE,BA,BC,BD,BE,CA,CB,CD,CE,DA,DB,DC,DE,EA,EB,EC、ED,AC,BA}となり合計は20通りになります。ABとBAを違うものとして考えるのがポイント。
Rの場合
library(Ryacas)
#nPr=n!/(n-r)!
yacas("(5!)/((5-2)!)")
expression(20)
#Rには順列を直接計算する函数はないので例えば相乗の函数prodを用いる。nPrはprod((n-r+1):n)と計算するが、この方法はr=0のときうまくいかない。
n<-5; r<-2
prod((n-r+1):n)
[1] 20
#なおRの場合、e1071というパッケージに含まれるpermutationsという函数は、
#引数にとった数までの順列のパターンをすべて表示してくれる。例えば
#permutations(3)とすれば、1から3までの数をすべて1回ずつ使った場合、
#どういう並べ方があるかを教えてくれる。
library(e1071)
permutations(3)
[,1] [,2] [,3]
[1,] 1 2 3
[2,] 2 1 3
[3,] 2 3 1
[4,] 1 3 2
[5,] 3 1 2
[6,] 3 2 1
pythonの場合
順列の総数は階乗を返す関数math.factorial()を使って以下のように算出する。整数int型を返すように、整数除算を行う//演算子を用いる。
import math as m
def permutations_count(n, r):
return m.factorial(n) // m.factorial(n - r)
print(permutations_count(5, 2))
print(permutations_count(5, 0))
#出力結果
20
1
SciPyには順列の総数を返す関数scipy.special.perm()が用意されている。デフォルトは第三引数exact=Falseで、浮動小数点数floatが返される。整数intで取得したい場合はexact=Trueとする必要があるので注意。なお、import scipyだけだとscipy.specialモジュールは読み込まれない。例のようにfrom scipy.special import permとしてperm()を実行するか、import scipy.specialとしてscipy.special.perm()を実行する。
from scipy.special import perm
print(perm(5, 2))
print(perm(5, 2, exact=True))
print(perm(5, 0, exact=True))
# 出力結果
20.0
20
1
総数だけでなく、リスト(配列)などから順列を生成して列挙する場合にはitertoolsモジュールのpermutations()関数を使う。第一引数にイテラブル(リストや集合set型)、第二引数に選択する個数を渡すと、その順列のイテレータを返す。全て列挙するにはforループで回す。有限個のイテレータなので、list()でリスト型に変換する事も可能で、リスト要素数をlen()で取得すると、階乗から算出した順列の総数と一致していることが確認できる。ちなみに第二引数を省略すると、すべての要素を選択する場合の順列が返される。
import itertools as itr
l = ['A','B','C','D','E']
p = itr.permutations(l, 2)
#形表示
print("Type:")
print(type(p))
# <class 'itertools.permutations'>
#順列一覧
print("Sequence without Repetition(5,2)")
for v in itr.permutations(l, 2):
print(v)
#リストにして出力
p_list = list(itr.permutations(l, 2))
print("Sequence without Repetition(5,2) → list")
print(p_list)
print(len(p_list))
#第二引数省略時
print("Sequence without Repetition(5,5)")
for v in itr.permutations(l):
print(v)
print(len(list(itr.permutations(l))))
出力結果
Type:
<class 'itertools.permutations'>
Sequence without Repetition(5,2)
('A', 'B')
('A', 'C')
('A', 'D')
('A', 'E')
('B', 'A')
('B', 'C')
('B', 'D')
('B', 'E')
('C', 'A')
('C', 'B')
('C', 'D')
('C', 'E')
('D', 'A')
('D', 'B')
('D', 'C')
('D', 'E')
('E', 'A')
('E', 'B')
('E', 'C')
('E', 'D')
Sequence without Repetition(5,2) → list
[('A', 'B'), ('A', 'C'), ('A', 'D'), ('A', 'E'), ('B', 'A'), ('B', 'C'), ('B', 'D'), ('B', 'E'), ('C', 'A'), ('C', 'B'), ('C', 'D'), ('C', 'E'), ('D', 'A'), ('D', 'B'), ('D', 'C'), ('D', 'E'), ('E', 'A'), ('E', 'B'), ('E', 'C'), ('E', 'D')]
20
Sequence without Repetition(5,5)
('A', 'B', 'C', 'D', 'E')
('A', 'B', 'C', 'E', 'D')
('A', 'B', 'D', 'C', 'E')
('A', 'B', 'D', 'E', 'C')
('A', 'B', 'E', 'C', 'D')
('A', 'B', 'E', 'D', 'C')
('A', 'C', 'B', 'D', 'E')
('A', 'C', 'B', 'E', 'D')
('A', 'C', 'D', 'B', 'E')
('A', 'C', 'D', 'E', 'B')
('A', 'C', 'E', 'B', 'D')
('A', 'C', 'E', 'D', 'B')
('A', 'D', 'B', 'C', 'E')
('A', 'D', 'B', 'E', 'C')
('A', 'D', 'C', 'B', 'E')
('A', 'D', 'C', 'E', 'B')
('A', 'D', 'E', 'B', 'C')
('A', 'D', 'E', 'C', 'B')
('A', 'E', 'B', 'C', 'D')
('A', 'E', 'B', 'D', 'C')
('A', 'E', 'C', 'B', 'D')
('A', 'E', 'C', 'D', 'B')
('A', 'E', 'D', 'B', 'C')
('A', 'E', 'D', 'C', 'B')
('B', 'A', 'C', 'D', 'E')
('B', 'A', 'C', 'E', 'D')
('B', 'A', 'D', 'C', 'E')
('B', 'A', 'D', 'E', 'C')
('B', 'A', 'E', 'C', 'D')
('B', 'A', 'E', 'D', 'C')
('B', 'C', 'A', 'D', 'E')
('B', 'C', 'A', 'E', 'D')
('B', 'C', 'D', 'A', 'E')
('B', 'C', 'D', 'E', 'A')
('B', 'C', 'E', 'A', 'D')
('B', 'C', 'E', 'D', 'A')
('B', 'D', 'A', 'C', 'E')
('B', 'D', 'A', 'E', 'C')
('B', 'D', 'C', 'A', 'E')
('B', 'D', 'C', 'E', 'A')
('B', 'D', 'E', 'A', 'C')
('B', 'D', 'E', 'C', 'A')
('B', 'E', 'A', 'C', 'D')
('B', 'E', 'A', 'D', 'C')
('B', 'E', 'C', 'A', 'D')
('B', 'E', 'C', 'D', 'A')
('B', 'E', 'D', 'A', 'C')
('B', 'E', 'D', 'C', 'A')
('C', 'A', 'B', 'D', 'E')
('C', 'A', 'B', 'E', 'D')
('C', 'A', 'D', 'B', 'E')
('C', 'A', 'D', 'E', 'B')
('C', 'A', 'E', 'B', 'D')
('C', 'A', 'E', 'D', 'B')
('C', 'B', 'A', 'D', 'E')
('C', 'B', 'A', 'E', 'D')
('C', 'B', 'D', 'A', 'E')
('C', 'B', 'D', 'E', 'A')
('C', 'B', 'E', 'A', 'D')
('C', 'B', 'E', 'D', 'A')
('C', 'D', 'A', 'B', 'E')
('C', 'D', 'A', 'E', 'B')
('C', 'D', 'B', 'A', 'E')
('C', 'D', 'B', 'E', 'A')
('C', 'D', 'E', 'A', 'B')
('C', 'D', 'E', 'B', 'A')
('C', 'E', 'A', 'B', 'D')
('C', 'E', 'A', 'D', 'B')
('C', 'E', 'B', 'A', 'D')
('C', 'E', 'B', 'D', 'A')
('C', 'E', 'D', 'A', 'B')
('C', 'E', 'D', 'B', 'A')
('D', 'A', 'B', 'C', 'E')
('D', 'A', 'B', 'E', 'C')
('D', 'A', 'C', 'B', 'E')
('D', 'A', 'C', 'E', 'B')
('D', 'A', 'E', 'B', 'C')
('D', 'A', 'E', 'C', 'B')
('D', 'B', 'A', 'C', 'E')
('D', 'B', 'A', 'E', 'C')
('D', 'B', 'C', 'A', 'E')
('D', 'B', 'C', 'E', 'A')
('D', 'B', 'E', 'A', 'C')
('D', 'B', 'E', 'C', 'A')
('D', 'C', 'A', 'B', 'E')
('D', 'C', 'A', 'E', 'B')
('D', 'C', 'B', 'A', 'E')
('D', 'C', 'B', 'E', 'A')
('D', 'C', 'E', 'A', 'B')
('D', 'C', 'E', 'B', 'A')
('D', 'E', 'A', 'B', 'C')
('D', 'E', 'A', 'C', 'B')
('D', 'E', 'B', 'A', 'C')
('D', 'E', 'B', 'C', 'A')
('D', 'E', 'C', 'A', 'B')
('D', 'E', 'C', 'B', 'A')
('E', 'A', 'B', 'C', 'D')
('E', 'A', 'B', 'D', 'C')
('E', 'A', 'C', 'B', 'D')
('E', 'A', 'C', 'D', 'B')
('E', 'A', 'D', 'B', 'C')
('E', 'A', 'D', 'C', 'B')
('E', 'B', 'A', 'C', 'D')
('E', 'B', 'A', 'D', 'C')
('E', 'B', 'C', 'A', 'D')
('E', 'B', 'C', 'D', 'A')
('E', 'B', 'D', 'A', 'C')
('E', 'B', 'D', 'C', 'A')
('E', 'C', 'A', 'B', 'D')
('E', 'C', 'A', 'D', 'B')
('E', 'C', 'B', 'A', 'D')
('E', 'C', 'B', 'D', 'A')
('E', 'C', 'D', 'A', 'B')
('E', 'C', 'D', 'B', 'A')
('E', 'D', 'A', 'B', 'C')
('E', 'D', 'A', 'C', 'B')
('E', 'D', 'B', 'A', 'C')
('E', 'D', 'B', 'C', 'A')
('E', 'D', 'C', 'A', 'B')
('E', 'D', 'C', 'B', 'A')
120
なおitertools.permutations()では、要素が値ではなく位置に基づいて扱われる。値が重複していても特に考慮されない。
import itertools as itr
l = ['a', 'a']
for v in itr.permutations(l, 2):
print(v)
#出力結果
('a', 'a')
('a', 'a')
これは以下で説明する
- itertools.combinations()
- itertools.combinations_with_replacement()
についても同様である。
組み合わせ(combination, choose)
$nCr=nPr/r!$あるいは$n!/(r!×(n-r)!)$。異なるn個の中から選んだ異なるr個との組み合わせ数の事。記号Cで表す。例えば5人{A、B、C、D、E}の中から2人を選ぶ組み合わせを考えると_{AB}、{CD}、{AC}_…のようになり合計10通り。{AB}と{BA}のチームを同じと考えるので順列の総数の半分となる。ちなみにr=0の場合の組み合わせはやはり{}の1通りのみ。
Rの場合
library(Ryacas)
#yacasでは組合せnCr=nPr/r!はBin(n,r) 。
#bin はbinomial coeffients(2項係数)から来ている。
#これは2項係数の係数がnCrだからである。
yacas("Bin(5,2)")
expression(10)
#Rで組み合わせの数を求めるには函数chooseを用いる。
#nCrを求めたければchoose(n, r)となる。
n<-5; r<-2
choose(n, r)
[1] 10
#なおRではcombnという函数を用いると、ありうる組み合わせの
#すべてを行列の形で表示させることができる。
people <- c("A", "B", "C", "D")
combn(people, 3)
[,1] [,2] [,3] [,4]
[1,] "A" "A" "A" "B"
[2,] "B" "B" "C" "C"
[3,] "C" "D" "D" "D"
pythonの場合
組み合わせの総数は階乗を返す関数math.factorial()を使って以下のように算出する。整数int型を返すように、整数除算を行う//演算子を用いる。
import math as m
def combinations_count(n, r):
return m.factorial(n) // (m.factorial(n - r) * m.factorial(r))
print(combinations_count(5, 2))
print(combinations_count(5, 0))
# 出力結果
10
1
SciPyには組み合わせの総数を返す関数scipy.special.perm()が用意されている。scipy.special.perm()と同様に、デフォルトは第三引数exact=Falseで、浮動小数点数floatが返される。整数intで取得したい場合はexact=Trueとする必要があるので注意。繰り返しになるが、import scipyだけだとscipy.specialモジュールは読み込まれないので注意。例のようにfrom scipy.special import combとしてcomb()を実行するか、import scipy.specialとしてscipy.special.comb()を実行する。
from scipy.special import comb
print(comb(5, 2))
print(comb(5, 2, exact=True))
print(comb(5, 0, exact=True))
# 出力結果
10.0
10
1
なお標準ライブラリのみを使ってmath.factorial()を利用するより高速処理を実現する以下の様なアルゴリズムも存在する。
Is there a math nCr function in python? - Stack Overflow
from operator import mul
from functools import reduce
def combinations_count(n, r):
r = min(r, n - r)
numer = reduce(mul, range(n, n - r, -1), 1)
denom = reduce(mul, range(1, r + 1), 1)
return numer // denom
print(combinations_count(5, 2))
print(combinations_count(5, 0))
# 出力結果
10
1
総数だけでなく、リスト(配列)などから順列を生成して列挙する場合にはitertoolsモジュールのcombinations()関数を使う。第一引数にイテラブル(リストや集合set型)、第二引数に選択する個数を渡すと、その順列のイテレータを返す。全て列挙するにはforループで回す。有限個のイテレータなので、list()でリスト型に変換する事も可能で、リスト要素数をlen()で取得すると、階乗から算出した順列の総数と一致していることが確認できる。ちなみに第二引数は省略出来ない。
import itertools as itr
l = ['A','B','C','D','E']
p = itr.combinations(l, 2)
#形表示
print("Combination without Repetition:Type")
print(type(p))
# <class 'itertools.permutations'>
#組み合わせ一覧
print("Combination without Repetition(5,2)")
for v in itr.combinations(l, 2):
print(v)
#リストにして出力
p_list = list(itr.combinations(l, 2))
print("Combination without Repetition(5,2) → list")
print(p_list)
print(len(p_list))
#第二引数省略時
print("Combination without Repetition(5,1)")
for v in itr.combinations(l,1):
print(v)
print(len(list(itr.combinations(l,1))))
print("Combination without Repetition(5,5)")
for v in itr.combinations(l,5):
print(v)
print(len(list(itr.combinations(l,5))))
出力結果
Combination without Repetition:Type
<class 'itertools.combinations'>
Combination without Repetition(5,2)
('A', 'B')
('A', 'C')
('A', 'D')
('A', 'E')
('B', 'C')
('B', 'D')
('B', 'E')
('C', 'D')
('C', 'E')
('D', 'E')
Combination without Repetition(5,2) → list
[('A', 'B'), ('A', 'C'), ('A', 'D'), ('A', 'E'), ('B', 'C'), ('B', 'D'), ('B', 'E'), ('C', 'D'), ('C', 'E'), ('D', 'E')]
10
Combination without Repetition(5,1)
('A',)
('B',)
('C',)
('D',)
('E',)
5
Combination without Repetition(5,5)
('A', 'B', 'C', 'D', 'E')
1
重複組み合わせの総数算出とリストから生成/列挙
重複組み合わせは、異なるn個のものから重複を許してr個選ぶ場合の数。その総数は、異なる$n+r -1$個のものからr個選ぶ組み合わせの数に等しい。
pythonの場合
上で定義した組み合わせの総数を算出する関数を使えばよい。
import math as m
def combinations_count(n, r):
return m.factorial(n) // (m.factorial(n - r) * m.factorial(r))
def combinations_with_replacement_count(n, r):
return combinations_count(n + r - 1, r)
print(combinations_with_replacement_count(5, 2))
print(combinations_with_replacement_count(5, 0))
#出力結果
15
1
上述のscipy.special.comb()では、第四引数repetition=Trueとすると重複組合せの総数が取得可能。
from scipy.special import comb
print(comb(5, 2, exact=True,repetition=True))
print(comb(5, 0, exact=True, repetition=True))
# 出力結果
15
1
総数だけでなく、リスト(配列)などから順列を生成して列挙する場合にはitertoolsモジュールのcombinations_with_replacement()関数を使う。第一引数にイテラブル(リストや集合set型)、第二引数に選択する個数を渡すと、その順列のイテレータを返す。全て列挙するにはforループで回す。有限個のイテレータなので、list()でリスト型に変換する事も可能で、リスト要素数をlen()で取得すると、階乗から算出した順列の総数と一致していることが確認できる。ちなみに第二引数はやはり省略出来ない。
import itertools as itr
l = ['A','B','C','D','E']
p = itr.combinations_with_replacement(l, 2)
#形表示
print("Combination with Repetition:Type")
print(type(p))
# <class 'itertools.permutations'>
#組み合わせ一覧
print("Combination with Repetition(5,2)")
for v in itr.combinations_with_replacement(l, 2):
print(v)
#リストにして出力
p_list = list(itr.combinations_with_replacement(l, 2))
print("Combination with Repetition(5,2) → list")
print(p_list)
print(len(p_list))
#第二引数省略時
print("Combination with Repetition(5,1)")
for v in itr.combinations_with_replacement(l,1):
print(v)
print(len(list(itr.combinations(l,1))))
print("Combination with Repetition(5,5)")
for v in itr.combinations_with_replacement(l,5):
print(v)
print(len(list(itr.combinations_with_replacement(l,5))))
出力結果
Combination with Repetition:Type
<class 'itertools.combinations_with_replacement'>
Combination with Repetition(5,2)
('A', 'A')
('A', 'B')
('A', 'C')
('A', 'D')
('A', 'E')
('B', 'B')
('B', 'C')
('B', 'D')
('B', 'E')
('C', 'C')
('C', 'D')
('C', 'E')
('D', 'D')
('D', 'E')
('E', 'E')
Combination with Repetition(5,2) → list
[('A', 'A'), ('A', 'B'), ('A', 'C'), ('A', 'D'), ('A', 'E'), ('B', 'B'), ('B', 'C'), ('B', 'D'), ('B', 'E'), ('C', 'C'), ('C', 'D'), ('C', 'E'), ('D', 'D'), ('D', 'E'), ('E', 'E')]
15
Combination with Repetition(5,1)
('A',)
('B',)
('C',)
('D',)
('E',)
5
Combination with Repetition(5,5)
('A', 'A', 'A', 'A', 'A')
('A', 'A', 'A', 'A', 'B')
('A', 'A', 'A', 'A', 'C')
('A', 'A', 'A', 'A', 'D')
('A', 'A', 'A', 'A', 'E')
('A', 'A', 'A', 'B', 'B')
('A', 'A', 'A', 'B', 'C')
('A', 'A', 'A', 'B', 'D')
('A', 'A', 'A', 'B', 'E')
('A', 'A', 'A', 'C', 'C')
('A', 'A', 'A', 'C', 'D')
('A', 'A', 'A', 'C', 'E')
('A', 'A', 'A', 'D', 'D')
('A', 'A', 'A', 'D', 'E')
('A', 'A', 'A', 'E', 'E')
('A', 'A', 'B', 'B', 'B')
('A', 'A', 'B', 'B', 'C')
('A', 'A', 'B', 'B', 'D')
('A', 'A', 'B', 'B', 'E')
('A', 'A', 'B', 'C', 'C')
('A', 'A', 'B', 'C', 'D')
('A', 'A', 'B', 'C', 'E')
('A', 'A', 'B', 'D', 'D')
('A', 'A', 'B', 'D', 'E')
('A', 'A', 'B', 'E', 'E')
('A', 'A', 'C', 'C', 'C')
('A', 'A', 'C', 'C', 'D')
('A', 'A', 'C', 'C', 'E')
('A', 'A', 'C', 'D', 'D')
('A', 'A', 'C', 'D', 'E')
('A', 'A', 'C', 'E', 'E')
('A', 'A', 'D', 'D', 'D')
('A', 'A', 'D', 'D', 'E')
('A', 'A', 'D', 'E', 'E')
('A', 'A', 'E', 'E', 'E')
('A', 'B', 'B', 'B', 'B')
('A', 'B', 'B', 'B', 'C')
('A', 'B', 'B', 'B', 'D')
('A', 'B', 'B', 'B', 'E')
('A', 'B', 'B', 'C', 'C')
('A', 'B', 'B', 'C', 'D')
('A', 'B', 'B', 'C', 'E')
('A', 'B', 'B', 'D', 'D')
('A', 'B', 'B', 'D', 'E')
('A', 'B', 'B', 'E', 'E')
('A', 'B', 'C', 'C', 'C')
('A', 'B', 'C', 'C', 'D')
('A', 'B', 'C', 'C', 'E')
('A', 'B', 'C', 'D', 'D')
('A', 'B', 'C', 'D', 'E')
('A', 'B', 'C', 'E', 'E')
('A', 'B', 'D', 'D', 'D')
('A', 'B', 'D', 'D', 'E')
('A', 'B', 'D', 'E', 'E')
('A', 'B', 'E', 'E', 'E')
('A', 'C', 'C', 'C', 'C')
('A', 'C', 'C', 'C', 'D')
('A', 'C', 'C', 'C', 'E')
('A', 'C', 'C', 'D', 'D')
('A', 'C', 'C', 'D', 'E')
('A', 'C', 'C', 'E', 'E')
('A', 'C', 'D', 'D', 'D')
('A', 'C', 'D', 'D', 'E')
('A', 'C', 'D', 'E', 'E')
('A', 'C', 'E', 'E', 'E')
('A', 'D', 'D', 'D', 'D')
('A', 'D', 'D', 'D', 'E')
('A', 'D', 'D', 'E', 'E')
('A', 'D', 'E', 'E', 'E')
('A', 'E', 'E', 'E', 'E')
('B', 'B', 'B', 'B', 'B')
('B', 'B', 'B', 'B', 'C')
('B', 'B', 'B', 'B', 'D')
('B', 'B', 'B', 'B', 'E')
('B', 'B', 'B', 'C', 'C')
('B', 'B', 'B', 'C', 'D')
('B', 'B', 'B', 'C', 'E')
('B', 'B', 'B', 'D', 'D')
('B', 'B', 'B', 'D', 'E')
('B', 'B', 'B', 'E', 'E')
('B', 'B', 'C', 'C', 'C')
('B', 'B', 'C', 'C', 'D')
('B', 'B', 'C', 'C', 'E')
('B', 'B', 'C', 'D', 'D')
('B', 'B', 'C', 'D', 'E')
('B', 'B', 'C', 'E', 'E')
('B', 'B', 'D', 'D', 'D')
('B', 'B', 'D', 'D', 'E')
('B', 'B', 'D', 'E', 'E')
('B', 'B', 'E', 'E', 'E')
('B', 'C', 'C', 'C', 'C')
('B', 'C', 'C', 'C', 'D')
('B', 'C', 'C', 'C', 'E')
('B', 'C', 'C', 'D', 'D')
('B', 'C', 'C', 'D', 'E')
('B', 'C', 'C', 'E', 'E')
('B', 'C', 'D', 'D', 'D')
('B', 'C', 'D', 'D', 'E')
('B', 'C', 'D', 'E', 'E')
('B', 'C', 'E', 'E', 'E')
('B', 'D', 'D', 'D', 'D')
('B', 'D', 'D', 'D', 'E')
('B', 'D', 'D', 'E', 'E')
('B', 'D', 'E', 'E', 'E')
('B', 'E', 'E', 'E', 'E')
('C', 'C', 'C', 'C', 'C')
('C', 'C', 'C', 'C', 'D')
('C', 'C', 'C', 'C', 'E')
('C', 'C', 'C', 'D', 'D')
('C', 'C', 'C', 'D', 'E')
('C', 'C', 'C', 'E', 'E')
('C', 'C', 'D', 'D', 'D')
('C', 'C', 'D', 'D', 'E')
('C', 'C', 'D', 'E', 'E')
('C', 'C', 'E', 'E', 'E')
('C', 'D', 'D', 'D', 'D')
('C', 'D', 'D', 'D', 'E')
('C', 'D', 'D', 'E', 'E')
('C', 'D', 'E', 'E', 'E')
('C', 'E', 'E', 'E', 'E')
('D', 'D', 'D', 'D', 'D')
('D', 'D', 'D', 'D', 'E')
('D', 'D', 'D', 'E', 'E')
('D', 'D', 'E', 'E', 'E')
('D', 'E', 'E', 'E', 'E')
('E', 'E', 'E', 'E', 'E')
126
文字列からアナグラムを作成
pythonの場合
itertools.permutations()を使うと、文字列の並び替え(アナグラム)を簡単に作成できる。一文字ずつのタプルを文字列に結合してリスト化するには以下のようにする。
import itertools as itr
s = 'arc'
#リスト出力
print("list:")
for v in itr.permutations(s):
print(v)
# ('a', 'r', 'c')
# ('a', 'c', 'r')
# ('r', 'a', 'c')
# ('r', 'c', 'a')
# ('c', 'a', 'r')
# ('c', 'r', 'a')
#文字列出力
print("Text:")
anagram_list = [''.join(v) for v in itr.permutations(s)]
print(anagram_list)
#出力結果
list:
('a', 'r', 'c')
('a', 'c', 'r')
('r', 'a', 'c')
('r', 'c', 'a')
('c', 'a', 'r')
('c', 'r', 'a')
Text:
['arc', 'acr', 'rac', 'rca', 'car', 'cra']
ここではリストやタプルの要素を文字列に連結するjoin()メソッドと、リスト内包表記を利用している。
Pythonで文字列を連結(結合)
Pythonリスト内包表記の使い方
複数のリストからの直積(デカルト積)生成
直積(デカルト積)は、複数の集合から要素を一つずつ取り出した組み合わせの集合。例えば2つのリストがあったとき、すべてのペアの組み合わせのリストが直積となる。
直積集合 - Wikipedia
デカルト座標系におけるX軸の目盛とY軸の目盛の直積に加え、トランプのデッキにおけるトランプの13ランク{A, K, Q, J, 10, 9, 8, 7, 6, 5, 4, 3, 2} と4スーツ{♠, ♥, ♦, ♣} の直積が著名である(4×13=52枚)。
pythonの場合
Pythonで複数のリストの直積(デカルト積)を生成するitertools.product
Pythonで複数のリストの直積(デカルト積)を生成するにはitertools.product()を使う。引数に2つのリストを指定するとitertools.product型のオブジェクトが返るが、itertools.product型はイテレータなので、それをそのままprint()しても中身は出力されない。
- forループで列挙して各リストの要素の組み合わせがタプルで取得できる。最後まで辿り着いたイテレータを再度forループでまわしても何も出力されないので注意。
- タプルではなくそれぞれの要素を別々に取得することも可能で、その場合は各リストをネストしたforループ(多重ループ)と同じ結果が得られる。
Pythonでタプルやリストをアンパック(複数の変数に展開して代入) - list()でリスト化することも可能で、この場合タプルを要素とするリストとなる。
import itertools as itr
import pprint
l1 = ['Heart','Diamond','Club','Spade']
l2 = ['A','2','3','4','5','6','7','8','9','10','J','Q','K']
p = itr.product(l1, l2)
#形表示
print("Type:")
print(p)
# <itertools.product object at 0x1026edd80>
print(type(p))
# <class 'itertools.product'>
#直積内容列記(単一For)
print("Product(Single For)")
for v in p:
print(v)
#何も出力されない。
for v in p:
print(v)
#直積内容列記(Unpack)
print("Product(Unpack)")
for v1,v2 in itr.product(l1, l2):
print(v1,v2)
#直積内容列記(単一For)
print("Product(Double For)")
for v1 in l1:
for v2 in l2:
print(v1, v2)
#リストにして出力
l_p = list(itr.product(l1, l2))
print("Product(List)")
pprint.pprint(l_p)
print(len(l_p))
print(type(l_p))
# <class 'list'>
print(type(l_p[0]))
# <class 'tuple'>
出力結果
Type:
<itertools.product object at 0x7fe6e4bc3680>
<class 'itertools.product'>
Product(Single For)
('Heart', 'A')
('Heart', '2')
('Heart', '3')
('Heart', '4')
('Heart', '5')
('Heart', '6')
('Heart', '7')
('Heart', '8')
('Heart', '9')
('Heart', '10')
('Heart', 'J')
('Heart', 'Q')
('Heart', 'K')
('Diamond', 'A')
('Diamond', '2')
('Diamond', '3')
('Diamond', '4')
('Diamond', '5')
('Diamond', '6')
('Diamond', '7')
('Diamond', '8')
('Diamond', '9')
('Diamond', '10')
('Diamond', 'J')
('Diamond', 'Q')
('Diamond', 'K')
('Club', 'A')
('Club', '2')
('Club', '3')
('Club', '4')
('Club', '5')
('Club', '6')
('Club', '7')
('Club', '8')
('Club', '9')
('Club', '10')
('Club', 'J')
('Club', 'Q')
('Club', 'K')
('Spade', 'A')
('Spade', '2')
('Spade', '3')
('Spade', '4')
('Spade', '5')
('Spade', '6')
('Spade', '7')
('Spade', '8')
('Spade', '9')
('Spade', '10')
('Spade', 'J')
('Spade', 'Q')
('Spade', 'K')
Product(Unpack)
Heart A
Heart 2
Heart 3
Heart 4
Heart 5
Heart 6
Heart 7
Heart 8
Heart 9
Heart 10
Heart J
Heart Q
Heart K
Diamond A
Diamond 2
Diamond 3
Diamond 4
Diamond 5
Diamond 6
Diamond 7
Diamond 8
Diamond 9
Diamond 10
Diamond J
Diamond Q
Diamond K
Club A
Club 2
Club 3
Club 4
Club 5
Club 6
Club 7
Club 8
Club 9
Club 10
Club J
Club Q
Club K
Spade A
Spade 2
Spade 3
Spade 4
Spade 5
Spade 6
Spade 7
Spade 8
Spade 9
Spade 10
Spade J
Spade Q
Spade K
Product(Double For)
Heart A
Heart 2
Heart 3
Heart 4
Heart 5
Heart 6
Heart 7
Heart 8
Heart 9
Heart 10
Heart J
Heart Q
Heart K
Diamond A
Diamond 2
Diamond 3
Diamond 4
Diamond 5
Diamond 6
Diamond 7
Diamond 8
Diamond 9
Diamond 10
Diamond J
Diamond Q
Diamond K
Club A
Club 2
Club 3
Club 4
Club 5
Club 6
Club 7
Club 8
Club 9
Club 10
Club J
Club Q
Club K
Spade A
Spade 2
Spade 3
Spade 4
Spade 5
Spade 6
Spade 7
Spade 8
Spade 9
Spade 10
Spade J
Spade Q
Spade K
Product(List)
[('Heart', 'A'),
('Heart', '2'),
('Heart', '3'),
('Heart', '4'),
('Heart', '5'),
('Heart', '6'),
('Heart', '7'),
('Heart', '8'),
('Heart', '9'),
('Heart', '10'),
('Heart', 'J'),
('Heart', 'Q'),
('Heart', 'K'),
('Diamond', 'A'),
('Diamond', '2'),
('Diamond', '3'),
('Diamond', '4'),
('Diamond', '5'),
('Diamond', '6'),
('Diamond', '7'),
('Diamond', '8'),
('Diamond', '9'),
('Diamond', '10'),
('Diamond', 'J'),
('Diamond', 'Q'),
('Diamond', 'K'),
('Club', 'A'),
('Club', '2'),
('Club', '3'),
('Club', '4'),
('Club', '5'),
('Club', '6'),
('Club', '7'),
('Club', '8'),
('Club', '9'),
('Club', '10'),
('Club', 'J'),
('Club', 'Q'),
('Club', 'K'),
('Spade', 'A'),
('Spade', '2'),
('Spade', '3'),
('Spade', '4'),
('Spade', '5'),
('Spade', '6'),
('Spade', '7'),
('Spade', '8'),
('Spade', '9'),
('Spade', '10'),
('Spade', 'J'),
('Spade', 'Q'),
('Spade', 'K')]
52
<class 'list'>
<class 'tuple'>
ここまでの説明では引数を便宜上「リスト」としてきたが、イテラブルオブジェクトであればタプルでもリストでもrangeオブジェクトでもなんでもいい。また、引数にはイテラブルオブジェクトを2個以上指定できる。
import itertools as itr
import pprint
t = ('one', 'two')
d = {'key1': 'value1', 'key2': 'value2'}
r = range(2)
#デフォルト(辞書オブジェクトはKeyが参照される)
print("Default")
l_p = list(itr.product(t, d, r))
pprint.pprint(l_p)
#辞書オブジェクトのKey指定
print("keys")
l_p = list(itr.product(t, d.keys(), r))
pprint.pprint(l_p)
#デフォルト
print("values")
l_p = list(itr.product(t, d.values(), r))
pprint.pprint(l_p)
出力結果
Default
[('one', 'key1', 0),
('one', 'key1', 1),
('one', 'key2', 0),
('one', 'key2', 1),
('two', 'key1', 0),
('two', 'key1', 1),
('two', 'key2', 0),
('two', 'key2', 1)]
keys
[('one', 'key1', 0),
('one', 'key1', 1),
('one', 'key2', 0),
('one', 'key2', 1),
('two', 'key1', 0),
('two', 'key1', 1),
('two', 'key2', 0),
('two', 'key2', 1)]
values
[('one', 'value1', 0),
('one', 'value1', 1),
('one', 'value2', 0),
('one', 'value2', 1),
('two', 'value1', 0),
('two', 'value1', 1),
('two', 'value2', 0),
('two', 'value2', 1)]
- 結果から分かるように、辞書オブジェクトをそのままイテレートするとキーkeyが使われる。値valueを使いたい場合はvalues()メソッドを使う。
Pythonの辞書(dict)のforループ処理(keys, values, items) - range()についての詳細は以下の記事を参照。
Pythonのrange関数の使い方
Γ関数の対数値
尤度計算等では対数値が求まれば良いので、Γ関数の対数値の直接計算で事足ります。
Rの場合
対数値を与える関数lgamma(n+1)、lchoose(n, r)が用意されている。これらは対数値を直接計算するもので、後から対数をとっている訳ではない。
#例えば choose(1000000,1000) がどれくらいの大きさかを
#知りたければ、次のようにする。つまり、百万人の中から千人を抽出
#する可能性は 1.507833e+3432 通りある。
x <- lchoose(1000000,1000)/log(10) # 自然対数値を常用対数値に変換
x
[1] 3432.178
10^(x-3432) # 仮数部を計算
[1] 1.507833
pythonの場合
math.lgamma(x) はガンマ関数の自然対数を返す。
# GAMMA_05
import math as m
# log{Γ(1)}
a = m.lgamma(1)
# log{Γ(3.5)}
b = m.lgamma(3.5)
print("logΓ(1) = {}".format(a))
print("logΓ(3.5) = {}".format(b))
#出力結果
logΓ(1) = 0.0
logΓ(3.5) = 1.2009736023470738
scipy.special.gammaln() はガンマ関数の自然対数を高精度で計算する。
# GAMMA_06
from scipy.special import gammaln
# [logΓ(-3.5),logΓ(1),logΓ(10)]
a = gammaln([-3.5, 1, 10])
a = np.round(a, 3)
print(a)
#出力結果
[-1.309 0. 12.802]
そんな感じで以下続報…