- (2020年11月20日までの更新分)Rのみで実装
- (2021年3月4日以降)python併記に着手
- (2021年7月30日)同心環Tagに移行。
解析学の基本的な部分を形成する数学の分野の一つである。局所的な変化を捉える微分と局所的な量の大域的な集積を扱う積分の二本の柱からなり、分野としての範囲を確定するのは難しいが、大体多変数実数値関数の微分と積分に関わる事柄(逆関数定理やベクトル解析も)を含んでいる。
微分(Derivative)…ある関数のある点での接線、あるいは接平面を考える演算である。数学的に別の言い方をすると、基本的には複雑な関数を線型近似して捉えようとする考え方である。従って、微分は線型写像になる。但し、多変数関数の微分を線型写像として捉える考え方は20世紀に入ってからのものである。微分方程式はこの考え方の自然な延長にある。
積分(Integrate)…幾何学的には、曲線、あるいは曲面と座標軸とに挟まれた領域の面積(体積)を求めることに相当している。ベルンハルト・リーマンは(一変数の)定積分の値を、長方形近似の極限として直接的に定義し、連続関数は積分を有することなどを証明した。彼の定義による積分をリーマン積分と呼んでいる。
微分と積分はまったく別の概念でありながら密接な関連性を持ち、一変数の場合、互いに他の逆演算としての意味を持っている(微分積分学の基本定理)。微分は傾き、積分は面積を表す。
正直、高校生の頃は微分(Differential)や積分(Integrate)の様な解析学(Mathematical Analysis)的アプローチが大嫌いでした。状況に応じて行き当たりばったり的に節操なく考え方が切り替わり、それぞれの丸暗記を強要される感じがとても苦手だったのです。
微分公式一覧(基礎から発展まで)
積分公式一覧(基礎から発展まで)
【初心者向け】三角関数と指数・対数関数の「巡回性」について。
それが最近になって「解析学の主目的は近似値の精度向上であり、その為になら手段なんて選んでられない(方法論的一貫性への執着心など犬にでも食わせてしまえ!!)」なる激烈なモットーを知り、発想上のコペルニクス的逆転に至りました。
【初心者向け】「泳ぐ」数理について。
これって考えてみたら、アルゴリズム(Algorithm)の、ひいては数理(Mathematical Things)の**基本概念**(Basic Cocept)そのものの具現ではないですか!!
#「半径と直径」および「半径と円周長」の間の往復
【Rで球面幾何学】単位円と単位球①「半径1」と「直径2」の関係について。
概ね半径(Radius)rと直径(Diameter)2rと円周長(Circumference)2πrの関係については、ピタゴラスの定理(Pythagorean Theorem)r^2=rcos(θ)^2+rsin(θ)^2と、近似円概念(Approximate Circle Concept)そのものの定義から以下が自明の場合(Trivial Case)とされます。
【初心者向け】ピタゴラスの定理あるいは三平方の定理からの出発
【初心者向け】「円そのもの」の近似から派生した角度と経度の概念の起源

- 半径がrの時、直径は2r。直径がdの時、半径rはd/2。
- 半径がrの時、円周長は2πr。円周長がcの時、半径rはc/2π。
- 直径がdの時、円周長はdπ。円周長がcの時、直径dはc/π。
小学生の頃、「円周長=直径×3.14」「円の面積=半径×半径×3.14」と教わって直径と半径の使い分けに悩んだ記憶がありますが、要するに半径+半径は直径と表記されるルールだっただけなのですね。この辺りの自明性から疑って掛かったのがτ(タウ)論争となります。
数学定数τ(タウ)
オイラーの等式よりも美しい
要するに、如何なる数理上の自明性も必ず何らかの形では反証される可能性を秘めているという話…だからこそ、メンテナンス上の都合からもゼロからの積み上げで出来ている必要があるのです。
#「円周長と円の面積」および「球の体積と表面積」の往復
この辺りから微分(Differential)や積分(Integrate)の概念がおもむろに登場。
- 円の面積πr^2を半径rで微分すると円周の長さ2πrとなる。逆に円周の長さ2πrを半径rで積分すると円の面積πr^2になる。
- 球の体積4/3πr^3を半径rで微分すると球の表面積4πr^2、逆に球の表面積4πr^2を半径rで積分すると球の体積**4/3πr^3となる。
- 球の表面積4πr^2を半径rで微分すると円周長2πr、逆に円周長2πrを半径rで積分すると球の表面積4πr^2となる。
Rの場合
とりあえずR標準関数だけで検証可能な範囲。
#半径rの円の面積(pi*r^2)をrで微分すると
#円周の長さ(2*pi*r)となる。
D01<-expression(pi*r^2)
D(D01,"r")
pi * (2 * r)
#半径rの球の体積(4/3*pi*r^3)をrで微分すると
#球の表面積(4*pi*r^2)となる。
D02<-expression(4/3*pi*r^3)
D(D02,"r")
4/3 * pi * (3 * r^2)
さらにはライブラリRyacas導入によって可能となる検証範囲。
#ライブラリ読み込み
library(Ryacas)
#半径rの円の面積(pi*r^2)をrで微分すると
#円周の長さ(2*pi*r)となる。
yacas("D(r) pi * r^2")
expression(pi * (2 * r))
#逆に円周の長さ(2*pi*r)をrで積分すると
#半径rの円の面積(pi*r^2)になる。
yacas("Integrate(r) pi * (2 * r)")
expression(pi * r^2)
#半径rの球の体積(4/3*pi*r^3)をrで微分すると
#球の表面積(4*pi*r^2)となる。
yacas("D(r) 4/3 * pi * r^3")
expression(r^2 * (4 * pi))
#逆に球の表面積(4*pi*r^2)をrで積分すると
#半径rの球の体積(4/3*pi*r^3)となる。
yacas("Integrate(r) r^2 * (4 * pi)")
expression(r^3 * (4 * pi)/3)
pythonの場合
道具としてはSympy一択ですね。
半径rの円の面積πr^2 ⇄ 円周長2πr
import sympy as sp
r,f,g,h = sp.symbols('r,f,g,h')
#元関数
f=sp.pi*r**2
#半径rの円の面積(pi*r^2)をrで微分すると
#円周の長さ(2*pi*r)となる。
g=sp.diff(f,r,1)
#逆に円周の長さ(2*pi*r)をrで積分すると
#半径rの円の面積(pi*r^2)になる。
h=sp.integrate(g,r)
#画面表示
sp.init_printing()
display(f)
print(sp.latex(f))
display(g)
print(sp.latex(g))
display(h)
print(sp.latex(h))
元関数
\pi r^{2}
微分結果
2 \pi r
積分結果
\pi r^{2}
半径rの球の体積(4/3pir^3) ⇄ 球の表面積(4pir^2)
import sympy as sp
r,f,g,h = sp.symbols('r,f,g,h')
#元関数
f=sp.Rational(4,3)*sp.pi*r**3
#半径rの球の体積(4/3*pi*r^3)をrで微分すると
#球の表面積(4*pi*r^2)となる。
g=sp.diff(f,r,1)
#逆に球の表面積(4*pi*r^2)をrで積分すると
#半径rの球の体積(4/3*pi*r^3)となる。
h=sp.integrate(g,r)
#画面表示
sp.init_printing()
display(f)
print(sp.latex(f))
display(g)
print(sp.latex(g))
display(h)
print(sp.latex(h))
元関数
\frac{4 \pi r^{3}}{3}
微分結果
4 \pi r^{2}
積分結果
\frac{4 \pi r^{3}}{3}
ちなみに引数の変遷は所謂「微積分における冪乗算の不定積分公式」通り。
\int x^b dx=\frac{1}{β+1} x^{β+1}
ただしこの計算式にはβ=-1の時に分母が0になる問題があり、実際には別の計算方法で代用されています。
【数理考古学】冪乗算(Exponentiation)の微積分
import sympy as sp
a,x,f,g,h = sp.symbols('a,x,f,g,h,i,j')
#元関数
f=a**x
#f'(x)一階微分
g=sp.diff(f,r,1)
#f''(x)二階微分
h=sp.diff(f,r,2)
#f'(x)一階積分
i=sp.integrate(g,r)
#f''(x)二階積分
j=sp.integrate(i,r)
#画面表示
sp.init_printing()
display(f)
print(sp.latex(f))
display(g)
print(sp.latex(g))
display(h)
print(sp.latex(h))
display(i)
print(sp.latex(i))
display(j)
print(sp.latex(j))
元関数
a^{x}
一階微分
a^{x} \log{\left(a \right)}
二階微分
a^{x} \log{\left(a \right)}^{2}
一階積分
\begin{cases} \frac{a^{x}}{\log{\left(a \right)}} & \text{for}\: \log{\left(a \right)} \neq 0 \\x & \text{otherwise} \end{cases}
二階積分
\begin{cases} \begin{cases} \frac{a^{x}}{\log{\left(a \right)}^{2}} & \text{for}\: \log{\left(a \right)}^{2} \neq 0 \\\frac{x}{\log{\left(a \right)}} & \text{otherwise} \end{cases} & \text{for}\: \left(a \geq 0 \wedge a < 1\right) \vee a > 1 \\\frac{x^{2}}{2} & \text{otherwise} \end{cases}
では以降、より具体的に見ていきましょう。
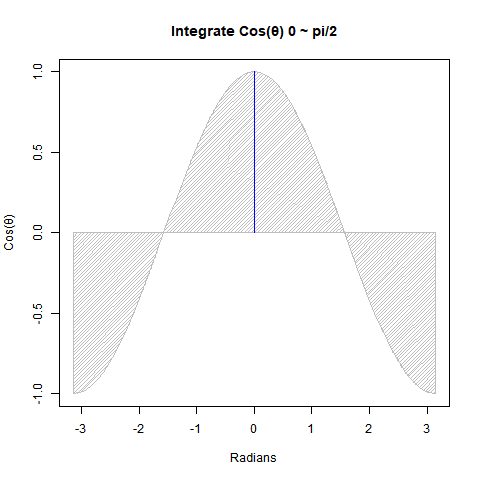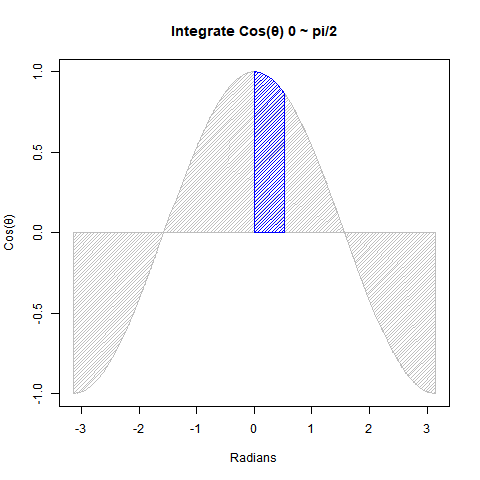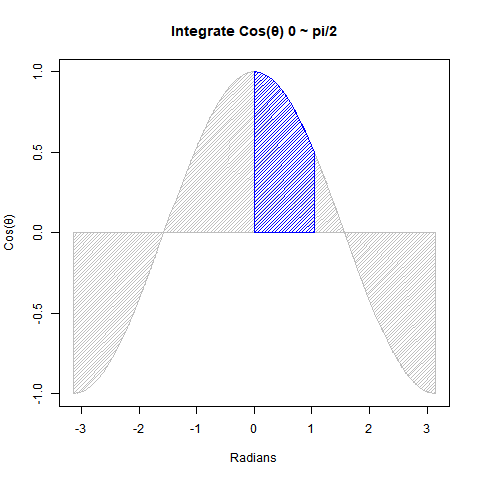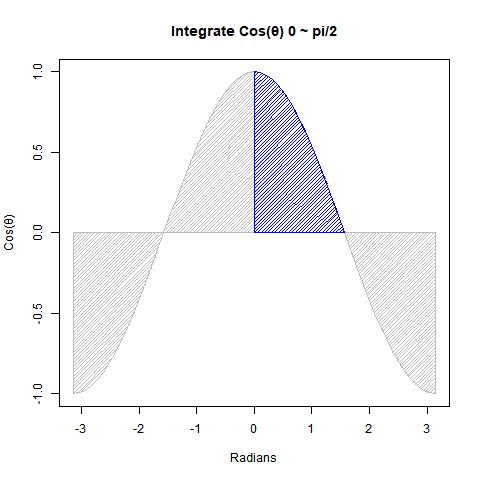
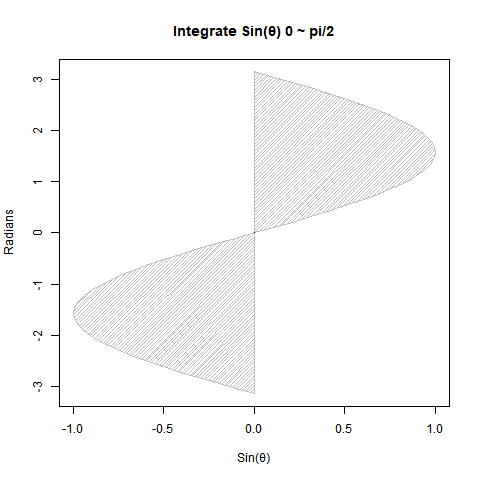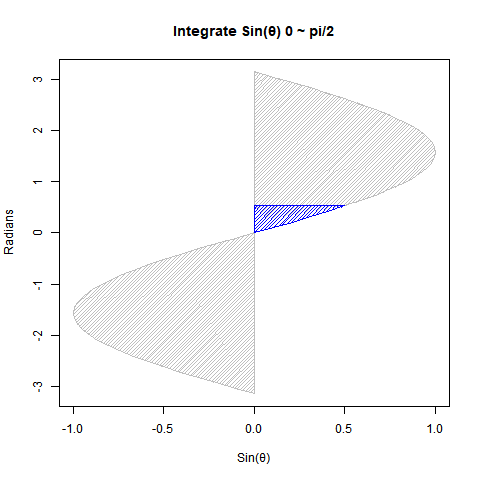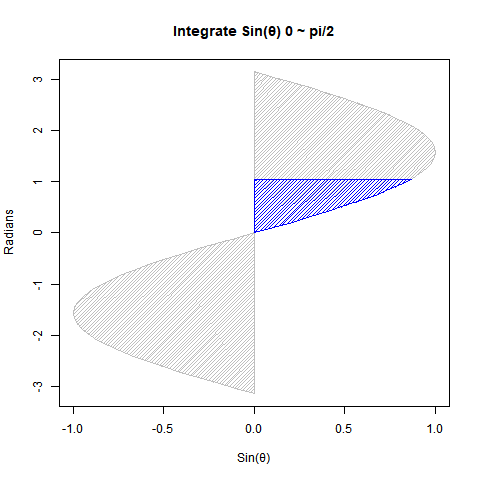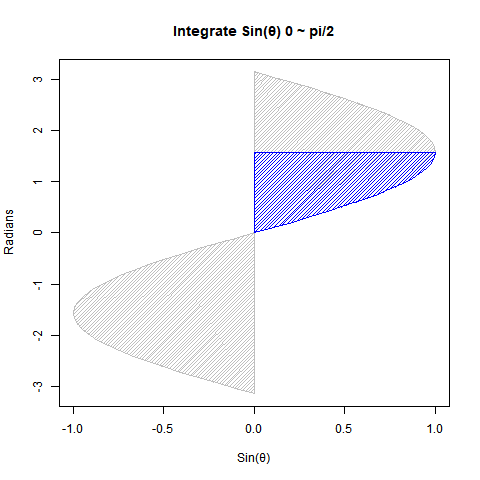
Cos(θ)とSin(θ)の数値積分結果
まずは円関係の微積分における基本中の基本。Cos(θ)とSin(θ)は位相がπ/2ラジアン(90度)ズレただけの同じ波なので、以下の数値積分結果に互換性があるのです。
【初心者向け】三角関数と数値積分(単位円上の面積4が円の面積πに対応)
①Cos(θ)を0からπ/2ラジアン(90度)まで数値積分すると1になる。同様にSin(θ)を0からπ/2ラジアン(90度)まで数値積分しても1となる。半径rに対応?
② Cos(θ)を-π/2ラジアン(90度)_からπ/2ラジアン(90度)まで数値積分すると2となる。Sin(θ)を0ラジアン(0度)からπラジアン(180度)まで数値積分しても2となる。直径2rに対応?
- 矩形近似領域の「単位辺」…θ(-π/2または-90度→0→π/2または90度。あるいは0→πラジアンまたは180度)
-
矩形近似領域の「積層辺」…Cos(θ)=1→0→1もしくはSin(θ)=0→1→0

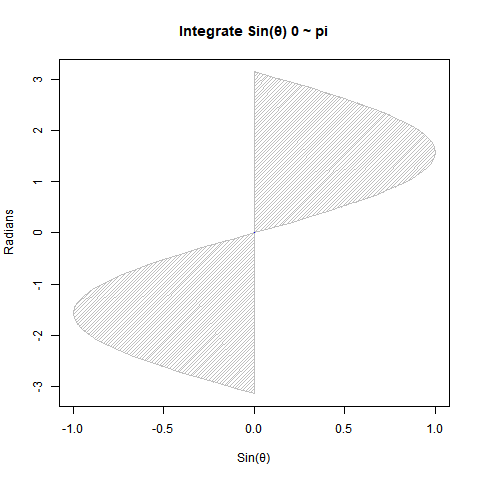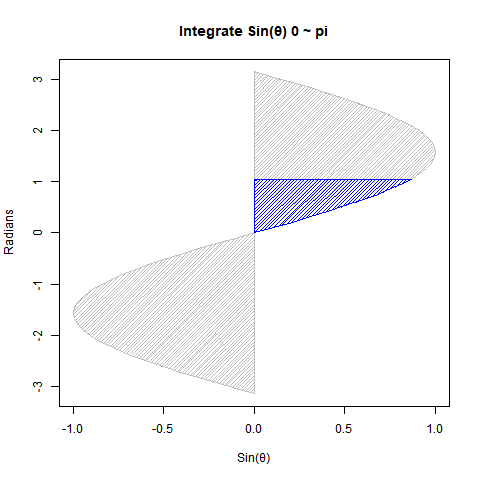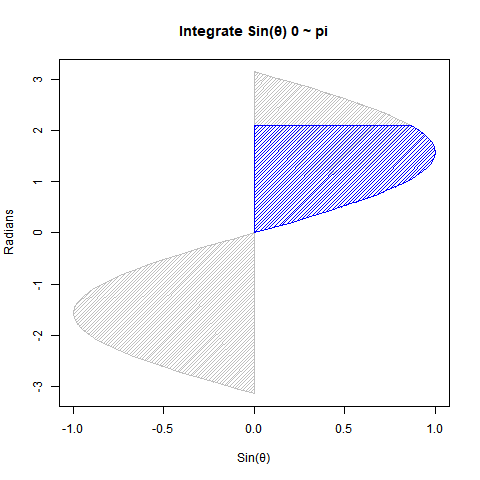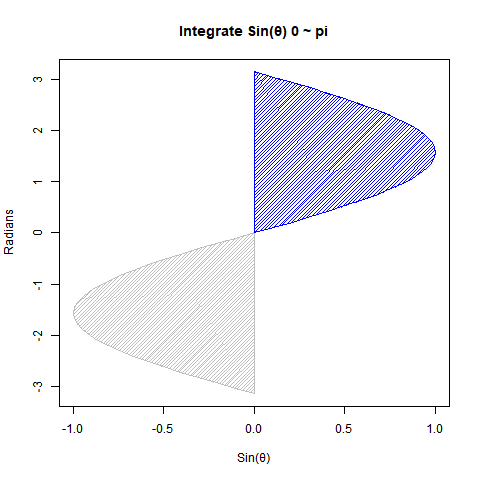
円周長2πr ⇄ 円の面積πr^2
三角形の面積の求め方(高さ*底辺)÷2を援用する形で高さが半径r、幅が円周長2πrの直角三角形を積層したイメージ。
- 矩形近似領域の「単位辺」…半径r
- 矩形近似領域の「積層辺」…πr=(半径r+半径r)×π/2
#話を半径1の単位円に限定すると、その面積はπとなる。
pi
[1] 3.141593
#π*Cos(θ)(θ=0~pi/2)の数値積分結果
f1<-function(x){cos(x)*pi}
integrate(f1,0,pi/2)
3.141593 with absolute error < 3.5e-14
#π*Sin(θ)(θ=0~pi/2)の数値積分結果
f2<-function(x){sin(x)*pi}
integrate(f2,0,pi/2)
3.141593 with absolute error < 3.5e-14
積層イメージの図示は、時間が取れたらそのうち…
#円周長2πr ⇄ 球の表面積4πr^2
円筒の側面積の求め方円周2πr×高さを援用して幅rΔΘで刻まれた同心円周2πrcos(Θ)をπ/2から-π/2にかけて積層したイメージ。ないしは同心円周2πrsin(Θ)を0からπにかけて積層したイメージ。
- 矩形近似領域の「単位辺」…2r=半径r×Cos(θ)(θ=-π/2ラジアン(-90度) ~ π/2ラジアン(90度))ないしはSin(θ)(θ=0ラジアン(0度) ~ πラジアン(180度))
- 矩形近似領域の「積層辺」…2πr=(半径r+半径r)×π
#話を半径1の単位球に限定すると、その表面積は4πとなる。
4*pi
[1] 12.56637
#2π*Cos(θ)(θ=-pi/2~pi/2)の数値積分結果
f3<-function(x){cos(x)*2*pi}
integrate(f3,-pi/2,pi/2)
12.56637 with absolute error < 1.4e-13
#2π*Sin(θ)(θ=0~pi)の数値積分結果
f4<-function(x){sin(x)*2*pi}
integrate(f4,0,pi)
12.56637 with absolute error < 1.4e-13
考え方としては単位円筒(Unit Cylinder)を加工して単位球面(Unit Sphere)に変換するプロセスと同じ筈。ただし…
【初心者向け】「単位円筒」から「単位球面」へ


上掲のアルゴリズムによる計算結果
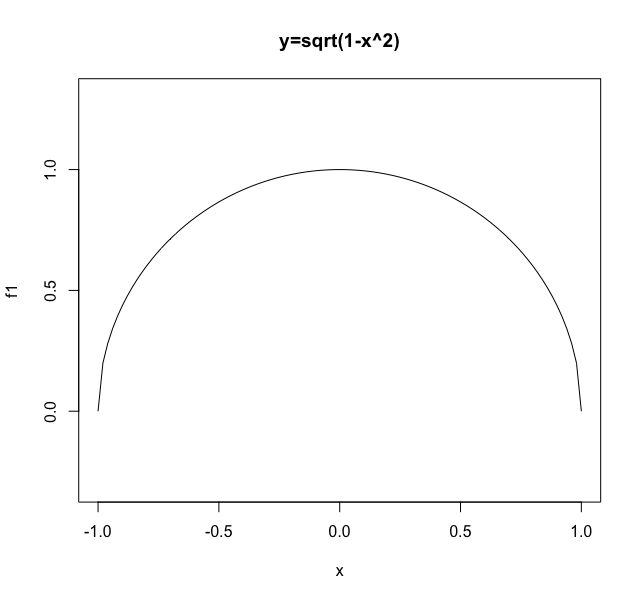
#「曲率」の算出
f0<-function(x) sqrt(1-x^2)
plot(f0,xlim=c(-1,1),ylim=c(0,1),asp=1,main="y=sqrt(1-x^2)")
#この式に円周長2πr^2を掛けた「高さごとの円の断面の周長」を足し合わせる。
f1<-function(x) sqrt(1-x^2)*2*pi
#とりあえず単位円計算対象とする。
integrate(f1,-1,1)
9.869604 with absolute error < 6.3e-09
#何故か精度が一定以上にならない。後で戻ってきて再挑戦…
手打ちで台形近似に挑戦した結果(やはり精度が一定以上にならない。)
#件の関数
f1<-function(x) sqrt(1-x^2)*2*pi
#台形近似
f2<-function(x){
c0<-seq(-1,1,length=x)
c1<-f1(c0)
#刻んだ短冊の幅は2/x
c2<-(c1[1:x-1]+c1[2:x])*2/(x-1)/2
sum(c2)
}
#算盤の玉みたいな状態(面積半分)からスタート。
> f2(3)
[1] 6.283185
#精度が一定以上に上がらない(というか収束してる?)。
> f2(5)
[1] 8.582991
> f2(10)
[1] 9.485197
> f2(100)
[1] 9.859003
> f2(1000)
[1] 9.869273
> f2(10000)
[1] 9.869594
円の面積πr^2 ⇄ 球の体積4/3πr^3
まずは円柱の体積の求め方底面積πr^2×高さ2rを援用。幅rΔΘで刻まれた球の断層πr^2cos(Θ)をπ/2から-π/2にかけて積層したイメージ、ないしは球の断層πr^2sin(Θ)を0からπにかけて積層したイメージに到達する。そして球の面積は、それをすっぽり包む円柱の面積の2/3(円錐は1/3)。
- 矩形近似領域の「単位辺」…2r=半径r*Cos(θ)(θ=-π/2ラジアン(-90度)→π/2ラジアン(90度))ないしはSin(θ)(θ=0ラジアン(0度)→πラジアン(180度))
- 矩形近似領域の「積層辺」…πr^2=半径r×半径r×π
- こうして出来上がった円柱の体積イメージを2/3に。
#話を半径1の単位球に限定すると、その体積は4/3πとなる。
4/3*pi
[1] 4.18879
#π*Cos(θ)(θ=-pi/2~pi/2)*2/3の数値積分結果
f5<-function(x){cos(x)*pi}
integrate(f5,-pi/2,pi/2)
6.283185 with absolute error < 7e-14
6.283185*2/3
[1] 4.18879
#π*Sin(θ)(θ=0~pi)*2/3の数値積分結果
f6<-function(x){sin(x)*pi}
integrate(f6,0,pi)
6.283185 with absolute error < 7e-14
6.283185*2/3
[1] 4.18879
積層イメージの図示は、時間が取れたらそのうち…
#結局、中高生の頃の私は具体的に何に躓(つまず)いたのか?
こうして全体像を俯瞰してみた結果、問題点は2つあった事に気付きました。
- 微積分計算はぶっちゃけ「単位辺」と「積層辺」を掛け合わせた面積としてイメージされる矩形近似領域が構成出来てナンボ。それを実現する為なら本当に「手段を選ばない」。
- とはいえ一応、例えば上掲の様な円関係の微積分計算では三角関数の微積分計算を中心に展開するといった数理的一貫性なら存在するのだが、当然低学年の児童はそこまで習わない。それで「半径r」「直径2r」「円周長2πr」「円の面積πr^2」「球の表面積4πr^2」「球の体積4/3π^3」の求め方それぞれを公式として強制的に暗記させられる一方、方便としてそれぞれについて、本筋から離れた「行き当たりばったり的な解釈」が与えられてきた。これでは全体像のイメージに到達出来ない。
前者の著名な例の一つが、微積分不可能な状況を打破する為に創造された「実在しない超関数」デルタ関数とも。しかも、後から「実は実在する」論が登場して大騒ぎに。
デルタ関数
デルタ関数は関数に似てはいるが、実は関数ではない。これを関数だと認めると、数学での分類の上ですっきりしない部分が出てくるらしいのである。それで数学では関数 (Function) ではなく超関数 (Distribution) というものに分類されている。しかし物理学徒はそのようなことには無頓着なのだ。
そして後者の問題は「児童への性教育」問題と構造が似ています。低学年では適当にお茶を濁して「詳しくは高学年で習ってね」と問題を先送り。一方、高学年では「これについては低学年でもう習ったよね」と問題を素通りしてしまうのです。これでは必要な知識が身に付く筈がありません。
近似円概念(Approximate circle concept)の限界としての「メルカトル図法の歪み」
ところで、こうしたアプローチからは解決の難しい問題も存在します。その著名な実例の一つが「メルカトル図法の歪み」ですね。
メルカトル図法 - Wikipedia

統計言語Rによる実装例(テクスチャは要ダウンロード)
library(rgl)
spheres3d (c(0,0,0),texture= "~/Desktop/350px-Mercator-projection.png", radius=1, color="white",alpha=0.8)
movie3d(spin3d(axis=c(0,0,1),rpm=4),duration=15,fps= 10,movie="~/Desktop/test009")
いや、むしろTexture Mappingによって問題が消失するとも?
【Python画像処理】メルカトル図法と正距方位図法
メルカトル図法(幅2πr高さπrの矩形→全球)





正距方位図法(半径$\frac{π}{2}の円盤→半球$)




正距方位図法(半径πの円盤→全球)




N次元球の表面積と体積の求め方。
こちらでで触れたガンマ関数(Γ Function)の応用例。
【Python演算処理】階乗と順列と組み合わせ
正直私にとってはパラダイムシフトでした。まさしくこれまでずっと探してきた「半径/直径・円周長/円の面積・球の表面積/体積の連続処理」が可能になったんです。ヒントは$\sqrt{\pi}$、すなわちガウス積分に潜んでいたんですね。
n次元球の体積 - EMANの統計力学 - EMANの物理学
まずはn次元球の表面積S_nを,n次元球の体積V_nを半径rで微分して導出する。そもそも$V_n$を微分するとは、半径をdrだけ変化させたときの$V_n$の変化率を求める事に他ならない。半径をdrだけ変化させると,体積は表面積$S_n$に厚みdrを掛けた分だけ変化するのだから,変化率は$S_n$だと考る訳である.
S_n=\frac{dV_n}{dr}=\frac{d (C_nr^n)}{dr}=n c_n r^{n-1}
そしてN次元球体の体積$I_n=\pi^\frac{n}{2}$について、n個の変数($x_1, x_2, …,x_n$)をn次元のデカルト座標と見て,これを半径rにのみ注目して極座標に変換していくと被積分関数はrのみの関数になる.
r^2=x_1^2+x_2^2+x_3^2+…x_n^2
r以外の残りの変数というのは全て角度に関するものなので、それだけ積分した結果は球の表面積を表す。なぜなら,$I_n$というのはn次元空間の全域についての積分であり,極座標に変換した結果、rを変化させながら全空間を塗りつぶしていく、つまり表面積$S_n$にdrを掛けたものを塗り重ねていくイメージだからである.
I^n=\int_{0}^{\infty}e^{-r^2}S_ndr\\
=\int_{0}^{\infty}e^{-r^2}n c_n r^{n-1}dr\\
=n c_n \int_{0}^{\infty}e^{-r^2} r^{n-1}dr
ここで$t=r^2$という変数変換を行う.
n c_n \int_{0}^{\infty}e^{-t} t^{\frac{n-1}{2}}(\frac{1}{2}t^{-\frac{1}{2}})dr\\
=\frac{n}{2}c_n \int_{0}^{\infty}e^{-t} t^{\frac{n}{2}-1}dt
これでΓ関数が代入可能な式形となった。
\Gamma (z)=\int_{0}^{\infty}e^{-t}t^{z-1}dt
すなわち
I_n = \frac{n}{2}c_n \Gamma (\frac{n}{2})\\
=c_n \Gamma (\frac{n}{2}+1)
よって
c_n = \frac{\pi^{\frac{n}{2}}}{\Gamma(\frac{n}{2}+1)}
すなわちn次元球の体積は以下となる。
V_n = \frac{\pi^{\frac{n}{2}}}{\Gamma(\frac{n}{2}+1)}r^2
つまり半径rのn次元球の体積は $c_n r^n$、表面積は$n c_nr^{n−1}$となります。
①$n=1$ のとき$C_n=\frac{\pi^{\frac{1}{2}}}{\Gamma(\frac{1}{2}+1)}=2$
Rの場合
f0 <- function(n) pi^(n/2)/gamma(n/2+1)
> f0(1)
[1] 2
pythonの場合
import math as m
def f0(n):
return m.pi**(n/2)/m.gamma(n/2+1)
print(f0(1))
#出力結果
1.9999999999999998
- 1次元球の体積は2rとなり、既知の結果と一致する。
②$n=2$ のとき$C_n=\frac{\pi^{\frac{2}{2}}}{\Gamma(\frac{2}{2}+1)}=\pi$
Rの場合
f0 <- function(n) pi^(n/2)/gamma(n/2+1)
> f0(2)
[1] 3.141593
> pi
[1] 3.141593
pythonの場合
import math as m
def f0(n):
return m.pi**(n/2)/m.gamma(n/2+1)
print(f0(2))
print(m.pi)
#出力結果
3.141592653589793
3.141592653589793
- 2次元球の体積は$\pi r^2$、表面積は$2 \pi r$となり、既知の結果と一致する。
③$n=3$ のとき$C_n=\frac{\pi^{\frac{3}{2}}}{\Gamma(\frac{3}{2}+1)}=\frac{3}{4} \pi$
Rの場合
f0 <- function(n) pi^(n/2)/gamma(n/2+1)
> f0(3)
[1] 4.18879
> 4/3*pi
[1] 4.18879
pythonの場合
import math as m
def f0(n):
return m.pi**(n/2)/m.gamma(n/2+1)
print(f0(3))
print(4/3*m.pi)
#出力結果
4.1887902047863905
4.1887902047863905
- 3次元球の体積は$\frac{3}{4} \pi r^3$、表面積は$4 \pi r^2$となり、既知の結果と一致する。
④$n=4$ のとき$C_n=\frac{\pi^{\frac{4}{2}}}{\Gamma(\frac{4}{2}+1)}=\frac{1}{2} \pi^2$
Rの場合
f0 <- function(n) pi^(n/2)/gamma(n/2+1)
> f0(4)
[1] 4.934802
> 1/2*pi^2
[1] 4.934802
pythonの場合
import math as m
def f0(n):
return m.pi**(n/2)/m.gamma(n/2+1)
print(f0(4))
print(1/2*m.pi**2)
#出力結果
4.934802200544679
4.934802200544679
- 4次元球の体積は$\frac{1}{2} r^4$、表面積は$2 \pi^2 r^3$となる。
Qiitaで同じ内容をΓ関数を用いず定義する投稿も見つけました。
n次元球の体積と表面積
a_n = \left\{
\begin{array}{ll}
\frac{\pi^{\frac{n}{2}}}{\frac{2}{n}!} & (n = Even) \\
\frac{2}{n!!} (2 \pi)^{\frac{n-1}{2}}& (n = Odd)
\end{array}
\right.
この時、半径rのn次元球の体積は $a_n r^n$、表面積は$n a_nr^{n−1}$となる。
①$n=1$ のとき$a_n=\frac{2}{1!!}(2π)^0=2$
- 1次元球の体積は2rとなり、既知の結果と一致する。
②$n=2$ のとき$a_n=\frac{2}{1!}(2π)^1=\pi$
- 2次元球の体積は$\pi r^2$、表面積は$2 \pi r$となり、既知の結果と一致する。
③$n=3$ のとき$a_n=\frac{2}{3!!}(2 \pi)^1=\frac{4}{3} \pi$
- 3次元球の体積は$\frac{4}{3} \pi r^3$、表面積は$4 \pi r^2$となり、既知の結果と一致する。
④$n=4$ のとき$a_n=\frac{\pi^2}{2!}=\frac{1}{2} \pi^2$
- 4次元球の体積は$\frac{1}{2} r^4$、表面積は$2 \pi^2 r^3$となる。
こちらの投稿でも、ガンマ関数を使えば$a_n=\frac{\pi^{\frac{n}{2}}}{\Gamma(\frac{n}{2}+1)}$ 、パイ関数を使えば$a_n=\frac{\pi^{\frac{n}{2}}}{\Pi(\frac{n}{2})}$と表せる事が指摘されています。
そんな感じで以下続報・・・