数理(Mathematical Thing)の世界は、賽の河原の様にパラダイムシフト到来による全体構造見直しを恐れつつ、自明の場合(Trival Case)の範囲を広げていく地道な作業によって興成されています。「半径が1なら直径は2」なる通念(Common Wisdom)ですら、以下の様に定義の厳密化に当たっての相応に精密な検証を免れ得ないのです。そして、その都度「鬼子」が…「鬼子」が…
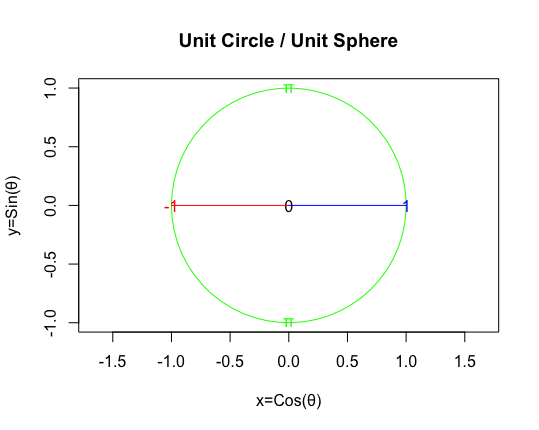
# 単位円/単位球(Unit Circle / Unit Sphere)
theta <- seq(pi,-pi,length=60)
plot(cos(theta),sin(theta),asp=1,type="l",col=rgb(0,1,0), main="Unit Circle / Unit Sphere", xlab="x=Cos(θ)", ylab="y=Sin(θ)")
text(0, 0, "0",col=rgb(0,0,0))
text(1, 0, "1",col=rgb(0,0,1))
text(-1, 0, "-1",col=rgb(1,0,0))
text(0, 1, "π",col=rgb(0,1,0))
text(0, -1, "π",col=rgb(0,1,0))
segments(0,0,1,0,col=rgb(0,0,1))
segments(0,0,-1,0,col=rgb(1,0,0))
【初心者向け】「単位円筒」から「単位球面」へ

①とある円弧(Circular Arc)/球表面(Sphere Surface)上の任意の観測原点(Origin)から観測される距離が全て一致する観測点(Distination)を、原蹠(Portal)に対する対蹠(Antipodal=たいしょ, 北極に対する南極あるいはその逆の位置関係)と位置付ける。
②もしその円弧/球表面が真円(True Circle)/真球(True Sphere)だったとしたら、原蹠と対蹠を結ぶ直線距離(Direct Distance)が直径(Diameter)、その直線上の中点がその円(Circle)/球(Sphere)の中心(Center)、それぞれの円弧(Circular Arc)/球表面(Sphere Surface)上の任意の点までの直線距離が半径(Radius)となる。
③逆に整理すると以下となる。
- 真円の円弧(Circular Arc of True Circle)/真球の表面(Sphere Surface of True Sphere)上における任意の点(Any point)の中心からの直線距離、すなわち半径は全て等しい。この場合を単位円(Unit Circle)/単位球(Unit Sphere)と呼ぶ。
- 半径を1と規定するなら、それぞれを原蹠とする対蹠との直線距離、すなわち直径は全て等しく2となる。
- また中心0を基準に考えると、原蹠までの直線距離は1、対蹠までの直線距離は-1となる。
この概念を「自明の理」として成立させる為には、さらに以下の数理の導入(Introduce)が必要となります。
①「半径、すなわち単位円の円弧/単位球の表面上の任意の点の中心からの直線距離は全て等しい」を自明の理とするにはピタゴラスの定理(Pythagorean theorem)概念の導入が不可欠。
【初心者向け】ピタゴラスの定理あるいは三平方の定理からの出発

②「単位円の円弧/単位球の表面上における任意の原蹠と対蹠を結ぶ実際の距離」をπ(3.141593…)とする計算がまた別途必要。
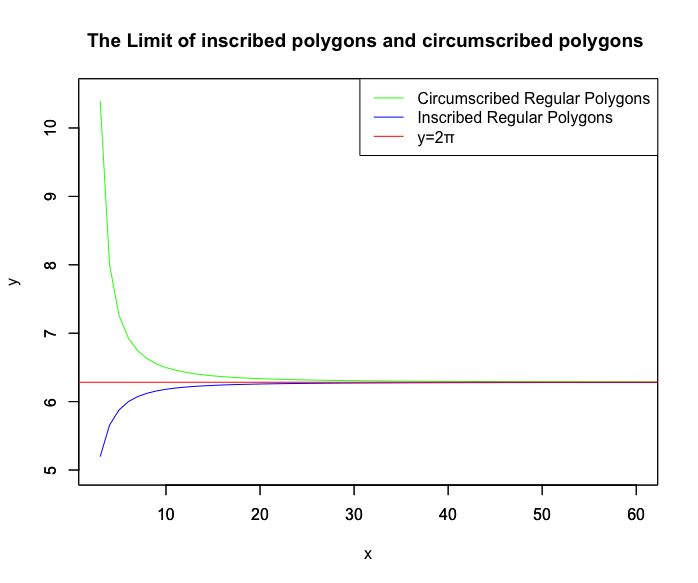
【初心者向け】挟み撃ち定理(Squeeze Theorem)による円周率πの近似

③「中心0を基準に考えた場合、原蹠までの直線距離を1とすれば対蹠までの直線距離は-1となる」を自明の理とするには数直線の概念導入が不可欠。この時点で「整数列においては偶数列と奇数列が交互に現れる」特徴も利用可能となる。
【Rで球面幾何学】等差数列(算術数列)① 数直線(Number Line)概念の導入(Introduction)について。
【Rで球面幾何学】等差数列(算術数列)②数直線(Number Line)概念から同心円集合(concentric set)概念へ


④こうして「半径が1なら直径は2」が自明の理として定まると、以下の計算結果もまたほぼ自動的に導入される。
【初心者向け】半径・直径・円周長・円の面積・球の表面積・球の体積の計算上の往復
- 半径がrの時、直径は2r。直径がdの時、半径rはd/2。
- 半径がrの時、円周長は2πr。円周長がcの時、半径rはc/2π。
- 直径がdの時、円周長はdπ。円周長がcの時、直径dはc/π。
- 円の面積πr^2を半径rで微分すると円周の長さ2πrとなる。逆に円周の長さ2πrを半径rで積分すると円の面積πr^2になる。
- 球の体積4/3πr^3を半径rで微分すると球の表面積4πr^2、逆に球の表面積4πr^2を半径rで積分すると球の体積**4/3πr^3となる。
- 球の表面積4πr^2を半径rで微分すると円周長2πr、逆に円周長2πrを半径rで積分すると球の表面積4πr^2となる。

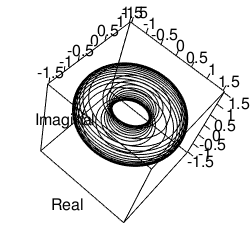
⑤ここで興味深いのが、同時にやはりほぼ自動的に「同心円集合を構成する片側無限等差数列は、さらに単位円の円弧/単位球の表面上の任意の点それぞれが同心円集合を構成する」特徴も導入される辺り。つまり例えば大円の半径(Major Radius)と小円の半径(Minor Radius)の組み合わせで表されるトーラス構造が全体を表す概念の一つとして利用可能となる。望む、望まないに関わらず…
【Rで球面幾何学】等差数列(算術数列)②数直線(Number Line)概念から同心円集合(concentric set)概念へ

【Rで球面幾何学】「単位円筒」から「トーラス構造」へ

かくして、不穏な空気が漂い始めた辺りで以下続報…