(2020年03月07日)初投稿
(2021年04月15日)texを導入。
今回の投稿の出発点はここ。
【初心者向け】「円そのもの」の近似から派生した角度概念の起源
尺度としては60*60=360を分割数に据えた度数法(Degree measure)と、半径rの円の周長が2πrである点に注目した弧度法(Radian measure)辺りが二大巨塔と目されています。
それでは人類はどういう経緯で「半径rの円の周長は2πr」なる結論に到達したのでしょう?
「挟み撃ち定理(Squeeze Theorem)」なる古典的流儀
古くから試みられ続けてきたのは「対象円に外接する正多角形と内接する正多角形の辺長計差を、ただひたすら角度を増やしながら計測し続ける」地道な方法。確かに収束率が悪く、より高速で精度が高いアルゴリズムも数多く開発されてきたのですが、手間自体に関しては天才数学者ガウス(独:Johann Carl Friedrich Gauß,羅:Carolus Fridericus Gauss、1777年〜1855年)が1の冪根の巡回性を発見し、コンピューター言語上では「2πをnで割った数列をCos関数に与えた結果をX軸、Sin関数に与えた結果をY軸に配すると正N角形を描く」だけで良くなった今日では、随分とカジュアルに試せる内容となっています。
1の原始冪根
巡回群(cyclic group/monogenous group)

# CIC=Circumscribed & Inscribed Circle(外接円と内接円)
# NoS=Number of Sides(辺の数)
CIC<-function(NoS){
c0<-seq(0,2*pi,length=60)
cx<-cos(c0)
cy<-sin(c0)
# 外接円の描画
plot(cx,cy,asp=1,type="l",col=rgb(1,0,0),xlim=c(-1,1),ylim=c(-1,1),main="
Circumscribed & Inscribed Circle",xlab="Cos(θ)",ylab="Sin(θ)")
par(new=T)#上書き指定
# 内接多角形の描画
p0<-seq(0,2*pi,length=NoS+1)
px<-cos(p0)
py<-sin(p0)
plot(px,py,asp=1,type="l",col=rgb(0,1,0),xlim=c(-1,1),ylim=c(-1,1),main="",xlab="",ylab="")
par(new=T)#上書き指定
# 内接円の描画
plot(cx*cos(pi/NoS),cy*cos(pi/NoS),asp=1,type="l",col=rgb(0,0,1),xlim=c(-1,1),ylim=c(-1,1),main="",xlab="",ylab="")
# 凡例
NPolysides<-paste0("Regular ",NoS, " sides Polysides")
legend("bottomright", legend=c("Circumscribed Circle",NPolysides,"Inscribed Circle"), lty=c(1,1,1), col=c(rgb(1,0,0),rgb(0,1,0),rgb(0,0,1)))
# 補助線とテキストの追加
segments(0,0,1,0,col=rgb(1,0,0))
text(1,0,"R",col=rgb(1,0,0),cex=1.5)
text((px[1]+px[2])/2+0.05,(py[1]+py[2])/2,"A",col=rgb(0,1,0),cex=1.5)
segments(0,0,px[2]*cos(pi/NoS),py[2]*cos(pi/NoS),col=rgb(0,0,1))
text(px[2]*cos(pi/NoS),py[2]*cos(pi/NoS),"r",col=rgb(0,0,1),cex=1.5)
}
# アニメーション
library("animation")
Time_Code=c(2,2,2,3,3,3,4,4,4,5,5,5,6,6,6,7,7,7,8,8,8,9,9,9,10,10,10)
saveGIF({
for (i in Time_Code){
CIC(i)
}
}, interval = 0.1, movie.name = "CIC01.gif")
一辺の長さがaの正n角形に外接する円の半径**r**
- $r=\frac{a}{2\tan(\frac{π}{n})}$
- $a=r(2\tan(\frac{π}{n}))$
一辺の長さがAの正n角形に内接する円の半径**R**
- $R=\frac{A}{2\tan(\frac{π}{n})cos(\frac{π}{n})}$
- $A=R(2\tan(\frac{π}{n})cos(\frac{π}{n}))$
一辺の長さがaの正n角形の外接円の半径と内接円の半径の関係
1.$r=Rcos(\frac{π}{n})$
2.$R=\frac{r}{cos(\frac{π}{n})}$
外接円を単位円(Unit Circle)としたのが上記アニメーション。
- 外接円の半径**R**は単位円の定義に従って1
- これに内接する正多辺形の1辺の長さ**A**は$2\tan(\frac{π}{辺数})cos(\frac{π}{辺数})$
- 外接円に内接する正多辺形の内接円の半径**r**は$cos(\frac{π}{辺数})$
この法則を上手く使えばa*nすなわち「対象円に外接する正n角形の全周」と「対象円に内接する正n角形の全周」で「半径1の円の全周=2π(=6.283185…)」を挟み撃ちにする形で_円周率「π(3.141593…)をある程度の精度まで求められる筈です。要するに「**対象円に内接する正n角形の一辺の長さ=$a_0$」「対象円に外接する正n角形の一辺の長さ=$a_1$」と置くと「$n(a_1-a_0)$」で近似されるのです。

Regular_Polygon_draw03<-function(x) {
# グラフの色の決定
Black<-rgb(0,0,0)
Red<-rgb(1,0,0)
Magenta<-rgb(1,0,1)
Blue<-rgb(0,0,1)
Green<-rgb(0,1,0)
Cyan<-rgb(0,1,1)
Yellow<-rgb(1,1,0)
Gray<-"#888888"
# タイトル定義
Main_title<-c("The Limit of inscribed polygons and circumscribed polygons")
x_title<-c("Real number")
y_title<-c("Imaginary number")
# グラフのスケール決定
gs_x<-c(-1,1)
gs_y<-c(-1,1)
# Circumscribed circle(外接多角形)
f1_name<-c("Circumscribed Polygon")
f0<-function(x){exp(x*(0+1i))}
c1<-seq(-pi,pi,length=x+1)
c1_r<-Re(f0(c1))
c1_i<-Im(f0(c1))
# Regular_Polygon(中間円)
f2_name<-c("Inner circle")
c2<-seq(-pi,pi,length=100)
c2_r<-Re(f0(c2))
c2_i<-Im(f0(c2))
# Inscribed circle(内接多角形)
f3_name<-c("Inscribed Polygon")
scl<-cos(pi/x)
# グラフ描画
plot(c1_r,c1_i,asp=1,xlim=gs_x,ylim=gs_y,type="l",col=Green, main=Main_title,xlab=x_title,ylab=y_title)
par(new=T)#上書き指定
plot(c2_r*scl,c2_i*scl,asp=1,xlim=gs_x,ylim=gs_y,type="l",col=Black, main="",xlab="",ylab="")
par(new=T)#上書き指定
plot(c1_r*scl,c1_i*scl,asp=1,xlim=gs_x,ylim=gs_y,type="l",col=Blue, main="",xlab="",ylab="")
# 基準線
abline(h=0)
abline(v=0)
# 凡例描画
legend("topleft", legend=c(f1_name,f2_name,f3_name),lty=c(1,1,1),col=c(Green,Black,Blue))
}
library("animation")
Time_Code=c(3,3,4,4,5,5,6,6,7,7,8,8,9,9,10,11,12,13,14,15,20,25,30,35,40,45,50,60,70,80,90,100)
saveGIF({
for (i in Time_Code){
Regular_Polygon_draw03(i)
}
}, interval = 0.1, movie.name = "TEST01.gif")
# グラフの色の決定
Black<-rgb(0,0,0)
Red<-rgb(1,0,0)
Magenta<-rgb(1,0,1)
Blue<-rgb(0,0,1)
Green<-rgb(0,1,0)
Cyan<-rgb(0,1,1)
Yellow<-rgb(1,1,0)
Gray<-"#888888"
# タイトル
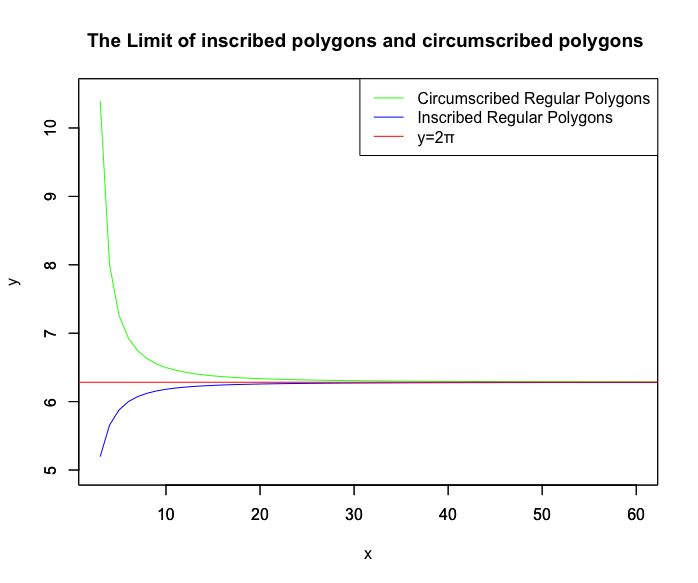
Main_title<-c("The Limit of inscribed polygons and circumscribed polygons ")
x_title<-c("x")
y_title<-c("y")
# x軸=多角形の範囲(3~100)
c0<-seq(3,100,length=98)
# グラフのスケール決定
gs_x<-c(3,60)
gs_y<-c(5,10.5)
# 基準円に外接する正多角形
f1_name<-c("Circumscribed Regular Polygons")
# CRPal=Circumscribed Regular Polygons all around
CRPal<-function(n) {(2*tan(pi/n))*n}
c1<-CRPal(c0)
# 基準円に内接する正多角形
f2_name<-c("Inscribed Regular Polygons")
# IRPal=Inscribed Regular Polygons all around
IRPal<-function(n) {(2*tan(pi/n))*cos(pi/n)*n}
c2<-IRPal(c0)
# 描画
plot(c0,c1,xlim=gs_x,ylim=gs_y,type="l",col=Green, main=Main_title,xlab=x_title,ylab=y_title)
par(new=T)#上書き指定
plot(c0,c2,xlim=gs_x,ylim=gs_y,type="l",col=Blue, main="",xlab="",ylab="")
abline(h=pi*2,col=Red)
legend("topright", legend=c(f1_name,f2_name,"y=2π"),lty=c(1,1,1),col=c(Green,Blue,Red))
こうして近年ではπ(pi≈3.141593)や2π(2*pi≈6.283185)の近似値が、その気になれば誰でも容易に求められる様になりました。
pi
[1] 3.141593
2*pi
[1] 6.283185
IRPal<-function(n) {(2*tan(pi/n))*cos(pi/n)*n}
IRPal(60)
[1] 6.280315