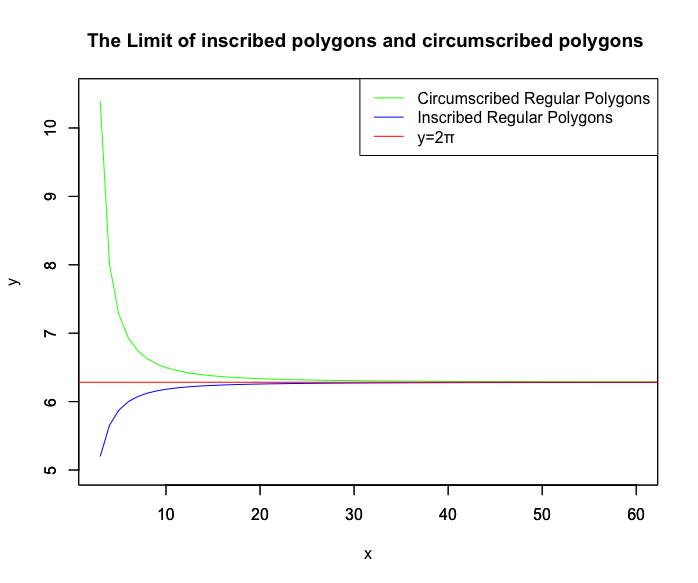
コンピューターなどが稼働する加算直積可能世界(Countable and Productable Sets)は、残念ながら「辺長が無限小(1/Inf)で辺数が無限大(Inf)」と定義される円そのもの(Circle itself)を直接は扱えません。それで概念上、必要にして十分なだけの辺数(NoS=Number of Sides)を備えた正多辺形(Regular PolySides)を用意し、これを代替操作対象としてきたのです。例えば、その起源がシュメール文明(紀元前3500年〜紀元前2350年頃)まで遡るとされる60進法に由来する60角形…
正多角形による円の近似
# CVCM=等速円運動(Constant Velocity Circular Motion)
# Radian=角度(60分割)
CVCM<-function(Radian){
c0<-seq(0,2*pi,length=60)
cx<-cos(c0)
cy<-sin(c0)
plot(cx,cy,asp=1,type="l",col=rgb(0,1,0),main="Constant Velocity Circular Motion",xlab="cos(θ)",ylab="sin(θ)")
# 塗りつぶし(円)
polygon(cx, #x
cy, #y
density=c(30), #塗りつぶす濃度
angle=c(45), #塗りつぶす斜線の角度
col=c(200,200,200)) #塗りつぶす色
text(cx[Radian],cy[Radian],"%",col=rgb(1,0,0))
segments(cx[Radian],cy[Radian],0,0,col=rgb(1,0,0))
# 凡例
legend("bottomright", legend=c("side=2π/1τ","radius=1"), lty=c(1,1), col=c(rgb(0,1,0),rgb(1,0,0)))
}
# アニメーション
library("animation")
Time_Code=seq(1,59, length=30)
saveGIF({
for (i in Time_Code){
CVCM(i)
}
}, interval = 0.1, movie.name = "CVCM01.gif")
とりあえずこうした考え方を近似円概念(Approximate Circle Concept)と呼ぶ事にします。見掛けはほとんど円そのもの。しかも「必要にして十分なだけの辺数を備えた正多辺形への代替」に成功した副産物として角度の概念の導入が可能となるのです。
角度概念の起源
そもそも「円そのもの」の各頂点は中心からの垂線(Perpendicular)と直角に交わるとされているので、それぞれを含む水平線(Horizon)も引ける訳です。近似円概念を直交座標系(Rectangular Coordinate System / Orthogonal Coordinate System)に射影(Projiection)する際の基本ですね。例えば半径1の単位円を原点(0,0)に射影する場合は以下となります。
- 円の上端の座標=(0,1)
- 円の下端の座標=(0,-1)
- 円の左端の座標=(-1,0)
- 円の右端の座標=(1,0)
後はどう分割結果を反映させるかですね。尺度としては_60*60=360_を分割数に据えた度数法(Degree measure)と、半径rの円の周長が2πrである点に注目した弧度法(Radian measure)辺りが二大巨塔と目されています。後者は当然、それに先立って半径rの場合の円周長2πrが求められる必要がありました。
【初心者向け】挟み撃ち定理(Squeeze Theorem)による円周率πの近似
弧度法とは?度数法との違いと表・求め方

| radians | degrees | Cos | Sin | |
|---|---|---|---|---|
| 1 | 0.00 | 0.00 | 1.00 | 0.00 |
| 2 | 0.10 | 6.00 | 0.99 | 0.10 |
| 3 | 0.21 | 12.00 | 0.98 | 0.21 |
| 4 | 0.31 | 18.00 | 0.95 | 0.31 |
| 5 | 0.42 | 24.00 | 0.91 | 0.41 |
| 6 | 0.52 | 30.00 | 0.87 | 0.50 |
| 7 | 0.63 | 36.00 | 0.81 | 0.59 |
| 8 | 0.73 | 42.00 | 0.74 | 0.67 |
| 9 | 0.84 | 48.00 | 0.67 | 0.74 |
| 10 | 0.94 | 54.00 | 0.59 | 0.81 |
| 11 | 1.05 | 60.00 | 0.50 | 0.87 |
| 12 | 1.15 | 66.00 | 0.41 | 0.91 |
| 13 | 1.26 | 72.00 | 0.31 | 0.95 |
| 14 | 1.36 | 78.00 | 0.21 | 0.98 |
| 15 | 1.47 | 84.00 | 0.10 | 0.99 |
| 16 | 1.57 | 90.00 | 0.00 | 1.00 |
| 17 | 1.68 | 96.00 | -0.10 | 0.99 |
| 18 | 1.78 | 102.00 | -0.21 | 0.98 |
| 19 | 1.88 | 108.00 | -0.31 | 0.95 |
| 20 | 1.99 | 114.00 | -0.41 | 0.91 |
| 21 | 2.09 | 120.00 | -0.50 | 0.87 |
| 22 | 2.20 | 126.00 | -0.59 | 0.81 |
| 23 | 2.30 | 132.00 | -0.67 | 0.74 |
| 24 | 2.41 | 138.00 | -0.74 | 0.67 |
| 25 | 2.51 | 144.00 | -0.81 | 0.59 |
| 26 | 2.62 | 150.00 | -0.87 | 0.50 |
| 27 | 2.72 | 156.00 | -0.91 | 0.41 |
| 28 | 2.83 | 162.00 | -0.95 | 0.31 |
| 29 | 2.93 | 168.00 | -0.98 | 0.21 |
| 30 | 3.04 | 174.00 | -0.99 | 0.10 |
| 31 | 3.14 | 180.00 | -1.00 | 0.00 |
| 32 | 3.25 | 186.00 | -0.99 | -0.10 |
| 33 | 3.35 | 192.00 | -0.98 | -0.21 |
| 34 | 3.46 | 198.00 | -0.95 | -0.31 |
| 35 | 3.56 | 204.00 | -0.91 | -0.41 |
| 36 | 3.67 | 210.00 | -0.87 | -0.50 |
| 37 | 3.77 | 216.00 | -0.81 | -0.59 |
| 38 | 3.87 | 222.00 | -0.74 | -0.67 |
| 39 | 3.98 | 228.00 | -0.67 | -0.74 |
| 40 | 4.08 | 234.00 | -0.59 | -0.81 |
| 41 | 4.19 | 240.00 | -0.50 | -0.87 |
| 42 | 4.29 | 246.00 | -0.41 | -0.91 |
| 43 | 4.40 | 252.00 | -0.31 | -0.95 |
| 44 | 4.50 | 258.00 | -0.21 | -0.98 |
| 45 | 4.61 | 264.00 | -0.10 | -0.99 |
| 46 | 4.71 | 270.00 | -0.00 | -1.00 |
| 47 | 4.82 | 276.00 | 0.10 | -0.99 |
| 48 | 4.92 | 282.00 | 0.21 | -0.98 |
| 49 | 5.03 | 288.00 | 0.31 | -0.95 |
| 50 | 5.13 | 294.00 | 0.41 | -0.91 |
| 51 | 5.24 | 300.00 | 0.50 | -0.87 |
| 52 | 5.34 | 306.00 | 0.59 | -0.81 |
| 53 | 5.45 | 312.00 | 0.67 | -0.74 |
| 54 | 5.55 | 318.00 | 0.74 | -0.67 |
| 55 | 5.65 | 324.00 | 0.81 | -0.59 |
| 56 | 5.76 | 330.00 | 0.87 | -0.50 |
| 57 | 5.86 | 336.00 | 0.91 | -0.41 |
| 58 | 5.97 | 342.00 | 0.95 | -0.31 |
| 59 | 6.07 | 348.00 | 0.98 | -0.21 |
| 60 | 6.18 | 354.00 | 0.99 | -0.10 |
| 61 | 6.28 | 360.00 | 1.00 | -0.00 |
# 角度(ラディアン/度)とCos(θ)/Sin(θ)の対応
c0<-seq(0,2*pi,length=61)
c1<-seq(0,360,length=61)
cx<-cos(c0)
cy<-sin(c0)
TR01<- data.frame(radians=c0,degrees=c1,Cos=cx,Sin=cy)
library(xtable)
print(xtable(TR01),type="html")
これではあまりに解りにくいので、初学者向けにこういう図も出回っている様です。試験向けに暗記するならこっち?

とりあえず_半径1,周長2πの単位円_(Unit Circle)の円弧上において、角度さえ求められれば自動的に決定するx座標が正弦波(Sine wave)、y座標が余弦波(Cosin wave)という認識。
【初心者向け】物理学における「単位円筒(Unit Cylinder)」の概念について。

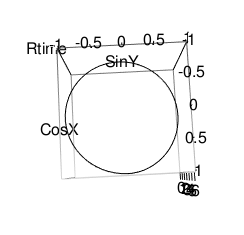
XY軸(円弧)

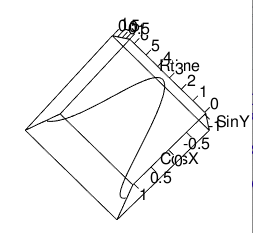
XZ軸(Cos波)

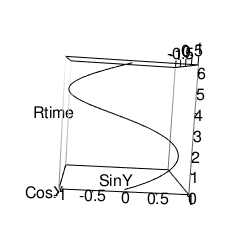
YZ軸(Sin波)

【初心者向け】三角関数と指数・対数関数の「巡回性」について。


【Rで球面幾何学】オイラーの公式を導出したマクローリン級数の限界?

【Rで球面幾何学】オイラーの公式とは、そもそも何か?

地球儀上における経度(longitude)の概念はこれに由来するとも。
緯度経度とは?
ならば緯度の概念は何処から発祥したのでしょう…それについては、以下続報。
