【初心者向け】三角関数と指数・対数関数の「巡回性」について。

今回は大上段に構えて既存知識(Existing Knowledge)の点検(Inspection)と保守(Maintenance)という話から始めましょう。

数理的問題解決方法(Mathematical Problem Solving)の世界は、特に厳密な手続きを必要とします。「すでに正しいことが明らかになっている事柄を基にして別の新しい事柄が正しいことを説明していく」演繹法(Deduction)の論理(Logic)と「いくつかの具体例を調べて共通性を見付ける」帰納法(Induction)や「既習の内容との類似性に着目して新しい事柄を見いだす」類推法(Analogy)の論理を突き合わせ、適切かつ合理的な手続き(Method)に従って粛々と点検(Inspection)と再点検(Re-inspection)を重ねていくのです。
小学校算数科数学的な考え方「演繹的な考え方」
適切なって英語でなんて言うの？

appropriateは「規定のルールに合致する」
suitableは「状況的にふさわしい」
properは「社会的な基準に照らし合わせ、礼儀にかなっている」
rightは「大まかに回答として間違ってない、道義的に正しいと見做される」

それではおもむろに自分の三角関数(Trigonometric Function)についての知識の保守点検作業に入ります。

三角関数 - Wikipedia

平面三角法における、角の大きさと線分の長さの関係を記述する関数の族(Famiry)および、それらを拡張して得られる関数の総称である。鋭角を扱う場合、その値は対応する直角三角形の二辺の長さの比となり三角比(Triangular Ratio)とも呼ばれる。三角法に由来する三角関数という呼び名のほかに、半径1の単位円(Unit Circle)を用いた定義に由来する円関数（Circular Function）という呼び名もある。

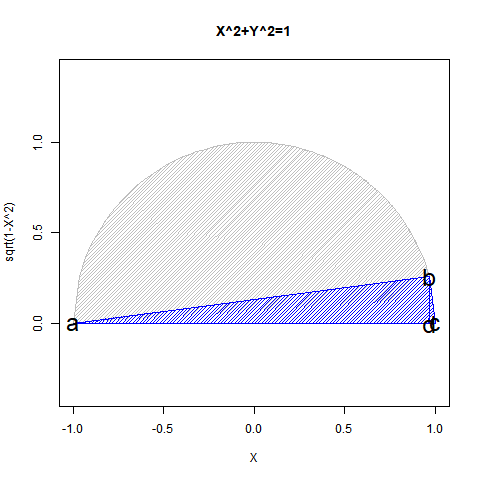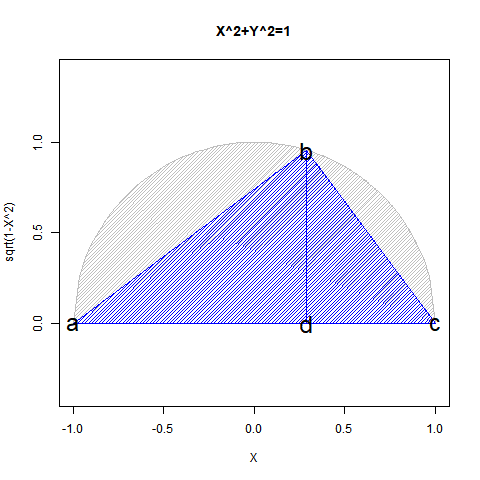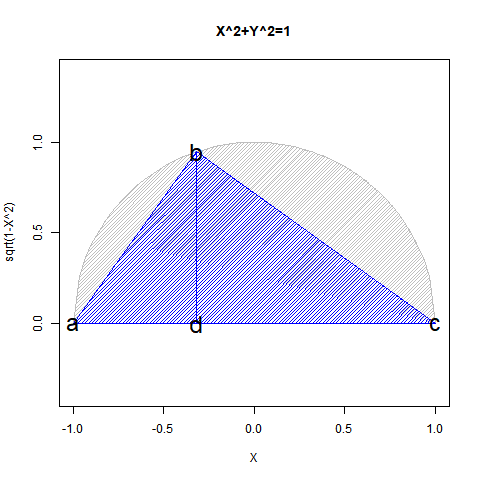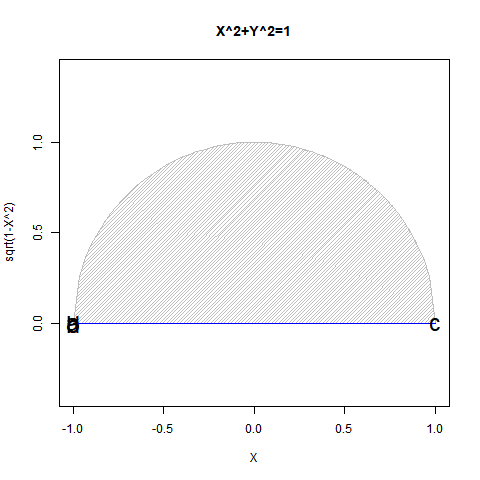
①ある意味「安楽椅子数学者(Armchair Mathematician)」っぽい雰囲気が漂う三角比(Triangular Ratio)の世界には演繹法(Deduction)の産物という印象がある。実際には測量技術の流れもあるから帰納法(Induction)と完全に無縁でもないだろうが「半円しか描けない」制約を自力で乗り越えられなかった事実は動かない。
【Rで球面幾何学】「半円しか描けなかった」世界の思い出？

②一方、現在につながる円関数（Circular Function）の世界は天体や等速円運動の物理的観測から出発した帰納法(Induction)の産物と言える。
【初心者向け】物理学における「単位円筒(Unit Cylinder)」の概念について。
XY軸（円弧）

XZ軸（Cos波）

YZ軸（Sin波）

特に sin, cos は幾何学的にも解析学的にも良い性質を持っているので、様々な分野で用いられる。例えば波や電気信号などは正弦関数と余弦関数を組み合わせることで表現することができる。この事実はフーリエ級数およびフーリエ変換の理論として知られ、音声などの信号の合成や解析の手段として利用されている。

他にもベクトルの外積や内積は正弦関数および余弦関数を用いて表すことができ、ベクトルを図形に対応づけることができる。

三角関数の基礎定理①ピタゴラスの定理。

ピタゴラスの定理(Pythagorean Theorem)…円概念(Circle Concept)/球面概念(Sphere Concept)そのものを構築する基本演算。
【初心者向け】ピタゴラスの定理あるいは三平方の定理からの出発

• 半径r=sqrt(x座標^2+y座標^2)…ただし直交座標系(Cartesian Coordinate System){x座標,y座標}において円の中心(Center)が原点{0,0}の場合。半径1の単位円(Unit Circle)sqrt(x^2+y^2)=1のr倍の同心円集合(Concentric Set)を構築する。y=±sqrt(1-x^2)あるいはx=±sqrt(1-y^2)の計算集合(Calculation Set)に従ってそれぞれの座標を求める。
• 半径r=sqrt(x座標^2+y座標^2+z座標^2)…ただし直交座標系{x座標,y座標,z座標}において円の中心が原点{0,0,0}の場合。半径1の単位球面(Unit Sphere)sqrt(x^2+y^2+z^2)=1のr倍の同心球面集合(Homocentric Sphere Set)を構築する。xy面ではy=sqrt(1-x^2)あるいはx=sqrt(1-y^2)、xz面ではz=sqrt(1-x^2)あるいはx=sqrt(1-z^2)、yz面ではz=sqrt(1-z^2)あるいはx=sqrt(1-z^2)の計算でそれぞれの座標を求める。

私が思うに、ここで確実にしっかり把握すべきは「数直線概念(Number Line Concept)」との連続性です。
【Rで球面幾何学】等差数列(算術数列)②数直線概念から同心円集合概念へ

何故なら実はピタゴラスの定理(Pythagorean Theorem)は、二項展開 (binomial expansion)の以下の特殊型に過ぎず直交の概念と深く関わってくるからです。

• 余弦定理(cosine formula)a^2=(b-c)^2=b^2+c^2−2bc*cos(α)においてα=90度(π/2ラジアン)の場合、cos(α)=0なのでa^2=b^2+c^2−2bc*0=b^2+c^2となる。

【初心者向け】パスカルの三角形と二項定理または二項展開

あと(現在の私にはまだちゃんとした形で説明出来ませんが)ここでの半径rの概念はその後ノルム(Norm)の概念に拡張される筈で、そういう意識も重要そうです。
ノルムとは - コトバンク
ノルムの意味とL1，L2，L∞ノルム
関数の内積とノルムの定義を総ざらい！意外に重要な単元！
ハミルトンの四元数(quaternion)がRe+Xi+Yj+Zkで表されるのもこれですね。そう、ノルムはスカラー量…
【Rで球面幾何学】ハミルトンの四元数は何を表しているのか？


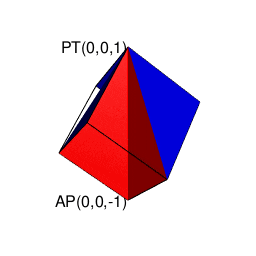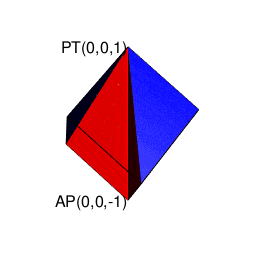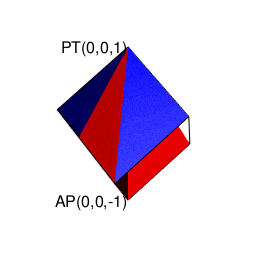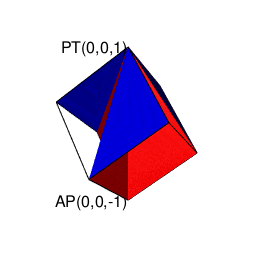
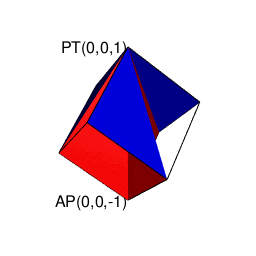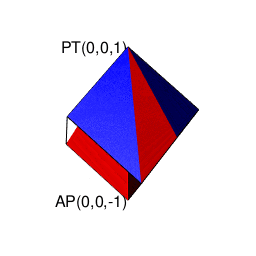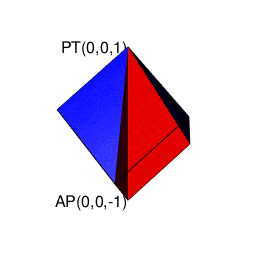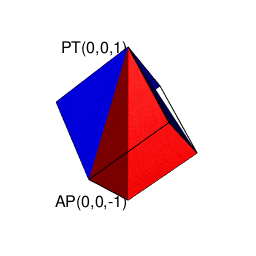
【Rで球面幾何学】そもそも「内積」とは「外積」とは何か？

三角関数の基礎定理②合成角の公式。

三角関数の合成公式

• α(-180度<=α<=180度あるいは-πラジアン<=α<=πラジアン)が与えられcos(α)=b/sqrt(a^2+b^2),sin(α)=a/sqrt(a^2+b^2)の条件が満たされる時、a×sin(θ)+b×cos(θ)=sqrt(a^2+b^2)×sin(θ+α)
  
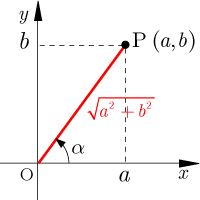
• β(-180度<=α<=180度あるいは-πラジアン<=α<=πラジアン)が与えられcos(β)=a/sqrt(a^2+b^2),sin(β)=b/sqrt(a^2+b^2)の条件が満たされる時、a×sin(θ)+b×cos(θ)=sqrt(a^2+b^2)×cos(θ-β)
  

統計言語Rによる検算結果

#theta_a(pi/3ラジアン(60度)=1.047198
theta_a<-pi/3
> pi/3
[1] 1.047198

#theta_c=π/4ラジアン(45度)=0.7853982
> theta_c
[1] 0.7853982
> pi/4
[1] 0.7853982

#a×sin(θ)+b×cos(θ)=sin(θ+α)
> a<-sin(theta_a)
> a
[1] 0.8660254
> b<-cos(theta_a)
> b
[1] 0.5
> a*sin(theta_c)+b*cos(theta_c)
[1] 0.9659258
> sin(theta_a+theta_c)
[1] 0.9659258

#a×sin(θ)+b×cos(θ)=cos(α-θ)
> a<-cos(theta_a)
> a
[1] 0.5
> b<-sin(theta_a)
> b
[1] 0.8660254
> a*sin(theta_c)+b*cos(theta_c)
[1] 0.9659258
> cos(theta_c-theta_a)
[1] 0.9659258

この様に半径1の単位円(Unit Circle)上では半径1=sqrt(a^2+b^2)と置けるので、上掲式は以下の様に統合されるのです。

• (三角形の内角の和が180度(πラジアン)でそのうち1角が90度(π/2ラジアン)を占める)直角三角形の特徴から合計が90度(π/2ラジアン)となる角a0b/b0a=α(-180度<=α<=180度あるいは-πラジアン<=α<=πラジアン),0ba/ab0=β(90度~-90度あるいはπ/2ラジアン~-π/2ラジアン)が与えられ、X成分(X Elements)a=cos(α)=sin(β),Y成分(Y Elements)b=cos(β)=sin(α)と置ける時、a×sin(θ)+b×cos(θ)=cos(θ-β)=sin(θ+α)
  

統計言語Rによるグラフ化

#複素平面（球面）
Complex_plane<-function(x){
theta<-c(seq(0, pi, length=180),seq(-pi, 0, length=180))
dr<-seq(0,2*pi,length=360)

plot(cos(theta),sin(theta),asp=1,xlim=c(-1,1), ylim=c(-1,1), type="l", main="Unit Circle",xlab="X Elements(Cos(θ))", ylab="Y Elements(Sin(θ))")

#線を引く
segments(cos(dr[x]),0,0,0,col=rgb(0,1,0),lwd=2)
segments(cos(dr[x]),sin(dr[x]),cos(dr[x]),0,col=rgb(0,0,1),lwd=2)
segments(cos(dr[x]),sin(dr[x]),0,0,col=rgb(1,0,0),lwd=2)

#文字追加
text(c(cos(dr[x]),cos(dr[x]),0),c(0,sin(dr[x]),0), labels=c("a","b","0"),col=c(rgb(0,1,0),rgb(0,0,1),rgb(1,0,0)),cex=c(2,2,2))

#内積を塗りつぶす
polygon(c(cos(dr[x]),cos(dr[x]),0), #x
c(sin(dr[x]),0,0), #y
density=c(30), #塗りつぶす濃度
angle=c(45),　 　　　#塗りつぶす斜線の角度
col=c(200,200,200)) 　#塗りつぶす色
legend("bottomleft", legend=c("a=Cos(θ)","b=Sin(θ)","sqrt(a^2+b^2)=1", "inner product"), lty=c(1,1),col =c(rgb(0,1,0),rgb(0,0,1),rgb(1,0,0),c(200,200,200)))

}
#アニメーションさせてみる。

library("animation")
Time_Code=c(1,15,30,45,60,75,90,105,120,135,150,165,180,195,210,225,240,255,270,285,300,315,330,345)
saveGIF({
for (i in Time_Code){
　　Complex_plane(i)
}
}, interval = 0.1, movie.name = "TEST.gif")

統計言語Rによる検算結果

#theta_a(pi/3ラジアン(60度)
theta_a<-pi/3
#theta_b(pi/6ラジアン(30度)
theta_b<-pi/6
#theta_a+theta_b=π/2ラジアン(90度)
theta_a+theta_b
> pi/3+pi/6
[1] 1.570796
> pi/2
[1] 1.570796

#theta_c=π/4ラジアン(45度)=0.7853982
> theta_c
[1] 0.7853982
> pi/4
[1] 0.7853982

#a=cos(theta_a)=sin(theta_b)
> a<-cos(theta_a)
> cos(theta_a)
[1] 0.5
> sin(theta_b)
[1] 0.5

#b=sin(theta_a)=cos(theta_b)
> b<-sin(theta_a)
> sin(theta_a)
[1] 0.8660254
> cos(theta_b)
[1] 0.8660254

#a×sin(θ)+b×cos(θ)=cos(theta_b-θ)=sin(θ+theta_a)
> a*sin(theta_c)+b*cos(theta_c)
[1] 0.9659258
> cos(theta_c-theta_b)
[1] 0.9659258
> sin(theta_c+theta_a)
[1] 0.9659258

実はこの表現には問題があり、集合論(Set Theory)的に言い直そうとすると、とりあえずこうなります。

• (三角形の内角の和がπラジアンでそのうち1角がπ/2ラジアンを占める)直角三角形の特徴から合計がπ/2ラジアン(π/2ラジアン)となる角集合(Angle Set)a0b/b0a=αn((n1→n2=n1→…)=(0ラジアン→2πラジアン=0ラジアン…)),0ba/ab0=βm(m=n+π/2ラジアン)が与えられ、X座標集合(X Coordinate Set)Xn((n1→n2→n3→n4→n1→…){1→0→-1→0→1→…}=cos(αn)=sin(βm),Y座標集合(Y Coordinate Set)Yn((n1→n2→n3→n4→n1→…){0→1→0→-1→0→…}=sin(αn)=-cos(βm)と置ける時、Xn×cos(θ)+Ym×sin(θ)=cos(θ-αn)=sin(θ+αn)
  

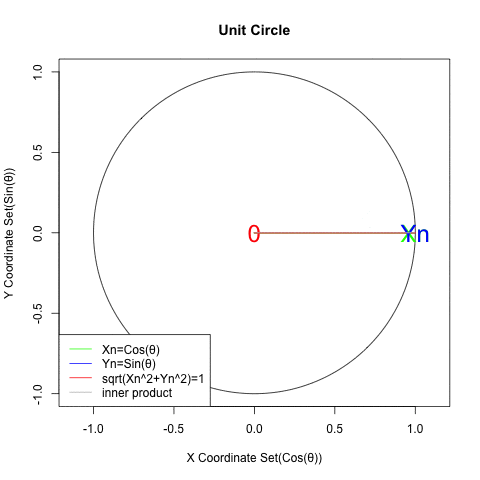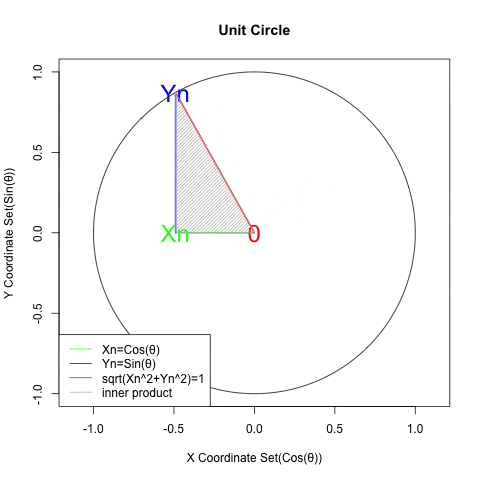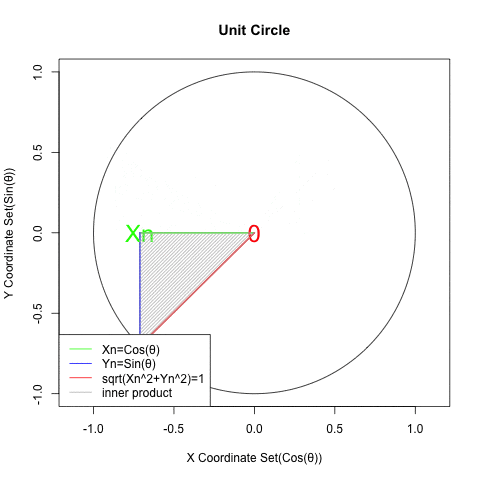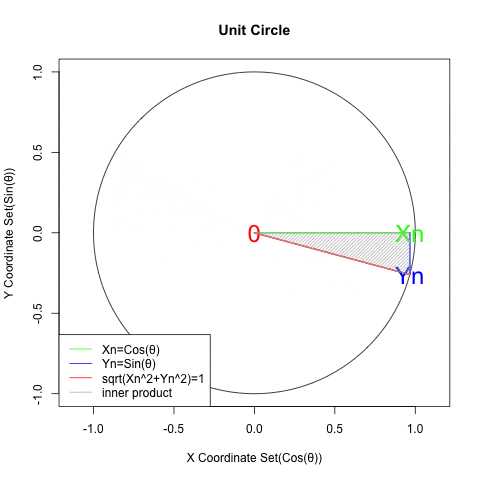
統計言語Rによるグラフ化

#複素平面（球面）
Complex_plane<-function(x){
theta<-c(seq(0, pi, length=180),seq(-pi, 0, length=180))
dr<-seq(0,2*pi,length=360)

plot(cos(theta),sin(theta),asp=1,xlim=c(-1,1), ylim=c(-1,1), type="l", main="Unit Circle",xlab="X Coordinate Set(Cos(θ))", ylab="Y Coordinate Set(Sin(θ))")

#線を引く
segments(cos(dr[x]),0,0,0,col=rgb(0,1,0),lwd=2)
segments(cos(dr[x]),sin(dr[x]),cos(dr[x]),0,col=rgb(0,0,1),lwd=2)
segments(cos(dr[x]),sin(dr[x]),0,0,col=rgb(1,0,0),lwd=2)

#文字追加
text(c(cos(dr[x]),cos(dr[x]),0),c(0,sin(dr[x]),0), labels=c("Xn","Yn","0"),col=c(rgb(0,1,0),rgb(0,0,1),rgb(1,0,0)),cex=c(2,2,2))

#内積を塗りつぶす
polygon(c(cos(dr[x]),cos(dr[x]),0), #x
c(sin(dr[x]),0,0), #y
density=c(30), #塗りつぶす濃度
angle=c(45),　 　　　#塗りつぶす斜線の角度
col=c(200,200,200)) 　#塗りつぶす色
legend("bottomleft", legend=c("Xn=Cos(θ)","Yn=Sin(θ)","sqrt(Xn^2+Yn^2)=1", "inner product"), lty=c(1,1),col =c(rgb(0,1,0),rgb(0,0,1),rgb(1,0,0),c(200,200,200)))

}
#アニメーションさせてみる。

library("animation")
Time_Code=c(1,15,30,45,60,75,90,105,120,135,150,165,180,195,210,225,240,255,270,285,300,315,330,345)
saveGIF({
for (i in Time_Code){
　　Complex_plane(i)
}
}, interval = 0.1, movie.name = "UC01.gif")

統計言語Rによる検算結果

#theta_a(90度=π/2ラジアン単位の回転)
theta_a<-c(0,pi/2,pi,3*pi/2,2*pi)
> theta_a
[1] 0.000000 1.570796 3.141593 4.712389 6.283185
#1周2πでリセット
> theta_a%%(2*pi)
[1] 0.000000 1.570796 3.141593 4.712389 0.000000

#theta_b(theta_aの90度=π/2ラジアン位相ずれ)
> theta_b<-theta_a+pi/2
> theta_b
[1] 1.570796 3.141593 4.712389 6.283185 7.853982
> theta_b-theta_a
[1] 1.570796 1.570796 1.570796 1.570796 1.570796
> theta_b%%(2*pi)
[1] 1.570796 3.141593 4.712389 0.000000 1.570796

#theta_c=π/4ラジアン(45度)=0.7853982
> theta_c
[1] 0.7853982
> pi/4
[1] 0.7853982

#Xn=cos(theta_a)=sin(theta_b)
>Xn<-cos(theta_a)
> round(cos(theta_a), digits=4)
[1]  1  0 -1  0  1
> round(sin(theta_b), digits=4)
[1]  1  0 -1  0  1

#Yn=sin(theta_a)=cos(theta_b)
> Yn<-sin(theta_a)
> round(sin(theta_a),digits=4)
[1]  0  1  0 -1  0
round(cos(theta_b),digits=4)
[1]  0 -1  0  1  0

#Xn×sin(θ)+Yn×cos(θ)=cos(θ-theta_b)=sin(θ+theta_a)
> Xn*sin(theta_c)+Yn*cos(theta_c)
[1]  0.7071068  0.7071068 -0.7071068 -0.7071068  0.7071068
> cos(theta_c-theta_b)
[1]  0.7071068 -0.7071068 -0.7071068  0.7071068  0.7071068
> sin(theta_c+theta_a)
[1]  0.7071068  0.7071068 -0.7071068 -0.7071068  0.7071068

そう、それまでの方法ではbがマイナスの場合cos(π/2),cos(3π/2)の計算が狂ってしまうのです。bがマイナスの場合も視野に入れると以下の様に計算しないといけません。

• Yn=sin(theta_a)=-cos(theta_b)
• Xn×sin(θ)+Yn×cos(θ)=cos(θ-theta_a)

統計言語Rによる検算結果

#Yn=sin(theta_a)=-cos(theta_b)
> Yn<-sin(theta_a)
> round(sin(theta_a),digits=4)
[1]  0  1  0 -1  0
> round(-cos(theta_b),digits=4)
[1]  0  1  0 -1  0

#Xn×sin(θ)+Yn×cos(θ)=cos(θ-theta_a)=sin(θ+theta_a)
> Xn*sin(theta_c)+Yn*cos(theta_c)
[1]  0.7071068  0.7071068 -0.7071068 -0.7071068  0.7071068
> cos(theta_c-theta_a)
[1]  0.7071068  0.7071068 -0.7071068 -0.7071068  0.7071068
> sin(theta_c+theta_a)
[1]  0.7071068  0.7071068 -0.7071068 -0.7071068  0.7071068

三角関数の合成の問題で、sinθまたはcosθの係数が負の場合はどう処理するのですか？

a×Sin(θ)-b×Cos(θ)=sqrt(a^2+b^2)Sin(θ-a)
Sin(θ),Cos(θ)の係数が正なら括弧の中の角は第一象限
Sin(θ)が負、Cos(θ)が正なら第二象限
Sin(θ),Cos(θ)が負なら第三象限
Sin(θ)が正、Cos(θ)が負なら第四象限

三角関数の基礎定理③加法定理。

加法定理(Addition Theorem)…角αと角βを足し合わせ角γにする際のCos(γ)とSin(γ)を求める式である。
【初心者向け】「加法定理の幾何学的証明」に挑戦。

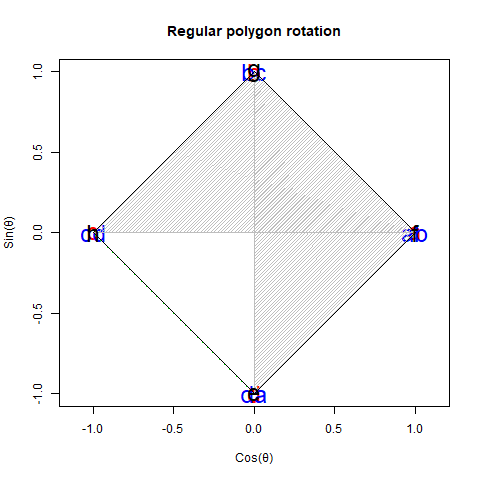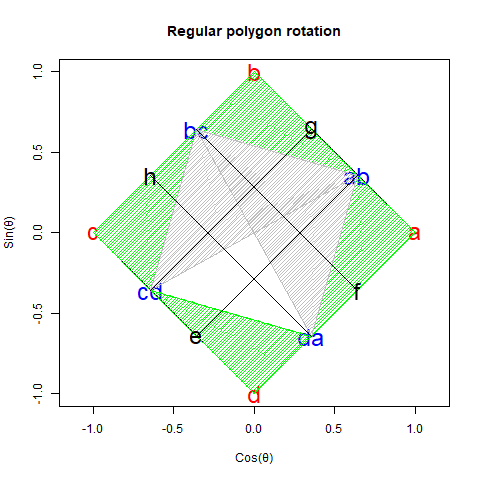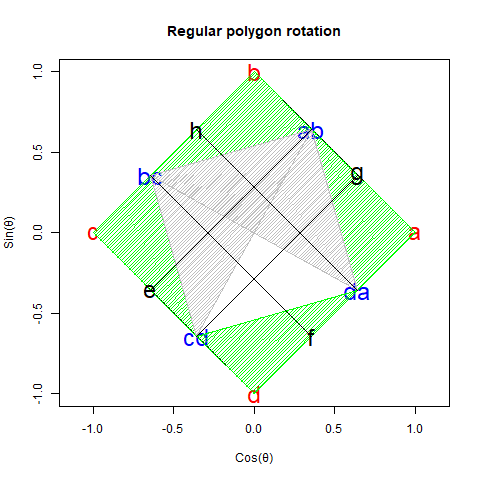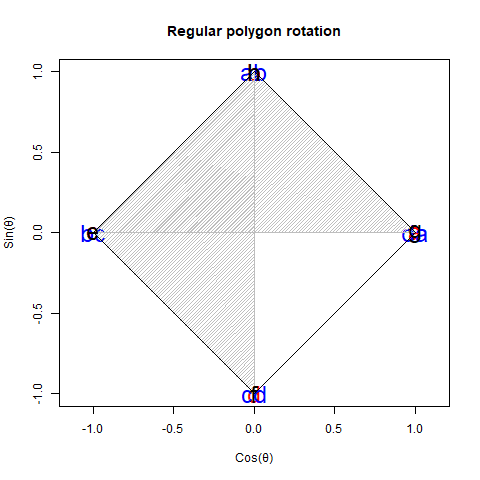
加算

• Cos(α+β)=Cos(α)Cos(β)-Sin(α)Sin(β)
• Sin(α+β)=Cos(α)Sin(β)+Sin(α)Cos(β)
• Tan(α+β)=(Tan(α)+Tan(β))/(1-Tan(α)Tan(β))

減算

• Cos(α-β)=Cos(α)Cos(β)+Sin(α)Sin(β)
• Sin(α-β)=Sin(α)Cos(β)-Cos(α)Sin(β)
• Tan(α-β)=(Tan(α)-Tan(β))/(1+Tan(α)Tan(β))

ちなみに学校教育では以下も習います。

倍角の公式

• Cos(2a)=Cos(a)^2-Sin(a)^2=1-2*Sin(α)^2
• Sin(2α)=2*Sin(α)*Cos(α)
• Tan(2a)=2*tan(α)/1-Tan(α)^2

３倍角の公式

• Cos(3α)=4*Cos(α)^3-3*cos(α)
• Sin(3α)=3*Sin(α)^3-4*Sin(α)

半角の公式

• Cos(α/2)^2=(1+Cos(α))/2
• Sin(α/2)^2=(1-Cos(α))/2
• Tan(α/2)^2=(1-Cos(α))/(1+Cos(α))

積和の公式

• Sin(α)*Cos(β)=(Sin(α+β)+Sin(α-β))/2
• Cos(α)*Sin(β)=(Sin(α+β)-Sin(α-β))/2
• Cos(α)*Cos(β)=(Cos(α+β)+Cos(α-β))/2
• Sin(α)*Sin(β)=(Cos(α+β)-Cos(α-β))/2

和積の公式

• Sin(α)+Sin(β)=2*Sin((α+β)/2)*Cos((α-β)/2)
• Cos(α)-Cos(β)=2*Cos((α+β)/2)*Sin((α-β))/2)
• Cos(α)+Cos(β)=2*Cos((α+β)/2)*Cos((α-β))/2)
• Cos(α)-Cos(β)=-2*Sin((α+β)/2)*Sin((α-β)/2)

三角関数の基礎定理④三角不等式との関係について。

三角不等式(Triangle Inequality)
【初心者向け】「三角不等式(Triangle Inequality)」の体感方法？
‖x+y‖<=‖x‖+‖y‖

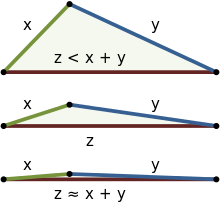
• ‖x‖と‖y‖が同一直線上にある場合のみ‖x+y‖=‖x‖+‖y‖が成立。その時の三角形の面積は0に退化する。

単位円(Unit Circle)上の直径を長編とする直角三角形では、正弦定理（Law of Sines）a/sin(a)+b/sin(b)+c/sin(c)~2rの特殊形たるターレスの定理(Thales' theorem)によって必ずその対角がπ/2ラジアン(90度)となり、残り2角α,βの合計も三角形の内角の和がπラジアン(180度)である事からπ/2ラジアン(90度)と定まる。
【初心者向け】三角関数と指数・対数関数の「巡回性」について。

• この時‖x+y‖=‖x‖+‖y‖が成立するのはcos(θ)=0かsin(θ)=0の場合のみ。

ちなみに単位円において三角比(Triangular ratio)概念が通用する範囲は以下の6通り。
【Rで球面幾何学】「半円しか描けなかった」世界の思い出？

• 第一象限(cos(θ)>=0,sin(θ)>=0)のみ。
• 第一象限とそれに隣接する第二象限(cos(θ)=1→0→-1,sin(θ)=0→1→0)。
• 第一象限とそれに隣接する第四象限(cos(θ)=0→1→0,sin(θ)=1→0→-1)。
• 第三象限(cos(θ)<=0,sin(θ)<=0)のみ。
• 第三象限とそれに隣接する第四象限(cos(θ)=1→0→-1,sin(θ)=0→-1→0)。
• 第三象限とそれに隣接する第二象限(cos(θ)=0→-1→0,sin(θ)=1→0→-1)。

三角関数の基礎定理⑤極座標系。

三角関数というと極座標系（Polar Coordinates System）を思い浮かべる人も多いと思います。

①二次元空間におけるデカルト座標(x,y)の極座標系上における表現

• 原点(0,0)からの距離r=sqrt(x^2+y^2)
• x=r*cos(φ)
• y=r*sin(φ)

②三次元空間におけるデカルト座標(x,y,z)の極座標系上における表現

• 原点(0,0,0)からの距離r=sqrt(x^2+y^2+z^2)
• x=r*sin(θ)cos(φ)
• y=r*sin(θ)sin(φ)
• z=r*cos(θ)

三角関数の基本定理⑥高校レベルの公式一覧の再確認

以降は高校レベルの三角関数の公式一覧を再確認しながら全体像の俯瞰を試みます。学童時代の私はこうした公式一覧全ての暗記を強要され、それで一旦は完全に算数に挫折したのです。
三角関数の公式一覧

• Cos(θ)^2+Sin(θ)^2=1(ピタゴラスの定理の応用)
• Tan(θ)=Sin(θ)/Cos(θ)(Tangent関数の定義)
• 1+Tan(θ)^2=1/Cos(θ)^2

Cosine関数の基本公式

• Cos(-θ)=Cos(θ)(符号の逆転)
• Cos(θ+2nπ)=Cos(θ)(1回転)
• Cos(θ+π/2)=-Sin(θ)(θ+π/2の三角関数)
• Cos(π/2-θ)=Sin(θ)(π/2-θの三角関数)
• Cos(θ+π)=-Cos(θ)(θ+πの三角関数)
• Cos(π-θ)=-Cos(θ)(π-θの三角関数)

Sine関数の基本公式

• Sin(-θ)=-Sin(θ)(符号の逆転)
• Sin(θ+2nπ)=Sin(θ)(1回転)
• Sin(θ+π/2)=Cos(θ)(θ+π/2の三角関数)
• Sin(π/2-θ)=Cos(θ)(π/2-θの三角関数)
• Sin(θ+π)=-Sin(θ)(θ+πの三角関数)
• Sin(π-θ)=Sin(θ)(π-θの三角関数)

Tangent関数の基本公式

• Tan(-θ)=-Tan(θ)(符号の逆転)
• Tan(θ+2nπ)=Tan(θ)(1回転)
• Tan(θ+π/2)=-1/Tan(θ)(θ+π/2の三角関数)
• Tan(π/2-θ)=1/Tan(θ)(π/2-θの三角関数)
• Tan(θ+π)=Tan(θ)(θ+πの三角関数)
• Tan(π-θ)=-Tan(θ)(π-θの三角関数)

#周期性検証の準備(θ)
> d0<-pi/8
> d0
[1] 0.3926991

#周期性検証の準備(θの周期)
> d1<-seq(-5,5,length=11)
> d1
 [1] -5 -4 -3 -2 -1  0  1  2  3  4  5

#基本公式

#Cos(θ)^2+Sin(θ)^2=1
> cos(d0)^2+sin(d0)^2
[1] 1
#Tan(θ)=Sin(θ)/Cos(θ)
> tan(d0)
[1] 0.4142136
> sin(d0)/cos(d0)
[1] 0.4142136
#1+Tan(θ)^2=1/Cos(θ)^2
> 1+tan(d0)^2
[1] 1.171573
> 1/cos(d0)^2
[1] 1.171573

#Cosine関数の基本公式

#Cos(-θ)=Cos(θ)(符号の逆転)
> cos(-d0)
[1] 0.9238795
> cos(d0)
[1] 0.9238795
#Cos(θ+2nπ)=Cos(θ)(1回転)
> cos(d0)
[1] 0.9238795
> cos(d0+d1*pi)
[1]  0.9238795 -0.9238795  0.9238795 -0.9238795  0.9238795 -0.9238795  0.9238795
[8] -0.9238795  0.9238795
#Cos(θ+π/2)=-Sin(θ)(θ+π/2の三角関数)
> cos(d0+pi/2)
[1] -0.3826834
> -sin(d0)
[1] -0.3826834
#Cos(π/2-θ)=Sin(θ)(π/2-θの三角関数)
> cos(pi/2-d0)
[1] 0.3826834
> sin(d0)
[1] 0.3826834
#Cos(θ+π)=-Cos(θ)(θ+πの三角関数)
> cos(d0+pi)
[1] -0.9238795
> -cos(d0)
[1] -0.9238795
#Cos(θ-π)=-Cos(θ)(θ-πの三角関数)
> cos(pi-d0)
[1] -0.9238795
> -cos(d0)
[1] -0.9238795

#Sine関数の基本公式

#Sin(-θ)=-Sin(θ)(符号の逆転)
> sin(-d0)
[1] -0.3826834
> -sin(d0)
[1] -0.3826834
#Sin(θ+2nπ)=Sin(θ)(1回転)
> sin(d0)
[1] 0.3826834
> sin(d0+d1*2*pi)
 [1] 0.3826834 0.3826834 0.3826834 0.3826834 0.3826834 0.3826834 0.3826834 0.3826834
 [9] 0.3826834 0.3826834 0.3826834
#Sin(θ+π/2)=Cos(θ)(θ+π/2の三角関数)
> sin(d0+pi/2)
[1] 0.9238795
> cos(d0)
[1] 0.9238795
#Sin(π/2-θ)=Cos(θ)(π/2-θの三角関数)
> sin(pi/2-d0)
[1] 0.9238795
> cos(d0)
[1] 0.9238795
#Sin(θ+π)=-Sin(θ)(θ+πの三角関数)
> sin(d0+pi)
[1] -0.3826834
> -sin(d0)
[1] -0.3826834
#Sin(θ+π)=-Sin(θ)(θ+πの三角関数)
> sin(pi-d0)
[1] 0.3826834
> sin(d0)
[1] 0.3826834

#Tangent関数の基本公式

#Tan(-θ)=-Tan(θ)(符号の逆転)
> tan(-d0)
[1] -0.4142136
> -tan(d0)
[1] -0.4142136
#Tan(θ+2nπ)=Tan(θ)(1回転)
> tan(d0)
[1] 0.4142136
> tan(d0+d1*2*pi)
 [1] 0.4142136 0.4142136 0.4142136 0.4142136 0.4142136 0.4142136 0.4142136 0.4142136
 [9] 0.4142136 0.4142136 0.4142136
#Tan(θ+π/2)=-1/Tan(θ)(θ+π/2の三角関数)
> tan(d0+pi/2)
[1] -2.414214
> -1/tan(d0)
[1] -2.414214
#Tan(π/2-θ)=1/Tan(θ)(π/2-θの三角関数)
> tan(pi/2-d0)
[1] 2.414214
> 1/tan(d0)
[1] 2.414214
#Tan(θ+π)=Tan(θ)(θ+πの三角関数)
> tan(d0+pi)
[1] 0.4142136
> tan(d0)
[1] 0.4142136
Tan(π-θ)=-Tan(θ)(π-θの三角関数)
> tan(pi-d0)
[1] -0.4142136
> -tan(d0)
[1] -0.4142136

複素数平面(Complex Plane)概念の導入。

上掲の様に等速円運動(Constant Velocity Circular Motion)の観察結果から、円描画関数がX軸とY軸で位相が半分ズレた2つの単振動(x軸=cos(θ),y軸=sin(θ))によって構成される事自体は先行して自明の場合(Trival Case)となりました。その事実を一つの数式で表すにはどうしたら良いでしょうか。(三次方程式の解を表す為に発案された)虚数(Imaginary Number)i^2=-1の概念と複素数(Complex Representation)(X,Yi)=cos(θ)+sin(θ)iの導入はまさにこの観点から導入される運びとなったのです。

c0<-seq(-1,1,length=21)
c0
r1=complex(real=0,imaginary=1)
f1<-function(x)r1^(2*x)
round(f1(c0),digit=4)
r2=complex(real=0,imaginary=-1)
f2<-function(x)r2^(2*x)
round(f2(c0),digit=4)
cmp01<-f1(c0)
cmp02<-f2(c0)

#c0=添字集合In(n=-1->1)
> c0<-seq(-1,1,length=21)
> c0
 [1] -1.0 -0.9 -0.8 -0.7 -0.6 -0.5 -0.4 -0.3 -0.2 -0.1  0.0  0.1  0.2  0.3  0.4  0.5  0.6
[18]  0.7  0.8  0.9  1.0

#Xi=(0,1i)^2xはπ/2ラジアン単位(90度)で　以下の様に推移
#(-1,0i)→(0,-1i)→(1,0i)→(0,1i)→(-1,0i)
#要するに「-1から反時計回り」
> r1=complex(real=0,imaginary=1)
> f1<-function(x)r1^(2*x)
> round(f1(c0),digit=4)
 [1] -1.0000+0.0000i -0.9511-0.3090i -0.8090-0.5878i -0.5878-0.8090i -0.3090-0.9511i
 [6]  0.0000-1.0000i  0.3090-0.9511i  0.5878-0.8090i  0.8090-0.5878i  0.9511-0.3090i
[11]  1.0000+0.0000i  0.9511+0.3090i  0.8090+0.5878i  0.5878+0.8090i  0.3090+0.9511i
[16]  0.0000+1.0000i -0.3090+0.9511i -0.5878+0.8090i -0.8090+0.5878i -0.9511+0.3090i
[21] -1.0000+0.0000i

#Xi=(0,-1i)^2xはπ/2ラジアン単位(90度)で　以下の様に推移
#(-1,0i)→(0,1i)→(1,0i)→(0,-1i)→(-1,0i)
#要するに「-1から時計回り」
r2=complex(real=0,imaginary=-1)
> f2<-function(x)r2^(2*x)
> round(f2(c0),digit=4)
 [1] -1.0000+0.0000i -0.9511+0.3090i -0.8090+0.5878i -0.5878+0.8090i -0.3090+0.9511i
 [6]  0.0000+1.0000i  0.3090+0.9511i  0.5878+0.8090i  0.8090+0.5878i  0.9511+0.3090i
[11]  1.0000+0.0000i  0.9511-0.3090i  0.8090-0.5878i  0.5878-0.8090i  0.3090-0.9511i
[16]  0.0000-1.0000i -0.3090-0.9511i -0.5878-0.8090i -0.8090-0.5878i -0.9511-0.3090i
[21] -1.0000+0.0000i

有名なオイラーの等式(Eulerian Identity)e^πi=-1が円を描くのも、かかる等比数列-1^x=((0,±1i)^2)^x=(0,±1i)^2xの作用。

#y=(0,1i)^2x「-1から反時計回り」
cmp01<-f1(c0)
cmp01x<-Re(cmp01)
cmp01y<-Im(cmp01)
plot(cmp01x,cmp01y,asp=1,type="l",xlim=c(-1,1),ylim=c(-1,1),main="y=(0,1i)^2x",xlab="Real",ylab="Imaginaly")
cmp02<-f2(c0)

#y=(0,-1i)^2x「-1から時計回り」
cmp02<-f2(c0)
cmp02x<-Re(cmp02)
cmp02y<-Im(cmp02)
plot(cmp02x,cmp02y,asp=1,type="l",xlim=c(-1,1),ylim=c(-1,1),main="y=(0,-1i)^2x",xlab="Real",ylab="Imaginaly")

実際-1から-2の間をN分割した添字集合を与えられた複素数関数の出力結果を-πからπの間を同様にN分割した角θの集合と比較すると、実数部がCos(θ),虚数部がSin(θ)の出力結果と一致します。残された問題は等速円運動を構成するX要素=cos(θ)やY要素=sin(θ)の周期が2π(n=-π→π)なのに対し、かかる複素数関数の周期が4(n=-1→1→1)である点。とりあえずその都度、円の半径(Radius)に円周上を移動させたい距離を掛ければ「移動距離の齟齬」問題自体は解決しますが、これが正解とは到底思えません。

c1<-seq(-1,1,length=21)
c1
c2<-seq(-pi,pi,length=21)
c2
r0=complex(real=0,imaginary=1)
f0<-function(x)r0^(2*x)
cmp0<-f0(c1)
cmp01x<-Re(cmp0)
cmp01x
cmp01x*pi
cmp01y<-Im(cmp0)
cmp01y
cmp01y*pi


#c1=添字集合In(n=-1->1)
> c1<-seq(-1,1,length=21)
> c1
 [1] -1.0 -0.9 -0.8 -0.7 -0.6 -0.5 -0.4 -0.3 -0.2 -0.1  0.0  0.1  0.2  0.3  0.4  0.5  0.6
[18]  0.7  0.8  0.9  1.0

#c2=添字集合Ln(n=-π->π)
> c2<-seq(-pi,pi,length=21)
> c2
 [1] -3.1415927 -2.8274334 -2.5132741 -2.1991149 -1.8849556 -1.5707963 -1.2566371
 [8] -0.9424778 -0.6283185 -0.3141593  0.0000000  0.3141593  0.6283185  0.9424778
[15]  1.2566371  1.5707963  1.8849556  2.1991149  2.5132741  2.8274334  3.1415927

#複素数関数の出力結果を得る。
>r0=complex(real=0,imaginary=1)
>f0<-function(x)r0^(2*x)
> cmp0<-f0(c1)
> cmp01x<-Re(cmp0)

#複素数関数の実数部は、その分割数に応じた
#角度θを与えられたCos(θ)関数の出力に一致。
> round(cmp01x,digit=4)
 [1] -1.0000 -0.9511 -0.8090 -0.5878 -0.3090  0.0000  0.3090  0.5878  0.8090  0.9511
[11]  1.0000  0.9511  0.8090  0.5878  0.3090  0.0000 -0.3090 -0.5878 -0.8090 -0.9511
[21] -1.0000
> round(cos(c2),digit=4)
 [1] -1.0000 -0.9511 -0.8090 -0.5878 -0.3090  0.0000  0.3090  0.5878  0.8090  0.9511
[11]  1.0000  0.9511  0.8090  0.5878  0.3090  0.0000 -0.3090 -0.5878 -0.8090 -0.9511
[21] -1.0000

#複素数関数の虚数部は、その分割数に応じた
#角度θを与えられたSin(θ)関数の出力に一致。
> cmp01y<-Im(cmp0)
> round(cmp01y,digit=4)
 [1]  0.0000 -0.3090 -0.5878 -0.8090 -0.9511 -1.0000 -0.9511 -0.8090 -0.5878 -0.3090
[11]  0.0000  0.3090  0.5878  0.8090  0.9511  1.0000  0.9511  0.8090  0.5878  0.3090
[21]  0.0000
> round(sin(c2),digit=4)
 [1]  0.0000 -0.3090 -0.5878 -0.8090 -0.9511 -1.0000 -0.9511 -0.8090 -0.5878 -0.3090
[11]  0.0000  0.3090  0.5878  0.8090  0.9511  1.0000  0.9511  0.8090  0.5878  0.3090
[21]  0.0000

#複素数関数の出力結果をN倍しても半径Nの円が出現するだけ。
#しかし少なくとも円周上の移動距離は一致する。
> cmp01x*pi
 [1] -3.1415927 -2.9878322 -2.5416018 -1.8465818 -0.9708055  0.0000000  0.9708055
 [8]  1.8465818  2.5416018  2.9878322  3.1415927  2.9878322  2.5416018  1.8465818
[15]  0.9708055  0.0000000 -0.9708055 -1.8465818 -2.5416018 -2.9878322 -3.1415927
> cmp01y*pi
 [1]  0.0000000 -0.9708055 -1.8465818 -2.5416018 -2.9878322 -3.1415927 -2.9878322
 [8] -2.5416018 -1.8465818 -0.9708055  0.0000000  0.9708055  1.8465818  2.5416018
[15]  2.9878322  3.1415927  2.9878322  2.5416018  1.8465818  0.9708055  0.0000000

そう、オイラーの等式(Eulerian Identity)e^πi=-1をやたらと神聖視してる人達には大変残念なお知らせですが、実はこの数式に登場するπはここでいう「円周上を移動させたい距離」に過ぎず、それが半周分=πラジアンだと出発点(1,0i)の対蹠(Antipodal)(-1,0i)まで到達するというだけの話に過ぎないのです。
【Rで球面幾何学】「世界で一番美しい公式」オイラーの等式の罠？

本当は「2つでセット」。


そして与える距離によって…

ここまで見てきてやっと「移動したい距離×複素関数の出力結果」を添字として与えられた自然指数関数が「出発点を(-1,0i)から(1,0i)に変更し（与えられた移動距離はそのまま継承しつつ）円の半径を1に保つ」働きをしている事が明らかになります。如何なる数理の組み合わせで実現しているかまでは現段階では分かりません。現段階で明らかになっているのは「自然対数関数も同じ役割を果たす」「ただし根がネイピア数の場合しか完全には機能しない」事くらい。
【Rで球面幾何学】指数関数や対数関数における「ネイピア数周期」の意味について。

三角関数の微積分とその巡回性について。

正弦波の位相変遷の法則は基本中の基本。
サイン波（正弦波、sine wave、sinusoidal wave） - Wikipedia

正弦関数として観測可能な周期的変化を示す波動のことで、その波形は正弦曲線（sine curve）もしくはシヌソイド (Sinusoid) と呼ばれ、数学、信号処理、電気工学およびその他の分野において重要な働きをする。

コサイン波形（Cosine wave=余弦波）もシヌソイドと言われる。これは、正弦波が後方にシフトされたもので波形が同一（Sin(θ+π/2)=Cos(θ)）だからである。

1. cos(x+pi/2)=-sin(x)（位相+90度、一階微分と同じ）
2. cos(x-pi/2)=sin(x)（位相-90度、一階積分と同じ）

Waves01<-function(prm){

#関数定義

f0=function(x)  cos(x)
f1=function(x)  sin(x)
f2=function(x)  -sin(x)
f3=function(x)  cos(x+prm)
f4=function(x)  cos(x-prm)
#正弦波描写

plot(f0,type="l",xlim=c(-pi,pi),ylim=c(-1,1),main="cos(x+pi/2)=-sin(x), cos(x-pi/2)=sin(x)",xlab="Frequency",ylab="Amplitude")
par(new=T) #上書き指定
plot(f1,type="l",xlim=c(-pi,pi),col=rgb(1,1,0),ylim=c(-1,1),main="",xlab="",ylab="")
par(new=T) #上書き指定
plot(f2,type="l",xlim=c(-pi,pi),col=rgb(0,1,1),ylim=c(-1,1),main="",xlab="",ylab="")
par(new=T) #上書き指定
plot(f3,type="l",xlim=c(-pi,pi),col=rgb(0,0,1),ylim=c(-1,1),main="",xlab="",ylab="")
par(new=T) #上書き指定
plot(f4,type="l",xlim=c(-pi,pi),col=rgb(1,0,0),ylim=c(-1,1),main="",xlab="",ylab="")

#凡例

legend("bottomleft", legend=c("Cos(θ)","Sin(θ)","-Sin(θ)","Cos(θ+π/x)","Cos(θ-π/x)"), lty=c(1,1,1,1,1), col=c(rgb(0,0,0),rgb(1,1,0),rgb(0,1,1),rgb(0,0,1),rgb(1,0,0)))
}

library("animation")
Time_Code=seq(0,pi/2,length=15)
saveGIF({
for (i in Time_Code){
　Waves01(i)
}
}, interval = 0.1, movie.name = "CosSin01.gif")

1. cos(x+pi)=-cos(x)（位相+180度、二階微分と同じ）
2. cos(x-pi)=-cos(x)（位相-180度、二階積分と同じ）

Waves02<-function(prm){

#関数定義

f0=function(x)  cos(x)
f1=function(x)  -cos(x)
f2=function(x)  cos(x+prm)
f3=function(x)  cos(x-prm)
#正弦波描写

plot(f0,type="l",xlim=c(-pi,pi),ylim=c(-1,1),main="cos(x+pi)=cos(x-pi)=-cos(x)",xlab="Frequency",ylab="Amplitude")
par(new=T) #上書き指定
plot(f1,type="l",xlim=c(-pi,pi),col=rgb(1,0,1),ylim=c(-1,1),main="",xlab="",ylab="")
par(new=T) #上書き指定
plot(f2,type="l",xlim=c(-pi,pi),col=rgb(0,0,1),ylim=c(-1,1),main="",xlab="",ylab="")
par(new=T) #上書き指定
plot(f3,type="l",xlim=c(-pi,pi),col=rgb(1,0,0),ylim=c(-1,1),main="",xlab="",ylab="")

#凡例

legend("bottomleft", legend=c("Cos(θ)","-Cos(θ)","Cos(θ+π/x)","Cos(θ-π/x)"), lty=c(1,1,1,1), col=c(rgb(0,0,0),rgb(1,0,1),rgb(0,0,1),rgb(1,0,0)))
}

library("animation")
Time_Code=seq(0,pi,length=15)
saveGIF({
for (i in Time_Code){
　Waves02(i)
}
}, interval = 0.1, movie.name = "CosCos01.gif")

ちなみに統計言語Rから呼び出せる汎用代数ライブラリRyhacasは、こういう「頭が悪く見えそうな」単純過ぎる位相変遷を扱ってくれません。単なる計算機のくせにお高くとまりやがって…

library(Ryacas)
#Cos(x+Pi/2)

yac("Cos(x+Pi/2)")
[1] "Cos(x+Pi/2)"
yac("TrigSimpCombine(Cos(x+Pi/2))")
[1] "Cos(Pi/2+x)"

#Cos(x-Pi/2)
yac("Cos(x-Pi/2)")
[1] "Cos(x-Pi/2)"
yac("TrigSimpCombine(Cos(x-Pi/2))")
[1] "Cos(Pi/2-x)"

#Cos(x+Pi)
yac("Cos(x+Pi)")
[1] "Cos(x+Pi)"
yac("TrigSimpCombine(Cos(x+Pi))")
[1] "Cos(Pi+x)"
#Cos(x-Pi)
yac("Cos(x-Pi)")
[1] "Cos(x-Pi)"
yac("TrigSimpCombine(Cos(x-Pi))")
[1] "Cos(Pi-x)"

実質ここでやってるのは三角関数の微積分そのもので、そういう「頭が良く見えそうな」の問題なら喜んで解いてくれます。

1. Cos(θ)を微分すると-Sin(θ)となる（位相+90度）。
2. Cos(θ)を積分するとSin(θ)となる（位相-90度）。
3. Sin(θ)を微分するとCos(θ)となる（位相+90度）。
4. Sin(θ)を微分すると-Cos(θ)となる（位相+90度）。
5. Cos(θ)を2階微分すると-Cos(θ)となる（位相+180度）。
6. Cos(θ)を2階積分すると-Cos(θ)となる（位相-180度）。

library(Ryacas)

#Cos(θ)を微分すると-Sin(θ)となる（位相-90度）。
yac("D(x) Cos(x)")
[1] "-Sin(x)"

#Sin(θ)を微分するとCos(θ)となる（位相-90度）。
yac("D(x) Sin(x)")
[1] "Cos(x)"

#Cos(θ)を積分するとSin(θ)となる（位相+90度）。
yac("Integrate(x) Cos(x)")
[1] "Sin(x)"

#Sin(θ)を微分すると-Cos(θ)となる（位相+90度）。
yac("Integrate(x) Sin(x)")
[1] "-Cos(x)"
#Cos(θ)を2階微分すると-Cos(θ)となる（位相+180度）。
yac("D(x,2) Cos(x)")
[1] "-Cos(x)"

#Cos(θ)を2階積分すると-Cos(θ)となる（位相-180度）。
yac("Integrate(x) Cos(x)")
[1] "Sin(x)"
yac("Integrate(x) Sin(x)")
[1] "-Cos(x)"

つまり三角関数の微積分は「４階で１周期」するのです。解析学（Mathematical Analysis）の分野は正弦波をその様に捉えます。

三角関数の微分（それぞれが-90度の変遷に対応）

1. Cos(θ)→-Sin(θ)→-Cos(θ)→Sin(θ)→Cos(θ)
2. Sin(θ)→Cos(θ)→-Sin(θ)→-Cos(θ)→Sin(θ)

三角関数の積分（それぞれが+90度の変遷に対応）

1. Cos(θ)→Sin(θ)→-Cos(θ)→-Sin(θ)→Cos(θ)
2. Sin(θ)→-Cos(θ)→-Sin(θ)→Cos(θ)→Sin(θ)

library(Ryacas)

#Cos波の微分（位相変遷-90度、４回で１周）
yac("D(x,1) Cos(x)")
[1] "-Sin(x)"
yac("D(x,2) Cos(x)")
[1] "-Cos(x)"
yac("D(x,3) Cos(x)")
[1]"Sin(x)"
yac("D(x,4) Cos(x)")
[1] "Cos(x)"

#Sin波の微分（位相変遷-90度、４回で１周）

yac("D(x,1) Sin(x)")
[1] "Cos(x)"
yac("D(x,2) Sin(x)")
[1] "-Sin(x)"
yac("D(x,3) Sin(x)")
[1] "-Cos(x)"
yac("D(x,4) Sin(x)")
[1] "Sin(x)"

#Cos波の積分（位相変遷+90度、４回で１周）

yac("Integrate(x) Cos(x)")
[1] "Sin(x)"
yac("Integrate(x) Sin(x)")
[1] "-Cos(x)"
yac("Integrate(x) -Cos(x)")
[1] "-Sin(x)"
yac("Integrate(x) -Sin(x)")
[1] "Cos(x)"

#Sin波の積分（位相変遷+90度、４回で１周）

yac("Integrate(x) Sin(x)")
[1] "-Cos(x)"
yac("Integrate(x) -Cos(x)")
[1] "-Sin(x)"
yac("Integrate(x) -Sin(x)")
[1] "Cos(x)"
yac("Integrate(x) Cos(x)")
[1] "Sin(x)"

ところで、こうした性質を備えた関数は三角関数のみに限りません。

指数関数や対数関数の「微積分」とその巡回性について。

こうした性質は指数関数（Exponential function）や対数関数（Logarithm function）と似ており、解析学（Mathematical Analysis）の分野はこれをセットで扱います。
【Rで球面幾何学】指数・対数関数の発見

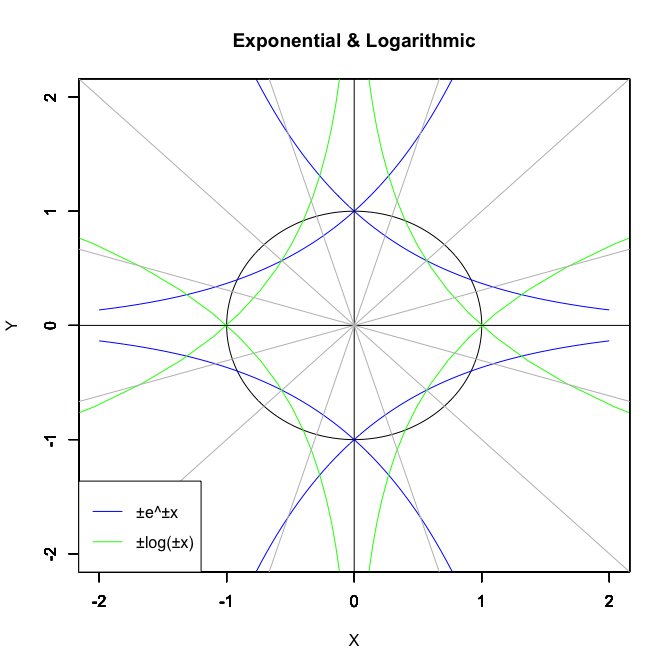
指数関数内における±90度位相変遷

-90度（微分）方向…exp(θ)→-exp(-θ)→-exp(-θ)→exp(-θ)→exp(θ)
+90度（積分）方向…exp(θ)→exp(-θ)→-exp(-θ)→-exp(θ)→exp(θ)

対数関数内における±90度位相変遷

-90度（微分）方向…log(θ)→-log(θ)→-log(-θ)→log(-θ)→log(θ)
+90度（積分）方向…log(θ)→log(-θ)→-log(-θ)→-log(θ)→log(θ)

指数・対数関数間変遷を含む±90度位相変遷

指数関数

-90度（微分）方向…exp(θ)→log(θ)→-exp(θ)→-log(θ)→exp(θ)
+90度（積分）方向…exp(θ)→-log(θ)→-exp(θ)→log(θ)→exp(θ)

対数関数

-90度（微分）方向…log(θ)→-exp(θ)→-log(θ)→exp(θ)→log(θ)
+90度（積分）方向…log(θ)→exp(θ)→-log(θ)→-exp(θ)→log(θ)

もちろんYacasばかりか、解析学そのものがこういう「頭が悪く見えそうな」時代遅れの位相変遷を微分や積分の範疇では取り扱ってくれません。しかしながら、こうした共通点への注目から数学者レオンハルド・オイラー（Leonhard Euler, 1707年〜1783年）はマクローリン展開（Maclaurin expansion） を用いてオイラーの公式（Euler's formula）e^Θ=cos(Θ)+sin(Θ)iを発想したのでした。
【Rで球面幾何学】オイラーの公式を導出したマクローリン級数
【Rで球面幾何学】オイラーの公式とは、そもそも何か？

以下続報…