【初心者向け】「三角不等式(Triangle Inequality)」の体感方法？

まずは基本中の基本から。
三角不等式(Triangle Inequality)
‖x+y‖<=‖x‖+‖y‖

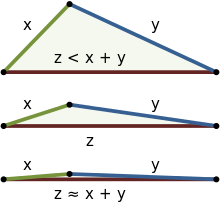
• ‖x‖と‖y‖が同一直線上にある場合のみ‖x+y‖=‖x‖+‖y‖が成立。その時の三角形の面積は0に退化する。

単位円(Unit Circle)上の直径を長編とする直角三角形では、正弦定理（Law of Sines）a/sin(a)+b/sin(b)+c/sin(c)~2rの特殊形たるターレスの定理(Thales' theorem)によって必ずその対角がπ/2ラジアン(90度)となり、残り2角α,βの合計も三角形の内角の和がπラジアン(180度)である事からπ/2ラジアン(90度)と定まる。
【初心者向け】三角関数と指数・対数関数の「巡回性」について。

#CFS=Circle Function Single
CFS<-function(Radian){
cx<-seq(-1,1,length=60)
f0<-function(x) sqrt(1-x^2)
cy<-f0(cx)
plot(cx,cy,asp=1,type="l",main="Mean proportional",xlab="X",ylab="sqrt(1-X^2)")

#塗りつぶし（背景）
polygon(cx, #x
cy, #y
density=c(30), #塗りつぶす濃度
angle=c(45),　 　　　#塗りつぶす斜線の角度
col=c(200,200,200)) 　#塗りつぶす色

#塗りつぶし（三角）
polygon(c(-1,cx[Radian],1), #x
c(0,cy[Radian],0), #y
density=c(30), #塗りつぶす濃度
angle=c(45),　 　　　#塗りつぶす斜線の角度
col=rgb(0,0,1)) 　#塗りつぶす色
#線追加（三角）
segments(cx[Radian],cy[Radian],cx[Radian],0,col=rgb(1,0,0))

#文字追加
text(c(-1,cx[Radian],1,cx[Radian]),c(0,cy[Radian],0,0), labels=c("a","d","c","b"),col=c(rgb(0,0,0),rgb(1,0,0),rgb(0,0,0),rgb(1,0,0)),cex=c(2,2,2,2))
text(0,0,labels="0",col=rgb(0,1,0),cex=2)

}
#アニメーション
library("animation")
Time_Code=rev(seq(1,59, length=30))
saveGIF({
for (i in Time_Code){
　CFS(i)
}
}, interval = 0.1, movie.name = "CFS01.gif")

#CFS90Sift=Circle Function Single 90Sift
CFS90Sift<-function(Radian){
cx<-seq(-1,1,length=60)
f0<-function(x) sqrt(1-x^2)
cy<-f0(cx)
plot(cy,cx,asp=1,type="l",main="Mean proportional",xlab="sqrt(1-Y^2)",ylab="Y")

#塗りつぶし（背景）
polygon(cy, #x
cx, #y
density=c(30), #塗りつぶす濃度
angle=c(45),　 　　　#塗りつぶす斜線の角度
col=c(200,200,200)) 　#塗りつぶす色

#塗りつぶし（三角）
polygon(c(0,cy[Radian],0), #x
c(-1,cx[Radian],1), #y
density=c(30), #塗りつぶす濃度
angle=c(45),　 　　　#塗りつぶす斜線の角度
col=rgb(0,0,1)) 　#塗りつぶす色

#線追加（三角）
segments(cy[Radian],cx[Radian],0,cx[Radian],col=rgb(1,0,0))

#文字追加
text(c(0,cy[Radian],0,0),c(1,cx[Radian],-1,cx[Radian]), labels=c("a","d","c","b"),col=c(rgb(0,0,0),rgb(1,0,0),rgb(0,0,0),rgb(1,0,0)),cex=c(2,2,2,2))
text(0,0,labels="0",col=rgb(0,1,0),cex=2)
}

#アニメーション
library("animation")
Time_Code=rev(seq(1,59, length=30))
saveGIF({
for (i in Time_Code){
　CFS90Sift(i)
}
}, interval = 0.1, movie.name = "CFS90Sift01.gif")

• この時‖x+y‖=‖x‖+‖y‖が成立するのはcos(θ)=0かsin(θ)=0の場合のみ。

ちなみに単位円において三角比(Triangular ratio)概念が通用する範囲は以下の6通り。
【Rで球面幾何学】「半円しか描けなかった」世界の思い出？

• 第一象限(cos(θ)>=0,sin(θ)>=0)のみ。
• 第一象限とそれに隣接する第二象限(cos(θ)=1→0→-1,sin(θ)=0→1→0)。
• 第一象限とそれに隣接する第四象限(cos(θ)=0→1→0,sin(θ)=1→0→-1)。
• 第三象限(cos(θ)<=0,sin(θ)<=0)のみ。
• 第三象限とそれに隣接する第四象限(cos(θ)=1→0→-1,sin(θ)=0→-1→0)。
• 第三象限とそれに隣接する第二象限(cos(θ)=0→-1→0,sin(θ)=1→0→-1)。

とりあえず現時点では役立てる方法を思いつきませんがRavi変換や相加相乗平均の不等式(Additive Geometric Mean Inequality)a+B>=2sqrt(a×b)(a=bの時のみ等号が成立)との関係が深い事でも知られています。
Ravi変換
相加相乗平均の不等式とそのエレガントな証明

証明

長さがそれぞれa,b,cであるような3つの線分に関して, 三角不等式「一番長い辺が他の2つの辺の和より小さい」が成立する時,a,b,cを3辺とする三角形が成立する。

数式化すると、

• a+b>c
• b+c>a
• c+a>b

1文字(ここではaにする)について整理すると、

• a>c−b
• b+c>a
• a>b−c

まとめて

• |b−c|

特にmax{a,b,c}=aである時a>|b−c|であるから

• a

これを「一番長い辺が他の2つの辺の和より小さい」と表した。

ところでコンピューター言語においては容易に「区間や条件や個数を定めて発生させた乱数データ」を通常の数列の様に扱う事が可能です。

ND<-function(x){
cx<-rnorm(1000)
cy<-rnorm(1000)
plot(cx,cy,xlim=c(-4,4),ylim=c(-4,4),main="Normal Distribution",xlab="",ylab="")
}
#アニメーション
library("animation")
Time_Code=seq(1,16,length=16)
saveGIF({
for (i in Time_Code){
　ND(i)
}
}, interval = 0.1, movie.name = "ND01.gif")

中心推定付

ND<-function(x){
cx<-rnorm(1000)
cy<-rnorm(1000)
plot(cx,cy,xlim=c(-4,4),ylim=c(-4,4),main="Normal Distribution",xlab="",ylab="")
text(mean(cx),mean(cy),"X",col=rgb(0,1,0))
}
#アニメーション
library("animation")
Time_Code=seq(1,16,length=16)
saveGIF({
for (i in Time_Code){
　ND(i)
}
}, interval = 0.1, movie.name = "ND01.gif")

同心円表示付(N=1000)

ND<-function(x){
cx<-rnorm(1000)
cy<-rnorm(1000)
plot(cx,cy,xlim=c(-4,4),asp=1,ylim=c(-4,4),main="Normal Distribution",xlab="",ylab="")
c0<-seq(-pi,pi,length=61)
cx0<-cos(c0)
cy0<-sin(c0)
par(new=T)#上書き指定
plot(cx0+mean(cx),cy0+mean(cy),type="l",asp=1,xlim=c(-4,4),ylim=c(-4,4),main="",xlab="",ylab="",col=rgb(0,1,0))
par(new=T)#上書き指定
plot(cx0*2+mean(cx),cy0*2+mean(cy),type="l",asp=1,xlim=c(-4,4),ylim=c(-4,4),main="",xlab="",ylab="",col=rgb(0,1,0))
par(new=T)#上書き指定
plot(cx0*3+mean(cx),cy0*3+mean(cy),type="l",asp=1,xlim=c(-4,4),ylim=c(-4,4),main="",xlab="",ylab="",col=rgb(0,1,0))
text(mean(cx),mean(cy),"X",col=rgb(0,1,0))
}
#アニメーション
library("animation")
Time_Code=seq(1,16,length=16)
saveGIF({
for (i in Time_Code){
　ND(i)
}
}, interval = 0.1, movie.name = "ND02.gif")

同心円表示付(N=100)

ND<-function(x){
cx<-rnorm(100)
cy<-rnorm(100)
plot(cx,cy,xlim=c(-4,4),asp=1,ylim=c(-4,4),main="Normal Distribution",xlab="",ylab="")
c0<-seq(-pi,pi,length=61)
cx0<-cos(c0)
cy0<-sin(c0)
par(new=T)#上書き指定
plot(cx0+mean(cx),cy0+mean(cy),type="l",asp=1,xlim=c(-4,4),ylim=c(-4,4),main="",xlab="",ylab="",col=rgb(0,1,0))
par(new=T)#上書き指定
plot(cx0*2+mean(cx),cy0*2+mean(cy),type="l",asp=1,xlim=c(-4,4),ylim=c(-4,4),main="",xlab="",ylab="",col=rgb(0,1,0))
par(new=T)#上書き指定
plot(cx0*3+mean(cx),cy0*3+mean(cy),type="l",asp=1,xlim=c(-4,4),ylim=c(-4,4),main="",xlab="",ylab="",col=rgb(0,1,0))
text(mean(cx),mean(cy),"X",col=rgb(0,1,0))
}
#アニメーション
library("animation")
Time_Code=seq(1,16,length=16)
saveGIF({
for (i in Time_Code){
　ND(i)
}
}, interval = 0.1, movie.name = "ND03.gif")

同心円表示付(N=10)

ND<-function(x){
cx<-rnorm(10)
cy<-rnorm(10)
plot(cx,cy,xlim=c(-4,4),asp=1,ylim=c(-4,4),main="Normal Distribution",xlab="",ylab="")
c0<-seq(-pi,pi,length=61)
cx0<-cos(c0)
cy0<-sin(c0)
par(new=T)#上書き指定
plot(cx0+mean(cx),cy0+mean(cy),type="l",asp=1,xlim=c(-4,4),ylim=c(-4,4),main="",xlab="",ylab="",col=rgb(0,1,0))
par(new=T)#上書き指定
plot(cx0*2+mean(cx),cy0*2+mean(cy),type="l",asp=1,xlim=c(-4,4),ylim=c(-4,4),main="",xlab="",ylab="",col=rgb(0,1,0))
par(new=T)#上書き指定
plot(cx0*3+mean(cx),cy0*3+mean(cy),type="l",asp=1,xlim=c(-4,4),ylim=c(-4,4),main="",xlab="",ylab="",col=rgb(0,1,0))
text(mean(cx),mean(cy),"X",col=rgb(0,1,0))
}
#アニメーション
library("animation")
Time_Code=seq(1,16,length=16)
saveGIF({
for (i in Time_Code){
　ND(i)
}
}, interval = 0.1, movie.name = "ND04.gif")

三次元だとこんな感じ。こうした画像の、ガウスが「円の面積がπなら1辺の長さはsqrt(π)に決まってるじゃん!!」と問答無用で殴りかかってくる感じが好きです。

library(rgl)
Rtime<-seq(0,2*pi,length=60)
cx<-rnorm(1000)
cy<-rnorm(1000)
cz<-rnorm(1000)
plot3d(cx,cy,cz,type="p",xlim=c(-4,4),ylim=c(-4,4),zlim=c(-4,4))
movie3d(spin3d(axis=c(0,0,1),rpm=5),duration=10,fps=25,movie="~/Desktop/r06")

そして実際、数学再勉強者としてそういう部分がこうした概念の再獲得に役立ったりしてるのです。 例えば以下。

吉田武「オイラーの贈物」「基礎理論(Basic Theory)」より

連続性(Continuity)を扱う数直線(Number line)上においては端点(End Point)の設定により以下の記法(Notation)を用いる。

> c0<-seq(0,10,length=11)
> c0
 [1]  0  1  2  3  4  5  6  7  8  9 10
#閉区間(Closed Interval)[a,b](a<=x<=b)
> c0[c0>=3 & c0<=6]
[1] 3 4 5 6
#開区間(Open Interval)(a,b)(a<x<b)
> c0[c0>3 & c0<6]
[1] 4 5
#半開区間(Semi-Open Interval)[a,b)(a=<x<b)
> c0[c0>=3 & c0<6]
[1] 3 4 5
#半開区間(Semi-Open Interval)(a,b](a<=>x>a)
> c0[c0>3 & c0<=6]
[1] 4 5 6

ここで絶対値(Absolute Value)|x|の概念を導入しよう。xの符号の正負に関りなくその大きさのみを取り出す。定義(Definition)は以下。

#|x|≡x(x>=0の時)
> abs(6)
[1] 6
#|x|≡-x(x<0の時)
> abs(-6)
[1] 6

この記号を用いれば不等式を以下の様に簡潔に表せる。

> c0<-seq(-5,5,length=11)
> c0
 [1] -5 -4 -3 -2 -1  0  1  2  3  4  5
#不等式-a<x<a
#|x|<a(ただしa>0)
> c0[c0>-3 & c0<3]
[1] -2 -1  0  1  2
#幾何学的に考えれば数直線上の0を中心とした幅2aの中に数xが存在する事を意味する。

とっさに想起したのが「0除算が発生する為、X<=0やy<=0の場合が扱えない一次関数や数列」でした。数学再学習者とはいえ、あくまで「はじめにコンピューターありき」なんですね。

三角不等式の証明

二数a,bの正負を場合分けする事により、容易に以下を得る。

• |a,b|=|a|*|b|

また任意のa,bに対して以下が成り立つので、

• -|a|<=a<=|a|
• -|b|<=b<=|b|
   

辺々を加え以下が成立する。

• -(|a|+|b|)<=a+b<=|a|+|b|

これは絶対値の定義によって以下の様に書け三角不等式(Triangle Inequalty)と呼ばれる。

• |a+b|<=|a|+|b|

等号はa>=0の時成り立つ。この式でaを(a-b)に置き換えると、

• |(a-b)+b|=|a|<=|a-b|+|b|

より

• |a|-|b|<=|a-b|

を得る。これは最も基本的な不等式である。

さて、こうした数理の再学習にあたって私はどうしたか？　なんと「実験」とか始めたのです。

#数列単位で比較出来る。
c(1,2,3)>c(2,1,3)
[1] FALSE TRUE FALSE

#最小-5、最大5の乱数10個で試してみる。
a=round(runif(10,-5,5))
a
[1] -1 1 1 -1 -1 -3 4 4 -3 3
abs(a)
[1] 1 1 1 1 1 3 4 4 3 3

b=round(runif(10,-5,5))
b
[1] 1 -3 4 4 -4 3 -3 4 4 3
abs(b)
[1] 1 3 4 4 4 3 3 4 4 3
a==b
[1] FALSE FALSE FALSE FALSE FALSE FALSE FALSE TRUE FALSE TRUE
a!=b
[1] TRUE TRUE TRUE TRUE TRUE TRUE TRUE FALSE TRUE FALSE
a>b
[1] FALSE TRUE FALSE FALSE TRUE FALSE TRUE FALSE FALSE FALSE
a<b
[1] TRUE FALSE TRUE TRUE FALSE TRUE FALSE FALSE TRUE FALSE
a<=b
[1] TRUE FALSE TRUE TRUE FALSE TRUE FALSE TRUE TRUE TRUE
a>=b
[1] FALSE TRUE FALSE FALSE TRUE FALSE TRUE TRUE FALSE TRUE

#式の動作の確認
abs(a*b)==abs(a)*abs(b)
[1] TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE
-(abs(a)+abs(b))<=a+b
[1] TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE
-(abs(a)+abs(b))<=a+b
[1] TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE
a+b<=abs(a)+abs(b)
[1] TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE
abs(a)-abs(b)<=abs(a-b)
[1] TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE

こうやって私は「正規分布の半径3以上で急速に収束していく感じ」を次第に捉えていったのでした。思えば遠くに来たもんだ…
【初心者向け】誤差関数(ERF)と相補誤差関数 (ERFC)。

そういえば、あえて一昔前の教科書を選んだ事で「コンピューター革命」を実感する場面も。

循環小数(recurring decimal)0.3333…(無限に続く)について

• A=0.3333…(無限に続く)

とする。両辺を10倍して

10A=3.33333…(無限に続く)=3+A

よって

• 9A=3

よって

• A=1/3

0.9999…(無限に続く)を途中で1と置いている訳だが、有理数(rational number)のこうした側面を認めないと実数(real number)の連続性(continuity)仮定が崩壊してしまう。

コンピューター処理が普及したらあまり気にされなくなった案件…

#通常ライブラリには、そもそも循環小数への配慮自体がない。
1/3*10
[1] 3.333333

#代数ライブラリyacasは逆に約分自体をしない。
library(Ryacas)
yacas("1/3*10")
expression(10/3)

エンジニアというより、むしろ数学教育者に読んで欲しい内容。「実験」って楽しいの…