一般に三平方の定理(Three square theorem)」あるいはピタゴラスの定理(Pythagorean Theorem)として知られるX^2+Y^2=Z^2の式、すなわち単位円(Unit Circle、半径1の円弧)上ではx^2+y^2=1、単位球面(Unit Circle、半径1の球面)上ではx^2+y^2+z^2=1となる定理について。
【初心者向け】ピタゴラスの定理あるいは三平方の定理からの出発

「半円しか描けなかった」世界
しばしばyの値をxで求める関数に変換されたy=sqrt(1-x^2)の形式でも用いられますが、この形だとx^2>1の時、平方根の概念で扱い切れなくなって答えが出ません。xの値をyで求める関数に変換されたx=sqrt(1-y^2)の場合も、やはりy^2>1の時答えが出ず、従って数学史のある段階までこの関数は「半円ずつしか描けない」「従ってy=sqrt(1-x^2)とy=-sqrt(1-x^2)、あるいはx=sqrt(1-y^2)とx=-sqrt(1-y^2)の式のセットで運用するもの」と考えられていたのでした。
Xの関数としてYを求めた場合の「半円しか描けない」
平方根展開時に0除算が発生しないのは第一象限(X=>0かつY=>0)と第二象限(X=<0かつY=>0)となります。
#CFS=Circle Function Single
CFS<-function(Radian){
cx<-seq(-1,1,length=60)
f0<-function(x) sqrt(1-x^2)
cy<-f0(cx)
plot(cx,cy,asp=1,type="l",main="X^2+Y^2=1",xlab="X",ylab="sqrt(1-X^2)")
#塗りつぶし(背景)
polygon(cx, #x
cy, #y
density=c(30), #塗りつぶす濃度
angle=c(45), #塗りつぶす斜線の角度
col=c(200,200,200)) #塗りつぶす色
#塗りつぶし(三角)
polygon(c(-1,cx[Radian],1), #x
c(0,cy[Radian],0), #y
density=c(30), #塗りつぶす濃度
angle=c(45), #塗りつぶす斜線の角度
col=rgb(0,0,1)) #塗りつぶす色
#線追加(三角)
segments(cx[Radian],cy[Radian],cx[Radian],0,col=c(100,100,100))
#文字追加
text(c(-1,cx[Radian],1,cx[Radian]),c(0,cy[Radian],0,0), labels=c("a","b","c","d"),col=c(rgb(0,0,0),rgb(0,0,0),rgb(0,0,0),rgb(0,0,0)),cex=c(2,2,2,2))
}
#アニメーション
library("animation")
Time_Code=rev(seq(1,59, length=30))
saveGIF({
for (i in Time_Code){
CFS(i)
}
}, interval = 0.1, movie.name = "CFS02.gif")
%matplotlib nbagg
import math as m
import cmath as c
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.animation as animation
#単位円データ作成
c0=np.linspace(0,m.pi,61,endpoint = True)
s0=[]
for num in range(len(c0)):
s0.append(complex(m.cos(c0[num]),m.sin(c0[num])))
s1=np.array(s0)
plt.style.use('default')
fig = plt.figure()
#関数定義
def unit_circle(n):
plt.cla()
#スポーク線描画
for num in range(len(s1)):
plt.plot([0,s1[num].real],[0,s1[num].imag],color="gray",lw=0.5);
#円周描画
plt.plot(s1.real,s1.imag,color="blue", label="Unit Cylinder")
plt.ylim([0,1.1])
plt.xlim([-1.1,1.1])
plt.title("Pythagorean Theorem")
plt.xlabel("Real")
plt.ylabel("Imaginal")
ax = fig.add_subplot(111)
ax.set_aspect('equal', adjustable='box')
ax.legend(loc='upper right')
#補助線描画
plt.axvline(0, 0, 1,color="purple")
plt.axhline(0, 0, 1,color="purple")
#移動線描画
plt.plot([0,s1[n].real],[0,s1[n].imag],color="red",lw=1)
plt.plot([s1[n].real,s1[n].real],[0,s1[n].imag],color="green",lw=1)
plt.plot([1,s1[n].real],[0,s1[n].imag],color="green",lw=1)
plt.plot([-1,s1[n].real],[0,s1[n].imag],color="green",lw=1)
plt.fill([1,s1[n].real,-1,1],[0,s1[n].imag,0,0],color="lightgreen")
plt.text(-1, 0, "A")
plt.text(1, 0, "B")
plt.text(s1[n].real, s1[n].imag, "C")
plt.text(s1[n].real, 0, "D")
ani = animation.FuncAnimation(fig, unit_circle, interval=50,frames=len(s1))
ani.save("desktop/output02.gif", writer="pillow")
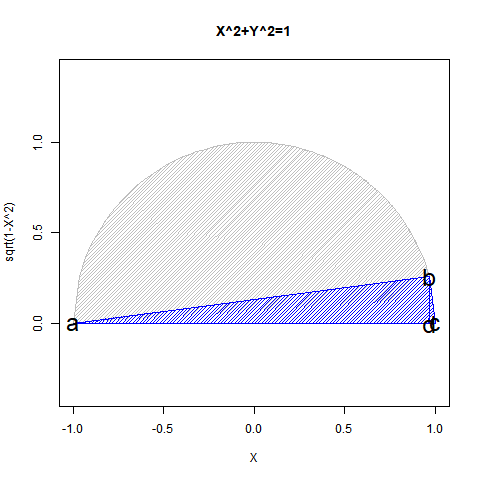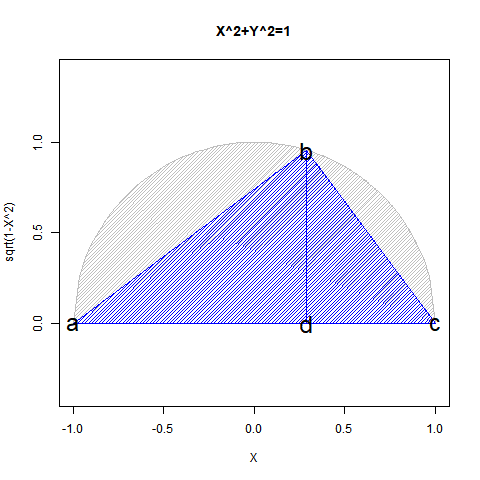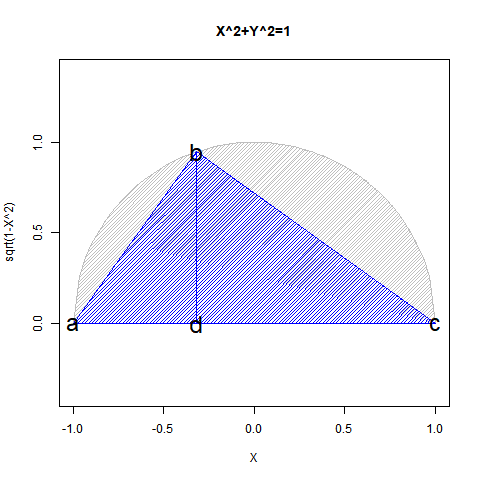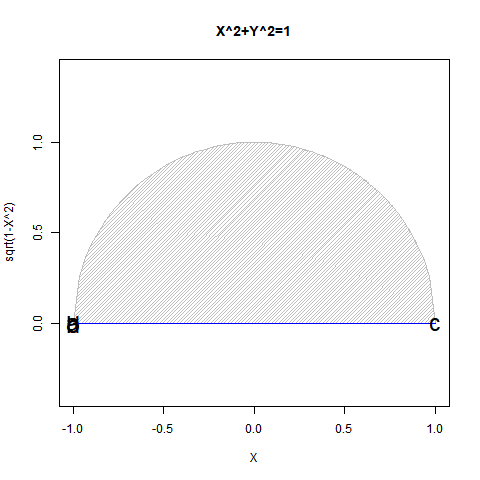
xの値が1から0を経て-1に推移する関数y=sqrt(1-x^2)の内容は三角関数(Trigonometric Function)的に表現(Expression)すると、角度θの0ラジアン(0度)からπ/2ラジアン(90度)を経てπラジアン(180度)に推移する変遷を扱った形となります。頂点bおよび頂点dのx座標値がCos(θ),頂点bのy座標値がSin(θ)に対応。
【初心者向け】「円そのもの」の近似から派生した角度概念の起源
CFD<-function(Radian){
cx<-seq(-1,1,length=60)
f0<-function(x) sqrt(1-x^2)
cy<-f0(cx)
plot(cx,cy,asp=1,type="l",xlim=c(-1,1),ylim=c(-1,1),main="X^2+Y^2=1",xlab="X",ylab="sqrt(1-X^2) &-sqrt(1-X^2) ")
par(new=T)#上書き指定
plot(cx,-1*cy,asp=1,type="l",xlim=c(-1,1),ylim=c(-1,1),main="",xlab="",ylab="")
#塗りつぶし(上背景)
polygon(cx, #x
cy, #y
density=c(30), #塗りつぶす濃度
angle=c(45), #塗りつぶす斜線の角度
col=c(200,200,200)) #塗りつぶす色
#塗りつぶし(下背景)
polygon(cx, #x
-cy, #y
density=c(30), #塗りつぶす濃度
angle=c(45), #塗りつぶす斜線の角度
col=c(200,200,200)) #塗りつぶす色
#塗りつぶし(上三角)
polygon(c(-1,cx[Radian],1), #x
c(0,cy[Radian],0), #y
density=c(30), #塗りつぶす濃度
angle=c(45), #塗りつぶす斜線の角度
col=rgb(0,0,1)) #塗りつぶす色
#塗りつぶし(下三角)
cx1<-rev(cx)
cy1<-rev(cy)*-1
polygon(c(1,cx1[Radian],-1), #x
c(0,cy1[Radian],0), #y
density=c(30), #塗りつぶす濃度
angle=c(45), #塗りつぶす斜線の角度
col=rgb(1,0,0)) #塗りつぶす色
#線追加(三角)
segments(cx[Radian],cy[Radian],cx[Radian],0,col=rgb(0,0,1))
segments(cx1[Radian],cy1[Radian],cx1[Radian],0,col=rgb(1,0,0))
#文字追加
text(c(-1,cx[Radian],1,cx[Radian],-cx[Radian],-cx[Radian]),c(0,cy[Radian],0,0,-cy[Radian],0), labels=c("a","b","c","d","e","f"),col=c(rgb(0,0,0),rgb(0,0,0),rgb(0,0,0),rgb(0,0,0),rgb(0,0,0)),cex=c(2,2,2,2,2,2))
#凡例
legend("bottomright", legend=c("sqrt(1-X^2)","-sqrt(1-X^2)"), lty=c(1,1), col=c(rgb(0,0,1),rgb(1,0,0)))
}
#アニメーション
library("animation")
Time_Code=rev(seq(1,59, length=30))
saveGIF({
for (i in Time_Code){
CFD(i)
}
}, interval = 0.1, loop=TRUE, movie.name = "CFD01.gif")
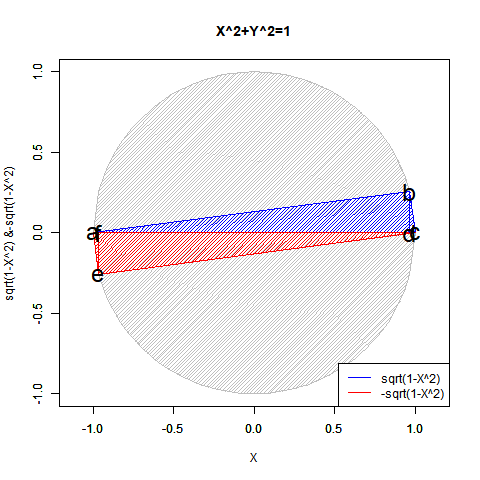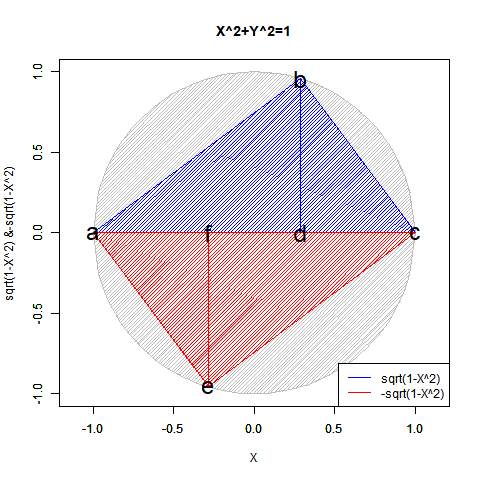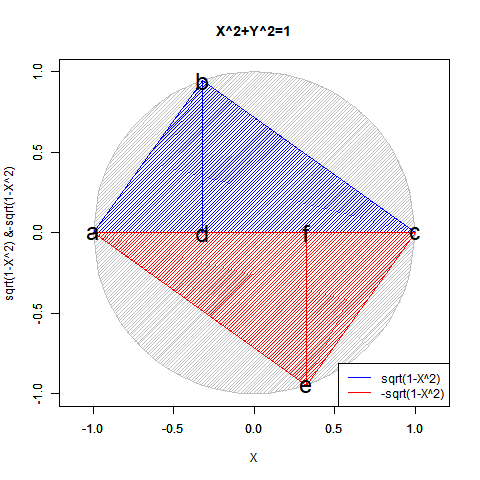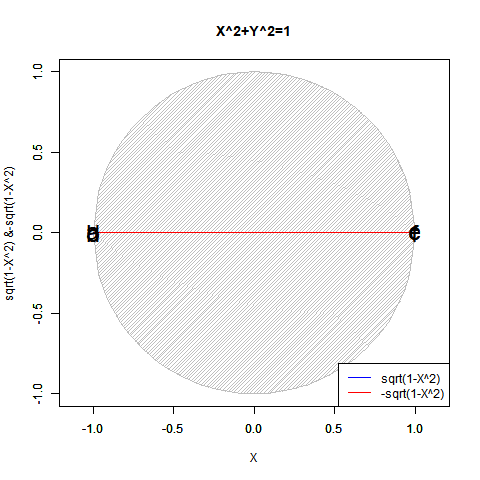
xの値が-1から0を経て1に推移する関数y=sqrt(1-x^2)の内容は三角関数(Trigonometric Function)的に表現(Expression)すると、角度θのπラジアン(180度)から3/4πラジアン(270度)あるいは-π/2ラジアン(-90度)を経て2πラジアン(360度)あるいは0ラジアン(0度)に推移する変遷を扱った形となります。頂点eおよび頂点fのx座標値がCos(θ),頂点eのy座標値がSin(θ)に対応。
【Rで球面幾何学】「円そのもの」の近似から派生した角度概念の起源
あれ? 複素共役/複素共軛(Complex Conjugate)の実数部分の動きと同じではありませんか?
複素共役 - Wikipedia
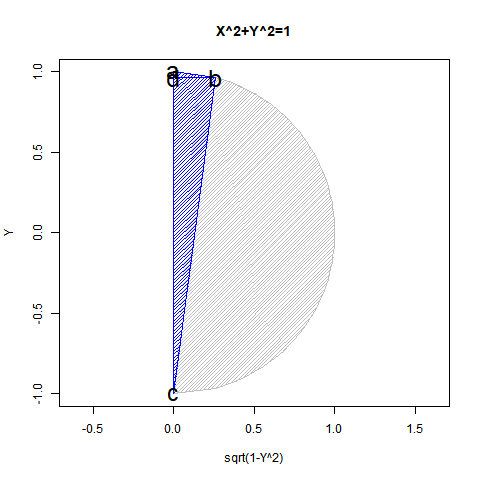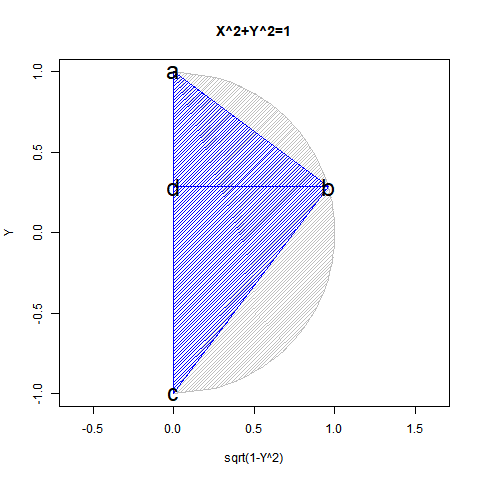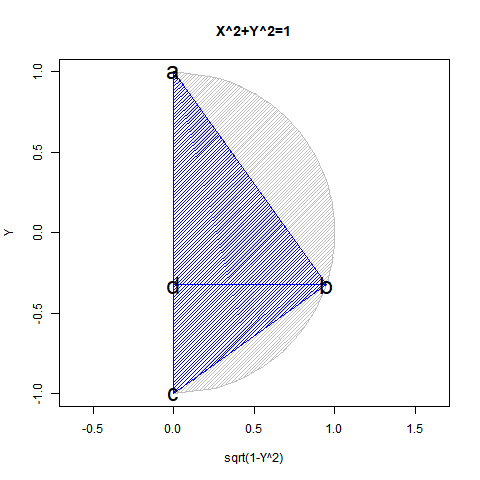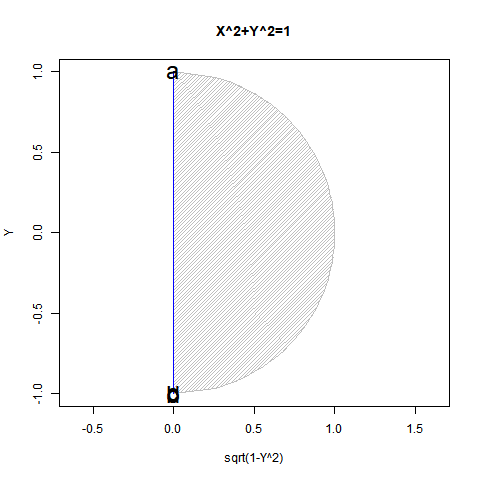
#Yの関数としてXを求めた場合の「半円しか描けない」
平方根展開時に0除算が発生しないのは第一象限(Y=>0かつX=>0)と第四象限(Y=<0かつX=>0)となります。
#CFS90Sift=Circle Function Single 90Sift
CFS90Sift<-function(Radian){
cx<-seq(-1,1,length=60)
f0<-function(x) sqrt(1-x^2)
cy<-f0(cx)
plot(cy,cx,asp=1,type="l",main="X^2+Y^2=1",xlab="sqrt(1-Y^2)",ylab="Y")
#塗りつぶし(背景)
polygon(cy, #x
cx, #y
density=c(30), #塗りつぶす濃度
angle=c(45), #塗りつぶす斜線の角度
col=c(200,200,200)) #塗りつぶす色
#塗りつぶし(三角)
polygon(c(0,cy[Radian],0), #x
c(-1,cx[Radian],1), #y
density=c(30), #塗りつぶす濃度
angle=c(45), #塗りつぶす斜線の角度
col=rgb(0,0,1)) #塗りつぶす色
#線追加(三角)
segments(cy[Radian],cx[Radian],0,cx[Radian],col=c(100,100,100))
#文字追加
text(c(0,cy[Radian],0,0),c(1,cx[Radian],-1,cx[Radian]), labels=c("a","b","c","d"),col=c(rgb(0,0,0),rgb(0,0,0),rgb(0,0,0),rgb(0,0,0)),cex=c(2,2,2,2))
}
#アニメーション
library("animation")
Time_Code=rev(seq(1,59, length=30))
saveGIF({
for (i in Time_Code){
CFS90Sift(i)
}
}, interval = 0.1, movie.name = "CFS90Sift01.gif")
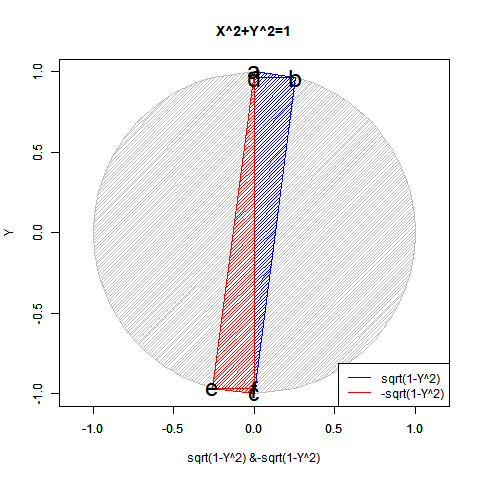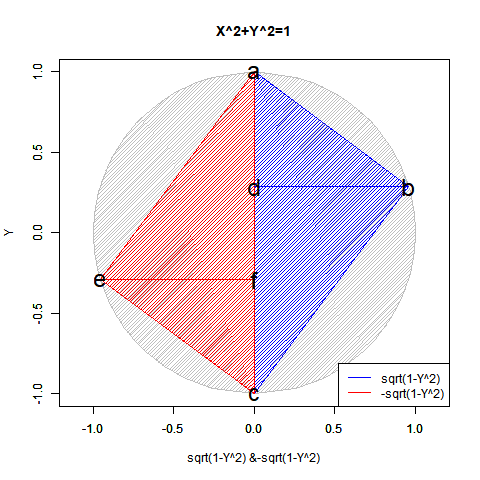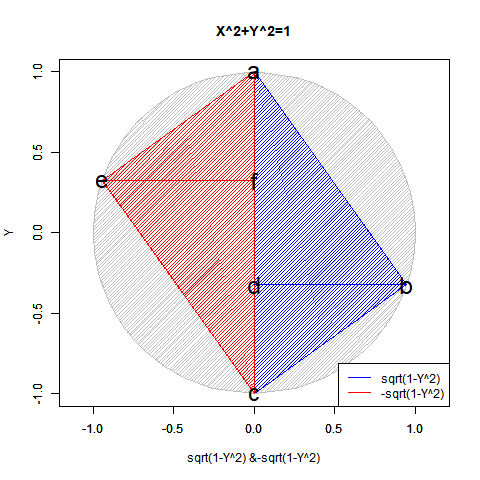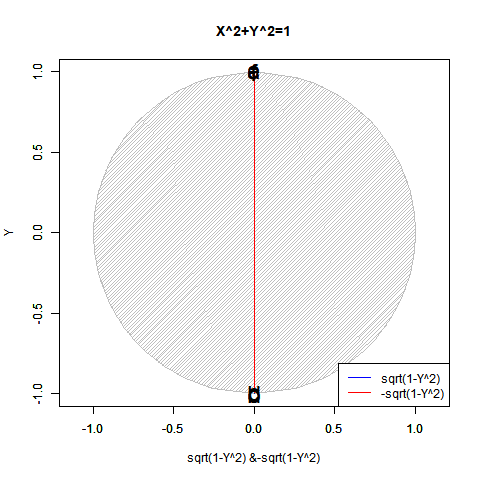
yの値が1から0を経て-1に推移する関数x=sqrt(1-y^2)の内容は三角関数(Trigonometric Function)的に表現(Expression)すると、角度θのπ/2ラジアン(90度)から0ラジアン(0度)を経て3/4πラジアン(270度)あるいは-πラジアン(-90度)に推移する変遷を扱った形となります。頂点bのx座標値がCos(θ),頂点bおよび頂点dのy座標値がSin(θ)に対応。
【Rで球面幾何学】「円そのもの」の近似から派生した角度概念の起源
#CFD90Sift=Circle Function Double 90Sift
CFD90Sift<-function(Radian){
cx<-seq(-1,1,length=60)
f0<-function(x) sqrt(1-x^2)
cy<-f0(cx)
plot(cy,cx,asp=1,type="l",xlim=c(-1,1),ylim=c(-1,1),main="X^2+Y^2=1",xlab="sqrt(1-Y^2) &-sqrt(1-Y^2)",ylab="Y")
par(new=T)#上書き指定
plot(cy*-1,cx,asp=1,type="l",xlim=c(-1,1),ylim=c(-1,1),main="",xlab="",ylab="")
#塗りつぶし(上背景)
polygon(cy, #x
cx, #y
density=c(30), #塗りつぶす濃度
angle=c(45), #塗りつぶす斜線の角度
col=c(200,200,200)) #塗りつぶす色
#塗りつぶし(下背景)
polygon(-cy, #x
cx, #y
density=c(30), #塗りつぶす濃度
angle=c(45), #塗りつぶす斜線の角度
col=c(200,200,200)) #塗りつぶす色
#塗りつぶし(上三角)
polygon(c(0,cy[Radian],0), #x
c(-1,cx[Radian],1), #y
density=c(30), #塗りつぶす濃度
angle=c(45), #塗りつぶす斜線の角度
col=rgb(0,0,1)) #塗りつぶす色
#塗りつぶし(下三角)
cx1<-rev(cx)
cy1<-rev(cy)*-1
polygon(c(0,cy1[Radian],0), #x
c(1,cx1[Radian],-1), #y
density=c(30), #塗りつぶす濃度
angle=c(45), #塗りつぶす斜線の角度
col=rgb(1,0,0)) #塗りつぶす色
#線追加(三角)
segments(cy[Radian],cx[Radian],0,cx[Radian],col=rgb(0,0,1))
segments(cy1[Radian],cx1[Radian],0,cx1[Radian],col=rgb(1,0,0))
#文字追加
text(c(0,cy[Radian],0,0,-cy[Radian],0),c(1,cx[Radian],-1,cx[Radian],-cx[Radian],-cx[Radian]), labels=c("a","b","c","d","e","f"),col=c(rgb(0,0,0),rgb(0,0,0),rgb(0,0,0),rgb(0,0,0),rgb(0,0,0)),cex=c(2,2,2,2,2,2))
#凡例
legend("bottomright", legend=c("sqrt(1-Y^2)","-sqrt(1-Y^2)"), lty=c(1,1), col=c(rgb(0,0,1),rgb(1,0,0)))
}
#アニメーション
library("animation")
Time_Code=rev(seq(1,59, length=30))
saveGIF({
for (i in Time_Code){
CFD90Sift(i)
}
}, interval = 0.1, movie.name = "CFD90Sift02.gif")
yの値が-1から0を経て1に推移する関数x=sqrt(1-y^2)の内容は三角関数(Trigonometric Function)的に表現(Expression)すると、角度θのπ/2ラジアン(90度)から2πラジアン(360度)あるいは0ラジアン(0度)を経て3/4πラジアン(270度)あるいは-π/2ラジアン(-90度)に推移する変遷を扱った形となります。頂点eおよび頂点fのx座標値がCos(θ),頂点eのy座標値がSin(θ)に対応。
【Rで球面幾何学】「円そのもの」の近似から派生した角度概念の起源
あれ? 複素共役/複素共軛(Complex Conjugate)の虚数部分の動きと同じではありませんか?
複素共役 - Wikipedia
ちなみに角adbと角cdbが直角、すなわちπ/2ラジアン(90度)に保たれ続けるので、三角形の内角の和がπラジアン(180度)となる性質から(その残りである)角dbc=角dab(角度θに従って0ラジアン(0度)からπラジアン(180度)にかけて変遷)と角bcd=角dab(角度-θに従ってπラジアン(180度)から0ラジアン(0度)にかけて遷移)の和もまた直角に保たれ続けます。半径Rの円に内接する三角形ABCにおける正弦定理(law of sines)線分AB/Sin(角BCA)=線分BC/Sin(角CAB)=線分CA/Sin(角ABC)=2πRの特殊例。
#合わせて「3/4までは円が描ける」世界
要するにこうしたアプローチによっては手が出せなかったのは、第三象限(X=<0かつY=<0)のみだったとも考えられる訳です。
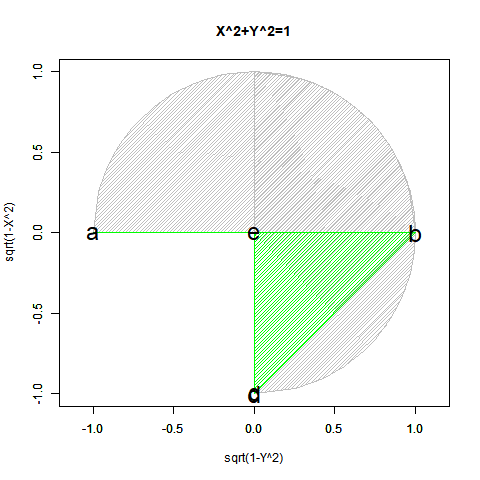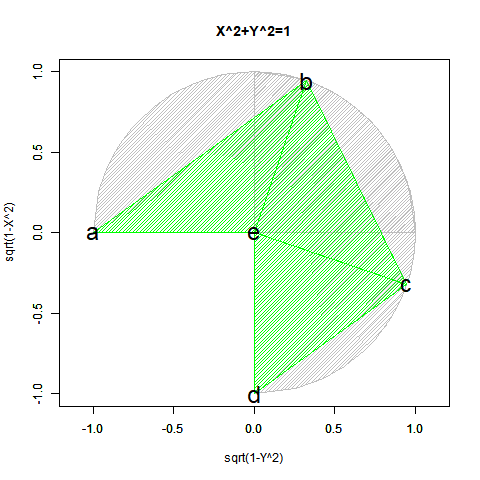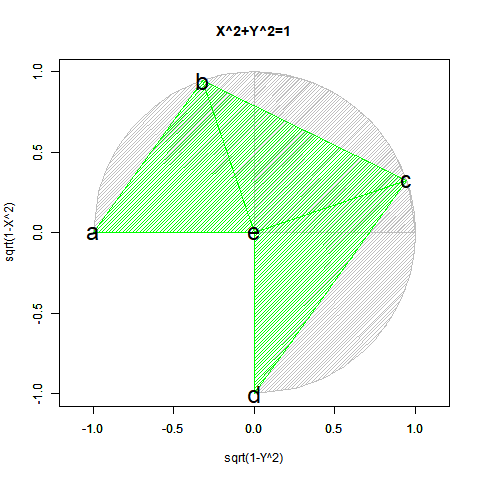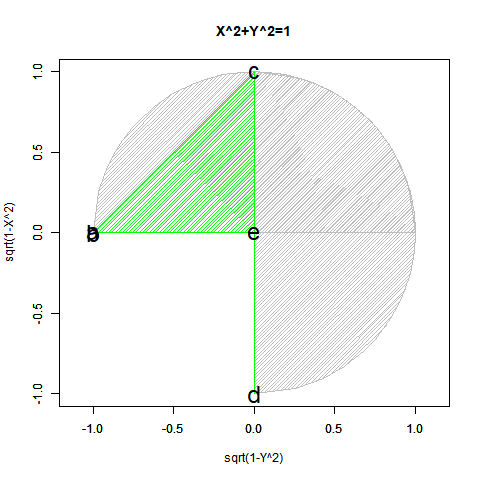
#CFC=Circle Function Closs
CFC<-function(Radian){
cx<-seq(-1,1,length=60)
f0<-function(x) sqrt(1-x^2)
cy<-f0(cx)
plot(cx,cy,asp=1,type="l",xlim=c(-1,1),ylim=c(-1,1),main="X^2+Y^2=1",xlab="sqrt(1-Y^2)",ylab="sqrt(1-X^2)")
par(new=T)#上書き指定
plot(cy,cx,asp=1,type="l",xlim=c(-1,1),ylim=c(-1,1),main="",xlab="",ylab="")
#塗りつぶし(X軸)
polygon(cx, #x
cy, #y
density=c(30), #塗りつぶす濃度
angle=c(45), #塗りつぶす斜線の角度
col=c(200,200,200)) #塗りつぶす色
#塗りつぶし(Y軸)
polygon(cy, #x
cx, #y
density=c(30), #塗りつぶす濃度
angle=c(45), #塗りつぶす斜線の角度
col=c(200,200,200)) #塗りつぶす色
#塗りつぶし(三角)
cx1<-rev(cx)
cy1<-rev(cy)
polygon(c(-1,cx[Radian],cy1[Radian],0,0,-1), #x
c(0,cy[Radian],cx1[Radian],-1,0,0), #y
density=c(30), #塗りつぶす濃度
angle=c(45), #塗りつぶす斜線の角度
col=rgb(0,1,0)) #塗りつぶす色
#線追加(三角)
segments(cx[Radian],cy[Radian],0,0,col=rgb(0,1,0))
segments(cy1[Radian],cx1[Radian],0,0,col=rgb(0,1,0))
#文字追加
text(c(-1,cx[Radian],cy1[Radian],0,0),c(0,cy[Radian],cx1[Radian],-1,0), labels=c("a","b","c","d","e"),col=c(rgb(0,0,0),rgb(0,0,0),rgb(0,0,0),rgb(0,0,0)),cex=c(2,2,2,2,2))
}
#アニメーション
library("animation")
Time_Code=rev(c(1:60))
saveGIF({
for (i in Time_Code){
CFC(i)
}
}, interval = 0.1, movie.name = "CFC001.gif")
そして人類はこの壁を複素数の導入によって乗り越える事になるのです。
【Rで球面幾何学】「世界で一番美しい公式」オイラーの等式の罠?