【Rで球面幾何学】「世界で一番美しい公式」オイラーの等式の罠？

• (2020年5月5日)初投稿
• (2021年4月29日)pythonによる実装を追加。

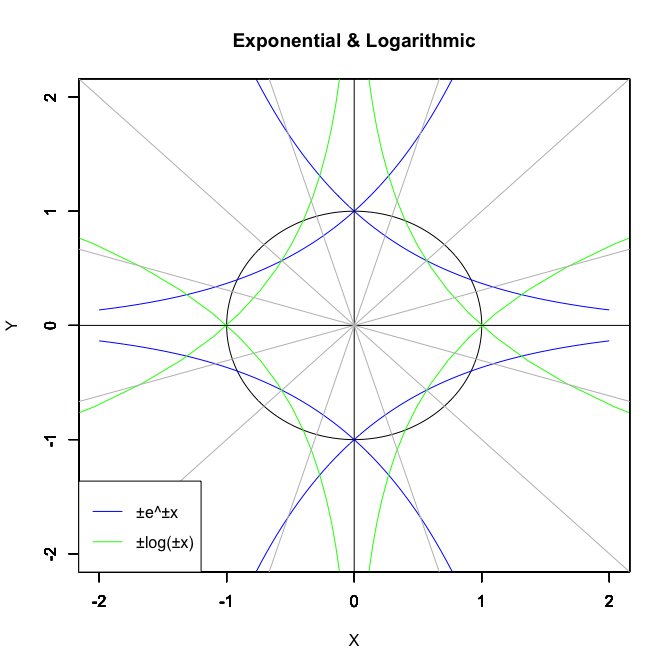
【初心者向け】指数・対数関数の発見

ヤコブ・ベルヌーイ（Jakob Bernoulli、1654年〜1705年）が導出した指数関数e^xに複素数πiを代入すると、所謂「世界で一番美しい方程式」オイラーの等式（Eulers identity）e^πi=(1+πi/N)^N=-1となって半円を描きます。ちなみにそういう具合に式を拡張したの自体は弟子のレオンハルト・オイラー（Leonhard Euler, 1707年〜1783年）の功績。

#オイラーの等式（ヤコブ・ベルヌーイ方式による作図）

Eulers_identity<-function(n){
rim01<-pi*complex(real=0,imaginary=1)
Tarm=c(complex(real=1,imaginary=0),seq(rim01/n,rim01/n,length=n))
Reduce(function(a,b) {a+a*b}, Tarm, accumulate = T)

}
theta <- seq(pi, -pi, length=360) #円周率（ラジアン表記）

Eulers_identity00_plot<-function(n){
plot(cos(theta), sin(theta), xlim=c(-2,1),ylim=c(0,4),type="l",col=rgb(0,1,0), asp=1,main="Euler’s identity", xlab="Real Expanse", ylab="Imaginary Expanse")
par(new=T) # 上書き指定

plot(Re(Eulers_identity(n)),Im(Eulers_identity(n)),asp=1,xlim=c(-2,1),ylim=c(0,4),asp=1,type="l",main="", xlab="", ylab="")

text(0, 0, "0",col=rgb(0,0,0))
text(1, 0, "1",col=rgb(0,0,1))
text(-1, 0, "-1",col=rgb(1,0,0))
text(0, 1, "π",col=rgb(0,1,0))
segments(0,0,1,0,col=rgb(0,0,1))
segments(0,0,-1,0,col=rgb(1,0,0))
}

#アニメーションさせてみる。
library("animation")
Time_Code=c(1,2,4,8,16,32,64,128)
saveGIF({
for (i in Time_Code){
　　Eulers_identity00_plot(i)
}
}, interval = 0.1, movie.name = "TEST01.gif")

オイラー自身はジョン・ネイピア（John Napier, 1550年〜1617年）の対数表の底「0.9999999」と師匠ベルヌーイの考案したベルヌーイ試行の概念を組み合わせた式(1-1/N)^Nより出発してe^Xi=(1-Xi/N)^Nへと到達したと考えられています。e^πi=(1-πi/N)^N=-1で、反対周りの半円を描きます。

#オイラーの等式（オイラー方式による作図）

Eulers_identity<-function(n){
rim01<-pi*complex(real=0,imaginary=1)
Tarm=c(complex(real=1,imaginary=0),seq(rim01/n,rim01/n,length=n))
Reduce(function(a,b) {a-a*b}, Tarm, accumulate = T)

}
theta <- seq(pi, -pi, length=360) #円周率（ラジアン表記）

Eulers_identity00_plot<-function(n){
plot(cos(theta), sin(theta), xlim=c(-2,1),ylim=c(-4,0),asp=1,type="l",col=rgb(0,1,0), main="Euler’s identity", xlab="Real Expanse", ylab="Imaginary Expanse")
par(new=T) # 上書き指定

plot(Re(Eulers_identity(n)),Im(Eulers_identity(n)),asp=1,xlim=c(-2,1),ylim=c(-4,0),type="l",main="", xlab="", ylab="")

text(0, 0, "0",col=rgb(0,0,0))
text(1, 0, "1",col=rgb(0,0,1))
text(-1, 0, "-1",col=rgb(1,0,0))
text(0, 1, "π",col=rgb(0,1,0))
segments(0,0,1,0,col=rgb(0,0,1))
segments(0,0,-1,0,col=rgb(1,0,0))
}

#アニメーションさせてみる。
library("animation")
Time_Code=c(1,2,4,8,16,32,64,128)
saveGIF({
for (i in Time_Code){
　　Eulers_identity00_plot(i)
}
}, interval = 0.1, movie.name = "TEST02.gif")

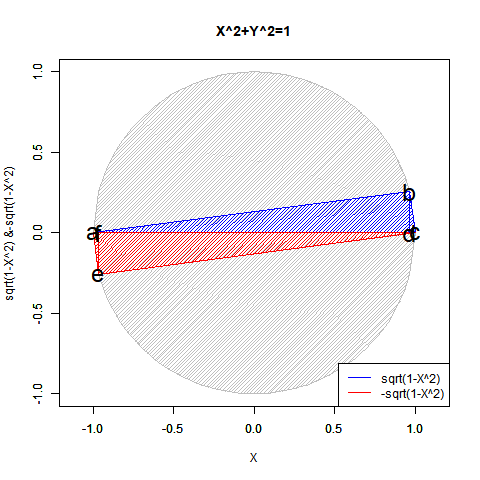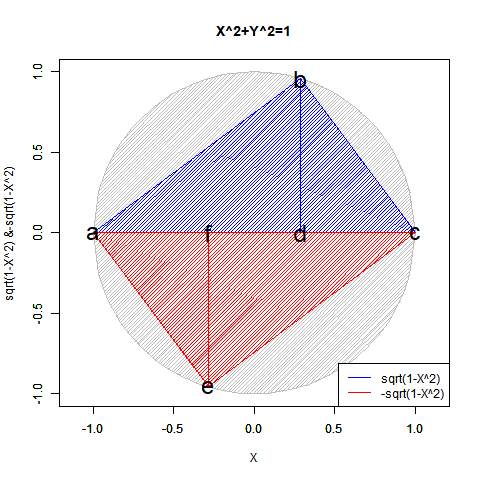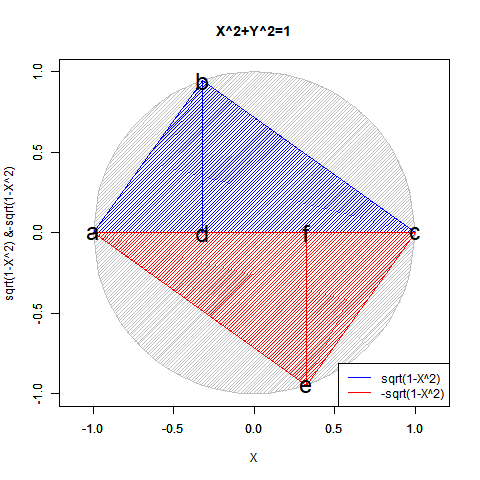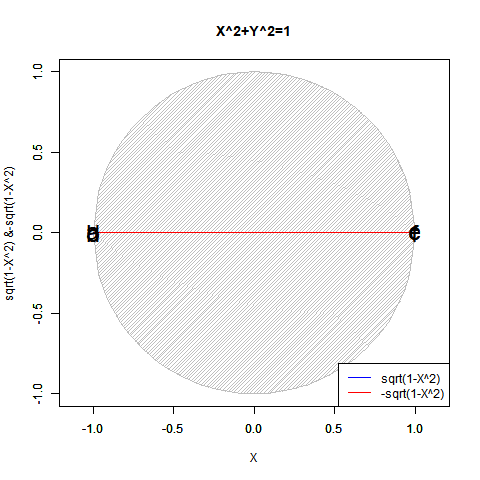
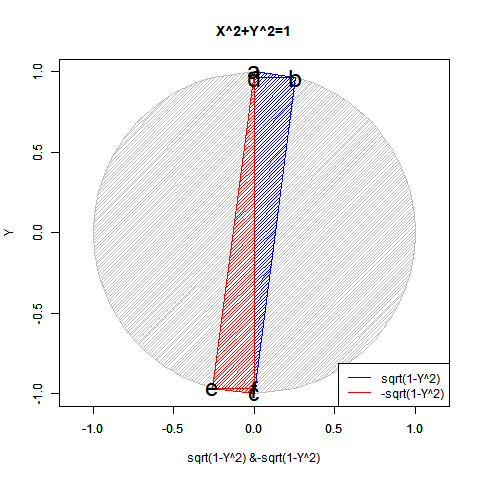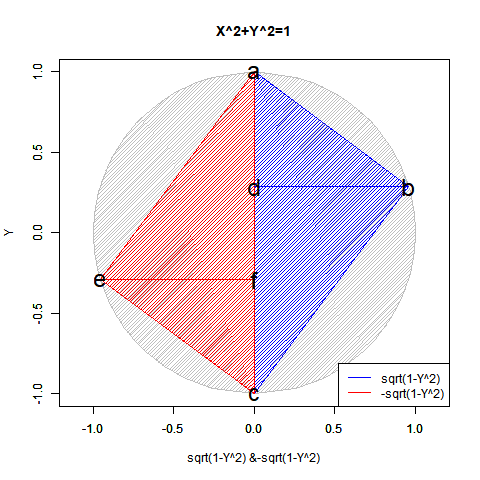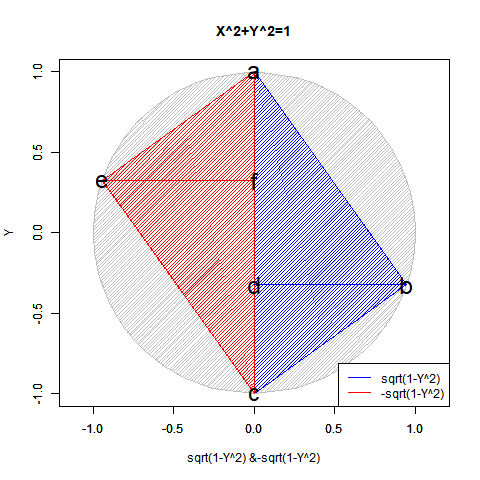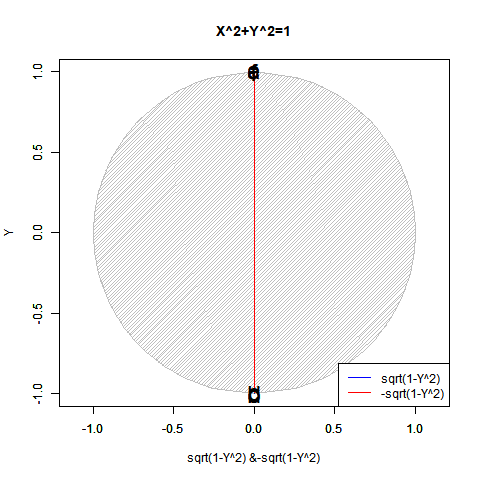
この２つの計算結果は複素図表上において共役関係にあり、両方あわせてe^πi=(1±πi/N)^N=-1と表記し、三平方の定理（ピタゴラスの定理）を応用した円関数x^2+y^2=1を単位円描写に援用した±sqrt(1-x^2)と並べて論じられる事もあったりします。

#オイラーの等式（全周分）

Eulers_identity<-function(n){
rim01<-pi*complex(real=0,imaginary=1)
Tarm=c(complex(real=1,imaginary=0),seq(rim01/n,rim01/n,length=n))
Reduce(function(a,b) {a+a*b}, Tarm, accumulate = T)

}
theta <- seq(pi, -pi, length=360) #円周率（ラジアン表記）
#グラフを描画してみる。
Eulers_identity01_plot<-function(n){
ei01<-Eulers_identity(n)
ei02<-Conj(ei01)
plot(cos(theta), sin(theta),asp=1, xlim=c(-2,1),ylim=c(-4,4),type="l",col=rgb(0,1,0), main="Euler’s identity", xlab="Real Expanse", ylab="Imaginary Expanse")
par(new=T) # 上書き指定
plot(Re(ei01),Im(ei01),asp=1,xlim=c(-2,1),ylim=c(-4,4),type="l",main="", xlab="", ylab="")
par(new=T) # 上書き指定
plot(Re(ei02),Im(ei02),asp=1,xlim=c(-2,1),ylim=c(-4,4),type="l",main="", xlab="", ylab="")
text(0, 0, "0",col=rgb(0,0,0))
text(1, 0, "1",col=rgb(0,0,1))
text(-1, 0, "-1",col=rgb(1,0,0))
text(0, 1, "π",col=rgb(0,1,0))
text(0, -1, "π",col=rgb(0,1,0))
segments(0,0,1,0,col=rgb(0,0,1))
segments(0,0,-1,0,col=rgb(1,0,0))
}

#アニメーションさせてみる。

library("animation")
Time_Code=c(1,2,4,8,16,32,64,128)
saveGIF({
for (i in Time_Code){
　　Eulers_identity01_plot(i)
}
}, interval = 0.1, movie.name = "TEST03.gif")

【Rで球面幾何学】「半円しか描けなかった」世界の思い出？

実は、かかる解釈こそが罠。何故ならオイラーの等式（Euler's identity）e^πi=(1±1/N)^N=-1なる式はあくまでオイラーの公式（Euler's Fomula）e^θi=Cos(θ)+Sin(θi)＝(1+θi/N)^N=-(1-θi/N)^Nの特別解に過ぎず、こちらには「半円しか描けない」なんて制約は全く存在しないからなのです… 

###オイラーの公式（1/4周分、反時計回り）

Eulers_identity<-function(n){
rim01<-0.5*pi*complex(real=0,imaginary=1)
Tarm=c(complex(real=1,imaginary=0),seq(rim01/n,rim01/n,length=n))
Reduce(function(a,b) {a+a*b}, Tarm, accumulate = T)

}
theta <- seq(pi, -pi, length=360) #円周率（ラジアン表記）
#グラフを描画してみる。
Eulers_identity01_plot<-function(n){
ei01<-Eulers_identity(n)
ei02<-Conj(ei01)
plot(cos(theta), sin(theta),asp=1, xlim=c(-2,1),ylim=c(-4,4),type="l",col=rgb(0,1,0), main="Euler’s identity", xlab="Real Expanse", ylab="Imaginary Expanse")
par(new=T) # 上書き指定
plot(Re(ei01),Im(ei01),asp=1,xlim=c(-2,1),ylim=c(-4,4),type="l",main="", xlab="", ylab="")
#par(new=T) # 上書き指定
#plot(Re(ei02),Im(ei02),asp=1,xlim=c(-2,1),ylim=c(-4,4),type="l",main="", xlab="", ylab="")
text(0, 0, "0",col=rgb(0,0,0))
text(1, 0, "1",col=rgb(0,0,1))
text(-1, 0, "-1",col=rgb(1,0,0))
text(0, 1, "π",col=rgb(0,1,0))
text(0, -1, "π",col=rgb(0,1,0))
segments(0,0,1,0,col=rgb(0,0,1))
segments(0,0,-1,0,col=rgb(1,0,0))
}

#アニメーションさせてみる。

library("animation")
Time_Code=c(1,2,4,8,16,32,64,128)
saveGIF({
for (i in Time_Code){
　　Eulers_identity01_plot(i)
}
}, interval = 0.1, movie.name = "TEST04.gif")

###オイラーの公式（半周分、反時計回り）

Eulers_identity<-function(n){
rim01<-pi*complex(real=0,imaginary=1)
Tarm=c(complex(real=1,imaginary=0),seq(rim01/n,rim01/n,length=n))
Reduce(function(a,b) {a+a*b}, Tarm, accumulate = T)

}
theta <- seq(pi, -pi, length=360) #円周率（ラジアン表記）
#グラフを描画してみる。
Eulers_identity01_plot<-function(n){
ei01<-Eulers_identity(n)
ei02<-Conj(ei01)
plot(cos(theta), sin(theta),asp=1, xlim=c(-2,1),ylim=c(-4,4),type="l",col=rgb(0,1,0), main="Euler’s identity", xlab="Real Expanse", ylab="Imaginary Expanse")
par(new=T) # 上書き指定
plot(Re(ei01),Im(ei01),xlim=c(-2,1),asp=1,ylim=c(-4,4),type="l",main="", xlab="", ylab="")
#par(new=T) # 上書き指定
#plot(Re(ei02),Im(ei02),asp=1,xlim=c(-2,1),ylim=c(-4,4),type="l",main="", xlab="", ylab="")
text(0, 0, "0",col=rgb(0,0,0))
text(1, 0, "1",col=rgb(0,0,1))
text(-1, 0, "-1",col=rgb(1,0,0))
text(0, 1, "π",col=rgb(0,1,0))
text(0, -1, "π",col=rgb(0,1,0))
segments(0,0,1,0,col=rgb(0,0,1))
segments(0,0,-1,0,col=rgb(1,0,0))
}

#アニメーションさせてみる。

library("animation")
Time_Code=c(1,2,4,8,16,32,64,128)
saveGIF({
for (i in Time_Code){
　　Eulers_identity01_plot(i)
}
}, interval = 0.1, movie.name = "TEST05.gif")

###オイラーの公式（3/4周分、反時計回り）

Eulers_identity<-function(n){
rim01<-1.5*pi*complex(real=0,imaginary=1)
Tarm=c(complex(real=1,imaginary=0),seq(rim01/n,rim01/n,length=n))
Reduce(function(a,b) {a+a*b}, Tarm, accumulate = T)

}
theta <- seq(pi, -pi, length=360) #円周率（ラジアン表記）
#グラフを描画してみる。
Eulers_identity01_plot<-function(n){
ei01<-Eulers_identity(n)
ei02<-Conj(ei01)
plot(cos(theta), sin(theta),asp=1,xlim=c(-2,1),ylim=c(-4,4),type="l",col=rgb(0,1,0), main="Euler’s identity", xlab="Real Expanse", ylab="Imaginary Expanse")
par(new=T) # 上書き指定
plot(Re(ei01),Im(ei01),asp=1,xlim=c(-2,1),ylim=c(-4,4),type="l",main="", xlab="", ylab="")
#par(new=T) # 上書き指定
#plot(Re(ei02),Im(ei02),asp=1,xlim=c(-2,1),ylim=c(-4,4),type="l",main="", xlab="", ylab="")
text(0, 0, "0",col=rgb(0,0,0))
text(1, 0, "1",col=rgb(0,0,1))
text(-1, 0, "-1",col=rgb(1,0,0))
text(0, 1, "π",col=rgb(0,1,0))
text(0, -1, "π",col=rgb(0,1,0))
segments(0,0,1,0,col=rgb(0,0,1))
segments(0,0,-1,0,col=rgb(1,0,0))
}

#アニメーションさせてみる。

library("animation")
Time_Code=c(1,2,4,8,16,32,64,128)
saveGIF({
for (i in Time_Code){
　　Eulers_identity01_plot(i)
}
}, interval = 0.1, movie.name = "TEST06.gif")

###オイラーの公式（１周分、反時計回り）

Eulers_identity<-function(n){
rim01<-2*pi*complex(real=0,imaginary=1)
Tarm=c(complex(real=1,imaginary=0),seq(rim01/n,rim01/n,length=n))
Reduce(function(a,b) {a+a*b}, Tarm, accumulate = T)

}
theta <- seq(pi, -pi, length=360) #円周率（ラジアン表記）
#グラフを描画してみる。
Eulers_identity01_plot<-function(n){
ei01<-Eulers_identity(n)
ei02<-Conj(ei01)
plot(cos(theta), sin(theta),asp=1, xlim=c(-2,1),ylim=c(-4,4),type="l",col=rgb(0,1,0), main="Euler’s identity", xlab="Real Expanse", ylab="Imaginary Expanse")
par(new=T) # 上書き指定
plot(Re(ei01),Im(ei01),asp=1,xlim=c(-2,1),ylim=c(-4,4),type="l",main="", xlab="", ylab="")
#par(new=T) # 上書き指定
#plot(Re(ei02),Im(ei02),asp=1,xlim=c(-2,1),ylim=c(-4,4),type="l",main="", xlab="", ylab="")
text(0, 0, "0",col=rgb(0,0,0))
text(1, 0, "1",col=rgb(0,0,1))
text(-1, 0, "-1",col=rgb(1,0,0))
text(0, 1, "π",col=rgb(0,1,0))
text(0, -1, "π",col=rgb(0,1,0))
segments(0,0,1,0,col=rgb(0,0,1))
segments(0,0,-1,0,col=rgb(1,0,0))
}

#アニメーションさせてみる。

library("animation")
Time_Code=c(1,2,4,8,16,32,64,128)
saveGIF({
for (i in Time_Code){
　　Eulers_identity01_plot(i)
}
}, interval = 0.1, movie.name = "TEST07.gif")

###オイラーの公式（２周分、反時計回り）

Eulers_identity<-function(n){
rim01<-4*pi*complex(real=0,imaginary=1)
Tarm=c(complex(real=1,imaginary=0),seq(rim01/n,rim01/n,length=n))
Reduce(function(a,b) {a+a*b}, Tarm, accumulate = T)

}
theta <- seq(pi, -pi, length=360) #円周率（ラジアン表記）
#グラフを描画してみる。
Eulers_identity01_plot<-function(n){
ei01<-Eulers_identity(n)
ei02<-Conj(ei01)
plot(cos(theta), sin(theta),asp=1, xlim=c(-2,1),ylim=c(-4,4),type="l",col=rgb(0,1,0), main="Euler’s identity", xlab="Real Expanse", ylab="Imaginary Expanse")
par(new=T) # 上書き指定
plot(Re(ei01),Im(ei01),asp=1,xlim=c(-2,1),ylim=c(-4,4),type="l",main="", xlab="", ylab="")
#par(new=T) # 上書き指定
#plot(Re(ei02),Im(ei02),asp=1,xlim=c(-2,1),ylim=c(-4,4),type="l",main="", xlab="", ylab="")
text(0, 0, "0",col=rgb(0,0,0))
text(1, 0, "1",col=rgb(0,0,1))
text(-1, 0, "-1",col=rgb(1,0,0))
text(0, 1, "π",col=rgb(0,1,0))
text(0, -1, "π",col=rgb(0,1,0))
segments(0,0,1,0,col=rgb(0,0,1))
segments(0,0,-1,0,col=rgb(1,0,0))
}

#アニメーションさせてみる。

library("animation")
Time_Code=c(1,2,4,8,16,32,64,128,256,512,1024)
saveGIF({
for (i in Time_Code){
　　Eulers_identity01_plot(i)
}
}, interval = 0.1, movie.name = "TEST08.gif")

当然、正反対方向に展開しても同じ結果となります。

###オイラーの公式（1/4周分、時計回り）

Eulers_identity<-function(n){
rim01<-0.5*pi*complex(real=0,imaginary=1)
Tarm=c(complex(real=1,imaginary=0),seq(rim01/n,rim01/n,length=n))
Reduce(function(a,b) {a+a*b}, Tarm, accumulate = T)

}
theta <- seq(pi, -pi, length=360) #円周率（ラジアン表記）
#グラフを描画してみる。
Eulers_identity01_plot<-function(n){
ei01<-Eulers_identity(n)
ei02<-Conj(ei01)
plot(cos(theta), sin(theta),asp=1,xlim=c(-2,1),ylim=c(-4,4),type="l",col=rgb(0,1,0), main="Euler’s identity", xlab="Real Expanse", ylab="Imaginary Expanse")
#par(new=T) # 上書き指定
#plot(Re(ei01),Im(ei01),asp=1,xlim=c(-2,1),ylim=c(-4,4),type="l",main="", xlab="", ylab="")
par(new=T) # 上書き指定
plot(Re(ei02),Im(ei02),asp=1,xlim=c(-2,1),ylim=c(-4,4),type="l",main="", xlab="", ylab="")
text(0, 0, "0",col=rgb(0,0,0))
text(1, 0, "1",col=rgb(0,0,1))
text(-1, 0, "-1",col=rgb(1,0,0))
text(0, 1, "π",col=rgb(0,1,0))
text(0, -1, "π",col=rgb(0,1,0))
segments(0,0,1,0,col=rgb(0,0,1))
segments(0,0,-1,0,col=rgb(1,0,0))
}

#アニメーションさせてみる。

library("animation")
Time_Code=c(1,2,4,8,16,32,64,128)
saveGIF({
for (i in Time_Code){
　　Eulers_identity01_plot(i)
}
}, interval = 0.1, movie.name = "TEST09.gif")

###オイラーの公式（半周分、時計回り）

Eulers_identity<-function(n){
rim01<-pi*complex(real=0,imaginary=1)
Tarm=c(complex(real=1,imaginary=0),seq(rim01/n,rim01/n,length=n))
Reduce(function(a,b) {a+a*b}, Tarm, accumulate = T)

}
theta <- seq(pi, -pi, length=360) #円周率（ラジアン表記）
#グラフを描画してみる。
Eulers_identity01_plot<-function(n){
ei01<-Eulers_identity(n)
ei02<-Conj(ei01)
plot(cos(theta), sin(theta),asp=1, xlim=c(-2,1),ylim=c(-4,4),type="l",col=rgb(0,1,0), main="Euler’s identity", xlab="Real Expanse", ylab="Imaginary Expanse")
#par(new=T) # 上書き指定
#plot(Re(ei01),Im(ei01),asp=1,xlim=c(-2,1),ylim=c(-4,4),type="l",main="", xlab="", ylab="")
par(new=T) # 上書き指定
plot(Re(ei02),Im(ei02),asp=1,xlim=c(-2,1),ylim=c(-4,4),type="l",main="", xlab="", ylab="")
text(0, 0, "0",col=rgb(0,0,0))
text(1, 0, "1",col=rgb(0,0,1))
text(-1, 0, "-1",col=rgb(1,0,0))
text(0, 1, "π",col=rgb(0,1,0))
text(0, -1, "π",col=rgb(0,1,0))
segments(0,0,1,0,col=rgb(0,0,1))
segments(0,0,-1,0,col=rgb(1,0,0))
}

#アニメーションさせてみる。

library("animation")
Time_Code=c(1,2,4,8,16,32,64,128)
saveGIF({
for (i in Time_Code){
　　Eulers_identity01_plot(i)
}
}, interval = 0.1, movie.name = "TEST10.gif")

###オイラーの公式（3/4周分、時計回り）

Eulers_identity<-function(n){
rim01<-1.5*pi*complex(real=0,imaginary=1)
Tarm=c(complex(real=1,imaginary=0),seq(rim01/n,rim01/n,length=n))
Reduce(function(a,b) {a+a*b}, Tarm, accumulate = T)

}
theta <- seq(pi, -pi, length=360) #円周率（ラジアン表記）
#グラフを描画してみる。
Eulers_identity01_plot<-function(n){
ei01<-Eulers_identity(n)
ei02<-Conj(ei01)
plot(cos(theta), sin(theta),asp=1, xlim=c(-2,1),ylim=c(-4,4),type="l",col=rgb(0,1,0), main="Euler’s identity", xlab="Real Expanse", ylab="Imaginary Expanse")
#par(new=T) # 上書き指定
#plot(Re(ei01),Im(ei01),asp=1,xlim=c(-2,1),ylim=c(-4,4),type="l",main="", xlab="", ylab="")
par(new=T) # 上書き指定
plot(Re(ei02),Im(ei02),asp=1,xlim=c(-2,1),ylim=c(-4,4),type="l",main="", xlab="", ylab="")
text(0, 0, "0",col=rgb(0,0,0))
text(1, 0, "1",col=rgb(0,0,1))
text(-1, 0, "-1",col=rgb(1,0,0))
text(0, 1, "π",col=rgb(0,1,0))
text(0, -1, "π",col=rgb(0,1,0))
segments(0,0,1,0,col=rgb(0,0,1))
segments(0,0,-1,0,col=rgb(1,0,0))
}

#アニメーションさせてみる。

library("animation")
Time_Code=c(1,2,4,8,16,32,64,128)
saveGIF({
for (i in Time_Code){
　　Eulers_identity01_plot(i)
}
}, interval = 0.1, movie.name = "TEST11.gif")

###オイラーの公式（１周分、時計回り）

Eulers_identity<-function(n){
rim01<-2*pi*complex(real=0,imaginary=1)
Tarm=c(complex(real=1,imaginary=0),seq(rim01/n,rim01/n,length=n))
Reduce(function(a,b) {a+a*b}, Tarm, accumulate = T)

}
theta <- seq(pi, -pi, length=360) #円周率（ラジアン表記）
#グラフを描画してみる。
Eulers_identity01_plot<-function(n){
ei01<-Eulers_identity(n)
ei02<-Conj(ei01)
plot(cos(theta), sin(theta),asp=1, xlim=c(-2,1),ylim=c(-4,4),type="l",col=rgb(0,1,0), main="Euler’s identity", xlab="Real Expanse", ylab="Imaginary Expanse")
#par(new=T) # 上書き指定
#plot(Re(ei01),Im(ei01),asp=1,xlim=c(-2,1),ylim=c(-4,4),type="l",main="", xlab="", ylab="")
par(new=T) # 上書き指定
plot(Re(ei02),Im(ei02),asp=1,xlim=c(-2,1),ylim=c(-4,4),type="l",main="", xlab="", ylab="")
text(0, 0, "0",col=rgb(0,0,0))
text(1, 0, "1",col=rgb(0,0,1))
text(-1, 0, "-1",col=rgb(1,0,0))
text(0, 1, "π",col=rgb(0,1,0))
text(0, -1, "π",col=rgb(0,1,0))
segments(0,0,1,0,col=rgb(0,0,1))
segments(0,0,-1,0,col=rgb(1,0,0))
}

#アニメーションさせてみる。

library("animation")
Time_Code=c(1,2,4,8,16,32,64,128)
saveGIF({
for (i in Time_Code){
　　Eulers_identity01_plot(i)
}
}, interval = 0.1, movie.name = "TEST12.gif")

###オイラーの公式（２周分、時計回り）

Eulers_identity<-function(n){
rim01<-4*pi*complex(real=0,imaginary=1)
Tarm=c(complex(real=1,imaginary=0),seq(rim01/n,rim01/n,length=n))
Reduce(function(a,b) {a+a*b}, Tarm, accumulate = T)

}
theta <- seq(pi, -pi, length=360) #円周率（ラジアン表記）
#グラフを描画してみる。
Eulers_identity01_plot<-function(n){
ei01<-Eulers_identity(n)
ei02<-Conj(ei01)
plot(cos(theta), sin(theta),asp=1, xlim=c(-2,1),ylim=c(-4,4),type="l",col=rgb(0,1,0), main="Euler’s identity", xlab="Real Expanse", ylab="Imaginary Expanse")
#par(new=T) # 上書き指定
#plot(Re(ei01),Im(ei01),asp=1,xlim=c(-2,1),ylim=c(-4,4),type="l",main="", xlab="", ylab="")
par(new=T) # 上書き指定
plot(Re(ei02),Im(ei02),asp=1,xlim=c(-2,1),ylim=c(-4,4),type="l",main="", xlab="", ylab="")
text(0, 0, "0",col=rgb(0,0,0))
text(1, 0, "1",col=rgb(0,0,1))
text(-1, 0, "-1",col=rgb(1,0,0))
text(0, 1, "π",col=rgb(0,1,0))
text(0, -1, "π",col=rgb(0,1,0))
segments(0,0,1,0,col=rgb(0,0,1))
segments(0,0,-1,0,col=rgb(1,0,0))
}

#アニメーションさせてみる。

library("animation")
Time_Code=c(1,2,4,8,16,32,64,128,256,512,1024)
saveGIF({
for (i in Time_Code){
　　Eulers_identity01_plot(i)
}
}, interval = 0.1, movie.name = "TEST13.gif")

#pythonによる実装
pythonのreduce関数は途中値を出力しません。
Python Tips： functools.reduce() を活用したい
高階関数の使い方！Pythonでreduceを使う方法【初心者向け】 | TechAcademyマガジン
こういう場合にはaccumulate()関数を使うのです。
Reduce() vs Accumulate() in Python

%matplotlib nbagg
import math as m
import cmath as c
import numpy as num
import matplotlib.pyplot as plt
from functools import reduce
from itertools import accumulate
import matplotlib.animation as animation

def Napier_culc(ABS,n):
    RIM=ABS*m.pi*(0+1j)
    Tarm0=num.repeat(RIM/n,n)
    Tarm=num.concatenate([[(1+0j)], Tarm0])
    return accumulate(Tarm,lambda x,y:x+x*y)

#単位円データ作成
c0=num.linspace(0,2*m.pi,61,endpoint = True)
s0=[]
for nm in range(len(c0)):
    s0.append(complex(m.cos(c0[nm]),m.sin(c0[nm])))
s1=num.array(s0)
plt.style.use('default')
fig = plt.figure(111)

#関数定義
def Eulerien_Identity(n):
    plt.cla()
    #ネイピア数算出
    ei01=num.array(list(Napier_culc(ABS,Time_Code[n])))
    EI0=[]
    for nm in range(len(ei01)):
        EI0.append(ei01[nm].conjugate())
    ei02=num.array(EI0)
    #円周描画
    plt.plot(s1.real,s1.imag,color="green", label="Circle")
    plt.plot(ei01.real,ei01.imag,color="blue", label="(1+1/n)^n")
    plt.plot(ei02.real,ei02.imag,color="red", label="(1-1/n)^n")
    plt.xlim([-m.pi,m.pi])
    plt.ylim([-m.pi,m.pi])
    plt.title("Eulerean Identity")
    plt.xlabel("Real")
    plt.ylabel("Imaginal")
    ax = fig.add_subplot()
    ax.set_aspect('equal', adjustable='box')
    #補助線描画
    plt.axvline(0, 0, 1,color="black")
    plt.axhline(0, 0, 1,color="black")
    plt.plot([-1,0],[0,0],color="red",lw=1)
    plt.plot([0,1],[0,0],color="blue",lw=1)
    ax.text(0, 0, "0",color="black",size=13)
    ax.text(1, 0, "1",color="blue",size=13)
    ax.text(-1, 0, "-1",color="red",size=13)
    ax.text(0, 1, "π",color="green",size=13)
    ax.text(0, -1, "-π",color="green",size=13)
    #凡例描画
    ax.legend(loc='lower right')

ABS=1
Time_Code=[1,2,4,8,16,32,64,128]

#Eulerien_Identity(0)
#plt.show()

ani = animation.FuncAnimation(fig, Eulerien_Identity, interval=100,frames=len(Time_Code))
ani.save("EI01.gif", writer="pillow")

ABS=1.5(3/4周)の場合

ABS=2(1周)の場合…おや「河童巻き」が巻き切らない？　という事は…

ABS=6(3周)の場合…この程度のネイピア数の計算精度では、もはや「河童巻き」に見えない程のユルユル状態…

そう、実は分枝点切断の概念を持ち出すまでもなく$e^πi$関数は、最初からネイピア数の計算精度に応じた螺旋軌道しか描かないのです。

ABS=6
Time_Code=[1,2,4,8,16,32,64,128,256,512,1024,2048]

#オイラーの方便?
ところで、私は以前から「オイラーの等式は世界で一番美しい方程式」と言い広めた最初期の人物の一人があの大数学者ガウスだった事が気に掛かっていたのです。
オイラーの等式 - Wikipedia

カール・フリードリヒ・ガウスは「この式を見せられた学生がすぐにその意味を理解できなければ、その学生は第一級の数学者には決してなれない(If this formula was not immediately apparent to a student on being told it, the student would never be a first-class mathematician.) 」と指摘している。

もしかしたらこれも「（虚数が嫌われていた時代に密かにその啓蒙活動を続けた）ガウスの方便」の一環だったのでは？