時はまさに近世も成熟期に入った18世紀。自然指数関数(Natural Exponential function)と自然対数関数(Natural Logarithmic function)の概念を纏め上げ、マクローリン級数 (Maclaurin series) の概念を知ったばかりの数学者レオンハルド・オイラー(Leonhard Euler, 1707年〜1783年)は、三角関数(Trigonometric Function)の概念と自然指数関数/自然対数関数の概念が統合可能なのではないかと考えました。
【Rで球面幾何学】オイラーの公式を導出したマクローリン級数

そもそも指数関数や対数関数はどういう概念なのでしょう?
自然指数関数と自然対数関数の値の範囲。ただし
- n={-∞→-2→-1→0→1→2→∞}
- N={-∞,…,-2,-1,0,1,2,…,∞}
- m={exp(-∞):=0→exp(-2)=1/exp(2)=1/exp(1)^2→exp(-1)=1/exp(1)→exp(0)=1,exp(1)→exp(2)=exp(1)^2→exp(∞):=∞}
- M={exp(-∞):=0,…,→exp(-2)=1/exp(2)=1/exp(1)^2→exp(-1)=1/exp(1),exp(0)=1,exp(1),exp(2)=exp(1)^2,…,exp(∞):=∞}
とする。
- 自然指数関数Y=e^nの範囲=M
- 自然指数関数Y=log(m)の範囲=N
- 自然指数関数Y=e^-nの値の範囲=rev(M)
- 自然指数関数Y=log(-m)の値の範囲=rev(N)
- 自然指数関数Y=-e^nの値の範囲=-M
- 自然指数関数Y=-log(m)の値の範囲=-N
- 自然指数関数Y=-e^-nの値の範囲=-rev(M)
- 自然指数関数X=-log(-m)の値の範囲=-rev(N)
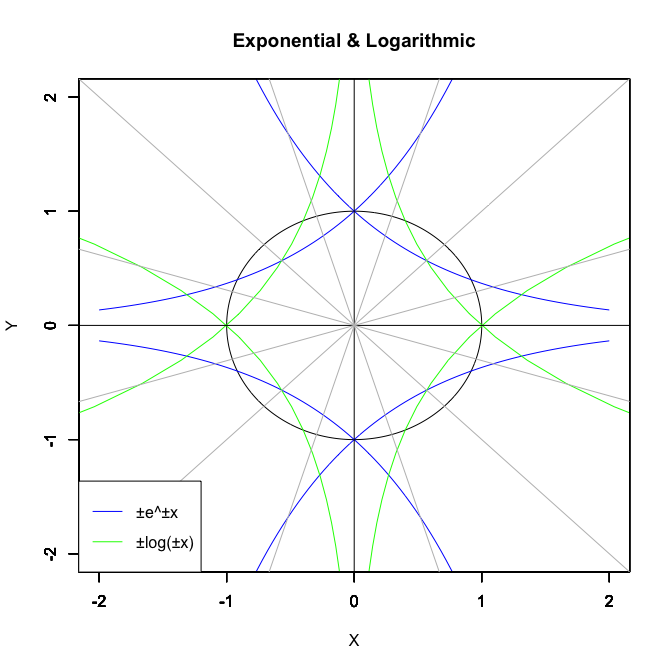
統計言語Rによる作図例
# 各指数関数・対数関数の交差点
Graph_scale_x<-c(-2,2)
Graph_scale_y<-c(-2,2)
theta <- seq(pi, -pi, length=360)
plot(cos(theta), sin(theta),asp=0,xlim=Graph_scale_x,ylim=Graph_scale_y,type="l",col=rgb(0,0,0), main="Exponential & Logarithmic", xlab="X", ylab="Y")
par(new=T)#上書き指定
# 指数関数
e0<-function(x){exp(x)}
plot(e0,asp=0,xlim=Graph_scale_x,ylim=Graph_scale_y,type="l",col=rgb(0,0,1), main="",xlab="",ylab="")
par(new=T)#上書き指定
e1<-function(x){exp(-x)}
plot(e1,asp=0,xlim=Graph_scale_x,ylim=Graph_scale_y,type="l",col=rgb(0,0,1), main="",xlab="",ylab="")
par(new=T)#上書き指定
e2<-function(x){-1*exp(x)}
plot(e2,asp=0,xlim=Graph_scale_x,ylim=Graph_scale_y,type="l",col=rgb(0,0,1), main="",xlab="",ylab="")
par(new=T)#上書き指定
e3<-function(x){-1*exp(-x)}
plot(e3,asp=0,xlim=Graph_scale_x,ylim=Graph_scale_y,type="l",col=rgb(0,0,1), main="",xlab="",ylab="")
par(new=T)#上書き指定
# 対数関数
tc <- seq(-6, 6, length=60) #-6から6までを60等分
l0<-function(x){exp(x)}
tcvals0 <- l0(tc) #それぞれの縦軸の値
plot(tcvals0,tc,asp=0,xlim=Graph_scale_x,ylim=Graph_scale_y,type="l",col=rgb(0,1,0), main="",xlab="",ylab="")
par(new=T)#上書き指定
l1<-function(x){exp(-x)}
tcvals1 <- l1(tc) #それぞれの縦軸の値
plot(tcvals1,tc,asp=0,xlim=Graph_scale_x,ylim=Graph_scale_y,type="l",col=rgb(0,1,0), main="",xlab="",ylab="")
par(new=T)#上書き指定
l2<-function(x){-1*exp(x)}
tcvals2 <- l2(tc) #それぞれの縦軸の値
plot(tcvals2,tc,asp=0,xlim=Graph_scale_x,ylim=Graph_scale_y,type="l",col=rgb(0,1,0), main="",xlab="",ylab="")
par(new=T)#上書き指定
l3<-function(x){-1*exp(-x)}
tcvals3 <- l3(tc) #それぞれの縦軸の値
plot(tcvals3,tc,asp=0,xlim=Graph_scale_x,ylim=Graph_scale_y,type="l",col=rgb(0,1,0), main="",xlab="",ylab="")
# 90度(π/2)の補助線
abline(h=0)
abline(v=0)
# 45度(π/4)の補助線
segments(-8,-8,8,8,col=c(128,128,128))
segments(-8,8,8,-8,col=c(128,128,128))
# 18度(π/10)/72度の補助線
segments(-8,-(sin(pi/10))*8,8,(sin(pi/10))*8,col=c(128,128,128))
segments(-8,(sin(pi/10))*8,8,-1*(sin(pi/10))*8,col=c(128,128,128))
segments(-(sin(pi/10))*8,-8,(sin(pi/10))*8,8,col=c(128,128,128))
segments*1*8,-8,-1*(sin(pi/10))*8,8,col=c(128,128,128))
legend("bottomleft", legend=c("±e^±x","±log(±x)"),lty=c(1,1),col=c(rgb(0,0,1),rgb(0,1,0)))
ちなみに三角関数や自然指数・対数関数の様に有限回数の加減乗除算や冪算で表せない関数を超越関数(Transcendental Function)といいます。
超越関数(transcendental function)とは
ネイピア数の発見
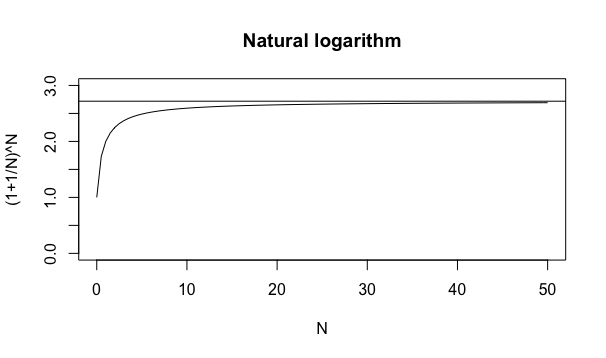
①大数の弱法則(WLLN: Weak Law of Large Numbers) の発見者たるヤコブ・ベルヌーイ(Jakob Bernoulli、1654年〜1705年)とその弟子レオンハルト・オイラー(Leonhard Euler, 1707年〜1783年)は、「各出目の出現確率が均等に1/6の六面体サイコロを6回降って特定の目が1回も出ない確率」なる概念を数式的に抽象化した(1-1/N)^Nの式を通じてネイピア数1/e=0.3678794の概念に到達した。
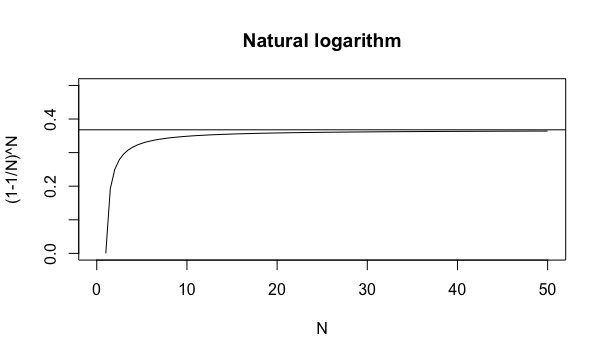
統計言語Rによる作図例
# オイラーの「ネイピアの対数表」に基づく算出方法
f0=function(x){(1-1/x)^x}
# グラフ化してみる。
plot(f0, xlim=c(0,50),ylim=c(0,0.5),lty =1,main="Natural logarithm", xlab="N", ylab="(1-1/N)^N")
# 自然対数1/eと比較。
abline(h=exp(-1))#exp(-1)=0.3678794...
-
大数の弱法則(WLLN:Weak Law of Large Numbers)…独立同分布/独立同一分布に従う可積分な確率変数の無限列X1,X2,…Xnとその平均μが与えられた時、標本平均(Sample Mean)(X1, X2,…Xn)/n(ただしn>=1)_の取る値が平均μの近傍から外れる確率は、nの値さえ大きくとれば、いくらでも小さく出来るとする考え方。
【初心者向け】記述統計学と代表値
【無限遠点を巡る数理】無限遠点としての正規分布と分散概念の歴史 -
独立同分布/独立同一分布(Independent and Identically Distributed; IID,i.i.d.,iid)…確率論と統計学において、確率変数の列やその他の系が、それぞれの確率変数が他の確率変数と同じ確率分布を持ち、かつ、それぞれ互いに独立している場合をいう。例えば6面体サイコロで各出目の確率は毎回1/6であり、その前後の出目の影響を受けない(メモリレス性)。「独立同分布/独立同一分布」なる確率分布自体が存在する訳ではない点に注意。
-
可積分(Integrable)…ニュートンが17世紀にケプラー問題を解いて微分積分学や古典力学が発祥して以降追求されてきた「求積法で完全に解ける」範囲。例えば「物差しの目盛は収束などしてはいけない」ルールに従って指数・対数関数や三角関数を「収束しない基準」として採用したフーリエ解析(Fourier Analysis)におけるフーリエ展開(Fourier Expansion)/フーリエ逆展開(Fourier Inverse Expansion)は、その立ち場故に指数・対数関数や三角関数そのものを直接は扱えない(決して収束しないからこそ正負の目盛りが無限に続き微積分演算の対象となり得ない)。あえてこの制約を破ろうとしたのがラプラス変換となる。
-
確率変数(Random Variable)…ある確率のセットが変数として存在し、しかも概ねそうした確率の合計が1となる様に正規化(Normalization)された状態モデルを指す。例えばコインの出目は{表,裏}のいずれかで、それぞれの目が出る確率は1/2(P(X)=1/2(x=0,1))。6面体サイコロを投げて出る目は{1,2,3,4,5,6}のいずれかで、それぞれの目が出る確率は1/6(P(X)=1/6(x=1,2,3,4,5,6))。3の目が出る確率も1/6(P(X=3)=1/6,P(3)=1/6)。一般化するとP(X)=1/N(X=1,2,3…N)となる。ちなみにこの様に出目の出現確率が均等となる分布を離散一様分布(Discrete Uniform Distribution)という。
離散一様分布
連続一様分布1
連続一様分布2
先に述べた(1-1/N)^N(各出目の出現確率が均等に1/NのN面体サイコロをN回降って特定の目が1回も出ない確率)なる概念も、この考え方の延長線上に導出されたのである。
ところで、ここに挙げた(1-1/N)^Nなる式は円グラフ(Pie Chart)に配した離散一様分布(Discrete Uniform Distribution)P(X)=1/N(X=1,2,3…N)のNを分割回数0(分割数1)から分割数無限(Inf(inity),分割数はInf(inity)-1=Inf(inity))に増やしていく過程に重なります。特定の出目が1回も出ない確率は各柱の頂点に現れるので、ピタゴラスの定理(Pythagorean Theorem)sqrt(x^2+y^2)ないしはsqrt(x^2+y^2+z^2)に導かれる形で「原点{0,0}ないしは{0,0,0}を共有しユークリッド距離(Euclidean Distance)を同じくする半径(Radius)r」の集合(Set)が最終的に円(Circle)や球面(Sphere)を描く訳です。
【初心者向け】ピタゴラスの定理あるいは三平方の定理からの出発

統計言語Rによる作図例
# FN01=Find the number of Napier 01
FN01<-function(NoS){
pie.data<-rep(1, NoS)
names0<-NULL
for(i in 1:NoS){
names0<-c(names0,paste0(i,"/",NoS))
}
names(pie.data)<-names0
pie(pie.data, col = heat.colors(NoS),main = "Probability of losing the Antipodal point")
}
# アニメーション
library("animation")
Time_Code=c(1,1,1,2,2,2,3,3,3,4,4,4,5,5,5,6,6,6,7,7,8,8,9,9,10,10,11,12,13,14,15,16)
saveGIF({
for (i in Time_Code){
FN01(i)
}
}, interval = 0.1, movie.name = "FN01.gif")
分割回数0(分割数1)…当たりが引けない確率(1-1/1)^1=0(「未開封のくじ引きセット」同様、必ず当たり籤が含まれている状態なので、それを引けない確率は0)。ちなみにこの時の頂点間を結ぶ辺長計は2πr=6.283185r(rは半径。つまり円周長そのもの)。
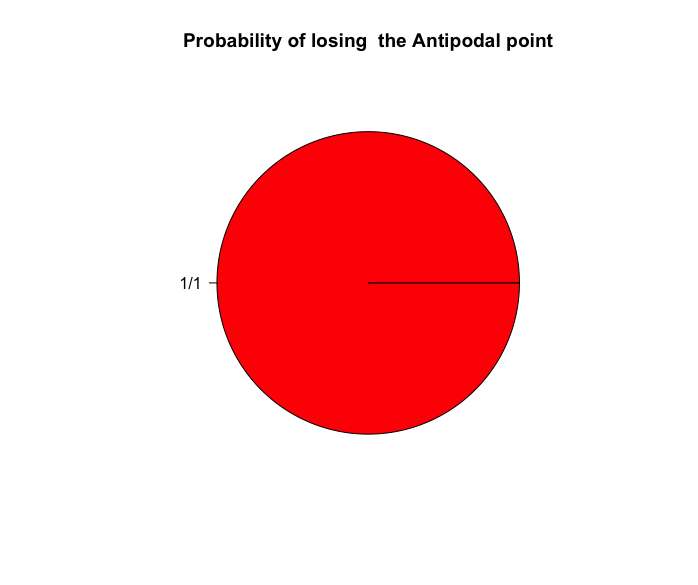
分割回数1(分割数2)…当たりが引けない確率(1-1/2)^2=0.25(1/4)。ちなみにこの時の頂点間を結ぶ辺長計は4r(rは半径。つまり半径×4=直径×2)。
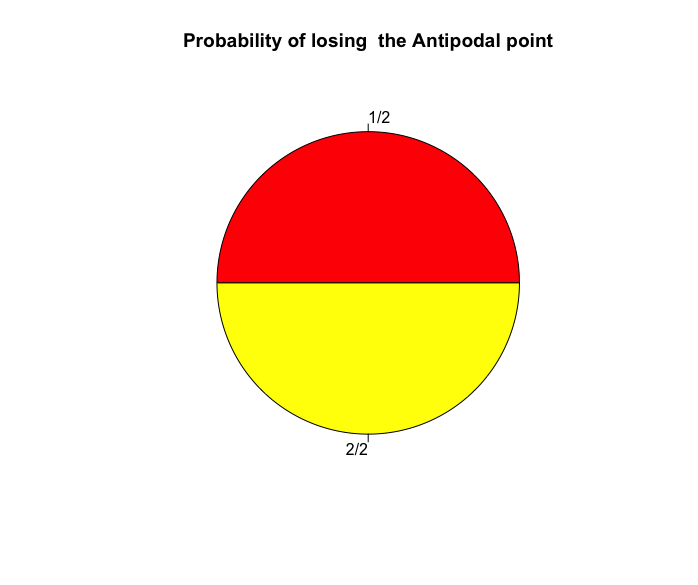
分割回数2(分割数3)…当たりが引けない確率(1-1/3)^3=0.2962963。ちなみにこの時の頂点間を結ぶ辺長計は6r(rは半径。つまり正三角形の1辺2r*3)。
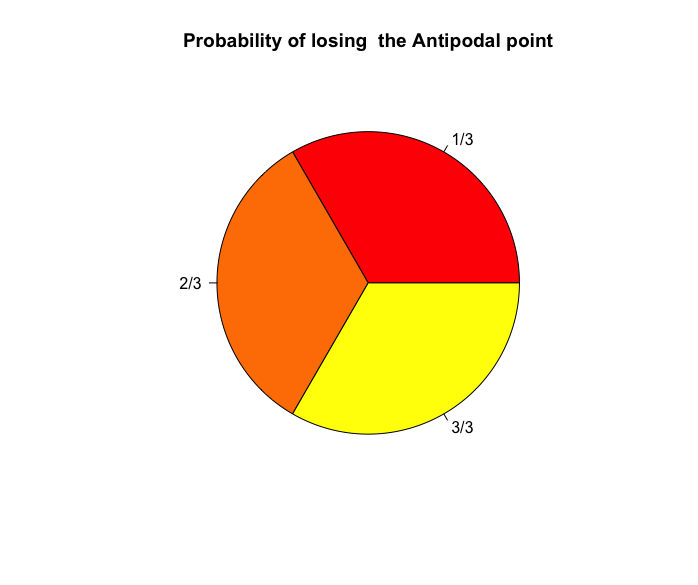
分割回数3(分割数4)…当たりが引けない確率(1-1/4)^4=0.3164062。ちなみにこの時の頂点間を結ぶ辺長計は4sqrt(2)r=5.656854r(rは半径。対角線sqrt(2)×4)。
こうして「頂点間を結ぶ辺長計」を求める振る舞いは「円に内接する多角形の辺長計と内接する多角形の辺長計の左がなくなるまで辺数Nを増やす」方法で半径(Radius)rの円周長2πr=6.283185rを求める**「挟み撃ち法**(Squeeze Theorem)」と重なります。
【初心者向け】挟み撃ち定理による円周率πの近似

そう、実は最終的に収束する数字こそ異なるとはいえ「exp(-1)=ネイピア数1/eの求め方」と「円周率πの求め方」は添字(Index)Nを共有していたのです。
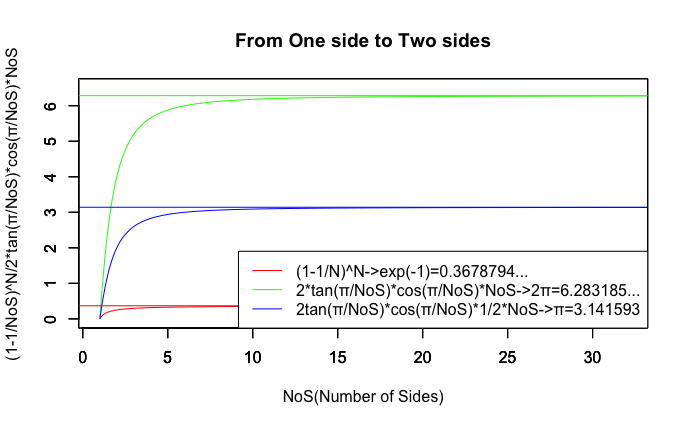
統計言語Rによる作図例
# オイラーの「ネイピアの対数表」に基づく算出方法
cx0<-seq(1,70,length=700)
f0<-function(x){(1-1/x)^x}
cy0<-f0(cx0)
# グラフ化してみる。
plot(cx0,cy0,xlim=c(1,32),ylim=c(0,6.5),type="l",col=rgb(1,0,0),main="From One side to Two sides", xlab="NoS(Number of Sides)", ylab="(1-1/NoS)^N/2*tan(π/NoS)*cos(π/NoS)*NoS")
par(new=T)#上書き指定
# 円周計算
cx1=seq(1,70,length=700)
f1=function(x) 2*tan(pi/x)*cos(pi/x)*x
cy1<-f1(cx1)
plot(cx1,cy1,xlim=c(1,32),ylim=c(0,6.5),type="l",col=rgb(0,1,0),main="", xlab="", ylab="")
par(new=T)#上書き指定
# 面積計算
cx2=seq(1,70,length=700)
f2=function(x) tan(pi/x)*cos(pi/x)*x
cy2<-f2(cx2)
plot(cx2,cy2,xlim=c(1,32),ylim=c(0,6.5),type="l",col=rgb(0,0,1),main="", xlab="", ylab="")
# 自然対数1/eと比較。
abline(h=exp(-1),col=rgb(1,0,0))#exp(-1)=0.3678794...
abline(h=pi,col=rgb( 0,0,1))#2π=6.283185...
abline(h=2*pi,col=rgb(0,1,0))#2π=6.283185...
# 凡例
legend("bottomright", legend=c("(1-1/N)^N->exp(-1)=0.3678794...","2*tan(π/NoS)*cos(π/NoS)*NoS->2π=6.283185...","2tan(π/NoS)*cos(π/NoS)*1/2*NoS->π=3.141593"),lty=c(1,1),col=c(rgb(1,0,0),rgb(0,1,0),rgb(0,0,1)))
②さらにベルヌーイとオイラーは「一年で元金が倍になる夢の金融商品において、複利計算でさらに利益を上げられる上限」なる概念を数式的に抽象化した(1+1/N)^Nの式の究極解としてネイピア数e=2.718282そのものにも到達。

# 統計解析言語Rによる確認例。
Principal_growth1<-function(op){
# 増加基準単位となる元本を1=100/100=100%と置く。
Principal<-1
# 関数グラフ化
f0=function(x){(x*(Principal+1/op))^op}
plot(f0, xlim=c(0,1),ylim=c(0,3),lty =1,type="s",main="Principal growth on Compound interest", xlab="Operation period", ylab="Principal growth rate (100% base)")
# 凡例を書き添える 。
legend("topleft", legend=c("Compound interest"), lty =c(1))
}
# アニメーションさせてみる。
library("animation")
Time_Code=c(1,2,3,4,5,10,20,30,40,50)
saveGIF({
for (i in Time_Code){
Principal_growth1(i)
}
}, interval = 0.1, movie.name = "TEST.gif")
# ヤコブ・ベルヌイの複利計算法に基づく算出方法
f0=function(x){(1+1/x)^x}
# グラフ化してみる。
plot(f0, xlim=c(0,50),ylim=c(0,3),lty =1,main="Natural logarithm", xlab="N", ylab="(1+1/N)^N")
# 自然対数eと比較。
abline(h=exp(1))#exp(1)=2.718282...
ネイピア数の逆数exp(-1)=1/exp(1)(=0.3678794)の計算が0分割(分割数1)の概念から出発するのに対し、その逆数たるネイピア数exp(1)(=2.718282)の計算は「距離2の直線」から出発します。前者を半径(Radius)rの世界とすれば後者は直径(Diameter){-r,0,r}あるいは共役概念(Conjugated Concept)との関わりが深い球表面上の対蹠(Antipodes)の世界であり、両者の鮮やかな対比は何らかの形での「境界線」を暗示している様です。
共役とは - コトバンク
-
ネイピア数exp(1)=2.718282を求める式(1+1/n)^nは(元金により生じた利子を次期の元金に組み入れていく)複利計算法においては単複利状態「元手1,区間範囲1における利率が2倍」から出発し「期間分割に対応して前期までの利率が元金に加えられる」「ただし区間分割数に対応して利率も割られる」設定で計算すると、どうしても区間分割数を無限に増やしても超えられない「元金増率の壁」に突き当たる事を意味している。「距離2の直線」には、こういう顕現の仕方もあるという事。
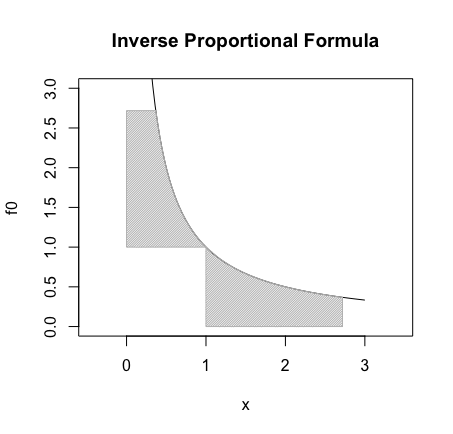
【数列】連続複利とネイピア数 ”e” - またネイピア数は解析学などの世界では「x=1,y=1の時にx×yの面積が1となる反比例関数y=1/xにおいて、次にx×yの面積が1となるxの区間{1,x}のxとその時のyの値を求めよ」なる設問の形で登場し、この問題の正解はx=exp(1)(=2.718282),y=exp(-1)(=0.3678794)。解き方としてはx^(-1)の定積分から出発して式(1+x)^(1/x)を導出してその極限を求める。そう、この計算方法もやはり「距離2の直線」から出発するのである。
自然対数の底eの定義
反比例関数y=1/xにおいて「面積1となる区間(exp(-1)×exp(1)=1)」
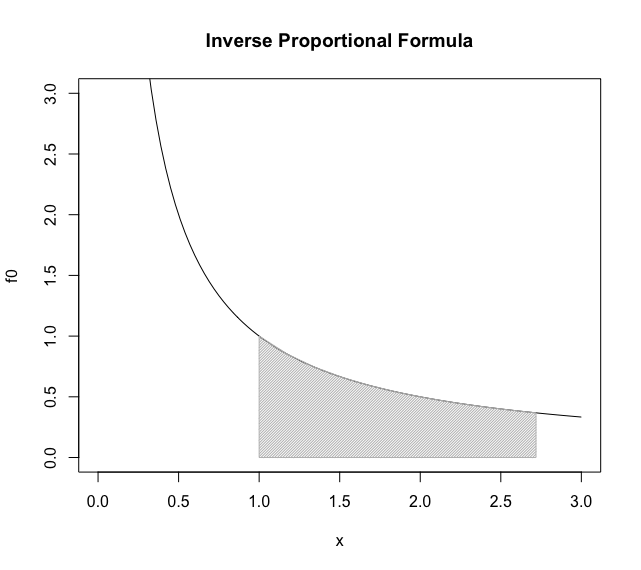
統計言語Rによる作図例(片側)
f0<-function(x){1/x}
plot(f0,xlim=c(0,3),ylim=c(0,3),main="Inverse Proportional Formula")
# 該当箇所の塗り潰し
sqx<-seq(1,exp(1),length=11)
sqy<-f0(sqx)
polygon(
c(1,sqx,exp(1)), #x
c(0,sqy,0), #y
density=c(50), #塗りつぶす濃度
angle=c(45), #塗りつぶす斜線の角度
col=c(200,200,200)) #塗りつぶす色
f0<-function(x){1/x}
plot(f0,asp=1,xlim=c(0,3),ylim=c(0,3),main="Inverse Proportional Formula")
# 該当箇所の塗り潰し
sqx0<-seq(1,exp(1),length=11)
sqy0<-f0(sqx0)
polygon(
c(1,sqx0,exp(1)), #x
c(0,sqy0,0), #y
density=c(50), #塗りつぶす濃度
angle=c(45), #塗りつぶす斜線の角度
col=c(200,200,200)) #塗りつぶす色
sqx1<-seq(exp(-1),1,length=11)
sqy1<-f0(sqx1)
polygon(
c(0,0,exp(-1),sqx1,0), #x
c(1,exp(1),exp(1),sqy1,1), #y
density=c(50), #塗りつぶす濃度
angle=c(45), #塗りつぶす斜線の角度
col=c(200,200,200)) #塗りつぶす色
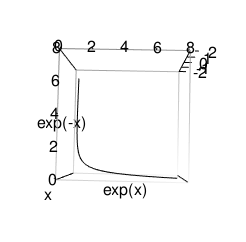
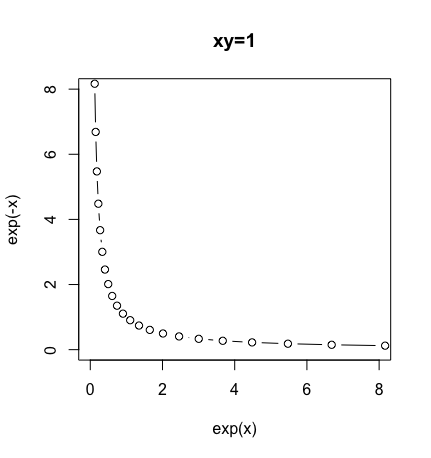
なのでX軸にexp(x)、y軸にexp(x)を置くとxy面に関数xy=1の演算結果集合(Operation Result Set)が現れます。

library(rgl)
c0<-seq(-2.1,2.1,by=0.2)
cx<-exp(c0)
cy<-exp(-c0)
cz<-c0
plot3d(cx,cy,cz,type="l",xlim=c(0,8),ylim=c(0,8),zlim=c(-2,2),xlab="exp(x)",ylab="exp(-x)",zlab="x")
movie3d(spin3d(axis=c(0,0,1),rpm=5),duration=10,fps=25,movie="~/Desktop/r10")
c0<-seq(-2.1,2.1,by=0.2)
cx<-exp(c0)
cy<-exp(-c0)
plot(cx,cy,xlim=c(0,8),type="b",ylim=c(0,8),main="xy=1",xlab="exp(x)",ylab="exp(-x)")
cx<-seq(-2.1,2.1,by=0.2)
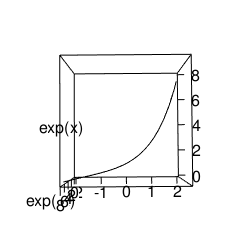
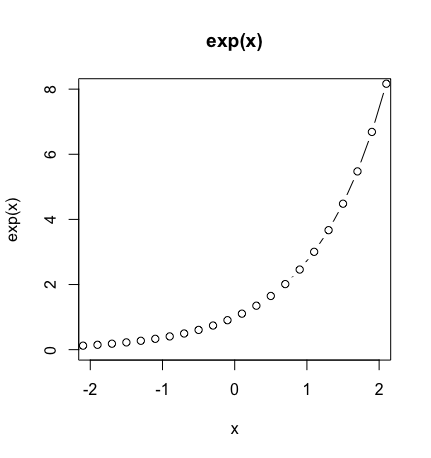
cy<-exp(c0)
plot(cx,cy,type="b",xlim=c(-2,2),ylim=c(0,8),main="exp(x)",xlab="x",ylab="exp(x)")
cx<-seq(-2.1,2.1,by=0.2)
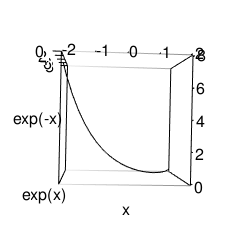
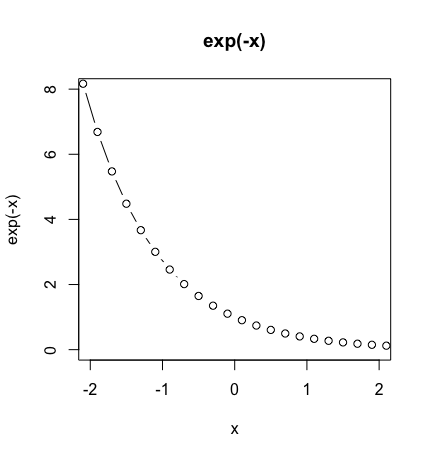
cy<-exp(-c0)
plot(cx,cy,type="b",xlim=c(-2,2),ylim=c(0,8),main="exp(-x)",xlab="x",ylab="exp(-x)")
一方、自然対数関数Log(x)は自然指数関数e^xの座標を90度回転させたものに他なりりません。
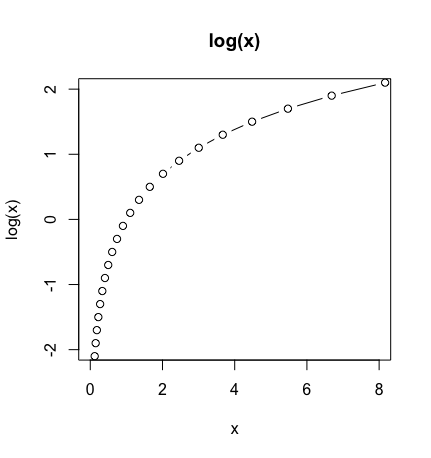
cx<-seq(-2.1,2.1,by=0.2)
cy<-exp(c0)
plot(cy,cx,type="b",xlim=c(0,8),ylim=c(-2,2),main="log(x)",xlab="x",ylab="log(x)")
c0<-seq(-2.1,2.1,by=0.2)
cx<-exp(-c0)
cy<-exp(c0)
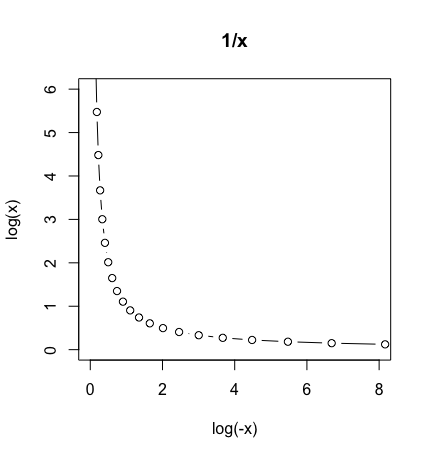
plot(cx,cy,type="b",xlim=c(0,8),ylim=c(0,6),main="1/x",xlab="log(-x)",ylab="log(x)")
exp(c0)とexp(-c0))を足して2で割ったのがCosh(x)関数となります。式を見てわかる様に最大値が半減して1が最低値になっていますね。その逆数1/Cosh(x)がSech(x)です。
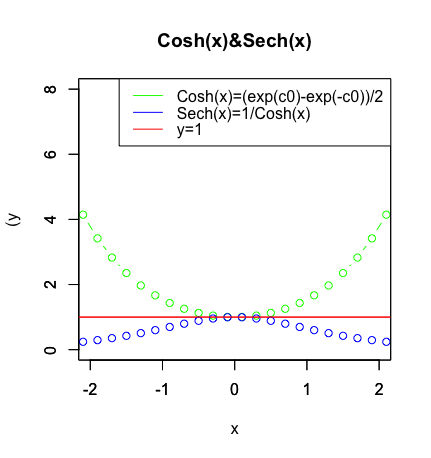
cx<-seq(-2.1,2.1,by=0.2)
cy<-(exp(c0)+exp(-c0))/2
plot(cx,cy,type="b",xlim=c(-2,2),ylim=c(0,8),main="Cosh(x)&Sech(x)",xlab="x",ylab="(y",col=rgb(0,1,0))
segments(-8,1,8,1,col=rgb(1,0,0))
par(new=T)
plot(cx,1/cy,type="b",xlim=c(-2,2),ylim=c(0,8),main="",xlab="",ylab="",col=rgb(0,0,1))
segments(-8,1,8,1,col=rgb(1,0,0))
# 凡例
legend("topright", legend=c("Cosh(x)=(exp(c0)-exp(-c0))/2","Sech(x)=1/Cosh(x)","y=1"),lty=c(1,1,1),col=c(rgb(0,1,0),rgb(0,0,1),rgb(1,0,0)))
exp(x)からexp(-x))を引いて2で割ったのがSinh(x)関数となります。その逆数1/Sinh(x)がCosech(x)で、両者は座標{1,1}と座標{1,1}で接します。
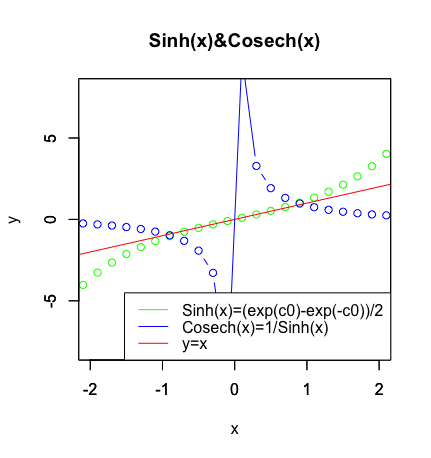
cx<-seq(-2.1,2.1,by=0.2)
cy<-(exp(c0)-exp(-c0))/2
plot(cx,cy,type="b",xlim=c(-2,2),ylim=c(-8,8),main="Sinh(x)&Cosech(x)",xlab="x",ylab="y",col=rgb(0,1,0))
par(new=T)
plot(cx,1/cy,type="b",xlim=c(-2,2),ylim=c(-8,8),main="",xlab="",ylab="",col=rgb(0,0,1))
segments(-8,-8,8,8,col=rgb(1,0,0))
# 凡例
legend("bottomright", legend=c("Sinh(x)=(exp(c0)-exp(-c0))/2","Cosech(x)=1/Sinh(x)","y=x"),lty=c(1,1,1),col=c(rgb(0,1,0),rgb(0,0,1),rgb(1,0,0)))
Sinh(x)をSinh(-x))で割ったのがTanh(x)関数となります。その逆数1/Tanh(x)がCoth(x)となります。どちらも原点周りの収束に関係してくる関数ですね。
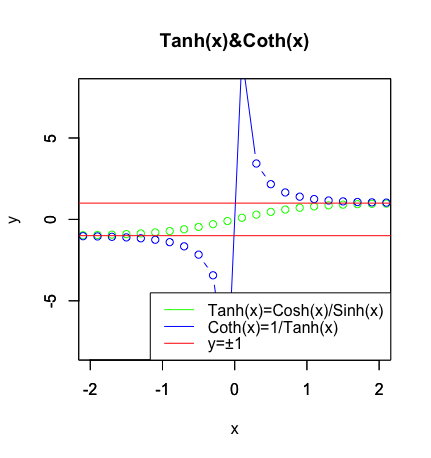
cx<-seq(-2.1,2.1,by=0.2)
cy<-(exp(c0)-exp(-c0))/(exp(c0)+exp(-c0))
plot(cx,cy,type="b",xlim=c(-2,2),ylim=c(-8,8),main="Tanh(x)&Coth(x)",xlab="x",ylab="y",col=rgb(0,1,0))
par(new=T)
plot(cx,1/cy,type="b",xlim=c(-2,2),ylim=c(-8,8),main="",xlab="",ylab="",col=rgb(0,0,1))
segments(-8,-1,8,-1,col=rgb(1,0,0))
segments(-8,1,8,1,col=rgb(1,0,0))
# 凡例
legend("bottomright", legend=c("Tanh(x)=Cosh(x)/Sinh(x)","Coth(x)=1/Tanh(x)","y=±1"),lty=c(1,1,1),col=c(rgb(0,1,0),rgb(0,0,1),rgb(1,0,0)))
このTanh(x)の振幅幅-1~+1を確率論などでの利用に適した「中心1/2、最大値1,最小値0の振幅」に調整したのがシグモイド関数(Sigmoid Function)1/(1+exp(a*x))=(tanh(ax/2)+1)/2となります。生物の神経細胞が持つ性質をモデル化したもので、導関数をシグモイド関数自身で簡単に導出できる為、微分成分が必要となるバックプロパゲーションに適しています。ニューラルネットワークにおける活性化関数などで用いられます。
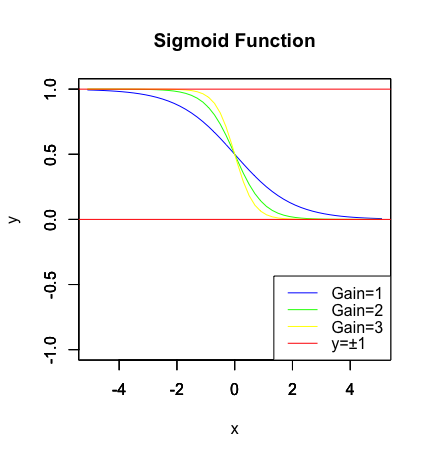
【初心者向け】ロジスティック方程式とその関連範囲
cx<-seq(-5.1,5.1,by=0.2)
f0<-function(a,x) 1/(1+exp(a*x))
cy1<-f0(1,cx)
cy2<-f0(2,cx)
cy3<-f0(3,cx)
plot(cx,cy1,type="l",xlim=c(-5,5),ylim=c(-1,1),main="Sigmoid Function",xlab="x",ylab="y",col=rgb(0,0,1))
par(new=T)
plot(cx,cy2,type="l",xlim=c(-5,5),ylim=c(-1,1),main="",xlab="",ylab="",col=rgb(0,1,0))
par(new=T)
plot(cx,cy3,type="l",xlim=c(-5,5),ylim=c(-1,1),main="",xlab="",ylab="",col=rgb(1,1,0))
segments(-8,0,8,0,col=rgb(1,0,0))
segments(-8,1,8,1,col=rgb(1,0,0))
# 凡例
legend("bottomright", legend=c("Gain=1","Gain=2","Gain=3","y=1/y=0"),lty=c(1,1,1,1),col=c(rgb(0,0,1),rgb(0,1,0),rgb(1,1,0),rgb(1,0,0)))
ちなみに式(1+x)^(1/x)を使っての実際のネイピア数導出過程
> f1<-function(x){(1+x)^(1/x)}
> f1(1)
[1] 2
> f1(0.1)
[1] 2.593742
> f1(0.01)
[1] 2.704814
> f1(0.001)
[1] 2.716924
> f1(0.0001)
[1] 2.718146
> f1(0.00001)
[1] 2.718268
ところで、このサイトでは円を描く時、概ね以下のどれかのアルゴリズムを使っています。まだ投稿本文で本格的に触れる段階まで至ってませんが、実は裏舞台は既に「虚数と複素数と複素平原まみれ」だったりするのです。
- 群論の大源流の一つともなった「1の冪乗根(Root of Unity)」概念に起源を有するガウスの巡回群理論。小難しい背景理論なんて理解してなくても
c0=seq(-pi,pi,length=NoS);cx=cos(c0);cy=sin(c0)(NoS(Number of Sides)=描く多角形の辺数+巡回を完成させる為の1)の構文さえ覚えていれば使える。
1の冪根(Root of Unity) - Wikipedia -
- ご存知オイラーの公式(Eulerian Formula)e^πi=cos(θ)+sin(θ)i。回転行列とか使わなくても円/球表面上の座標/図形が回転させられるのが魅力。
【Rで球面幾何学】ジンバルロック(?)やリサージュ曲線(?)との邂逅。
ただし迂闊にcos(θ)+sin(θ)iの式をに一般化した数式Cos(θ)+Cos(θ-π/NoS)i(NoS=Number of Sides)なんぞを振り回そうとすると「奴が来る」…
【無限遠点を巡る数理】「ティンダロスの猟犬問題」を世に解き放つ。 -
虚数の定義i=(-1)^2を発展させた円描画式(0±1i)^2x。そう、ここでも2が出てくるのである。ある意味、まさかの小学校の頃習った等差数列概念(Geometric Sequence Concept=幾何数列概念)と複素数概念のマリアージュ。
等比数列(幾何数列)①その基本的性質について。
等比数列(幾何数列)②同心円集合に射影する準備
等比数列(幾何数列)③振動関数を巡る収束と拡散。
等比数列(幾何数列)④公比Dが正の場合の収束と拡散, そして対数尺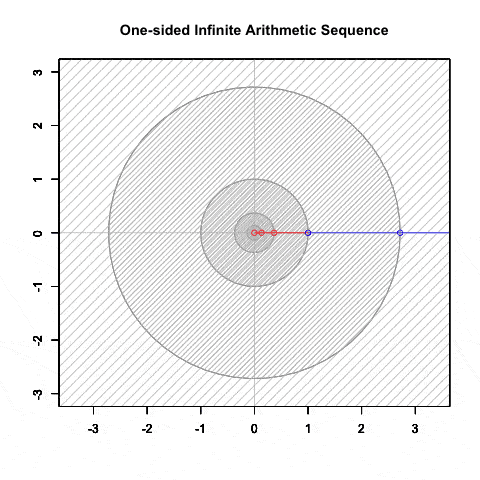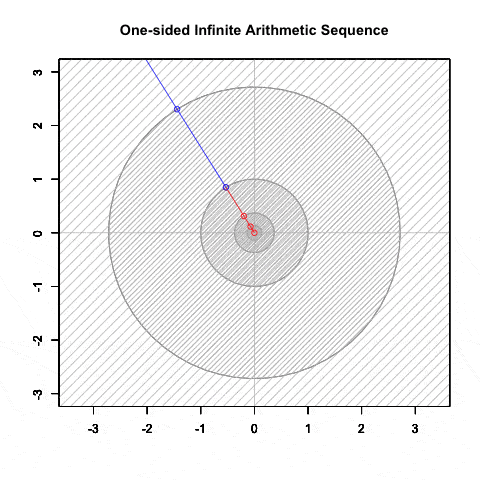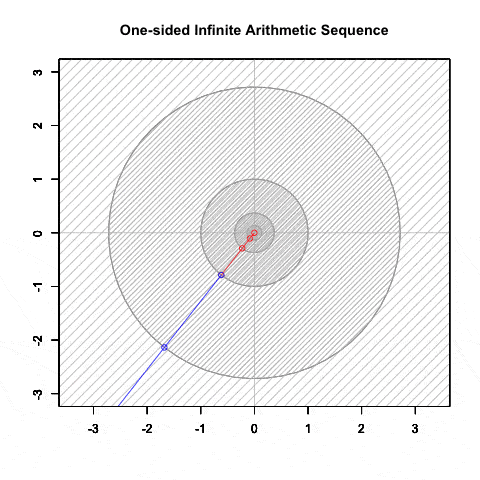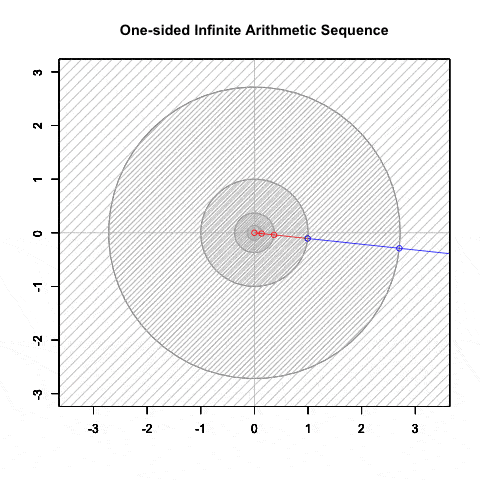
まだまだ全然知識が至ってなくて十分に語れてない箇所の方が全然多いのですが、実はこうした全てが、やはり直径(Diameter){-r,0,r}や対蹠(Antipodes)概念と密接に結びついている様に見えるのです。そこでも繰り返し対蹠間を直線距離で結ぶ「2のコース」から円周/球表面上を結ぶ「πのコース」への拡張過程が現れるのですが…実際、こちら側の世界でもネイピア数を求める数式と円周率を求める数式が添字Nを共有してたりする訳ですが…
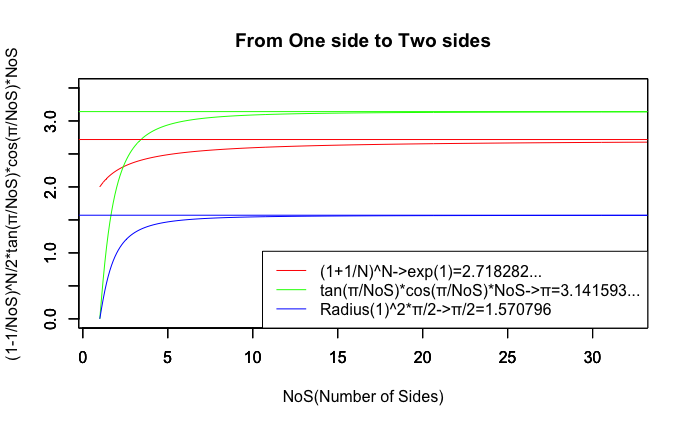
統計言語Rによる作図例
# オイラーの「ネイピアの対数表」に基づく算出方法
cx0<-seq(1,70,length=700)
f0<-function(x){(1+1/x)^x}
cy0<-f0(cx0)
# グラフ化してみる。
plot(cx0,cy0,xlim=c(1,32),ylim=c(0,3.5),type="l",col=rgb(1,0,0),main="From One side to Two sides", xlab="NoS(Number of Sides)", ylab="(1-1/NoS)^N/2*tan(π/NoS)*cos(π/NoS)*NoS")
par(new=T)#上書き指定
# 円周計算
cx1=seq(1,70,length=700)
f1=function(x) tan(pi/x)*cos(pi/x)*x
cy1<-f1(cx1)
plot(cx1,cy1,xlim=c(1,32),ylim=c(0,3.5),type="l",col=rgb(0,1,0),main="", xlab="", ylab="")
par(new=T)#上書き指定
# 面積計算
cx2=seq(1,70,length=700)
f2=function(x) tan(pi/x)*cos(pi/x)*x/2
cy2<-f2(cx2)
plot(cx2,cy2,xlim=c(1,32),ylim=c(0,3.5),type="l",col=rgb(0,0,1),main="", xlab="", ylab="")
# 自然対数1/eと比較。
abline(h=exp(1),col=rgb(1,0,0))#exp(1)=2.718282...
abline(h=pi/2,col=rgb( 0,0,1))#π/2=1.570796...
abline(h=pi,col=rgb(0,1,0))#π=3.141593...
# 凡例
legend("bottomright", legend=c("(1+1/N)^N->exp(1)=2.718282...","tan(π/NoS)*cos(π/NoS)*NoS->π=3.141593...","Radius(1)^2*π/2->π/2=1.570796"),lty=c(1,1),col=c(rgb(1,0,0),rgb(0,1,0),rgb(0,0,1)))
…実際の具体的アプローチは割とそれぞれ個性的だったりします。例えば「(「挟み撃ち法」を含む)多角形近似法」に淡々と地道に事務的に隙間を詰めてくる繊細な雰囲気があるのに対して…
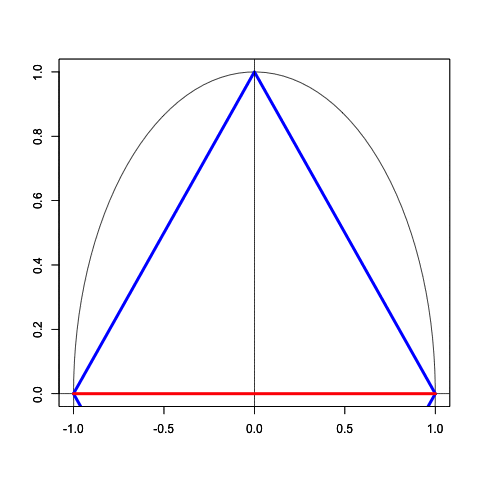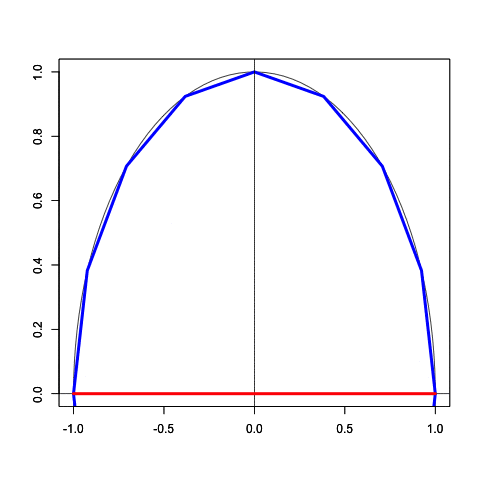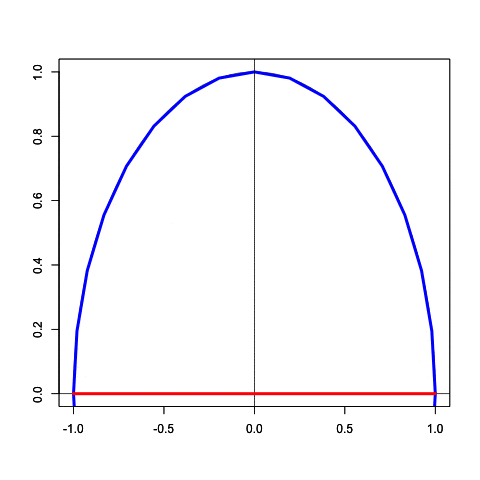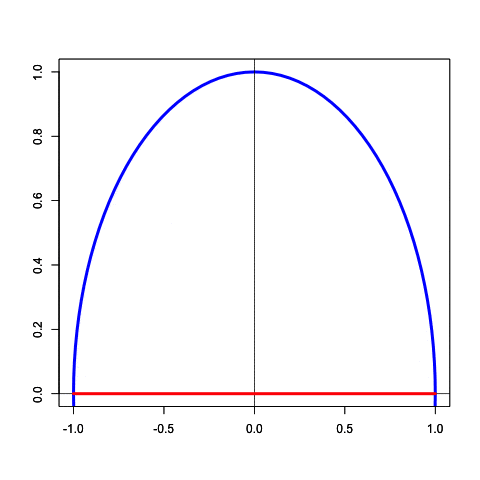
統計言語Rによる作図例
Regular_Polygon_draw03<-function(x) {
# グラフの色の決定
Black<-rgb(0,0,0)
Red<-rgb(1,0,0)
Magenta<-rgb(1,0,1)
Blue<-rgb(0,0,1)
Green<-rgb(0,1,0)
Cyan<-rgb(0,1,1)
Yellow<-rgb(1,1,0)
Gray<-"#888888"
# タイトル定義
Main_title<-c("The Limit of inscribed polygons and circumscribed polygons")
x_title<-c("Real number")
y_title<-c("Imaginary number")
# グラフのスケール決定
gs_x<-c(-1,1)
gs_y<-c(0,1)
# Circumscribed circle(外接多角形)
f1_name<-c("Circumscribed Polygon")
f0<-function(x){exp(x*(0+1i))}
c1<-seq(-pi,pi,length=x+1)
c1_r<-Re(f0(c1))
c1_i<-Im(f0(c1))
# Regular_Polygon(中間円)
f2_name<-c("Inner circle")
c2<-seq(-pi,pi,length=128)
c2_r<-Re(f0(c2))
c2_i<-Im(f0(c2))
# Inscribed circle(内接多角形)
f3_name<-c("Inscribed Polygon")
scl<-cos(pi/x)
# グラフ描画
plot(c2_r,c2_i,xlim=gs_x,ylim=gs_y,type="l",col=Black, main="",xlab="",ylab="")
par(new=T)#上書き指定
plot(c1_r,c1_i,lwd=4,xlim=gs_x,ylim=gs_y,type="l",col=Blue, main="",xlab="",ylab="")
# 基準線
abline(h=0)
abline(v=0)
segments(-1,0,1,0,lwd=4,col=Red)
# 凡例描画
# legend("topleft", legend=c(f1_name,f2_name,f3_name),lty=c(1,1,1),col=c(Green,Black,Blue))
}
library("animation")
Time_Code=c(4,4,4,8,8,8,16,16,16,32,32,32,64,64,128,128)
saveGIF({
for (i in Time_Code){
Regular_Polygon_draw03(i)
}
}, interval = 0.1, movie.name = "Compound_Interest19.gif")
ベルヌーイやオイラーの考案した数式(1±πi/n)^nの振る舞いの豪快さと来たら…
【Rで球面幾何学】「世界で一番美しい公式」オイラーの等式の罠?

(オイラーの公式を導出した)マクローリン級数 (Maclaurin series)を複素平面展開すると本当に円を描いているか微妙なエピソードも含め、古代から脈々と受け継がれてきた数学史の雄大さを忍ばせます。思えば遠くに来たもんだ…・
【Rで球面幾何学】オイラーの公式を導出したマクローリン級数の限界?

③そして両者が逆数関係にある事から既存の対数関数論を敷衍する形で自然指数関数(Natural Exponential Function)y=e^xと自然対数関数(Natural Logarithm Function)x=e^yあるいはy=log(x)が発案されたとされています。
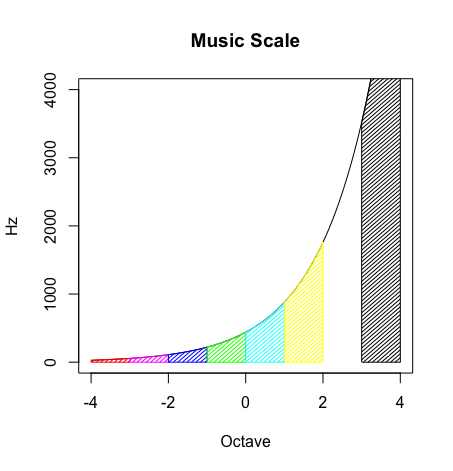

- ところで「(「挟み撃ち法」を含む)多角形近似法」の片手間に計算しても「半径rの円の面積はπr^2」なのは動かない様である。他の証明方法との循環状態に陥らないモンテカルロ法(Monte Carlo method)の結果もそうなる。
【初心者向け】「モンテカルロ法」概説
- ならば数理(Mathematical Things)の世界は、それについて何か上手い説明を見つけなければならない。定積分の世界ではこれを便宜上、各辺長が半径rとπrの矩形の面積として計算する。とりあえず高さが半径rなのは自明の場合(Trival Case)として、何処からπrの概念が飛び出してくるかというと円周2πrの半分。いわゆる扇算の概念、ホールケーキを切り分ける時の様に切り出すそれぞれの小切片が三角形となるので面積も半分になるという考え方を使う訳である。この説明は完全に「(あえて直径の概念を導入せずに済まそうとする)半径(radius)の世界」もの。こうした考え方の延長線上において球の表面積も「幅=円周長2πr」×「高さ2r」=4πrの矩形で求めると説明された訳ですが、何せ「高さ2r」ですからこちらは「(むしろ直径の概念から出発する)直径(Diameter)の世界」。学童時代の私はこの辺りの飛躍について行けなくて算数に挫折してしまったのである。ちなみに後にメルカトル図法の概念を知り「無理はそこで顕現していたのか」と改めて思った次第。
【初心者向け】半径・直径・円周長・円の面積・球の表面積・球の体積の計算上の往復

- そして2年前の年末に突然思い立ってベルヌーイやオイラーやガウスが活躍した近世数学の世界から再勉強を始めた訳だが…その結果ぼんやりと見えてきたのが、どうやら「(あえて直径の概念を導入せずに済まそうとする)半径(radius)の世界」は主にX-Y平面、「(むしろ直径の概念から出発する)直径(Diameter)の世界」は主にZ軸概念の追加に際して現れるという驚愕の真相。
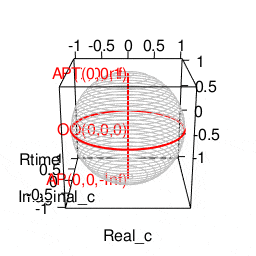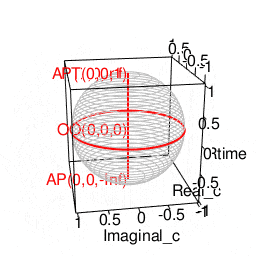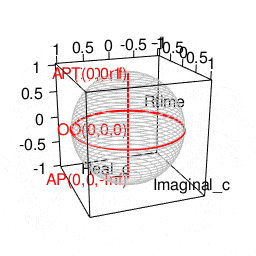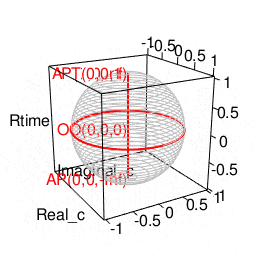
ああ一刻も早くこの発見を小学校の頃の自分に伝えたい!! ただこうした考え方の拡張は拡張で、深入りすると次第にルマルシャンの小箱(Lament Configuration)が開いて「ハミルトンの四元数(Hamilton's Quaternion)」とか「リーマン球面(Riemann sphere)」といったさらに理解に努力を要する気難しい隣人がどんどん勝手に増え始める。まさしくリアル「メイド・イン・アビス」の世界…
【Rで球面幾何学】ハミルトンの四元数は何を表しているのか?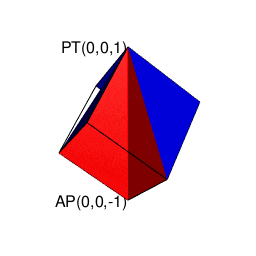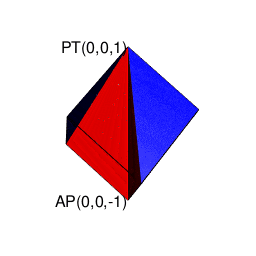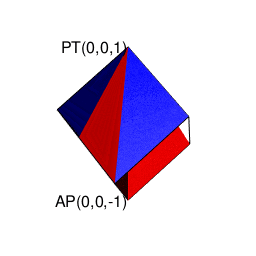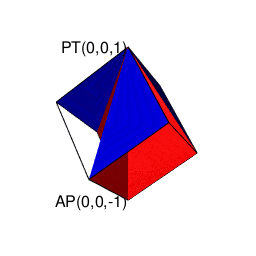
無限遠点と拡張された複素平面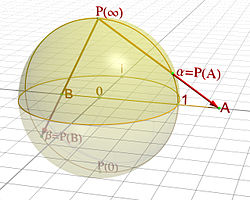
「関脇・正代『メイドインアビス』を見て感動」記事が大反響 ナナチ役の声優・井澤詩織さん「応援するしかないでしょ…!」
かくして話はやっと冒頭の頃の話題に戻るのです。ベルヌーイ(Johann Bernoulli, 1667年~1748年)やオイラー(Leonhard Euler, 1707年~1783年)が確率論の研究の一環として数式(1-1/n)^nに取り組み、その結果として自然指数関数(Natural Exponential Function)y=e^xや自然対数関数(Natural Logarithm Function)x=e^yあるいはy=log(x)などが発案された訳ですが、その背景には中心極限定理(CLT=Central Limit Theorem)の概念を何とか数理(Mathematical Things)の世界に持ち込みたいなる遠大な野望が存在し、その衣鉢を継いだのがガウス(Carolus Fridericus Gauss、1777年~1855年)だったという流れ。歴史的には17世紀後半~19世紀前半の展開…
大数の法則と中心極限定理の意味と関係
【初心者向け】「三角不等式(Triangle Inequality)」の体感方法?


- このマリモみたいな曖昧模糊とした円状/球状分布こそがCLTの本来の姿で、統計技術が未発達だった(それどころか確率論自体が賭博師のいかがわしい悪徳とのみ認識されていた)時代には真の意味で箸にも棒にも掛からない「無限遠点(Inf(inity))=我々の認識可能範囲外を跋扈する絶対他者の領域」だったといえる。そもそもそれへの観測線(Observational line)や観測円(Observational Circle)や観測球面(Observational Sphere)の構築自体が(「神の見えざる手」の恩恵を否定する)不敬行為と弾劾されては本当に話にならない。
「箸にも棒にもかからない」とは?意味と語源・使い方を解説 - しかし時代は確実に変遷していく。欧州においてその節目はあるいは(彼ら自身がかかる中世的伝統への反逆者だった)絶対王政時代の啓蒙君主達がこぞって天文学者や化学者や物理学者や数学者といった科学者のパトロンとなり、その彼らが偏見の払拭に貢献した時代だったのかもしれない(まさしくベルヌーイやオイラーが生きた時代の出来事)。その一方で、私の記憶が正しければ、消費経済を支える主体が王侯貴族や高階聖職者といった伝統的インテリ層から産業革命の波に乗ったブルジョワ成金や庶民に推移しつつあった時代に生まれ、かかる新興消費者層への配慮を余儀なくされたガウスはどうしてこれへの予測線(Prediction line)/予測円(Prediction Circle)/予測球面(Prediction Sphere)の基準として放物線(Parabola)-x^2を選んだかについて特に言及も書き残しもしていない。おそらくはそれを「自然界に存在する最も自然な運動の一つ」と考えるコンセンサスならそれ以前から存在し、以降膨大なデータの積み上げによって実際それが多くの特徴ある分布においてある種の無限遠点(Inf(inity))、すなわちサンプル数Nの増大によってそれぞれが個性を失う極限と見做せる統計結果が不可逆的に観測されてしまった今日では、それを疑う人もまた途絶えてしまったのであろう。
衝突予測線と衝突危険
しかしながら放物線関数(Parabola Function)-x^2自体はY軸に沿って無限小-Inf(inity)に発散(Divergence)する関数であり、そのままではCLTに直接重ね合わせる事が出来ません。そこで自然指数関数(Natural Exponential Function)y=e^xの出番となる訳ですが、その事自体がこの関数が添字(Index)として与えられる変数についてどの様な働きをするかについての説明になっている訳です。
- 二次元直交座標系(2Dimensional Cartesian Coordinate System)x,yについて、y=<0の範囲をy=0~1の範囲に、y=>0の範囲をy=1~Inf(inity)の範囲に**射影**(Projection)する。
- その結果y=>0の範囲では元座標系におけるY軸に沿った無限小-Inf(inity)への発散が1への収束(Convergence)に(押し潰された分だけ量を増大させながら)変換される。
どういう事か具体的に見ていきましょう。ちなみにグラフを重ねる為、放物線関数(Parabola Function)-x^2のY軸に1を足しています。
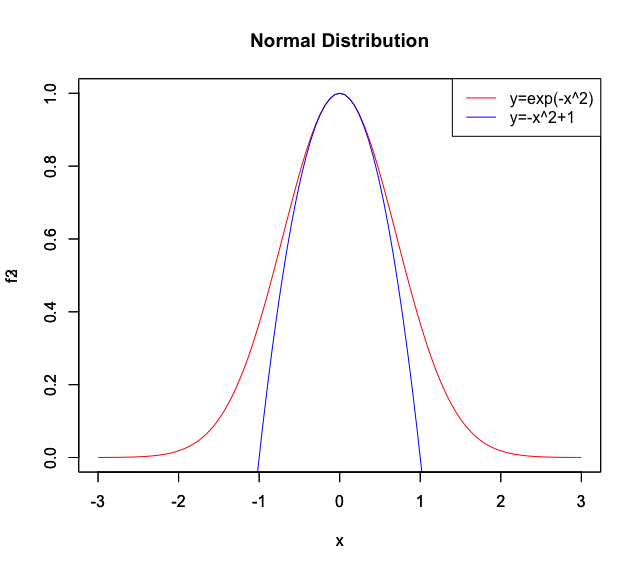
統計言語Rによる作図例
f2<-function(x){exp(-x^2)}
f3<-function(x){-x^2+1}
plot(f2, xlim=c(-3,3),ylim=c(0,1),main="Normal Distribution",col=rgb(1,0,0))
par(new=T)#上書き指定
plot(f3, xlim=c(-3,3),ylim=c(0,1),main="",col=rgb(0,0,1))
# 凡例
legend("topright", legend=c("y=exp(-x^2)","y=-x^2+1"),lty=c(1,1),col=c(rgb(1,0,0),rgb(0,0,1)))
確かに見事にy=<0の領域がy=0~1の領域に射影され、Y軸に沿った**無限小**-Inf(inity)への発散が(押し潰された分だけ量を増大させながら)0への収束に変換されています。有名な「**左右対象の釣鐘状曲線**(bell curve)」は、この様なプロセスを経て合成されたものだったのです。ここで気になるのがその時Y>=0の領域では何が起こっているのか…
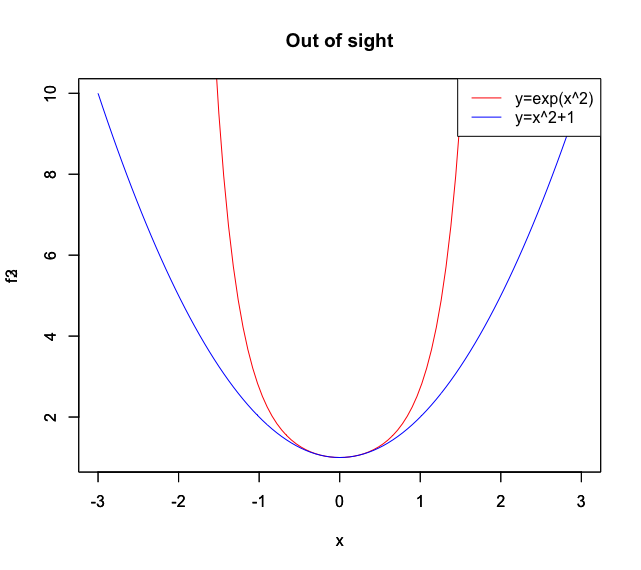
統計言語Rによる作図例
f8<-function(x){exp(x^2)}
f9<-function(x){x^2+1}
plot(f8, xlim=c(-3,3),ylim=c(0,10),main="",col=rgb(1,0,0))
par(new=T)#上書き指定
plot(f9, xlim=c(-3,3),ylim=c(0,10),main="",col=rgb(0,0,1))
# 凡例
legend("topright", legend=c("y=exp(x^2)","y=x^2+1"),lty=c(1,1),col=c(rgb(1,0,0),rgb(0,0,1)))
予想通りY軸に沿っての無限大Inf(inity)への発散が量的に増大していますが、現時点でこの数理(Mathematical Things)を有効活用する方法は見つかっていない様です。
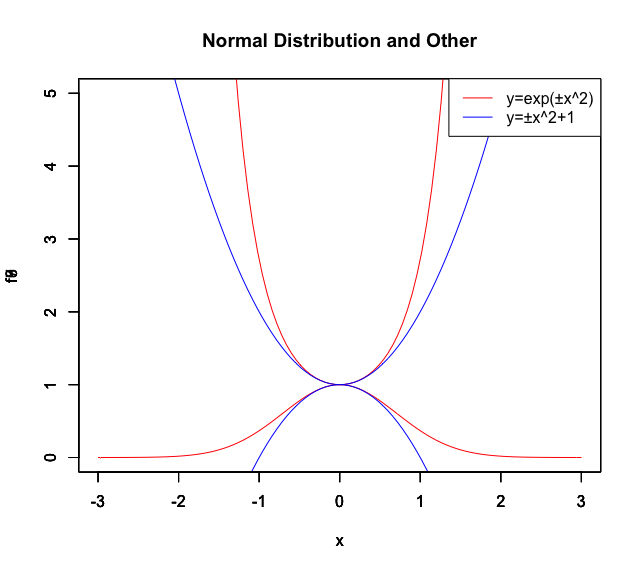
統計言語Rによる作図例
f6<-function(x){exp(-x^2)}
f7<-function(x){-x^2+1}
f8<-function(x){exp(x^2)}
f9<-function(x){x^2+1}
plot(f6, xlim=c(-3,3),ylim=c(0,5),main="Normal Distribution and Other",col=rgb(1,0,0))
par(new=T)#上書き指定
plot(f7, xlim=c(-3,3),ylim=c(0,5),main="",col=rgb(0,0,1))
par(new=T)#上書き指定
plot(f8, xlim=c(-3,3),ylim=c(0,5),main="",col=rgb(1,0,0))
par(new=T)#上書き指定
plot(f9, xlim=c(-3,3),ylim=c(0,5),main="",col=rgb(0,0,1))
# 凡例
legend("topright", legend=c("y=exp(±x^2)","y=±x^2+1"),lty=c(1,1),col=c(rgb(1,0,0),rgb(0,0,1)))
全体像を俯瞰すると、何が起こっているのかよりはっきりと解りますね。しかし人類のこの方面への挑戦は、歴史のこの時点ではまだまだ始まったばかりだったのです。
- この図形を確率論の世界に持ち込む為には、まずその面積を求め、さらにこれを1に変換する必要があった。それでガウスはまずCLTの本来の姿たる半径rの同心円状分布の面積を求めた集合(Set)Cr(r=0→Inf(inity)){0,…,πr^2,…,Inf(inity)}から出発し、0から無限遠点Inf(inity)までの範囲の定積分から半径1の単位円(Unit Circle)の面積πを一辺がscrt(π)の矩形で求める式を完成させ、このscrt(π)を関数y=exp(-x^2)が描く釣鐘状図形の面積としたのである。何を言ってるか分からない人も少なくないと思うが、実は私もこの過程自体は全然理解出来てない。
ガウス積分の公式 - いずれにせよ、事がここまで到ればこの釣鐘状図形の面積を1に変換して確率変数(Random Variable)Xと確率密度(Probability Density)Yの関係に対応させた関数Px(x=-Inf(inity)→0→Inf(inity))を導出し、確率変数上の任意の区間の確率密度(面積)が求め尽くされ、さらなる使い勝手向上を求めてその分布(Distribution)の具合を平均(Mean)と分散(Variance)なる2つのパラメーター(Parameter)で調整する仕組みが追加されるのは時間の問題となった。かくして完成したシステムが(多くの人間が自動車や飛行機やコンピューターの様な文明の利器同様にブラックボックスの利用者に留まる事に満足する様になった)所謂正規分布(Normal Distribution)の概念だったという訳である。
正規分布とは

- ところでガウスの時代にはまだ観測誤差(Observational Error)の概念があるばかりで、観測対象そのものが分散(Variance)しているという概念は存在していなかった(何しろ当時の観測対象は天体であり、分散してる筈がなかった)。だからガウス当人がこうした仕組み全体を整えたとは限らないのだが、詳しい事は現時点では分からない。
【無限遠点を巡る数理】無限遠点(Infinity)としての正規分布と分散概念の歴史
ここに見られる(Z軸に沿って展開する)釣鐘状曲線と(XY面上で展開する)同心円状分布の関係については、以下のグラフを見れば一発で理解できると思います。問題は「(カンブリア爆発期以降、一部の生物が視覚とそれに呼応する脊髄と運動機関のフィードバック体系を獲得する過程で依存する様になった)原始デカルト座標系 (Primitive Cartesian Coordinate System)」の制約上、この概念の三次元以上版をそう簡単にはイメージ出来ない辺りにあるのですが…
【初心者向け】正規分布(Normal Distribution)とは何か?

この辺りの自然指数関数(Natural Exponential Function)y=e^xの応用例としては(自然指数関数の提示する幾何学的急増の可能性に刺激されて執筆された)マルサス「人口論(An Essay on the Principle of Population, 1798年)」への回答として研究が始まったロジスティク方程式(Logistic Equation)も著名。これについてもそのうち触れたいと考えています。
【初心者向け】ロジスティック方程式とその関連範囲

指数法則(Power law)
おもむろに基礎的話題に戻ります。
①a^0=1
^0の結果は1となる。
3^0
[1] 1
2^0
[1] 1
1^0
[1] 1
0^0
[1] 1
②a^-n=1/a^n
a=1の場合の結果は全て1となる。
ただしa≠0で、m、nが正の数の場合。
library(Ryacas)
# 1の段
yac("1^-1") #1/1^1
[1] "1"
yac("1^-2") #1/1^2
[1] "1"
yac("1^-3") #1/1^3
[1] "1"
# 2の段
yac("2^-1") #1/2^1
[1] "1/2"
yac("2^-2") #1/2^2
[1] "1/4"
yac("2^-3") #1/2^3
[1] "1/8"
# 3の段
yac("3^-1") #1/3^1
[1] "1/3"
yac("3^-2") #1/3^2
[1] "1/9"
yac("3^-3") #1/3^3
[1] "1/27"
③a^m*a^n=a^(m+n)
この性質を利用して乗算を加算に単純化可能。
2^3*2^4
[1] 128
2^(3+4)
[1] 128
④ (a^m)^n = a^(m*n)
この性質を利用して累乗算を乗算に単純化可能。
(2^3)^4
[1] 4096
2^(3*4)
[1] 4096
⑤a^m/a^n=a^(m-n)
この性質を利用して除算を減算に単純化可能。
ただしa≠0、b≠0で、m、nが整数の場合。
library(Ryacas)
# 計算結果
yac("2^3/2^4")
[1] "1/2"
yacas("2^(3-4)")
[1] "1/2"
⑥(ab)^n=a^nb^n
実はここに列記した指数関数7大法則の中では、次に述べる(a/b)^n=a^n/b^n法則同様にあまり使われない。
(2*3)^4
[1] 1296
2^4*3^4
[1] 1296
⑦(a/b)^n=a^n/b^n
ちなみにこうしてわざわざYacasを使ったのは、この計算があくまで有理数(Rational Number)すなわち分数(Fraction)で表せる範囲に留まっている事を示すため。
library(Ryacas)
# 計算結果
yac("(2/3)^4")
[1] "16/81"
yac("2^4/3^4")
[1] "16/81"
対数法則(Logarithmic law)
指数関数y=a^xをx=a^yに変形すると対数関数y=log(x,base=a)となり、当然上掲の指数法則がそのまま逆対応する。
①log(1,base=a)=0
ただしaが1でない正の数の場合。指数関数で底(base,root)が0になってはいけない様に、対数関数ではそれが1になってはならない。なおLog関数はbase=指数の時に1を返す。
log(1,base=1)
[1] NaN
警告メッセージ:
計算結果が NaN になりました
log(1,base=2)
[1] 0
log(2,base=2)
[1] 1
log(1,base=3)
[1] 0
log(3,base=3)
[1] 1
②log(-n,base=a)=1/log(n,base=a)
ただしmもnも正の数でaが1でない正の数の場合。
こういう時計算機代数ソフトウェアYacasは役に立たない。
log(1/2,base=2)
[1] -1
1/log(1/2,base=2)
[1] -1
③log(m^n,base=a)=n*log(m,base=a)
ただしmもnも,aが1でない正の数の場合。
ここでは乗算が指数上の累乗算に置換される。
log(3^4,base=2)
[1] 6.33985
4*log(3,base=2)
[1] 6.33985
④log(m*n,base=a)=log(m,base=a)+log(n,base=a)
ここでは加算が指数上の乗算に置換される。
log(3*4,base=2)
[1] 3.584963
log(3,base=2)+log(4,base=2)
[1] 3.584963
⑤log(b,base=a)-log(c,base=a)=log(b/c,base=a)
ここでは減算が指数上の除算に置換される。
log(3/4,base=2)
[1] -0.4150375
log(3,base=2)-log(4,base=2)
[1] -0.4150375
⑥log(a,base=b)=log(b,base=c)/log(a,base=c)
しばしば根(base,root)の変換式と呼ばれる。cをネイピア数とすれば自然対数への変換公式となる。
log(2,base=3)
[1] 0.6309298
log(2,base=4)/log(3,base=4)
[1] 0.6309298
> log(2)/log(3)
[1] 0.6309298
この辺の「演算変換」についてもそのうちまとめます。とりあえず以下続報…