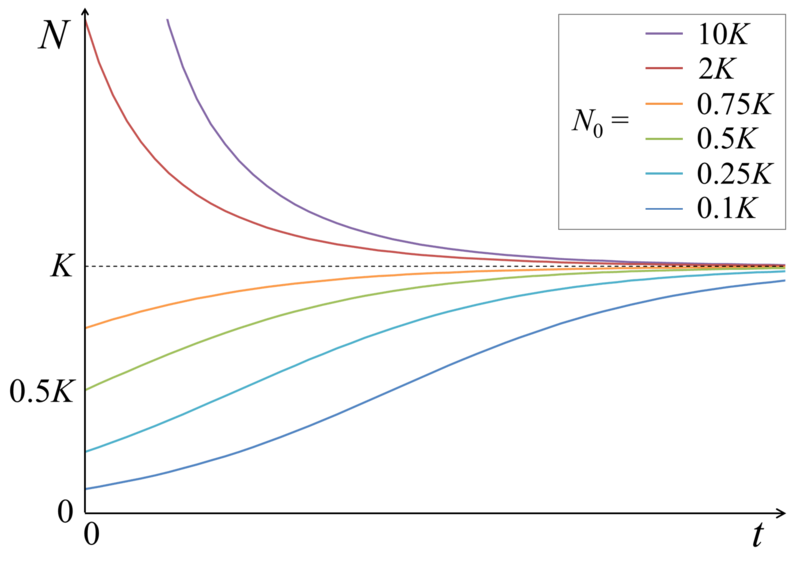
元来理論的には個体数ゼロからも個体数無限からも出発出来ないジレンマを抱えつつ、ゼロと無限の中点としての環境収容力Kすら状況に応じてさらに揺らぎ続けるロジスティック方程式(Logistic Equation)dN/dt=rN(1-N/K)に関するメモ。
- dN/dt…時間t時点における個体数Nの増減加速度。環境収容力K>Nの時増大、K=0の時均衡、K<Nの時減少。
- r…内的自然増加率(intrinsic rate of natural increase/intrinsic natural growth rate/intrinsic growth rate/biotic potential)、個体辺りの出生率b-個体辺りの死亡率dで求められる。
- N…個体数(Number)
- K…環境収容力(Carrying Capacity)
シグモイド関数やロジット関数との関係
ロジスティック方程式は対数関数を導入しNt=K/(1±exp^rK(t0(時間tの原点)-t(時間t時点)))と表す事も出来ます。
- Nt…時間t時点における個体数Nの増減率。
- K…環境収容力(Carrying Capacity)
- r…内的自然増加率(intrinsic rate of natural increase/intrinsic natural growth rate/intrinsic growth rate/biotic potential)、個体辺りの出生率b-個体辺りの死亡率dで求められる。
- t0…時間tの原点
- t…時間t0からの経過時間
さらに計算を単純化する為にこう置きます。
- 内部自然増加率r=a(gain)
- 環境収容力K=1
- 時間tの原点t0=0
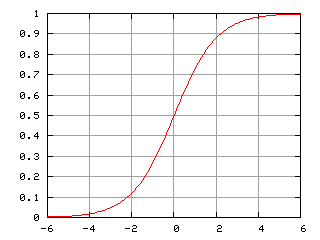
さらに(t0(初期時間),Inf(無限遠点))→(N0(初期個体数),K(環境収容力))の範囲を(-Inf,Inf)→(0,1)の範囲に射影したのがシグモイド関数(Sigmoid Function)1/(1+exp^-ax)、さらにgain=1と置いたのが標準シグモイド関数(Standard Sigmoid Function)となります。
シグモイド関数 - Wikipedia
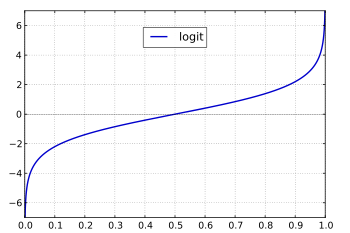
シグモイド関数はその逆関数たるロジット関数(logit Function)log(x/(1-x))=log(x)-log(1-x)(ただしxの範囲は(0,1))と併せて様々な局面で用いられます。
ロジット - Wikipedia
マルサス方程式との関係
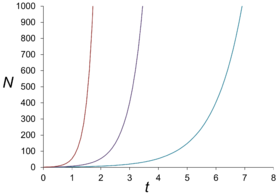
これらの関数はマルサス方程式(Malthusian Equation)dN/dt=rN=N0*exp^rtの自然かつ自明的な拡張とされています。
- dN/dt…時間t時点における個体数Nの増加率増減率。
- r…内的自然増加率(intrinsic rate of natural increase/intrinsic natural growth rate/intrinsic growth rate/biotic potential)、個体辺りの出生率b-個体辺りの死亡率dで求められる。
- t0…時間tの原点
- t…時間t0からの経過時間
- N0…時間t0時点の個体数
- N…時間t時点の個体数
「個体数ゼロからも個体数無限からも出発出来ないジレンマ」はこの時点で既に埋め込まれています。またこの方程式は(ロジスティック方程式も含め)理論上(時間tが無限遠Infinityに到達した時点で達成される筈の)最終的な状況、すなわち個体数0や個体数無限を扱う事も出来ません。
確率分布との関係
シグモイド曲線自体は常に連続した時系列に沿ってのみ現れるわけではありません。例えば正規分布(Normal Distribution)における累積分布関数(CDF=Cumulative Distribution Function)とか。正規分布に従ってステップ関数(0,1)がランダムに追加され続けるモデルなどでは、数が増えるにつれその分布がシグモイド曲線に収束していく形となります。
【初心者向け】正規分布(Normal Distribution)とは何か? - Qiita

また個体数はあくまで拡張も疑う余地もない1次元代表値ですが、多変量解析の世界ではN次元評価軸のどれを代表値として抽出するか自体がテクニックの一部となってくるのです。
因子分析(factor analysis) - Wikipedia
Rで因子分析やってみた
主成分分析(principal component analysis; PCA) - Wikipedia
主成分分析の考え方
その人工知能技術への応用
人工知能技術の中核の一つたる活性化関数(Activation Function)/伝達関数(Transfer Function)においては「この写真に映っているのは犬ではなく猫である」といった最終結論に到達する為に「次段階で何らかの解釈導入が可能な形に整理された出力の連鎖」が求められるのであり、こうした試金石的標準関数が必要に応じて総動員されるのです。
活性化関数 - Wikipedia