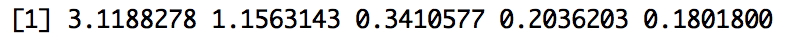Rで因子分析やってみた

今更感ありますが、R言語で因子分析を試してみたのでそのメモを書きます。

因子分析とは

因子分析とは、ある観測された変数（質問項 目への回答など）が、どのような潜在的な変 数（観測されない、仮定された変数）から影響 を受けているかを探る手法。

因子分析より引用

ざっくり言うと、複数の観測変数の背後にある潜在的な要因を明らかにするための分析です。
例えば、定期試験で国語、社会、英語、数学、理科のテストを行ったとします。
もし、数学、理科の点数が高い人がいれば、理系科目が得意そうですよね。
この「数学、理科の点数が高い」という背景にある理系能力という潜在的な因子を探るのが因子分析です。

分析用データ

今回分析するデータは、統計教育推進委員会が提供する国語, 英語, 数学, 物理, 化学の5科目の成績データをダウンロードして使用します。このデータを使ってR言語で因子分析を行い、5科目の成績に影響を与える潜在因子を探索したいと思います。

5科目の成績データ

データ読み込み

先ほどダウンロードした5科目の成績データをR言語で記述したプログラムから読み込みます。このとき、ダウンロードしたファイルをcsv形式に変換し、不要な空白のセル等は削除しておくと良いです。
データを読み込むプログラムは以下の通りです。

data <- read.csv(file="ファイルパス.csv",
                   header=T, fileEncoding="Shift-JIS", row.names=1)

因子数の決定

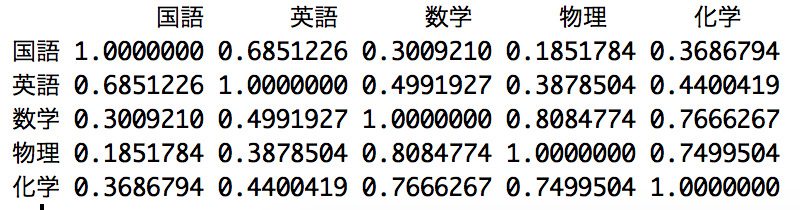
抽出する因子数を決定するために、相関行列を算出した後、その行列の固有値を算出します。

• 相関行列
• 相関行列は関数cor()で算出することができます。

cor <- cor(data)

#出力
cor

相関行列

• 固有値
• 固有値および固有ベクトルは関数eigen()で算出することができます。
• 固有値は$values,固有ベクトルは$vectorsに格納されます。

eigen <- eigen(cor)$values

#出力
eigen

固有値

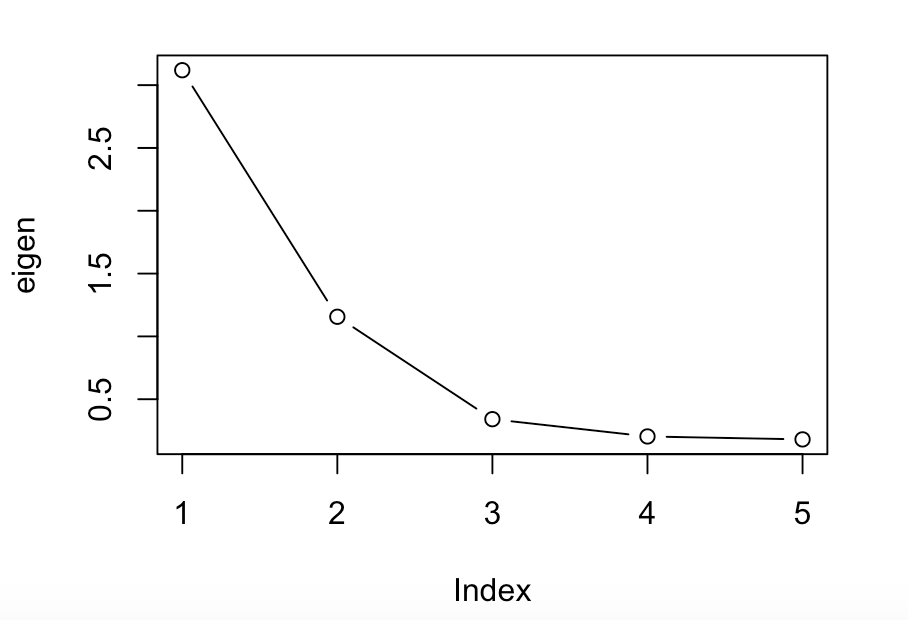
• スクリープロット
• 先ほど算出した固有値の減衰をスクリープロットで見て因子数を決定します。
• スクリープロットの描画は関数plot()を使用します。

#type="b"でグラフ上に点と線両方を表示
plot(eigen, type="b")

スクリープロット

因子数

算出された固有値のうち、1より大きい固有値は2つで、スクリープロットの固有値減衰をみると、第3固有値以降は減衰が緩やかになっていますので、今回は因子数を2として因子分析を行います。

因子分析

R言語には因子分析を行うための標準関数が用意されています。
因子分析は関数factanal()で行うことができます。
なお、標準関数では初期解の算出方法は最尤法のみ、因子の回転法はバリマックス回転(直行回転)かプロマックス回転(斜行回転)のみとなっております。

• 直行回転
• 因子間の相関を仮定しない
• 斜行回転
• 因子間の相関を仮定する

(psychパッケージ等を利用すれば初期解の算出法や因子の回転法などの選択の幅が広がります)

今回は、バリマックス回転法で因子分析を行いたいと思います。

factanal <- factanal(x=data,factors=2,rotation="varimax")
#出力(cutoff=0で全ての因子負荷量を表示)
print(factanal,　cutoff=0)

結果

結果の見かた

• uniquenesses
  • factanal()では共通性の値が出力されないかわりに独自性(1-共通性)の値が出力されます。
  • 共通性は、各測定値に対して、共通因子の部分がどの程度あるのかを示す指標。

今回の分析結果では、どの項目も共通因子からある程度影響を受けていることがわかります。

• Loadings
• 因子負荷
• 観測変数に対して共通因子がどの程度影響を与えているかを示したもの。

今回の分析結果では、第一因子は数学、物理、化学が高い因子負荷量を示しており、第二因子は国語、英語が高い因子負荷量を示していることがわかります。

• SS loadings

• 因子寄与

• その因子が全体分散のうちどの程度を説明しているか。

• Proportion Var

• 因子寄与率

• その因子が全体分散のうちどの程度の割合を説明しているか。

• Cumulative Var

• 累積寄与率

• 因子寄与率を大きい順に足していったもの。

• そこまでの因子で全体の情報量のどの程度が説明されているかを示す。

• 今回の分析結果では、2つの因子で5項目の全分散を説明する割合が78%であることがわかります。

分析結果まとめ

• 固有値の変化(3.1188278 1.1563143 0.3410577 0.2036203 0.1801800)より、2因子構造が妥当
• 第一因子は数学、物理、化学が高い因子負荷量を示しており、第二因子は国語、英語が高い因子負荷量を示していることから、第一因子を理系能力、第二因子を文系能力と命名します。
• ２因子で全体の分散を説明する割合は78%。

以上です。Rを使えば中の数式がわからなくても簡単に因子分析ができます。
今後はpsychパッケージなどを使ってもっと色々試してみたいと思います。