【初心者向け】正規分布(Normal Distribution)とは何か？

#確率密度(Probability Density)とは何か？

パラメーター（Parameter）が平均（Average）=0,標準偏差(SD=Standard Deviation)=1の場合の標準正規分布（Standard Normal Distribution）が以下。

#確率密度関数（PDF=Probability Density Function）
f1<-function(x){dnorm(x,mean=0, sd=1)}
plot(f1,xlim=c(-5,5),ylim=c(0,1),col=rgb(1,0,0),main="Standard Normal Distribution",xlab="X",ylab="Normal Distribution")

par(new=T) #上書き

#累積分布関数（CDF=Cumulative Distribution Function）
f2<-function(x){pnorm(x,mean=0, sd=1)}
plot(f2,xlim=c(-5,5),ylim=c(0,1),col=rgb(0,0,1),main="",xlab="",ylab="")

#凡例
legend("topleft", legend=c("PDF=Probability Density Function","CDF=Cumulative Distribution Function"), lty=c(1,1), col=c(rgb(1,0,0),rgb(0,0,1)))

pythonの場合
【Pyrhon演算処理】確率密度空間と累積分布空間①記述統計との狭間

#正規分布の基本的性質

• 確率密度関数では平均値と最頻値と中央値が一致する（標準偏差=1の時のそれは0.3989423）。累積分布関数では中央がx=0となる（y=0.5）。
• 「パラメーター」である平均値を中心に左右対称となる。（直線x=μに関して対称）
  x軸が漸近線である。
• 「パラメーター」である分散（標準偏差）が大きくなると、確率密度関数では曲線の山は低くなり、左右に広がって平らになる。累積分布関数では傾きが小さくなり幅も広がる。分散が小さくなると確率密度関数では山が高くなり、より尖った形となる。累積分布関数では傾きが大きくなり幅が狭まる。

###確率密度関数（PDF=Probability Density Function）

#確率密度関数（μ=0, σ2=0.4）
f1<-function(x){dnorm(x,mean=0, sd=0.4)}
plot(f1,xlim=c(-5,5),ylim=c(0,1),col=rgb(0,0,1),main="Probability Density Function(PDF)",xlab="X",ylab="Normal Distribution")

par(new=T) #上書き

#確率密度関数（μ=0, σ2=1.0）
f1<-function(x){dnorm(x,mean=0, sd=1.0)}
plot(f1,xlim=c(-5,5),ylim=c(0,1),col=rgb(1,0,0),main="",xlab="",ylab="")

par(new=T) #上書き

#確率密度関数（μ=0, σ2=4.0）
f1<-function(x){dnorm(x,mean=0, sd=4.0)}
plot(f1,xlim=c(-5,5),ylim=c(0,1),col=rgb(1,1,0),,main="",xlab="",ylab="")

par(new=T) #上書き 

#確率密度関数（μ=-2, σ2=0.7）
f1<-function(x){dnorm(x,mean=-2, sd=0.7)}
plot(f1,xlim=c(-5,5),ylim=c(0,1),col=rgb(0,1,0),,main="",xlab="",ylab="")

#凡例
legend("topright", legend=c("μ=0, σ2=0.4","μ=0, σ2=1.0","μ=0, σ2=4.0","μ=-2, σ2=0.7"), lty=c(1,1,1,1), col=c(rgb(0,0,1),rgb(1,0,0),rgb(1,1,0),rgb(0,1,0)))

pythonの場合
【Pyrhon演算処理】確率密度空間と累積分布空間①記述統計との狭間

###累積分布関数（CDF=Cumulative Distribution Function）

#累積分布関数（μ=0, σ2=0.4）
f1<-function(x){pnorm(x,mean=0, sd=0.4)}
plot(f1,xlim=c(-5,5),ylim=c(0,1),col=rgb(0,0,1),main="Cumulative Distribution Function(CDF)",xlab="X",ylab="Normal Distribution")

par(new=T) #上書き

#累積分布関数（μ=0, σ2=1.0）
f1<-function(x){pnorm(x,mean=0, sd=1.0)}
plot(f1,xlim=c(-5,5),ylim=c(0,1),col=rgb(1,0,0),main="",xlab="",ylab="")

par(new=T) #上書き

#累積分布関数（μ=0, σ2=4.0）
f1<-function(x){pnorm(x,mean=0, sd=4.0)}
plot(f1,xlim=c(-5,5),ylim=c(0,1),col=rgb(1,1,0),,main="",xlab="",ylab="")

par(new=T) #上書き 

#累積分布関数（μ=-2, σ2=0.7）
f1<-function(x){pnorm(x,mean=-2, sd=0.7)}
plot(f1,xlim=c(-5,5),ylim=c(0,1),col=rgb(0,1,0),,main="",xlab="",ylab="")

#凡例
legend("bottomright", legend=c("μ=0, σ2=0.4","μ=0, σ2=1.0","μ=0, σ2=4.0","μ=-2, σ2=0.7"), lty=c(1,1,1,1), col=c(rgb(0,0,1),rgb(1,0,0),rgb(1,1,0),rgb(0,1,0)))

pythonの場合
【Pyrhon演算処理】確率密度空間と累積分布空間①記述統計との狭間

ちなみに標準正規分布は積分して面積を求めると結果が1となります。これを100%状態と考え、その時点の分布のx座標を求めるのが確率密度概念（Probability Density Concept）となる訳です。

integrate(dnorm,-Inf,Inf)
1 with absolute error < 9.4e-05

この概念に従って統計言語Rのqnorm関数は第一引数に確率を受けて、確率密度を返し、pnorm関数は第一引数に確率密度を受けて、確率を返します。

#確率点（quantile）計算、引数=確率,平均,標準偏差、返り値=確率密度
qnorm(0.95,0,1)
[1] 1.644854

#累積分布（cdf）、引数=確率密度,平均,標準偏差、返り値=確率
pnorm(1.6448,0,1)
[1] 0.9499945

#積分による検証
integrate(dnorm , -Inf, 1.6448)
0.9499945 with absolute error < 8.6e-08

#確率密度関数（μ=0, σ2=1）
f0<-function(x){dnorm(x,mean=0, sd=1)}
plot(f0,xlim=c(-4,4),ylim=c(0,0.4),main="Probability Density Function(PDF)",xlab="X",ylab="Normal Distribution")

#塗りつぶし
x0 <- seq(-5, 1.6448, length=50 ) # x範囲を50分割
y0 <- dnorm(x0)# x座標に対応する曲線上の値（y座標）
xvals <- c(x0, 1.6448)
yvals <- c(y0, 0)
polygon( xvals, yvals, col=rgb(1,0,0))

#文字追加
text( 0, 0.2, "95%" )
text(2,0.1, "1.64" ) 

###qqnorm関数

そのデータが正規分布に従っているかどうかをチェックするには、qqnorm関数を用います。この関数に、データを与えると、対象データの順序標本（昇順に並べたデータ）と、正規分布から選ばれた同数の順序分位点に対してプロットした散布図を作ります。

#統計言語Rによる作図例
x<-rnorm(100,mean=0, sd=1)

#qqnorm(データ名) Q－Qプロットを描画する
qqnorm(x)

#qqline(データ名） 完全な正規分布に従うときの予想線lwd=n 線の太さ（デフォルトは1）col="色名" 1:黒 2:赤 3:青 4:緑 5:水色 6:茶
qqline(x, lwd=2, col="red" )

#大数の法則（LLN=Law of Large Numbers）に従った収束(Convergence)が起こった結果の顕現(Appearance)としての確率密度関数と累積分布関数。

ところで確率密度関数（PDF=Probability Density Function）とは、度数分布（Frequency Distribution）を表すグラフの一つであるヒストグラム（Histogram）上において大数の法則（LLN=Law of Large Numbers）に従った収束(Convergence)が起こった結果の顕現(Appearance)といえそうなのです。

#確率密度関数（PDF=Probability Density Function）の集約過程
PDF<-function(x){rnorm(x,mean=0, sd=1)}
Probability_Density_Function<-function(x){
hist(PDF(x),col=rgb(0,1,0))
rug(PDF(x))
}

#アニメーション
library("animation")
Time_Code=c(1,3,5,7,10,25,50,75,100,250,500,750,1000,2500,5000,7500,10000,25000,50000,75000,100000)
saveGIF({
for (i in Time_Code){
　Probability_Density_Function(i)
}
}, interval = 0.1, movie.name = "PDF01.gif")

N=100の場合（揺らぎが激しい）
頻度ポリゴンを描く関数 hist2d() (パッケージ：gplots)

z_axis<-rnorm(100,mean=0, sd=1)
x_axis<-rnorm(100,mean=0, sd=1)
y_axis<-rnorm(100,mean=0, sd=1)
SND100 <- data.frame(X=x_axis, Y=y_axis,Z=z_axis)

X軸-Y軸

library(gplots)
SND_hist2d<-function(x){

# 遠近法プロット (persp) のためのデータをhist2d() を使用して作成
h2d <- hist2d(SND100$X, SND100$Y, show=FALSE, same.scale=TRUE, nbins=c(20,30))
# 遠近法プロット (persp) 描画
persp( h2d$x, h2d$y, h2d$counts,
ticktype="detailed", theta=x, phi=30,
expand=0.5, shade=0.5, col="cyan", ltheta=-30,main="SND with hist2d()",xlab="x",ylab="y",zlab="counts")
}

#アニメーション
library("animation")
Time_Code=seq(0,350,length=36)
saveGIF({
for (i in Time_Code){
　SND_hist2d(i)
}
}, interval = 0.1, movie.name = "SND_hist2d.gif")

X軸-Z軸

library(gplots)
SND_hist2d<-function(x){

# 遠近法プロット (persp) のためのデータをhist2d() を使用して作成
h2d <- hist2d(SND100$X, SND100$Z, show=FALSE, same.scale=TRUE, nbins=c(20,30))
# 遠近法プロット (persp) 描画
persp( h2d$x, h2d$y, h2d$counts,
ticktype="detailed", theta=x, phi=30,
expand=0.5, shade=0.5, col="cyan", ltheta=-30,main="SND with hist2d()",xlab="x",ylab="z",zlab="counts")
}

#アニメーション
library("animation")
Time_Code=seq(0,350,length=36)
saveGIF({
for (i in Time_Code){
　SND_hist2d(i)
}
}, interval = 0.1, movie.name = "SND_hist2d.gif")

Y軸-Z軸

library(gplots)

SND_hist2d<-function(x){
# 遠近法プロット (persp) のためのデータをhist2d() を使用して作成
h2d <- hist2d(SND100$Y, SND100$Z, show=FALSE, same.scale=TRUE, nbins=c(20,30))
# 遠近法プロット (persp) 描画
persp( h2d$x, h2d$y, h2d$counts,
ticktype="detailed", theta=x, phi=30,
expand=0.5, shade=0.5, col="cyan", ltheta=-30,main="SND with hist2d()",xlab="y",ylab="z",zlab="counts")
}

#アニメーション
library("animation")
Time_Code=seq(0,350,length=36)
saveGIF({
for (i in Time_Code){
　SND_hist2d(i)
}
}, interval = 0.1, movie.name = "SND_hist2d.gif")

N=100000の場合（ほとんど揺らがない）

標準正規分布のデータ生成（N=100000）

x_axis<-rnorm(100000,mean=0, sd=1)
y_axis<-rnorm(100000,mean=0, sd=1)
SND100000 <- data.frame(X=x_axis, Y=y_axis)

標準正規分布（N=100000）の描画

library(gplots)

SND100000_hist2d<-function(x){
# 遠近法プロット (persp) のためのデータをhist2d() を使用して作成
h2d <- hist2d(SND100000$X,SND100000$Y, show=FALSE, same.scale=TRUE, nbins=c(20,30))
# 遠近法プロット (persp) 描画
persp( h2d$x, h2d$y, h2d$counts,
ticktype="detailed", theta=x, phi=30,
expand=0.5, shade=0.5, col="cyan", ltheta=-30,main="SND with hist2d()",xlab="x",ylab="y",zlab="counts")
}

#アニメーション
library("animation")
Time_Code=seq(0,350,length=36)
saveGIF({
for (i in Time_Code){
　SND100000_hist2d(i)
}
}, interval = 0.1, movie.name = "SND100000_hist2d.gif")

まぁ一言で言うとこういう世界観の話…
【初心者向け】「三角不等式(Triangle Inequality)」の体感方法？

一方、累積分布関数とは経験分布関数（Empirical distribution function）が大数の法則（LLN=Law of Large Numbers）に従った収束(Convergence)を起こした結果の顕現(Appearance)といえそうなのです。
＊要するに累積分布関数も経験分布関数もある意味、無数のステップ関数の集合と規定可能？　おや、ディラックのデルタ関数が仲間にして欲しそうな目付きでこちらを見ています。仲間に加えますか？

累積分布関数（CDF=Cumulative Distribution Function）の収束過程

CDF<-function(x){rnorm(x,mean=0, sd=1)}
Cumulative_Distribution_Function<-function(x){
plot.ecdf(CDF(x))
}

#アニメーション
library("animation")
Time_Code=c(1,3,5,7,10,25,50,75,100,250,500,750,1000,2500,5000,7500,10000,25000,50000,75000,100000)
saveGIF({
for (i in Time_Code){
　Cumulative_Distribution_Function(i)
}
}, interval = 0.1, movie.name = "CDF01.gif")

考え方としては確率密度関数を積分すると累積分布関数、逆に累積分布関数を微分すると確率密度関数になる様です。

#pythonへの移行(順次)

とりあえず以下はほとんど元記事の引き写しです。
1. Pythonで学ぶ統計学　2. 確率分布[scipy.stats徹底理解]

##確率密度関数(PDF=Probability Density Function)

import sympy as sp
import numpy as np
import pandas as pd
from scipy import stats
import matplotlib.pyplot as plt

# 等差数列を生成
X = np.arange(start=-4, stop=4, step=0.1)

# pdfで確率密度関数を生成
norm_pdf = stats.norm.pdf(x=X, loc=0, scale=1) # 期待値(平均)=0, 標準偏差(分散)=1 

# 可視化
plt.plot(X, norm_pdf)
plt.xlabel("確率変数X", fontsize=13)
plt.ylabel("確率密度pdf", fontsize=13)
plt.show()

5%~95%の信頼区間設定

import sympy as sp
import numpy as np
import pandas as pd
from scipy import stats
import matplotlib.pyplot as plt

# 等差数列を生成
X = np.arange(start=-4, stop=4, step=0.1)

# pdfで確率密度関数を生成
norm_pdf = stats.norm.pdf(x=X, loc=0, scale=1) # 期待値(平均)=0, 標準偏差(分散)=1 

# ppfで累積分布関数05％に当たる変数を取得
q_05 = stats.norm.ppf(q=0.05, loc=0, scale=1) 
print('累積分布関数05％点の確率変数：', q_05)
# pdfで当該変数の確率密度を取得
v_05 = stats.norm.pdf(x=q_05, loc=0, scale=1)
print('累積分布関数05％点の確率密度：', v_05)

# ppfで累積分布関数95％に当たる変数を取得
q_95 = stats.norm.ppf(q=0.95, loc=0, scale=1) 
print('累積分布関数95％点の確率変数：', q_95)
# pdfで当該変数の確率密度を取得
v_95 = stats.norm.pdf(x=q_95, loc=0, scale=1)
print('累積分布関数95％点の確率密度：', v_95)

x1=np.arange(start=np.round(q_05,decimals=1),stop=np.round(q_95,decimals=1),step=0.1)
x0=np.concatenate((
    [q_05],
    x1,
    [q_95,q_05])) 
y0=np.concatenate((
    [0],
    stats.norm.pdf(x=x1, loc=0, scale=1),
    [0,0])) 

# 可視化
plt.plot(X, norm_pdf,color="blue")
plt.fill(x0,y0,color="skyblue",alpha=0.5)
plt.xlabel("確率変数X", fontsize=13)
plt.ylabel("確率密度pdf", fontsize=13)
plt.show()

累積分布関数05％点の確率変数： -1.6448536269514729
累積分布関数05％点の確率密度： 0.10313564037537128
累積分布関数95％点の確率変数： 1.6448536269514722
累積分布関数95％点の確率密度： 0.10313564037537139

##累積分布関数(CDF=Cumulative Distribution Function)

import sympy as sp
import numpy as np
import pandas as pd
from scipy import stats
import matplotlib.pyplot as plt

# 等差数列を生成
X = np.arange(start=-4, stop=4, step=0.1)

# cdfで累積分布関数を生成
norm_cdf = stats.norm.cdf(x=X, loc=0, scale=1) # 期待値(平均)=0, 標準偏差(分散)=1 

# 可視化
plt.plot(X, norm_cdf)
plt.xlabel("確率変数X", fontsize=13)
plt.ylabel("累積分布関数cdf", fontsize=13)
plt.show()

75%までの累積分布関数

import sympy as sp
import numpy as np
import pandas as pd
from scipy import stats
import matplotlib.pyplot as plt

# 等差数列を生成
X = np.arange(start=-4, stop=4, step=0.1)

# cdfで累積分布関数を生成
norm_cdf = stats.norm.cdf(x=X, loc=0, scale=1) # 期待値(平均)=0, 標準偏差(分散)=1 

# cdfで累積分布関数75％に当たる変数を取得
q_75 = stats.norm.ppf(q=0.75, loc=0, scale=1) 
print('累積分布関数75％点の確率変数：', q_75)
# cdfで当該変数の確率密度を取得
v_75 = stats.norm.cdf(x=q_75, loc=0, scale=1)
print('累積分布関数75％点の確率密度：', v_75)

x1=np.arange(start=-4,stop=np.round(q_75,decimals=1),step=0.1)
x0=np.concatenate((
    [-4],
    x1,
    [q_75,-4])) 
y0=np.concatenate((
    [0],
    stats.norm.cdf(x=x1, loc=0, scale=1),
    [0,0])) 

# 可視化
plt.plot(X, norm_cdf)
plt.fill(x0,y0,color="skyblue",alpha=0.5)
plt.xlabel("確率変数X", fontsize=13)
plt.ylabel("累積分布関数cdf", fontsize=13)
plt.show()

累積分布関数75％点の確率変数： 0.6744897501960817
累積分布関数75％点の確率密度： 0.75

全く同一のパラメータによる確率密度関数の計算結果

import sympy as sp
import numpy as np
import pandas as pd
from scipy import stats
import matplotlib.pyplot as plt

# 等差数列を生成
X = np.arange(start=-4, stop=4, step=0.1)

# cdfで累積分布関数を生成
norm_cdf = stats.norm.pdf(x=X, loc=0, scale=1) # 期待値(平均)=0, 標準偏差(分散)=1 

# cdfで累積分布関数75％に当たる変数を取得
q_75 = stats.norm.ppf(q=0.75, loc=0, scale=1) 
print('確率密度関数75％点の確率変数：', q_75)
# cdfで当該変数の確率密度を取得
v_75 = stats.norm.pdf(x=q_75, loc=0, scale=1)
print('確率密度関数75％点の確率密度：', v_75)

x1=np.arange(start=-4,stop=np.round(q_75,decimals=1),step=0.1)
x0=np.concatenate((
    [-4],
    x1,
    [q_75,-4])) 
y0=np.concatenate((
    [0],
    stats.norm.pdf(x=x1, loc=0, scale=1),
    [0,0])) 

# 可視化
plt.plot(X, norm_cdf)
plt.fill(x0,y0,color="skyblue",alpha=0.5)
plt.xlabel("確率変数X", fontsize=13)
plt.ylabel("確率密度関数pdf", fontsize=13)
plt.show()

確率密度関数75％点の確率変数： 0.6744897501960817
確率密度関数75％点の確率密度： 0.317776572684107

##QQプロット
【統計学】Q-Qプロットの仕組みをアニメーションで理解する。

教科書的な説明をすると、「Q-Qプロットとは得られたデータと理論分布を比較し、その類似度を調べるためのグラフ」となります。類似していればプロットした点が直線に並ぶ、そうです。

さまざま分布のQQプロットを描画してみる

import math as n
import numpy as np 
import scipy.stats as stats
import matplotlib.pyplot as plt

def qqplot(dist):
    plt.hist(dist, bins=30)
    plt.show()
    stats.probplot(dist, dist="norm", plot=plt)
    plt.show()

###正規分布
正規分布に従う乱数は、当然QQプロット上に一直線に並びます。

qqplot(np.random.randn(10000))

###一様分布（Uniform distribution)
中央から遠ざかるほど、正規分布と比べた場合の裾の重さ(確率分布の裾がガウス分布のように指数関数的に減衰せず、それよりも緩やかに減衰する)が際立ちます。
一様分布

qqplot(np.random.rand(10000))

###混合ガウス分布（GMM=Gaussian Mixture Model)
混合ガウス分布（GMM）の意味と役立つ例 - 具体例で学ぶ数学
＊＊クラスター分析＊＊やEMアルゴリズムへの入口。
EMアルゴリズム - Wikipedia
混合正規分布モデル(GMM)とEMアルゴリズム
EMアルゴリズム徹底解説

dist = [np.random.normal(-3,1) if np.random.randint(2) else np.random.normal(3,1) for _ in range(10000)]
qqplot(dist)

dist = [np.random.normal(-5,1) if np.random.randint(3) 
   else np.random.normal(3,5) for _ in range(10000)]
qqplot(dist)

###Beta分布(β-distribution)
ベータ分布 - Wikipedia
ベータ分布の意味と平均・分散の導出 | 高校数学の美しい物語

ベータ分布は「コイン投げにおける表が出る確率の予測分布」という解釈ができます。

• 表が出る確率xxが不明であるコインを何回か投げ、表がmm回，裏がnn回出たとする。
• この時「表が出る確率の予測値」は、大雑把にパラメータが(a,b)=(m+1,n+1)であるベータ分布に従うと考える事が出来る。

• (a,b)=(1,1) の時、ベータ分布は青い直線のように一様分布となる。つまり，m=n=0の時（そもそもコインを投げていないとき）は「情報が全く無いのでxxは一様分布に従う」と解釈される。
• (a,b)=(2,3)(a,b)=(2,3)の時、ベータ分布は赤い曲線の様になる。つまりm=1,n=2の時は「表が出る確率は$\frac{1}{3}$に近そうだけど，試行回数が少ないので$\frac{1}{3}$からは遠い値かもしれない」と解釈される。
• (a,b)=(4,7)の時、ベータ分布は緑の曲線の様になる。つまりm=3,n=6の時は「表が出る確率は$\frac{1}{3}$に近そうで、さきほどより試行回数が多いのでより自信を持って$\frac{1}{3}$に近いと言える」と解釈される。

こうした全体像は、より正確は「事前分布を一様分布とし，尤度が二項分布（コイン投げ）であるときの事後分析がベータ分布になる」と表現されます。

qqplot(np.random.beta(0.5,0.5,10000))

###t分布(t-distribution)
t分布 - Wikipedia

連続確率分布の一つであり、正規分布する母集団の平均と分散が未知で標本サイズが小さい場合に平均を推定する問題に利用される。また2つの平均値の差の統計的有意性を検討するt検定で利用される。この分布はνによるが、元の正規分布の母標準偏差σにはよらないという重要な性質を持っている。自由度 ν が ∞（無限大）に近づくにつれ、t分布は正規分布に近づく。

裾が重い(確率分布の裾がガウス分布のように指数関数的に減衰せず、それよりも緩やかに減衰する)分布の代表例の一つ。

qqplot(stats.t.rvs(5, size=100000))

###対数正規分布(Log-Normal Distribution)
対数正規分布 - Wikipedia

確率変数Yが正規分布に従う時$e^Y$が従う分布をいう。あくまで「正規分布の対数」ではなく「対数を取ると正規分布になる」点に注意。

確率密度関数

累積分布関数

対数正規分布の例と平均，分散 | 高校数学の美しい物語

各人が持っている資産の分布は対数正規分布っぽいと言われています。これを（少し強引ですが）説明してみます。

• 人間は最初みんな資産をCだけ持っている。人生のとあるイベントiによって資産は$e^{Y_i}$倍される。ただし$Y_i$は確率変数である。
• イベント1からnまで起こった後の資産は$Ce^{Y_1+Y_2+\cdots+Y_n}$である。
• 各$Y_i$がどのような分布に従うかは分からないが（長い時間経過したとき資産が減る人も増える人も同じくらいいるだろうということで）$Y_1+Y_2+\cdots +Y_n$の期待値は0と考える。
• よって中心極限定理よりnがそれなりに大きければ$Y=Y_1+Y_2+\cdots+Y_n$は正規分布に従うと考えられる。つまり，資産$Ce^Yは対数正規分布に従う。

なお，対数正規分布は裾が重い分布であり「お金持ちがけっこう多い」ことを表しています。

そういえば$e^Y=(1+\frac{Y}{n})^n$で、これは「出目の数がnで、それぞれの出現確率が均等に$\frac{1}{n}のサイコロをn回振った場合$」に対応するのでした。ちなみに球状座標系への対蹠の概念追加から出発するオイラーの多面体定理$Vertex（頂点数）-Edge(辺数）＋Face(面数)$によって「出目の数がnで、それぞれの出現確率が均等に$\frac{1}{n}$のサイコロ」は「正二面体(コイン)」「正四面体」「正六面体」「正八面体」「正十二面体」「正二十面体」「（辺長無限小、辺数無限大の）球」の7種類しか存在しない事が明らかになっています。
【オイラーの多面体定理と正多面体】とある「球面幾何学」の出発点…

qqplot(np.exp(np.random.normal(100,0.5,10000)))

そういえばR時代には「分布の裾の重さ」と「(CosθやSinθの形で現れる)水平線状曲線」の相似が気になって円分布データをQQプロットに放り込んだのです。

X = np.linspace(start=-1, stop=1, num=50,endpoint=True)
Y=np.sqrt(1-X**2)

plt.plot(X, Y,marker = 'o',color="blue")
plt.show()
#qqplot(Y)

X = np.linspace(start=-1, stop=1, num=50,endpoint=True)
Y=np.sqrt(1-X**2)

#plt.plot(X, Y,marker = 'o',color="blue")
#plt.show()
qqplot(Y)

ここに登場する「円状分布」なる概念は相関係数の楕円性に由来すます。線形代数における固有値や固有ベクトルの概念とも関わってくる要所といえましょう。
【Python演算処理】行列演算の基本④大源流における記述統計学との密接な関連性?

ところで「円状分布」には、以下の概念とも相似性が見て取れるのです。

###誤差関数(Error Function)

X = np.linspace(start=-np.pi, stop=np.pi, num=50,endpoint=True)
y0=[]
for nm in range(len(X)):
    y0.append(n.erf(X[nm]))
Y=np.array(y0)

plt.plot(X, Y,marker = 'o',color="blue")
plt.show()
#qqplot(Y)

X = np.linspace(start=-np.pi, stop=np.pi, num=50,endpoint=True)
y0=[]
for nm in range(len(X)):
    y0.append(n.erf(X[nm]))
Y=np.array(y0)

#plt.plot(X, Y,marker = 'o',color="blue")
#plt.show()
qqplot(Y)

###相補誤差関数(Complementary Error Function)

X = np.linspace(start=-np.pi, stop=np.pi, num=50,endpoint=True)
y0=[]
for nm in range(len(X)):
    y0.append(n.erfc(X[nm]))
Y=np.array(y0)

plt.plot(X, Y,marker="o",color="blue")
plt.show()
#qqplot(Y)

X = np.linspace(start=-np.pi, stop=np.pi, num=50,endpoint=True)
y0=[]
for nm in range(len(X)):
    y0.append(n.erfc(X[nm]))
Y=np.array(y0)

#plt.plot(X, Y,marker="o",color="blue")
#plt.show()
qqplot(Y)

ちなみにELFC(x)=1-ERF(x)なのでそれぞれをX軸とY軸に取るとこうなります。

a = np.linspace(start=-np.pi, stop=np.pi, num=50,endpoint=True)
x0=[]
for nm in range(len(a)):
    x0.append(n.erf(a[nm]))
X=np.array(x0)
y0=[]
for nm in range(len(a)):
    y0.append(n.erfc(a[nm]))
Y=np.array(y0)

plt.plot(X, Y,marker = 'o',color="blue")
plt.show()

より具体的には…

• 円状尺に円状尺自身を射影すると「半面のみをこちら側に向けた」球面尺が現れる(円周→対蹠の射影)。
  【初心者向け】複素共役のアニメーション表示について。
  
  
  
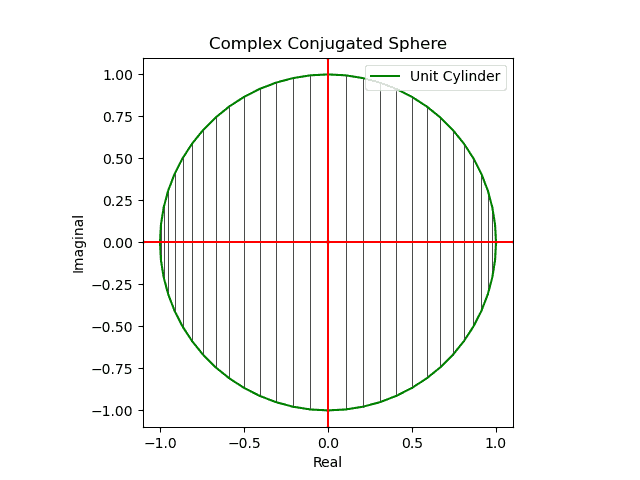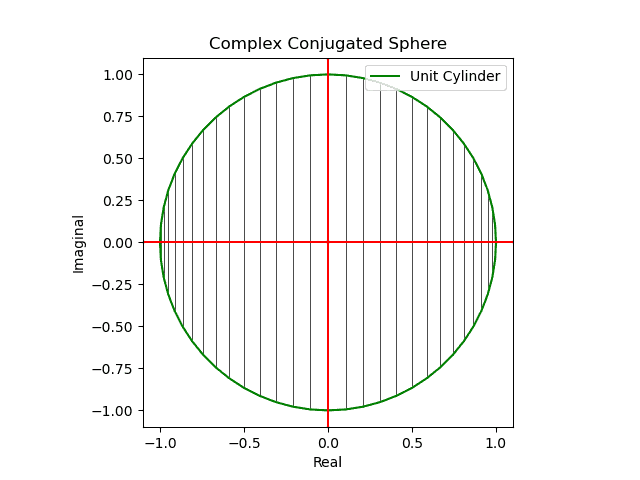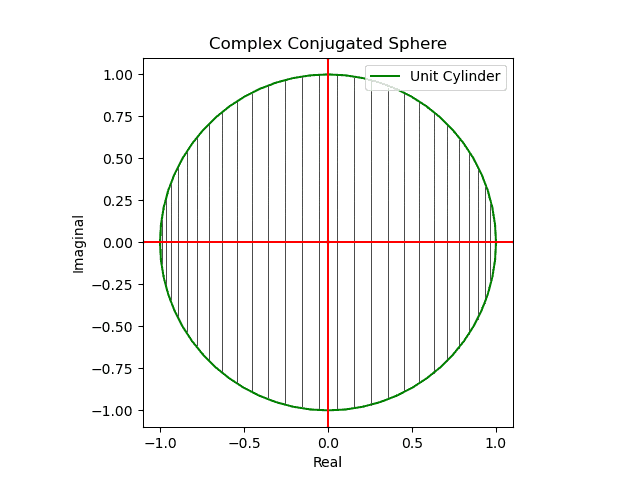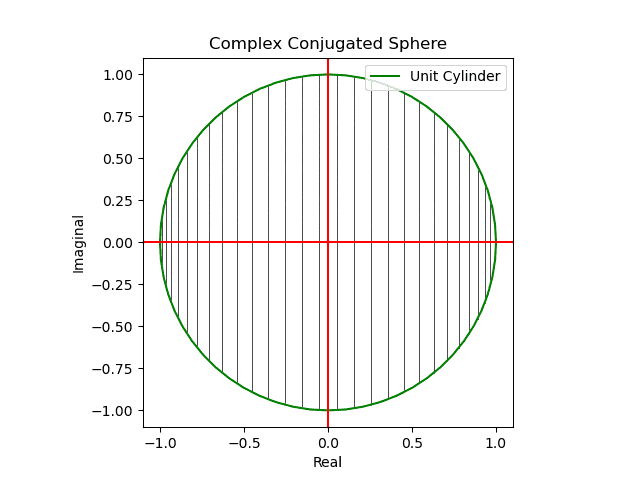
• 同じ円状尺に誤差関数の値を射影すると「(ブラックホールの重力レンズ効果の様に)裏側まで見通せる」球面尺が現れる(円周→円周の射影)。
  【数理考古学】誤差関数(ERF)と相補誤差関数 (ERFC)。
  
• ただし人間の主観的視覚は(生得的にそれを誤差として切り捨てる方向に進化してきたので)両者の違いをほぼに認識出来ない。

とりあえず以下続報…