【Python演算処理】行列演算の基本④大源流における記述統計学との密接な関連性?

私が最初に線形代数を学んだのはこの本でした。
マンガ　線形代数入門　はじめての人でも楽しく学べる
しばらくはこの本に従って解説を進めていきたいと思います。

第一章「行列って何？　線形代数って何？」

まずは直線性(Linearity=グラフとして表した時に直線となるような数学的関係)とは何か説明する為、以下の中学校で習う公式から出発します。

ax+bx=c

確率の期待値(平均)の場合

E(aX+bY)=aE(X)+bE(Y)

微分の場合

(af(x)+bg(x))'=af'(x)+bg'(x)

ax+bx=cの場合、代数方程式(Algebraic Formula)の表現(Expression)では以下となります。
【数理考古学】代数方程式について。

ax+bx-c=0

これを行列(Matrix)で表してみましょう。

行列の行とは横の事、列とは縦の事。合わせると縦と横に数字を綺麗に並べたものといえる。日本では数学用語Matrixを和訳する際にこれを「行と列の組み合わせ」と捉えたのでかかる表現が採用されたが、英語では窓口に並ぶ行列の事をQueueという。

マトリックス - Wikipedia

本来は「子宮」を意味するラテン語（< Mater母+ix）に由来するMatrixの音写で（英語では「メイトリクス」）、そこから何かを生み出すものを意味する。この「生み出す機能」に着目して命名されることが多い。また、子宮状の形状・状態に着目して命名される場合もある。

日本語にあえて翻訳する場合は「基盤」「基質」などの訳語が当てられることがあるが、原語で強く感じられる「生み出す機能」や「形状」が伝わりにくく、必ずしも評判が良くない。例えば「母体」あるいは「子宮体」ならばニュアンスも伝わるのだろうが、このような訳語はほとんど採用されていない。結局、カタカナで表記されることが多い。

生物学や医学では「間質」という言葉も使われている(例：細胞間質)。

材料学では「母材」、鉱物学では「母岩」という訳語も使われている(複合材料の母材)。

• SFドラマ「ドクター・フー（1963年-）」88話「Deadly Assassin（1976年）」に登場する用語。知識が集積された仮想空間のことを「マトリックス」と呼んでいる。
• 聖悠紀の漫画作品「超人ロック」シリーズ(1967年~)において、超能力者が他人に変身するときに、他人の身体からコピーして自分の体を作り変える遺伝子情報を遺伝子マトリクスと呼んでいる。
• ウィリアム・ギブスンのサイバーパンクSF小説「ニューロマンサー（1984年）」「カウント・ゼロ（1986年）」「モナリザ・オーバードライブ（1988年）」「記憶屋ジョニィ（1981年）」「クローム襲撃（1982年）」、あるいは「記憶屋ジョニィ」を基にした映画「ＪＭ(Johnny Mnemonic,1995年）での用語。それらの作品において、コンピューター・ネットワーク上のサイバースペース（電脳空間）に築かれた「仮想現実空間」、人類の全コンピューター・システムから引き出されたデータの「視覚的再現」、「共感覚幻想」のことを「マトリックス」と呼んでいる。
• 上掲のサイバーパンク文学上の文脈から映画「マトリックス三部作(1999年~2003年)」でも「コンピュータの作り出した仮想現実」をそう呼んでいる。ちなみに「MATRIX」という言葉自体はボードリヤールの著書「シミュラークルとシミュレーション(Simulacres et simulation,1981年)」の中にも掲げられており、そこに登場する「シミュラークル=不換紙幣(本位貨幣すなわち正貨たる金貨や銀貨との兌換が保障されない法定紙幣（Fiat Money）で、政府の信用において流通する事から信用紙幣（英: Faith Money）とも呼ばれる)の様に、単に特定の実体と紐付けられたラベルに留まらない記号そのもの」の概念こそが出所となったという見方もある。作中ではハードカバーのボードリヤールの本が映るシーンも見られ、2作目からボードリヤール本人をアドバイザーに迎える計画があったが、断られたという。
  【雑想】「自己の専有と疎外の終わり」?
  【データベース消費】 穿り返すと案外根深い？

これが数理的にどういうニュアンスになるかというと…

import sympy as sp
a,b,c,x,y = sp.symbols('a,b,c,x,y')
A = sp.Matrix([[a,b,c]])
X = sp.Matrix([[x],[y],[-1]])
AX=A*X
expr00 =ax[0]
expr01 = sp.solve(expr00,y)
expr02 = sp.solve(expr00,x)
expr03 = sp.solve(expr00,c)
sp.init_printing()
display(A)
display(X) 
display(AX)
print(sp.latex(A)+sp.latex(X)+"="+sp.latex(AX))
display(expr00)
print(sp.latex(expr00)+"=0")
display(expr01)
print("y="+sp.latex(expr01))
display(expr02)
print("x="+sp.latex(expr02))
display(expr03)
print(sp.latex(expr03)+"=c")

\left[\begin{matrix}a & b & c\end{matrix}\right]\left[\begin{matrix}x\\y\\-1\end{matrix}\right]=\left[\begin{matrix}a x + b y - c\end{matrix}\right] \\
a x + b y - c=0 \\
y=\left[ \frac{- a x + c}{b}\right] \\
x=\left[ \frac{- b y + c}{a}\right] \\
\left[ a x + b y\right]=c

全体像を構築しようとすると行列に「-1」なる成分を追加する必要が生じますが、これは複式簿記における「借方(左側)」と「貸方(右側)」の関係の定義に対応します。そう歴史上における複式簿記の導入とは実は経済分野における会計処理の代数計算化に他ならなかったのです!!
【数理考古学】三次方程式(cubic equation)から虚数(Imaginary Number)へ。

例えば300円のコーヒーと350円の紅茶しかメニューが存在しない喫茶店において、1日の売り上げを知りたいとすれば、その日のコーヒーの注文回数をx杯、紅茶の注文回数をy杯と置いて「300x+350y」の計算が成立します。

import sympy as sp
a,b,c,x,y = sp.symbols('a,b,c,x,y')
A = sp.Matrix([[a,b,c]])
X = sp.Matrix([[x],[y],[-1]])
AX=A*X
expr00 =AX[0]
expr01 = sp.solve(expr00,y)
expr02 = sp.solve(expr00,x)
expr03 = sp.solve(expr00,c)
Aa=A.subs([(a,300),(b,350)])
expr00a = expr00.subs([(a,300),(b,350)])
expr01a = expr01[0].subs([(a,300),(b,350)])
expr02a = expr02[0].subs([(a,300),(b,350)])
expr03a = expr03[0].subs([(a,300),(b,350)])
sp.init_printing()
display(Aa)
display(X) 
display(Aa*X)
print(sp.latex(Aa)+sp.latex(X)+"="+sp.latex(Aa*X))
display(expr00a)
print(sp.latex(expr00a)+"=0")
display(expr01a)
print("y="+sp.latex(expr01a))
display(expr02a)
print("x="+sp.latex(expr02a))
display(expr03a)
print(sp.latex(expr03a)+"=c")

\left[\begin{matrix}300 & 350 & c\end{matrix}\right]\left[\begin{matrix}x\\y\\-1\end{matrix}\right]=\left[\begin{matrix}- c + 300 x + 350 y\end{matrix}\right] \\
- c + 300 x + 350 y=0 \\
y=\frac{c}{350} - \frac{6 x}{7} \\
x=\frac{c}{300} - \frac{7 y}{6} \\
300 x + 350 y=c

Sympyが自動的に約分を施すせいで元データすなわち「特定の実体と紐付けられたラベル」のイメージから離れ始めてますね。それではこの喫茶店の1週間の売り上げをランダムに生成してみましょう。とりあえず売り上げ幅は0杯から50杯とします。

import sympy as sp
a,b,x,y = sp.symbols('a,b,x,y')
A = sp.Matrix([[a,b]])
X = sp.Matrix([[x],[y]])
AX=A*X
expr00 =AX[0]
Aa=A.subs([(a,300),(b,350)])
Xr=sp.randMatrix(2,7, min=0, max=50)
sp.init_printing()
display(Aa)
display(X) 
display(Aa*X)
print(sp.latex(Aa)+sp.latex(X)+"="+sp.latex(Aa*X))
display(Xr) 
display(Aa*Xr)
print(sp.latex(Aa)+sp.latex(Xr)+"="+sp.latex(Aa*Xr))

\left[\begin{matrix}300 & 350\end{matrix}\right]\left[\begin{matrix}x\\y\end{matrix}\right]=\left[\begin{matrix}300 x + 350 y\end{matrix}\right] \\
\left[\begin{matrix}300 & 350\end{matrix}\right]\left[\begin{matrix}18 & 4 & 41 & 49 & 4 & 41 & 33\\10 & 5 & 6 & 23 & 9 & 6 & 35\end{matrix}\right]=\left[\begin{matrix}8900 & 2950 & 14400 & 22750 & 4350 & 14400 & 22150\end{matrix}\right]

ああ、これはもう立派な統計データですね!!
かくしてデータ処理の主体がnumpyを介してpadasに推移する。
Pythonで改行コードLF「\n」を削除する

import sympy as sp
import numpy as np
import pandas as pd
a,b,x,y = sp.symbols('a,b,x,y')
A = sp.Matrix([[300,350]])
X = sp.Matrix([[18,4,41,49,4,41,33],[10,5,6,23,9,6,35]])
X1=X.row_insert(2, A*X)
x=X1.transpose()
df=pd.DataFrame(np.matrix(x),columns=['Coffe', 'Tea', 'Total'])
sp.init_printing()
display(A)
display(X) 
display(A*X)
print(sp.latex(Aa)+sp.latex(X)+"="+sp.latex(Aa*X))
display(x)
org=df.to_html()
print(org.replace('\n', ''))

\left[\begin{matrix}18 & 10 & 8900\\4 & 5 & 2950\\41 & 6 & 14400\\49 & 23 & 22750\\4 & 9 & 4350\\41 & 6 & 14400\\33 & 35 & 22150\end{matrix}\right]

	Coffe	Tea	Total
0	18	10	8900
1	4	5	2950
2	41	6	14400
3	49	23	22750
4	4	9	4350
5	41	6	14400
6	33	35	22150

だから以下の様な記述統計諸元が計算可能となります。

import sympy as sp
import numpy as np
import pandas as pd
X = sp.Matrix([[18,4,41,49,4,41,33],[10,5,6,23,9,6,35]])
df=pd.DataFrame(np.matrix(X.transpose()),columns=['Coffee', 'Tea'])
sp.init_printing()
display(X.transpose())
print(sp.latex(X.transpose()))
org=df.to_html()
print(org.replace('\n', ''))
print(df.astype({'Coffee': int, 'Tea': int}).describe())

\left[\begin{matrix}18 & 10\\4 & 5\\41 & 6\\49 & 23\\4 & 9\\41 & 6\\33 & 35\end{matrix}\right]

	Coffee	Tea
0	18	10
1	4	5
2	41	6
3	49	23
4	4	9
5	41	6
6	33	35

          Coffee        Tea
count   7.000000   7.000000
mean   27.142857  13.428571
std    18.488091  11.326328
min     4.000000   5.000000
25%    11.000000   6.000000
50%    33.000000   9.000000
75%    41.000000  16.500000
max    49.000000  35.000000

      Coffee Tea
count      7   7
unique     5   6
top        4   6
freq       2   2

このうちcountは成分の個数(1週間分のデータなので7個)、uniqueはユニークな（一意な）値の要素の個数に対応します。
【初心者向け】記述統計学と代表値
要約統計量についてまとめてみた

クォンタイル(パーセンタイル)/四分位(Quantile)

以下の要素から構成される要約統計量(Summary Statistics)。

• 最小値(Min)
• 第1四分位(1st Quartile=25%)
• 中央値(Median=50%)
• 第3四分位（3rd Quartile=75%）
• 最大値(Max)

以下の形で統計的代表値の候補となります。

• 散布度基準の一つである範囲(Range)は最小値(Min)と最大値（Max)から構成される(最大値-最小値)。
• 分布の中心にある中央値(Median)は、候補データが複数存在する場合にはその平均を取る。年収リストの様な中央値と平均が異なる分布では、概ね中央値の方が平均値を下回る。平均値(Mean)より外れ値の影響に対してロバスト(頑強)とされる。
  【初心者向け】平均と標準偏差、中央値と平均偏差

人工知能・機械学習のときには過学習 (オーバーフィッティング) に気をつけよう！～過学習とその対処法～

中央絶対偏差はすべてのデータから中央値を引き、すべて絶対値を取り、それらの中央値を求めた結果です。標準偏差のかわりに使うときは、中央絶対偏差に1.4826をかけて補正する必要があります。

中央値(Median)は平均値(Mean)ほど外れ値の影響を受けない事の簡単な検証。

import sympy as sp
import numpy as np
import pandas as pd
df1=pd.DataFrame([300,300,300,300,400,400,400,2000,9000])
df2=pd.DataFrame([300,300,300,300,400,400,400,2000,12000])
print("mean1=" + str(df1.mean()))
print("median1=" + str(df1.median()))
print("mean2=" + str(df2.mean()))
print("median2=" + str(df2.median()))

mean1=0    1488.888889
dtype: float64
median1=0    400.0
dtype: float64
mean2=0    1822.222222
dtype: float64
median2=0    400.0
dtype: float64

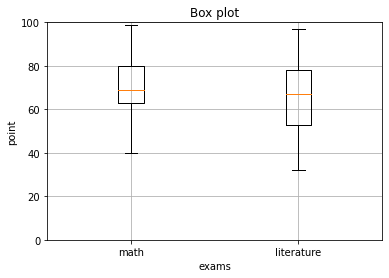
いわゆる「箱髭図(Box Plot)」はこのデータから起こされます。

【プログラマーのための統計学】箱ひげ図

%matplotlib inline
import matplotlib.pyplot as plt

# 数学の点数
math = [74, 65, 40, 62, 85, 67, 82, 71, 60, 99]
# 国語の点数
literature = [81, 62, 32, 67, 41, 50, 85, 70, 67, 97]
# 点数のタプル
points = (math, literature)

# 箱ひげ図
fig, ax = plt.subplots()

bp = ax.boxplot(points)
ax.set_xticklabels(['math', 'literature'])

plt.title('Box plot')
plt.xlabel('exams')
plt.ylabel('point')
# Y軸のメモリのrange
plt.ylim([0,100])
plt.grid()

# 描画
plt.show()

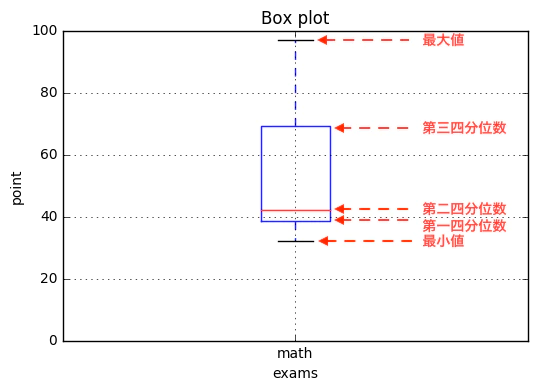
それぞれの意味はこうなっています。

箱ひげ図の場合、最大値、最小値が極端であった場合、ヒゲが長くなります。外れ値を考慮する箱ひげ図の場合は、ヒゲの長さは、最大値側、最小値側でそれぞれ、箱の1.5倍以下とし、それを超えるデータは、外れ値とみなします。

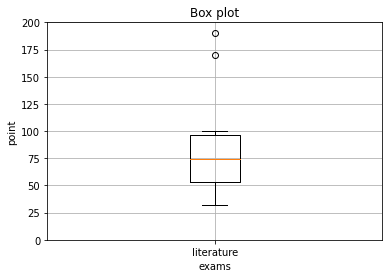
pythonのmatplotlibでは、外れ値を自動で検出してくれるようです。以下のコードでは、国語の点数結果に170点、190点を追加してみました。テストは100点満点なので、この2つは外れ値になるはずです。グラフの目盛りは200までに増やしています。これでグラフを作成してみます。

%matplotlib inline
import matplotlib.pyplot as plt

# 国語の点数
literature = [81, 62, 32, 67, 41, 50, 85, 100, 170, 190]
# 点数のタプル
points = (literature)

# 箱ひげ図
fig, ax = plt.subplots()

bp = ax.boxplot(points)
ax.set_xticklabels(['literature'])

plt.title('Box plot')
plt.xlabel('exams')
plt.ylabel('point')
# Y軸のメモリのrange
plt.ylim([0,200])
plt.grid()

# 描画
plt.show()

グラフの上部の方に、◯が2つできました。この2つは、170点、190点が外れ値としてみなされたものです。pythonのmatplotlibでは、特に外れ値を定義しなくても、このように自動で判別してくれるようなので、非常に便利ですね。

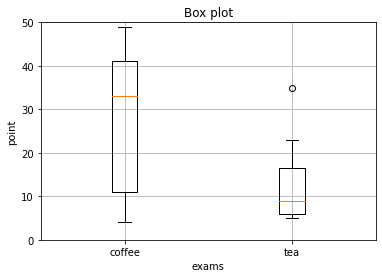
独自に「外れ値」を除外する仕組みが備わっていたりもするのですね。ちなみに今回の「とある架空の喫茶店の7日分の売り上げ(データランダム生成)」をプロットするとこんな感じに。

%matplotlib inline
import matplotlib.pyplot as plt

# コーヒーの売り上げ
coffee = [18,4,41,49,4,41,33]
# 紅茶の売り上げ
tea = [10,5,6,23,9,6,35]
# 点数のタプル
points = (coffee, tea)

# 箱ひげ図
fig, ax = plt.subplots()

bp = ax.boxplot(points)
ax.set_xticklabels(['coffee', 'tea'])

plt.title('Box plot')
plt.xlabel('exams')
plt.ylabel('point')
# Y軸のメモリのrange
plt.ylim([0,50])
plt.grid()

# 描画
plt.show()

なんとランダム生成データなのに外れ値が検出されてしまいました?

範囲(Range)と最頻値(Mode)

以下の要素から構成される要約統計量(Summary Statistics)。

• 範囲(Range)…散布度基準の一つだが、あまり普及してない。最大値(Max)-最小値(Min)。度数分布（Frequency Distribution）の表現形態の一つたるヒストグラム（Histogram）では「階級(Class)の最大値-階級(Class)の最小値」と計算される。
• 最頻値(Mode)…日本工業規格の定義では「離散分布の場合は確率関数が，連続分布の場合は密度関数が最大となる確率変数の値。分布が多峰性の場合は，それぞれの極大値を与える確率変数の値」と定めている。Pandasのdescribe関数ではTopが最頻値、freqがその出現回数を表す。

そう、連続分布を度数分布表(Histogram)で離散的に表す過程はしばしば、「データ分布の(確率密度に対応した)クラス分けの最適化」なる分析過程を必要とするのです。
【初心者向け】度数分布と最頻値

試しに「とある架空の喫茶店の7日分の売り上げ(データランダム生成)」をプロットすると…

%matplotlib inline
import numpy as np
import matplotlib.pyplot as plt

# コーヒーの売り上げ
coffee = [18,4,41,49,4,41,33]
# 紅茶の売り上げ
tea = [10,5,6,23,9,6,35]

plt.hist([coffee, tea], stacked=False)
# 描画
plt.show()

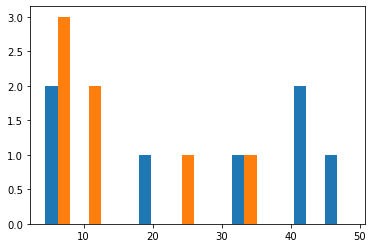
まぁ当然の帰結として見るからに有意性の感じられない結果を迎えました。これではクラス分けを最適化する意欲も起こりません。

平均(Mean)と偏差（Deviation）と分散（Dispersion）

ここで共通して使用する要約統計量(Summary Statistics)は以下です。

• 平均(Mean)

とりあえず「とある架空の喫茶店の7日分の売り上げ(データランダム生成)」における偏差(Deviation)、すなわち「データの各数値より、その平均を引いた残り」概念から出発します。数理的にいうと「平均値(mean)を原点とする分布への射影結果」といったイメージですね。

import sympy as sp
import numpy as np
import pandas as pd
x=np.matrix([8900,2950,14400,22750,4350,14400,22150])
y=pd.DataFrame([8900,2950,14400,22750,4350,14400,22150])
org=y.to_html()
print(org.replace('\n', ''))
print("元データ:" + str(x))
print("平均:" + str(np.round(np.mean(x))))
print("偏差:" + str(np.round(x-np.mean(x))))
print("標本分散:" + str(np.round(np.var(x))))
print("不偏分散:" + str(np.round(y.var())))
print("標本偏差:" + str(np.round(np.std(x))))
print("標準偏差:" + str(np.round(y.std())))
print("偏差の絶対値:" + str(np.round(abs(x-np.mean(x)))))
print("平均偏差=偏差の絶対値の平均:" + str(np.round(np.sum(abs(x-np.mean(x))))/len(x)))

	0
0	8900
1	2950
2	14400
3	22750
4	4350
5	14400
6	22150

元データ:[[ 8900  2950 14400 22750  4350 14400 22150]]
平均:12843.0
偏差:[[-3943. -9893.  1557.  9907. -8493.  1557.  9307.]]
標本分散:53595306.0
不偏分散:0    62527857.0
dtype: float64
標本偏差:7321.0
標準偏差:0    7907.0
dtype: float64
偏差の絶対値:[[3943. 9893. 1557. 9907. 8493. 1557. 9307.]]
平均偏差=偏差の絶対値の平均:44657.0

何やらややこしい計算を重ねた末に「標本分散(Sample Dispersion)/標本偏差(Sample Dispersion)」「不偏分散(Unbiased Dispersion)/標準偏差(Standard Deviation)」「平均偏差(Mean Deviation)」の3組に到達します。どういう事なのでしょうか? 順を追って見ていく事にしましょう。

偏差(Deviation)の合計自体は0

統計学的画像再構成法であるOSEMアルゴリズムの基礎論

まずは(母平均μ（ミュー）を中心位置、母標準偏差σ（シグマ）をばらつき具合とする未知の分布によって構成される)母集合(Parameter=パラメータ)からn個の標本集合(Sample Set)$[x_1,…,x_n]$を抽出し、その「標本平均(Sample Mean)」を求めます。

\hat{μ}=\overline{x} = \frac{1}{n}\sum_{ i = 1 }^{ n } x_i

この標本集合の偏差(Deviation)すなわち各データから平均値を引いた結果の合計は必ず0となります。

\sum_{ i = 1 }^{ n } x_i-\overline{x}=(x_1-\overline{x})+…+(x_n-\overline{x})=0

試しに「とある架空の喫茶店の7日分の売り上げ(データランダム生成)」で計算すると…

import sympy as sp
import numpy as np
import pandas as pd
from scipy import stats
a=[8900,2950,14400,22750,4350,14400,22150]
print("リスト表現")
print(a)
print("平均")
print(np.round(np.mean(a)))
print("偏差")
print(a-np.round(np.mean(a)))
print("偏差計")
print(sum(a-np.round(np.mean(a))))

リスト表現
[8900, 2950, 14400, 22750, 4350, 14400, 22150]
平均
12843.0
偏差
[-3943. -9893.  1557.  9907. -8493.  1557.  9307.]
偏差計
-1.0

四捨五入による誤差の結果、中心が「ちょうど0」にはなりませんが、イメージ的には大体こんな感じ。群論でいうと「加法単位元と加法逆元が設定された加法群」に射影された状態に該当する様です。統計学における標準化(Standardization)にはそういうニュアンスもあったのですね。
【数理考古学】群論概念(Group Theory Concept)①基本定義

ただし、この考え方ではデータのばらつき具合を把握出来ないので、さらに考え方を発展させなくてはいけません。

標本分散(Sample Dispersion)/標本偏差(Sample Dispersion)

numpyがデフォルトで立拠する分散と偏差の概念です。

• 標本分散(Sample Dispersion)…偏差^2の合計/標本数

s^2 = \frac{1}{n}\sum_{i=1}^{n}  (x_i – \bar{x})^2

• 標本偏差(Sample Dispersion)…標本分散の平方根

s = \sqrt{\frac{1}{n}\displaystyle \sum_{ i = 1 }^{ n } (x_i-\overline{x})^2}

上掲の「架空の喫茶店NO枚日の売り上げ」の例でいうと、その開店が1週間限定だったら全データが列記されている事になり、こちらの計算が採用されます。

不偏分散(Sample Dispersion)/標準偏差(Sample Dispersion)

padasが立拠する分散と偏差の概念です。何やら出自が胡散臭い「平均への回帰」理論を使いますが、確かに計算上はこちらの方が正解に近づくのです。
平均への回帰 -Wikipedia
【初心者向け】標本分散と不偏分散

• 不偏分散(Unbiased Dispersion)…偏差^2の合計/（標本数-1）

s^2 = \frac{1}{n-1}\sum_{i=1}^{n}  (x_i – \bar{x})^2

• 標準偏差(Standard Deviation)…不偏分散の平方根

S = \sqrt{\frac{1}{n-1}\displaystyle \sum_{ i = 1 }^{ n } (x_i-\overline{x})^2}

上掲の「架空の喫茶店NO枚日の売り上げ」の例でいうと、そのデータは連日の売り上げ集合から7日分だけ抽出した結果なら「母分散は別に実際する」と想定せざるを得なくなり、こちらの計算が採用されます。確かにまぁ、普通はそう考えるものなんです?

• ちなみにいわゆる「正規分布(Normal Distribution)」が平均(中央値0)同様にパラメーターとして使用する分散(中央値1)は、この不偏分散の方です。
  【初心者向け】正規分布とは何か？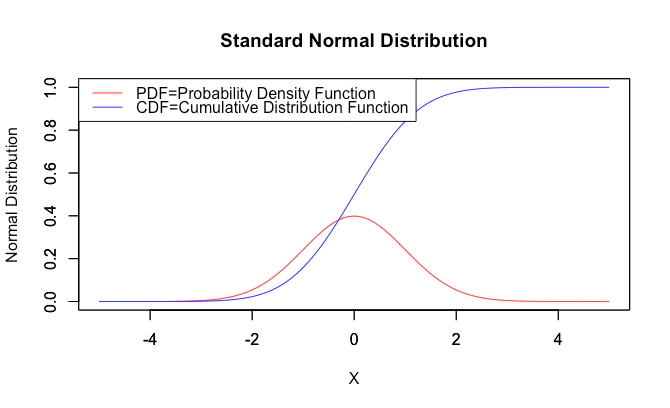
  
  
  
  
  

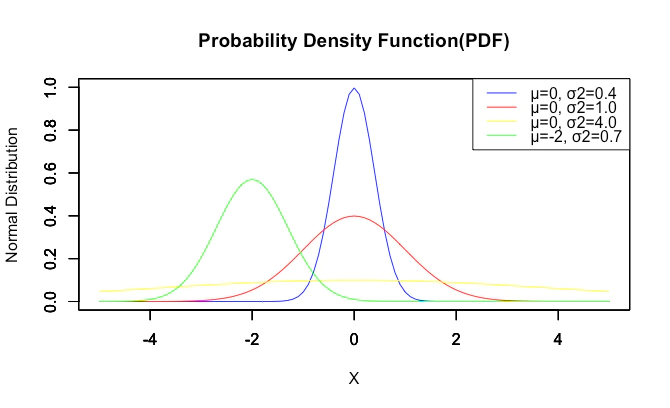
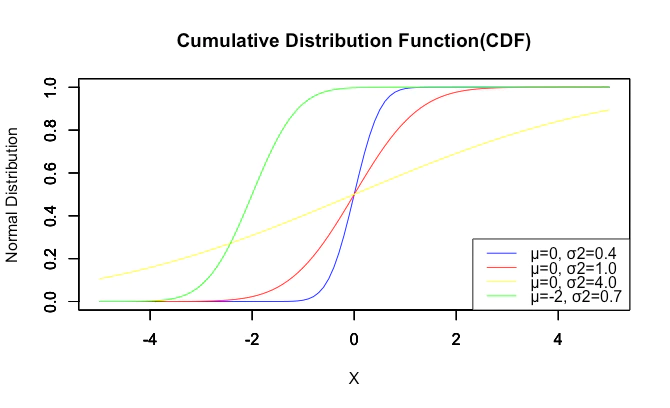
• ちなみにnumpyのstd関数も引数としてddof=1を与える事で不偏分散/標準偏差を扱う様になります。ddofはDelta Degrees of Freedomの略との事。
  numpy.varやnumpy.stdの自由度

import sympy as sp
import numpy as np
import pandas as pd
from scipy import stats
a=[8900,2950,14400,22750,4350,14400,22150]
print("リスト表現")
print(a)
print("np var ddof=0")
print(np.var(a,ddof=0))
print("np std ddof=0")
print(np.std(a,ddof=0))
print("np var ddof=1")
print(np.var(a,ddof=1))
print("np std ddof=1")
print(np.std(a,ddof=1))
x=pd.DataFrame(a,columns=["Daily Total"])
print("Dataframe表現")
print(x)
print("np var ddof=0")
print(np.round(x.var(),decimals=2))
print("np var ddof=1")
print(np.round(x.std(),decimals=2))

リスト表現
[8900, 2950, 14400, 22750, 4350, 14400, 22150]
np var ddof=0
53595306.12244898
np std ddof=0
7320.88151266287
np var ddof=1
62527857.14285714
np std ddof=1
7907.455794555993
Dataframe表現
   Daily Total
0         8900
1         2950
2        14400
3        22750
4         4350
5        14400
6        22150
np var ddof=0
Daily Total    62527857.14
dtype: float64
np var ddof=1
Daily Total    7907.46
dtype: float64

「統計学における自由度」の考え方自体はこちらを参照して下さい。
自由度 | 統計学の時間 | 統計WEB - BellCurve

自由度(Degrees of Freedom)とは、ある変数において自由な値をとることのできるデータの数。例えばn個のデータ$x_1,x_2,…x_n$があるとき、これらはどれも自由な値を取りうるので自由度はnである。

ところが平均値$\bar{x}=a$の時、平均値が変わらないようにする為に$n-1$個の$x_i$は自由な値を取りうるが、n個目の$x_n$は自由な値を取る事が出来ず、この時自由度はn-1となる。一般にn個のデータの間でk個の条件があるとき、自由度はn-kとなる。

あれ、もしかしてこの話、四元数a+bi+cj+dkにおいてijkのうちどれか2つが決まると残りの選択範囲が狭められる件と重なる？
【Rで球面幾何学】ハミルトンの四元数(Hamilton's Quaternion)は何を表しているのか？
ijk=-1

ji-k=-1(iを戻す場合)

ji-k=-1(jを戻す場合)

jki=-1

kj-i=-1

kij=-1

ik-j=-1

ところで「原点ゼロからの自乗を取る」とは行列演算の二次形式で表現すると以下となります。
【Python演算処理】行列演算の基本③パスカルの三角形から二次形式へ

\left[\begin{matrix}a & b\end{matrix}\right]\left[\begin{matrix}0 & 0\\0 & 1\end{matrix}\right]\left[\begin{matrix}a\\b\end{matrix}\right]=\left[\begin{matrix}b^{2}\end{matrix}\right]

【参考】二次形式行列における「マスキング」

import sympy as sp
a,b = sp.symbols('a,b')
#Rows
x=sp.Matrix([[a,b]])
#Columns
y=sp.Matrix([[a],[b]])
a00=sp.Matrix([[1,1],[1,1]])
a11=sp.Matrix([[1,0],[0,0]])
a12=sp.Matrix([[0,1],[0,0]])
a21=sp.Matrix([[0,0],[1,0]])
a22=sp.Matrix([[0,0],[0,1]])
sp.init_printing()
display(x) 
display(a00) 
display(a11) 
display(a12) 
display(a21) 
display(a22) 
display(y) 
display(sp.simplify(x*a00*y)) 
print(sp.latex(x)+sp.latex(a00)+sp.latex(y)+"="+sp.latex(sp.simplify(x*a00*y)))
display(sp.simplify(x*a11*y)) 
print(sp.latex(x)+sp.latex(a11)+sp.latex(y)+"="+sp.latex(sp.simplify(x*a11*y)))
display(sp.simplify(x*a12*y)) 
print(sp.latex(x)+sp.latex(a12)+sp.latex(y)+"="+sp.latex(sp.simplify(x*a12*y)))
display(sp.simplify(x*a21*y)) 
print(sp.latex(x)+sp.latex(a21)+sp.latex(y)+"="+sp.latex(sp.simplify(x*a21*y)))
display(sp.simplify(x*a22*y)) 
print(sp.latex(x)+sp.latex(a22)+sp.latex(y)+"="+sp.latex(sp.simplify(x*a22*y)))

\left[\begin{matrix}a & b\end{matrix}\right]\left[\begin{matrix}1 & 1\\1 & 1\end{matrix}\right]\left[\begin{matrix}a\\b\end{matrix}\right]=\left[\begin{matrix}\left(a + b\right)^{2}\end{matrix}\right]\\
\left[\begin{matrix}a & b\end{matrix}\right]\left[\begin{matrix}1 & 0\\0 & 0\end{matrix}\right]\left[\begin{matrix}a\\b\end{matrix}\right]=\left[\begin{matrix}a^{2}\end{matrix}\right]\\
\left[\begin{matrix}a & b\end{matrix}\right]\left[\begin{matrix}0 & 1\\0 & 0\end{matrix}\right]\left[\begin{matrix}a\\b\end{matrix}\right]=\left[\begin{matrix}a b\end{matrix}\right]\\
\left[\begin{matrix}a & b\end{matrix}\right]\left[\begin{matrix}0 & 0\\1 & 0\end{matrix}\right]\left[\begin{matrix}a\\b\end{matrix}\right]=\left[\begin{matrix}a b\end{matrix}\right]\\
\left[\begin{matrix}a & b\end{matrix}\right]\left[\begin{matrix}0 & 0\\0 & 1\end{matrix}\right]\left[\begin{matrix}a\\b\end{matrix}\right]=\left[\begin{matrix}b^{2}\end{matrix}\right]

$\sqrt{x^2}=x$があまりに自明の場合(Trival Case)っぽく見えるので、それがユークリッド距離演算$\sqrt{0+x^2}$によって等長性が保証された空間への射影とも見て取れる事をつい失念してしまいます。そもそも、それら全てがいわゆる正規分布のBellCurve自体がこの方法によって(極座標系における)円状分布から平面に射影された結果である事に対応しているのですね。
【初心者向け】正規分布(Normal Distribution)とは何か？

• ただしこの空間自体は(中心を定める為の)スカラー演算と(そうして検出された中心からの距離を扱う)加減算の概念こそ存在するものの(ベクトル空間ではある)、まだ角度の概念を備えていない（内積が計算可能なベクトル計量空間ではない）。

平均偏差(Mean Deviation)

標準偏差も標本偏差も平均(Mean)の概念を代表値に選ぶ点は同じですが、平均偏差は中央値(Median)を代表値とする要約統計量(Summary Statistics)です。
【初心者向け】平均と標準偏差、中央値と平均偏差

• 平均偏差(Mean Deviation)

s = \frac{1}{n}\sum_{i=1}^{n}  |x_i – \bar{x}|

試しに「とある架空の喫茶店の7日分の売り上げ(データランダム生成)」で計算すると…

import sympy as sp
import numpy as np
import pandas as pd
from scipy import stats
a=[8900,2950,14400,22750,4350,14400,22150]
print("リスト表現")
print(a)
print("平均")
print(np.round(np.mean(a)))
print("偏差")
print(a-np.round(np.mean(a)))
print("偏差の絶対値")
print(abs(a-np.round(np.mean(a))))
print("偏差の絶対値計")
print(sum(abs(a-np.round(np.mean(a)))))

リスト表現
[8900, 2950, 14400, 22750, 4350, 14400, 22150]
平均
12843.0
偏差
[-3943. -9893.  1557.  9907. -8493.  1557.  9307.]
偏差の絶対値
[3943. 9893. 1557. 9907. 8493. 1557. 9307.]
偏差の絶対値計
44657.0

そういえば正規化(Feature Scaling)には「最小値0、最大値1への正規化(Min-Max Normalization)」なんて考え方もあるのです。

x'=\frac{x-min(x)}{max(x)-min(x)}

import sympy as sp
import numpy as np
import pandas as pd
from scipy import stats
a=[8900,2950,14400,22750,4350,14400,22150]
print("リスト表現")
print(a)
print("Min(0)-Max(1) Normalization")
print((a-np.round(min(a)))/(max(a)-min(a)))

リスト表現
[8900, 2950, 14400, 22750, 4350, 14400, 22150]
Min(0)-Max(1) Normalization
[0.30050505 0.         0.57828283 1.         0.07070707 0.57828283
 0.96969697]

群論的志向様式に寄せるなら「最小値-1、最大値1への正規化(Min-Max Normalization)」なんて考え方も出来るかもしれません。

x'=2\frac{x-min(x)}{max(x)-min(x)}-1

import sympy as sp
import numpy as np
import pandas as pd
from scipy import stats
a=[8900,2950,14400,22750,4350,14400,22150]
print("リスト表現")
print(a)
print("Min(-1)-Max(1) Normalization")
print(((a-np.round(min(a)))/(max(a)-min(a)))*2-1)

リスト表現
[8900, 2950, 14400, 22750, 4350, 14400, 22150]
Min(-1)-Max(1) Normalization
[-0.3989899  -1.          0.15656566  1.         -0.85858586  0.15656566
  0.93939394]

本来ならこれらは状況によって使い分けるのが正しいのでしょうが、結果として一時期(特に20世紀後半)不偏分散/標準偏差を絶対視するイデオロギーが広まりました。この辺り本当に注意が必要です。

標準得点（z得点）への変換と偏差値（Deviation Value）

Z値とは

Z値とは、標準偏差の単位で観測統計量とその仮説母集団パラメータの差を測定するZ検定の統計量です。

観測値をZ値に変換することを標準化と呼びます。母集団の観測値を標準化するには、対象の観測値から母集団平均を引き、その結果を母集団の標準偏差で除算します。この計算結果が、対象の観測値に関連付けられるZ値です。

Z値を使用して、帰無仮説を棄却するかどうかを判断できます。帰無仮説を棄却するかどうかを判断するには、Z値を棄却値と比較します。これは、ほとんどの統計の教科書の標準正規表に示されています。棄却値は、両側検定の場合はZ1-α/2、片側検定の場合はZ1-αです。Z値の絶対値が棄却値より大きい場合、帰無仮説を棄却します。そうでない場合、帰無仮説を棄却できません。

• Z得点(Z Value)…$\frac{偏差}{標準偏差}$
• 偏差値(Deviation Value)…Z得点*10+50

【python】pandasでデータを標準得点（z得点）に変換

データの正規化（標準化）とは、データを分散1、平均0に変換する操作である。

Pythonで正規化・標準化（リスト、NumPy配列、pandas.DataFrame）

①z得点と偏差値の計算(デフォルト)

import sympy as sp
import numpy as np
import pandas as pd
from scipy import stats
a=[8900,2950,14400,22750,4350,14400,22150]
A1=stats.zscore(a)
print("z得点")
print(A1)
A2=A1*10+50
print("偏差値")
print(A2)
x=pd.DataFrame(a,columns=["Daily Total"])
X1=x.apply(stats.zscore)
print("z得点")
print(X1)
X2=X1*10+50
print("偏差値")
print( X2)

z得点 \\
[-0.53857683 -1.35132048  0.21269882  1.35327185 -1.16008668  0.21269882
  1.27131451] \\
偏差値 \\
[44.61423172 36.48679517 52.1269882  63.53271848 38.39913318 52.1269882
 62.71314505]

z得点
   Daily Total
0    -0.538577
1    -1.351320
2     0.212699
3     1.353272
4    -1.160087
5     0.212699
6     1.271315
偏差値
   Daily Total
0    44.614232
1    36.486795
2    52.126988
3    63.532718
4    38.399133
5    52.126988
6    62.713145

②z得点と偏差値の計算(ddof=0)=$\frac{偏差}{標本偏差}$(*10+50)

import sympy as sp
import numpy as np
import pandas as pd
from scipy import stats
a=[8900,2950,14400,22750,4350,14400,22150]
A1=stats.zscore(a,ddof=0)
print("z得点")
print(A1)
A2=A1*10+50
print("偏差値")
print(A2)
x=pd.DataFrame(a,columns=["Daily Total"])
X1=x.apply(stats.zscore,ddof=0)
print("z得点")
print(X1)
X2=X1*10+50
print("偏差値")
print( X2)

z得点 \\
[-0.53857683 -1.35132048  0.21269882  1.35327185 -1.16008668  0.21269882
  1.27131451] \\
偏差値 \\
[44.61423172 36.48679517 52.1269882  63.53271848 38.39913318 52.1269882
 62.71314505]

z得点
   Daily Total
0    -0.538577
1    -1.351320
2     0.212699
3     1.353272
4    -1.160087
5     0.212699
6     1.271315
偏差値
   Daily Total
0    44.614232
1    36.486795
2    52.126988
3    63.532718
4    38.399133
5    52.126988
6    62.713145

③z得点と偏差値の計算(ddof=1)=$\frac{偏差}{標準偏差}$(*10+50)

import sympy as sp
import numpy as np
import pandas as pd
from scipy import stats
a=[8900,2950,14400,22750,4350,14400,22150]
A1=stats.zscore(a,ddof=1)
print("z得点")
print(A1)
A2=A1*10+50
print("偏差値")
print(A2)
x=pd.DataFrame(a,columns=["Daily Total"])
X1=x.apply(stats.zscore,ddof=1)
print("z得点")
print(X1)
X2=X1*10+50
print("偏差値")
print( X2)

z得点 \\
[-0.49862525 -1.25107966  0.19692084  1.25288628 -1.07403157  0.19692084
  1.17700852] \\
偏差値 \\
[45.01374747 37.48920335 51.96920843 62.52886278 39.25968432 51.96920843
 61.77008522]

z得点
   Daily Total
0    -0.498625
1    -1.251080
2     0.196921
3     1.252886
4    -1.074032
5     0.196921
6     1.177009
偏差値
   Daily Total
0    45.013747
1    37.489203
2    51.969208
3    62.528863
4    39.259684
5    51.969208
6    61.770085

母集団からのランダムサンプリングの場合は③が使われます。偏差値が百点満点のテスト(最低得点0点,最高得点100点)のイメージに立脚する評価空間ながら、大元のZ得点の特徴から0点以下や100点以上も扱える点に注意して下さい。しかしまぁ大抵は例えデータとして現れても外れ値(Outliers)として切り捨てられてしまう事でしょう。

• 言葉としての「偏差値」が20世紀の受験戦争以降一般にも定着しましたが、その過程でその内容についての誤解も広まりました。この辺りもまた注意が必要です。
  【無限遠点を巡る数理】無限遠点としての正規分布と分散概念の歴史

こうして全体像を俯瞰してみると統計データにおける標準化(スカラー倍率を抽出して増減範囲を1にまとめ行列演算的に対角化する)と行列演算における標準化(同じくスカラー倍率を抽出して値1の直行行列概念を援用)にある種の相似性が見て取れるのです。
２次形式の標準化

正規分布(Normal Distribution)を母集合分布として想定した展開

正規分布を母集合分布として想定すると何が嬉しいって、以下の様な計算が可能となるのです。

標準誤差（SE：Standard Srror）

標準偏差と標準誤差

推定量の標準偏差であり、標本から得られる推定量そのもののバラつき（＝精度）を表します。一般に「標本平均の標準偏差」を意味し、その計算に「中心極限定理」を使います。

「中心極限定理」は、平均μ、分散σに従う母集団からサンプルサイズnの標本を抽出する時、その平均値の分布はnが大きくなるにつれ正規分布$N(μ,\frac{σ^2}{N})$に近づくと考えます。すなわち標本平均の標準偏差は以下に近づくのです。

\sqrt{\frac{σ^2}{N}}=\frac{σ}{\sqrt{N}}

ただし、標本の分散は$σ^2$ではなく不偏分散$s^2$を用いることから、標本平均の標準偏差（＝標準誤差SE）は標準偏差sを用いて次の式から計算できます。

SE=\frac{s}{\sqrt{N}}=\frac{\sqrt{\frac{1}{n-1}\displaystyle \sum_{ i = 1 }^{ n } (x_i-\overline{x})^2}}{\sqrt{N}}

標準誤差は、母集団から抽出された標本から標本平均を求める場合、標本平均の値が母平均に対してどの程度ばらついているかを表すものです。サンプルサイズが大きくなると標準誤差は小さくなります。

「統計備忘録」 標準誤差

標準誤差はｎの二乗根に反比例することになりますから、サンプルサイズを４倍にすれば標準誤差は半分になります。

import sympy as sp
import numpy as np
import pandas as pd
from scipy import stats
a=[126,224,34,25,199,89,178,14,38,11]
A1=np.std(a,ddof=1)
print("標準偏差")
print(A1)
A2=A1/np.sqrt(len(a))
print("標準誤差")
print(A2)

標準偏差
82.202730422346
標準誤差
25.994785801942832

統計的仮説検定(Testing of Statistical Hypothes)

Pythonで統計学を学ぶ(4)
頭がこんがらがってしまったので、以下にまとめ直しました。
【Pyrhon演算処理】確率密度空間と累積分布空間①記述統計との狭間
こういう定義もありますが…

統計科学事典，清水良一訳(https://www.ism.ac.jp/~ayaka/2017_gairon_1.pdf)

記述統計学とはデータのもっている主要な特性をより鮮明に表現するために，データを要約したり作表をしたりすること一般を指する。

まぁこの辺りが「とりあえず手元データ自体を母集合と考える」記述統計学(Descriptive Statistics)と「手元データは母集合から抽出した部分標本に過ぎない」と考える推計統計学(Inferential Statistics)の基本的態度の境界線となってくる訳で、そこに「大数の法則」概念より発展した正規分布の概念が密接に絡んでくる訳です。
記述統計学と推計統計学の違い

相関係数(Correlation Coefficient)から単回帰分析(Simple Regression Analysis)へ。

相関係数の意味と求め方 - 公式と計算例

\begin{align*} r &= \frac{s_{xy}}{s_xs_y} \\[5pt] &= \frac{\frac{1}{n(-1)}\sum_{i=1}^n(x_i-\overline{x})(y_i-\overline{y})}{\sqrt{\frac{1}{n(-1)}\sum_{i=1}^n(x_i-\overline{x})^2}\sqrt{\frac{1}{n(-1)}\sum_{i=1}^n(y_i-\overline{y})^2}} \end{align*}=\frac{\sum_{i=1}^n(x_i-\overline{x})(y_i-\overline{y})}{\sqrt{\sum_{i=1}^n(x_i-\overline{x})^2}\sqrt{\sum_{i=1}^n(y_i-\overline{y})^2}}

相関係数を求めるには、共分散をそれぞれの変数の標準偏差で割ります。
具体的には次の6つのステップで求めます。

①それぞれの変数の平均値を求める。
②それぞれの変数の偏差（数値－平均値）を求める。
③それぞれの変数の分散（偏差の二乗平均）を求める。
④それぞれの変数の標準偏差（分散の正の平方根）を求める。
⑤共分散（偏差の積の平均）を求める。
⑥共分散を2つの変数の標準偏差の積で割って相関係数を得る。

式にもあります様に($\frac{1}{n}$項だろうが$\frac{1}{n-1}$項だろうが最終的に分母と分子で打ち消し合うので)標本相関係数(Sample Correlation Coefficient)と不偏相関係数(Unbiased Correlation Coefficient)は一致します。

import sympy as sp
import numpy as np
import pandas as pd
from scipy import stats

#元データ
#A~Eさんの英語(x)と数学(y)のテスト結果。
x=[50,60,70,80,90]
y=[40,70,90,60,100]
print("データx")
print(x)
print("データy")
print(y)

#①それぞれの変数の平均値を求める。
x_mean=np.mean(x)
print("x平均")
print(x_mean)
y_mean=np.mean(y)
print("y平均")
print(y_mean)

#②それぞれの変数の偏差（数値－平均値）を求める。
x_deviation=x-x_mean
print("x偏差")
print(x_deviation)
y_deviation=y-y_mean
print("y偏差")
print(y_deviation)

#③それぞれの変数の分散（偏差の二乗平均）を求める。
x_sample_var=np.var(x,ddof=0)
x_unbiased_var=np.var(x,ddof=1)
print("x標本分散")
print(x_sample_var)
print("x不偏分散")
print(x_unbiased_var)
y_sample_var=np.var(y,ddof=0)
y_unbiased_var=np.var(y,ddof=1)
print("y標本分散")
print(y_sample_var)
print("y不偏分散")
print(y_unbiased_var)

#④それぞれの変数の標準偏差（分散の正の平方根）を求める。
x_sample_std=np.std(x,ddof=0)
x_unbiased_std=np.std(x,ddof=1)
print("x標本偏差")
print(x_sample_std)
print("x不偏偏差")
print(x_unbiased_std)
y_sample_std=np.std(y,ddof=0)
y_unbiased_std=np.std(y,ddof=1)
print("y標本偏差")
print(y_sample_std)
print("y不偏偏差")
print(y_unbiased_std)

#⑤**共分散**（偏差の積の平均）を求める。
xy_sample_cov=sum(x_deviation*y_deviation)/len(x)
xy_unbiased_cov=sum(x_deviation*y_deviation)/(len(x)-1)
print("xy標本共分散")
print(xy_sample_cov)
print(np.cov(x,y,bias=True))
print("x不偏共分散")
print(xy_unbiased_cov)
print(np.cov(x,y,bias=False))

#⑥共分散を2つの変数の標準偏差の積で割って相関係数を得る。
xy_sample_cor=sum(x_deviation*y_deviation)/len(x)
xy_unbiased_cor=sum(x_deviation*y_deviation)/len(x)
print("xy共分散")
print(np.corrcoef(x,y))

データx
[50, 60, 70, 80, 90]
データy
[40, 70, 90, 60, 100]
x平均
70.0
y平均
72.0
x偏差
[-20. -10.   0.  10.  20.]
y偏差
[-32.  -2.  18. -12.  28.]
x標本分散
200.0
x不偏分散
250.0
y標本分散
456.0
y不偏分散
570.0
x標本偏差
14.142135623730951
x不偏偏差
15.811388300841896
y標本偏差
21.354156504062622
y不偏偏差
23.874672772626646
xy標本共分散
220.0
[[200. 220.]
 [220. 456.]]
x不偏共分散
275.0
[[250. 275.]
 [275. 570.]]
xy共分散
[[1.        0.7284928]
 [0.7284928 1.       ]]

numpy.cov()は共分散行列、numpy.corrcoef()は相関行列を返しますが、これはこう見ます。
[[1つ目のデータと1つ目のデータ, 1つ目のデータと2つ目のデータ],
[2つ目のデータと1つ目のデータ, 2つ目のデータと2つ目のデータ]]

NumPyの共分散を求める関数np.cov関数の使い方
Pythonで相関係数を求める方法を現役エンジニアが解説【初心者向け】

相関係数は−1から1までの値をとり、1であれば2つの変数の値は完全に同期している事になります。対象によって相関係数の意味はかなり変わってきますが、一般的見方は以下。

• −1〜−0.7…強い負の相関
• −0.7〜−0.4…かなりの負の相関
• −0.4〜−0.2…やや負の相関
• −0.2〜0.2…ほとんど相関なし
• 0.2〜0.4…やや正の相関
• 0.4〜0.7…かなりの正の相関
• 0.7〜1…強い正の相関

単なる線形関係ではなく、楕円関数を介した結びつきとなります。
【初心者向け】方形描画関数①三角関数との関係。


背景に固有値と固有ベクトルの概念が存在する?
【Python演算処理】行列演算の基本③パスカルの三角形から二次形式へ

このデータでは「強い正の相関」が検出されたので、さらに最小二乗法(Least Squares Method)による単回帰分析(Simple Regression Analysis)へと進みます。

Numpyだけで回帰分析その4。polyfit()について。

import numpy as np
import matplotlib.pyplot as plt
from scipy import stats

#元データ
#A~Eさんの英語(x)と数学(y)のテスト結果。
xo=[50,60,70,80,90]
yo=[40,70,90,60,100]
print("データx")
print(xo)
print("データy")
print(yo)

#Z得点化
x=stats.zscore(x,ddof=1)
y=stats.zscore(y,ddof=1)
print("データx(標準化)")
print(np.round(x,decimals=3))
print("データy(標準化)")
print(np.round(y,decimals=3))

# 近似線の係数を算出
k = np.polyfit(x, y, 1)
a,b=k
#適当にx軸の両端の値
x_reg = np.array([-1.5, 1.5])
#直線の式を作って配列xを代入
y_reg = a * x_reg + b

plt.scatter(x,y)
plt.plot(x_reg, y_reg, color="red")
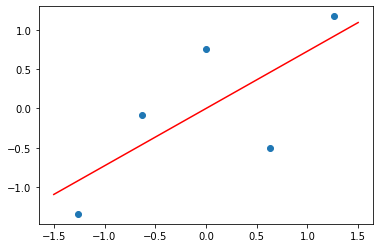
plt.show()

データx
[50, 60, 70, 80, 90]
データy
[40, 70, 90, 60, 100]
データx(標準化)
[-1.265 -0.632 -0.     0.632  1.265]
データy(標準化)
[-1.34  -0.084  0.754 -0.503  1.173]

21世紀は数理モデルの時代?

冒頭に述べた様に「行列」の原語たる「Matrix」には「不換紙幣の如く特定の実体の代替物を超えた何か」なる深淵なニュアンスまで存在するものの、かかる考え方を20世紀末に広めたフランスの思想家ボードリヤールなどは、それほどポジティブな意味では捉えていなかった様なのです。この辺り、同時期広まった「仮想(Virtual)」概念に通じるものがあります。当時はまだまだ「人間の知性は数理を超越して実存する」なる信念が健在だったのです。
仮想とは - IT用語辞典 e-Words

実際、当時その「シニフィエ(Signifié=意味されるもの。当時の流行語の一つ)」の領域は随分と被っていました。惜しくも1980年代末から1990年代にかけては著者高齢化に伴うハイファンタジー小説やTV系サイバーパンク文学の衰退、AI冬の時代の到来を迎え、これに有名なウォシャウスキー姉妹(当時は兄弟)監督映画「マトリックス(Matrix)三部作(1999年~2003年)」の成功が続いた訳ですが、かかる時代をDeep Blue(IBMが開発したチェス専用スーパーコンピュータ)が乗り越え(人間の知性の慎ましい模倣ではなく)ただひたすら「数理モデルの洗練」を目指す第三次AIブームが始まる訳です。
シニフィアンとシニフィエ - Wikipedia
「TV系サイバーパンク」という不思議なジャンル
AI冬の時代とは!？AIの過去と今後について
ディープ・ブルー (コンピュータ) - Wikipedia
ディープラーニング - Wikipedia

ようやくこうした景色の一端まで辿り着く事ができました。次回以降はさらにこの考え方を広げていきたいと思います。