【Python演算処理】行列演算の基本③パスカルの三角形から二次形式へ

【Python演算処理】パスカルの三角形と二項定理または二項展開
この投稿で紹介した乗法公式（式の展開公式）に登場するに乗算式を行列の二次形式で表現すると、それぞれこうなります。
【Python演算処理】行列演算の基本①基本的四則演算と積(Product)

import sympy as sp
a,b = sp.symbols('a,b')
#Rows
x=sp.Matrix([[a,b]])
#Columns
y=sp.Matrix([[a],[b]])
a=sp.Matrix([[1,1],[1,1]])
sp.init_printing()
display(x) 
display(a) 
display(y) 
display(sp.simplify(x*a*y)) 
print(sp.latex(x)+sp.latex(a)+sp.latex(y)+"="+sp.latex(sp.simplify(x*a*y)))

\left[\begin{matrix}a & b\end{matrix}\right]\left[\begin{matrix}1 & 1\\1 & 1\end{matrix}\right]\left[\begin{matrix}a\\b\end{matrix}\right]=\left[\begin{matrix}\left(a + b\right)^{2}\end{matrix}\right]

import sympy as sp
a,b = sp.symbols('a,b')
#Rows
x=sp.Matrix([[a,b]])
#Columns
y=sp.Matrix([[a],[b]])
a=sp.Matrix([[1,-1],[-1,1]])
sp.init_printing()
display(x) 
display(a) 
display(y) 
display(sp.simplify(x*a*y)) 
print(sp.latex(x)+sp.latex(a)+sp.latex(y)+"="+sp.latex(sp.simplify(x*a*y)))

\left[\begin{matrix}a & b\end{matrix}\right]\left[\begin{matrix}1 & -1\\-1 & 1\end{matrix}\right]\left[\begin{matrix}a\\b\end{matrix}\right]=\left[\begin{matrix}\left(a - b\right)^{2}\end{matrix}\right]

import sympy as sp
a,b = sp.symbols('a,b')
#Rows
x=sp.Matrix([[a,b]])
#Columns
y=sp.Matrix([[a],[b]])
a=sp.Matrix([[-1,1],[1,-1]])
sp.init_printing()
display(x) 
display(a) 
display(y) 
display(sp.simplify(x*a*y)) 
print(sp.latex(x)+sp.latex(a)+sp.latex(y)+"="+sp.latex(sp.simplify(x*a*y)))

\left[\begin{matrix}a & b\end{matrix}\right]\left[\begin{matrix}-1 & 1\\1 & -1\end{matrix}\right]\left[\begin{matrix}a\\b\end{matrix}\right]=\left[\begin{matrix}- \left(a - b\right)^{2}\end{matrix}\right]

import sympy as sp
a,b = sp.symbols('a,b')
#Rows
x=sp.Matrix([[a,b]])
#Columns
y=sp.Matrix([[a],[b]])
a=sp.Matrix([[-1,-1],[-1,-1]])
sp.init_printing()
display(x) 
display(a) 
display(y) 
display(sp.simplify(x*a*y)) 
print(sp.latex(x)+sp.latex(a)+sp.latex(y)+"="+sp.latex(sp.simplify(x*a*y)))

\left[\begin{matrix}a & b\end{matrix}\right]\left[\begin{matrix}-1 & -1\\-1 & -1\end{matrix}\right]\left[\begin{matrix}a\\b\end{matrix}\right]=\left[\begin{matrix}- \left(a + b\right)^{2}\end{matrix}\right]

• ここで二次形式行列と二次方程式を結ぶ為に使った「全ての成分が1か-1の行列」をアダマール行列(Hadamard Matrix)という。
  アダマール行列の定義と性質
• しばしば「全ての成分が1か-1のアダマール行列」はスカラーと混同されるが、その背景にはもっと深淵なレベルの数理が横たわっている様にも窺える。
  【Python演算処理】行列演算の基本①基本的四則演算と積

行列から対角角成分のみを抜き出すとこんな感じ。
対角行列 - Wikipedia

import sympy as sp
a,b = sp.symbols('a,b')
#Rows
x=sp.Matrix([[a,b]])
#Columns
y=sp.Matrix([[a],[b]])
a=sp.Matrix([[1,0],[0,1]])
sp.init_printing()
display(x) 
display(a) 
display(y) 
display(sp.simplify(x*a*y)) 
print(sp.latex(x)+sp.latex(a)+sp.latex(y)+"="+sp.latex(sp.simplify(x*a*y)))

\left[\begin{matrix}a & b\end{matrix}\right]\left[\begin{matrix}1 & 0\\0 & 1\end{matrix}\right]\left[\begin{matrix}a\\b\end{matrix}\right]=\left[\begin{matrix}a^{2} + b^{2}\end{matrix}\right]

行列から非対角成分のみを抜き出すとこんな感じ。
交代行列 - Wikipedia

import sympy as sp
a,b = sp.symbols('a,b')
#Rows
x=sp.Matrix([[a,b]])
#Columns
y=sp.Matrix([[a],[b]])
a=sp.Matrix([[0,1],[1,0]])
sp.init_printing()
display(x) 
display(a) 
display(y) 
display(sp.simplify(x*a*y)) 
print(sp.latex(x)+sp.latex(a)+sp.latex(y)+"="+sp.latex(sp.simplify(x*a*y)))

\left[\begin{matrix}a & b\end{matrix}\right]\left[\begin{matrix}0 & 1\\1 & 0\end{matrix}\right]\left[\begin{matrix}a\\b\end{matrix}\right]=\left[\begin{matrix}2 a b\end{matrix}\right]

さて、これらの直感的に思いつく初歩的行列操作にはそれぞれ数理的に一体どんな説明がつくのでしょうか？

#行列操作の基礎①二次形式
まずは二次形式そのものの概念について理解を深めましょう。
二次形式の意味，微分，標準形など
二次形式とは，二次の項のみからなる多項式の事。対称行列A、変数を縦に並べた列ベクトルx、転置記号Tを用いて$x^TAx$なるコンパクトな形で書けます。

import sympy as sp
x1,x2 = sp.symbols('x1,x2')
a=sp.Matrix([[x1],[x2]])
b=a.transpose()
sp.init_printing()
display(a) 
display(b) 
print(sp.latex(a)+"^T="+sp.latex(b))

\left[\begin{matrix}x_{1}\\x_{2}\end{matrix}\right]^T=\left[\begin{matrix}x_{1} & x_{2}\end{matrix}\right]

二次形式における表現

import sympy as sp
a11,a12,a21,a22,x1,x2 = sp.symbols('a11,a12,a21,a22,x1,x2')
a=sp.Matrix([[a11,a12],[a21,a22]])
y=sp.Matrix([[x1],[x2]])
x=y.transpose()
sp.init_printing()
display(x) 
display(a)
display(y)
display(x*a*y)
print(sp.latex(x)+sp.latex(a)+sp.latex(y)+"="+sp.latex(x*a*y))

\left[\begin{matrix}x_{1} & x_{2}\end{matrix}\right]\left[\begin{matrix}a_{11} & a_{12}\\a_{21} & a_{22}\end{matrix}\right]\left[\begin{matrix}x_{1}\\x_{2}\end{matrix}\right]=\left[\begin{matrix}x_{1} \left(a_{11} x_{1} + a_{21} x_{2}\right) + x_{2} \left(a_{12} x_{1} + a_{22} x_{2}\right)\end{matrix}\right]

結果が$3x_1^2-2x_1x_2+3x_2^2$となる代入。

import sympy as sp
a11,a12,a21,a22,x1,x2 = sp.symbols('a11,a12,a21,a22,x1,x2')
a=sp.Matrix([[a11,a12],[a21,a22]])
y=sp.Matrix([[x1],[x2]])
x=y.transpose()
b=a.subs([(a11,3),(a12,-1),(a21,-1),(a22,4)])
sp.init_printing()
display(x) 
display(b)
display(y)
display(x*b*y)
print(sp.latex(x)+sp.latex(b)+sp.latex(y)+"="+sp.latex(x*b*y))

\left[\begin{matrix}x_{1} & x_{2}\end{matrix}\right]\left[\begin{matrix}3 & -1\\-1 & 4\end{matrix}\right]\left[\begin{matrix}x_{1}\\x_{2}\end{matrix}\right]=\left[\begin{matrix}x_{1} \left(3 x_{1} - x_{2}\right) + x_{2} \left(- x_{1} + 4 x_{2}\right)\end{matrix}\right]

シグマ形式における表現

x^TAx=\sum_{i=1}^{n}\sum_{j=1}^{n}A_{ij}x_{i}x_{j}

import sympy as sp
a11,a12,a21,a22,x1,x2= sp.symbols('a11,a12,a21,a22,x1,x2')
i,j,n=sp.symbols('i,j,n', integer = True)
Org=sp.Matrix([[a11,a12],[a21,a22]])
Var=sp.Matrix([[x1*x1,x1*x2],[x1*x2,x2*x2]])
Trg=sp.summation(sp.summation(Org[i,j]*Var[i,j],(j,0,1)),(i,0,1) )
sp.init_printing()
display(Org)
display(Var)
display(Trg)
print("x^TAx="+sp.latex(Trg))

x^TAx=a_{11} x_{1}^{2} + a_{12} x_{1} x_{2} + a_{21} x_{1} x_{2} + a_{22} x_{2}^{2}

結果が$3x_1^2-2x_1x_2+3x_2^2$となる代入。

import sympy as sp
a11,a12,a21,a22,x1,x2= sp.symbols('a11,a12,a21,a22,x1,x2')
i,j,n=sp.symbols('i,j,n', integer = True)
Org0=sp.Matrix([[a11,a12],[a21,a22]])
Org=Org0.subs([(a11,3),(a12,-1),(a21,-1),(a22,4)])
Var=sp.Matrix([[x1*x1,x1*x2],[x1*x2,x2*x2]])
Trg=sp.summation(sp.summation(Org[i,j]*Var[i,j],(j,0,1)),(i,0,1) )
sp.init_printing()
display(Org)
display(Var)
display(Trg)
print("x^TAx="+sp.latex(Trg))

x^TAx=3 x_{1}^{2} - 2 x_{1} x_{2} + 4 x_{2}^{2}

ところで上で$x_1^2+2X_1X_2+X_2^2$に対応する二次形式行列から(マスキング概念の援用で)強引に対角角成分のみを抽出したら$x_1^2+X_2^2$だけが残りました。この様な操作を対角化（Diagonalization）といい、計算の正しい全体像は以下となります。
対角化 - Wikipedia
対角行列 - Wikipedia

import sympy as sp
a11,a12,a21,a22= sp.symbols('a11,a12,a21,a22')
x=sp.Matrix([[a11,a12],[a21,a22]])
x1=x.det()
y1=x.eigenvals()
y2=x.eigenvects()
y3=x.diagonalize()
sp.init_printing()
display(x)
display(x1)
display(y1)
display(y2)
display(y3)  
print(sp.latex(x)+"行列式"+sp.latex(x1)
      +"→"+"固有値"+sp.latex(y1)
      +"固有ベクトル"+sp.latex(y2)
      +"→対角化"+ sp.latex(y3))

\left[\begin{matrix}a_{11} & a_{12}\\a_{21} & a_{22}\end{matrix}\right]行列式a_{11} a_{22} - a_{12} a_{21} \\
→固有値\left\{ \frac{a_{11}}{2} + \frac{a_{22}}{2} - \frac{\sqrt{a_{11}^{2} - 2 a_{11} a_{22} + 4 a_{12} a_{21} + a_{22}^{2}}}{2} : 1, \  \frac{a_{11}}{2} + \frac{a_{22}}{2} + \frac{\sqrt{a_{11}^{2} - 2 a_{11} a_{22} + 4 a_{12} a_{21} + a_{22}^{2}}}{2} : 1\right\} \\
固有ベクトル\left[ \left( \frac{a_{11}}{2} + \frac{a_{22}}{2} - \frac{\sqrt{a_{11}^{2} - 2 a_{11} a_{22} + 4 a_{12} a_{21} + a_{22}^{2}}}{2}, \  1, \  \left[ \left[\begin{matrix}- \frac{2 a_{12}}{a_{11} - a_{22} + \sqrt{a_{11}^{2} - 2 a_{11} a_{22} + 4 a_{12} a_{21} + a_{22}^{2}}}\\1\end{matrix}\right]\right]\right), \  \left( \frac{a_{11}}{2} + \frac{a_{22}}{2} + \frac{\sqrt{a_{11}^{2} - 2 a_{11} a_{22} + 4 a_{12} a_{21} + a_{22}^{2}}}{2}, \  1, \  \left[ \left[\begin{matrix}- \frac{2 a_{12}}{a_{11} - a_{22} - \sqrt{a_{11}^{2} - 2 a_{11} a_{22} + 4 a_{12} a_{21} + a_{22}^{2}}}\\1\end{matrix}\right]\right]\right)\right] \\
→対角化\left( \left[\begin{matrix}- \frac{2 a_{12}}{a_{11} - a_{22} + \sqrt{a_{11}^{2} - 2 a_{11} a_{22} + 4 a_{12} a_{21} + a_{22}^{2}}} & \frac{2 a_{12}}{- a_{11} + a_{22} + \sqrt{a_{11}^{2} - 2 a_{11} a_{22} + 4 a_{12} a_{21} + a_{22}^{2}}}\\1 & 1\end{matrix}\right], \  \left[\begin{matrix}\frac{a_{11}}{2} + \frac{a_{22}}{2} - \frac{\sqrt{a_{11}^{2} - 2 a_{11} a_{22} + 4 a_{12} a_{21} + a_{22}^{2}}}{2} & 0\\0 & \frac{a_{11}}{2} + \frac{a_{22}}{2} + \frac{\sqrt{a_{11}^{2} - 2 a_{11} a_{22} + 4 a_{12} a_{21} + a_{22}^{2}}}{2}\end{matrix}\right]\right)

• 式自体は複雑だが計算自体はコンピューターに任せてしまうものとする。ここで重要なのは「対角化の計算結果は固有ベクトル(列ベクトル=縦ベクトル)を行で連ねた(横に並べた)変換行列と、その変換結果としての固有値を対角線上に並べた対角行列のセットで示される」なる全体イメージの獲得(この考え方の延長線上にジョルダン標準形への変換が現れる)。
• Sympyの出力を見る限り、省略はされているものの、一応以下の場合を自明解として含むっぽい?

\begin{bmatrix}1 & 0\\0 & 1\end{bmatrix}

それでは具体的に以下の行列を代入した結果を求めていきましょう。

\begin{bmatrix}1 & 1\\1 & 1\end{bmatrix}

import sympy as sp
x=sp.Matrix([[1,1],[1,1]])
y1=x.eigenvals()
y2=x.eigenvects()
y3=x.diagonalize()
sp.init_printing()
display(x) 
display(y1)
display(y2)
display(y3)  
print(sp.latex(x)+"→"+"固有値"+sp.latex(y1)+"固有ベクトル"+sp.latex(y2)+"→対角化"+ sp.latex(y3))

\left[\begin{matrix}1 & 1\\1 & 1\end{matrix}\right]行列式0 \\
→固有値\left\{ 0 : 1, \  2 : 1\right\} \\
固有ベクトル\left[ \left( 0, \  1, \  \left[ \left[\begin{matrix}-1\\1\end{matrix}\right]\right]\right), \  \left( 2, \  1, \  \left[ \left[\begin{matrix}1\\1\end{matrix}\right]\right]\right)\right] \\
→対角化\left( \left[\begin{matrix}-1 & 1\\1 & 1\end{matrix}\right], \  \left[\begin{matrix}0 & 0\\0 & 2\end{matrix}\right]\right)

• 行列式の結果が0なのに答えが算出されている。ある種の極限解っぽい？
• どうやらこの辺りに、ずっと悩んできた「偶数系と奇数系の分離」問題の回答も潜んでいるのかもしれない？

偶数系(スカラー)から奇数系への変換行列?:\begin{bmatrix}-1 & 1\\1 & 1\end{bmatrix}\\
その結果現れる奇数系行列?:\begin{bmatrix}0 & 0\\0 & 2\end{bmatrix}

それ以外の行列の代入結果

Pythonで線形代数!固有値と固有ベクトルを求める

\begin{bmatrix}3 & 0\\1 & 2\end{bmatrix}

import sympy as sp
a11,a12,a21,a22= sp.symbols('a11,a12,a21,a22')
x0=sp.Matrix([[a11,a12],[a21,a22]])
x=x0.subs([(a11,3),(a12,0),(a21,1),(a22,2)])
x1=x.det()
y1=x.eigenvals()
y2=x.eigenvects()
y3=x.diagonalize()
sp.init_printing()
display(x)
display(x1)
display(y1)
display(y2)
display(y3)  
print(sp.latex(x)+"行列式"+sp.latex(x1)
      +"→"+"固有値"+sp.latex(y1)
      +"固有ベクトル"+sp.latex(y2)
      +"→対角化"+ sp.latex(y3))

\left[\begin{matrix}3 & 0\\1 & 2\end{matrix}\right]行列式6 \\
→固有値\left\{ 2 : 1, \  3 : 1\right\} \\
固有ベクトル\left[ \left( 2, \  1, \  \left[ \left[\begin{matrix}0\\1\end{matrix}\right]\right]\right), \  \left( 3, \  1, \  \left[ \left[\begin{matrix}1\\1\end{matrix}\right]\right]\right)\right]→ \\
対角化\left( \left[\begin{matrix}0 & 1\\1 & 1\end{matrix}\right], \  \left[\begin{matrix}2 & 0\\0 & 3\end{matrix}\right]\right)

二次形式の意味，微分，標準形など

\begin{bmatrix}3 & -1\\-1 & 3\end{bmatrix}

import sympy as sp
a11,a12,a21,a22= sp.symbols('a11,a12,a21,a22')
x0=sp.Matrix([[a11,a12],[a21,a22]])
x=x0.subs([(a11,3),(a12,-1),(a21,-1),(a22,3)])
x1=x.det()
y1=x.eigenvals()
y2=x.eigenvects()
y3=x.diagonalize()
sp.init_printing()
display(x)
display(x1)
display(y1)
display(y2)
display(y3)  
print(sp.latex(x)+"行列式"+sp.latex(x1)
      +"→"+"固有値"+sp.latex(y1)
      +"固有ベクトル"+sp.latex(y2)
      +"→対角化"+ sp.latex(y3))

\left[\begin{matrix}3 & -1\\-1 & 3\end{matrix}\right]行列式8 \\
→固有値\left\{ 2 : 1, \  4 : 1\right\} \\
固有ベクトル\left[ \left( 2, \  1, \  \left[ \left[\begin{matrix}1\\1\end{matrix}\right]\right]\right), \  \left( 4, \  1, \  \left[ \left[\begin{matrix}-1\\1\end{matrix}\right]\right]\right)\right] \\
→対角化\left( \left[\begin{matrix}1 & -1\\1 & 1\end{matrix}\right], \  \left[\begin{matrix}2 & 0\\0 & 4\end{matrix}\right]\right)

二次形式$3x^2−2xy+3y^2$を以下の様に変数変換します。

\begin{bmatrix}X\\Y\end{bmatrix}=\frac{1}{\sqrt{2}}\begin{bmatrix}1 & 1\\1 & -1\end{bmatrix}\begin{bmatrix}x\\y\end{bmatrix}

すると以下の様にクロスタームがないきれいな二次形式に変換されます。

3x^2−2xy+3y^2 \\
=2(\frac{x}{\sqrt{2}}+\frac{y}{\sqrt{2}})^2+4(\frac{x}{\sqrt{2}}+\frac{y}{\sqrt{2}})^2 \\
=2X^2+4Y^2

平方完成の多変数バージョンです。この様に一般に二次形式$x^TAx$を標準形になおすことは，対称行列Aの対角化に対応します。

対称行列の固有値と固有ベクトルの性質の証明

\begin{bmatrix}5 & 2\\2 & 2\end{bmatrix}

import sympy as sp
a11,a12,a21,a22= sp.symbols('a11,a12,a21,a22')
x0=sp.Matrix([[a11,a12],[a21,a22]])
x=x0.subs([(a11,5),(a12,2),(a21,2),(a22,2)])
x1=x.det()
y1=x.eigenvals()
y2=x.eigenvects()
y3=x.diagonalize()
sp.init_printing()
display(x)
display(x1)
display(y1)
display(y2)
display(y3)  
print(sp.latex(x)+"行列式"+sp.latex(x1)
      +"→"+"固有値"+sp.latex(y1)
      +"固有ベクトル"+sp.latex(y2)
      +"→対角化"+ sp.latex(y3))

\left[\begin{matrix}5 & 2\\2 & 2\end{matrix}\right]行列式6 \\
→固有値\left\{ 1 : 1, \  6 : 1\right\} \\
固有ベクトル\left[ \left( 1, \  1, \  \left[ \left[\begin{matrix}- \frac{1}{2}\\1\end{matrix}\right]\right]\right), \  \left( 6, \  1, \  \left[ \left[\begin{matrix}2\\1\end{matrix}\right]\right]\right)\right] \\
→対角化\left( \left[\begin{matrix}-1 & 2\\2 & 1\end{matrix}\right], \  \left[\begin{matrix}1 & 0\\0 & 6\end{matrix}\right]\right)

固有方程式は$\lambda^2-7\lambda+6=0$なので，固有値は$\lambda=1,6$。

• $\lambda=1$に対応する固有ベクトル

\begin{bmatrix}1\\-2\end{bmatrix}

• $\lambda=6$に対応する固有ベクトル

\begin{bmatrix}2\\1\end{bmatrix}

固有値は実数で，二本の固有ベクトルは直交する！

かくしてここに直交行列(Orthogonal Matrix)の概念が乱入してくる訳です。
直交行列 - Wikipedia

固有値，固有ベクトルの定義と具体的な計算方法

\begin{bmatrix}3&1\\2&2\end{bmatrix}

import sympy as sp
a11,a12,a21,a22= sp.symbols('a11,a12,a21,a22')
x0=sp.Matrix([[a11,a12],[a21,a22]])
x=x0.subs([(a11,3),(a12,1),(a21,2),(a22,2)])
x1=x.det()
y1=x.eigenvals()
y2=x.eigenvects()
y3=x.diagonalize()
sp.init_printing()
display(x)
display(x1)
display(y1)
display(y2)
display(y3)  
print(sp.latex(x)+"行列式"+sp.latex(x1)
      +"→"+"固有値"+sp.latex(y1)
      +"固有ベクトル"+sp.latex(y2)
      +"→対角化"+ sp.latex(y3))

\left[\begin{matrix}3 & 1\\2 & 2\end{matrix}\right]行列式4 \\
→固有値\left\{ 1 : 1, \  4 : 1\right\} \\
固有ベクトル\left[ \left( 1, \  1, \  \left[ \left[\begin{matrix}- \frac{1}{2}\\1\end{matrix}\right]\right]\right), \  \left( 4, \  1, \  \left[ \left[\begin{matrix}1\\1\end{matrix}\right]\right]\right)\right] \\
→対角化\left( \left[\begin{matrix}-1 & 1\\2 & 1\end{matrix}\right], \  \left[\begin{matrix}1 & 0\\0 & 4\end{matrix}\right]\right)

以下の式より出発する。

A-\lambda I=\begin{bmatrix} 3-\lambda & 1\\ 2 & 2-\lambda \end{bmatrix}

これより特性方程式は$(3-\lambda)(2-\lambda)-2=0$。これを解くと$\lambda=1, 4$となり固有値が求まる。

・ $\lambda=1$に対応する固有ベクトルは以下の解である。

(A-I)\overrightarrow{x}=\begin{bmatrix} 2&1\\ 2&1\end{bmatrix}\overrightarrow{x}=0

• よってその固有ベクトルは以下の定数倍と求まる。

\begin{bmatrix}1\\-2\end{bmatrix}

• $\lambda=4λ=4$に対応する固有ベクトルは以下の解である。

(A-4I)\overrightarrow{x}=\begin{bmatrix} -1&1\\ 2&-2\end{bmatrix}

• よってその固有ベクトルは以下の定数倍と求まる。

\begin{bmatrix}1\\1\end{bmatrix}

• なお固有ベクトルで重要なのは向きのみ（長さは自由に決めれる）なので$k\overrightarrow{x}(k\neq 0)$もまたその$\overrightarrow{x}$の固有値$\lambda$に対応する固有ベクトルとなる。
  実際、Sympyの計算には随所に「約分」が見て取れる。

三次以上でも同様です。三次の場合，特性方程式が三次方程式になる＆固有ベクトルを三本求めるために三回連立方程式を解かないといけないのでかなりめんどうですが、各種試験では平気で出題されるのでできるようにしておきましょう。

上記の手順だけでは不十分な場合（AA が対角化できない場合）も稀に登場します。しかし，実際工学的に登場する行列はほとんどが対角化できる＆対角化できない場合を厳密に議論するのはけっこうめんどうなので省略します。特性方程式が重解を持たない場合は問題なしです！

特に重要なのは「対称行列の固有値と固有ベクトルは全て実数でかつ直交する(すなわち直交行列となる)」なる定理っぽい(棒読み)。
ところどころ「Sympyの計算結果」と「説明」の第一列目の向きが反転している様に見えるのだけど、気のせい?

学部1年で習う線形代数の一つの目標は固有値の概念を理解することだと思います。

なるほど、いつの間にかそんな領域まで踏み込んでいたんですね。

Python（SymPy）で学ぶ行列の固有値とJordan標準形

\begin{bmatrix}1&2\\3&2\end{bmatrix}

import sympy as sp
a11,a12,a21,a22= sp.symbols('a11,a12,a21,a22')
x0=sp.Matrix([[a11,a12],[a21,a22]])
x=x0.subs([(a11,1),(a12,2),(a21,3),(a22,2)])
x1=x.det()
y1=x.eigenvals()
y2=x.eigenvects()
y3=x.diagonalize()
sp.init_printing()
display(x)
display(x1)
display(y1)
display(y2)
display(y3)  
print(sp.latex(x)+"行列式"+sp.latex(x1)
      +"→"+"固有値"+sp.latex(y1)
      +"固有ベクトル"+sp.latex(y2)
      +"→対角化"+ sp.latex(y3))

\left[\begin{matrix}1 & 2\\3 & 2\end{matrix}\right]行列式-4  \\
→固有値\left\{ -1 : 1, \  4 : 1\right\} \\
固有ベクトル\left[ \left( -1, \  1, \  \left[ \left[\begin{matrix}-1\\1\end{matrix}\right]\right]\right), \  \left( 4, \  1, \  \left[ \left[\begin{matrix}\frac{2}{3}\\1\end{matrix}\right]\right]\right)\right] \\
→対角化\left( \left[\begin{matrix}-1 & 2\\1 & 3\end{matrix}\right], \  \left[\begin{matrix}-1 & 0\\0 & 4\end{matrix}\right]\right)

この様にn次正方行列に対し、線型独立な固有ベクトルがn個ある場合には行列を対角化することができますが、一般には線形独立な固有ベクトルの個数はnより小さくなります。

\begin{bmatrix}1&-2\\2&5\end{bmatrix}

import sympy as sp
a11,a12,a21,a22= sp.symbols('a11,a12,a21,a22')
x0=sp.Matrix([[a11,a12],[a21,a22]])
x=x0.subs([(a11,1),(a12,2),(a21,-2),(a22,5)])
x1=x.det()
y1=x.eigenvals()
y2=x.eigenvects()
sp.init_printing()
display(x)
display(x1)
display(y1)
display(y2)
print(sp.latex(x)+"行列式"+sp.latex(x1)
      +"→"+"固有値"+sp.latex(y1)
      +"固有ベクトル"+sp.latex(y2))

\left[\begin{matrix}1 & 2\\-2 & 5\end{matrix}\right]行列式9 \\
→固有値\left\{ 3 : 2\right\} \\
固有ベクトル\left[ \left( 3, \  2, \  \left[ \left[\begin{matrix}1\\1\end{matrix}\right]\right]\right)\right]

例えばこの行列は固有値３（縮重度は２）を持ちますが、固有ベクトルが（定数倍の自由度を除いて）ただ一つしかないので正則行列が作れず、行列を対角化することができません。そういう場合も適切な変換行列を用いてジョルダン標準形に変形する事が出来ます。

import sympy as sp
a11,a12,a21,a22= sp.symbols('a11,a12,a21,a22')
x0=sp.Matrix([[a11,a12],[a21,a22]])
x=x0.subs([(a11,1),(a12,2),(a21,-2),(a22,5)])
q=x.jordan_form()
Q=sp.Matrix([[-2,1],[-2,0]])
J=Q.inv()*x*Q
sp.init_printing()
display(x)
print(sp.latex(x))
display(q)
print(sp.latex(q))
display(Q)
print(sp.latex(Q))
display(J)
print(sp.latex(J))

\left[\begin{matrix}1 & 2\\-2 & 5\end{matrix}\right]→\left( \left[\begin{matrix}-2 & 1\\-2 & 0\end{matrix}\right], \  \left[\begin{matrix}3 & 1\\0 & 3\end{matrix}\right]\right) \\
J=\left[\begin{matrix}-2 & 1\\-2 & 0\end{matrix}\right]^{-1}\left[\begin{matrix}1 & 2\\-2 & 5\end{matrix}\right]\left[\begin{matrix}-2 & 1\\-2 & 0\end{matrix}\right]=\left[\begin{matrix}3 & 1\\0 & 3\end{matrix}\right]

Jordan標準形と呼ばれる形をした行列を考えることのメリットの一つとして、その累乗が対角化可能な行列同様に簡単に求められる事が挙げられます。

行列のn乗の求め方と例題

• まずは正方数列Aを対角化する、すなわち$D=P^{-1}AP$,$A=P^{-1}DP$となる変換行列Pと対角行列Dの固有対を求める。

\begin{bmatrix}3&1\\2&2\end{bmatrix}

import sympy as sp
a11,a12,a21,a22= sp.symbols('a11,a12,a21,a22')
x0=sp.Matrix([[a11,a12],[a21,a22]])
x=x0.subs([(a11,3),(a12,1),(a21,2),(a22,2)])
x1=x.det()
y1=x.eigenvals()
y2=x.eigenvects()
y3=x.diagonalize()
sp.init_printing()
display(x)
display(x1)
display(y1)
display(y2)
display(y3)  
print(sp.latex(x)+"行列式"+sp.latex(x1)
      +"→"+"固有値"+sp.latex(y1)
      +"固有ベクトル"+sp.latex(y2)
      +"→対角行化"+ sp.latex(y3))

\left[\begin{matrix}3 & 1\\2 & 2\end{matrix}\right]行列式4 \\
→固有値\left\{ 1 : 1, \  4 : 1\right\} \\
固有ベクトル\left[ \left( 1, \  1, \  \left[ \left[\begin{matrix}- \frac{1}{2}\\1\end{matrix}\right]\right]\right), \  \left( 4, \  1, \  \left[ \left[\begin{matrix}1\\1\end{matrix}\right]\right]\right)\right] \\
→対角行列化\left( \left[\begin{matrix}-1 & 1\\2 & 1\end{matrix}\right], \  \left[\begin{matrix}1 & 0\\0 & 4\end{matrix}\right]\right)

• n乗の計算が大幅に省力化されるが、$A^n=P^{-1}D^nP$を求めると同じ結果となる。

import sympy as sp
a11,a12,a21,a22= sp.symbols('a11,a12,a21,a22')
n=sp.symbols('n', integer = True)
A=sp.Matrix([[3,1],[2,2]])
D=sp.Matrix([[1,0],[0,4]])
P=sp.Matrix([[-1,1],[2,1]])
Pr=P.inv()
sp.init_printing()
display(Pr*D*P)
print("D=P^{-1}AP="+sp.latex(Pr)+sp.latex(A)+sp.latex(P)+"="+sp.latex(D))
display(Pr*A*P)
print("A=P^{-1}DP="+sp.latex(Pr)+sp.latex(D)+sp.latex(P)+"="+sp.latex(A))
display(P)
display(Pr)
display(A**n)
print("A^n="+sp.latex(A**n))
display(P*D**n*Pr) 
print("A^n=P^{-1}D^nP="+sp.latex(Pr)+sp.latex(D**n)+sp.latex(Pr)+"="+sp.latex(P*D**n*Pr))

D=P^{-1}AP=\left[\begin{matrix}- \frac{1}{3} & \frac{1}{3}\\\frac{2}{3} & \frac{1}{3}\end{matrix}\right]\left[\begin{matrix}3 & 1\\2 & 2\end{matrix}\right]\left[\begin{matrix}-1 & 1\\2 & 1\end{matrix}\right]=\left[\begin{matrix}1 & 0\\0 & 4\end{matrix}\right] \\
A=P^{-1}DP=\left[\begin{matrix}- \frac{1}{3} & \frac{1}{3}\\\frac{2}{3} & \frac{1}{3}\end{matrix}\right]\left[\begin{matrix}1 & 0\\0 & 4\end{matrix}\right]\left[\begin{matrix}-1 & 1\\2 & 1\end{matrix}\right]=\left[\begin{matrix}3 & 1\\2 & 2\end{matrix}\right] \\
A^n=\left[\begin{matrix}\frac{2 \cdot 4^{n}}{3} + \frac{1}{3} & \frac{4^{n}}{3} - \frac{1}{3}\\\frac{2 \cdot 4^{n}}{3} - \frac{2}{3} & \frac{4^{n}}{3} + \frac{2}{3}\end{matrix}\right]\\
A^n=P^{-1}D^nP=\left[\begin{matrix}- \frac{1}{3} & \frac{1}{3}\\\frac{2}{3} & \frac{1}{3}\end{matrix}\right]\left[\begin{matrix}1 & 0\\0 & 4^{n}\end{matrix}\right]\left[\begin{matrix}- \frac{1}{3} & \frac{1}{3}\\\frac{2}{3} & \frac{1}{3}\end{matrix}\right]=\left[\begin{matrix}\frac{2 \cdot 4^{n}}{3} + \frac{1}{3} & \frac{4^{n}}{3} - \frac{1}{3}\\\frac{2 \cdot 4^{n}}{3} - \frac{2}{3} & \frac{4^{n}}{3} + \frac{2}{3}\end{matrix}\right]

• 対角化出来ない正方数列Aの場合は$J=Q^{-1}JQ$,$J=Q^{-1}JQ$となる変換行列Qとジョルダン標準形Jの対を求めると同様にn乗の計算が省力化される。

対角化可能な正方行列と異なり$J=Q^{-1}AQ$のみが成立し$A=P^{-1}JP$は成立しない点に注意。

\begin{bmatrix}1&-2\\2&5\end{bmatrix}

import sympy as sp
a11,a12,a21,a22= sp.symbols('a11,a12,a21,a22')
x=sp.Matrix([[a11,a12],[a21,a22]])
A=x.subs([(a11,1),(a12,2),(a21,-2),(a22,5)])
q=A.jordan_form()
Q=sp.Matrix([[-2,1],[-2,0]])
Qr=Q.inv()
J=sp.Matrix([[3,1],[0,3]])
sp.init_printing()
display(q)
print(sp.latex(A)+"→"+sp.latex(q))
display(A)
display(Qr*A*Q)
print("J=Q^{-1}AQ="+sp.latex(Qr)+sp.latex(A)+sp.latex(Q)+"="+sp.latex(Qr*A*Q))
display(Q)
display(Pr)
display(A**n)
print("A^n="+sp.latex(A**n))
display(J**n)
print("J^n="+sp.latex(J**n))

\left[\begin{matrix}1 & 2\\-2 & 5\end{matrix}\right]→\left( \left[\begin{matrix}-2 & 1\\-2 & 0\end{matrix}\right], \  \left[\begin{matrix}3 & 1\\0 & 3\end{matrix}\right]\right) //
J=Q^{-1}AQ=\left[\begin{matrix}0 & - \frac{1}{2}\\1 & -1\end{matrix}\right]\left[\begin{matrix}1 & 2\\-2 & 5\end{matrix}\right]\left[\begin{matrix}-2 & 1\\-2 & 0\end{matrix}\right]=\left[\begin{matrix}3 & 1\\0 & 3\end{matrix}\right] \\
A^n=\left[\begin{matrix}3^{n} - 2 \cdot 3^{n - 1} n & 2 \cdot 3^{n - 1} n\\- 2 \cdot 3^{n - 1} n & 3^{n} + 2 \cdot 3^{n - 1} n\end{matrix}\right] \\
J^n=\left[\begin{matrix}3^{n} & 3^{n - 1} n\\0 & 3^{n}\end{matrix}\right]

そしてどうやらジョルダン標準形への変換は固有空間から広義固有空間への拡大に対応する様なんです？(棒読み)

今こそJordan標準形と向き合う

ベクトル空間上の線形写像は行列によって表現することができる。特に線形変換は線形写像であるから、これも行列によって表現可能である。

行列というのは線形変換をある基底に対して表現したものに過ぎず、基底の取り方によって姿を変え得る。唯一不変なのはその背後にある線形変換Tであり、線形変換を通して行列の振る舞いを考えることがJordan標準形の理解へと繋がる。

Jordan標準形になっていないn次正方行列Bを考える。Bをあるベクトル空間V上の線形変換Tの表現行列であると考えると、これは基底として広義固有ベクトル以外のものを選んだ場合であると解釈できる。これをJordan標準形に変形する事は、基底を広義固有ベクトルに取り替えることを意味する。

結局、線形変換の基底として広義固有ベクトルを選んだ場合の表現行列こそが、Jordan標準形の正体なのである。

おそらくジョルダン標準形への変換では$J=Q^{-1}AQ$のみが成立し$A=P^{-1}JP$は成立しない事と関わってくるのでしょうが、現時点では私の理解可能な範囲を超えています。

それと${}_nC_n=1$が現れるか右端に到達するまで計算を続けるジョルダン細胞(Jordan Block)のn乗の計算方法に何となくパスカルの三角形との関連性が見て取れる気もしますが、この辺りも現時点では私の理解可能な範囲を超えています。
行列のn乗の求め方と例題
ジョルダン標準形の意味と求め方
ジョルダン細胞のn乗 [物理のかぎしっぽ]
ジョルダン細胞とn乗の計算 - 新米夫婦のふたりごと

#行列操作の基礎②二次形式の微分
二次形式の意味，微分，標準形など

二次形式$x^TAxの微分（勾配ベクトル）は2Axとなります。ちなみに勾配ベクトル(Gradient)$\nabla f$とは各変数での微分を並べたベクトルのことです。
勾配ベクトルの意味と例題

$3x_1^2-2x_1x_2+4x_2^2$の場合

• $x_1$で偏微分すると$6x_1-2x_2$。
• $x_2$で偏微分すると$-2x_1+8x_2$。

import sympy as sp
x1,x2 = sp.symbols('x1,x2')

#元関数
f=3*x1**2-2*x1*x2+4*x2**2

#x1について偏微分
g=sp.diff(f,x1,1)

#x2について偏微分
h=sp.diff(f,x2,1)

#画面表示
sp.init_printing()
display(f) 
print(sp.latex(f))
display(g) 
print(sp.latex(g))
display(h) 
print(sp.latex(h))

3 x_{1}^{2} - 2 x_{1} x_{2} + 4 x_{2}^{2}\frac{dy}{dx_1}=6 x_{1} - 2 x_{2}\\
3 x_{1}^{2} - 2 x_{1} x_{2} + 4 x_{2}^{2}\frac{dy}{dx_2}=- 2 x_{1} + 8 x_{2}

よって勾配ベクトルは以下。

\begin{bmatrix}6x_1-2x_2\\-2x_1+8x_2\end{bmatrix}

ところでこの二次方程式に対応する対称行列は以下でした。

\begin{bmatrix}3&-1\\-1&4\end{bmatrix}

よって以下が成立します。

2Ax=2\begin{bmatrix}3&-1\\-1&4\end{bmatrix} \begin{bmatrix}X_1\\x_2\end{bmatrix}

• 具体例で確認しましたが，一般の二次形式の微分が$2Ax$になることも，成分計算で証明できます。
• ちなみに，１変数の場合は「$ax^2$の微分が$2ax$になる」高校数学の微分公式となります。
  【数理考古学】冪乗算(Exponentiation)の微積分

#行列操作の基礎③二次形式と行列のトレース
二次形式の意味，微分，標準形など

二次形式は行列のトレースを用いて$x^{T}Ax=tr(Axx^T)$の形で表現する事も出来ます。統計とかでときどき使う公式です。

import sympy as sp
a11,a12,a21,a22= sp.symbols('a11,a12,a21,a22')
x1,x2= sp.symbols('x1,x2')
A=sp.Matrix([[a11,a12],[a21,a22]])
X=sp.Matrix([[x1],[x2]])
XT=X.transpose()
Trg=A*X*XT
display(A)
print("A="+sp.latex(A))
display(X)
display(XT)
print("X^T="+sp.latex(X)+"^T="+ sp.latex(XT))
display(Trg)
print("tr(AXX^T)=tr("+sp.latex(Trg)+")="+ sp.latex(Trg.trace()))

A=\left[\begin{matrix}a_{11} & a_{12}\\a_{21} & a_{22}\end{matrix}\right] \\
X^T=\left[\begin{matrix}x_{1}\\x_{2}\end{matrix}\right]^T=\left[\begin{matrix}x_{1} & x_{2}\end{matrix}\right] \\
tr(AXX^T)=tr(\left[\begin{matrix}x_{1} \left(a_{11} x_{1} + a_{12} x_{2}\right) & x_{2} \left(a_{11} x_{1} + a_{12} x_{2}\right)\\x_{1} \left(a_{21} x_{1} + a_{22} x_{2}\right) & x_{2} \left(a_{21} x_{1} + a_{22} x_{2}\right)\end{matrix}\right])=x_{1} \left(a_{11} x_{1} + a_{12} x_{2}\right) + x_{2} \left(a_{21} x_{1} + a_{22} x_{2}\right)

統計分野でも行列計算は重要な役割を果たしているのですね。
書評『統計のための行列代数』
詳し内容についての勉強はこれからです。

行列のトレースのいろんな性質とその証明

トレースは正方行列に対して定まる実数で、行列式と並ぶ重要な量ですが行列式と違ってその定義は非常に単純(対角要素の和)です！ それが行列Aの固有値の和になっているのも重要な特徴の一つです。

Aの固有値を\lambda_1,\cdots,\lambda_nとおく。 \\
\mathrm{tr}\:A=\displaystyle\sum_{i=1}^n\lambda_i

実際に計算してみましょう。
これを「非常に単純」と断言する「高校数学の美しい物語」管理人って鬼過ぎじゃなくて？　まぁ「足したら確かに同じ」なんですが…(積分定数が存在する事による)不定積分の「不定性」が定積分では消えてしまうのと同じトリックを感じずにはいられません!!
【数理考古学】冪乗算(Exponentiation)の微積分

\begin{bmatrix}2&4\\-1&3\end{bmatrix}

import sympy as sp
a11,a12,a21,a22= sp.symbols('a11,a12,a21,a22')
x=sp.Matrix([[a11,a12],[a21,a22]])
A=x.subs([(a11,2),(a12,4),(a21,-1),(a22,3)])
T=A.trace()
e=A.eigenvals()
sp.init_printing()
display(A)
display(T)
print("tr("+sp.latex(A)+")="+sp.latex(T))
display(e)
print("固有値"+sp.latex(e))

tr(\left[\begin{matrix}2 & 4\\-1 & 3\end{matrix}\right])=5 \\
固有値\left\{ \frac{5}{2} - \frac{\sqrt{15} i}{2} : 1, \  \frac{5}{2} + \frac{\sqrt{15} i}{2} : 1\right\} \\
(\frac{5}{2} - \frac{\sqrt{15} i}{2})+(\frac{5}{2} + \frac{\sqrt{15} i}{2} )=5

その基本的性質

1． tr(r*A)=r*tr(A) \\
2． tr(A+B)=tr(A)+tr(B) \\
3． tr(A^T)=tr(A) \\
4.tr(AB^T)=sum_{i=1}^n\sum_{j=1}^na_{ij}b_{ij} \\
5.tr(AB)=tr(BA)

1〜3いずれもトレースの定義より明らかです。

• 1と2はトレースの線形性を表しています。
• 3は対角要素が転置によって影響を受けない事に対応します。

4.5は，積ABのトレースの話です。

• 4の右辺は行列Aと行列Bの内積であり，しばしばお目にかかります。サイズ2の場合について実際に計算してみましょう。

import sympy as sp
a11,a12,a21,a22= sp.symbols('a11,a12,a21,a22')
b11,b12,b21,b22= sp.symbols('b11,b12,b21,b22')
i,j=sp.symbols('i,j', integer = True)
A=sp.Matrix([[a11,a12],[a21,a22]])
B=sp.Matrix([[b11,b12],[b21,b22]])
BT=B.transpose()
ABT=A*BT
Trg=sp.summation(sp.summation(A[i,j]*B[i,j],(j,0,1)),(i,0,1) )
display(A)
print("A="+sp.latex(A))
display(B)
display(BT)
print("B^T="+sp.latex(B)+"^T→"+ sp.latex(BT))
display(ABT)
print("AB^T="+sp.latex(ABT))
display(ABT.trace())
display(Trg)
print("tr(AB^T)=\sum_{i=1}^n\sum_{j=1}^na_{ij}b_{ij}="+sp.latex(Trg))

A=\left[\begin{matrix}a_{11} & a_{12}\\a_{21} & a_{22}\end{matrix}\right] \\
B^T=\left[\begin{matrix}b_{11} & b_{12}\\b_{21} & b_{22}\end{matrix}\right]^T→\left[\begin{matrix}b_{11} & b_{21}\\b_{12} & b_{22}\end{matrix}\right] \\
AB^T=\left[\begin{matrix}a_{11} b_{11} + a_{12} b_{12} & a_{11} b_{21} + a_{12} b_{22}\\a_{21} b_{11} + a_{22} b_{12} & a_{21} b_{21} + a_{22} b_{22}\end{matrix}\right] \\
tr(AB^T)=\sum_{i=1}^n\sum_{j=1}^na_{ij}b_{ij}=a_{11} b_{11} + a_{12} b_{12} + a_{21} b_{21} + a_{22} b_{22}

• 5はトレースの交換法則で、4から証明できます。これも重要です！

4よりtr(AB)=\sum_{i=1}^n\sum_{j=1}^na_{ij}b_{ji}=\sum_{i=1}^n\sum_{j=1}^nb_{ij}a_{ji}=tr(BA)

注：3つの積についてtr(ABC)=tr(CAB)=tr(BCA)は成立しますが，tr(ABC)=tr(ACB)などは成立するとは限りません。

#行列操作の基礎④対称行列と反対称行列

対称行列と反対称行列の性質・分解公式
証明はこちらのサイトでご確認ください。

まずは転置操作による分類から出発します。

import sympy as sp
a,b,c,d = sp.symbols('a, b,c,d')
x=sp.Matrix([[a,b],[c,d]])
y=x.transpose()
sp.init_printing()
display(x) 
display(y) 
print(sp.latex(x)+"^T="+sp.latex(y))

\left[\begin{matrix}a & b\\c & d\end{matrix}\right]^T=\left[\begin{matrix}a & c\\b & d\end{matrix}\right]

正方行列Aが対称行列である事は転置すなわち$A^T=A$と表現される。

• 逆を言えば転置しても成分が同じ正方行列が対称行列である。

import sympy as sp
a,b,c,d = sp.symbols('a, b,c,d')
x=sp.Matrix([[a,b],[c,d]])
X=x.subs([(a,1),(b,0),(c,-0),(d,-1)])
y=x.transpose()
Y=X.transpose()
Z=X.inv()
sp.init_printing()
display(X) 
display(Y)
display(Z)
print(sp.latex(X)+"^T="+sp.latex(Y))
print(sp.latex(X)+"^{-1}="+sp.latex(Z))

\left[\begin{matrix}1 & 0\\0 & -1\end{matrix}\right]^T=\left[\begin{matrix}1 & 0\\0 & -1\end{matrix}\right]\\
\left[\begin{matrix}1 & 0\\0 & -1\end{matrix}\right]^{-1}=\left[\begin{matrix}1 & 0\\0 & -1\end{matrix}\right]

この場合、同時に逆行列でもありますが…

正方行列Aが反対称行列である事は転置すなわち$A^T=-A$によって示される。

• 逆を言えば転置によって-1倍される正方行列が反対称行列である。

import sympy as sp
a,b,c,d = sp.symbols('a, b,c,d')
x=sp.Matrix([[a,b],[c,d]])
X=x.subs([(a,0),(b,1),(c,-1),(d,0)])
y=x.transpose()
Y=X.transpose()
Z=X.inv()
sp.init_printing()
display(X) 
display(Y)
display(-Y)
print(sp.latex(X)+"^T="+sp.latex(Y))
print(sp.latex(X)+"*-1="+sp.latex(-Y))

\left[\begin{matrix}0 & 1\\-1 & 0\end{matrix}\right]^T=\left[\begin{matrix}0 & -1\\1 & 0\end{matrix}\right] \\
\left[\begin{matrix}0 & 1\\-1 & 0\end{matrix}\right]*-1=\left[\begin{matrix}0 & 1\\-1 & 0\end{matrix}\right]

そして…

• 反対称行列の対角成分は0である(二乗して0になる数が0しかない)。
• 対称行列かつ反対称行列である行列は零行列に限る(実際には、しばしばスカラーと混同される「全ての成分が同じ値で埋め尽くされたアダマール行列およびそのスカラー倍」も含まれる気もする？)。

また任意の正方行列𝐴は以下の式によって対称行列と反対称行列の和に分解する事が可能であり、かつそれが両者の和に分解する唯一の方法である。

A=\frac{A+A^T}{2}+\frac{A-A^T}{2}

import sympy as sp
a,b,c,d = sp.symbols('a, b,c,d')
x=sp.Matrix([[a,b],[c,d]])
X=x.subs([(a,1),(b,0),(c,-0),(d,1)])
Y=x.subs([(a,0),(b,1),(c,1),(d,0)])
sp.init_printing()
display(X) 
display(Y)
display(X+Y)
print(sp.latex(X)+"+"+sp.latex(Y)+"="+sp.latex(X+Y))

\left[\begin{matrix}1 & 0\\0 & 1\end{matrix}\right]+\left[\begin{matrix}0 & 1\\1 & 0\end{matrix}\right]=\left[\begin{matrix}1 & 1\\1 & 1\end{matrix}\right]

指数関数におけるcosh(x)(カテナリー)とsinh(x)(双曲線関数)の分離、およびその発展形として登場した三角関数における**Cos(θ)とSin(θ)**の分離に際しても活用された登場した概念ですね。
行列・関数・多項式に共通する有名な性質

【初心者向け】指数・対数関数の発見とそれ以降の発展について。

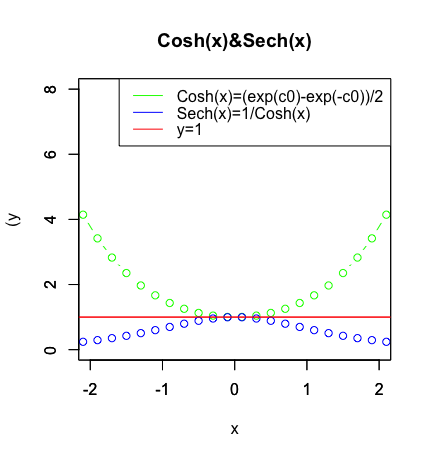
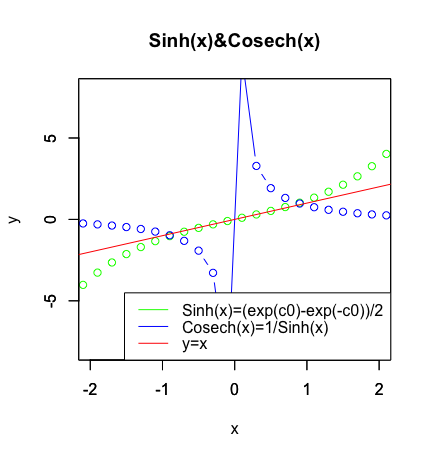
e^{x}=\frac{e^{x}+e^{-x}}{2}+\frac{e^{x}-e^{-x}}{2}

【数理考古学】群論とシミュレーション原理④群導出演算としてのオイラーの公式(Eulerien Formula)

e^{iθ}=\cos(θ)+\sin(θ)i=\frac{e^{θi}+e^{-θi}}{2}+\frac{e^{θi}-e^{-θi}}{2i}

$A^T=-A$となる交代行列（alternating matrix, antisymmetric matrix, skew symmetric matrix=反対称行列，歪対称行列）」は、さらに以下の特徴も備えます。
交代行列の定義と性質

• 実交代行列の固有値は全て実部が0となる。

実対称行列の固有値は，必ず実数である事は別記事で紹介しています。
対称行列の固有値と固有ベクトルの性質の証明
実交代行列にも同様に，固有値に面白い性質があります。実交代行列の固有値は全て実部が0となるのです。実数であることと，虚部が0であることは同値ですから，実対称行列の性質は「固有値の虚部が0である」とも言い換えられます。

もう一つ，交代行列に関する定理を紹介します。交代行列が固有値λを持つとき，-λも固有値になるのです。共役複素数について「実数係数多項式=0という方程式に関してzが解なら$\overline{z}$も解である」という話がありましたが、なんだかそれに似ていますね。
共役複素数の覚えておくべき性質

import sympy as sp
a11,a12,a21,a22= sp.symbols('a11,a12,a21,a22')
x0=sp.Matrix([[a11,a12],[a21,a22]])
x=x0.subs([(a11,0),(a12,-1),(a21,1),(a22,0)])
x1=x.det()
y1=x.eigenvals()
y2=x.eigenvects()
y3=x.diagonalize()
sp.init_printing()
display(x)
display(x1)
display(y1)
display(y2)
display(y3)  
print(sp.latex(x)+"行列式"+sp.latex(x1))
print("→"+"固有値"+sp.latex(y1))
print("固有ベクトル"+sp.latex(y2))
print("→対角化"+ sp.latex(y3))

\left[\begin{matrix}0 & -1\\1 & 0\end{matrix}\right]行列式1 \\
→固有値\left\{ - i : 1, \  i : 1\right\} \\
固有ベクトル\left[ \left( - i, \  1, \  \left[ \left[\begin{matrix}- i\\1\end{matrix}\right]\right]\right), \  \left( i, \  1, \  \left[ \left[\begin{matrix}i\\1\end{matrix}\right]\right]\right)\right] \\
→対角化\left( \left[\begin{matrix}- i & i\\1 & 1\end{matrix}\right], \  \left[\begin{matrix}- i & 0\\0 & i\end{matrix}\right]\right)

確かに交代行列の固有値には虚部しかなく、しかも±対で現れてますね。
#行列操作の基礎⑤直交行列

ところで冒頭と「対称行列と反対称行列の和に分解」に登場した以下の2行列、転置の結果がそれ自身であり(対称行列の特徴)、かつ逆行列(反対称行列)だったりします。

import sympy as sp
a,b,c,d = sp.symbols('a, b,c,d')
x=sp.Matrix([[a,b],[c,d]])
X=x.subs([(a,1),(b,0),(c,-0),(d,1)])
y=x.transpose()
Y=X.transpose()
Z=X.inv()
sp.init_printing()
display(X) 
display(Y)
display(Z)
print(sp.latex(X)+"^T="+sp.latex(Y))
print(sp.latex(X)+"^{-1}="+sp.latex(Z))

\left[\begin{matrix}1 & 0\\0 & 1\end{matrix}\right]^T=\left[\begin{matrix}1 & 0\\0 & 1\end{matrix}\right] \\
\left[\begin{matrix}1 & 0\\0 & 1\end{matrix}\right]^{-1}=\left[\begin{matrix}1 & 0\\0 & 1\end{matrix}\right]

import sympy as sp
a,b,c,d = sp.symbols('a, b,c,d')
x=sp.Matrix([[a,b],[c,d]])
X=x.subs([(a,0),(b,1),(c,1),(d,0)])
y=x.transpose()
Y=X.transpose()
Z=X.inv()
sp.init_printing()
display(X) 
display(Y)
display(Z)
print(sp.latex(X)+"^T="+sp.latex(Y))
print(sp.latex(X)+"^{-1}="+sp.latex(Z))

\left[\begin{matrix}0 & 1\\1 & 0\end{matrix}\right]^T=\left[\begin{matrix}0 & 1\\1 & 0\end{matrix}\right] \\
\left[\begin{matrix}0 & 1\\1 & 0\end{matrix}\right]^{-1}=\left[\begin{matrix}0 & 1\\1 & 0\end{matrix}\right]

要するにこれらは直交行列(Orthogonal Matrix)なのですね。

直交行列の５つの定義と性質の証明

1.$U^T=U^{-1}$
2.Uのn本の行ベクトルが正規直交基底をなす
3.Uのn本の列ベクトルが正規直交基底をなす
4.任意の$x\in \mathbb{R}^n$に対して∥Ux∥=∥x∥
5.任意の$x,y\in\mathbb{R}^n$に対してUx⋅Uy=x⋅y

2.3における「正規直交」とは，全てのベクトルの長さが1で異なる二本のベクトルの内積が 0であることを意味します。
基底 (線型代数学) - Wikipedia
4は「変換でベクトルのノルム（長さ）が変わらない(等長性)」，5は「変換で二つのベクトルの内積が変わらない」ことを表しています。

その性質

• 直交行列の行列式は1または-1である。
• 直交行列の逆行列もまた直交行列である。
• 対称行列は直交行列で対角化できる。

なお

ちなみに「対称行列は直交行列で対角化できる」は、複素数バージョンだと「エルミート行列はユニタリー行列で対角化できる」となります。

import sympy as sp
a11,a12,a21,a22= sp.symbols('a11,a12,a21,a22')
x0=sp.Matrix([[a11,a12],[a21,a22]])
X1=x0.subs([(a11,1),(a12,0),(a21,0),(a22,1)])
X1Det=X1.det()
X1Eval=X1.eigenvals()
X1Evec=X1.eigenvects()
X1Dig=X1.diagonalize()
X2=x0.subs([(a11,0),(a12,1),(a21,1),(a22,0)])
X2Det=X2.det()
X2Eval=X2.eigenvals()
X2Evec=X2.eigenvects()
X2Dig=X2.diagonalize()
sp.init_printing()
display(X1)
display(X1Det)
display(X1Eval)
display(X1Evec)
display(X1Evec)  
display(X1Dig)  
print(sp.latex(X1)+"行列式"+sp.latex(X1Det))
print("→"+"固有値"+sp.latex(X1Eval))
print("固有ベクトル"+sp.latex(X1Evec))
print("→対角化"+ sp.latex(X1Dig))
display(X2)
display(X2Det)
display(X2Eval)
display(X2Evec)
display(X2Evec)
display(X2Dig)
print(sp.latex(X2)+"行列式"+sp.latex(X2Det))
print("→"+"固有値"+sp.latex(X2Eval))
print("固有ベクトル"+sp.latex(X2Evec))
print("→対角化"+ sp.latex(X2Dig))

対角成分

\left[\begin{matrix}1 & 0\\0 & 1\end{matrix}\right]行列式1 \\
→固有値\left\{ 1 : 2\right\} \\
固有ベクトル\left[ \left( 1, \  2, \  \left[ \left[\begin{matrix}1\\0\end{matrix}\right], \  \left[\begin{matrix}0\\1\end{matrix}\right]\right]\right)\right] \\
→対角化\left( \left[\begin{matrix}1 & 0\\0 & 1\end{matrix}\right], \  \left[\begin{matrix}1 & 0\\0 & 1\end{matrix}\right]\right)

反対角成分

\left[\begin{matrix}0 & 1\\1 & 0\end{matrix}\right]行列式-1 \\
→固有値\left\{ -1 : 1, \  1 : 1\right\} \\
固有ベクトル\left[ \left( -1, \  1, \  \left[ \left[\begin{matrix}-1\\1\end{matrix}\right]\right]\right), \  
\left( 1, \  1, \  \left[ \left[\begin{matrix}1\\1\end{matrix}\right]\right]\right)\right] \\
→対角化\left( \left[\begin{matrix}-1 & 1\\1 & 1\end{matrix}\right], \  \left[\begin{matrix}-1 & 0\\0 & 1\end{matrix}\right]\right)

ところでWikipediaに気になる記述があるのです。
直交行列 - Wikipedia

n次直交行列全体の集合をn次直交群といいO(n)と書く。行列式の値が1となる直交行列全体の集合を特殊直交群(Special Orthogonal Matrix)といいSO(n) と書く。

え？　もしかして群論は特殊でない(長さが1でない)直交群も想定してるというの?

#三次形式?

二次形式の意味，微分，標準形など

複素数の二次形式を考えるときはエルミート行列が登場します。三次形式というものも一応あるみたいです。

ここから先は完全に「パスカルの三角形」の世界から離れてしまいます。

import sympy as sp
a,b,c = sp.symbols('a,b,c')
#Rows
x=sp.Matrix([[a,b,c]])
#Columns
y=sp.Matrix([[a],[b],[c]])
a=sp.Matrix([[1,1,1],[1,1,1],[1,1,1]])
sp.init_printing()
display(x) 
display(a) 
display(y) 
display(sp.simplify(x*a*y)) 
print(sp.latex(x)+sp.latex(a)+sp.latex(y)+"="+sp.latex(sp.simplify(x*a*y)))

\left[\begin{matrix}a & b & c\end{matrix}\right]\left[\begin{matrix}1 & 1 & 1\\1 & 1 & 1\\1 & 1 & 1\end{matrix}\right]\left[\begin{matrix}a\\b\\c\end{matrix}\right]=\left[\begin{matrix}\left(a + b + c\right)^{2}\end{matrix}\right]

そんな感じで以下続報…