【初心者向け】平均(Mean)と標準偏差(Standard Deviation)、中央値(Median)と平均偏差(Mean Absolute Deviation)

統計学史上においてはガウス（Carolus Fridericus Gauss、1777年〜1855年）が最小二乗法（least squares method）を発表して以降、平方損失系（平均系）尺度、すなわち正規分布に紐付けられた標本分散（Sample Variance）/不偏分散（Unbiased Variance）/不偏標本分散（Unbiased Sample Variance）および標準偏差（SD=standard deviation）の偏重が続いてきたとされています。
【無限遠点を巡る数理】無限遠点としての正規分布と分散概念の歴史

それでは他にどういう考え方があるのでしょうか？

標準偏差と平均偏差の使い分け

簡単な数値シミュレーションをして、標準偏差と平均偏差が最も小さくなる時の代表値がそれぞれ平均値と中央値になることを確かめてみましょう。

今回の検証ではR言語を使い確率分布からデータをランダムに発生させます。ここで正規分布を採用すると、平均値と中央値のずれがほとんどないと予想できるので、あえて違う確率分布（対数正規分布）を用います。

統計言語Rによる検証

# データの生成
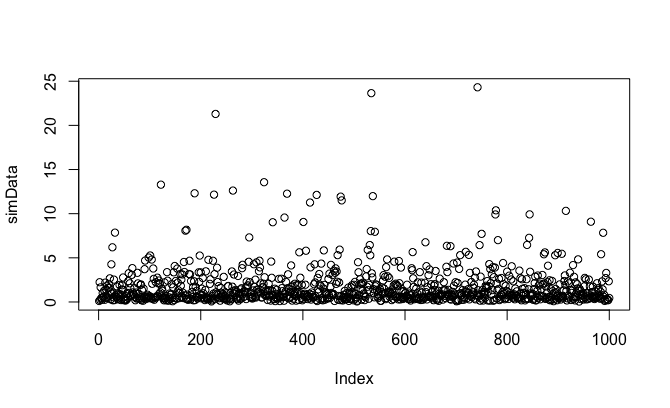
simData <- rlnorm(1000)
plot(simData)

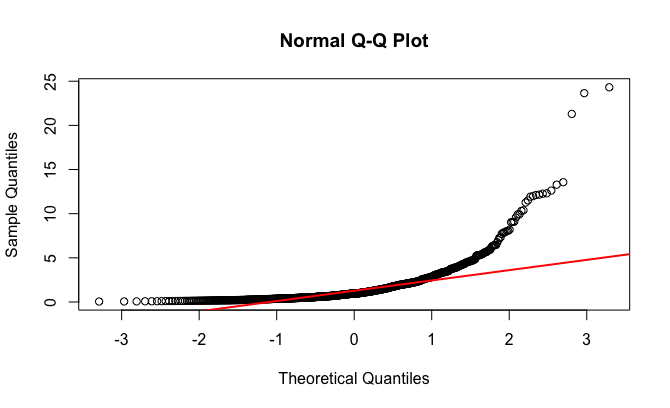
#分布が正規分布と懸け離れている事の確認
qqnorm(simData)
qqline(simData, lwd=2, col="red" )

最低値（Max）と最高値（Min）の計算

生成したデータの最低値と最高値を計算します。最初に最低値を分布の代表値と仮定し、標準偏差と平均偏差をそれぞれ求めます。

次に最低値よりも少しだけ大きな値を代表値とし、データの最大値を代表値とする場合まで次々に繰り返します。

そして最後に、すべての計算結果からいつ標準偏差と平均偏差が最小になるかを調べます。
＊手元のPCで計算してみた時にはminDataは0.04240865、maxDataは65.70159、numIterationは656592となりました。

変数の準備

#最小値と最大値の取得
minData <- min(simData)
minData
[1] 0.05256874
maxData <- max(simData)
maxData
[1] 24.31248

#繰り返しの回数を求める
numIteration<- round((maxData - minData)/0.0001)
numIteration
[1] 242599

SD/ADデータの準備

#計算結果の保存用配列を作成
## 標準偏差用
arrSD <- NULL
## 平均偏差用
arrAD <- NULL

for (i in 1:numIteration){
repData <- minData + 0.0001 * i

resSD <- sqrt(sum((simData - repData)^2)/length(simData))
resAD <- sum(abs(simData - repData))/length(simData)

arrSD <- c(arrSD, resSD)
arrAD <- c(arrAD, resAD)
}

データ後処理

標準偏差と平均偏差を保存したデータの中かからいつ値が最小になったのかを求めます。

シミュレーション本体

# SDが最小となるような代表値
minData + 0.0001 * which.min(arrSD)
[1] 1.708869
# ADが最小となるような代表値
minData + 0.0001 * which.min(arrAD)
[1] 0.9646687

SD/ADが最小となるような代表値

計算の結果、SDが最小となるような代表値は1.708909、ADが最小となるような代表値は0.9827087でした。では、最後にこのデータの平均と中央値を計算してみます。

統計言語Rによる検証

mean(simData)
[1] 1.708847
median(simData)
[1] 0.9662305

最終結論

計算結果は、平均値が1.708862、中央値が0.9834444でした。正確な一致ではありませんが、おおよそ標準偏差が最小となるような代表値は、データの平均値であり、平均偏差が最小となるような代表値はデータの中央値であることがわかります。

とりあえずこういう考え方を学びました。

• おおよそ標準偏差が最小となるような代表値はデータの平均値である。
• おおよそ平均偏差が最小となるような代表値はデータの中央値である。

で、こういう話も。
平均値と中央値の違い

中央値は平均値と異なり外れ値の影響を受けません。この性質のことを「外れ値に対してロバストである（頑健性がある）」と言います。

一方、平均値と中央値が異なる時、分布は平均値より中央値側に偏りが出ます。例えば年収や資産など、お金についてのデータをとると平均値より中央値が低くなることが殆どです。

以下続報…