- (2020年05月02日)初投稿
- (2021年03月以降)Tex,pyrhon部を追加。
冒頭言は内容が古くなったので差し替えます。
【数理考古学】とある実数列の規定例①等差数列から加法整数群へ
【数理考古学】とある実数列の規定例②等比数列から乗法群へ
【数理考古学】とある実数列の規定例③オイラーの等式が意味するもの?
それでは代数方程式(Algebraic Formula)とは何か?
吉田武「オイラーの贈物」「基礎理論(Basic Theory)」より…
実数(Real Number)は有理数と無理数から構成されている。有理数(Rational Number)」とは比(Ratio)で書ける数、整数も含めた広い意味での分数の事であり、無理数(Irrational Number)とはかかる表現が不可能な数をいう。
*こうした立場からすると両者は「有比数」「無比数」と呼ぶのが正しい。
- 式(Formula)において、数や文字の掛け算で表された一つの単位を項(Term)という。また、項の中で注目している文字以外の文字や数を係数(Coefficient)という。
- 一つの項からなる式を単項式(Monomial)」、複数の項からなる式を多項式(Polynomial)」あるいは整式(Integral Expression)」という。
- 二つの多項式の割り算すなわち商(Quotient)」の形で与えられる式を有理式(Rational Expression)あるいは分数式(Fractional Expression)」という。これは数の概念における整数から有理数への拡張の、式の概念に対する敷衍となっている。
- またk個のaの積をa^kと書きaのk乗と読む。このkを指数(Expornent)という。
そレではいよいよ本題の代数方程式(Algebraic Formula)の定義に入ります。
[代数方程式の性質 [物理のかぎしっぽ]]
(http://hooktail.sub.jp/algebra/AlgebraicEq/)
吉田武「オイラーの贈物」「基礎理論(Basic Theory)」より…
数学において公式(Fomura)とは多くの場合恒等式(Identity)を意味するが、その定義は「どの様な値を代入しても両辺が等しくなる」式である。
これに対し「ある特定の値でなければ統合が成立しない式」を方程式(Equatation)と呼び、その値を根(Root)あるいは解(Solution)と言う。
- 求めるべき量を未知数(Unknown)といいx,y,zなどのアルファベット後半の文字を使う。一方、定数値はa,b,cなど前半の文字を使うのが慣例である。
数学でよく使う記号、アルファベット、ギリシャ文字 - 特に未知数が冪(べき、power)による多項式の形式で与えられた方程式を代数方程式(Algebraic Equitation)という。冪は累乗ともいう。未知の指数をその項の次数(Degree)といい、一番大きい次数をもってその方程式の次数という。
【式の計算】 単項式と多項式の次数の数え方 - 大数学者ガウス(C.F.Gauss, 1777年〜1855年
)は「n次代数方程式はn個の根を複素数の範囲に持つ」事を証明した。これは代数学の基本定理と呼ばれている。
代数学の基本定理とその初等的な証明
もっと単純化すると…
未知数xを含む方程式(Formula)f(x)=0には様々な形式があり、このうち代数的演算(Algebraic operations、加減算、乗除算、冪根)を有限回用いて表せるものを代数方程式(Algebraic Formula)という。
# 代数的演算
3+2
[1] 5
3-2
[1] 1
3*2
[1] 6
3/2
[1] 1.5
3^2
[1] 9
# 平方根
sqrt(2)
[1] 1.414214
2^0.5
[1] 1.414214
# 三乗根
2^(1/3)
[1] 1.259921
一次方程式(Equitation of First Degree,Linear Equitation)
吉田武「オイラーの贈物」「基礎理論(Basic Theory)」より…
代数方程式の最も簡単な例はxの一次方程式(Equitation of First Degree,Linear Equitation)ax+b=0である。
xの係数a≠0の時、定数項(Constant Term)を移項(Transposition)し、両辺をaで割って一次方程式の根の公式x=-b/aを得る。
係数a=0で、さらにb=0の時、方程式は不定(Indeterminate)といい、この時根は無数に存在する。b≠0の時は不能(Inconsistent)といい、この場合根は一つも存在しない。
不定(Indeterminate)の場合
xの方程式x*0-0==0を解くとx=xとなる。
Rの場合
library(Ryacas)
yacas("Solve(x*0-0==0,x)")
[1] "{x==x}"
pythonの場合
import sympy
sympy.var('x')
Sol1=sympy.solve (x*0-0==0, x)
sympy.init_printing()
if Sol1==[]:
print("Can't solve!!")
else:
display(Sol1[0])
print(sympy.latex(Sol1[0]))
# 出力
Can't solve!!
不能(Inconsistent)の場合
xの方程式x*0-b=0を解くと{}(解なし)となる。bの値が何であっても結果は変わらない。
library(Ryacas)
yacas("Solve(x*0-b==0,x)")
[1] "{}"
yacas("Solve(x*0-3==0,x)")
[1] "{}"
yacas("Solve(x*0-5==0,x)")
[1] "{}"
pythonの場合
import sympy
sympy.var('x,b')
Sol1=sympy.solve (x*0-b==0, x)
sympy.init_printing()
if Sol1==[]:
print("Can't solve!!")
else:
display(Sol1[0])
print(sympy.latex(Sol1[0]))
# 出力
Can't solve!!
x-2=0の場合
- 左辺の定数項-2を右辺に移項し2とする。
あるいは
- 両辺に2を加える。
どちらも結果はx=2となる。
Rの場合
# 統計言語R(with YACAS)による実行例
library(Ryacas)
yacas("Solve(x-2==0,x)")
Yacas vector:
[1] x == 2
pythonの場合
import sympy
sympy.var('x')
Sol1=sympy.solve (x-2, x)
sympy.init_printing()
if Sol1==[]:
print("Can't solve!!")
else:
display(Sol1[0])
print(sympy.latex(Sol1[0]))
# 出力
2
2
2x+6=0の場合
- 両辺から6を引く。
- 両辺を2で割る。
答えはx=-3となる。
Rの場合
# 統計言語R(with YACAS)による実行例
library(Ryacas)
yacas("Solve(2*x+6==0,x)")
Yacas vector:
[1] x == -3
pythonの場合
import sympy
sympy.var('x')
Sol1=sympy.solve (2*x+6, x)
sympy.init_printing()
if Sol1==[]:
print("Can't solve!!")
else:
display(Sol1[0])
print(sympy.latex(Sol1[0]))
# 出力
-3
-3
二次方程式(Equitation of Second Degree,Quadratic Equitation)
基本中の基本ax^2+bx+c==0の場合
Rの場合
# 統計言語R(with YACAS)による実行例
library(Ryacas)
yac("Solve(a*x^2+b*x+c==0,x)")
[1] "{x==(Sqrt(b^2-4*a*c)-b)/(2*a),x==(-(b+Sqrt(b^2-4*a*c)))/(2*a)}"
pythonの場合
import sympy
sympy.var('x,a,b,c')
Sol1=sympy.solve ((a*x)**2+b*x+c, x)
sympy.init_printing()
if Sol1==[]:
print("Can't solve!!")
else:
for i in Sol1:
display(i)
print(sympy.latex(i))
\frac{- b + \sqrt{- 4 a^{2} c + b^{2}}}{2 a^{2}}\\
- \frac{b + \sqrt{- 4 a^{2} c + b^{2}}}{2 a^{2}}
ax^2-b=0の場合
- ax^2=bに変形。
- x^2=b/aに変形。
- x=±sqrt(b/a)に変形。
よって答えは±sqrt(b/a)の2つとなる。
Rの場合
# 統計言語R(with YACAS)による実行例
library(Ryacas)
yacas("Solve(a*x^2+b==0,x)")
Yacas vector:
[1] x == root(abs(b/a), 2) * complex_cartesian(cos(argument(-(b/a))/2), sin(argument(-(b/a))/2))
[2] x == root(abs(b/a), 2) * complex_cartesian(cos((argument(-(b/a)) + 2 * pi)/2), sin((argument(-(b/a)) + 2 * pi)/2))
pythonの場合
import sympy
sympy.var('x,a,b')
Sol1=sympy.solve (a*x**2+b, x)
sympy.init_printing()
if Sol1==[]:
print("Can't solve!!")
else:
display(Sol1[0])
print(sympy.latex(Sol1[0]))
- \sqrt{- \frac{b}{a}}
2x^2-1=0の場合
- 2x^2=1に変形
- x^2=1/2に変形
- x=±sqrt(1/2)に変形
よって答えは±sqrt(1/2)の2つとなる。
Rの場合
# 統計言語R(with YACAS)による実行例
library(Ryacas)
yacas("Solve(2*x^2-1==0,x)")
Yacas vector:
[1] x == root(1/2, 2) x == -root(1/2, 2)
sqrt(1/2)
[1] 0.7071068
-sqrt(1/2)
[1] -0.7071068
pythonの場合
import sympy
sympy.var('x')
Sol1=sympy.solve (2*x**2-1, x)
sympy.init_printing()
if Sol1==[]:
print("Can't solve!!")
else:
display(Sol1[0])
print(sympy.latex(Sol1[0]))
- \frac{\sqrt{2}}{2}
ただし代数方程式の解き方は1種類とは限りません。
(x+m)^2-n=0の場合
- (x+m)^2=nに変形
- 平方根を取るとx+m=±sqrt(n)
- x=±sqrt(n)-mに変形
よって答えは±sqrt(n)-mの2つとなる。
Rの場合
# 統計言語R(with YACAS)による実行例
library(Ryacas)
yacas("Solve((x+m)^2-n==0,x)")
Yacas vector:
[1] x == (root(4 * m^2 - 4 * (m^2 - n), 2) - 2 * m)/2 x == -(2 * m + root(4 * m^2 - 4 * (m^2 - n), 2))/2
pythonの場合
import sympy
sympy.var('x,m,n')
Sol1=sympy.solve ((x+m)**2-n, x)
sympy.init_printing()
if Sol1==[]:
print("Can't solve!!")
else:
for i in Sol1:
display(i)
print(sympy.latex(i))
- m - \sqrt{n}\\- m + \sqrt{n}
(x+2)^2-3=0の場合
- (x+2)^2=3に変形
- 平方根を取るとx+2=±sqrt(3)
- x=±sqrt(3)-2に変形
よって答えは±sqrt(3)-2の2つとなる。
Rの場合
# 統計言語R(with YACAS)による実行例
library(Ryacas)
yacas("Solve((x+2)^2-3==0,x)")
Yacas vector:
[1] x == (root(12, 2) - 4)/2 x == -(root(12, 2) + 4)/2
# +の場合の解答
sqrt(3)-2
[1] -0.2679492
(sqrt(12)-4)/2
[1] -0.2679492
# -の場合の解答
-(sqrt(3)-2)
[1] 0.2679492
-(sqrt(12)-4)/2
[1] 0.2679492
pythonの場合
import sympy
sympy.var('x')
Sol1=sympy.solve ((x+2)**2-3, x)
sympy.init_printing()
if Sol1==[]:
print("Can't solve!!")
else:
for i in Sol1:
display(i)
print(sympy.latex(i))
-2 - \sqrt{3}\\-2 + \sqrt{3}
ax^2+bx+c=0あるいはax^2+2bx+c=0の場合
以下の根の公式(Root formula<)を使う。
- ax^2+bx+cの場合、x=(-b±sqrt(b^2-4ac))/2a
- ax^2+2bx+cの場合、x=(-b±sqrt(b^2-ac))/a
これは因数分解出来なくても解けるパターンとなる。
Rの場合
# 統計言語R(with YACAS)による実行例
library(Ryacas)
yacas("Solve((a*x)^2+b*x+c==0,x)")
Yacas vector:
[1] x == (root(b^2 - 4 * (a^2 * c), 2) - b)/(2 * a^2) x == -(b + root(b^2 - 4 * (a^2 * c), 2))/(2 * a^2)
yacas("Solve((a*x)^2+2*b*x+c==0,x)")
Yacas vector:
[1] x == (root(4 * b^2 - 4 * (a^2 * c), 2) - 2 * b)/(2 * a^2) x == -(2 * b + root(4 * b^2 - 4 * (a^2 * c), 2))/(2 * a^2)
pythonの場合
import sympy
sympy.var('x,a,b,c')
Sol1=sympy.solve ((a*x)**2+b*x+c, x)
sympy.init_printing()
if Sol1==[]:
print("Can't solve!!")
else:
for i in Sol1:
display(i)
print(sympy.latex(i))
\frac{- b + \sqrt{- 4 a^{2} c + b^{2}}}{2 a^{2}}\\- \frac{b + \sqrt{- 4 a^{2} c + b^{2}}}{2 a^{2}}
結論的にいえば,二次方程式の重解の場合,「1つしかない」のが「解」であり 「同じものが2つある」のが「根」である.
異なる概念を混同しているのが今の高校教科書である.
「根」はrootから来ている言葉だ. 「根」という言葉は今の高校数学では「根号」とか「平方根」というところに残っているだけだ. しかし√という記号はもともとrootのrから来ているのだから, 毎日「根」は使っている.
「根」は「根っこ」であり「大地」である. こんなすばらしい言葉を高校数学から追放した現在の教科書の罪は深い。
x^2-3x+2=0の場合
- 根の公式x=(-b±sqrt(b^2-4ac))/2aから(-(-3)±sqrt((-3)^2-412))/(2*1)=(3±1)/2
よって答えは1と2の2つとなる。
Rの場合
# 統計言語R(with YACAS)による実行例
library(Ryacas)
yacas("Solve(x^2-3*x+2==0,x)")
Yacas vector:
[1] x == 1 x == 2
yacas("Solve((1*x)^2+(-3)*x+2==0,x)")
Yacas vector:
[1] x == 1 x == 2
pythonの場合
import sympy
sympy.var('x,a,b,c')
Sol1=sympy.solve ((a*x)**2+b*x+c, x)
sympy.init_printing()
if Sol1==[]:
print("Can't solve!!")
else:
for i in Sol1:
display(i)
print(sympy.latex(i))
1\\2
因数分解が可能な場合
因数分解を行うにはacx^2+(ad+bc)x+bd=0→(ax+b)(cx+d)=0の関係に注目して定数a,b,c,dを決定する必要がある。具体的には二次方程式の各係数から次の「たすき掛け」関係を満たす値を試行錯誤して発見する。
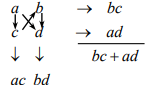
x^2-3x+2=0の例では
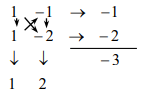
より、a=1,b=-1,c=1,d=-2となり
- x^2-3x+2=(x-1)(b-2)=0
よってx=1 or x=2となる。
Rの場合
# 統計言語R(with YACAS)による実行例
library(Ryacas)
yacas("Factor(x^2-3*x+2)")
expression((x - 2) * (x - 1))
yacas("Simplify((x-2)*(x-1))")
expression(x^2 - 3 * x + 2)
pythonの場合
import sympy
sympy.var('x')
a=sympy.factor(x**2-3*x+2)
b=sympy.simplify(a)
sympy.init_printing()
display(b)
print(sympy.latex(b))
\left(x - 2\right) \left(x - 1\right)
三次方程式(Cubic Equation)
Python (SymPy) で方程式・連立方程式を解く、数列を求める
Rの場合
# 統計言語R(with YACAS)による実行例
library(Ryacas)
yac("Solve(a*x^3+b*x^2+c*x+d==0,x)")
[1] "{x==((9*a*b*c-27*a^2*d-2*b^3)/(54*a^3)+Sqrt(((3*a*c-b^2)/(9*a^2))^3+((9*a*b*c-27*a^2*d-2*b^3)/(54*a^3))^2))^(1/3)+((9*a*b*c-27*a^2*d-2*b^3)/(54*a^3)-Sqrt(((3*a*c-b^2)/(9*a^2))^3+((9*a*b*c-27*a^2*d-2*b^3)/(54*a^3))^2))^(1/3)-b/(3*a),x==Complex(-(b/(3*a)+(((9*a*b*c-27*a^2*d-2*b^3)/(54*a^3)+Sqrt(((3*a*c-b^2)/(9*a^2))^3+((9*a*b*c-27*a^2*d-2*b^3)/(54*a^3))^2))^(1/3)+((9*a*b*c-27*a^2*d-2*b^3)/(54*a^3)-Sqrt(((3*a*c-b^2)/(9*a^2))^3+((9*a*b*c-27*a^2*d-2*b^3)/(54*a^3))^2))^(1/3))/2),Sqrt(3/4)*(((9*a*b*c-27*a^2*d-2*b^3)/(54*a^3)+Sqrt(((3*a*c-b^2)/(9*a^2))^3+((9*a*b*c-27*a^2*d-2*b^3)/(54*a^3))^2))^(1/3)-((9*a*b*c-27*a^2*d-2*b^3)/(54*a^3)-Sqrt(((3*a*c-b^2)/(9*a^2))^3+((9*a*b*c-27*a^2*d-2*b^3)/(54*a^3))^2))^(1/3))),x==Complex(-(b/(3*a)+(((9*a*b*c-27*a^2*d-2*b^3)/(54*a^3)+Sqrt(((3*a*c-b^2)/(9*a^2))^3+((9*a*b*c-27*a^2*d-2*b^3)/(54*a^3))^2))^(1/3)+((9*a*b*c-27*a^2*d-2*b^3)/(54*a^3)-Sqrt(((3*a*c-b^2)/(9*a^2))^3+((9*a*b*c-27*a^2*d-2*b^3)/(54*a^3))^2))^(1/3))/2),-Sqrt(3/4)*(((9*a*b*c-27*a^2*d-2*b^3)/(54*a^3)+Sqrt(((3*a*c-b^2)/(9*a^2))^3+((9*a*b*c-27*a^2*d-2*b^3)/(54*a^3))^2))^(1/3)-((9*a*b*c-27*a^2*d-2*b^3)/(54*a^3)-Sqrt(((3*a*c-b^2)/(9*a^2))^3+((9*a*b*c-27*a^2*d-2*b^3)/(54*a^3))^2))^(1/3)))}"
Pythonの場合
import sympy
sympy.var('x,a,b,c,d')
Sol1=sympy.solve (a*x**3+b*x**2+c*x+d,x)
sympy.init_printing()
if Sol1==[]:
print("Can't solve!!")
else:
for i in Sol1:
display(i)
print(sympy.latex(i))
解1
- \frac{- \frac{3 c}{a} + \frac{b^{2}}{a^{2}}}{3 \sqrt[3]{\frac{\sqrt{- 4 \left(- \frac{3 c}{a} + \frac{b^{2}}{a^{2}}\right)^{3} + \left(\frac{27 d}{a} - \frac{9 b c}{a^{2}} + \frac{2 b^{3}}{a^{3}}\right)^{2}}}{2} + \frac{27 d}{2 a} - \frac{9 b c}{2 a^{2}} + \frac{b^{3}}{a^{3}}}} - \frac{\sqrt[3]{\frac{\sqrt{- 4 \left(- \frac{3 c}{a} + \frac{b^{2}}{a^{2}}\right)^{3} + \left(\frac{27 d}{a} - \frac{9 b c}{a^{2}} + \frac{2 b^{3}}{a^{3}}\right)^{2}}}{2} + \frac{27 d}{2 a} - \frac{9 b c}{2 a^{2}} + \frac{b^{3}}{a^{3}}}}{3} - \frac{b}{3 a}
解2
- \frac{- \frac{3 c}{a} + \frac{b^{2}}{a^{2}}}{3 \left(- \frac{1}{2} - \frac{\sqrt{3} i}{2}\right) \sqrt[3]{\frac{\sqrt{- 4 \left(- \frac{3 c}{a} + \frac{b^{2}}{a^{2}}\right)^{3} + \left(\frac{27 d}{a} - \frac{9 b c}{a^{2}} + \frac{2 b^{3}}{a^{3}}\right)^{2}}}{2} + \frac{27 d}{2 a} - \frac{9 b c}{2 a^{2}} + \frac{b^{3}}{a^{3}}}} - \frac{\left(- \frac{1}{2} - \frac{\sqrt{3} i}{2}\right) \sqrt[3]{\frac{\sqrt{- 4 \left(- \frac{3 c}{a} + \frac{b^{2}}{a^{2}}\right)^{3} + \left(\frac{27 d}{a} - \frac{9 b c}{a^{2}} + \frac{2 b^{3}}{a^{3}}\right)^{2}}}{2} + \frac{27 d}{2 a} - \frac{9 b c}{2 a^{2}} + \frac{b^{3}}{a^{3}}}}{3} - \frac{b}{3 a}
解3
- \frac{- \frac{3 c}{a} + \frac{b^{2}}{a^{2}}}{3 \left(- \frac{1}{2} + \frac{\sqrt{3} i}{2}\right) \sqrt[3]{\frac{\sqrt{- 4 \left(- \frac{3 c}{a} + \frac{b^{2}}{a^{2}}\right)^{3} + \left(\frac{27 d}{a} - \frac{9 b c}{a^{2}} + \frac{2 b^{3}}{a^{3}}\right)^{2}}}{2} + \frac{27 d}{2 a} - \frac{9 b c}{2 a^{2}} + \frac{b^{3}}{a^{3}}}} - \frac{\left(- \frac{1}{2} + \frac{\sqrt{3} i}{2}\right) \sqrt[3]{\frac{\sqrt{- 4 \left(- \frac{3 c}{a} + \frac{b^{2}}{a^{2}}\right)^{3} + \left(\frac{27 d}{a} - \frac{9 b c}{a^{2}} + \frac{2 b^{3}}{a^{3}}\right)^{2}}}{2} + \frac{27 d}{2 a} - \frac{9 b c}{2 a^{2}} + \frac{b^{3}}{a^{3}}}}{3} - \frac{b}{3 a}
四次方程式(Quartic Equation)
Python (SymPy) で方程式・連立方程式を解く、数列を求める
Rの場合
# 統計言語R(with YACAS)による実行例
library(Ryacas)
yac("Solve(a*x^4+b*x^3+c*x^2+d*x+e==0,x)")
[1] "{x==(Sqrt((b/(2*a)+((((((((b*d)/a^2-(4*e)/a)*(-9)*c)/a-27*((4*c*e)/a^2-(d/a)^2-((b/a)^2*e)/a)-2*(-c/a)^3)/54+Sqrt(((3*((b*d)/a^2-(4*e)/a)-(c/a)^2)/9)^3+(((((b*d)/a^2-(4*e)/a)*(-9)*c)/a-27*((4*c*e)/a^2-(d/a)^2-((b/a)^2*e)/a)-2*(-c/a)^3)/54)^2))^(1/3)+(((((b*d)/a^2-(4*e)/a)*(-9)*c)/a-27*((4*c*e)/a^2-(d/a)^2-((b/a)^2*e)/a)-2*(-c/a)^3)/54-Sqrt(((3*((b*d)/a^2-(4*e)/a)-(c/a)^2)/9)^3+(((((b*d)/a^2-(4*e)/a)*(-9)*c)/a-27*((4*c*e)/a^2-(d/a)^2-((b/a)^2*e)/a)-2*(-c/a)^3)/54)^2))^(1/3)+c/(3*a))*b)/a-(2*d)/a)/(4*Sqrt(((((((b*d)/a^2-(4*e)/a)*(-9)*c)/a-27*((4*c*e)/a^2-(d/a)^2-((b/a)^2*e)/a)-2*(-c/a)^3)/54+Sqrt(((3*((b*d)/a^2-(4*e)/a)-(c/a)^2)/9)^3+(((((b*d)/a^2-(4*e)/a)*(-9)*c)/a-27*((4*c*e)/a^2-(d/a)^2-((b/a)^2*e)/a)-2*(-c/a)^3)/54)^2))^(1/3)+(((((b*d)/a^2-(4*e)/a)*(-9)*c)/a-27*((4*c*e)/a^2-(d/a)^2-((b/a)^2*e)/a)-2*(-c/a)^3)/54-Sqrt(((3*((b*d)/a^2-(4*e)/a)-(c/a)^2)/9)^3+(((((b*d)/a^2-(4*e)/a)*(-9)*c)/a-27*((4*c*e)/a^2-(d/a)^2-((b/a)^2*e)/a)-2*(-c/a)^3)/54)^2))^(1/3)+c/(3*a))^2/4-e/a)))^2-4*(((((((b*d)/a^2-(4*e)/a)*(-9)*c)/a-27*((4*c*e)/a^2-(d/a)^2-((b/a)^2*e)/a)-2*(-c/a)^3)/54+Sqrt(((3*((b*d)/a^2-(4*e)/a)-(c/a)^2)/9)^3+(((((b*d)/a^2-(4*e)/a)*(-9)*c)/a-27*((4*c*e)/a^2-(d/a)^2-((b/a)^2*e)/a)-2*(-c/a)^3)/54)^2))^(1/3)+(((((b*d)/a^2-(4*e)/a)*(-9)*c)/a-27*((4*c*e)/a^2-(d/a)^2-((b/a)^2*e)/a)-2*(-c/a)^3)/54-Sqrt(((3*((b*d)/a^2-(4*e)/a)-(c/a)^2)/9)^3+(((((b*d)/a^2-(4*e)/a)*(-9)*c)/a-27*((4*c*e)/a^2-(d/a)^2-((b/a)^2*e)/a)-2*(-c/a)^3)/54)^2))^(1/3)+c/(3*a))/2+Sqrt(((((((b*d)/a^2-(4*e)/a)*(-9)*c)/a-27*((4*c*e)/a^2-(d/a)^2-((b/a)^2*e)/a)-2*(-c/a)^3)/54+Sqrt(((3*((b*d)/a^2-(4*e)/a)-(c/a)^2)/9)^3+(((((b*d)/a^2-(4*e)/a)*(-9)*c)/a-27*((4*c*e)/a^2-(d/a)^2-((b/a)^2*e)/a)-2*(-c/a)^3)/54)^2))^(1/3)+(((((b*d)/a^2-(4*e)/a)*(-9)*c)/a-27*((4*c*e)/a^2-(d/a)^2-((b/a)^2*e)/a)-2*(-c/a)^3)/54-Sqrt(((3*((b*d)/a^2-(4*e)/a)-(c/a)^2)/9)^3+(((((b*d)/a^2-(4*e)/a)*(-9)*c)/a-27*((4*c*e)/a^2-(d/a)^2-((b/a)^2*e)/a)-2*(-c/a)^3)/54)^2))^(1/3)+c/(3*a))^2/4-e/a)))-(b/(2*a)+((((((((b*d)/a^2-(4*e)/a)*(-9)*c)/a-27*((4*c*e)/a^2-(d/a)^2-((b/a)^2*e)/a)-2*(-c/a)^3)/54+Sqrt(((3*((b*d)/a^2-(4*e)/a)-(c/a)^2)/9)^3+(((((b*d)/a^2-(4*e)/a)*(-9)*c)/a-27*((4*c*e)/a^2-(d/a)^2-((b/a)^2*e)/a)-2*(-c/a)^3)/54)^2))^(1/3)+(((((b*d)/a^2-(4*e)/a)*(-9)*c)/a-27*((4*c*e)/a^2-(d/a)^2-((b/a)^2*e)/a)-2*(-c/a)^3)/54-Sqrt(((3*((b*d)/a^2-(4*e)/a)-(c/a)^2)/9)^3+(((((b*d)/a^2-(4*e)/a)*(-9)*c)/a-27*((4*c*e)/a^2-(d/a)^2-((b/a)^2*e)/a)-2*(-c/a)^3)/54)^2))^(1/3)+c/(3*a))*b)/a-(2*d)/a)/(4*Sqrt(((((((b*d)/a^2-(4*e)/a)*(-9)*c)/a-27*((4*c*e)/a^2-(d/a)^2-((b/a)^2*e)/a)-2*(-c/a)^3)/54+Sqrt(((3*((b*d)/a^2-(4*e)/a)-(c/a)^2)/9)^3+(((((b*d)/a^2-(4*e)/a)*(-9)*c)/a-27*((4*c*e)/a^2-(d/a)^2-((b/a)^2*e)/a)-2*(-c/a)^3)/54)^2))^(1/3)+(((((b*d)/a^2-(4*e)/a)*(-9)*c)/a-27*((4*c*e)/a^2-(d/a)^2-((b/a)^2*e)/a)-2*(-c/a)^3)/54-Sqrt(((3*((b*d)/a^2-(4*e)/a)-(c/a)^2)/9)^3+(((((b*d)/a^2-(4*e)/a)*(-9)*c)/a-27*((4*c*e)/a^2-(d/a)^2-((b/a)^2*e)/a)-2*(-c/a)^3)/54)^2))^(1/3)+c/(3*a))^2/4-e/a))))/2,x==(-(b/(2*a)+((((((((b*d)/a^2-(4*e)/a)*(-9)*c)/a-27*((4*c*e)/a^2-(d/a)^2-((b/a)^2*e)/a)-2*(-c/a)^3)/54+Sqrt(((3*((b*d)/a^2-(4*e)/a)-(c/a)^2)/9)^3+(((((b*d)/a^2-(4*e)/a)*(-9)*c)/a-27*((4*c*e)/a^2-(d/a)^2-((b/a)^2*e)/a)-2*(-c/a)^3)/54)^2))^(1/3)+(((((b*d)/a^2-(4*e)/a)*(-9)*c)/a-27*((4*c*e)/a^2-(d/a)^2-((b/a)^2*e)/a)-2*(-c/a)^3)/54-Sqrt(((3*((b*d)/a^2-(4*e)/a)-(c/a)^2)/9)^3+(((((b*d)/a^2-(4*e)/a)*(-9)*c)/a-27*((4*c*e)/a^2-(d/a)^2-((b/a)^2*e)/a)-2*(-c/a)^3)/54)^2))^(1/3)+c/(3*a))*b)/a-(2*d)/a)/(4*Sqrt(((((((b*d)/a^2-(4*e)/a)*(-9)*c)/a-27*((4*c*e)/a^2-(d/a)^2-((b/a)^2*e)/a)-2*(-c/a)^3)/54+Sqrt(((3*((b*d)/a^2-(4*e)/a)-(c/a)^2)/9)^3+(((((b*d)/a^2-(4*e)/a)*(-9)*c)/a-27*((4*c*e)/a^2-(d/a)^2-((b/a)^2*e)/a)-2*(-c/a)^3)/54)^2))^(1/3)+(((((b*d)/a^2-(4*e)/a)*(-9)*c)/a-27*((4*c*e)/a^2-(d/a)^2-((b/a)^2*e)/a)-2*(-c/a)^3)/54-Sqrt(((3*((b*d)/a^2-(4*e)/a)-(c/a)^2)/9)^3+(((((b*d)/a^2-(4*e)/a)*(-9)*c)/a-27*((4*c*e)/a^2-(d/a)^2-((b/a)^2*e)/a)-2*(-c/a)^3)/54)^2))^(1/3)+c/(3*a))^2/4-e/a))+Sqrt((b/(2*a)+((((((((b*d)/a^2-(4*e)/a)*(-9)*c)/a-27*((4*c*e)/a^2-(d/a)^2-((b/a)^2*e)/a)-2*(-c/a)^3)/54+Sqrt(((3*((b*d)/a^2-(4*e)/a)-(c/a)^2)/9)^3+(((((b*d)/a^2-(4*e)/a)*(-9)*c)/a-27*((4*c*e)/a^2-(d/a)^2-((b/a)^2*e)/a)-2*(-c/a)^3)/54)^2))^(1/3)+(((((b*d)/a^2-(4*e)/a)*(-9)*c)/a-27*((4*c*e)/a^2-(d/a)^2-((b/a)^2*e)/a)-2*(-c/a)^3)/54-Sqrt(((3*((b*d)/a^2-(4*e)/a)-(c/a)^2)/9)^3+(((((b*d)/a^2-(4*e)/a)*(-9)*c)/a-27*((4*c*e)/a^2-(d/a)^2-((b/a)^2*e)/a)-2*(-c/a)^3)/54)^2))^(1/3)+c/(3*a))*b)/a-(2*d)/a)/(4*Sqrt(((((((b*d)/a^2-(4*e)/a)*(-9)*c)/a-27*((4*c*e)/a^2-(d/a)^2-((b/a)^2*e)/a)-2*(-c/a)^3)/54+Sqrt(((3*((b*d)/a^2-(4*e)/a)-(c/a)^2)/9)^3+(((((b*d)/a^2-(4*e)/a)*(-9)*c)/a-27*((4*c*e)/a^2-(d/a)^2-((b/a)^2*e)/a)-2*(-c/a)^3)/54)^2))^(1/3)+(((((b*d)/a^2-(4*e)/a)*(-9)*c)/a-27*((4*c*e)/a^2-(d/a)^2-((b/a)^2*e)/a)-2*(-c/a)^3)/54-Sqrt(((3*((b*d)/a^2-(4*e)/a)-(c/a)^2)/9)^3+(((((b*d)/a^2-(4*e)/a)*(-9)*c)/a-27*((4*c*e)/a^2-(d/a)^2-((b/a)^2*e)/a)-2*(-c/a)^3)/54)^2))^(1/3)+c/(3*a))^2/4-e/a)))^2-4*(((((((b*d)/a^2-(4*e)/a)*(-9)*c)/a-27*((4*c*e)/a^2-(d/a)^2-((b/a)^2*e)/a)-2*(-c/a)^3)/54+Sqrt(((3*((b*d)/a^2-(4*e)/a)-(c/a)^2)/9)^3+(((((b*d)/a^2-(4*e)/a)*(-9)*c)/a-27*((4*c*e)/a^2-(d/a)^2-((b/a)^2*e)/a)-2*(-c/a)^3)/54)^2))^(1/3)+(((((b*d)/a^2-(4*e)/a)*(-9)*c)/a-27*((4*c*e)/a^2-(d/a)^2-((b/a)^2*e)/a)-2*(-c/a)^3)/54-Sqrt(((3*((b*d)/a^2-(4*e)/a)-(c/a)^2)/9)^3+(((((b*d)/a^2-(4*e)/a)*(-9)*c)/a-27*((4*c*e)/a^2-(d/a)^2-((b/a)^2*e)/a)-2*(-c/a)^3)/54)^2))^(1/3)+c/(3*a))/2+Sqrt(((((((b*d)/a^2-(4*e)/a)*(-9)*c)/a-27*((4*c*e)/a^2-(d/a)^2-((b/a)^2*e)/a)-2*(-c/a)^3)/54+Sqrt(((3*((b*d)/a^2-(4*e)/a)-(c/a)^2)/9)^3+(((((b*d)/a^2-(4*e)/a)*(-9)*c)/a-27*((4*c*e)/a^2-(d/a)^2-((b/a)^2*e)/a)-2*(-c/a)^3)/54)^2))^(1/3)+(((((b*d)/a^2-(4*e)/a)*(-9)*c)/a-27*((4*c*e)/a^2-(d/a)^2-((b/a)^2*e)/a)-2*(-c/a)^3)/54-Sqrt(((3*((b*d)/a^2-(4*e)/a)-(c/a)^2)/9)^3+(((((b*d)/a^2-(4*e)/a)*(-9)*c)/a-27*((4*c*e)/a^2-(d/a)^2-((b/a)^2*e)/a)-2*(-c/a)^3)/54)^2))^(1/3)+c/(3*a))^2/4-e/a)))))/2,x==(((((((((b*d)/a^2-(4*e)/a)*(-9)*c)/a-27*((4*c*e)/a^2-(d/a)^2-((b/a)^2*e)/a)-2*(-c/a)^3)/54+Sqrt(((3*((b*d)/a^2-(4*e)/a)-(c/a)^2)/9)^3+(((((b*d)/a^2-(4*e)/a)*(-9)*c)/a-27*((4*c*e)/a^2-(d/a)^2-((b/a)^2*e)/a)-2*(-c/a)^3)/54)^2))^(1/3)+(((((b*d)/a^2-(4*e)/a)*(-9)*c)/a-27*((4*c*e)/a^2-(d/a)^2-((b/a)^2*e)/a)-2*(-c/a)^3)/54-Sqrt(((3*((b*d)/a^2-(4*e)/a)-(c/a)^2)/9)^3+(((((b*d)/a^2-(4*e)/a)*(-9)*c)/a-27*((4*c*e)/a^2-(d/a)^2-((b/a)^2*e)/a)-2*(-c/a)^3)/54)^2))^(1/3)+c/(3*a))*b)/a-(2*d)/a)/(4*Sqrt(((((((b*d)/a^2-(4*e)/a)*(-9)*c)/a-27*((4*c*e)/a^2-(d/a)^2-((b/a)^2*e)/a)-2*(-c/a)^3)/54+Sqrt(((3*((b*d)/a^2-(4*e)/a)-(c/a)^2)/9)^3+(((((b*d)/a^2-(4*e)/a)*(-9)*c)/a-27*((4*c*e)/a^2-(d/a)^2-((b/a)^2*e)/a)-2*(-c/a)^3)/54)^2))^(1/3)+(((((b*d)/a^2-(4*e)/a)*(-9)*c)/a-27*((4*c*e)/a^2-(d/a)^2-((b/a)^2*e)/a)-2*(-c/a)^3)/54-Sqrt(((3*((b*d)/a^2-(4*e)/a)-(c/a)^2)/9)^3+(((((b*d)/a^2-(4*e)/a)*(-9)*c)/a-27*((4*c*e)/a^2-(d/a)^2-((b/a)^2*e)/a)-2*(-c/a)^3)/54)^2))^(1/3)+c/(3*a))^2/4-e/a))-b/(2*a)+Sqrt((b/(2*a)-((((((((b*d)/a^2-(4*e)/a)*(-9)*c)/a-27*((4*c*e)/a^2-(d/a)^2-((b/a)^2*e)/a)-2*(-c/a)^3)/54+Sqrt(((3*((b*d)/a^2-(4*e)/a)-(c/a)^2)/9)^3+(((((b*d)/a^2-(4*e)/a)*(-9)*c)/a-27*((4*c*e)/a^2-(d/a)^2-((b/a)^2*e)/a)-2*(-c/a)^3)/54)^2))^(1/3)+(((((b*d)/a^2-(4*e)/a)*(-9)*c)/a-27*((4*c*e)/a^2-(d/a)^2-((b/a)^2*e)/a)-2*(-c/a)^3)/54-Sqrt(((3*((b*d)/a^2-(4*e)/a)-(c/a)^2)/9)^3+(((((b*d)/a^2-(4*e)/a)*(-9)*c)/a-27*((4*c*e)/a^2-(d/a)^2-((b/a)^2*e)/a)-2*(-c/a)^3)/54)^2))^(1/3)+c/(3*a))*b)/a-(2*d)/a)/(4*Sqrt(((((((b*d)/a^2-(4*e)/a)*(-9)*c)/a-27*((4*c*e)/a^2-(d/a)^2-((b/a)^2*e)/a)-2*(-c/a)^3)/54+Sqrt(((3*((b*d)/a^2-(4*e)/a)-(c/a)^2)/9)^3+(((((b*d)/a^2-(4*e)/a)*(-9)*c)/a-27*((4*c*e)/a^2-(d/a)^2-((b/a)^2*e)/a)-2*(-c/a)^3)/54)^2))^(1/3)+(((((b*d)/a^2-(4*e)/a)*(-9)*c)/a-27*((4*c*e)/a^2-(d/a)^2-((b/a)^2*e)/a)-2*(-c/a)^3)/54-Sqrt(((3*((b*d)/a^2-(4*e)/a)-(c/a)^2)/9)^3+(((((b*d)/a^2-(4*e)/a)*(-9)*c)/a-27*((4*c*e)/a^2-(d/a)^2-((b/a)^2*e)/a)-2*(-c/a)^3)/54)^2))^(1/3)+c/(3*a))^2/4-e/a)))^2-4*(((((((b*d)/a^2-(4*e)/a)*(-9)*c)/a-27*((4*c*e)/a^2-(d/a)^2-((b/a)^2*e)/a)-2*(-c/a)^3)/54+Sqrt(((3*((b*d)/a^2-(4*e)/a)-(c/a)^2)/9)^3+(((((b*d)/a^2-(4*e)/a)*(-9)*c)/a-27*((4*c*e)/a^2-(d/a)^2-((b/a)^2*e)/a)-2*(-c/a)^3)/54)^2))^(1/3)+(((((b*d)/a^2-(4*e)/a)*(-9)*c)/a-27*((4*c*e)/a^2-(d/a)^2-((b/a)^2*e)/a)-2*(-c/a)^3)/54-Sqrt(((3*((b*d)/a^2-(4*e)/a)-(c/a)^2)/9)^3+(((((b*d)/a^2-(4*e)/a)*(-9)*c)/a-27*((4*c*e)/a^2-(d/a)^2-((b/a)^2*e)/a)-2*(-c/a)^3)/54)^2))^(1/3)+c/(3*a))/2-Sqrt(((((((b*d)/a^2-(4*e)/a)*(-9)*c)/a-27*((4*c*e)/a^2-(d/a)^2-((b/a)^2*e)/a)-2*(-c/a)^3)/54+Sqrt(((3*((b*d)/a^2-(4*e)/a)-(c/a)^2)/9)^3+(((((b*d)/a^2-(4*e)/a)*(-9)*c)/a-27*((4*c*e)/a^2-(d/a)^2-((b/a)^2*e)/a)-2*(-c/a)^3)/54)^2))^(1/3)+(((((b*d)/a^2-(4*e)/a)*(-9)*c)/a-27*((4*c*e)/a^2-(d/a)^2-((b/a)^2*e)/a)-2*(-c/a)^3)/54-Sqrt(((3*((b*d)/a^2-(4*e)/a)-(c/a)^2)/9)^3+(((((b*d)/a^2-(4*e)/a)*(-9)*c)/a-27*((4*c*e)/a^2-(d/a)^2-((b/a)^2*e)/a)-2*(-c/a)^3)/54)^2))^(1/3)+c/(3*a))^2/4-e/a))))/2,x==(((((((((b*d)/a^2-(4*e)/a)*(-9)*c)/a-27*((4*c*e)/a^2-(d/a)^2-((b/a)^2*e)/a)-2*(-c/a)^3)/54+Sqrt(((3*((b*d)/a^2-(4*e)/a)-(c/a)^2)/9)^3+(((((b*d)/a^2-(4*e)/a)*(-9)*c)/a-27*((4*c*e)/a^2-(d/a)^2-((b/a)^2*e)/a)-2*(-c/a)^3)/54)^2))^(1/3)+(((((b*d)/a^2-(4*e)/a)*(-9)*c)/a-27*((4*c*e)/a^2-(d/a)^2-((b/a)^2*e)/a)-2*(-c/a)^3)/54-Sqrt(((3*((b*d)/a^2-(4*e)/a)-(c/a)^2)/9)^3+(((((b*d)/a^2-(4*e)/a)*(-9)*c)/a-27*((4*c*e)/a^2-(d/a)^2-((b/a)^2*e)/a)-2*(-c/a)^3)/54)^2))^(1/3)+c/(3*a))*b)/a-(2*d)/a)/(4*Sqrt(((((((b*d)/a^2-(4*e)/a)*(-9)*c)/a-27*((4*c*e)/a^2-(d/a)^2-((b/a)^2*e)/a)-2*(-c/a)^3)/54+Sqrt(((3*((b*d)/a^2-(4*e)/a)-(c/a)^2)/9)^3+(((((b*d)/a^2-(4*e)/a)*(-9)*c)/a-27*((4*c*e)/a^2-(d/a)^2-((b/a)^2*e)/a)-2*(-c/a)^3)/54)^2))^(1/3)+(((((b*d)/a^2-(4*e)/a)*(-9)*c)/a-27*((4*c*e)/a^2-(d/a)^2-((b/a)^2*e)/a)-2*(-c/a)^3)/54-Sqrt(((3*((b*d)/a^2-(4*e)/a)-(c/a)^2)/9)^3+(((((b*d)/a^2-(4*e)/a)*(-9)*c)/a-27*((4*c*e)/a^2-(d/a)^2-((b/a)^2*e)/a)-2*(-c/a)^3)/54)^2))^(1/3)+c/(3*a))^2/4-e/a))-b/(2*a)-Sqrt((b/(2*a)-((((((((b*d)/a^2-(4*e)/a)*(-9)*c)/a-27*((4*c*e)/a^2-(d/a)^2-((b/a)^2*e)/a)-2*(-c/a)^3)/54+Sqrt(((3*((b*d)/a^2-(4*e)/a)-(c/a)^2)/9)^3+(((((b*d)/a^2-(4*e)/a)*(-9)*c)/a-27*((4*c*e)/a^2-(d/a)^2-((b/a)^2*e)/a)-2*(-c/a)^3)/54)^2))^(1/3)+(((((b*d)/a^2-(4*e)/a)*(-9)*c)/a-27*((4*c*e)/a^2-(d/a)^2-((b/a)^2*e)/a)-2*(-c/a)^3)/54-Sqrt(((3*((b*d)/a^2-(4*e)/a)-(c/a)^2)/9)^3+(((((b*d)/a^2-(4*e)/a)*(-9)*c)/a-27*((4*c*e)/a^2-(d/a)^2-((b/a)^2*e)/a)-2*(-c/a)^3)/54)^2))^(1/3)+c/(3*a))*b)/a-(2*d)/a)/(4*Sqrt(((((((b*d)/a^2-(4*e)/a)*(-9)*c)/a-27*((4*c*e)/a^2-(d/a)^2-((b/a)^2*e)/a)-2*(-c/a)^3)/54+Sqrt(((3*((b*d)/a^2-(4*e)/a)-(c/a)^2)/9)^3+(((((b*d)/a^2-(4*e)/a)*(-9)*c)/a-27*((4*c*e)/a^2-(d/a)^2-((b/a)^2*e)/a)-2*(-c/a)^3)/54)^2))^(1/3)+(((((b*d)/a^2-(4*e)/a)*(-9)*c)/a-27*((4*c*e)/a^2-(d/a)^2-((b/a)^2*e)/a)-2*(-c/a)^3)/54-Sqrt(((3*((b*d)/a^2-(4*e)/a)-(c/a)^2)/9)^3+(((((b*d)/a^2-(4*e)/a)*(-9)*c)/a-27*((4*c*e)/a^2-(d/a)^2-((b/a)^2*e)/a)-2*(-c/a)^3)/54)^2))^(1/3)+c/(3*a))^2/4-e/a)))^2-4*(((((((b*d)/a^2-(4*e)/a)*(-9)*c)/a-27*((4*c*e)/a^2-(d/a)^2-((b/a)^2*e)/a)-2*(-c/a)^3)/54+Sqrt(((3*((b*d)/a^2-(4*e)/a)-(c/a)^2)/9)^3+(((((b*d)/a^2-(4*e)/a)*(-9)*c)/a-27*((4*c*e)/a^2-(d/a)^2-((b/a)^2*e)/a)-2*(-c/a)^3)/54)^2))^(1/3)+(((((b*d)/a^2-(4*e)/a)*(-9)*c)/a-27*((4*c*e)/a^2-(d/a)^2-((b/a)^2*e)/a)-2*(-c/a)^3)/54-Sqrt(((3*((b*d)/a^2-(4*e)/a)-(c/a)^2)/9)^3+(((((b*d)/a^2-(4*e)/a)*(-9)*c)/a-27*((4*c*e)/a^2-(d/a)^2-((b/a)^2*e)/a)-2*(-c/a)^3)/54)^2))^(1/3)+c/(3*a))/2-Sqrt(((((((b*d)/a^2-(4*e)/a)*(-9)*c)/a-27*((4*c*e)/a^2-(d/a)^2-((b/a)^2*e)/a)-2*(-c/a)^3)/54+Sqrt(((3*((b*d)/a^2-(4*e)/a)-(c/a)^2)/9)^3+(((((b*d)/a^2-(4*e)/a)*(-9)*c)/a-27*((4*c*e)/a^2-(d/a)^2-((b/a)^2*e)/a)-2*(-c/a)^3)/54)^2))^(1/3)+(((((b*d)/a^2-(4*e)/a)*(-9)*c)/a-27*((4*c*e)/a^2-(d/a)^2-((b/a)^2*e)/a)-2*(-c/a)^3)/54-Sqrt(((3*((b*d)/a^2-(4*e)/a)-(c/a)^2)/9)^3+(((((b*d)/a^2-(4*e)/a)*(-9)*c)/a-27*((4*c*e)/a^2-(d/a)^2-((b/a)^2*e)/a)-2*(-c/a)^3)/54)^2))^(1/3)+c/(3*a))^2/4-e/a))))/2}"
Pythonの場合
import sympy
sympy.var('x,a,b,c,d,e')
Sol1=sympy.solve (a*x**4+b*x**3+c*x**2+d*x+e,x)
sympy.init_printing()
if Sol1==[]:
print("Can't solve!!")
else:
for i in Sol1:
#display(i)
print(sympy.latex(i))
解1
\begin{cases} - \frac{\sqrt{- 2 \sqrt[3]{- \frac{\left(\frac{c}{a} - \frac{3 b^{2}}{8 a^{2}}\right)^{3}}{108} + \frac{\left(\frac{c}{a} - \frac{3 b^{2}}{8 a^{2}}\right) \left(- \frac{b \left(\frac{b \left(- \frac{c}{16 a} + \frac{3 b^{2}}{256 a^{2}}\right)}{a} + \frac{d}{4 a}\right)}{a} + \frac{e}{a}\right)}{3} - \frac{\left(\frac{b \left(- \frac{c}{2 a} + \frac{b^{2}}{8 a^{2}}\right)}{a} + \frac{d}{a}\right)^{2}}{8}} - \frac{2 c}{3 a} + \frac{b^{2}}{4 a^{2}}}}{2} - \frac{\sqrt{\frac{\frac{2 b \left(- \frac{c}{2 a} + \frac{b^{2}}{8 a^{2}}\right)}{a} + \frac{2 d}{a}}{\sqrt{- 2 \sqrt[3]{- \frac{\left(\frac{c}{a} - \frac{3 b^{2}}{8 a^{2}}\right)^{3}}{108} + \frac{\left(\frac{c}{a} - \frac{3 b^{2}}{8 a^{2}}\right) \left(- \frac{b \left(\frac{b \left(- \frac{c}{16 a} + \frac{3 b^{2}}{256 a^{2}}\right)}{a} + \frac{d}{4 a}\right)}{a} + \frac{e}{a}\right)}{3} - \frac{\left(\frac{b \left(- \frac{c}{2 a} + \frac{b^{2}}{8 a^{2}}\right)}{a} + \frac{d}{a}\right)^{2}}{8}} - \frac{2 c}{3 a} + \frac{b^{2}}{4 a^{2}}}} + 2 \sqrt[3]{- \frac{\left(\frac{c}{a} - \frac{3 b^{2}}{8 a^{2}}\right)^{3}}{108} + \frac{\left(\frac{c}{a} - \frac{3 b^{2}}{8 a^{2}}\right) \left(- \frac{b \left(\frac{b \left(- \frac{c}{16 a} + \frac{3 b^{2}}{256 a^{2}}\right)}{a} + \frac{d}{4 a}\right)}{a} + \frac{e}{a}\right)}{3} - \frac{\left(\frac{b \left(- \frac{c}{2 a} + \frac{b^{2}}{8 a^{2}}\right)}{a} + \frac{d}{a}\right)^{2}}{8}} - \frac{4 c}{3 a} + \frac{b^{2}}{2 a^{2}}}}{2} - \frac{b}{4 a} & \text{for}\: \frac{\left(\frac{c}{a} - \frac{3 b^{2}}{8 a^{2}}\right)^{2}}{12} - \frac{b \left(\frac{b \left(- \frac{c}{16 a} + \frac{3 b^{2}}{256 a^{2}}\right)}{a} + \frac{d}{4 a}\right)}{a} + \frac{e}{a} = 0 \\- \frac{\sqrt{- \frac{2 \left(- \frac{\left(\frac{c}{a} - \frac{3 b^{2}}{8 a^{2}}\right)^{2}}{12} + \frac{b \left(\frac{b \left(- \frac{c}{16 a} + \frac{3 b^{2}}{256 a^{2}}\right)}{a} + \frac{d}{4 a}\right)}{a} - \frac{e}{a}\right)}{3 \sqrt[3]{\frac{\left(\frac{c}{a} - \frac{3 b^{2}}{8 a^{2}}\right)^{3}}{216} - \frac{\left(\frac{c}{a} - \frac{3 b^{2}}{8 a^{2}}\right) \left(- \frac{b \left(\frac{b \left(- \frac{c}{16 a} + \frac{3 b^{2}}{256 a^{2}}\right)}{a} + \frac{d}{4 a}\right)}{a} + \frac{e}{a}\right)}{6} + \frac{\left(\frac{b \left(- \frac{c}{2 a} + \frac{b^{2}}{8 a^{2}}\right)}{a} + \frac{d}{a}\right)^{2}}{16} + \sqrt{\frac{\left(- \frac{\left(\frac{c}{a} - \frac{3 b^{2}}{8 a^{2}}\right)^{2}}{12} + \frac{b \left(\frac{b \left(- \frac{c}{16 a} + \frac{3 b^{2}}{256 a^{2}}\right)}{a} + \frac{d}{4 a}\right)}{a} - \frac{e}{a}\right)^{3}}{27} + \frac{\left(- \frac{\left(\frac{c}{a} - \frac{3 b^{2}}{8 a^{2}}\right)^{3}}{108} + \frac{\left(\frac{c}{a} - \frac{3 b^{2}}{8 a^{2}}\right) \left(- \frac{b \left(\frac{b \left(- \frac{c}{16 a} + \frac{3 b^{2}}{256 a^{2}}\right)}{a} + \frac{d}{4 a}\right)}{a} + \frac{e}{a}\right)}{3} - \frac{\left(\frac{b \left(- \frac{c}{2 a} + \frac{b^{2}}{8 a^{2}}\right)}{a} + \frac{d}{a}\right)^{2}}{8}\right)^{2}}{4}}}} + 2 \sqrt[3]{\frac{\left(\frac{c}{a} - \frac{3 b^{2}}{8 a^{2}}\right)^{3}}{216} - \frac{\left(\frac{c}{a} - \frac{3 b^{2}}{8 a^{2}}\right) \left(- \frac{b \left(\frac{b \left(- \frac{c}{16 a} + \frac{3 b^{2}}{256 a^{2}}\right)}{a} + \frac{d}{4 a}\right)}{a} + \frac{e}{a}\right)}{6} + \frac{\left(\frac{b \left(- \frac{c}{2 a} + \frac{b^{2}}{8 a^{2}}\right)}{a} + \frac{d}{a}\right)^{2}}{16} + \sqrt{\frac{\left(- \frac{\left(\frac{c}{a} - \frac{3 b^{2}}{8 a^{2}}\right)^{2}}{12} + \frac{b \left(\frac{b \left(- \frac{c}{16 a} + \frac{3 b^{2}}{256 a^{2}}\right)}{a} + \frac{d}{4 a}\right)}{a} - \frac{e}{a}\right)^{3}}{27} + \frac{\left(- \frac{\left(\frac{c}{a} - \frac{3 b^{2}}{8 a^{2}}\right)^{3}}{108} + \frac{\left(\frac{c}{a} - \frac{3 b^{2}}{8 a^{2}}\right) \left(- \frac{b \left(\frac{b \left(- \frac{c}{16 a} + \frac{3 b^{2}}{256 a^{2}}\right)}{a} + \frac{d}{4 a}\right)}{a} + \frac{e}{a}\right)}{3} - \frac{\left(\frac{b \left(- \frac{c}{2 a} + \frac{b^{2}}{8 a^{2}}\right)}{a} + \frac{d}{a}\right)^{2}}{8}\right)^{2}}{4}}} - \frac{2 c}{3 a} + \frac{b^{2}}{4 a^{2}}}}{2} - \frac{\sqrt{\frac{\frac{2 b \left(- \frac{c}{2 a} + \frac{b^{2}}{8 a^{2}}\right)}{a} + \frac{2 d}{a}}{\sqrt{- \frac{2 \left(- \frac{\left(\frac{c}{a} - \frac{3 b^{2}}{8 a^{2}}\right)^{2}}{12} + \frac{b \left(\frac{b \left(- \frac{c}{16 a} + \frac{3 b^{2}}{256 a^{2}}\right)}{a} + \frac{d}{4 a}\right)}{a} - \frac{e}{a}\right)}{3 \sqrt[3]{\frac{\left(\frac{c}{a} - \frac{3 b^{2}}{8 a^{2}}\right)^{3}}{216} - \frac{\left(\frac{c}{a} - \frac{3 b^{2}}{8 a^{2}}\right) \left(- \frac{b \left(\frac{b \left(- \frac{c}{16 a} + \frac{3 b^{2}}{256 a^{2}}\right)}{a} + \frac{d}{4 a}\right)}{a} + \frac{e}{a}\right)}{6} + \frac{\left(\frac{b \left(- \frac{c}{2 a} + \frac{b^{2}}{8 a^{2}}\right)}{a} + \frac{d}{a}\right)^{2}}{16} + \sqrt{\frac{\left(- \frac{\left(\frac{c}{a} - \frac{3 b^{2}}{8 a^{2}}\right)^{2}}{12} + \frac{b \left(\frac{b \left(- \frac{c}{16 a} + \frac{3 b^{2}}{256 a^{2}}\right)}{a} + \frac{d}{4 a}\right)}{a} - \frac{e}{a}\right)^{3}}{27} + \frac{\left(- \frac{\left(\frac{c}{a} - \frac{3 b^{2}}{8 a^{2}}\right)^{3}}{108} + \frac{\left(\frac{c}{a} - \frac{3 b^{2}}{8 a^{2}}\right) \left(- \frac{b \left(\frac{b \left(- \frac{c}{16 a} + \frac{3 b^{2}}{256 a^{2}}\right)}{a} + \frac{d}{4 a}\right)}{a} + \frac{e}{a}\right)}{3} - \frac{\left(\frac{b \left(- \frac{c}{2 a} + \frac{b^{2}}{8 a^{2}}\right)}{a} + \frac{d}{a}\right)^{2}}{8}\right)^{2}}{4}}}} + 2 \sqrt[3]{\frac{\left(\frac{c}{a} - \frac{3 b^{2}}{8 a^{2}}\right)^{3}}{216} - \frac{\left(\frac{c}{a} - \frac{3 b^{2}}{8 a^{2}}\right) \left(- \frac{b \left(\frac{b \left(- \frac{c}{16 a} + \frac{3 b^{2}}{256 a^{2}}\right)}{a} + \frac{d}{4 a}\right)}{a} + \frac{e}{a}\right)}{6} + \frac{\left(\frac{b \left(- \frac{c}{2 a} + \frac{b^{2}}{8 a^{2}}\right)}{a} + \frac{d}{a}\right)^{2}}{16} + \sqrt{\frac{\left(- \frac{\left(\frac{c}{a} - \frac{3 b^{2}}{8 a^{2}}\right)^{2}}{12} + \frac{b \left(\frac{b \left(- \frac{c}{16 a} + \frac{3 b^{2}}{256 a^{2}}\right)}{a} + \frac{d}{4 a}\right)}{a} - \frac{e}{a}\right)^{3}}{27} + \frac{\left(- \frac{\left(\frac{c}{a} - \frac{3 b^{2}}{8 a^{2}}\right)^{3}}{108} + \frac{\left(\frac{c}{a} - \frac{3 b^{2}}{8 a^{2}}\right) \left(- \frac{b \left(\frac{b \left(- \frac{c}{16 a} + \frac{3 b^{2}}{256 a^{2}}\right)}{a} + \frac{d}{4 a}\right)}{a} + \frac{e}{a}\right)}{3} - \frac{\left(\frac{b \left(- \frac{c}{2 a} + \frac{b^{2}}{8 a^{2}}\right)}{a} + \frac{d}{a}\right)^{2}}{8}\right)^{2}}{4}}} - \frac{2 c}{3 a} + \frac{b^{2}}{4 a^{2}}}} + \frac{2 \left(- \frac{\left(\frac{c}{a} - \frac{3 b^{2}}{8 a^{2}}\right)^{2}}{12} + \frac{b \left(\frac{b \left(- \frac{c}{16 a} + \frac{3 b^{2}}{256 a^{2}}\right)}{a} + \frac{d}{4 a}\right)}{a} - \frac{e}{a}\right)}{3 \sqrt[3]{\frac{\left(\frac{c}{a} - \frac{3 b^{2}}{8 a^{2}}\right)^{3}}{216} - \frac{\left(\frac{c}{a} - \frac{3 b^{2}}{8 a^{2}}\right) \left(- \frac{b \left(\frac{b \left(- \frac{c}{16 a} + \frac{3 b^{2}}{256 a^{2}}\right)}{a} + \frac{d}{4 a}\right)}{a} + \frac{e}{a}\right)}{6} + \frac{\left(\frac{b \left(- \frac{c}{2 a} + \frac{b^{2}}{8 a^{2}}\right)}{a} + \frac{d}{a}\right)^{2}}{16} + \sqrt{\frac{\left(- \frac{\left(\frac{c}{a} - \frac{3 b^{2}}{8 a^{2}}\right)^{2}}{12} + \frac{b \left(\frac{b \left(- \frac{c}{16 a} + \frac{3 b^{2}}{256 a^{2}}\right)}{a} + \frac{d}{4 a}\right)}{a} - \frac{e}{a}\right)^{3}}{27} + \frac{\left(- \frac{\left(\frac{c}{a} - \frac{3 b^{2}}{8 a^{2}}\right)^{3}}{108} + \frac{\left(\frac{c}{a} - \frac{3 b^{2}}{8 a^{2}}\right) \left(- \frac{b \left(\frac{b \left(- \frac{c}{16 a} + \frac{3 b^{2}}{256 a^{2}}\right)}{a} + \frac{d}{4 a}\right)}{a} + \frac{e}{a}\right)}{3} - \frac{\left(\frac{b \left(- \frac{c}{2 a} + \frac{b^{2}}{8 a^{2}}\right)}{a} + \frac{d}{a}\right)^{2}}{8}\right)^{2}}{4}}}} - 2 \sqrt[3]{\frac{\left(\frac{c}{a} - \frac{3 b^{2}}{8 a^{2}}\right)^{3}}{216} - \frac{\left(\frac{c}{a} - \frac{3 b^{2}}{8 a^{2}}\right) \left(- \frac{b \left(\frac{b \left(- \frac{c}{16 a} + \frac{3 b^{2}}{256 a^{2}}\right)}{a} + \frac{d}{4 a}\right)}{a} + \frac{e}{a}\right)}{6} + \frac{\left(\frac{b \left(- \frac{c}{2 a} + \frac{b^{2}}{8 a^{2}}\right)}{a} + \frac{d}{a}\right)^{2}}{16} + \sqrt{\frac{\left(- \frac{\left(\frac{c}{a} - \frac{3 b^{2}}{8 a^{2}}\right)^{2}}{12} + \frac{b \left(\frac{b \left(- \frac{c}{16 a} + \frac{3 b^{2}}{256 a^{2}}\right)}{a} + \frac{d}{4 a}\right)}{a} - \frac{e}{a}\right)^{3}}{27} + \frac{\left(- \frac{\left(\frac{c}{a} - \frac{3 b^{2}}{8 a^{2}}\right)^{3}}{108} + \frac{\left(\frac{c}{a} - \frac{3 b^{2}}{8 a^{2}}\right) \left(- \frac{b \left(\frac{b \left(- \frac{c}{16 a} + \frac{3 b^{2}}{256 a^{2}}\right)}{a} + \frac{d}{4 a}\right)}{a} + \frac{e}{a}\right)}{3} - \frac{\left(\frac{b \left(- \frac{c}{2 a} + \frac{b^{2}}{8 a^{2}}\right)}{a} + \frac{d}{a}\right)^{2}}{8}\right)^{2}}{4}}} - \frac{4 c}{3 a} + \frac{b^{2}}{2 a^{2}}}}{2} - \frac{b}{4 a} & \text{otherwise} \end{cases}
\begin{cases} - \frac{\sqrt{- 2 \sqrt[3]{- \frac{\left(\frac{c}{a} - \frac{3 b^{2}}{8 a^{2}}\right)^{3}}{108} + \frac{\left(\frac{c}{a} - \frac{3 b^{2}}{8 a^{2}}\right) \left(- \frac{b \left(\frac{b \left(- \frac{c}{16 a} + \frac{3 b^{2}}{256 a^{2}}\right)}{a} + \frac{d}{4 a}\right)}{a} + \frac{e}{a}\right)}{3} - \frac{\left(\frac{b \left(- \frac{c}{2 a} + \frac{b^{2}}{8 a^{2}}\right)}{a} + \frac{d}{a}\right)^{2}}{8}} - \frac{2 c}{3 a} + \frac{b^{2}}{4 a^{2}}}}{2} + \frac{\sqrt{\frac{\frac{2 b \left(- \frac{c}{2 a} + \frac{b^{2}}{8 a^{2}}\right)}{a} + \frac{2 d}{a}}{\sqrt{- 2 \sqrt[3]{- \frac{\left(\frac{c}{a} - \frac{3 b^{2}}{8 a^{2}}\right)^{3}}{108} + \frac{\left(\frac{c}{a} - \frac{3 b^{2}}{8 a^{2}}\right) \left(- \frac{b \left(\frac{b \left(- \frac{c}{16 a} + \frac{3 b^{2}}{256 a^{2}}\right)}{a} + \frac{d}{4 a}\right)}{a} + \frac{e}{a}\right)}{3} - \frac{\left(\frac{b \left(- \frac{c}{2 a} + \frac{b^{2}}{8 a^{2}}\right)}{a} + \frac{d}{a}\right)^{2}}{8}} - \frac{2 c}{3 a} + \frac{b^{2}}{4 a^{2}}}} + 2 \sqrt[3]{- \frac{\left(\frac{c}{a} - \frac{3 b^{2}}{8 a^{2}}\right)^{3}}{108} + \frac{\left(\frac{c}{a} - \frac{3 b^{2}}{8 a^{2}}\right) \left(- \frac{b \left(\frac{b \left(- \frac{c}{16 a} + \frac{3 b^{2}}{256 a^{2}}\right)}{a} + \frac{d}{4 a}\right)}{a} + \frac{e}{a}\right)}{3} - \frac{\left(\frac{b \left(- \frac{c}{2 a} + \frac{b^{2}}{8 a^{2}}\right)}{a} + \frac{d}{a}\right)^{2}}{8}} - \frac{4 c}{3 a} + \frac{b^{2}}{2 a^{2}}}}{2} - \frac{b}{4 a} & \text{for}\: \frac{\left(\frac{c}{a} - \frac{3 b^{2}}{8 a^{2}}\right)^{2}}{12} - \frac{b \left(\frac{b \left(- \frac{c}{16 a} + \frac{3 b^{2}}{256 a^{2}}\right)}{a} + \frac{d}{4 a}\right)}{a} + \frac{e}{a} = 0 \\- \frac{\sqrt{- \frac{2 \left(- \frac{\left(\frac{c}{a} - \frac{3 b^{2}}{8 a^{2}}\right)^{2}}{12} + \frac{b \left(\frac{b \left(- \frac{c}{16 a} + \frac{3 b^{2}}{256 a^{2}}\right)}{a} + \frac{d}{4 a}\right)}{a} - \frac{e}{a}\right)}{3 \sqrt[3]{\frac{\left(\frac{c}{a} - \frac{3 b^{2}}{8 a^{2}}\right)^{3}}{216} - \frac{\left(\frac{c}{a} - \frac{3 b^{2}}{8 a^{2}}\right) \left(- \frac{b \left(\frac{b \left(- \frac{c}{16 a} + \frac{3 b^{2}}{256 a^{2}}\right)}{a} + \frac{d}{4 a}\right)}{a} + \frac{e}{a}\right)}{6} + \frac{\left(\frac{b \left(- \frac{c}{2 a} + \frac{b^{2}}{8 a^{2}}\right)}{a} + \frac{d}{a}\right)^{2}}{16} + \sqrt{\frac{\left(- \frac{\left(\frac{c}{a} - \frac{3 b^{2}}{8 a^{2}}\right)^{2}}{12} + \frac{b \left(\frac{b \left(- \frac{c}{16 a} + \frac{3 b^{2}}{256 a^{2}}\right)}{a} + \frac{d}{4 a}\right)}{a} - \frac{e}{a}\right)^{3}}{27} + \frac{\left(- \frac{\left(\frac{c}{a} - \frac{3 b^{2}}{8 a^{2}}\right)^{3}}{108} + \frac{\left(\frac{c}{a} - \frac{3 b^{2}}{8 a^{2}}\right) \left(- \frac{b \left(\frac{b \left(- \frac{c}{16 a} + \frac{3 b^{2}}{256 a^{2}}\right)}{a} + \frac{d}{4 a}\right)}{a} + \frac{e}{a}\right)}{3} - \frac{\left(\frac{b \left(- \frac{c}{2 a} + \frac{b^{2}}{8 a^{2}}\right)}{a} + \frac{d}{a}\right)^{2}}{8}\right)^{2}}{4}}}} + 2 \sqrt[3]{\frac{\left(\frac{c}{a} - \frac{3 b^{2}}{8 a^{2}}\right)^{3}}{216} - \frac{\left(\frac{c}{a} - \frac{3 b^{2}}{8 a^{2}}\right) \left(- \frac{b \left(\frac{b \left(- \frac{c}{16 a} + \frac{3 b^{2}}{256 a^{2}}\right)}{a} + \frac{d}{4 a}\right)}{a} + \frac{e}{a}\right)}{6} + \frac{\left(\frac{b \left(- \frac{c}{2 a} + \frac{b^{2}}{8 a^{2}}\right)}{a} + \frac{d}{a}\right)^{2}}{16} + \sqrt{\frac{\left(- \frac{\left(\frac{c}{a} - \frac{3 b^{2}}{8 a^{2}}\right)^{2}}{12} + \frac{b \left(\frac{b \left(- \frac{c}{16 a} + \frac{3 b^{2}}{256 a^{2}}\right)}{a} + \frac{d}{4 a}\right)}{a} - \frac{e}{a}\right)^{3}}{27} + \frac{\left(- \frac{\left(\frac{c}{a} - \frac{3 b^{2}}{8 a^{2}}\right)^{3}}{108} + \frac{\left(\frac{c}{a} - \frac{3 b^{2}}{8 a^{2}}\right) \left(- \frac{b \left(\frac{b \left(- \frac{c}{16 a} + \frac{3 b^{2}}{256 a^{2}}\right)}{a} + \frac{d}{4 a}\right)}{a} + \frac{e}{a}\right)}{3} - \frac{\left(\frac{b \left(- \frac{c}{2 a} + \frac{b^{2}}{8 a^{2}}\right)}{a} + \frac{d}{a}\right)^{2}}{8}\right)^{2}}{4}}} - \frac{2 c}{3 a} + \frac{b^{2}}{4 a^{2}}}}{2} + \frac{\sqrt{\frac{\frac{2 b \left(- \frac{c}{2 a} + \frac{b^{2}}{8 a^{2}}\right)}{a} + \frac{2 d}{a}}{\sqrt{- \frac{2 \left(- \frac{\left(\frac{c}{a} - \frac{3 b^{2}}{8 a^{2}}\right)^{2}}{12} + \frac{b \left(\frac{b \left(- \frac{c}{16 a} + \frac{3 b^{2}}{256 a^{2}}\right)}{a} + \frac{d}{4 a}\right)}{a} - \frac{e}{a}\right)}{3 \sqrt[3]{\frac{\left(\frac{c}{a} - \frac{3 b^{2}}{8 a^{2}}\right)^{3}}{216} - \frac{\left(\frac{c}{a} - \frac{3 b^{2}}{8 a^{2}}\right) \left(- \frac{b \left(\frac{b \left(- \frac{c}{16 a} + \frac{3 b^{2}}{256 a^{2}}\right)}{a} + \frac{d}{4 a}\right)}{a} + \frac{e}{a}\right)}{6} + \frac{\left(\frac{b \left(- \frac{c}{2 a} + \frac{b^{2}}{8 a^{2}}\right)}{a} + \frac{d}{a}\right)^{2}}{16} + \sqrt{\frac{\left(- \frac{\left(\frac{c}{a} - \frac{3 b^{2}}{8 a^{2}}\right)^{2}}{12} + \frac{b \left(\frac{b \left(- \frac{c}{16 a} + \frac{3 b^{2}}{256 a^{2}}\right)}{a} + \frac{d}{4 a}\right)}{a} - \frac{e}{a}\right)^{3}}{27} + \frac{\left(- \frac{\left(\frac{c}{a} - \frac{3 b^{2}}{8 a^{2}}\right)^{3}}{108} + \frac{\left(\frac{c}{a} - \frac{3 b^{2}}{8 a^{2}}\right) \left(- \frac{b \left(\frac{b \left(- \frac{c}{16 a} + \frac{3 b^{2}}{256 a^{2}}\right)}{a} + \frac{d}{4 a}\right)}{a} + \frac{e}{a}\right)}{3} - \frac{\left(\frac{b \left(- \frac{c}{2 a} + \frac{b^{2}}{8 a^{2}}\right)}{a} + \frac{d}{a}\right)^{2}}{8}\right)^{2}}{4}}}} + 2 \sqrt[3]{\frac{\left(\frac{c}{a} - \frac{3 b^{2}}{8 a^{2}}\right)^{3}}{216} - \frac{\left(\frac{c}{a} - \frac{3 b^{2}}{8 a^{2}}\right) \left(- \frac{b \left(\frac{b \left(- \frac{c}{16 a} + \frac{3 b^{2}}{256 a^{2}}\right)}{a} + \frac{d}{4 a}\right)}{a} + \frac{e}{a}\right)}{6} + \frac{\left(\frac{b \left(- \frac{c}{2 a} + \frac{b^{2}}{8 a^{2}}\right)}{a} + \frac{d}{a}\right)^{2}}{16} + \sqrt{\frac{\left(- \frac{\left(\frac{c}{a} - \frac{3 b^{2}}{8 a^{2}}\right)^{2}}{12} + \frac{b \left(\frac{b \left(- \frac{c}{16 a} + \frac{3 b^{2}}{256 a^{2}}\right)}{a} + \frac{d}{4 a}\right)}{a} - \frac{e}{a}\right)^{3}}{27} + \frac{\left(- \frac{\left(\frac{c}{a} - \frac{3 b^{2}}{8 a^{2}}\right)^{3}}{108} + \frac{\left(\frac{c}{a} - \frac{3 b^{2}}{8 a^{2}}\right) \left(- \frac{b \left(\frac{b \left(- \frac{c}{16 a} + \frac{3 b^{2}}{256 a^{2}}\right)}{a} + \frac{d}{4 a}\right)}{a} + \frac{e}{a}\right)}{3} - \frac{\left(\frac{b \left(- \frac{c}{2 a} + \frac{b^{2}}{8 a^{2}}\right)}{a} + \frac{d}{a}\right)^{2}}{8}\right)^{2}}{4}}} - \frac{2 c}{3 a} + \frac{b^{2}}{4 a^{2}}}} + \frac{2 \left(- \frac{\left(\frac{c}{a} - \frac{3 b^{2}}{8 a^{2}}\right)^{2}}{12} + \frac{b \left(\frac{b \left(- \frac{c}{16 a} + \frac{3 b^{2}}{256 a^{2}}\right)}{a} + \frac{d}{4 a}\right)}{a} - \frac{e}{a}\right)}{3 \sqrt[3]{\frac{\left(\frac{c}{a} - \frac{3 b^{2}}{8 a^{2}}\right)^{3}}{216} - \frac{\left(\frac{c}{a} - \frac{3 b^{2}}{8 a^{2}}\right) \left(- \frac{b \left(\frac{b \left(- \frac{c}{16 a} + \frac{3 b^{2}}{256 a^{2}}\right)}{a} + \frac{d}{4 a}\right)}{a} + \frac{e}{a}\right)}{6} + \frac{\left(\frac{b \left(- \frac{c}{2 a} + \frac{b^{2}}{8 a^{2}}\right)}{a} + \frac{d}{a}\right)^{2}}{16} + \sqrt{\frac{\left(- \frac{\left(\frac{c}{a} - \frac{3 b^{2}}{8 a^{2}}\right)^{2}}{12} + \frac{b \left(\frac{b \left(- \frac{c}{16 a} + \frac{3 b^{2}}{256 a^{2}}\right)}{a} + \frac{d}{4 a}\right)}{a} - \frac{e}{a}\right)^{3}}{27} + \frac{\left(- \frac{\left(\frac{c}{a} - \frac{3 b^{2}}{8 a^{2}}\right)^{3}}{108} + \frac{\left(\frac{c}{a} - \frac{3 b^{2}}{8 a^{2}}\right) \left(- \frac{b \left(\frac{b \left(- \frac{c}{16 a} + \frac{3 b^{2}}{256 a^{2}}\right)}{a} + \frac{d}{4 a}\right)}{a} + \frac{e}{a}\right)}{3} - \frac{\left(\frac{b \left(- \frac{c}{2 a} + \frac{b^{2}}{8 a^{2}}\right)}{a} + \frac{d}{a}\right)^{2}}{8}\right)^{2}}{4}}}} - 2 \sqrt[3]{\frac{\left(\frac{c}{a} - \frac{3 b^{2}}{8 a^{2}}\right)^{3}}{216} - \frac{\left(\frac{c}{a} - \frac{3 b^{2}}{8 a^{2}}\right) \left(- \frac{b \left(\frac{b \left(- \frac{c}{16 a} + \frac{3 b^{2}}{256 a^{2}}\right)}{a} + \frac{d}{4 a}\right)}{a} + \frac{e}{a}\right)}{6} + \frac{\left(\frac{b \left(- \frac{c}{2 a} + \frac{b^{2}}{8 a^{2}}\right)}{a} + \frac{d}{a}\right)^{2}}{16} + \sqrt{\frac{\left(- \frac{\left(\frac{c}{a} - \frac{3 b^{2}}{8 a^{2}}\right)^{2}}{12} + \frac{b \left(\frac{b \left(- \frac{c}{16 a} + \frac{3 b^{2}}{256 a^{2}}\right)}{a} + \frac{d}{4 a}\right)}{a} - \frac{e}{a}\right)^{3}}{27} + \frac{\left(- \frac{\left(\frac{c}{a} - \frac{3 b^{2}}{8 a^{2}}\right)^{3}}{108} + \frac{\left(\frac{c}{a} - \frac{3 b^{2}}{8 a^{2}}\right) \left(- \frac{b \left(\frac{b \left(- \frac{c}{16 a} + \frac{3 b^{2}}{256 a^{2}}\right)}{a} + \frac{d}{4 a}\right)}{a} + \frac{e}{a}\right)}{3} - \frac{\left(\frac{b \left(- \frac{c}{2 a} + \frac{b^{2}}{8 a^{2}}\right)}{a} + \frac{d}{a}\right)^{2}}{8}\right)^{2}}{4}}} - \frac{4 c}{3 a} + \frac{b^{2}}{2 a^{2}}}}{2} - \frac{b}{4 a} & \text{otherwise} \end{cases}
\begin{cases} \frac{\sqrt{- 2 \sqrt[3]{- \frac{\left(\frac{c}{a} - \frac{3 b^{2}}{8 a^{2}}\right)^{3}}{108} + \frac{\left(\frac{c}{a} - \frac{3 b^{2}}{8 a^{2}}\right) \left(- \frac{b \left(\frac{b \left(- \frac{c}{16 a} + \frac{3 b^{2}}{256 a^{2}}\right)}{a} + \frac{d}{4 a}\right)}{a} + \frac{e}{a}\right)}{3} - \frac{\left(\frac{b \left(- \frac{c}{2 a} + \frac{b^{2}}{8 a^{2}}\right)}{a} + \frac{d}{a}\right)^{2}}{8}} - \frac{2 c}{3 a} + \frac{b^{2}}{4 a^{2}}}}{2} - \frac{\sqrt{- \frac{\frac{2 b \left(- \frac{c}{2 a} + \frac{b^{2}}{8 a^{2}}\right)}{a} + \frac{2 d}{a}}{\sqrt{- 2 \sqrt[3]{- \frac{\left(\frac{c}{a} - \frac{3 b^{2}}{8 a^{2}}\right)^{3}}{108} + \frac{\left(\frac{c}{a} - \frac{3 b^{2}}{8 a^{2}}\right) \left(- \frac{b \left(\frac{b \left(- \frac{c}{16 a} + \frac{3 b^{2}}{256 a^{2}}\right)}{a} + \frac{d}{4 a}\right)}{a} + \frac{e}{a}\right)}{3} - \frac{\left(\frac{b \left(- \frac{c}{2 a} + \frac{b^{2}}{8 a^{2}}\right)}{a} + \frac{d}{a}\right)^{2}}{8}} - \frac{2 c}{3 a} + \frac{b^{2}}{4 a^{2}}}} + 2 \sqrt[3]{- \frac{\left(\frac{c}{a} - \frac{3 b^{2}}{8 a^{2}}\right)^{3}}{108} + \frac{\left(\frac{c}{a} - \frac{3 b^{2}}{8 a^{2}}\right) \left(- \frac{b \left(\frac{b \left(- \frac{c}{16 a} + \frac{3 b^{2}}{256 a^{2}}\right)}{a} + \frac{d}{4 a}\right)}{a} + \frac{e}{a}\right)}{3} - \frac{\left(\frac{b \left(- \frac{c}{2 a} + \frac{b^{2}}{8 a^{2}}\right)}{a} + \frac{d}{a}\right)^{2}}{8}} - \frac{4 c}{3 a} + \frac{b^{2}}{2 a^{2}}}}{2} - \frac{b}{4 a} & \text{for}\: \frac{\left(\frac{c}{a} - \frac{3 b^{2}}{8 a^{2}}\right)^{2}}{12} - \frac{b \left(\frac{b \left(- \frac{c}{16 a} + \frac{3 b^{2}}{256 a^{2}}\right)}{a} + \frac{d}{4 a}\right)}{a} + \frac{e}{a} = 0 \\\frac{\sqrt{- \frac{2 \left(- \frac{\left(\frac{c}{a} - \frac{3 b^{2}}{8 a^{2}}\right)^{2}}{12} + \frac{b \left(\frac{b \left(- \frac{c}{16 a} + \frac{3 b^{2}}{256 a^{2}}\right)}{a} + \frac{d}{4 a}\right)}{a} - \frac{e}{a}\right)}{3 \sqrt[3]{\frac{\left(\frac{c}{a} - \frac{3 b^{2}}{8 a^{2}}\right)^{3}}{216} - \frac{\left(\frac{c}{a} - \frac{3 b^{2}}{8 a^{2}}\right) \left(- \frac{b \left(\frac{b \left(- \frac{c}{16 a} + \frac{3 b^{2}}{256 a^{2}}\right)}{a} + \frac{d}{4 a}\right)}{a} + \frac{e}{a}\right)}{6} + \frac{\left(\frac{b \left(- \frac{c}{2 a} + \frac{b^{2}}{8 a^{2}}\right)}{a} + \frac{d}{a}\right)^{2}}{16} + \sqrt{\frac{\left(- \frac{\left(\frac{c}{a} - \frac{3 b^{2}}{8 a^{2}}\right)^{2}}{12} + \frac{b \left(\frac{b \left(- \frac{c}{16 a} + \frac{3 b^{2}}{256 a^{2}}\right)}{a} + \frac{d}{4 a}\right)}{a} - \frac{e}{a}\right)^{3}}{27} + \frac{\left(- \frac{\left(\frac{c}{a} - \frac{3 b^{2}}{8 a^{2}}\right)^{3}}{108} + \frac{\left(\frac{c}{a} - \frac{3 b^{2}}{8 a^{2}}\right) \left(- \frac{b \left(\frac{b \left(- \frac{c}{16 a} + \frac{3 b^{2}}{256 a^{2}}\right)}{a} + \frac{d}{4 a}\right)}{a} + \frac{e}{a}\right)}{3} - \frac{\left(\frac{b \left(- \frac{c}{2 a} + \frac{b^{2}}{8 a^{2}}\right)}{a} + \frac{d}{a}\right)^{2}}{8}\right)^{2}}{4}}}} + 2 \sqrt[3]{\frac{\left(\frac{c}{a} - \frac{3 b^{2}}{8 a^{2}}\right)^{3}}{216} - \frac{\left(\frac{c}{a} - \frac{3 b^{2}}{8 a^{2}}\right) \left(- \frac{b \left(\frac{b \left(- \frac{c}{16 a} + \frac{3 b^{2}}{256 a^{2}}\right)}{a} + \frac{d}{4 a}\right)}{a} + \frac{e}{a}\right)}{6} + \frac{\left(\frac{b \left(- \frac{c}{2 a} + \frac{b^{2}}{8 a^{2}}\right)}{a} + \frac{d}{a}\right)^{2}}{16} + \sqrt{\frac{\left(- \frac{\left(\frac{c}{a} - \frac{3 b^{2}}{8 a^{2}}\right)^{2}}{12} + \frac{b \left(\frac{b \left(- \frac{c}{16 a} + \frac{3 b^{2}}{256 a^{2}}\right)}{a} + \frac{d}{4 a}\right)}{a} - \frac{e}{a}\right)^{3}}{27} + \frac{\left(- \frac{\left(\frac{c}{a} - \frac{3 b^{2}}{8 a^{2}}\right)^{3}}{108} + \frac{\left(\frac{c}{a} - \frac{3 b^{2}}{8 a^{2}}\right) \left(- \frac{b \left(\frac{b \left(- \frac{c}{16 a} + \frac{3 b^{2}}{256 a^{2}}\right)}{a} + \frac{d}{4 a}\right)}{a} + \frac{e}{a}\right)}{3} - \frac{\left(\frac{b \left(- \frac{c}{2 a} + \frac{b^{2}}{8 a^{2}}\right)}{a} + \frac{d}{a}\right)^{2}}{8}\right)^{2}}{4}}} - \frac{2 c}{3 a} + \frac{b^{2}}{4 a^{2}}}}{2} - \frac{\sqrt{- \frac{\frac{2 b \left(- \frac{c}{2 a} + \frac{b^{2}}{8 a^{2}}\right)}{a} + \frac{2 d}{a}}{\sqrt{- \frac{2 \left(- \frac{\left(\frac{c}{a} - \frac{3 b^{2}}{8 a^{2}}\right)^{2}}{12} + \frac{b \left(\frac{b \left(- \frac{c}{16 a} + \frac{3 b^{2}}{256 a^{2}}\right)}{a} + \frac{d}{4 a}\right)}{a} - \frac{e}{a}\right)}{3 \sqrt[3]{\frac{\left(\frac{c}{a} - \frac{3 b^{2}}{8 a^{2}}\right)^{3}}{216} - \frac{\left(\frac{c}{a} - \frac{3 b^{2}}{8 a^{2}}\right) \left(- \frac{b \left(\frac{b \left(- \frac{c}{16 a} + \frac{3 b^{2}}{256 a^{2}}\right)}{a} + \frac{d}{4 a}\right)}{a} + \frac{e}{a}\right)}{6} + \frac{\left(\frac{b \left(- \frac{c}{2 a} + \frac{b^{2}}{8 a^{2}}\right)}{a} + \frac{d}{a}\right)^{2}}{16} + \sqrt{\frac{\left(- \frac{\left(\frac{c}{a} - \frac{3 b^{2}}{8 a^{2}}\right)^{2}}{12} + \frac{b \left(\frac{b \left(- \frac{c}{16 a} + \frac{3 b^{2}}{256 a^{2}}\right)}{a} + \frac{d}{4 a}\right)}{a} - \frac{e}{a}\right)^{3}}{27} + \frac{\left(- \frac{\left(\frac{c}{a} - \frac{3 b^{2}}{8 a^{2}}\right)^{3}}{108} + \frac{\left(\frac{c}{a} - \frac{3 b^{2}}{8 a^{2}}\right) \left(- \frac{b \left(\frac{b \left(- \frac{c}{16 a} + \frac{3 b^{2}}{256 a^{2}}\right)}{a} + \frac{d}{4 a}\right)}{a} + \frac{e}{a}\right)}{3} - \frac{\left(\frac{b \left(- \frac{c}{2 a} + \frac{b^{2}}{8 a^{2}}\right)}{a} + \frac{d}{a}\right)^{2}}{8}\right)^{2}}{4}}}} + 2 \sqrt[3]{\frac{\left(\frac{c}{a} - \frac{3 b^{2}}{8 a^{2}}\right)^{3}}{216} - \frac{\left(\frac{c}{a} - \frac{3 b^{2}}{8 a^{2}}\right) \left(- \frac{b \left(\frac{b \left(- \frac{c}{16 a} + \frac{3 b^{2}}{256 a^{2}}\right)}{a} + \frac{d}{4 a}\right)}{a} + \frac{e}{a}\right)}{6} + \frac{\left(\frac{b \left(- \frac{c}{2 a} + \frac{b^{2}}{8 a^{2}}\right)}{a} + \frac{d}{a}\right)^{2}}{16} + \sqrt{\frac{\left(- \frac{\left(\frac{c}{a} - \frac{3 b^{2}}{8 a^{2}}\right)^{2}}{12} + \frac{b \left(\frac{b \left(- \frac{c}{16 a} + \frac{3 b^{2}}{256 a^{2}}\right)}{a} + \frac{d}{4 a}\right)}{a} - \frac{e}{a}\right)^{3}}{27} + \frac{\left(- \frac{\left(\frac{c}{a} - \frac{3 b^{2}}{8 a^{2}}\right)^{3}}{108} + \frac{\left(\frac{c}{a} - \frac{3 b^{2}}{8 a^{2}}\right) \left(- \frac{b \left(\frac{b \left(- \frac{c}{16 a} + \frac{3 b^{2}}{256 a^{2}}\right)}{a} + \frac{d}{4 a}\right)}{a} + \frac{e}{a}\right)}{3} - \frac{\left(\frac{b \left(- \frac{c}{2 a} + \frac{b^{2}}{8 a^{2}}\right)}{a} + \frac{d}{a}\right)^{2}}{8}\right)^{2}}{4}}} - \frac{2 c}{3 a} + \frac{b^{2}}{4 a^{2}}}} + \frac{2 \left(- \frac{\left(\frac{c}{a} - \frac{3 b^{2}}{8 a^{2}}\right)^{2}}{12} + \frac{b \left(\frac{b \left(- \frac{c}{16 a} + \frac{3 b^{2}}{256 a^{2}}\right)}{a} + \frac{d}{4 a}\right)}{a} - \frac{e}{a}\right)}{3 \sqrt[3]{\frac{\left(\frac{c}{a} - \frac{3 b^{2}}{8 a^{2}}\right)^{3}}{216} - \frac{\left(\frac{c}{a} - \frac{3 b^{2}}{8 a^{2}}\right) \left(- \frac{b \left(\frac{b \left(- \frac{c}{16 a} + \frac{3 b^{2}}{256 a^{2}}\right)}{a} + \frac{d}{4 a}\right)}{a} + \frac{e}{a}\right)}{6} + \frac{\left(\frac{b \left(- \frac{c}{2 a} + \frac{b^{2}}{8 a^{2}}\right)}{a} + \frac{d}{a}\right)^{2}}{16} + \sqrt{\frac{\left(- \frac{\left(\frac{c}{a} - \frac{3 b^{2}}{8 a^{2}}\right)^{2}}{12} + \frac{b \left(\frac{b \left(- \frac{c}{16 a} + \frac{3 b^{2}}{256 a^{2}}\right)}{a} + \frac{d}{4 a}\right)}{a} - \frac{e}{a}\right)^{3}}{27} + \frac{\left(- \frac{\left(\frac{c}{a} - \frac{3 b^{2}}{8 a^{2}}\right)^{3}}{108} + \frac{\left(\frac{c}{a} - \frac{3 b^{2}}{8 a^{2}}\right) \left(- \frac{b \left(\frac{b \left(- \frac{c}{16 a} + \frac{3 b^{2}}{256 a^{2}}\right)}{a} + \frac{d}{4 a}\right)}{a} + \frac{e}{a}\right)}{3} - \frac{\left(\frac{b \left(- \frac{c}{2 a} + \frac{b^{2}}{8 a^{2}}\right)}{a} + \frac{d}{a}\right)^{2}}{8}\right)^{2}}{4}}}} - 2 \sqrt[3]{\frac{\left(\frac{c}{a} - \frac{3 b^{2}}{8 a^{2}}\right)^{3}}{216} - \frac{\left(\frac{c}{a} - \frac{3 b^{2}}{8 a^{2}}\right) \left(- \frac{b \left(\frac{b \left(- \frac{c}{16 a} + \frac{3 b^{2}}{256 a^{2}}\right)}{a} + \frac{d}{4 a}\right)}{a} + \frac{e}{a}\right)}{6} + \frac{\left(\frac{b \left(- \frac{c}{2 a} + \frac{b^{2}}{8 a^{2}}\right)}{a} + \frac{d}{a}\right)^{2}}{16} + \sqrt{\frac{\left(- \frac{\left(\frac{c}{a} - \frac{3 b^{2}}{8 a^{2}}\right)^{2}}{12} + \frac{b \left(\frac{b \left(- \frac{c}{16 a} + \frac{3 b^{2}}{256 a^{2}}\right)}{a} + \frac{d}{4 a}\right)}{a} - \frac{e}{a}\right)^{3}}{27} + \frac{\left(- \frac{\left(\frac{c}{a} - \frac{3 b^{2}}{8 a^{2}}\right)^{3}}{108} + \frac{\left(\frac{c}{a} - \frac{3 b^{2}}{8 a^{2}}\right) \left(- \frac{b \left(\frac{b \left(- \frac{c}{16 a} + \frac{3 b^{2}}{256 a^{2}}\right)}{a} + \frac{d}{4 a}\right)}{a} + \frac{e}{a}\right)}{3} - \frac{\left(\frac{b \left(- \frac{c}{2 a} + \frac{b^{2}}{8 a^{2}}\right)}{a} + \frac{d}{a}\right)^{2}}{8}\right)^{2}}{4}}} - \frac{4 c}{3 a} + \frac{b^{2}}{2 a^{2}}}}{2} - \frac{b}{4 a} & \text{otherwise} \end{cases}
解2
\begin{cases} \frac{\sqrt{- 2 \sqrt[3]{- \frac{\left(\frac{c}{a} - \frac{3 b^{2}}{8 a^{2}}\right)^{3}}{108} + \frac{\left(\frac{c}{a} - \frac{3 b^{2}}{8 a^{2}}\right) \left(- \frac{b \left(\frac{b \left(- \frac{c}{16 a} + \frac{3 b^{2}}{256 a^{2}}\right)}{a} + \frac{d}{4 a}\right)}{a} + \frac{e}{a}\right)}{3} - \frac{\left(\frac{b \left(- \frac{c}{2 a} + \frac{b^{2}}{8 a^{2}}\right)}{a} + \frac{d}{a}\right)^{2}}{8}} - \frac{2 c}{3 a} + \frac{b^{2}}{4 a^{2}}}}{2} + \frac{\sqrt{- \frac{\frac{2 b \left(- \frac{c}{2 a} + \frac{b^{2}}{8 a^{2}}\right)}{a} + \frac{2 d}{a}}{\sqrt{- 2 \sqrt[3]{- \frac{\left(\frac{c}{a} - \frac{3 b^{2}}{8 a^{2}}\right)^{3}}{108} + \frac{\left(\frac{c}{a} - \frac{3 b^{2}}{8 a^{2}}\right) \left(- \frac{b \left(\frac{b \left(- \frac{c}{16 a} + \frac{3 b^{2}}{256 a^{2}}\right)}{a} + \frac{d}{4 a}\right)}{a} + \frac{e}{a}\right)}{3} - \frac{\left(\frac{b \left(- \frac{c}{2 a} + \frac{b^{2}}{8 a^{2}}\right)}{a} + \frac{d}{a}\right)^{2}}{8}} - \frac{2 c}{3 a} + \frac{b^{2}}{4 a^{2}}}} + 2 \sqrt[3]{- \frac{\left(\frac{c}{a} - \frac{3 b^{2}}{8 a^{2}}\right)^{3}}{108} + \frac{\left(\frac{c}{a} - \frac{3 b^{2}}{8 a^{2}}\right) \left(- \frac{b \left(\frac{b \left(- \frac{c}{16 a} + \frac{3 b^{2}}{256 a^{2}}\right)}{a} + \frac{d}{4 a}\right)}{a} + \frac{e}{a}\right)}{3} - \frac{\left(\frac{b \left(- \frac{c}{2 a} + \frac{b^{2}}{8 a^{2}}\right)}{a} + \frac{d}{a}\right)^{2}}{8}} - \frac{4 c}{3 a} + \frac{b^{2}}{2 a^{2}}}}{2} - \frac{b}{4 a} & \text{for}\: \frac{\left(\frac{c}{a} - \frac{3 b^{2}}{8 a^{2}}\right)^{2}}{12} - \frac{b \left(\frac{b \left(- \frac{c}{16 a} + \frac{3 b^{2}}{256 a^{2}}\right)}{a} + \frac{d}{4 a}\right)}{a} + \frac{e}{a} = 0 \\\frac{\sqrt{- \frac{2 \left(- \frac{\left(\frac{c}{a} - \frac{3 b^{2}}{8 a^{2}}\right)^{2}}{12} + \frac{b \left(\frac{b \left(- \frac{c}{16 a} + \frac{3 b^{2}}{256 a^{2}}\right)}{a} + \frac{d}{4 a}\right)}{a} - \frac{e}{a}\right)}{3 \sqrt[3]{\frac{\left(\frac{c}{a} - \frac{3 b^{2}}{8 a^{2}}\right)^{3}}{216} - \frac{\left(\frac{c}{a} - \frac{3 b^{2}}{8 a^{2}}\right) \left(- \frac{b \left(\frac{b \left(- \frac{c}{16 a} + \frac{3 b^{2}}{256 a^{2}}\right)}{a} + \frac{d}{4 a}\right)}{a} + \frac{e}{a}\right)}{6} + \frac{\left(\frac{b \left(- \frac{c}{2 a} + \frac{b^{2}}{8 a^{2}}\right)}{a} + \frac{d}{a}\right)^{2}}{16} + \sqrt{\frac{\left(- \frac{\left(\frac{c}{a} - \frac{3 b^{2}}{8 a^{2}}\right)^{2}}{12} + \frac{b \left(\frac{b \left(- \frac{c}{16 a} + \frac{3 b^{2}}{256 a^{2}}\right)}{a} + \frac{d}{4 a}\right)}{a} - \frac{e}{a}\right)^{3}}{27} + \frac{\left(- \frac{\left(\frac{c}{a} - \frac{3 b^{2}}{8 a^{2}}\right)^{3}}{108} + \frac{\left(\frac{c}{a} - \frac{3 b^{2}}{8 a^{2}}\right) \left(- \frac{b \left(\frac{b \left(- \frac{c}{16 a} + \frac{3 b^{2}}{256 a^{2}}\right)}{a} + \frac{d}{4 a}\right)}{a} + \frac{e}{a}\right)}{3} - \frac{\left(\frac{b \left(- \frac{c}{2 a} + \frac{b^{2}}{8 a^{2}}\right)}{a} + \frac{d}{a}\right)^{2}}{8}\right)^{2}}{4}}}} + 2 \sqrt[3]{\frac{\left(\frac{c}{a} - \frac{3 b^{2}}{8 a^{2}}\right)^{3}}{216} - \frac{\left(\frac{c}{a} - \frac{3 b^{2}}{8 a^{2}}\right) \left(- \frac{b \left(\frac{b \left(- \frac{c}{16 a} + \frac{3 b^{2}}{256 a^{2}}\right)}{a} + \frac{d}{4 a}\right)}{a} + \frac{e}{a}\right)}{6} + \frac{\left(\frac{b \left(- \frac{c}{2 a} + \frac{b^{2}}{8 a^{2}}\right)}{a} + \frac{d}{a}\right)^{2}}{16} + \sqrt{\frac{\left(- \frac{\left(\frac{c}{a} - \frac{3 b^{2}}{8 a^{2}}\right)^{2}}{12} + \frac{b \left(\frac{b \left(- \frac{c}{16 a} + \frac{3 b^{2}}{256 a^{2}}\right)}{a} + \frac{d}{4 a}\right)}{a} - \frac{e}{a}\right)^{3}}{27} + \frac{\left(- \frac{\left(\frac{c}{a} - \frac{3 b^{2}}{8 a^{2}}\right)^{3}}{108} + \frac{\left(\frac{c}{a} - \frac{3 b^{2}}{8 a^{2}}\right) \left(- \frac{b \left(\frac{b \left(- \frac{c}{16 a} + \frac{3 b^{2}}{256 a^{2}}\right)}{a} + \frac{d}{4 a}\right)}{a} + \frac{e}{a}\right)}{3} - \frac{\left(\frac{b \left(- \frac{c}{2 a} + \frac{b^{2}}{8 a^{2}}\right)}{a} + \frac{d}{a}\right)^{2}}{8}\right)^{2}}{4}}} - \frac{2 c}{3 a} + \frac{b^{2}}{4 a^{2}}}}{2} + \frac{\sqrt{- \frac{\frac{2 b \left(- \frac{c}{2 a} + \frac{b^{2}}{8 a^{2}}\right)}{a} + \frac{2 d}{a}}{\sqrt{- \frac{2 \left(- \frac{\left(\frac{c}{a} - \frac{3 b^{2}}{8 a^{2}}\right)^{2}}{12} + \frac{b \left(\frac{b \left(- \frac{c}{16 a} + \frac{3 b^{2}}{256 a^{2}}\right)}{a} + \frac{d}{4 a}\right)}{a} - \frac{e}{a}\right)}{3 \sqrt[3]{\frac{\left(\frac{c}{a} - \frac{3 b^{2}}{8 a^{2}}\right)^{3}}{216} - \frac{\left(\frac{c}{a} - \frac{3 b^{2}}{8 a^{2}}\right) \left(- \frac{b \left(\frac{b \left(- \frac{c}{16 a} + \frac{3 b^{2}}{256 a^{2}}\right)}{a} + \frac{d}{4 a}\right)}{a} + \frac{e}{a}\right)}{6} + \frac{\left(\frac{b \left(- \frac{c}{2 a} + \frac{b^{2}}{8 a^{2}}\right)}{a} + \frac{d}{a}\right)^{2}}{16} + \sqrt{\frac{\left(- \frac{\left(\frac{c}{a} - \frac{3 b^{2}}{8 a^{2}}\right)^{2}}{12} + \frac{b \left(\frac{b \left(- \frac{c}{16 a} + \frac{3 b^{2}}{256 a^{2}}\right)}{a} + \frac{d}{4 a}\right)}{a} - \frac{e}{a}\right)^{3}}{27} + \frac{\left(- \frac{\left(\frac{c}{a} - \frac{3 b^{2}}{8 a^{2}}\right)^{3}}{108} + \frac{\left(\frac{c}{a} - \frac{3 b^{2}}{8 a^{2}}\right) \left(- \frac{b \left(\frac{b \left(- \frac{c}{16 a} + \frac{3 b^{2}}{256 a^{2}}\right)}{a} + \frac{d}{4 a}\right)}{a} + \frac{e}{a}\right)}{3} - \frac{\left(\frac{b \left(- \frac{c}{2 a} + \frac{b^{2}}{8 a^{2}}\right)}{a} + \frac{d}{a}\right)^{2}}{8}\right)^{2}}{4}}}} + 2 \sqrt[3]{\frac{\left(\frac{c}{a} - \frac{3 b^{2}}{8 a^{2}}\right)^{3}}{216} - \frac{\left(\frac{c}{a} - \frac{3 b^{2}}{8 a^{2}}\right) \left(- \frac{b \left(\frac{b \left(- \frac{c}{16 a} + \frac{3 b^{2}}{256 a^{2}}\right)}{a} + \frac{d}{4 a}\right)}{a} + \frac{e}{a}\right)}{6} + \frac{\left(\frac{b \left(- \frac{c}{2 a} + \frac{b^{2}}{8 a^{2}}\right)}{a} + \frac{d}{a}\right)^{2}}{16} + \sqrt{\frac{\left(- \frac{\left(\frac{c}{a} - \frac{3 b^{2}}{8 a^{2}}\right)^{2}}{12} + \frac{b \left(\frac{b \left(- \frac{c}{16 a} + \frac{3 b^{2}}{256 a^{2}}\right)}{a} + \frac{d}{4 a}\right)}{a} - \frac{e}{a}\right)^{3}}{27} + \frac{\left(- \frac{\left(\frac{c}{a} - \frac{3 b^{2}}{8 a^{2}}\right)^{3}}{108} + \frac{\left(\frac{c}{a} - \frac{3 b^{2}}{8 a^{2}}\right) \left(- \frac{b \left(\frac{b \left(- \frac{c}{16 a} + \frac{3 b^{2}}{256 a^{2}}\right)}{a} + \frac{d}{4 a}\right)}{a} + \frac{e}{a}\right)}{3} - \frac{\left(\frac{b \left(- \frac{c}{2 a} + \frac{b^{2}}{8 a^{2}}\right)}{a} + \frac{d}{a}\right)^{2}}{8}\right)^{2}}{4}}} - \frac{2 c}{3 a} + \frac{b^{2}}{4 a^{2}}}} + \frac{2 \left(- \frac{\left(\frac{c}{a} - \frac{3 b^{2}}{8 a^{2}}\right)^{2}}{12} + \frac{b \left(\frac{b \left(- \frac{c}{16 a} + \frac{3 b^{2}}{256 a^{2}}\right)}{a} + \frac{d}{4 a}\right)}{a} - \frac{e}{a}\right)}{3 \sqrt[3]{\frac{\left(\frac{c}{a} - \frac{3 b^{2}}{8 a^{2}}\right)^{3}}{216} - \frac{\left(\frac{c}{a} - \frac{3 b^{2}}{8 a^{2}}\right) \left(- \frac{b \left(\frac{b \left(- \frac{c}{16 a} + \frac{3 b^{2}}{256 a^{2}}\right)}{a} + \frac{d}{4 a}\right)}{a} + \frac{e}{a}\right)}{6} + \frac{\left(\frac{b \left(- \frac{c}{2 a} + \frac{b^{2}}{8 a^{2}}\right)}{a} + \frac{d}{a}\right)^{2}}{16} + \sqrt{\frac{\left(- \frac{\left(\frac{c}{a} - \frac{3 b^{2}}{8 a^{2}}\right)^{2}}{12} + \frac{b \left(\frac{b \left(- \frac{c}{16 a} + \frac{3 b^{2}}{256 a^{2}}\right)}{a} + \frac{d}{4 a}\right)}{a} - \frac{e}{a}\right)^{3}}{27} + \frac{\left(- \frac{\left(\frac{c}{a} - \frac{3 b^{2}}{8 a^{2}}\right)^{3}}{108} + \frac{\left(\frac{c}{a} - \frac{3 b^{2}}{8 a^{2}}\right) \left(- \frac{b \left(\frac{b \left(- \frac{c}{16 a} + \frac{3 b^{2}}{256 a^{2}}\right)}{a} + \frac{d}{4 a}\right)}{a} + \frac{e}{a}\right)}{3} - \frac{\left(\frac{b \left(- \frac{c}{2 a} + \frac{b^{2}}{8 a^{2}}\right)}{a} + \frac{d}{a}\right)^{2}}{8}\right)^{2}}{4}}}} - 2 \sqrt[3]{\frac{\left(\frac{c}{a} - \frac{3 b^{2}}{8 a^{2}}\right)^{3}}{216} - \frac{\left(\frac{c}{a} - \frac{3 b^{2}}{8 a^{2}}\right) \left(- \frac{b \left(\frac{b \left(- \frac{c}{16 a} + \frac{3 b^{2}}{256 a^{2}}\right)}{a} + \frac{d}{4 a}\right)}{a} + \frac{e}{a}\right)}{6} + \frac{\left(\frac{b \left(- \frac{c}{2 a} + \frac{b^{2}}{8 a^{2}}\right)}{a} + \frac{d}{a}\right)^{2}}{16} + \sqrt{\frac{\left(- \frac{\left(\frac{c}{a} - \frac{3 b^{2}}{8 a^{2}}\right)^{2}}{12} + \frac{b \left(\frac{b \left(- \frac{c}{16 a} + \frac{3 b^{2}}{256 a^{2}}\right)}{a} + \frac{d}{4 a}\right)}{a} - \frac{e}{a}\right)^{3}}{27} + \frac{\left(- \frac{\left(\frac{c}{a} - \frac{3 b^{2}}{8 a^{2}}\right)^{3}}{108} + \frac{\left(\frac{c}{a} - \frac{3 b^{2}}{8 a^{2}}\right) \left(- \frac{b \left(\frac{b \left(- \frac{c}{16 a} + \frac{3 b^{2}}{256 a^{2}}\right)}{a} + \frac{d}{4 a}\right)}{a} + \frac{e}{a}\right)}{3} - \frac{\left(\frac{b \left(- \frac{c}{2 a} + \frac{b^{2}}{8 a^{2}}\right)}{a} + \frac{d}{a}\right)^{2}}{8}\right)^{2}}{4}}} - \frac{4 c}{3 a} + \frac{b^{2}}{2 a^{2}}}}{2} - \frac{b}{4 a} & \text{otherwise} \end{cases}
反比例式について
この辺の件に踏み込むのはまだ先になりそう?
Rの場合
# 統計言語R(with YACAS)による実行例
library(Ryacas)
yacas("Solve(x*y-1==0,x)")
Yacas vector:
[1] x == 1/y
yacas("Solve(x*y-1==0,y)")
Yacas vector:
[1] y == 1/x
pythonの場合①
import sympy
sympy.var('x,y')
Sol1=sympy.solve (x*y-1, x)
sympy.init_printing()
if Sol1==[]:
print("Can't solve!!")
else:
for i in Sol1:
display(i)
print(sympy.latex(i))
\frac{1}{y}
pythonの場合②
import sympy
sympy.var('x,a,b,c')
Sol1=sympy.solve ((a*x)**2+b*x+c, y)
sympy.init_printing()
if Sol1==[]:
print("Can't solve!!")
else:
for i in Sol1:
display(i)
print(sympy.latex(i))
\frac{1}{x}
二項展開(Binomial Expansion)の限界
二項定理(Binomial theorem)とも関連してくる領域となります。
【初心者向け】パスカルの三角形と二項定理または二項展開
ところで平方ピタゴラスの定理a^2=b^2+c^2は一般の2項展開(Binomial Expansion)(a±b)^2では扱い切れません。
【初心者向け】ピタゴラスの定理あるいは三平方の定理からの出発
その証明には「角度が90度(π/2ラジアン)という特別条件」あるいは「複素平面(Complex Plane)における単位円上の操作、すなわち虚数i^2=-1の概念の導入と共益複素数(Conjugate Complex Number)の相互打ち消し作用」を必要とするのです。
# 余弦定理(cosine formula)で角度が90度の場合
a^2=(b-c)^2=b^2+c^2−2bc*cos(α)
# ところでα=90度(π/2ラジアン)の場合、cos(α)=0
a^2=b^2+c^2−2bc*0=b^2+c^2
# オイラーの公式(Euler's Formula)あるいは
# 共益複素数(Conjugate Complex Number)同士の打ち消し作用を用いた証明。
1=e^0=e^(iθ-iθ)=e^iθ-e^iθ)
=(cos(θ)+sin(θ)i)(cos(θ)-sin(θ)i)
=cos(θ)^2+sin(θ)i-sin(θ)i-sin(θ)i^2
=cos(θ)^2+sin(θ)^2 #i^2=-1
さらなる先の展望
[代数曲線に触れる]
ユークリッド幾何学における平面代数曲線 (Plane Algebraic Curve)におけるx^2+y^2=a(aは実定数)。これは、実数の範囲で考えた時、以下となる。
- a > 0 なら円
- a = 0 なら原点一点
- a < 0 なら空集合
ただしa < 0 でも、複素数の範囲で解を考えればたくさんある。このように、代数曲線といってもどの範囲で解を考えるのか、どの体で解を考えるのかを明らかにしないと定かにはさだまらない。
実数の範囲で考えると一点や空集合なども「代数曲線」であることになり、直感に合わない。通常は、代数曲線といったら複素数解の全体をあらわすことが多い。
# 統計言語R(with YACAS)による実行例
library(Ryacas)
yacas("Solve(x^2+y^2-1==0,x)")
Yacas vector:
[1] x == root(abs(y^2 - 1), 2) * complex_cartesian(cos(argument(1 - y^2)/2), sin(argument(1 - y^2)/2))
[2] x == root(abs(y^2 - 1), 2) * complex_cartesian(cos((argument(1 - y^2) + 2 * pi)/2), sin((argument(1 - y^2) + 2 * pi)/2))
yacas("Solve(x^2+y^2-1==0,y)")
Yacas vector:
[1] y == root(abs(x^2 - 1), 2) * complex_cartesian(cos(argument(1 - x^2)/2), sin(argument(1 - x^2)/2))
[2] y == root(abs(x^2 - 1), 2) * complex_cartesian(cos((argument(1 - x^2) + 2 * pi)/2), sin((argument(1 - x^2) + 2 * pi)/2))
pythonの場合①
import sympy
sympy.var('x,y')
Sol1=sympy.solve (x**2+y**2-1, y)
sympy.init_printing()
if Sol1==[]:
print("Can't solve!!")
else:
for i in Sol1:
display(i)
print(sympy.latex(i))
- \sqrt{1 - x^{2}}\\\sqrt{1 - x^{2}}
pythonの場合②
import sympy
sympy.var('x,y')
Sol1=sympy.solve (x**2+y**2-1, y)
sympy.init_printing()
if Sol1==[]:
print("Can't solve!!")
else:
for i in Sol1:
display(i)
print(sympy.latex(i))
- \sqrt{1 - y^{2}}\\\sqrt{1 - y^{2}}
そうそう、こういうレベルの話まで出てきてしまう世界線でもあったのです…
【Rで球面幾何学】「半円しか描けなかった」世界の思い出?
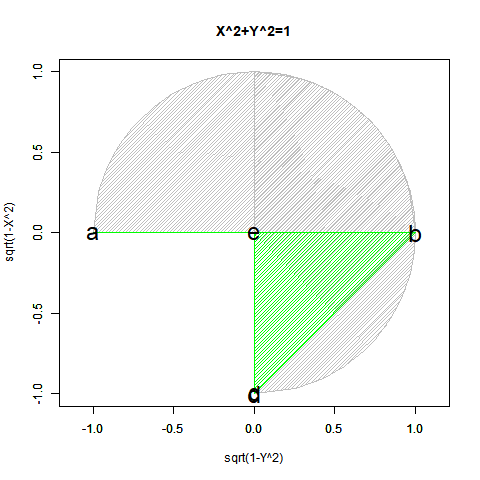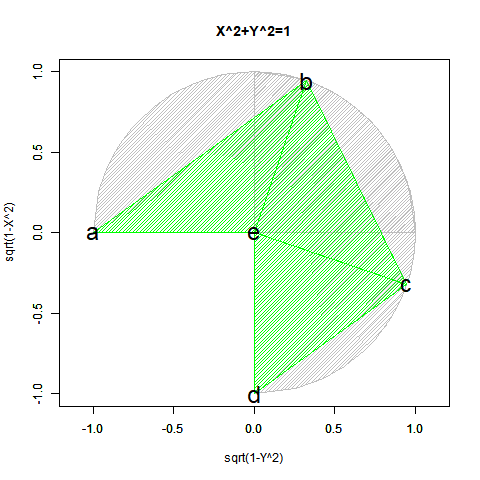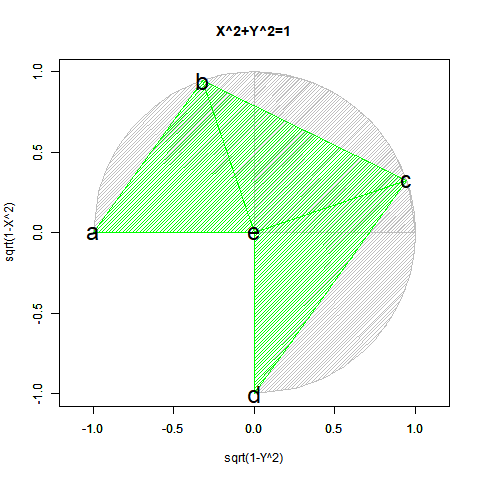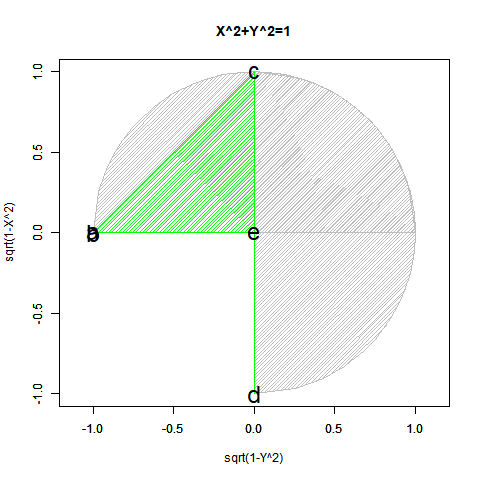
とりあえず、以下続報?