(2021年2月27日)Rによる投稿
(2021年4月08日)texとpythonによる追記
とりあえず、以下までに実数族に下属する(部分集合を構成する)整数族とネイピア族の振る舞いをまとめてきました。それぞれが実数全体を規定する戦略を備えている辺りが不穏ですね。
【数理考古学】とある実数列の規定例①等差数列から加法整数群へ
【数理考古学】とある実数列の規定例②等比数列から乗法群へ
今回は趣を変え、それらが置かれている座標系全体の成立過程について考察を深めて行きたいと思います。
0次元(Zero Dimension)
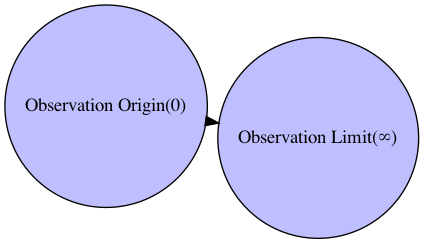
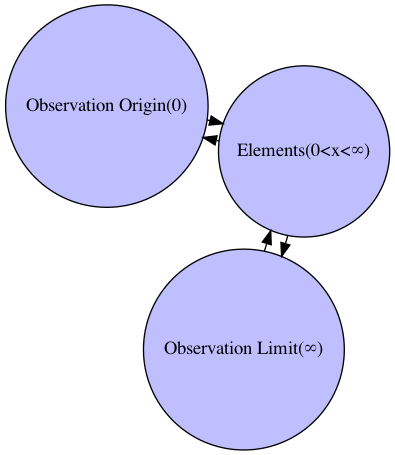
(それ自体は観測対象となり得ない)観測原点(Observation Origin)$0$と観測限界およびその向こう側(Observation Limit)$\infty$の間に「何もない」状態から出発します。群論(Group Theory)でいう空環概念(Empty/Nullary Ring Concept)に対応し、その元(Element)は空となります。
【初心者向け】群論概念②空環から整数環へ。
空環概念(Empty/Nullary Ring Concept)は「空和概念(Empty/Nullary Sum Concept)」の規約と「空積概念(Empty/Nullary Product Concept)」の規約の統合結果である。
①ここでいう「空和概念(Empty/Nullary Sum Concept)の規約」とは、群論(Group Theory)上における、空集合(Empty/Nullary Set)$\emptyset_n(n=0)=()$について「0個の因子を足し合わせた演算結果集合(Operation Result Set)で、加法単位元(Additive Identity)0に等しい(():=0)」とする規約をいう。
- 二項演算(Binary Operation)のうち、加減算(Addition and Subtraction)すなわち加法単位元(Additive Identity)$0+Α+Β(Α+(-Β))$においては任意の元(Any Element)$Α_n(n=0)()=Β_n(n=0)()=Γ_n(n=0)()=0$なので結合則(Associative Law)0+(Α+Β)+C+…=0+Α+(Β+C)+…も交換則(Commutative Law)0+Α+Β+…=0+Β+Α+…も成立し、その演算結果は閉じている(演算の都度0=()に戻る)。
②ここでいう「空積概念(Empty/Nullary Product Concept)の規約」とは、群論(Group Theory)における、空集合概念(Empty/Nullary Set)$\emptyset _n(n=0)=()$について「0個の因子を掛け合わせた演算結果集合(Operation Result Set)で、乗法単位元(Multiplicative Identity)1に等しい(():=1)」とする規約をいう。
- 二項演算(Binary Operation)のうち、乗除算(Multiplying and Dividing)すなわち乗法単位元(Multiplicative Identity)$1×Α×Β(Α×(1/Β))$においては任意の元(Any Element)$Α_n(n=0)()=Β_n(n=0)()=Γ_n(n=0)()=1$となるので結合則(Associative Law)1×(Α×Β)×C+…=1×Α×(Β×C)×…も交換則(Commutative Law)1×Α×Β×…=1×Β×Α×…も成立し、その演算結果は閉じている(演算の都度1=()に戻る)。
- 二項演算(Binary Operation)のうち、冪算(Exponentiation)それ自体こそ分配法則や交換法則を満たさないものの、その計算範囲自体は上掲の演算に内包され、自明の理としてその演算結果も同じ範囲で閉じている($…A^2=A×A,A^2=A,A^0=\frac{A}{A}=1,A^-1=\frac{1}{A},A^-2=\frac{1}{A×A},…・$)。
③この時点ではあくまで空集合$\emptyset _n(n=0)()=(加減算における単位元)0=(乗除算における単位元)1$と規約されるだけで$\emptyset _n(n=2)=(0,1)$が成立する訳ではない点に注意されたい。実際、単元集合(Singleton)/単位集合(Unit Set)$Α_n(n=1)=(0)$及び$Β_n(n=1)=(1)$、さらには二つを合算した集合$Γ_n(n=2)=(0,1)$全てが空環/空群$\emptyset(n=0)=()$と異なりそれ自体は群も環も構成しない。
- exp(-1)(0.3678794)を求めるベルヌーイの式(1-1/n)^nにおけるn=1(すなわち(1-1/1)^1=0)の場合に該当する。未開封のくじ引きセットの様なもので当たりなら必ず入っており「外れる確率」を計算しても0にしかならない。いわば観測自体成立していない、すなわち「閉じた目蓋の向こう側に全てが待っている」状態。実数概念など成立しようがないから、この時点では全てが虚数領域に留まっているともいえる。
# FN01=Find the number of Napier 01
FN01<-function(NoS){
pie.data<-rep(1, NoS)
names0<-NULL
for(i in 1:NoS){
names0<-c(names0,paste0(i,"/",NoS))
}
names(pie.data)<-names0
pie(pie.data, col = heat.colors(NoS),main = "Probability of losing the Antipodal point")
}
# アニメーション
library("animation")
Time_Code=c(1,1,1,2,2,2,3,3,3,4,4,4,5,5,5,6,6,6,7,7,8,8,9,9,10,10,11,12,13,14,15,16)
saveGIF({
for (i in Time_Code){
FN01(i)
}
}, interval = 0.1, movie.name = "FN01.gif")
しかしもちろん、ただ「瞼を開いた」だけで観測原点(Observation Origin)0と観測限界(Observation Limit)Inf(inity)の狭間に何かを見出せる訳ではありません。上掲の様にこの段階における観測結果集合はあくまで空集合、すなわち各観測結果の関係が全て互いに素なので次元抽出も相対設定も行えず、ある意味観測原点を中心に円弧状、もしくは球面状に均等に広がっているのみ。
- この状態はある意味、統計学における「統計対象に値しない」名義尺度(Nominal scale, Stanley Smith Stevens,1946年)、あるいは仮説検定において棄却される帰無仮説、すなわち「ここで証明したい事は証明不可能である」とする論拠に対応する。まさしく「(数理処理可能な有意味水準を超えるデータは)存在しない」状態の数理化という訳である。
確率変数とは
確率変数の尺度
帰無仮説(null hypothesis)
【数理考古学】とある実数列の規定例①等差数列から加法整数群へ


まるで禅問答の様ですが、この概念を幾何学的イメージに置き換えたのが以下。有向グラフ(Directed graph)で表すと「観測者側からの観測対象に対する一方的観察」と図示される点が重要。
Rによる表現例
これを実装した当時はまだ双方向で考えてました。
library(igraph)
par(mfrow=c(1,2),mar=c(3,3,3,3))
gd<-graph(c(
"Zero(0)","Inf(Inity)",
"Inf(Inity)","Zero(0)"
))
plot(gd,layout=layout.fruchterman.reingold)
pythonによる表現例
【Python演算処理】NetworkXライブラリを導入する。
空積概念(Empty/Nullary Product Concept)
- 観測限界を点と置いた場合、(0~$\infty$の範囲に渡る)観測原点との距離$x$は、何倍にしても何分の1にしても値は変わらない。
- ただし例外的に$\frac{x}{x}=1$となり、これが乗法単位元(Multiplicative
Identity)の概念の出発点になる。
空和概念(Empty/Nullary Sum Concept)
- 観測限界を(0~$\infty$の範囲に渡る)観測原点との距離$x$を半径とする円弧/球面と置いた場合、それをどんなに足し合わせても値は変わらない。
- ただし例外的に$x-x=0$となり、これが加法単位元(Additive Identity Identity)の概念の出発点になる。
まるである種の哲学論、というより般若心境における「色即是空色即是空」の境地? 科学的にはむしろ、実験しながら「有意差出ろ!! 有意差出ろ!!」と念じ続ける心境と重なります。つまりどちらかというと(乳幼児が生きているとされる、無意識と自我と超自我が未分離状態の)呪術的世界観に近いとも。そういえば機械学習の根幹部たる(人間の神経を模して活性化関数によって0と1の境界線をハンドリングする)パーセプトロン(Perceptron)概念もまた、この辺りの境界認識問題に関わってくるのです。
パーセプトロン-Wikipedia
心理学者・計算機科学者のフランク・ローゼンブラットが1957年に考案し、1958年に論文を発表した。モデルは同じく1958年に発表されたロジスティック回帰と等価である。
視覚と脳の機能をモデル化したものであり、パターン認識を行う。ただし学習については自明ではなく、特に多層パーセプトロンの機械学習に関する歴史は、それがパーセプトロンの歴史だと言っても過言ではない。
1960年代に爆発的なニューラルネットブームを巻き起こしたが、60年代末のミンスキーらによる、単層パーセプトロンは線形分離可能なものしか学習できないという指摘は、多層パーセプトロンの学習が当時まだよくわからなかったことから、一時研究を停滞させた。
影響を受けた変種といえるニューラルネットワークも多数提案されているが、それらについてはここでは略す。パーセプトロン自体はその後、ボルツマンマシンや、多層パーセプトロンの機械学習をある程度実用化したバックプロパゲーションなどによって1980年代に再興隆した後、1990年代にはまた停滞した。
21世紀に入った後の研究の進展などにより、より層を増やしたパーセプトロンでの機械学習を指すいわゆる「ディープラーニング」の実用化と、それによる画像認識などの成果により、2020年現在はブームにある。
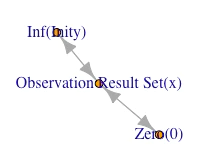
0.5次元(0.5 Dimension)
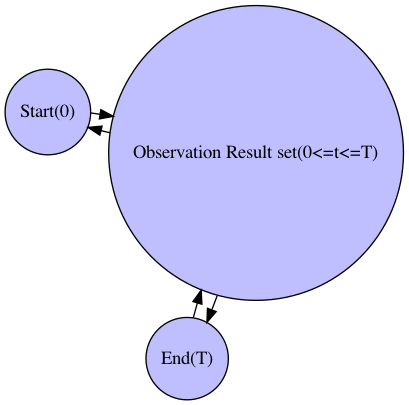
次元抽出や中心割り出しが可能そうな有望な観測結果集合が得られて初めて「統計科学的/確率論的アプローチ」が可能となります。
library(igraph)
par(mfrow=c(1,2),mar=c(3,3,3,3))
gd<-graph(c(
"Zero(0)","Observation Result Set(x)",
"Observation Result Set(x)","Zero(0)",
"Observation Result Set(x)","Inf(Inity)",
"Inf(Inity)","Observation Result Set(x)"
))
plot(gd,layout=layout.fruchterman.reingold)
pythonによる表現例
【Python演算処理】NetworkXライブラリを導入する。
- 次元抽出や中心割り出しが可能そうな有望な観測結果集合(Observation Result Set)が得られて初めて「統計科学的/確率論的アプローチ」が可能となる。最初の評価軸であるから、当然それはX軸や時間軸(t軸)の形で与えられる。
import networkx as nx
G = nx.DiGraph()
G.add_edge("Observation Origin(0)","Elements(0<x<∞)")
G.add_edge("Elements(0<x<∞)","Observation Limit(∞)")
G.add_edge("Elements(0<x<∞)","Observation Origin(0)",)
G.add_edge("Observation Limit(∞)","Elements(0<x<∞)")
nx.nx_agraph.view_pygraphviz(G, prog='fdp')
import networkx as nx
G = nx.DiGraph()
G.add_edge("Start(0)","Observation Result set(0<=t<=T)")
G.add_edge("Observation Result set(0<=t<=T)","End(T)")
G.add_edge("Observation Result set(0<=t<=T)","Start(0)")
G.add_edge("End(T)","Observation Result set(0<=t<=T)")
nx.nx_agraph.view_pygraphviz(G, prog='fdp')
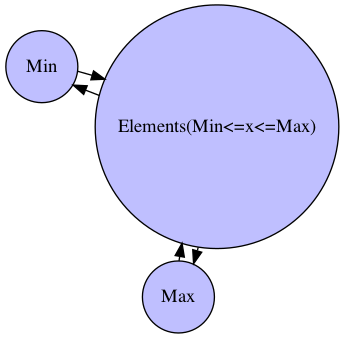
- 統計の対象となる実データには当然(観測不可能な)両極限は現れず、最大値(Max)と最小値(Min)がそれが推察可能な形で得られるとも限らない。
import networkx as nx
G = nx.DiGraph()
G.add_edge("Min","Elements(Min<=x<=Max)")
G.add_edge("Elements(Min<=x<=Max)","Max")
G.add_edge("Elements(Min<=x<=Max)","Min",)
G.add_edge("Max","Elements(Min<=x<=Max)")
nx.nx_agraph.view_pygraphviz(G, prog='fdp')
- この辺りのニュアンスも含め、確率変数の尺度(Stanley Smith Stevens,1946年)では「データ間の順位にのみ意味がある」順位尺度(Ordinal scale)から「データ間の差にのみ意味がある」間隔尺度(Interval scale)にかけてが該当する。
確率変数の尺度
この段階での中心的関心は「最大値と最小値の狭間に(平均や中央値や最頻値から)中心を見出す」事にあります。原則としてサンプル数nが多いほど信頼度(Reliability)が増えていきます。
ND<-function(x){
cx<-rnorm(10)
cy<-rnorm(10)
plot(cx,cy,xlim=c(-4,4),asp=1,ylim=c(-4,4),main="Normal Distribution",xlab="",ylab="")
c0<-seq(-pi,pi,length=61)
cx0<-cos(c0)
cy0<-sin(c0)
par(new=T)#上書き指定
plot(cx0+mean(cx),cy0+mean(cy),type="l",asp=1,xlim=c(-4,4),ylim=c(-4,4),main="",xlab="",ylab="",col=rgb(0,1,0))
par(new=T)#上書き指定
plot(cx0*2+mean(cx),cy0*2+mean(cy),type="l",asp=1,xlim=c(-4,4),ylim=c(-4,4),main="",xlab="",ylab="",col=rgb(0,1,0))
par(new=T)#上書き指定
plot(cx0*3+mean(cx),cy0*3+mean(cy),type="l",asp=1,xlim=c(-4,4),ylim=c(-4,4),main="",xlab="",ylab="",col=rgb(0,1,0))
text(mean(cx),mean(cy),"X",col=rgb(0,1,0))
}
# アニメーション
library("animation")
Time_Code=seq(1,16,length=16)
saveGIF({
for (i in Time_Code){
ND(i)
}
}, interval = 0.1, movie.name = "ND04.gif")
ND<-function(x){
cx<-rnorm(100)
cy<-rnorm(100)
plot(cx,cy,xlim=c(-4,4),asp=1,ylim=c(-4,4),main="Normal Distribution",xlab="",ylab="")
c0<-seq(-pi,pi,length=61)
cx0<-cos(c0)
cy0<-sin(c0)
par(new=T)#上書き指定
plot(cx0+mean(cx),cy0+mean(cy),type="l",asp=1,xlim=c(-4,4),ylim=c(-4,4),main="",xlab="",ylab="",col=rgb(0,1,0))
par(new=T)#上書き指定
plot(cx0*2+mean(cx),cy0*2+mean(cy),type="l",asp=1,xlim=c(-4,4),ylim=c(-4,4),main="",xlab="",ylab="",col=rgb(0,1,0))
par(new=T)#上書き指定
plot(cx0*3+mean(cx),cy0*3+mean(cy),type="l",asp=1,xlim=c(-4,4),ylim=c(-4,4),main="",xlab="",ylab="",col=rgb(0,1,0))
text(mean(cx),mean(cy),"X",col=rgb(0,1,0))
}
# アニメーション
library("animation")
Time_Code=seq(1,16,length=16)
saveGIF({
for (i in Time_Code){
ND(i)
}
}, interval = 0.1, movie.name = "ND03.gif")
ND<-function(x){
cx<-rnorm(1000)
cy<-rnorm(1000)
plot(cx,cy,xlim=c(-4,4),asp=1,ylim=c(-4,4),main="Normal Distribution",xlab="",ylab="")
c0<-seq(-pi,pi,length=61)
cx0<-cos(c0)
cy0<-sin(c0)
par(new=T)#上書き指定
plot(cx0+mean(cx),cy0+mean(cy),type="l",asp=1,xlim=c(-4,4),ylim=c(-4,4),main="",xlab="",ylab="",col=rgb(0,1,0))
par(new=T)#上書き指定
plot(cx0*2+mean(cx),cy0*2+mean(cy),type="l",asp=1,xlim=c(-4,4),ylim=c(-4,4),main="",xlab="",ylab="",col=rgb(0,1,0))
par(new=T)#上書き指定
plot(cx0*3+mean(cx),cy0*3+mean(cy),type="l",asp=1,xlim=c(-4,4),ylim=c(-4,4),main="",xlab="",ylab="",col=rgb(0,1,0))
text(mean(cx),mean(cy),"X",col=rgb(0,1,0))
}
# アニメーション
library("animation")
Time_Code=seq(1,16,length=16)
saveGIF({
for (i in Time_Code){
ND(i)
}
}, interval = 0.1, movie.name = "ND02.gif")
library(rgl)
Rtime<-seq(0,2*pi,length=60)
cx<-rnorm(1000)
cy<-rnorm(1000)
cz<-rnorm(1000)
plot3d(cx,cy,cz,type="p",xlim=c(-4,4),ylim=c(-4,4),zlim=c(-4,4))
movie3d(spin3d(axis=c(0,0,1),rpm=5),duration=10,fps=25,movie="~/Desktop/r06")
①平均値(Mean)に立脚する中心検知技法(Center Detecting Technique)は、外れ値(Outliers)の影響を受けやすいので、それを除去する技術が共に発展してきた。
【初心者向け】誤差関数(ERF)と相補誤差関数 (ERFC)。
②中央値(Median)は平均値(Mean)より外れ値に対してロバスト(頑強)であり、かつ富が富裕層に集中している状況の様な中央値と平均値が解離している状況での中央検知に威力を発揮する。
【初心者向け】平均と標準偏差、中央値と平均偏差
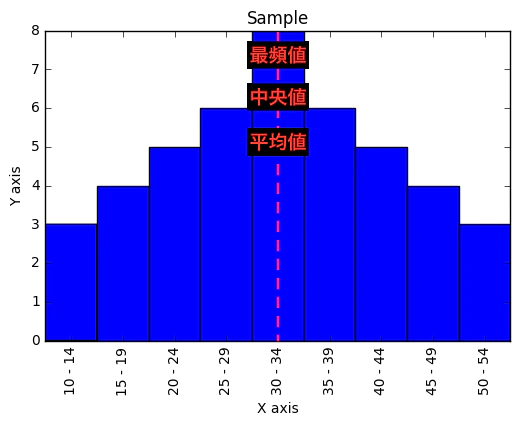
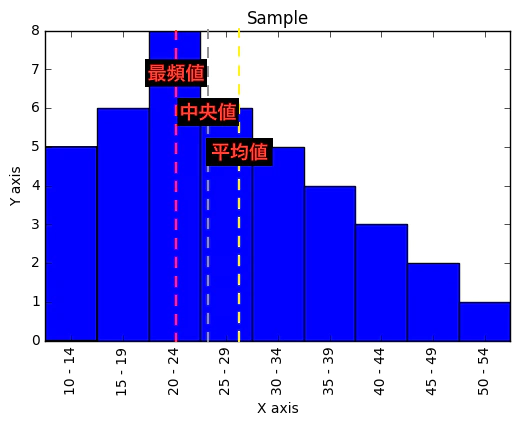
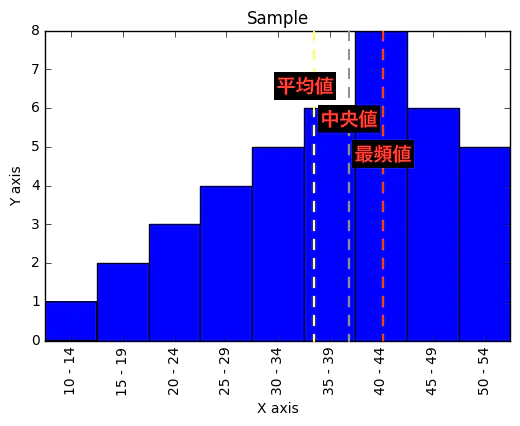
③正直、最頻値(Mode)に立脚する中央検知の意義はあまり研究されてないが、上掲二つのアプローチと併記して語られる事が多い。ピアソンの経験則によれば、ヒストグラムの分布が左右対称の場合は中央で重なる平均値・中央値・最頻値が、分布が左に偏る(右の裾野が広がる)場合には「最頻値・中央値・平均値」、分布が右に偏る(左の裾野が広がる)場合には「平均値・中央値・最頻値」の順に並ぶ事が多いという。
【初心者向け】度数分布/度数分布図と最頻値
【プログラマーのための統計学】平均値・中央値・最頻値
④さらにややこしい事に、現代における「統計科学的/確率論的アプローチ」は、かかる中央検知問題ばかりに拘泥している訳でもない。MCMC法の広まりや機械学習概念の台頭はそういう観点に関連してくる。
【初心者向け】「モンテカルロ法」概説

【初心者向け】ロジスティック方程式とその関連範囲
⑤確率楕円(Probability Ellipse)概念は、こうした考え方にさらに線形代数における固有値や固有ベクトル概念を加えた内容で、因子分析(Factor Analysis)の基礎。主成分分析(PCA=Principal Component Analysis)に至っては、同一平面上に展開する観測結果集合を複数の観測楕円に分割したりする。
Rによる楕円関数の実装例①

Cos_Waltz01<-function(Radius){
# 格子描画
grx=seq(-3,3,length=4)
gry01=rep(c(-1,1),2)
gry02=rep(c(1,-1),2)
plot(grx,gry01,type="l",asp=1,xlim=c(-1,1),ylim=c(-1,1),main="Cosine Waltz",xlab="x=-Cos(θ)→Sin(θ)→Cos(θ)→Sin(θ)→-Cos(θ)",ylab="Cos(θ)",col=rgb(0,0,0))
par(new=T)
plot(grx,gry02,type="l",asp=1,xlim=c(-1,1),ylim=c(-1,1),main="",xlab="",ylab="",col=rgb(0,0,0))
# 円描画
c0<-seq(0,pi*2,length=61)
cy<-cos(c0)
cx00<-cos(c0-pi*Radius)
cx01<-cos(c0-pi*Radius)-2
cx02<-cos(pi*Radius-c0)+2
par(new=T)
plot(cx00,cy,type="l",asp=1,xlim=c(-1,1),ylim=c(-1,1),main="",xlab="",ylab="",col=rgb(0,1,0))
for(i in 1:61)
{
segments(0,0,cx00[i],cy[i],col=rgb(0,1,0))
}
# 補助線
abline(h=0,col=rgb(1,0,0))
abline(v=0,col=rgb(1,0,0))
}
# アニメーション
library("animation")
Time_Code=seq(0, 4,length=61)
saveGIF({
for (i in Time_Code[1:60]){
Cos_Waltz01(i)
}
}, interval = 0.1, movie.name = "Cos_Waltz04.gif")
Cos_Waltz01<-function(Radius){
# 格子描画
grx=seq(-3,3,length=4)
gry01=rep(c(-1,1),2)
gry02=rep(c(1,-1),2)
plot(grx,gry01,type="l",xlim=c(-3,3),ylim=c(-1,1),main="Cosine Waltz",xlab="x=-Cos(θ)→Sin(θ)→Cos(θ)→Sin(θ)→-Cos(θ)",ylab="Cos(θ)",col=rgb(0,0,0))
par(new=T)
plot(grx,gry02,type="l",xlim=c(-3,3),ylim=c(-1,1),main="",xlab="",ylab="",col=rgb(0,0,0))
# 円描画
c0<-seq(0,pi*2,length=61)
cy<-cos(c0)
cx00<-cos(c0-pi*Radius)
cx01<-cos(c0-pi*Radius)-2
cx02<-cos(pi*Radius-c0)+2
par(new=T)
plot(cx00,cy,type="l",xlim=c(-3,3),ylim=c(-1,1),main="",xlab="",ylab="",col=rgb(0,1,0))
par(new=T)
plot(cx01,cy,type="l",xlim=c(-3,3),ylim=c(-1,1),main="",xlab="",ylab="",col=rgb(1,0,0))
par(new=T)
plot(cx02,cy,type="l",xlim=c(-3,3),ylim=c(-1,1),main="",xlab="",ylab="",col=rgb(0,0,1))
for(i in 1:61)
{
segments(0,0,cx00[i],cy[i],col=rgb(0,1,0))
}
for(i in 1:61)
{
segments(-2,0,cx01[i],cy[i],col=rgb(1,0,0))
}
for(i in 1:61)
{
segments(2,0,cx02[i],cy[i],col=rgb(0,0,1))
}
# 補助線
abline(h=0,col=rgb(1,0,0))
abline(v=0,col=rgb(1,0,0))
}
# アニメーション
library("animation")
Time_Code=seq(0, 4,length=61)
saveGIF({
for (i in Time_Code[1:60]){
Cos_Waltz01(i)
}
}, interval = 0.1, movie.name = "Cos_Waltz03.gif")
Pythonで綴る多変量解析 4-1. 因子分析(scikit-learn)
主成分分析を Python で理解する
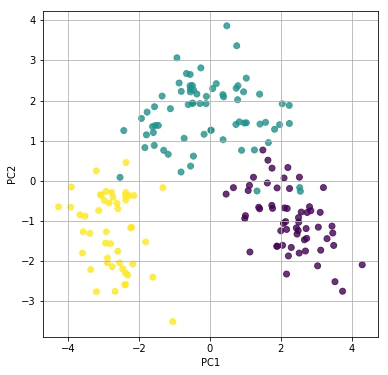
⑥適用する距離関数(Matric Function)の見直しは、かかる評価空間全体に影響を与える可能性がある。
【初心者向け】方形描画関数②距離空間との関係。
符号なし距離関数で作る魚眼レンズ効果

この投稿の目的は(こうした諸概念が現れる以前の)近世から近代にかけての数学者の足跡を追う事なので、とりあえずこのまま先を続けます。いずれにせよ興味深いのは、統計学の世界は実軸(Real Axis)を追加するごとに起こる視界狭窄(Vision Tunnel)と無縁な事で、これは統計学の座標系が原則として全て虚軸(Imaginal Axis)に分類される事を意味している可能性を示唆しているのです。
0次元を(乳幼児が生きているとされる、無意識と意識と超自我の境界線が存在しない)呪術的世界に擬えるなら、0.5次元は(ハイハイを始め、つかまり立ちを覚え、自分の足で歩き始める)経験主義的世界に該当します。哲学史の世界においては、人間が白紙状態(Tabula rasa)から経験の蓄積を始めると考える経験主義的立場と、経験知に対して先天的/生得的/先験的に(a priori)実存する認識が存在すると主張する観念論的立場が長年絶対的対立を続けてきましたが、虚数(Imaginal)概念が存在する数理の世界では、両者をこの様に連続的に統合的に扱う事が可能となるのですね。実際発達心理学によれば、人間の認知能力の成長は概ねこういう具合に進むとされています。
タブラ・ラサ | 現代美術用語辞典ver.2.0 - Artscape
アプリオリ - Wikipedia
1次元(1.0 Dimension)
中心検出に成功したら、いよいよこれを単位元(Identity Element)として反元(Inverse Elements)を設定し、群(Group)を定義する事が可能となります。確率変数の尺度(Stanley Smith Stevens,1946年)では比例尺度(Proportional Scale)に該当。これ以降、関数列(Function Sequance)を含む演算結果集合(Operation Result Set)が、観測結果集合(Ovsevation Result Set)と矛盾しない限り、その族(Famiry)を代表する形となります。
確率変数の尺度
library(igraph)
gd<-graph(edges=c("Zero(0)","Element(g)","Element(g)","Zero(0)","Element(g)","Inf(inity)","Inf(inity)","Element(g)","Zero(0)","Inverse(-g)","Inverse(-g)","Zero(0)","Inverse(-g)","-Inf(inity)","-Inf(inity)","Inverse(-g)"))
plot(gd,layout=layout.fruchterman.reingold)
pythonによる表現例
【Python演算処理】NetworkXライブラリを導入する。
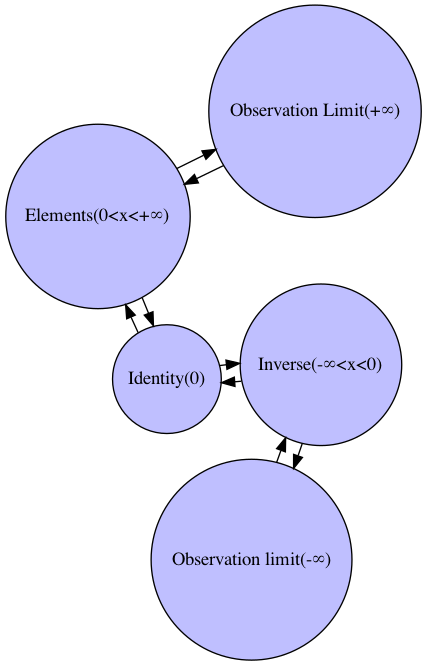
加法実数群(Additive Real Group)の場合
【数理考古学】とある実数列の規定例①等差数列から加法整数群へ
10進法(Decimal System)、すなわち10を法とする加法整数群(Additive Integer Group)の剰余類(Residue Class)の多層添字化によって理論上、小数点下を含む実数全体を扱える様に拡張された両側無限数列(Both-sides Infinite Sequance)。
乗法実数群(Multiplicative Real Group)の場合
【数理考古学】とある実数列の規定例②等比数列から乗法群へ
上掲の加法実数群(均等尺)を$-\infty→0,0→1,+\infty→\infty$に射影した片側無限数列(One-sides Infinite Sequance)。均等尺上の乗除算が加減算、冪乗算が乗算に置き換えられる。
【数理考古学】常用対数表を使った計算
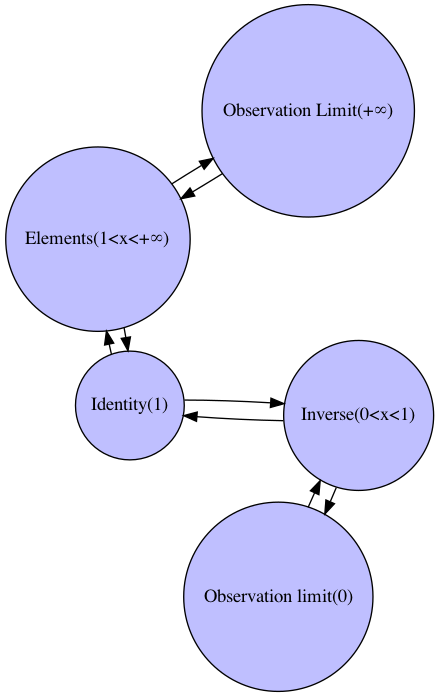
おやおや? 正負の概念が導入され、無限遠点$\infty$が無限大$+\infty$と無限小$-\infty$に引き裂かれると同時に、観測原点(Observation Origin)が座標上から消えてしまいました。このタイミングで偶奇(Parity)の概念が導入されるのは決して偶然でなく、どうやら「観測原点と観測対象の関係」もまた偶数系(Even System)と奇数系(Odd System)に引き裂かれてしまう様なのです。哲学でいう「(独我論や無我論と対比される)他我論」の登場ですね。それを数理の世界は「観測原点0が半径1の円弧を計測単位とする観測系を樹立すると、同時に観測対象たる1を観測原点とし、観測原点0を観測対象とする観測系を得る。前者を偶数系、後者を奇数系という」といった具合に説明し、この説明を用いると独我論と他我論と無我論の境界線が相対化によって消失してしまう訳です。
他我 - Wikipedia
トーラス座標系(Torus Coordinate System)と円筒座標系(Cylinder Coordinate System)の狭間
以前の投稿ではこの「独我」状態から…


この「我他相対」状態に直接飛躍すると説明してきました。
【数理考古学】とある実数列の規定例①等差数列から加法整数群へ


しかし実は「観測原点0が半径1の円弧を計測単位とする観測系を樹立した段階」からさらにこれに直交する実軸を考える場合、そこに現れるべきは円筒(Unit Cylinder)でなくドーナツ型のトーラス(単数形:torus, 複数形:tori)なのです。
Rによる実装例
library(rgl)
radians<-seq(0,60*pi,length=3000)
f0<-function(x){exp(x*(0+1i))}
f1<-function(x){sqrt(1-x^2)}
r0<-f0(radians)
c0<-seq(-1,1,length=1500)
# c1<-c(f1(c0)/2,-1*f1(c0)/2)
c1<-c(f1(c0),-1*f1(c0))
r1<-r0*(1+c1)
Real<-Re(r1)
Imaginal<-Im(r1)
Rtime<-c(seq(0,1,length=1500),seq(1,0,length=1500))
plot3d(Real,Imaginal,Rtime,type="l",xlim=c(-2,2),ylim=c(-2,2),zlim=c(0,2),xlab="",ylab="",zlab="")
# 大円描写
Real01<-Re(f0(radians))
Imaginal01<-Im(f0(radians))
Rtime01<-seq(1/2,1/2,length=3000)
points3d(Real01,Imaginal01,Rtime01,col=rgb(0,0,1))
# 小円描写
Real01<-Re(f0(radians))+1
Imaginal01<-Im(f0(radians))/2+1/2
Rtime01<-seq(0,0,length=3000)
points3d(Rtime01,Real01,Imaginal01,col=rgb(1,0,0))
movie3d(spin3d(axis=c(0,0,1),rpm=5),duration=10,fps=25,movie="~/Desktop/unit16")
pythonによる実装例
【Python演算処理】単位球面を巡る数理②そして単位トーラスへ



トーラスは座標系(Coordinate System)としては媒介変数t,p(0≦t≦2π,0≦p≦2π)を用いて以下の様に表します。
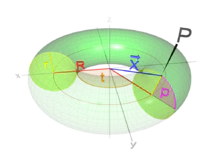
- x=大半径R×cos(t)+小半径r×cos(p)×cos(t)
- y=大半径R×cos(t)+小半径r×cos(p)×sin(t)
- z=小半径r×sin(p)
トーラスではなくなる極限状態は以下。
- 大半径R=0,小半径R=1の時、単位球面(Unit Sphere)を二重に描く。従って経緯度法(経度-180度~180度に対して緯度-90度~90度)や3次元極座標系(水平角φ=-π~πに対して垂直角0~π)は適用範囲を半分に減らしてなお球面上の全座標を示せるのはこれによる。
- 逆に大半径R=1,小半径R=0の時、Z=0となってただの単位円(Unit Circle)になる。
その中間過程に現れる大半径R=1,小半径R=1のトーラスを単位トーラス(Unit Torus)と呼ぶ事にしましょう。この単位トーラスをアイロンを掛けた様に平らに伸ばして円筒形座標系に移行するにはどうしたらいいでしょう?
- まずはトーラスを円筒状に展開する。この時高さは2π。中心線で分割するとπ×2。
- これを湾曲させて対蹠間の距離を2(片側の対蹠の座標が1なら-1)に到達させる。
おや、この操作には見覚えが…
i^2=e^{πi}=-1
Eulers_identity<-function(n){
rim01<-pi*complex(real=0,imaginary=1)
Tarm=c(complex(real=1,imaginary=0),seq(rim01/n,rim01/n,length=n))
Reduce(function(a,b) {a+a*b}, Tarm, accumulate = T)
}
# グラフを描画してみる。
Eulers_identity01_plot<-function(n){
ei01<-Eulers_identity(n)
ei02<-Conj(ei01)
# 背景描画
c00<-seq(-pi,pi,length=61)
c01<-exp(c00*(0+1i))
plot(c01+(0+1i),type="l",asp=1,xlim=c(-pi,pi),ylim=c(0,pi),main="Even Scale to Logarithmic Scale",xlab="Real",ylab="Imaginal")
par(new=T)
plot(c01+1,type="l",asp=1,xlim=c(-pi,pi),ylim=c(0,pi),main="",xlab="",ylab="")
par(new=T)
plot(c01-1,type="l",asp=1,xlim=c(-pi,pi),ylim=c(0,pi),main="",xlab="",ylab="")
par(new=T) # 上書き指定
plot(-Re(ei01)+1,Im(ei01),asp=1,xlim=c(-pi,pi),ylim=c(0,pi),type="l",main="", xlab="", ylab="",col=rgb(0,0,1))
par(new=T) # 上書き指定
plot(-Re(-ei02)-1,-Im(ei02),asp=1,xlim=c(-pi,pi),ylim=c(0,pi),type="l",main="", xlab="", ylab="",col=rgb(1,0,0))
segments(-2,0,2,0)
abline(h=(1+3/n)^n,col=c(200,200,200))
abline(h=(1+2.5/n)^n,col=c(200,200,200))
abline(h=(1+2/n)^n,col=c(200,200,200))
abline(h=(1+1.5/n)^n,col=c(200,200,200))
abline(h=(1+1/n)^n,col=rgb(0,1,0))
abline(h=(1+0.5/n)^n,,col=c(200,200,200))
abline(h=1,col=c(200,200,200))
abline(h=(1-0.5/n)^n,,col=c(200,200,200))
abline(h=(1-1/n)^n,col=rgb(0,1,0))
abline(h=(1-1.5/n)^n,col=c(200,200,200))
abline(h=(1-2/n)^n,col=c(200,200,200))
abline(h=(1-2.5/n)^n,col=c(200,200,200))
abline(h=(1-3/n)^n,col=c(200,200,200))
Text<-paste("(1±1/",n,")^",n,"=",round((1+1/n)^n,digits=4),"/",round((1-1/n)^n,digits=4))
legend("topleft", legend=c("π×(0+1i)","π×(0-1i)",Text), lty=c(1,1,1), col=c(rgb(0,0,1),rgb(1,0,0),rgb(0,1,0)))
}
# アニメーションさせてみる。
library("animation")
Time_Code=c(1,2,4,8,16,32,64,128)
saveGIF({
for (i in Time_Code){
Eulers_identity01_plot(i)
}
}, interval = 0.1, movie.name = "TEST.gif")
まだ関連数理を完全にはまとめ切れていませんが、基本方針としてはそう間違ってない気もしています。あくまで「補助線」の話に過ぎないので他の考え方も一杯出来そうだし。そんな感じで以下続報…