【Python演算処理】NetworkXライブラリを導入する。

R時代にはiGraphパッケージを使ってました。
Rとigraphを使ったネットワーク解析と可視化

pythonではNetworkXライブラリを使う様です。早速、自分のMacintoshにインストールしてみました。
【図解】Python NetworkXの使い方 | ネットワーク分析・可視化
【Python】NetworkX 2.0の基礎的な使い方まとめ
[python] Macにpygraphvizをインストールする

とりあえず以下の投稿の図示の差し替えに挑戦したいと思います。
【数理考古学】とある実数列の規定例③オイラーの等式e^πi=-1が意味するもの？

#０次元(Zero Dimension)
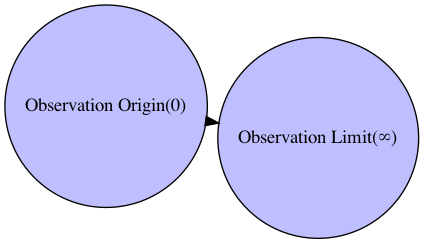
(それ自体は観測対象となり得ない)観測原点(Observation Origin)$0$と観測限界およびその向こう側(Observation Limit)$\infty$の間に「何もない」状態から出発する。群論(Group Theory)でいう空環概念(Empty/Nullary Ring Concept)に対応し、その元(Element)は空となる。
【初心者向け】群論概念②空環から整数環へ。

空環概念(Empty/Nullary Ring Concept)は「空和概念(Empty/Nullary Sum Concept)」の規約と「空積概念(Empty/Nullary Product Concept)」の規約の統合結果である。

①ここでいう「空和概念(Empty/Nullary Sum Concept)の規約」とは、群論(Group Theory)上における、空集合(Empty/Nullary Set)$\emptyset_n(n=0)=()$について「0個の因子を足し合わせた演算結果集合(Operation Result Set)で、加法単位元(Additive Identity)0に等しい(():=0)」とする規約をいう。

• 二項演算(Binary Operation)のうち、加減算(Addition and Subtraction)すなわち加法単位元(Additive Identity)$0+Α+Β(Α+(-Β))$においては任意の元(Any Element)$Α_n(n=0)()=Β_n(n=0)()=Γ_n(n=0)()=0$なので結合則(Associative Law)0+(Α+Β)+C+…=0+Α+(Β+C)+…も交換則(Commutative Law)0+Α+Β+…=0+Β+Α+…も成立し、その演算結果は閉じている(演算の都度0=()に戻る)。

②ここでいう「空積概念(Empty/Nullary Sum Concept)の規約」とは、群論(Group Theory)における、空集合概念(Empty/Nullary Set)$\emptyset _n(n=0)=()$について「0個の因子を掛け合わせた演算結果集合(Operation Result Set)で、乗法単位元(Multiplicative Identity)1に等しい(():=1)」とする規約をいう。

• 二項演算(Binary Operation)のうち、乗除算(Multiplying and Dividing)すなわち乗法単位元(Multiplicative Identity)$1×Α×Β(Α×(1/Β))$においては任意の元(Any Element)$Α_n(n=0)()=Β_n(n=0)()=Γ_n(n=0)()=1$となるので結合則(Associative Law)1×(Α×Β)×C+…=1×Α×(Β×C)×…も交換則(Commutative Law)1×Α×Β×…=1×Β×Α×…も成立し、その演算結果は閉じている(演算の都度1=()に戻る)。
• 二項演算(Binary Operation)のうち、冪算(Exponentiation)それ自体こそ分配法則や交換法則を満たさないものの、その計算範囲自体は上掲の演算に内包され、自明の理として演算結果も同じ範囲で閉じている($…A^2=A×A,A^2=A,A^0=\frac{A}{A}=1,A^-1=\frac{1}{A},A^-2=\frac{1}{A×A},…・$)。

③この時点ではあくまで空集合$\emptyset _n(n=0)()=(加減算における単位元)0=(乗除算における単位元)1$と規約されるだけで$\emptyset _n(n=2)=(0,1)$が成立する訳ではない点に注意されたい。

• 実際、単元集合(Singleton)/単位集合(Unit Set)$Α_n(n=1)=(0)$及び$Β_n(n=1)=(1)$、さらには二つを合算した集合$Γ_n(n=2)=(0,1)$全てが空環/空群$\emptyset(n=0)=()$と異なりそれ自体は群も環も構成しない。

まるで禅問答の様ですが、この概念を幾何学的イメージに置き換えたのが以下。有向グラフ(Directed graph)で表すと「観測者側からの観測対象に対する一方的観察」と図示される点が重要。

###空積概念(Empty/Nullary Sum Concept)

• 観測限界を点と置いた場合、(0~$\infty$の範囲に渡る)観測原点との距離$x$は、何倍にしても何分の1にしても値は変わらない。
• ただし例外的に$\frac{x}{x}=1$となり、これが乗法単位元(Multiplicative Identity)の概念の出発点になる。

import networkx as nx

G = nx.DiGraph()
G.add_edge("Observation Origin(0)","Observation Limit(∞)")
nx.nx_agraph.view_pygraphviz(G, prog='fdp') 

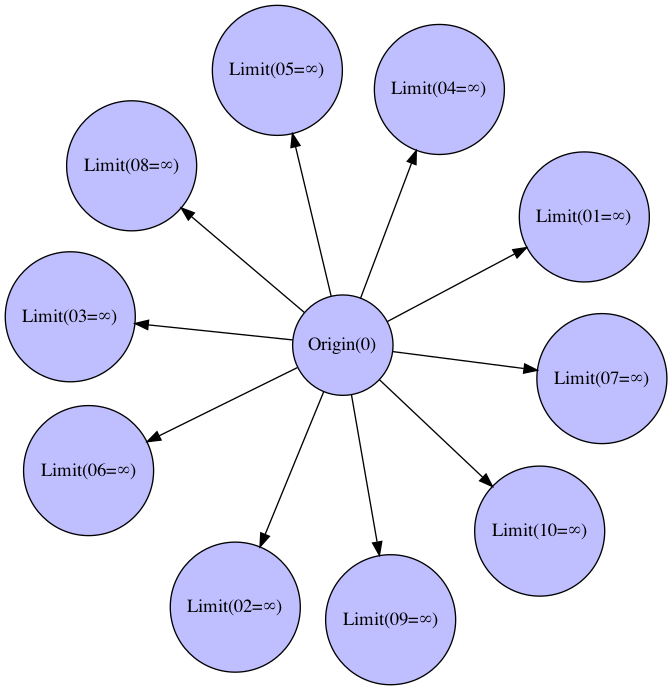
###空和概念(Empty/Nullary Sum Concept)

• 観測限界を(0~$\infty$の範囲に渡る)観測原点との距離$x$を半径とする円弧/球面と置いた場合、それをどんなに足し合わせても値は変わらない。
• ただし例外的に$x-x=0$となり、これが加法単位元(Additive Identity Identity)の概念の出発点になる。

import networkx as nx

G = nx.DiGraph()
G.add_edge("Origin(0)","Limit(01=∞)")
G.add_edge("Origin(0)","Limit(02=∞)")
G.add_edge("Origin(0)","Limit(03=∞)")
G.add_edge("Origin(0)","Limit(04=∞)")
G.add_edge("Origin(0)","Limit(05=∞)")
G.add_edge("Origin(0)","Limit(06=∞)")
G.add_edge("Origin(0)","Limit(07=∞)")
G.add_edge("Origin(0)","Limit(08=∞)")
G.add_edge("Origin(0)","Limit(09=∞)")
G.add_edge("Origin(0)","Limit(10=∞)")
nx.nx_agraph.view_pygraphviz(G, prog='fdp') 

• この状態はある意味、統計学における「統計対象に値しない」名義尺度(Nominal scale, Stanley Smith Stevens,1946年)、あるいは仮説検定において棄却される帰無仮説、すなわち「ここで証明したい事は証明不可能である」とする論拠に対応する。まさしく「(数理処理可能な有意味水準を超えるデータは)存在しない」状態の数理化という訳である。
  確率変数とは
  確率変数の尺度
  帰無仮説
  (null hypothesis)

#0.5次元(0.5 Dimension)

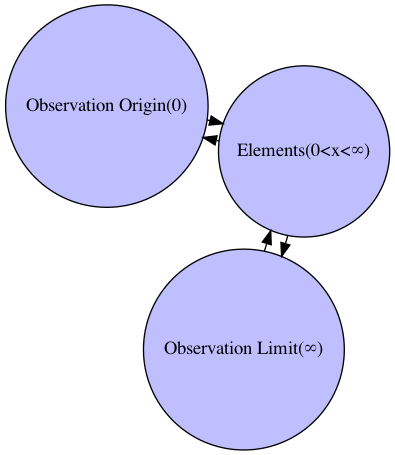
次元抽出や中心割り出しが可能そうな有望な観測結果集合(Observation Result Set)が得られて初めて「統計科学的/確率論的アプローチ」が可能となる。最初の評価軸であるから、当然それはX軸や時間軸(t軸)の形で与えられる。

import networkx as nx

G = nx.DiGraph()
G.add_edge("Observation Origin(0)","Elements(0<x<∞)")
G.add_edge("Elements(0<x<∞)","Observation Limit(∞)")
G.add_edge("Elements(0<x<∞)","Observation Origin(0)",)
G.add_edge("Observation Limit(∞)","Elements(0<x<∞)")
nx.nx_agraph.view_pygraphviz(G, prog='fdp') 

import networkx as nx

G = nx.DiGraph()
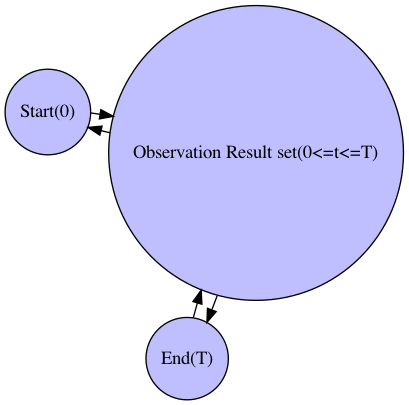
G.add_edge("Start(0)","Observation Result set(0<=t<=T)")
G.add_edge("Observation Result set(0<=t<=T)","End(T)")
G.add_edge("Observation Result set(0<=t<=T)","Start(0)")
G.add_edge("End(T)","Observation Result set(0<=t<=T)")
nx.nx_agraph.view_pygraphviz(G, prog='fdp') 

統計の対象となる実データには当然(観測不可能な)両極限は現れず、最大値(Max)と最小値(Min)がそれが推察可能な形で得られるとも限らない。

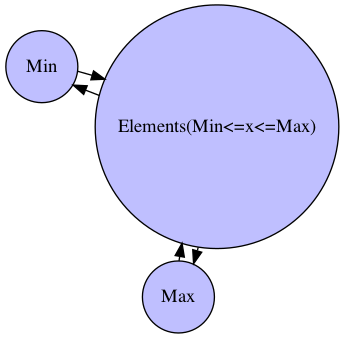
import networkx as nx

G = nx.DiGraph()
G.add_edge("Min","Elements(Min<=x<=Max)")
G.add_edge("Elements(Min<=x<=Max)","Max")
G.add_edge("Elements(Min<=x<=Max)","Min",)
G.add_edge("Max","Elements(Min<=x<=Max)")
nx.nx_agraph.view_pygraphviz(G, prog='fdp') 

この辺りのニュアンスも含め、確率変数の尺度(Stanley Smith Stevens,1946年)では「データ間の順位にのみ意味がある」順位尺度(Ordinal scale)から「データ間の差にのみ意味がある」間隔尺度(Interval scale)にかけてが該当する。
確率変数の尺度

#1次元(1.0 Dimension)

中心検出に成功したら、いよいよこれを単位元(Identity Element)として反元(Inverse Elements)を設定し、群(Group)を定義する事が可能となります。確率変数の尺度(Stanley Smith Stevens,1946年)では比例尺度(Proportional Scale)に該当。これ以降、関数列(Function Sequance)を含む演算結果集合(Operation Result Set)が、観測結果集合(Ovsevation Result Set)と矛盾しない限り、その族(Famiry)を代表する形となるのです。
確率変数の尺度

###加法実数群(Additive Real Group)の場合
【数理考古学】とある実数列の規定例①等差数列から加法整数群へ
10進法(Decimal System)、すなわち10を法とする加法整数群(Additive Integer Group)の剰余類(Residue Class)の多層添字化によって理論上、小数点下を含む実数全体を扱える様に拡張された両側無限数列(Both-sides Infinite Sequance)。

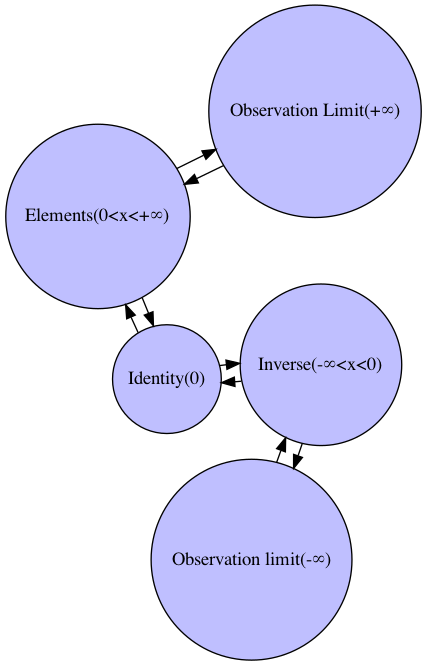
import networkx as nx

G = nx.DiGraph()
G.add_edge("Observation limit(-∞)","Inverse(-∞<x<0)")
G.add_edge("Inverse(-∞<x<0)","Identity(0)")
G.add_edge("Identity(0)","Elements(0<x<+∞)")
G.add_edge("Elements(0<x<+∞)","Observation Limit(+∞)")
G.add_edge("Inverse(-∞<x<0)","Observation limit(-∞)")
G.add_edge("Identity(0)","Inverse(-∞<x<0)")
G.add_edge("Elements(0<x<+∞)","Identity(0)")
G.add_edge("Observation Limit(+∞)","Elements(0<x<+∞)")

nx.nx_agraph.view_pygraphviz(G, prog='fdp')

##乗法実数群(Multiplicative Real Group)の場合
【数理考古学】とある実数列の規定例②等比数列から乗法群へ
上掲の加法実数群(均等尺)を$-\infty→0,0→1,+\infty→\infty$に射影した片側無限数列(One-sides Infinite Sequance)。均等尺上の乗除算が加減算、冪乗算が乗算に置き換えられる。

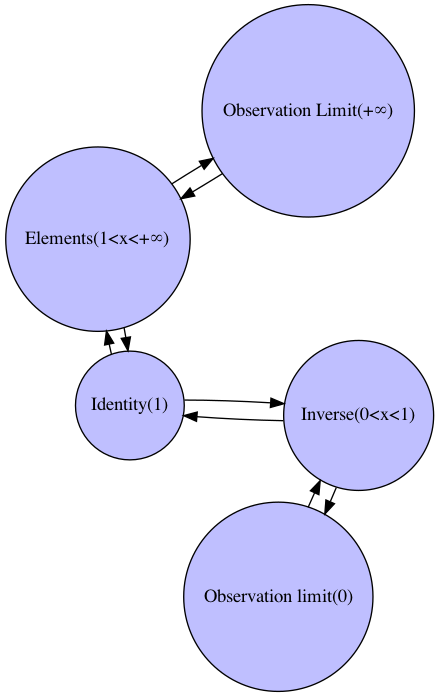
import networkx as nx

G = nx.DiGraph()
G.add_edge("Observation limit(0)","Inverse(0<x<1)")
G.add_edge("Inverse(0<x<1)","Identity(1)")
G.add_edge("Identity(1)","Elements(1<x<+∞)")
G.add_edge("Elements(1<x<+∞)","Observation Limit(+∞)")
G.add_edge("Inverse(0<x<1)","Observation limit(0)")
G.add_edge("Identity(1)","Inverse(0<x<1)")
G.add_edge("Elements(1<x<+∞)","Identity(1)")
G.add_edge("Observation Limit(+∞)","Elements(1<x<+∞)")

nx.nx_agraph.view_pygraphviz(G, prog='fdp')

おやおや？　正負の概念が導入され、無限遠点$\infty$が無限大$+\infty$と無限小$-\infty$に引き裂かれると同時に、観測原点(Observation Origin)が座標上から消えてしまいました。このタイミングで偶奇(Parity)の概念は導入されるのは決して偶然でなく、どうやら「観測原点と観測対象の関係」もまた偶数系(Even System)と奇数系(Odd System)に引き裂かれてしまった様なのです。

そんな感じで以下続報…