(2020年12月25日)Rによる投稿
(2021年04月08日)texとpythonによる追記
群概念(Group Concept)は空環概念(Empty/Nullary Ring Concept)から出発し、自明の場合(Trival Case)として自然数集合(Natural Set)や加法整数群(Additive Integer Group)概念に発展します。
【初心者向け】群論概念(Group Theory Concept)①基本定義

剰余類概念(Residue Class Concept)の出発点でもありますね。ここから「桁上がり(Carry)」「桁下がり(Borrow)」概念の導入(Introduction)を経てN進法(N-ary)の世界へと発展していくのです。
整数の加法群の剰余類
【初心者向け】N進法(N-ary)とp進数(p-adic)


群論概念(Group Theory Concept)における出発点としての空環概念(Empty/Nullary Ring Concept)
それは「空和概念(Empty/Nullary Sum Concept)」の規約と「空積概念(Empty/Nullary Product Concept)」の規約の統合結果です。
環 (数学) - Wikipedia
関係演算子としての記号 := と =: について教え乞う
- その各二項演算(Binary Operation)上の振る舞いは、単一の要素(Element=)しか備えない単元集合(Singleton)/単位集合(Unit Set)のそれと似ている。
単集合 - Wikipedia - これから一応全ての場合について検証するが「またつまらぬ物を斬ってしまった」感が物凄い(実は「ルパン三世(漫画原作1967年~、アニメ化1971年~)」の石川五右衛門がこのセリフを最初に口にしたのは原作漫画でもTVアニメシリーズでのなく劇場版映画の中でだったのは有名なトリビア)。
ルパン三世の石川五右衛門のセリフで、「また、つまらぬ物を斬ってしまった」というのがあったと思い - ルパン三世の石川五右衛... - Yahoo!知恵袋
斬鉄剣で斬ってしまったつまらぬもの一覧とは (ザンテツケンノムダヅカイとは) [単語記事] - ニコニコ大百科
①ここでいう「空和概念(Empty/Nullary Sum Concept)の規約」とは、群論(Group Theory)における、空集合概念(Empty/Nullary Set)$\emptyset_n(n=0)=()$について「0個の因子を足し合わせた空集合で、加法単位元(Additive Identity)0に等しい(():=0)」とする規約をいう。
- 二項演算(Binary Operation)のうち、加減算(Addition and Subtraction)すなわち加法単位元(Additive Identity)$0+Α+Β(Α+(-Β))$においては任意の元(Any Element)$Α_n(n=0)()=Β_n(n=0)()=Γ_n(n=0)()=0$なので結合則(Associative Law)0+(Α+Β)+C+…=0+Α+(Β+C)+…も交換則(Commutative Law)0+Α+Β+…=0+Β+Α+…も成立し、その演算結果は閉じている(演算の都度0=()に戻る)。
空和概念上で想定される加減算上の交換条件と結合条件
統計言語Rによる検証
# 加法単位元(Additive Identity)0の規定
> AI<-0
# 任意の元(Any Element)の規定
> Alpha<-0
> Beta<-0
> Gamma<-0
# 加算(Addition)
> AI+Alpha+Beta
[1] 0
> AI+Alpha+Beta+Gamma
[1] 0
# 減算(Subtraction)
# 2^2-1=3通り
> AI-Alpha+Beta
[1] 0
> AI+Alpha-Beta
[1] 0
> AI-Alpha-Beta
[1] 0
# 2^3-1=7通り
> AI-Alpha+Beta+Gamma
[1] 0
> AI+Alpha-Beta+Gamma
[1] 0
> AI+Alpha-Beta-Gamma
[1] 0
> AI-Alpha-Beta+Gamma
[1] 0
> AI-Alpha+Beta-Gamma
[1] 0
> AI+Alpha-Beta-Gamma
[1] 0
> AI-Alpha-Beta-Gamma
[1] 0
# 交換法則
> AI+Alpha-Beta
[1] 0
> AI-Beta+Alpha
[1] 0
> AI-Alpha+Beta
[1] 0
> AI+Beta-Alpha
[1] 0
# 結合法則
> AI+(-Alpha+Beta)+Gamma
[1] 0
> AI-Alpha+(Beta+Gamma)
[1] 0
> AI+(Alpha-Beta)+Gamma
[1] 0
> AI+Alpha+(-Beta+Gamma)
[1] 0
> AI+(Alpha+Beta)-Gamma
[1] 0
> AI+Alpha+(Beta-Gamma)
[1] 0
②ここでいう「空積概念(Empty/Nullary Sum Concept)の規約」とは、群論(Group Theory)における、空集合概念(Empty/Nullary Set)$\emptyset _n(n=0)=()$について「0個の因子を掛け合わせた演算結果集合(Operation Result Set)で、乗法単位元(Multiplicative Identity)1に等しい(():=1)」とする規約をいう。
- 二項演算(Binary Operation)のうち、乗除算(Multiplying and Dividing)すなわち乗法単位元(Multiplicative Identity)$1×Α×Β(Α×(1/Β))$においては任意の元(Any Element)$Α_n(n=0)()=Β_n(n=0)()=Γ_n(n=0)()=1$となるので結合則(Associative Law)1×(Α×Β)×C+…=1×Α×(Β×C)×…も交換則(Commutative Law)1×Α×Β×…=1×Β×Α×…も成立し、その演算結果は閉じている(演算の都度1=()に戻る)。
- 二項演算(Binary Operation)のうち、冪算(Exponentiation)それ自体こそ分配法則や交換法則を満たさないものの、その計算範囲自体は上掲の演算に内包され、自明の理として演算結果も同じ範囲で閉じている($…A^2=A×A,A^2=A,A^0=\frac{A}{A}=1,A^-1=\frac{1}{A},A^-2=\frac{1}{A×A},…・$)。
空積概念における乗除算上の交換条件と結合条件
統計言語Rによる検証
# 乗法単位元(Multiplicative Identity)1の規定
> MI<-1
# 任意の元(Any Element)の規定
> Alpha<-1
> Beta<-1
> Gamma<-1
# 乗算(Multiplying)
> MI*Alpha*Beta
[1] 1
> MI*Alpha*Beta*Gamma
[1] 1
# 除算(Dividing)
# 2^2-1=3通り
> MI*(1/Alpha)*Beta
[1] 1
> MI*Alpha*(1/Beta)
[1] 1
> MI*(1/Alpha)*(1/Beta)
[1] 1
# 2^3-1=7通り
> MI*(1/Alpha)*Beta*Gamma
[1] 1
> MI*Alpha*(1/Beta)*Gamma
[1] 1
> MI*Alpha*Beta*(1/Gamma)
[1] 1
> MI*(1/Alpha)*(1/Beta)*Gamma
[1] 1
> MI*(1/Alpha)*Beta*(1/Gamma)
[1] 1
> MI*Alpha*(1/Beta)*(1/Gamma)
[1] 1
> MI*(1/Alpha)*(1/Beta)*(1/Gamma)
[1] 1
# 交換法則
> MI*Alpha*(1/Beta)
[1] 1
> MI*(1/Beta)*Alpha
[1] 1
> MI*(1/Alpha)*Beta
[1] 1
> MI*Beta*(1/Alpha)
[1] 1
# 結合法則
> MI*((1/Alpha)*Beta)*Gamma
[1] 1
> MI*(1/Alpha)*(Beta*Gamma)
[1] 1
> MI*(Alpha*(1/Beta))*Gamma
[1] 1
> MI*Alpha*((1/Beta)*Gamma)
[1] 1
> MI*(Alpha*Beta)*(1/Gamma)
[1] 1
> MI*Alpha*(Beta*(1/Gamma))
[1] 1
③この時点ではあくまで空集合$\emptyset _n(n=0)()=(加減算における単位元)0=(乗除算における単位元)1$と規約されるだけで$\emptyset _n(n=2)=(0,1)$が成立する訳ではない点に注意されたい。実際、単元集合(Singleton)/単位集合(Unit Set)$Α_n(n=1)=(0)$及び$Β_n(n=1)=(1)$、さらには二つを合算した集合$Γ_n(n=2)=(0,1)$全てが空環/空群$\emptyset(n=0)=()$と異なりそれ自体は群も環も構成しない。理由は簡単。演算結果集合(Operation Result Set)が集合全体に対して閉じなくなってしまうからである。
自明の場合(Trival Case)としての自然数集合(Natural Set)/加法整数群(Additive Integer Group)への発展。
どういう事なのでしょう。まずは集合$Γ_n(n=1)=(1)$における「乗法単位元(Additive Identity)0を巡る加減算」に目を向けて見てみましょう。
統計言語Rによる検証
# 加法単位元(Additive Identity)0の規定
AI<-0
# 任意の元(Any Element)へのの規定
Alpha<-1
Beta<-1
Gamma<-1
# 加算(Addition)
AI+Alpha+Beta
[1] 2
AI+Alpha+Beta+Gamma
[1] 3
# 減算(Subtraction)
# 2^2-1=3通り
> AI-Alpha+Beta
[1] 0
> AI+Alpha-Beta
[1] 0
> AI-Alpha-Beta
[1] -2
# 2^3-1=7通り
> AI-Alpha+Beta+Gamma
[1] 1
> AI+Alpha-Beta+Gamma
[1] 1
> AI+Alpha-Beta-Gamma
[1] -1
> AI-Alpha-Beta+Gamma
[1] -1
> AI-Alpha+Beta-Gamma
[1] -1
> AI+Alpha-Beta-Gamma
[1] -1
> AI-Alpha-Beta-Gamma
[1] -3
# 交換法則
> AI+Alpha-Beta
[1] 0
> AI-Beta+Alpha
[1] 0
> AI-Alpha+Beta
[1] 0
> AI+Beta-Alpha
[1] 0
# 結合法則
> AI+(-Alpha+Beta)+Gamma
[1] 1
> AI-Alpha+(Beta+Gamma)
[1] 1
> AI+(Alpha-Beta)+Gamma
[1] 1
> AI+Alpha+(-Beta+Gamma)
[1] 1
> AI+(Alpha+Beta)-Gamma
[1] 1
> AI+Alpha+(Beta-Gamma)
[1] 1
無限再帰二項演算(Infinity Loop of Binary Operation)の働きによって数直線(Number Line)や座標系(Coordinate System)を構築するいわば距離(Distance)の概念が作用し始めてしまうのが原因ですね。
- $Α_n(n=0→+\infty)=(0,0+1=1,1+1=2,(1+1)+1=3,((1+1)+1)=4,…,+\infty)$
- $Α_n(n=0→-Inf)=(0,0-1=-1,(0-1)-1=-2,((0-1)-1)-1=-3,…,-\infty)$
そこで群/環としての閉性(Closure)を回復する為、以下の概念を導入します。
- 自然数集合(Natural Set)…初項(First Term)1/公差(Common Difference)1の等差数列(Arithmetic Sequence=算術数列)$N_n(n=1→\infty)(a0,an+(n-1)d,…)(ただしa0=初項,d=公差)={1,1+1=2,(1+1)+1=3,…,\infty}の形で規定される。
- 加法整数群(Additive Integer Group)…自然数集合$N_n$の概念に加法単位元0と逆元$-N_n$の概念を付加して群成立条件を満たした結果。初項(First Term)$-\infty$/終項(Last Term)+\infty/公差(Common Difference)1の等差数列$Z_n(n=-\infty→-3→-2→-1→0→1→2→3→+\infty)(-\infty,…,((0-1)-1)-1=-3,(0-1)-1=-2,0-1=-1,0,0+1=1,(0+1)2,((0+1)+1)+1,…,+\infty)$の形で規定される。
【初心者向け】群論概念(Group Theory Concept)①基本定義
Rの場合
元(Element)

逆元(Inverse Element)

群(Group)

pythonの場合
元(Element)

逆元(Inverse Element)

群(Group)

こう考えると幸いな事に少なくとも加法の範囲では距離の変化が連続しており(つまり等差数列を構築するので)各距離ごとで交換則も結合則も成立します(減法についても上掲の様な形で加法の一種で繰り込む形で事実上加減法の範囲で成立)。演算結果も閉じます。
距離(Distance)2(1+1)における交換則と結合則の成立(以下再帰的繰り返し)
統計言語Rによる検証
# 加法単位元(Additive Identity)0の規定
> AI<-0
# 任意の元(Any Element)の規定
> Alpha<-2
> Beta<-2
> Gamma<-2
# 加算(Addition)
> AI+Alpha+Beta
[1] 4
> AI+Alpha+Beta+Gamma
[1] 6
# 減算(Subtraction)
# 2^2-1=3通り
> AI-Alpha+Beta
[1] 0
> AI+Alpha-Beta
[1] 0
> AI-Alpha-Beta
[1] -4
# 2^3-1=7通り
> AI-Alpha+Beta+Gamma
[1] 2
> AI+Alpha-Beta+Gamma
[1] 2
> AI+Alpha-Beta-Gamma
[1] -2
> AI-Alpha-Beta+Gamma
[1] -2
> AI-Alpha+Beta-Gamma
[1] -2
> AI+Alpha-Beta-Gamma
[1] -2
> AI-Alpha-Beta-Gamma
[1] -6
# 交換法則
> AI+Alpha-Beta
[1] 0
> AI-Beta+Alpha
[1] 0
> AI-Alpha+Beta
[1] 0
> AI+Beta-Alpha
[1] 0
# 結合法則
> AI+(-Alpha+Beta)+Gamma
[1] 2
> AI-Alpha+(Beta+Gamma)
[1] 2
> AI+(Alpha-Beta)+Gamma
[1] 2
> AI+Alpha+(-Beta+Gamma)
[1] 2
> AI+(Alpha+Beta)-Gamma
[1] 2
> AI+Alpha+(Beta-Gamma)
[1] 2
距離(Distance)-1(0-1)における交換則と結合則の成立(以下再帰的繰り返し)
統計言語Rによる検証
# 加法単位元(Additive Identity)0の規定
> AI<-0
# 任意の元(Any Element)の規定
> Alpha<--1
> Beta<--1
> Gamma<--1
# 加算(Addition)
> AI+Alpha+Beta
[1] -2
> AI+Alpha+Beta+Gamma
[1] -3
# 減算(Subtraction)
# 2^2-1=3通り
> AI-Alpha+Beta
[1] 0
> AI+Alpha-Beta
[1] 0
> AI-Alpha-Beta
[1] 2
# 2^3-1=7通り
> AI-Alpha+Beta+Gamma
[1] -1
> AI+Alpha-Beta+Gamma
[1] -1
> AI+Alpha-Beta-Gamma
[1] 1
> AI-Alpha-Beta+Gamma
[1] 1
> AI-Alpha+Beta-Gamma
[1] 1
> AI+Alpha-Beta-Gamma
[1] 1
> AI-Alpha-Beta-Gamma
[1] 3
# 交換法則
> AI+Alpha-Beta
[1] 0
> AI-Beta+Alpha
[1] 0
> AI-Alpha+Beta
[1] 0
> AI+Beta-Alpha
[1] 0
# 結合法則
> AI+(-Alpha+Beta)+Gamma
[1] -1
> AI-Alpha+(Beta+Gamma)
[1] -1
> AI+(Alpha-Beta)+Gamma
[1] -1
> AI+Alpha+(-Beta+Gamma)
[1] -1
> AI+(Alpha+Beta)-Gamma
[1] -1
> AI+Alpha+(Beta-Gamma)
[1] -1
乗除算や冪算についてはこうは行きません。
- とりあえず整数の乗法結果集合(Multiplication Result Set)たる初項(First Term)0/公比(Common Ratio)1の等比数列(Geometric sequence=幾何数列)$A_n(n=0→Inf)(1,…,a×a^(n-1)d,…,Inf)(ただし1=乗法単位元,r=公比)を半群(Semigroup)と規定し、これと加法整数群を合わせた概念を整数環(Ring of Integers)と呼ぶ。
半群 - Wikipedia
整数環 - Wikipedia
ところでこの段階までは到達しないと(上掲の等差数列や等比数列の様な)添字単位(Index Unit)と周回単位(Cycle Unit)が織りなす添字集合(Index Set)の概念すら導入出来ません。
【初心者向け】添字化(Indexing)と単位化(Unitization)
するとこれはある種の循環論法(Circular Logic)?
循環論法 - Wikipedia
ハートリー近似
そして遂には視野外を虚数概念(Imaginary Concept)や四元数(Quaternion Concept)概念が跋扈する?
ところで現代人の観点からすれば、かかる整数環(Ring of Integers)の定義はいささか臆病すぎやしないでしょうか? 例えばN次元座標系(N-Dimensional Coordinate System)上では以下の様な数列が普通に登場するのです。
【初心者向け】線形関数(Linear Function)や絶対値関数(Absolute Value Function)
Z軸に沿ったX-Y面を巡る円錐座標系

X軸に沿ったY-Z面を巡る円錐座標系、あるいはY軸に沿ったX-Z面を巡る円錐座標系

- 二次元空間における平方展開(Square Deployment)$N^2(N=-\infty→-3,-2,-1,0,1,2,3→+\infty)=(-\infty,…,-9,-4,-1,0,1,4,9,…,+\infty)$
- 三次元空間における立方展開(Cubic Deployment)$N^3(N=-\infty→-3,-2,-1,0,1,2,3→+infty)=(-\infty,…,-27,-8,-1,0,1,8,27,…,\infty)$
こうした観察結果をそのまま表現(Expression)すると以下の様になるのではないでしょうか?
-
「2乗すると負数」の単位元は、もちろん自明の場合(Trival Case)として(実数関数x^2=1に対応する)虚数関数(Imaginary Function)$i^2=(0 \pm i)^{2x}=-1$となる。
【Rで球面幾何学】そもそも複素数Xi(x*(0+1i))はどう振る舞う?

-
この考え方の延長線上に自明の場合として四元数(Quaternion)$i^2(j=0でk=iもしくはk=0でj=iの時)=j^2(i=0でk=jもしくはk=0でi=jの時)=k^2(i=0でj=kもしくはj=0でi=kの時)=ijk=-1$が現れる。
【オイラーの多面体定理と正多面体】正方形における平方対角線(Square diagonal)と立方体における立方対角線(Cubic diagonal)の関係について。
Rで球面幾何学】ハミルトンの四元数は何を表しているのか?
ijk=-1の場合
ji-k=-1の場合
kj-i=-1の場合
ik-j=-1の場合
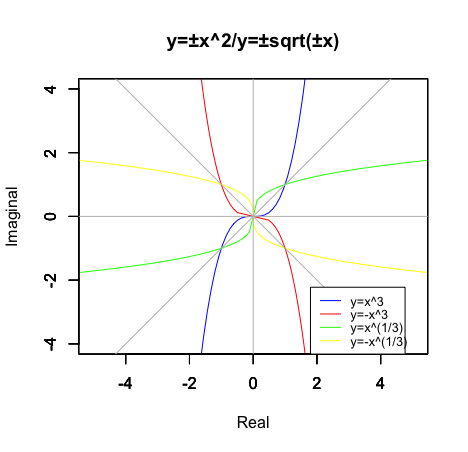
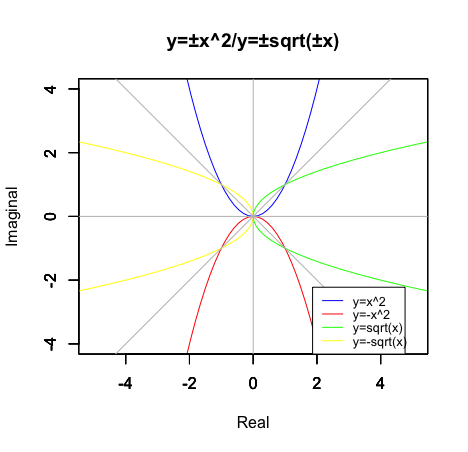
そして、かかる概念を援用すると見慣れた二次関数$y=±x^2$/三次関数$±y=x^3$が自明の場合として「(逆関数化によって)関数$x=y$/関数$x=-y$の軌跡を回転軸に向きを180度回転させられる」という結論に到達するのです。
統計言語Rによる検証
二次関数$y=±x^2$とその逆関数たる平方根関数y=$±x^{\frac{1}{2}}$
s00=seq(-3,3,length=41)
s01<-complex(re=s00,im=s00^2)
s02<-complex(re=s00^2,im=s00)
plot(s01,type="l",asp=1,xlim=c(-4,4),ylim=c(-4,4),main="y=±x^2/y=±sqrt(±x)",xlab="Real",ylab="Imaginal",col=rgb(0,0,1))
par(new=T)#上書き指定
plot(-s01,type="l",asp=1,xlim=c(-4,4),ylim=c(-4,4),main="",xlab="",ylab="",col=rgb(1,0,0))
par(new=T)#上書き指定
plot(s02,type="l",asp=1,xlim=c(-4,4),ylim=c(-4,4),main="",xlab="",ylab="",col=rgb(0,1,0))
par(new=T)#上書き指定
plot(-s02,type="l",asp=1,xlim=c(-4,4),ylim=c(-4,4),main="",xlab="",ylab="",col=rgb(1,1,0))
abline(h=0,col=c(200,200,200))
abline(v=0,col=c(200,200,200))
segments(-7,-7,7,7,col=c(200,200,200))
segments(-7,7,7,-7,col=c(200,200,200))
legend("bottomright", legend = c("y=x^2","y=-x^2","y=sqrt(x)","y=-sqrt(x)"), col=c(rgb(0,0,1),rgb(1,0,0),rgb(0,1,0),rgb(1,1,0)),lty =c(1,1,1,1),cex=0.8)
三次次関数y=$±x^3$とその逆関数たる立方根関数y=$±x^{\frac{1}{3}}$
s00=seq(-6,6,length=101)
s0h=seq(0,6,length=51)^(1/3)
s0r=c(-rev(s0h),s0h[2:51])
s01<-complex(re=s00,im=s00^3)
s01R<-complex(re=s00,im=s0r)
s02<-complex(re=-s00^3,im=s00)
s02R<-complex(re=-s0r,im=s00)
plot(s01,type="l",asp=1,xlim=c(-4,4),ylim=c(-4,4),main="y=±x^2/y=±sqrt(±x)",xlab="Real",ylab="Imaginal",col=rgb(0,0,1))
par(new=T)#上書き指定
plot(s01R,type="l",asp=1,xlim=c(-4,4),ylim=c(-4,4),main="",xlab="",ylab="",col=rgb(0,1,0))
par(new=T)#上書き指定
plot(s02,type="l",asp=1,xlim=c(-4,4),ylim=c(-4,4),main="",xlab="",ylab="",col=rgb(1,1,0))
par(new=T)#上書き指定
plot(s02R,type="l",asp=1,xlim=c(-4,4),ylim=c(-4,4),main="",xlab="",ylab="",col=rgb(1,0,0))
abline(h=0,col=c(200,200,200))
abline(v=0,col=c(200,200,200))
segments(-7,-7,7,7,col=c(200,200,200))
segments(-7,7,7,-7,col=c(200,200,200))
legend("bottomright", legend = c("y=x^3","y=-x^3","y=x^(1/3)","y=-x^(1/3)"), col=c(rgb(0,0,1),rgb(1,0,0),rgb(0,1,0),rgb(1,1,0)),lty =c(1,1,1,1),cex=0.8)
この様に一般化すると冪乗関数$x^n$の逆関数はN乗根関数$x^{\frac{1}{n}}となる訳ですが、何か重要な基本的事実を見落としてる様な…とりあえずそんな感じで以下続報。