(2020年10月16日)Rによる投稿
(2021年3月29日)tex部とpython部を追記
(2021年4月12日)回転方向を反時計回りで統一。
真の意味での「数学自体初学者自身の手になる、数学自体初学者の為の群論入門」。一歩間違えば「群盲象を評す」状態に陥ってしまいます。
群盲象を評す - Wikipedia
添字集合(Indexed Set)としての基本設定。
まずは基本規約。特定の二項演算(Binary Operation)の結果集合(Result Set)としての群(Group)は、原則として添字記法(Index notation=指数記法)Xnで表されます。
族 (数学) - Wikipedia
数学における族(Family)は、添字付けされた(Indexed)元(Elements=要素)の(一般には非可算無限個の)集まりXnを指し、対、n-組、列などの概念の一般化である。系(Collection)と呼ぶこともある。元がどのような対象であるかによって、点族、集合族(集合系)、関数族(関数系)などと呼ばれる。
集合Iから集合Xへの写像A:I→Xが与えられた時、これをXの元の集まりとみなしたものを、Iを添字集合(index set)とするXの元の族とし、添字集合Iの元を添字 (index)という。Iの要素を仮に i, j,… と表すとき、A(i), A(j),… の代わりに、通例 Ai, Aj,…といった記法を用い、この族を(Ai|i∈I),(Ai)i∈I,{Ai|i∈I},{Ai}i∈Iなどであらわす。これを添字記法などと呼ぶこともある。
明示的に「添字付けられた族(indexed family)」という場合もある。また、暗に適当な濃度の集合を添字集合として添字付けることができるような集まり、という意味で「族」という術語を用い、必ずしもはじめから族が添字付けられていない場合もある。添字があらかじめ与えられていない場合でも、族に対して何らかの操作を考えるときなどには添字があったほうが都合がよく、必要な基数をもつ集合をとって添字付けを与えるのが通例である。
そして上掲の[添字付けられた族」は、その内容を空環(Empty/Nullary Ring)→自然数集合(Natural Set)→加法整数群(Additive Integer Group)→整数環(Ring of Integers)の順に充実させていきます。
【初心者向け】群論概念(Group Theory Concept)②空環(Empty/Nullary Ring)から整数環(Ring of Integers)へ。

X軸に沿ったY-Z面を巡る円錐座標系、あるいはY軸に沿ったX-Z面を巡る円錐座標系

代数的構造(Algebraic Structure)の導入。
こうした記述から、どうやら群(Group)研究とは、その代数的構造(Algebraic Structure)を明らかにする学問だと考える様になったのです。
代数的構造 - Wikipedia
数学において代数的構造(Algebraic Structure)とは、集合に定まっている算法(演算ともいう)や作用によって決まる構造のことである。代数的構造の概念は、数学全体を少数の概念のみを用いて見通しよく記述するために架空の数学者ニコラ・ブルバキ(Nicolas Bourbaki, 活動時期1934年~、主著書「数学原論(Éléments de mathématique,1939年~)」)によって導入された。
代数的構造を持つ集合は代数系(algebraic system)であるといわれる。すなわち、代数系というのは、集合Aとそこでの算法(演算の規則)の族(Famiry)Rの組(A, R)のことを指す。
逆に、具体的なさまざまな代数系から、それらが共通してもつ原理的な性質を抽出して抽象化・公理化したものが代数的構造と呼ばれるのである。
なお、分野(あるいは人)によっては代数系そのもの、あるいは代数系のもつ算法族のことを代数的構造とよぶこともあるようである。 後者は代数系の代数構造とも呼ばれる。
現代では、代数学とは代数系を研究する学問のことであると捉えられている。
そして群論概念(Group Theory Concept)の登場
群論自体の内容については、現時点において以下の説明に頼りっ切りの状態です。
EMANの物理学・物理数学・群論の軽い説明
数学での群というのは英語ではGroupであり、まさにグループのイメージである。まず集合を考える。この集合の要素が次の4つの性質を持つ時、その集合のことを「群」と呼ぶ。
積もまた集合の要素になっていること…集合の要素からどれでも二つを選んで計算をした結果として何かが得られる共通のルールが定められているとする。この計算ルール、または計算結果のことを「積」と呼ぶことにしよう。「積」と呼んでいるが、それが掛け算だとは限らない。二つの要素を使って計算する何らかのルールがあればいいので、それが足し算であっても構わない。この時、同じものを二つ取り出して計算しても良いとする。さて、ここで一番大事なのは、結果として得られた積も同じ集合の要素になっていることである。計算ルールとその結果がグループ内の要素だけで完結していることを重視するわけだ。
結合法則が成り立つこと…結合法則というのはa(bc)=(ab)cというやつだ。先ほどは二つの要素を選んで計算をすると書いたが、二つの要素の積も同じ集合の要素なのだから、それに対してさらに別の要素を掛けることができる。こうして3つ以上の要素の積を考えることができるのだが、どこから計算しても同じ結果になることを保証するのがこの法則である。これによって、わざわざカッコを付けなくても3つの要素の積はabcのように書くだけで良くなる。
単位元が存在すること…単位元というのはae=ea=aとなるような要素eのことで、それはつまり、他のどんな要素との積を計算してももとと変わらない結果になるような要素である。それは掛け算のときの数字の1に似ている。
逆元が存在すること…逆元というのは、ax=xa=eとなるような要素xのことで、そのような要素をa^−1と表す。全ての要素にそれぞれ逆元がなければならない。
なぜこのような性質を持つものを重視してわざわざ「群」などという概念を作ったのだろうかと思うかも知れない。いや、私は思った。何か理由や目的があってこのような理論を作ったはずだ、などと疑ったわけだが、どうやら数学は「実用的な目的」のようなものをほとんど意識していないらしい。これらの組み合わせをもとにして広がる論理が面白かったので、こんなにも発展したのだろう。実際、他の組み合わせもちゃんと研究されているようで、条件をもう少し狭めた「半群」「モノイド」「マグマ」、逆に広げた「環」「体」といった概念もある。群だけが特別なのではなく、数学はすでに色々と調べ尽くしているというわけだ。
群と呼べる条件は上に書いた4つだけだからab=baは満たしていなくても構わない。積の順序を変えると違う結果になることが許されている。むしろ、積の順序を変えても同じ結果になる方が特別視されていて、そういうものも群の一種だが「可換群」あるいは「アーベル群」と呼ばれている。それ以外を「非可換群」あるいは「非アーベル群」と呼ぶ。
群論は、結果として、数学の代数的構造(Algebraic Structure)の分類をするのに役に立つ。
見た目やイメージが異なる別分野であっても、そこで使われている記号や計算内容のつながりを比較すると、全く同じ内容のことを実行しているに過ぎないと気付くことがある。そのような事例を沢山集めて名前を付けて分類することによって、「この分野のこの論理と、別分野のこの論理は同じ構造を持っている」だとか、「全体としては異なるが部分的に似た構造を持っている」だとかいうことがはっきり意識できるようになる。
計算だけとは限らない。図形を回転させたり反転させてみたり、座標変換をしたりするときの移動のパターンなどにも同じ構造を持つものがある。構造に着目して議論するので、図形だろうが記号だろうが、そういう見た目には縛られない。だから、図形の対称性や、理論の対称性などといったものにも関連した議論ができる。
このようなものが物理でどう役に立つかと言えば、結晶構造の分類や、量子力学に出てくる波動関数の対称性、座標変換の対称性などと関係しているところである。広い視点で考えを整理したり、新しいアイデアを持ち込んだりできるだろう。まだよく分かっていない時空の高次元の構造などを議論するのにも使えるのである。
例えば加法整数群(Additive Integer Group)の導出過程について。
Z_n(n=-\infty→-1→0→1→+\infty)\\=(-\infty,…,-3,-2,-1,0,1,2,3,…,+\infty)
【数理考古学】とある実数列の規定例①等差数列から加法整数群へ
【数理考古学】とある実数列の規定例②等比数列から乗法群へ
【数理考古学】とある実数列の規定例③オイラーの等式e^πi=-1が意味するもの?
①まず元(Element) として自然数集合(Natulal Set)、すなわち初項(First Term)$α=1$,公差(Common Difference)$d=1$,一般項(General Term)$α+(n-1)d$の等差数列(Arithmetic Sequence=算術数列)を準備する。
N_n(n=1→\infty)\\
=(1+(1-1)×1=1,1+(2-1)×1=2,1+(3-1)×1=3,…,1+(\infty-1)×1=\infty)\\
=(1,2,3,…,Inf(inity))
これは以下の様に再帰的に考えても良い。
N_n(n=1→\infty)\\
=(1,1+1=2,(1+1)+1=3,…,\infty+1=\infty)\\
=(1,2,3,…,Inf(inity))
どちらの場合も範囲に加法単位元(Additive Identity)0を加えても添字範囲が拡張されるだけで演算の連続性(Operation Continuity)そのものは維持され(結合法則((Associative Law))の成立)、演算結果(Operation Result)も閉じている(整数以外の数が登場する余地がない)。
-
Rの場合

-
pythonの場合
【Python演算処理】単位円筒(Unit Cylinder)の描画
②上掲の拡張自然数集合(?)$N_n(n=0→\infty)(0,1,2,3,…,\infty)$について逆元(Inverse Element)$-N_n(n=-\infty→0)=(-\infty,…,-3,-2,-1,0)$を準備する。この場合も「結合法則成立による演算の連続性の担保」は成立し、演算結果も閉じている。
-
Rの場合

-
pythonの場合
【Python演算処理】単位円筒(Unit Cylinder)の描画
③上掲二つの演算結果集合(Operation Result Set)を一つの集合に射影(Projection)した積(Product)が加法整数群となる。この場合も「結合法則成立による演算の連続性の担保」は成立し、演算結果も閉じている。
-
Rの場合

-
pythonの場合
【Python演算処理】単位円筒(Unit Cylinder)の描画
④こうして得られた整数集合(Integer Set)Zn(n=-Inf→-1→0→1→Inf){-Inf,…,-3,-2,-1,0,1,2,3,…,Inf}同士を乗算(Multiply)した結果集合(Operation Result Set)も1を乗法単位元(Multiple Identity)とし、逆元も存在し整数以外の数が登場する余地がないので群として成立する。それでこの概念を加法整数群に加え整数環(Integer Ring)と呼ぶ。ただし整数集合自体の等比数列(Geometric Sequence=幾何数列)αn(n=-Inf→0→Inf){α×r^(n-1)}(ただしα=初項(First Term),r=公比(Common Retio)){1/(α^Inf):=0,…,1/(a^2),1/(a^1)=1/α,α/α=1,α^1=a,α^2,…,a^Inf=Inf}や指数関数(Exponential Function)y=2^xの演算結果集合は添字が0以下の場合に整数以外を含んでしまうので半群(Semigroup)に分類される。
こうして全体像を俯瞰するうちに、なんとなく演算範囲を定めて面積を求める積分(Integral)の概念との発想の類似性を感じました。
【初心者向け】半径・直径・円周長・円の面積・球の表面積・球の体積の計算上の往復
こちらの世界もこちらの世界でよく広義積分(Improper Integral)integurate(f(x),lower=-Inf,upper=Inf)をintegurate(f(x),lower=-Inf,upper=0)とintegurate(f(x),lower=0,upper=Inf)に分解して計算するみたいな事をやりますよね。
より厳密な定義
ところでこの考え方は、より厳密には以下の様に規定される様なんです。
自己同型(Automorphism) - Wikipedia
「数学的対象(Mathematical Object)」から自分自身への「同型射(Isomorphism)」のことを言う。ある解釈においては、構造を保ちながら対象をそれ自身へと写像する方法のことで、その対象の「対称性」を表わしていると言える。対象の全ての自己同型の集合は群を成し「自己同型群(Automorphism Group)」と呼ばれる。大まかにいえば、自己同型は、「数学的対象」の「対称群」である。
- 「数学的対象(Mathematical Object)」…とりあえずここで集合論的に扱った「自然数列(Natural Sequance)」「整数(Integer Sequance)」といった諸概念が対応すると想定される。「一般的に遭遇する数学的対象として、数、順列、分割、行列、集合、関数、および関係などが挙げられる。数学の分科としての幾何学は、六角形、点、線、三角形、円、球、多面体、位相空間、および多様体のような対象を持つ。別の分科の代数学は、群、環、体、格子、および束といった対象を持つ。圏は、数学的対象を一斉に生じさせるものであるとともに、それ自体がひとつの数学的対象である。」
数学的対象 - Wikipedia
まだこうした考え方に正確には対応させられてないが、例えば「実数列( Real Sequance)」についてとりあえず以下の様に整数列(Integer Sequance)の十進法(Decimal System)による拡張形で考える立場を採用している。
【数理考古学】群論とシミュレーション原理⑧族の分類とそれに下属する演算集合の関係の整理 - 「同型射(Isomorphism)」あるいは単に同型(Isomorphic)…「数学において同型写像(isomorphism)である、あるいは同型(isomorphic)であるとは、準同型写像あるいは射であって逆射を持つ事を意味し(逆関数ではない)。2つの数学的対象が同型であるとはそれらの間に同型写像が存在することをいう。自己同型写像は始域と終域が同じ同型写像である。同型写像の興味は2つの同型な対象が写像を定義するのに使われる性質のみを使って区別できないという事実にある。したがって同型な対象はこれらの性質やその結果だけを考える限り同じものと考えてよい。また標準的な同型写像(canonical isomorphism) とは同型であるような標準的な写像を意味する。2つの対象が標準的に同型(canonically isomorphic)であるとは,それらの間に標準的な同型写像が存在することをいう。そして同型写像は圏論を用いて形式化される。ある圏の射f:X→Yが同型射であるとは両側逆射を持つことをいう。すなわちその圏における別の射g:Y→X があって$gf =1_X$かつ$fg=1_Y$となる。ただし$1_X$と$1_Y$はそれぞれXとYの恒等射である(対称式について、こんな面倒臭い考え方をする?)。」
恒等写像 - Wikipedia
表現が抽象的過ぎて何の話をしているかさっぱり分かりません。とりあえず私はプログラミングにおける利用を想定し、同じ添字化された元(Indexed Element)を族(Family)として共有する演算結果集合(Operation Result Set)をそれぞれ束ねたいと考える様になった訳ですが、これは現代数学の基準においては随分と粗雑な思考様式で、何処かのレベルで破綻をきたす様なのです。
数学のある分野,特に圏論では,等しいことと同型とを区別するのが大切である。等しい(つまり二つの対象が等号で結べる)とは2つの対象が全く同じであることであり,一方について正しいすべてのことは他方についても正しい.一方同型は一方の対象の構造のある指定された部分について正しいすべてのことは他方についても正しいことを意味する。
同型は明らかで従わざるを得ないように見えることもあるが,なお等号では結べない(例えば父子関係や兄弟関係といった系譜学的構造が完璧に一致する二つの家族は同型(isomorphism =Greek iso-,"same," and -morph,"form" or "shape") だがそれを構成する人々が異なるので等しくはない)。
- 統計の世界は真逆に「有意水準(Significance Level)が検定基準を満たさない範囲(確率論的に十分偶然と考えられる範囲に留まる)」すなわち「意味ある特徴が何も起こってない」「(比較対象間に)意味ある特徴上の差異が何も見出せない」状態からの脱却が出発点であり、そうやって検出された意味空間(Semantic Space)の内容吟味(Content Scrutiny)がこれに続く。
吟味したって英語でなんて言うの? - 例えば相関係数(Correlation Coefficient)は、比較対象に選んだ特徴が「(あたかも一対の比較対象が同一の存在であるかの様に)比例する場合(1)」「(あたかも一対の比較対象が互いにとって反存在であるかの様に)反比例する場合(-1)」「(あたかも一対の比較対象が互いに素であるかの様に)連動しない場合(0)」を連続的に検出するが、それぞれの極限値を検出する機会は滅多になく、その意味合いにおいてかかる分布は(無数の操作変数に左右される)ある種の開集合を形成していると目される。
【初心者向け】記述統計学と代表値 - 数学における圏論(Category Theory)には、何となく任意の比較対象のあらゆる差異を黙殺して共通数理のみを抽出しようとする(公理系から演繹的に証明される)定理絶対主義への批判から生じた節が見受けられる。もしかしたら上掲の様な「慎重な態度」はそういう側面に由来するのかもしれない。
圏論 - Wikipedia
圏論は数学をするための「高級言語」
逆にそこまで深く考えなくて良い「単純な場合」として例示されるのが以下。
-
論理的原子論(Logical Atomism)の早期の理論において「事実(Facts)」と「真である命題(True Propositions)」の間の形式的な関係はバートランド・ラッセルとルートヴィヒ・ヴィトゲンシュタインによって同型であると理論化された。この方向の考えの例はラッセルの「数理哲学概論(Introduction to Mathematical Philosophy,1919年)」などに見出される。
logical atomismとは - コトバンク
記号論理学とは何か - 群や環を含むほとんどの代数的構造に対して、準同型写像が同型写像であることと全単射であることは同値である。
全単射 - Wikipedia
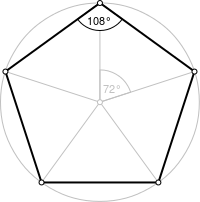
例えば1の5乗根が乗法についてなす群(巡回群)は正五角形の回転が合成についてなす群(回転群)に同型であると考えられる。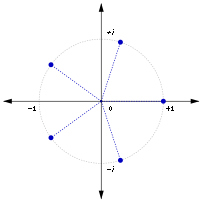
-
位相幾何学において射とは連続写像のことであるが、同型写像は同相写像あるいは双連続写像とも呼ばれる。
連続写像 - Wikipedia
連続写像の定義には,なぜ開集合の「逆像」をつかうのですか? -
解析学において射は可微分関数であり同型写像は微分同相とも呼ばれる。(リー群の事か?)。
リー群の入門的なこと
また2つのヒルベルト空間の間の同型写像は和とスカラー倍と内積を保つ全単射となる。
ヒルベルト空間 - EMANの量子力学 - EMANの物理学
またラプラス変換は難しい微分方程式を簡単な代数的方程式に写す同型写像である(ならばフーリエ変換は?)。
【Python演算処理】ラプラス変換/ラプラス逆変換を試す。
【数理考古学】とある実数列の規定例④フーリエ族とラプラス族概念の追加? -
有限次元ベクトル空間Vから二重双対空間への標準的な写像は標準的な同型写像となるが、その一方で有限次元ベクトル空間Vは双対空間に同型となるものの、一般に*標準的にもそう定まったとはいえない。
ベクトル空間 - Wikipedia
双対ベクトル空間 - Wikipedia - グラフ理論において,2つのグラフGとHの間の同型写像はGの頂点たちからHの頂点たちへの全単射fであって次の意味で「辺の構造」を保つものである:Gにおいて頂点uから頂点vに辺があるのは Hにおいてf(u)からf(v)に辺があるとき、かつそのときに限る。
グラフ同型 -Wikipedia - サイバネティックスの世界においては(Roger.C.ConantとW.Ross.Ashbyが提唱した)コナント=アシュベイ定理(Conant-Ashby theorem)に従う有効な調整器(Good Regulator)が、調整対象として選ばれたシステムとモデル的に同型と見做される。"Every Good Regulator of a system must be a model of that system"(あらゆる有効な調整器が、それが調整対象とするシステムの何らかのモデルとなっている)そして"Whether regulated or self-regulating an isomorphism is required between regulator part and the processing part of the system."(それが外挿的な形で達成されているか、あるいは自律的に達成されているかに関わらず、制御が成功しているという事はそのシステムの処理部と制御部と同型(isomorphism)のモデルが何らかの形で抽出されている事を意味する)である。この考え方には、ある意味回路方程式(Circuit Equation)を演算結果集合の族に取る演算子法(後にラプラス変換/逆変換と同型である事が数学的に証明された)の生みの親たるヘヴィサイド(Oliver Heaviside,1850年~1925年)の「数学は実験的科学であり、定義が先にくるわけではない」「私は消化のプロセスを知らないからといって食事をしないわけではない」発言との連続性が感じられる。システム同型とでも呼ぶべき?
特に重要なのが以下の2例となる。
対数と指数
$R^+$を正の実数のなす乗法群とし,Rを実数のなす加法群とする。
- 対数関数$\log:R^+→R$はすべての$x,y∈R^+$に対して$log(xy)=log(x)+log(y )$を満たすので,それは群準同型である。
- 指数関数$\exp:R →R^+$はすべての$x,y∈R^+$に対して$exp(x+y)=exp(x)exp (y)$を満たすので、これも準同型である。
- 恒等式$\log(exp(x))=x$および$exp(log(y))=y$はlogとexpが互いの逆関数であることを示している。logは準同型である逆関数を持つ準同型であるから群同型である。
logは同型だから、正の実数の積を実数の和に翻訳する。この機能により定規と対数表を用いて、あるいは対数スケールの計算尺を用いて実数を掛けることができる。
6を法とした整数
まずは以下の二つの群を考える。
- 0から5までの整数が6を法とした加法でなす群$(Z_6,+)$。
- 群$(Z_2×Z_3,+) $。
これはx座標が0か1でy座標が0か1か2の順序対で、加法はx座標は2を法とし、y 座標は3を法とする。これらの構造は以下の対応によって同型である:
- (0,0) → 0(0+0=0 mod 6)
- (2,0) → 0(6+0=6 mod 6)
- (1,1) → 1(3+4 mod 6)
- (0,2) → 2(0+8=8 mod 6)
- (1,0) → 3(3+0=3 mod 6)
- (0,1) → 4(0+4=4 mod 6)
- (1,2) → 5(3+8=11 mod 6)
あるいは一般に
- (a,b)→(3a+4b) mod 6.
例えば,(1,1)+(1,0)=(0, 1)であり,もう一方に翻訳すると1+3=4である.
これらの2つの群は集合が異なる元を含むという意味で違って「見える」にもかかわらず,それらは実際同型であり,構造は全く同じである.より一般に,2つの巡回群$Z_m$と$Z_n$の直積が$Z_{mn}$と同型であるのは、mとnが互いに素であるとき,かつそのときに限る。
自己同型の定義
自己同型の正確な定義は「数学的対象」の種類や、その対象上の「同型射」の定義によって変化する。
- 「自己同型」という言葉が意味を持つ最も一般性の高い領域は圏論と呼ばれる数学の抽象的な分野である。圏は、抽象的な対象(object)とそれらの対象の間の射(morphism)を扱う。圏論においては、(圏論的な意味で)同型でもあるような自己準同型(つまり、対象から対象自身への射である)である。圏論では、射は函数である必要もないし、対象が集合である必要もないので、この定義は非常に抽象的な定義である。しかし、より具体的な設定では、対象はある加法構造を持つであろうし、射はこの構造を保つであろう。
準同型 - Wikipedia -
抽象代数学の文脈では、「数学的対象」とは例えば、群、環、ベクトル空間といった代数的構造である。この場合は、同型は単に全単射な準同型である。(準同型の定義は代数構造の種類に依存する)
群準同型(Group Homomorphism) -wikipedia
環準同型(Ring Homomorphism) -wikipedia
作用素(Operator) -wikipedia - 恒等射は自明な自己同型(trivial automorphism)と呼ばれることもある。他の(恒等射ではない)自己同型は非自明な自己同型(nontrivial automorphisms)と呼ばれる。
とりあえず何を言ってるのかさっぱり分かりまぜん…orz
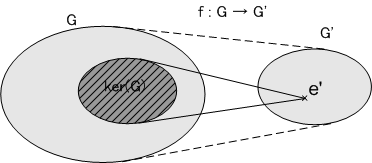
準同型写像の核
群Gの単位元eは必ず群G'の単位元e'に移されますが、もし写像が全射ならGの中には他にも e'に移される元があるかもしれません。
群Gの部分集合で準同写像によってe'に移されてしまうものをGの核と呼びます。ドイツ語で核をKernelといいますが、日本語でも核といわずカーネルとそのまま呼ぶ人がいます。核の大きさは,もちろん準同型写像によって変わりますが、最低で元1つ(単位元のみ)、最大で群Gそのものとなります。
準同型写像の核については「準同型写像fの核Kは正規部分群(Normal Subgroup)となる」定理がとても重要です。正規部分群の概念は群論の中でも非常に重要です。順番としては剰余類(Residue Class)あるいは傍系(coset=コセット)や商群(Quotient Group/Factor Group)から出てきた概念ですが、より現代的な捉え方としては,正規部分群を準同型写像の核として定義した方がスマートかも知れません。
正規部分群は、与えられた群から剰余群を構成するのに用いることができる。
G が群で、H がその部分群、g は G の元とする。このとき、
$gH=(gh:h \in H)$
をGにおけるHの(Hによる、Hに関する、Hを法とする)左剰余類(Left Coset)、
$Hg=(hg:h \in H)$
をGにおけるHの(Hによる、Hに関する、Hを法とする)右剰余類 (right coset) という。
文献によってはここでいうものと左右が逆になっているものもあるので注意を要する。Hが正規部分群である場合に限り左剰余類と右剰余類の両概念は一致する(これを以って正規部分群の定義とする場合もある)。剰余類は、この様にGにおいて何らかの部分群による左剰余類や右剰余類となるものの総称である。アーベル群や加法的に書かれた群では、g+H,H+gのような記号で剰余類を表すことがある。
商群$\frac{G}{G}$は自明群(ただ1つの元を持つ群)、$\frac{G}{(e)}$はGと同型になる。
商群$\frac{G}{N}$の位数、すなわち元の個数は、|G:N|すなわちNのGにおける指数に等しい。G が有限ならば、指数はGの位数をNの位数で割ったものにも等しい。GとNがともに無限でも $\frac{G}{N}$は有限かもしれないことに注意(例えば$\frac{Z}{2Z}$)。
例えば整数$\mathbb{Z}$が加法についてなす群と、すべての偶数からなる部分群$2\mathbb{Z}$を考える。$\mathbb{Z}$は可換群なので正規部分群である。剰余類は2つしかない:偶数全体の集合と奇数全体の集合である;したがって商群$\frac{\mathbb{Z}}{2\mathbb{Z}}$は2つの元を持つ巡回群となり、それは2を法とする加法をもつ集合(0,1)と同型である;インフォーマルに商群$\frac{\mathbb{Z}}{2\mathbb{Z}}$は2を法とする加法をもつ集合(0,1)に「等しい」と表現する事もある。
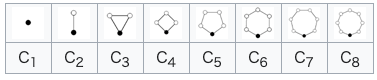
この例を少し一般化する。再び整数が加法についてなす群$\mathbb{Z}$を考える。nを任意の正整数とする。nのすべての倍数からなる$\mathbb{Z}$の部分群$n\mathbb{Z}$を考える。$\mathbb{Z}$は可換なのでその部分群$n\mathbb{Z}$は正規である。剰余類たちの集合は($n\mathbb{Z}$,$1+n\mathbb{Z}$,…,$(n−2)+n\mathbb{Z}$,$(n−1)+n\mathbb{Z}$) である。整数kは、kをnで割った余りをrとすると、剰余類$r+n\mathbb{Z}$に属する。商$\frac{\mathbb{z}}{n\mathbb{z}}$はnで割った「余り」の群と考えることができる。これは位数nの巡回群(Cyclic Group/Monogenous Group)である。
巡回群 - Wikipedia
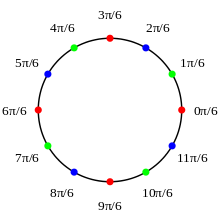
ここで1の12乗根全体を考える。これは単位円周に乗っているが、乗法についてアーベル群Gをなす。数が色つきの点で偏角とともに絵に描かれている。赤い点で示されている、1の4乗根全体のなす部分群Nを考える。この正規部分群は群を赤、緑、青で示される3つの剰余類に分ける。剰余類たちが3元からなる群をなすことを確認できる(赤の元と青の元の積は青、青の元の逆元は緑、など)。したがって、商群$\frac{G}{N}$は3色の群で、3つの元をもつ巡回群であることが分かる。
さらに実数が加法についてなす群$\mathbb{R}$とその整数からなる部分群$\mathbb{Z}$を考える。$\mathbb{R}$における$\mathbb{Z}$の剰余類はすべて、0≤a<1を実数として$a+\mathbb{Z}$の形の集合である。そのような剰余類を足すことは対応する実数を足し、結果が1以上ならば1を引くことによってなされる。商群$\frac{\mathbb{R}}{\mathbb{Z}}$は円周群$S^1$と同型であり、これは絶対値1の複素数が乗法についてなす群、あるいはそれに対応して、2次元で原点についての回転のなす群、すなわち「平面上における回転」を意味する特殊直交群SO(2)である。同型はf(a+Z)=exp(2πia)によって与えられる。SO(2)はさらに「球面上における回転」SO(3)に発展させる事が出来る。
SO(2) - EMANの物理数学
SO(3) - EMANの物理数学Gが可逆3×3実行列全体の乗法群で、Nがその行列式1の部分群であるとき、NはGにおいて正規である(なぜなら行列式を取る準同型の核なので)。Nの剰余類は与えられた行列式を持つ行列全体の集合であり、したがって$\frac{G}{N}$は非零実数のなす乗法群に同型である。群Nは特殊線型群SL(3)と呼ばれる。
特殊線型群 - Wikipediaアーベル群$Z4=\frac{Z}{4Z}$(すなわち4を法とする加法をもつ集合(0, 1, 2, 3))とその部分群 (0,2)を考える。商群$\frac{Z4}{(0,2)}$は((0,2),(1,3))である。これの群の単位元は(0, 2)であり、群の演算は(0,2)+(1,3)=(1,3)などとなる。部分群(0,2)と商群 ((0,2),(1,3))はともにZ2に同型である。
乗法群$G=Z_{n^2}^{*}$を考える。n乗剰余の集合Nは$G=Z_{n}^{*}$に同型な乗法的部分群である。このときNはGで正規であり、商群$\frac{G}{N}$は剰余類(N,(1+n)N,(1+n)2N, …,(1+n)n−1N)となる。Paillier暗号はGのランダムな元の剰余類をnの因数分解を知らずに決定することは難しいという予想に基づいている。
自己同型群
対象Xの自己同型全体が(真のクラスではなく)集合をなす場合、この集合は写像の合成の下に群をなす。この群をXの自己同型群と呼ぶ。これが群をなすことは、以下のことから簡単に確認できる。
- 閉性(Closure):2つの自己準同型の合成は再び自己準同型となる。
- 結合法則(Associativity): 射の合成は常に結合的である。
- 単位元(Identity): 対象からそれ自身への恒等写像は単位元となる。
- 逆元(Inverses): 定義より、全ての同型は逆写像を持つ。その逆写像も同型であり、また自己準同型でもあるため、それは自己同型となる。
圏Cの対象Xの自己同型群は、$Aut_C(X)$ あるいは、圏が前後関係より明らかな場合は、単に Aut(X) と書く。
-
初等的な算術(Elementary Arithmetic)では、整数の集合$\mathbb{Z}$は加法の下で群とみることができ、符号の反転が唯一の非自明な自己同型となる。しかし、環と考えた場合は自明な自己同型しか持たない。一般的に、符号反転は任意のアーベル群(Abelian Group)または可換群(Commutative Group)上の自己同型になるが、環や体ではそうならない。
アーベル群 - Wikipedia -
集合論では、集合X上の任意の置換(Permutation)が自己同型となる。Xの自己同型群は、Xの対称群(Symmetric Group)とも呼ばれる。
置換(数学) - Wikipedia
対称群 - Wikipedia
一般には組合せ論に属する話題となる。
【Python演算処理】階乗と順列と組み合わせ -
群の自己同型は、群からそれ自身への群同型である。非公式に言うと、構造を変化させない群上の置換である。すべての群Gに対して、像は内部自己同型(inner automorphism)の群 Inn(G) となり、核がGの中心となるような、自然な作用をもつ準同型G→Aut(G) が存在する。従ってGが自明な中心を持つならば、GをG自身の自己同型群に埋め込むことができる。
内部自己同型 - Wikipedia -
線型代数では、ベクトル空間Vの自己準同型が、線型変換(Linear Transformation=一次変換)あるいは線型写像(Linear Mapping)V→Vである。自己同型はV上の可逆な線型変換のことである。ベクトル空間が有限次元のとき、V の自己同型群は一般線型群(V)GL(V)と同じになる。
線型写像 - Wikipedia
一般線型群 -Wikipedia -
体の自己同型は、体から自分自身への全単射な環準同型である。有理数$\mathbb{Q}$や実数$\mathbb{R}$の場合には、非自明な体自己同型は存在しない。もしこれらが非自明な体自己同型を持つとすると全体への拡大ができない(なぜならば平方根を持つ数の性質を保たなくなるから)。複素数$\mathbb{C}$において非自明な自己同型は複素共役ただ一つであるが(選択公理を前提とすると)無限個(非可算個の)「ワイルド」な自己同型が存在する。体自己同型は体の拡大、特にガロア拡大の理論で重要である。ガロア拡大$\frac{L}{K}$の場合には、Kを各元ごとに固定するLの自己同型全体の部分群を拡大のガロア群と呼ぶ。
選択公理 - Wikipedia - p-進数の体$Q_p$は非自明な自己同型を持たない。
【初心者向け】N進法(N-ary)とp進数(p-adic) - グラフ理論では、グラフの自己同型(Automorphism of a Graph)は、頂点の置換で隣接関係を保つ写像のことを言う。
Graph Automorphism -
関係性の自己同型については、自己同型を保存する関係(relation-preserving automorphism)を参照の事。
Relation-preserving isomorphism - Wikipedia -
順序理論(Order Theory)については、順序自己同型(Order Automorphism)を参照の事。
Order isomorphism - Wikipedia
幾何学では、自己同型は空間の動き(motion)と呼ばれる。下記の特別な意味で使われる。
①計量幾何学(metric geometry)では、自己同型は、自己等長写像を意味し、自己同型群は等長群(isometry group)と呼ばれる。
等長写像 - Wikipedia
直交変換・ユニタリ変換
Xが実ベクトル空間であるとき、線形な等長変換として直交変換が対応する。これは直交行列T を用いて$T_x$と書くことができる。複素ベクトル空間では同様な写像にユニタリ変換(およびその行列表現としてのユニタリ行列)が対応する。
一般に、実ベクトル空間内の等長写像は直交行列Tとあるベクトルaを用いて$T_x+a$と書くことができる(アフィン変換)。このうち、|T| = 1であるものを特にユークリッドの運動と呼ぶが、これは "回転"と"平行移動"の二つの合成によってできるものである。等長写像はユークリッド空間の図形の間の合同をもたらすが、さらに一般に、リーマン多様体の間の等長写像(各点の微分が等長写像になるというように定義される)はその構造をすべて保存する。このような等長写像は運動と呼ばれ、運動の全体はある群をなす。
②リーマン面のカテゴリでは、自己同型は、あるリーマン面から自分自身への全単射な双正則(biholomorphic)写像をいう(共形写像とも言う)。 例えば、リーマン球面(Riemann Sphere)の自己同型はメビウス変換(Möbius transformation)$f(z)=\frac{az+b}{cz+d}$である。ここで、係数a,b,c,d はad−bc≠0を満足する複素定数である。
無限遠点(Infiinity)$\frac{1}{0}=∞$を一点追加して複素平面を拡張する手法で、複素射影直線$CP^1$あるいは拡張複素平面$\hat{\mathbf {C}}$ または$\hat{\mathbf {C}}∪{∞}$とも記述される。
純代数的には、無限遠点を追加した複素数全体は、拡張複素数として知られる数体系を構成する。無限を伴う算術は、通常の代数規則すべてに従う訳ではないので全体として体を構成しないが、幾何学的また解析学的に無限遠においてさえもよく振舞い、リーマン面とも呼ばれる1-次元複素多様体をなす。複素解析において有理型関数の洗練された理論で重要な役割を果たす。
幾何学的には複素数平面を実二次元球面へ立体射影したものの上で回転と平行移動により各点の位置と向きを変更したものを再度平面に立体射影することによって得られる。
これらの変換は「角度」を保ちつつ(「等角性」)、任意の「直線または円」を「直線または円」に写し(「円円対応」)、円に対して「対称な二点」をメビウス変換の像の円に関しても「対称な二点」に写す(「対称原理」)。
複素射影直線上の射影変換であり、その全体はメビウス群と呼ばれる射影一般線型群PGL(2, C)を成す。ちなみに「メビウス変換」の名はガウスの弟子メビウス(August Ferdinand Möbius、1790年~1868年)の業績に因むが、ほかにも射影変換や一次分数変換(あるいは単に一次変換)などと呼ばれることもある。
アウグスト・フェルディナント・メビウス -Wikipedia
③微分可能多様体Mの自己同型は、Mからそれ自身への微分同相写像である。自己同型群はDiff(M)と書く。
微分同相写像 - Wikipedia
局所微分同相写像 - Wikipedia
微分同相写像等の定義
④トポロジーでは、位相空間の間の準同型は、連続写像であり、位相空間の自己同型群は、空間から自分自身への同相群(Homeomorphism Group)である。この例は、全単射が同型となることは充分ではないことを示している。
位相群 - Wikipedia
とりあえず、現段階では上掲の様な「自然数列に単位元と逆元を加えて加法整数群とする」式の思考様式がそのうち様々な形で限界に到達することが確認出来た時点でよしとしておきます。そんな感じで以下続報…