【数理考古学】群論とシミュレーション原理①これまでの投稿内容のまとめ。
吃驚するほどグチャグチャになってしまったので整理を試みます。とりあえず私は群論を「クラスをメンバ変数とメンバメソッドの対で考える」オブジェクト志向プログラミングの延長線として把握しています。まずはその表現で語るとどうなるか見ていく事にしましょう。
族(Family)による分類
「そのクラスにおいてメンバメソッドが共有するメンバ変数」に該当する元集合(Element Set)=観測結果集合(Observation Result Set)を族(Family)と規定する。
- 独自表現なので特別にそう呼び分ける事に意義がある場合(すなわち、かかる観測結果集合を共有する演算結果集合が複数存在する事を強調したケース)以外には単に列(Sequence)と呼ぶ。
これまで扱ってきたのは以下辺り。
- 以下に登場する「さしあたって…と規定される」なる表現は、オブジェクト志向プログラミングでいうコンストラクタ(Constructor=オブジェクト生成関数)みたいなイメージ。「族のそれは更新される事がない」という意味合いにおいてある種の定数(集合)として機能する(数学にリテラルの概念が存在しないので、こういう表現にならざるを得ない?)が、もちろん実際のプログラミングの世界は、以下の様な「自然数・整数・実数の規定」の如き数の根本定義を自明の場合(Trival Case)として自動的に言及なく通過してしまう。
コンストラクタ - Wikipedia
定数 (プログラミング) - Wikipedia
import networkx as nx
G = nx.DiGraph()
G.add_edge("Rap Function1^n(関数列)","Sum(演算)")
G.add_edge("Sum(演算)","Natural(族)")
G.add_edge("Natural(族)","Grouping(演算)")
G.add_edge("Grouping(演算)","Integer(族)")
G.add_edge("Cyclic Function-1^n(関数列)","Unionize(演算)")
G.add_edge("Cyclic Function-1^n±1(関数列)","Unionize(演算)")
G.add_edge("Unionize(演算)","Crossing(演算)")
G.add_edge("Rap Function1^n(関数列)","Crossing(演算)")
G.add_edge("Crossing(演算)","Integer(族)")
G.add_edge("Integer(族)","Decimal System(演算)")
G.add_edge("Decimal System(演算)","Real(族)")
G.add_edge("Real(族)","Extraction:x=0→2(演算)")
G.add_edge("Extraction:x=0→2(演算)","2^x(演算)")
G.add_edge("2^x(演算)","Real(族)")
G.add_edge("Napierian(族)","2^x(演算)")
nx.nx_agraph.view_pygraphviz(G, prog='fdp')
自然数族(Natural Family)/自然数列(Natural Sequence)
観測原点(Observation Origin)0と観測極限(Observation Limit)∞を含まない等間隔に離散する開集合をなす。
\mathbb{N}_n(n=1→\infty)=(1,2,…,\infty-1)
import networkx as nx
G = nx.DiGraph()
G.add_edge("Rap Function1^n(関数列)","Sum(演算)")
G.add_edge("Sum(演算)","Natural(族)")
# G.add_edge("Natural(族)","Grouping(演算)")
# G.add_edge("Grouping(演算)","Integer(族)")
# G.add_edge("Cyclic Function-1^n(関数列)","Unionize(演算)")
# G.add_edge("Cyclic Function-1^n±1(関数列)","Unionize(演算)")
# G.add_edge("Unionize(演算)","Crossing(演算)")
# G.add_edge("Rap Function1^n(関数列)","Crossing(演算)")
# G.add_edge("Crossing(演算)","Integer(族)")
# G.add_edge("Integer(族)","Decimal System(演算)")
# G.add_edge("Decimal System(演算)","Real(族)")
# G.add_edge("Real(族)","Extraction:x=0→2(演算)")
# G.add_edge("Extraction:x=0→2(演算)","2^x(演算)")
# G.add_edge("2^x(演算)","Real(族)")
# G.add_edge("Napierian(族)","2^x(演算)")
nx.nx_agraph.view_pygraphviz(G, prog='fdp')
①さしあたって初項$α_1=1$,公差d=1,一般項$α_1+(n-1)d$の無限片側等差数列(One Side Infinity Arithmetic Sequence)の演算結果集合(Operation Result Set)で規定する。
等差数列 - Wikipedia
\mathbb{N}_n(n=1→\infty)=(1+(n-1)d,…)
循環論法っぽいので、あえてグラフには含めなかった(言い訳)。
循環論法とは
②周回関数(Rap Function)$1^n(n=-\infty→0→+infty)=(…,1,1,1,…)$の、とりあえず初項1からの総和(Sum)、すなわち算術級数(Arithmetic Series)でも規定される。
\mathbb{N}_n(n=1→\infty)=(…,\sum_{k=1}^{n}1^k,…)=(1^{n_1},1^{n_1}+1^{n_2},1^{n_1}+1^{n_2}+1^{n_3},…,n_\infty)=(1×1,1×2,1×3,…,n_\infty)=(1,2,3,…,n_\infty)
- ここで小学校時代には気付けなかった事に気付く。
等差数列の和を計算する2つの公式
等差数列の和の公式1:初項Ft(First Term)、末項Lt(Last Term)、項数nの等差数列$A^n$の総和(Sum)
\sum_{k=1}^{n}A_n=\frac{n}{2}(Ft+Lt)
初項Ft=1,末項Lt=1、項数nの場合の公式1
\sum_{k=1}^{n}A_n=\frac{n}{2}(1+1)=\frac{2n}{2}=n
等差数列の和の公式2:初項Ft、交差d(Common Difference)、項数nの等差数列$A^n$の総和
\sum_{k=1}^{n}A_n=\frac{n(2Ft+(n-1)d)}{2}
初項Ft(First Term)=1,交差d=1、項数nの場合の公式2
\sum_{k=1}^{n}A_n=\frac{n(2*1+(n-1)*1)}{2}=\frac{n(2+n-1)}{2}=\frac{n(n+1)}{2}
ところがこちらの公式は通用しない。
> f1<-function(n) (n*(n+1))/2
> f1(1)
[1] 1
> f1(2)
[1] 3
> f1(3)
[1] 6
> f1(4)
[1] 10
それで気の効いた説明ではあえて「ただし公比$d \neq 1$の場合」と断っている。冪乗算の微積分同様に$0<n<2$の範囲に特異点(Singularity)が存在し、自然数集合においてこの条件を満たすのは1のみとなる訳である。
冪乗算(Exponentiation)の微積分
-
関数列におけるε-δ論法では連続関数$\lim_{x \to a}f(x)=f(a)$の収束がxに依存する場合を各点収束、依存しない場合を一様収束とするが、これは「"とりあえず"が使える=xに依存しない」なので一様収束となるケース? それとも、そもそも収束しないので無関係?
関数列と関数項級
イプシロン-デルタ論法 - Wikipedia
単位元も反元も追加不可能なので群を構成しません。どういう事かは以下のアニメーションで直感的に理解可能です。
【Rで球面幾何学】等差数列(算術数列)②数直線概念から同心円集合概念へ
整数族(Integer Family)整数列(Integer Sequence)
無限少-∞と無限大+∞を含まない等間隔に離散する開集合をなす。
\mathbb{Z}_n(n=-\infty→0→+\infty)=(-\infty+1,…,-2,-1,0,1,2,…,+\infty-1)
import networkx as nx
G = nx.DiGraph()
# G.add_edge("Rap Function1^n(関数列)","Sum(演算)")
# G.add_edge("Sum(演算)","Natural(族)")
G.add_edge("Natural(族)","Grouping(演算)")
G.add_edge("Grouping(演算)","Integer(族)")
G.add_edge("Cyclic Function-1^n(関数列)","Unionize(演算)")
G.add_edge("Cyclic Function-1^n±1(関数列)","Unionize(演算)")
G.add_edge("Unionize(演算)","Crossing(演算)")
G.add_edge("Rap Function1^n(関数列)","Crossing(演算)")
G.add_edge("Crossing(演算)","Integer(族)")
# G.add_edge("Integer(族)","Decimal System(演算)")
# G.add_edge("Decimal System(演算)","Real(族)")
# G.add_edge("Real(族)","Extraction:x=0→2(演算)")
# G.add_edge("Extraction:x=0→2(演算)","2^x(演算)")
# G.add_edge("2^x(演算)","Real(族)")
# G.add_edge("Napierian(族)","2^x(演算)")
nx.nx_agraph.view_pygraphviz(G, prog='fdp')
①さしあたって自然数列$\mathbb{N}_n$に単位元0と逆元$\mathbb{N}_n^{-1}$を追加する群演算(Group Operation)の演算結果集合で規定する。その演算集合はZ軸(あるいは時間軸t)における断面曲率の変化を伴わない二次元極座標系、すなわち円筒座標系(Cylindrical Coordinate System)として観測される事になる。
【数理考古学】とある実数列の規定例①等差数列から加法整数群へ

- この操作の結果、観測原点の概念が消失し、観測限界∞が無限小-∞と無限大+∞に分解される点に注意。
- 虚数(Imaginal)として実軸外部に押し出される円筒半径は理論上どう設定しても良いが、実軸との対応を考えるとそれとの比が1:1と規定するのが最も都合が良い
②かかる観測結果集合は偶数群2nと奇数集合2n±1の直積、あるいは周期関数(Cyclic Function)$-1^n=±i^{2x}$と$-1^n±1=±i^{2x}±1$の直積(ただしn=0→1とし半周単位で分岐切断点を設定した場合)およびそれと周回関数$1^n$の交点を求める形でも規定される。


- ここで初めて「離散集合をなす整数列の補集合」としての虚数(Imaginal)概念が数理全体の説明として必要不可避となる。
ところで±1はこの座標系に追加される「奇数の最初の一対」でもあり、②が構成する群と後述するガウスの巡回群における「奇数図形が円を2分する数理」を組み合わせると、この時点における観測限界∞の無限小-∞と無限大+∞への分解を上手く説明出来たりするのである。
【数理考古学】群論とシミュレーション原理②群導出演算としてのガウスの巡回群
③偶奇の概念自体は商群(Quotient Group/Factor Group)を用いて複素数の概念を導入する事なく追加する事が可能である。
商群 - Wikipedia
整数$\mathbb{Z}$が加法についてなす群と、すべての偶数からなる部分群$2\mathbb{Z}$を考える。$\mathbb{Z}$は可換群なので正規部分群である。剰余類は2つしかない:偶数全体の集合と奇数全体の集合である;したがって商群$\frac{\mathbb{Z}}{2\mathbb{Z}}$は2つの元を持つ巡回群となり、それは2を法とする加法をもつ集合(0,1)と同型である;インフォーマルに商群$\frac{\mathbb{Z}}{2\mathbb{Z}}$は2を法とする加法をもつ集合(0,1)に「等しい」と表現する事もある。
ただしこの思考様式、あくまで整数列の実存を前提とした拡張なので、整数列そのものの規定には関わらない。また巡回群の概念を導入した以上、分割数が3以上となる段階で複素数概念導入が不可避となる。
【数理考古学】三次方程式から虚数へ。
実数族(Real Family)実数列(Real Sequence)
無限少-∞と無限大+∞を含まない連続的開集合をなす。
\mathbb{Z}_n(n=-\infty→0→+\infty)=(-\infty,…,-2,…,-1,…,0,…,1,…,2,…,+\infty)
import networkx as nx
G = nx.DiGraph()
# G.add_edge("Rap Function1^n(関数列)","Sum(演算)")
# G.add_edge("Sum(演算)","Natural(族)")
# G.add_edge("Natural(族)","Grouping(演算)")
# G.add_edge("Grouping(演算)","Integer(族)")
# G.add_edge("Cyclic Function-1^n(関数列)","Unionize(演算)")
# G.add_edge("Cyclic Function-1^n±1(関数列)","Unionize(演算)")
# G.add_edge("Unionize(演算)","Crossing(演算)")
# G.add_edge("Rap Function1^n(関数列)","Crossing(演算)")
# G.add_edge("Crossing(演算)","Integer(族)")
G.add_edge("Integer(族)","Decimal System(演算)")
G.add_edge("Decimal System(演算)","Real(族)")
G.add_edge("Real(族)","Extraction:x=0→2(演算)")
G.add_edge("Extraction:x=0→2(演算)","2^x(演算)")
G.add_edge("2^x(演算)","Real(族)")
G.add_edge("Napierian(族)","2^x(演算)")
nx.nx_agraph.view_pygraphviz(G, prog='fdp')
①さしあたって十進法(Decimal System)すなわち「10を法とする剰余類(0,1,2,3,4,5,6,7,8,9)を添字とする演算結果集合の任意の入れ子状態がなす演算結果集合」で規定する。
剰余類 - Wikipedia
- 山本義隆「少数と対数の概念(2018年)」は、ルネサンス期欧州が複式簿記概念の普及(最初は地中海商人が駆使するアラビア数学の一環として元ヴェネツィア商人の数学者が紹介した)によって単位元0と負数(「貸方」の逆元としての「借方」)の概念を獲得し他にも関わらず、さらにそれを少数の概念に発展させるのが遅れたのは「お金に少数の概念がなかったから」とする。大変興味深い仮説といえよう。群論が整数と少数の峻別(あるいは少数概念の排除)に血道を上げるのは、あるいはこの辺りの歴史に由来するのかもしれない
「数学の常識」が確立したのは意外に新しい
【数理考古学】三次方程式から虚数へ。
【初心者向け】添字化と単位化
この考え方は商群(Quotient Group/Factor Group)を用いた説明によってさらに一般化する事が出来る。
整数が加法についてなす群$\mathbb{Z}$を考える。nを任意の正整数とする。nのすべての倍数からなる$\mathbb{Z}$の部分群$n\mathbb{Z}$を考える。$\mathbb{Z}$は可換なのでその部分群$n\mathbb{Z}$は正規である。剰余類たちの集合は($n\mathbb{Z}$,$1+n\mathbb{Z}$,…,$(n−2)+n\mathbb{Z}$,$(n−1)+n\mathbb{Z}$) である。整数kは、kをnで割った余りをrとすると、剰余類$r+n\mathbb{Z}$に属する。商$\frac{\mathbb{z}}{n\mathbb{z}}$はnで割った「余り」の群と考えることができる。これは位数nの巡回群(Cyclic Group/Monogenous Group)である。
巡回群 - Wikipedia
ここで1の12乗根全体を考える。これは単位円周に乗っているが、乗法についてアーベル群Gをなす。数が色つきの点で偏角とともに絵に描かれている。赤い点で示されている、1の4乗根全体のなす部分群Nを考える。この正規部分群は群を赤、緑、青で示される3つの剰余類に分ける。剰余類たちが3元からなる群をなすことを確認できる(赤の元と青の元の積は青、青の元の逆元は緑、など)。したがって、商群$\frac{G}{N}$は3色の群で、3つの元をもつ巡回群であることが分かる。
さらに実数が加法についてなす群$\mathbb{R}$とその整数からなる部分群$\mathbb{Z}$を考える。$\mathbb{R}$における$\mathbb{Z}$の剰余類はすべて、0≤a<1を実数として$a+\mathbb{Z}$の形の集合である。そのような剰余類を足すことは対応する実数を足し、結果が1以上ならば1を引くことによってなされる。商群$\frac{\mathbb{R}}{\mathbb{Z}}$は円周群$S_1$と同型であり、これは絶対値1の複素数が乗法についてなす群、あるいはそれに対応して、2次元で原点についての回転のなす群、すなわち「平面上における回転」を意味する特殊直交群SO(2)である。同型はf(a+Z)=exp(2πia)によって与えられる。SO(2)はさらに「球面上における回転」SO(3)に発展させる事が出来る。
SO(2) - EMANの物理数学
SO(3) - EMANの物理数学
ここに現れる「$実数\mathbb{R}=実数\mathbb{R}_a(a=0→1)+整数\mathbb{Z}$」で考える思考様式は「$冪乗算2^x+実数\mathbb{R}_n(n=0→2)$」で考える②の思考様式の大源流かもしれない(とりあえず思いついたのでメモがてら)。
②「0から2までの正の実数」と2の冪乗算を組み合わせて正の実数に対応させ、それを群演算した演算結果集合もこの族を規定する。
2^n(n=-\infty→+\infty)=(2^{-\infty}=\frac{1}{\infty}=0,…,2^{-2}=\frac{1}{2^2}=\frac{1}{4},…,2^{-1}=\frac{1}{2},…,2^0=\frac{2}{2}=1,…,2^1=2,…,2^2=4,…,2^{+\infty}=\infty)
2の冪乗算を用いた正の整数の表現例
| Values | Explessions | |
|---|---|---|
| 1 | 1 | 2^0 |
| 2 | 2 | 2^1 |
| 3 | 3 | 2^0+2^1 / 2^log(3,base=2) |
| 4 | 4 | 2^2 |
| 5 | 5 | 2^2+2^0 |
| 6 | 6 | 2^2+2^1 |
| 7 | 7 | 2^2+2^log(3,base=2) |
| 8 | 8 | 2^3 |
そう、まさにこの辺りが$-1 \rightleftharpoons n \rightleftharpoons +1$あるいは$0 \rightleftharpoons n \rightleftharpoons 2$を運動範囲とする単振動(Simple Vibration)概念の出発点となるのである。
③実数列を(確率の合計を1=100%と計算する)確率密度空間(Probability Density Space)の概念で掌握する統計学(Statistics)の考え方では、間隔尺度(Interval Scale)が「自然数族を十進法導入によって連続化した空間に配置される観測結果集合」、比例尺度(Ratio Scale)が「それにさらに群演算を加えた(すなわち中心を検出して単位元とし、元と逆元を定める操作を経た)連続空間に配置される観測結果集合」に対応し、後者が二群間の相関係数(Correlation Coefficient)や線形回帰性(Linear Regression)などを導出する出発点となる。
確率密度関数 - Wikipedia
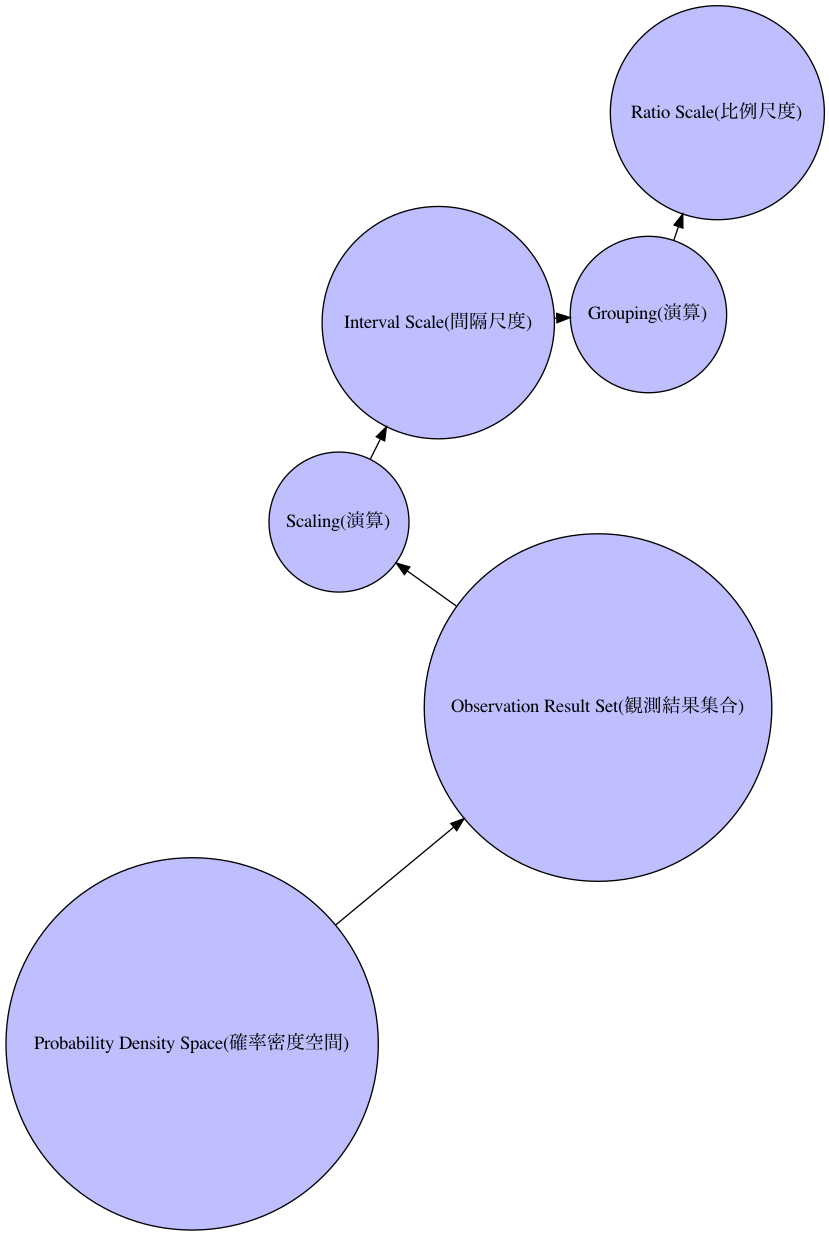
import networkx as nx
G = nx.DiGraph()
G.add_edge("Probability Density Space(確率密度空間)","Observation Result Set(観測結果集合)")
G.add_edge("Observation Result Set(観測結果集合)","Scaling(演算)")
G.add_edge("Scaling(演算)","Interval Scale(間隔尺度)")
G.add_edge("Interval Scale(間隔尺度)","Grouping(演算)")
G.add_edge("Grouping(演算)","Ratio Scale(比例尺度)")
nx.nx_agraph.view_pygraphviz(G, prog='fdp')
【初心者向け】平均と標準偏差、中央値と平均偏差
【初心者向け】標本分散と不偏分散
【初心者向け】度数分布(Frequency Table)/度数分布図と最頻値(Mode)
【初心者向け】記述統計学と代表値
線形回帰とは何か - Qiita
- この操作においても観測原点の概念が消失し、観測限界∞が無限小-∞と無限大+∞に分解される点に注意。データの平均や中央値や最頻値のどれかを代表値(Representative Value)と定めた段階で、このプロセスは既に始まっているのである。
ネイピア族(Napierian Family)
実数列の指数写像(Exponential Map)と対数写像(Logarithmic Map)を「登り坂の数だけ下り坂がある」観点から併合した独自概念である。
【トーラス構造と古典数学】等比数列(幾何数列)②同心円集合に射影する準備


import networkx as nx
G = nx.DiGraph()
# G.add_edge("Napierian(-2)(族)","指数写像(-1)(演算)")
# G.add_edge("指数写像(-1)(演算)","Napierian(-1)(族)")
# G.add_edge("Napierian(-1)(族)","対数写像(-1)(演算)")
# G.add_edge("対数写像(-1)(演算)","Napierian(-2)(族)")
G.add_edge("Napierian(-1)(族)","指数写像(0)(演算)")
G.add_edge("指数写像(0)(演算)","Real(族)")
G.add_edge("Real(族)","対数写像(0)(演算)")
G.add_edge("対数写像(0)(演算)","Napierian(-1)(族)")
G.add_edge("Real(族)","指数写像(+1)(演算)")
G.add_edge("指数写像(+1)(演算)","Napierian(+1)(族)")
G.add_edge("Napierian(+1)(族)","対数写像(+1)(演算)")
G.add_edge("対数写像(+1)(演算)","Real(族)")
# G.add_edge("Napierian(+1)(族)","指数写像(+2)(演算)")
# G.add_edge("指数写像(+2)(演算)","Napierian(+2)(族)")
# G.add_edge("Napierian(+2)(族)","対数写像(+2)(演算)")
# G.add_edge("対数写像(+2)(演算)","Napierian(+1)(族)")
nx.nx_agraph.view_pygraphviz(G, prog='fdp')
- この演算の無限連続性に触れた説明にまだ出会えてないので仮設定。この辺りから族を単なる(コンピューター言語における)定数と看做すのが難しくなってくる。
- この演算結果集合では実数列上における乗除算が対数写像上における加減算に置き換わる。
【数理考古学】常用対数表を使った計算
$\log xy=\log x+\log y$
$\log\frac{x}{y}=\log x-\log y$
①指数写像(-∞が0、0が1、+∞が∞に射影される)
exp(x)(x=-\infty→0→+\infty)=(exp(-\infty)=\frac{1}{exp(\infty)}=0,…,exp(-1)=\frac{1}{exp(1)},…,exp(0)=\frac{exp(1)}{exp(1)}=1,…,exp(1),…,exp(+\infty)=\infty)
②対数写像…直接計算出来ないので、まずは「0から2までの正の対数」とLog(2)の組み合わせから任意の正の対数を求め、さらにその真数部を逆数化した結果を逆元に設定する。
【数理考古学】冪乗算の微積分
$\log2$を用いた対数の表現例
| Numbers | Explessions | Values | |
|---|---|---|---|
| 1 | log(1) | log(2^1)+log(1/2) | 0 |
| 2 | log(2) | log(2^1) | 0.6931472 |
| 3 | log(3) | log(3/2)+log(2^1) | 1.098612 |
| 4 | log(4) | log(2^2) | 1.386294 |
| 5 | log(5) | log(5/4)+log(2^2) | 1.609438 |
| 6 | log(6) | log(3/2)+log(2^2) | 1.791759 |
| 7 | log(7) | log(7/4)+log(2^2) | 1.94591 |
| 8 | log(8) | log(2^3) | 2.079442 |
ところで指数関数や対数関数はしばしばオイラーの公式(Eulerian Formula)$e^{θi}=\cos(θ)+\sin(θ)i$と紐付けて語られるが、実はこの演算自体はネイピア族に属していない(後述)。その事についてノーベル賞を受賞した物理学者朝永振一郎博士(1906年~1979年)は高校時代から気付いており「中学生には解けない(逆を言えば高校生以上なら解けて不思議でない)問題」と指摘している。この発想がネイピア族と(後述する)ピタゴラス族を分離する数理抽出を目指す最初のモチベーションとなった。
【無限遠点を巡る数理】オイラーの公式と等比数列④「中学生には難しいが高校生なら気付くレベル」?
とにかくネイピア族自体の数理はそれとは随分と異なる形で独自展開する。
【初心者向け】ロジスティック方程式とその関連範囲
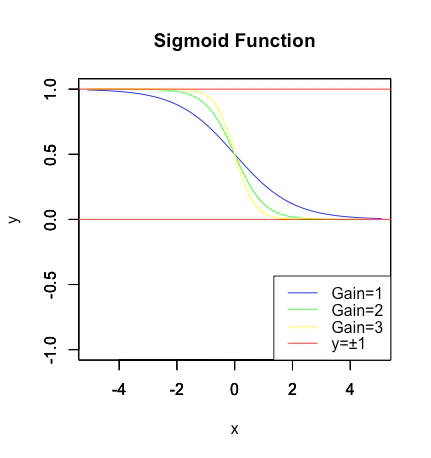
例えば生物の神経細胞が持つ性質のモデル化で、ニューラルネットワークにおける活性化関数などで用いられるシグモイド関数(Sigmoid Function)$\frac{1}{1+e^{ax}}=\frac{tanh(\frac{ax}{2})+1}{2}$辺りがその著名な代表例の一つとなる。
【初心者向け】指数・対数関数の発見とそれ以降の発展について。 - Qiita
ピタゴラス族(Pythagorean Family)
さしあたって絶対値(半径)1を与えられたピタゴラスの定理(Pythagorean Theorem)$x^2+y^2=1$が描く円弧/球面上の任意の座標集合(球状集合)についての独自表現。
数理考古学】ピタゴラスの定理あるいは三平方の定理からの出発
半径r^2=x^2+y^2+z^2+…\\
特に二次元で半径1の時、y=\sqrt{1-x^2},x=\sqrt{1-y^2}
- 以下の概念を網羅する説明にまだ出会えてないのでとりあえず仮設定
- この集合自体は単位元も反元も備えないので群を構成しない。その辺りの特徴は自然数列と似ている。
(高校数学で習う様な)2項展開(Binomial Expansion)$(a±b)^2$の範囲では扱い切れず、その証明に「角度が90度(π/2ラジアン)という特別条件」や「複素平面(Complex Plane)における単位円上の操作、すなわち虚数(Imaginal)$i^2=−1$概念の導入と共益複素数(Conjugate Complex Number)の相互打ち消し作用」などを必要とする。
【初心者向け】パスカルの三角形と二項定理または二項展開
全体像はこんな感じとなります。ある意味、始まりも終わりもなく、大小の比較も不可能な「虚無の世界」の顕現そのもの…
【初心者向け】複素共役のアニメーション表示について。



何がややこしいって、ゲームプログラミングにおける当たり判定(2点間の絶対値を求めて相対距離を計測する)やモンテカルロ法における円の面積や球の体積の算出(ランダムに置かれる点が円/球の内側か外側か判定する)に使われるピタゴラスの定理そのものには、それに含まれる各点の座標を特定する数理が含まれていないのです。
【初心者向け】「モンテカルロ法」概説
なのでそを担当する別の演算群(Operation Group)が存在します。オブジェクト志向プログラミングでいうところの「そのクラスにおいてメンバ変数を共有するメンバメソッド群」に該当。
メンバ変数とメンバメソッド | Java入門
-
0次元の場合…代数方程式$x^2+y^2=0$を解くと$y=±x$ないしは$x=±y$となり、かかる一対の線形関数(Linear function)の交点、すなわちxy軸の中心(0,0)、複素平面(Complex Plane)実軸(Real Axis)上における0の一点(一切の広がりを備えない半径0の円)としか観測されない。この考え方はN次球へも拡張可能である(任意の次元数上において「点=一切の広がりを備えない半径0の球面」としてしか観測されない)。
【Python演算処理】「N次球概念導入による円/球関係の数理の統合」? -
1次元の場合…ピタゴラス族と実数列の交点は2点のみ、すなわちxy軸上の(1,0)(-1,0)あるいは複素平面実軸上の-1、1だけとなる。交代級数(Alternating Series)に該当する演算結果集合と重なる。
【数理考古学】解析学史に「虚数概念」をもたらした交代級数 -
2次元の場合…代数方程式$x^2+y^2=1$を解くと$y=±\sqrt{1-x^2}$ないしは$x=±\sqrt{1-y^2}$となり、それぞれ前者はy=0、後者はx=0を分枝切断線(Branch cut line=到達不可能な特異点)とする半円2本を描く。演算結果集合としては極座標系(Polar Coordinates System)(r,θ)上の円(Circle)=半径1の単位円×半径(Radius)R=観測結果集合とする円周群=リー群$S_0$=1次元トーラス×半径(Radius)rに該当。
【Rで球面幾何学】等差数列(算術数列)②数直線概念から同心円集合概念へ

-
3次元の場合…三次元極座標系(3D Polar Coordinate System)(半径r,水平角φ,垂直角θ)は、三次元トーラス多様体$S_3$=四元数(Quaternion)上における「縦回転も横回転も伴わない場合(すなわ大半径Rに直交する交点を中心に±Rの線分伸ばした接線の両端を対蹠に取った場合)」がなす球状集合に該当する。
【数理考古学】群論とシミュレーション原理⑥二次元トーラス概念への発展


ちなみに以下の演算の結果集合が「リー群$S_0$=一次元トーラス=円周群」を充分近似するには条件があります。
①ガウスの巡回群(Gaussian Cyclic Group)の場合。
【数理考古学】群論とシミュレーション原理②群導出演算としてのガウスの巡回群
円周上に現れる正n角形が充分に円の定義たる「辺数∞、辺長$\frac{1}{∞}=0$」の条件を満たす事(このサイトでは正60角形を採用するケースが多い)。ただしこの演算に限ってはnをどれだけ小さく取っても、その元が円周群の元をはみ出す事がない。
一辺の長さがaの正n角形に外接する円の半径r
- $r=\frac{a}{2\tan(\frac{π}{n})}$
- $a=r(2\tan(\frac{π}{n}))$
一辺の長さがAの正n角形に内接する円の半径R
- $R=\frac{A}{2\tan(\frac{π}{n})cos(\frac{π}{n})}$
- $A=R(2\tan(\frac{π}{n})cos(\frac{π}{n}))$
一辺の長さがaの正n角形の外接円の半径と内接円の半径の関係
- $r=Rcos(\frac{π}{n})$
- $R=\frac{r}{cos(\frac{π}{n})}$
外接円を単位円(Unit Circle)としたのが上記アニメーション。
- 外接円の半径Rは単位円の定義に従って1
- これに内接する正多辺形の1辺の長さAは$2\tan(\frac{π}{辺数})\cos(\frac{π}{辺数})$
- 外接円に内接する正多辺形の内接円の半径rは$\cos(\frac{π}{辺数})$
この演算の極限には半径1の単位円の場合における円周長として2πが現れる。半径rの場合に一般化すると算数段階で習う2πrとなる。
②虚数冪(Imaginal Exponentiation)$e^{θi}$の場合。
【数理考古学】群論とシミュレーション原理④群導出演算としてのオイラーの公式
ネイピア数e(2.71828)が充分近似出来ている事。
③公比-1の等比数列$-1^x=±i^{2x}$の場合。
【数理考古学】群論とシミュレーション原理⑤群導出演算としての「公比-1の等比数列」
「周回関数(Rap Function)$α^n$の冪根αが十分1に近く」かつ「周期関数(Cyclyc Function)$−1^n$の冪根βが十分-1に近い」場合に限られる。
0<公比<1の時…純粋な1次元展開により0へ向けて収束。
公比>1の時…純粋な1次元展開により無限大に向けて発散。
0>公比>-1の時…振幅の幅が0に向けて狭まっていく。
公比<-1の時…振幅の幅が無限大に向けて広がっていく。
④解析学的アプローチ
【数理考古学】群論とシミュレーション原理③群導出演算としての解析学的アプローチ
Z軸について、円の表面積や体積を求める際には半径(Radius)=単純振動を、球面座標を求める際には三角関数(Cos(θ))を採用する。
【Python演算処理】半径・直径・円周長・円の面積・球の表面積・球の体積の計算上の往復 - Qiita
考え方の中核は以下の球の表面積を求める式$4πr^2$や球の体積を求める式$\frac{4}{3}πr^3$を導出する三重積分三重積分にある。
{\int U(x,y,z)dV=\int_{0}^{2π}\int_{0}^{π}\int_{0}^{1}U(r,θ,φ)r^2\sinθdrdθdφ\\ =\int_{0}^{2π}\int_{0}^{π}\int_{0}^{1}\begin{vmatrix} \frac{∂x}{∂r} & \frac{∂x}{∂θ} & \frac{∂x}{∂φ}\\ \frac{∂y}{∂r} & \frac{∂y}{∂θ} & \frac{∂y}{∂φ}\\ \frac{∂z}{∂r} & \frac{∂z}{∂θ} & \frac{∂z}{∂φ} \end{vmatrix} drdθdφ }
極座標系(r,φ,θ,…)積分範囲の積み重ね方に注目すると以下となっている。
- まずは角度φ=0→2πφ=0→2πの範囲で積分して円周2πrに到達。
- さらに角度θ=0→πθ=0→πの範囲で積分を重ね**球の表面積****$4πr^2$に到達。
- さらに半径r=0→1r=0→1の範囲で積分を重ね球の体積$\frac{4}{3}πr^3$に到達。
垂直角θ(0~πラジアンのπ範囲)を水平角φ(-πラジアン~0~+πラジアンの2π範囲)の半分に取るのが特徴で、地球儀上で緯度(±90度)の概念が経度(±180度)で表されるのも同じ数理に基づく。
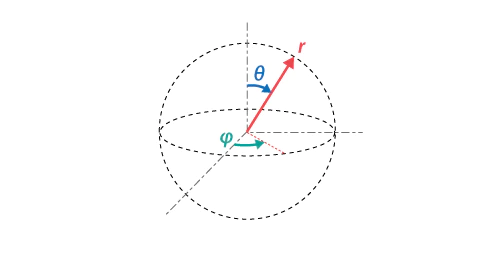
二次元空間(円弧)におけるデカルト座標系(x,y)と極座標系(r,φ)の相互変換
- 原点(0,0)からの距離$r=\sqrt{x^2+y^2}$
- $φ(-π \rightleftharpoons +π)=-(\arctan^2(x,y)-\frac{π}{2})$
- $x=r×\cos(φ)$
- $y=r×\sin(φ)$
三次元空間(球面)におけるデカルト座標系(x,y,z)と極座標系(r,φ,θ)の相互変換
- 原点(0,0,0)からの距離$r=\sqrt{x^2+y^2+z^2}$
- $φ(-π \rightleftharpoons +π)=-(\arctan^2(x,y)-\frac{π}{2})$
- $θ(-\frac{π}{2} \rightleftharpoons +\frac{π}{2})=-(\arctan^2(\sqrt{x^2+y^2+z^2},z)-\frac{π}{2})$
- $x=r×\sin(θ)\cos(φ)$
- $y=r×\sin(θ)\sin(φ)$
- $z=r×\cos(θ)$
そして、この辺りから円描画に関係する単振動(Simple Vibration)概念が、偶数系$-1 \rightleftharpoons n \rightleftharpoons +1$と奇数系$0 \rightleftharpoons n \rightleftharpoons 2$の2種類存在する事が俄然意味を持ち始めるのです。
【トーラス構造と古典数学】「単位円筒」から「トーラス構造」へ

import networkx as nx
G = nx.DiGraph()
G.add_edge("Real(族)","Extraction:x=-1 →1(演算)")
G.add_edge("指数写像(exp(xπi/2))(演算)","Extraction:x=-1 →1(演算)")
G.add_edge("Extraction:x=-1 →1(演算)","指数写像(exp((x±1)πi/2))(演算)")
G.add_edge("Extraction:x=-1 →1(演算)","指数写像(exp(xπi/2))(演算)")
G.add_edge("指数写像(exp((x±1)πi/2))(演算)","Extraction:x=-1 →1(演算)")
G.add_edge("Pythagorean(族)=偶数系","指数写像(exp(xπi/2))(演算)")
G.add_edge("Pythagorean±1(族)=奇数系","指数写像(exp((x±1)πi/2))(演算)")
G.add_edge("指数写像(exp(xπi/2))(演算)","Pythagorean(族)=偶数系")
G.add_edge("指数写像(exp((x±1)πi/2))(演算)","Pythagorean±1(族)=奇数系")
nx.nx_agraph.view_pygraphviz(G, prog='fdp')
- ここで引いた「補助線」は、等速円運動(Constant Velocity Circular Motion)やオイラーの公式(Eulerian formula)$e^{θi}=\cos(θ)+\sin(θ)i$が立脚する「1軸で回転する円状/球状集合」の概念に由来する。
【数理考古学】群論とシミュレーション原理④群導出演算としてのオイラーの公式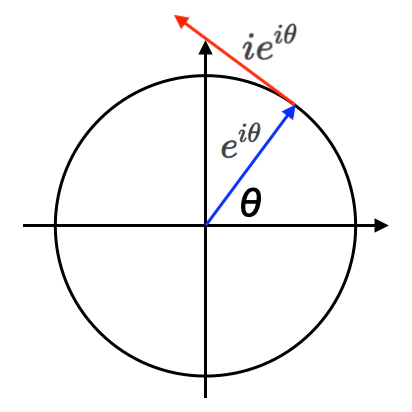
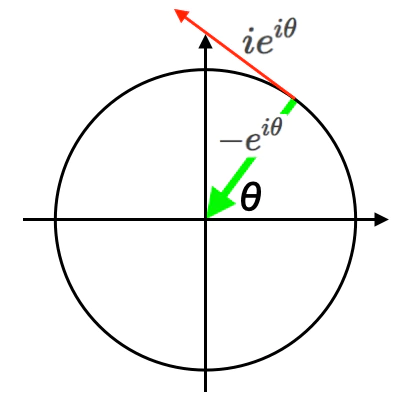
- そしてかかる「1軸で回転する円状/球状集合」に2番目の直行回転軸を与えると、両者の合成結果として3番目の直行回転軸が勝手に追加されるのが三次元トーラス多様体$S_3$=四元数(Quaternion)概念の基本原理となる(リー群$S_1$の次が$S_2$でなく$S_3$なのはこの為)。。
【数理考古学】群論とシミュレーション原理⑦三次元トーラスとしての四元数概念導入
完全に「気分は宇宙飛行士」じゃないですか…
ガウス族(Gauss Family)
「ある母集団から無作為抽出した標本の平均は標本の大きさを大きくすると母平均に近づく」とするベルヌーイの大数弱の法則を拡張して数式化した中心極限定理(CLT=Central Limit Theorem)に対応する観測結果集合。いわゆる正規分布(Normal Distribution)概念の表現としての「ベルカーブ」を指す独自表現。
【初心者向け】正規分布(Normal Distribution)とは何か?

f(x)=\frac{1}{\sqrt{2π}σ}e^{-\frac{(x-μ)^2}{2σ^2}}(-∞<x<+∞)\\
確率変数Xの期待値E(X)=平均μ\\
確率変数Xの分散V(X)=分散σ^2
import networkx as nx
G = nx.DiGraph()
G.add_edge("放物線-x^2(関数)","指数写像exp(-x^2)(演算)")
G.add_edge("指数写像exp(-x^2)(演算)","正規化(演算)")
G.add_edge("正規化(演算)","Gaussian(族)")
nx.nx_agraph.view_pygraphviz(G, prog='fdp')
①演算結果集合としては放物線関数$y=-x^2$の対数写像$y=e^{-x^2}$から出発する。実際の統計学で使う式はこの全体を確立密度空間に対応させた複雑な内容となるが、この曲線自体が備える数理的本質そのものは変わらない。
【初心者向け】指数・対数関数の発見とそれ以降の発展について。

② (全体を1=100%と考える確立密度空間に立脚する)統計学における相関係数や線形回帰といった数理処理の出発点(観測結果集合を演算結果集合に近づける為に遂行する外れ値除去の技法)でもある。かかる概念は、この演算結果集合を上掲のピタゴラス群に射影するとよりはっきりと見て取れる。
erf(x)=\frac{2}{\sqrt{π}}\int_{0}^{x}e^{-t^2}dt\\
erfc(x)=1-erf(x)=\frac{2}{\sqrt{π}}\int_{x}^{∞}e^{-t^2}dt=e^{-x^2}erfcx(x)\\
ω(x)=e^{-x^2}erfcx(ix)
- 通常のピタゴラス群の正面図では中心の反対側の対蹠を観測限界に設定するので裏半分が視野外となるのに対し、この場合は円の辺縁部を観測限界に設定する。その結果「**重力レンズ効果によって裏側まで見通せるブラックホールの景観」**が現れるが、人間の視覚はこの部分を誤差として切り捨ててしまうので、両者の違いに案外気付かない。
【数理考古学】誤差関数(ERF)と相補誤差関数 (ERFC)。
そもそも媒介変数として離心率εを導入した関数$\frac{1}{1+ε\cos(θ)}$(θ=−π→+π)において円(楕円)と放物線と双曲線は連続して現れるのです。
二次曲線の性質
【無限遠点を巡る数理】離心率①二次曲線(楕円,放物線,双曲線)の極座標表示からの出発
- 上掲のピタゴラス族との元の共有範囲は離心率ε=0の場合のみ。
離心率ε=0の時に半径1の単位円$y=±\sqrt{1-x^2}$
つまりリー群$S_0$=円周群=一次元トーラス。
離心率0<ε<1の時に楕円$y=\sqrt{b^2(1-\frac{x^2}{a^2})}$
離心率ε=1の時に放物線を横にした$y=\frac{1}{2}±\sqrt{x}$
離心率ε>1の時に双曲線$y=\sqrt{b^2(\frac{x^2}{a^2}-1)}$
そして離心率εが無限大∞に近くにつれ**原点{0,0}**へと収束。
そんな感じで以下続報…