とりあえず物理学における等速円運動=単位円筒(Unit Cylinder, 半径1,高さ2もしくは2π)概念から出発します。
【初心者向け】物理学における「単位円筒」概念について。



連動して動くX軸やY軸と異なりZ軸は独立しているのでどうとも差し替えが効きます。上掲は等尺(Even Schale)すなわち自然数集合(Natulal Set)Nnないしは加法整数群(Additive Integer Group)Zn=1を添字単位(Index Unit)とし、ラジアン尺(Radian Schale)=射影ピッチ(Projection Pitch)=2のπ尺(π Schale)を周期単位(Cycle Unit)に設定した場合で、周期単位を何度も繰り返せば「円柱に見えるだけの周回密度を備えた立体表現」が実現する訳です。
- 例えば半径R=1で周期単位2πの単位円筒(Unit Cylinder)で考える。
角速度 - Wikipedia -
角速度(Angular Velocity)が(半径1と同じ)1Radian/s(ラジアン毎秒)の場合には射影ピッチ=2πとなり、毎秒高さ2πの円筒追加が観測される。
【初心者向け】物理学における「単位円筒(Unit Cylinder)」の概念について。

XY軸(円弧)
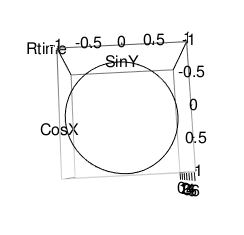
ZX軸(Cos波)
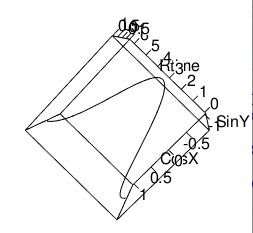
ZY軸(Sin波)
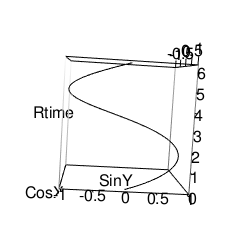
-
角速度が「2πのn倍」Radian/sの場合には射影ピッチ=1となり、毎秒高さ1の円筒追加が観測される。

かくして完成形はこんな感じに。
【初心者向け】「単位円筒」から「単位球面」へ

-
自然数集合(Natulal Set)…初項(First Term)α=1,公差(Common Difference)d=1,一般項(General Term)α+(n-1)dの等差数列(Arithmetic sequence=算術数列)Nn(n=1→Inf(inity)){1+(1-1)×1=1,1+(2-1)×1=2,1+(3-1)×1=3,…,1+(Inf(inity)-1)×1=Inf(inity)}={1,2,3,…,Inf(inity)}概念から出発する。これは単純化して再帰的にNn(n=1→Inf(inity)){1,1+1=2,(1+1)+1=3,…,Inf(inity)+1=Inf(inity)}と考えても良い。
【Rで球面幾何学】等差数列(算術数列)① 数直線概念の導入について。
その添字単位および周期単位は座標系そのもの(Coordinate System Itself)に観測原点(Observation Origin)の1点で固定されているだけなので、全体として同心円構造(Concentric Set Structure)/同心球面構造(Concentric SphereSetStructure)を構成する。XY座標上に置かれてはいるものの実質上、半径(Radius)Rと角度θによって表記(Expression)される極座標系(Polar Coordinates System)といって良い。
【Rで球面幾何学】等差数列(算術数列)②数直線概念から同心円集合概念へ

-
等尺(Even Scale)=加法整数群(Additive Integer Group)Zn(n=-Inf→-1→0→1→Inf){-Inf,…,-3,-2,-1,0,1,2,3,…,Inf}…自然数集合に加法単位元(Additive Identity)0と逆元(Inverse Element)-Nn(n=-Inf→0){-Inf,…,-3,-2,-1,0}を射影(Projection)した積(Product)。群(Group)成立条件を満たす。
【初心者向け】群論(Group Theory)概念の根幹


-
ラジアン尺(Radian Schale)=π尺(π Schale)πn(n=-Infπ=-Inf→-1→0→1→Infπ=Inf){-Inf,…,-3π,-2π,-π,0,π,2π,3π,…,Inf}…単位円筒(Unit Cylinder)概念を単位化(Unitization)したものだが、そのままでは射影ピッチ=2となる。
ラジアン - Wikipedia
ピッチとは何? Weblio辞書
添字単位(Index Unit)や周期単位(Cycle Unit)の概念はおそらく数学上の合同式(Congruent Expression)概念と重なってくるのでしょうが、そちらの定義が難しく全然理解出来ないので、とりあえず独自形式で表現しておきます。
数学で「法とする」とは、どういう意味でしょうか?
整数の合同 - Wikipedia
その起源は管理会計(Management Accounting)?
人類が最初にこうした座標概念(Coordinate Concept)に到達したのは、おそらく会計(Accounting)の世界においてでした。複式簿記(Double-Entry Bookkeeping System)の記法(Expression)では時系列が期首(Beginning)から期末(Ending)にかけて区切られた会計年度(Fiscal Year)の連続として表され、さらにその中身が(月初から月末にかけて区切られた)12ケ月、365日/366日などといった単位で仕切られます。この場合、会計年度が添字単位(Index Unit)、月や週や日などが周期単位(Cycle Unit)となる訳です。
<Weblio英会話コラム>「平成29年」「平成29年度」は英語でどう言う?
[fiscal とは 意味・読み方・表現 | Weblio英和辞書](fiscal とは 意味・読み方・表現 | Weblio英和辞書)
さらには閏年の概念を加え「4年+閏日」の尺度で考える事も可能で、この場合には年単位の会計年度(Fiscal Year)への射影ピッチ=1/4となります。
閏年 - Wikipedia
文献上での体系的紹介こそ(オスマン帝国台頭に伴うイタリア諸都市の地中海貿易への影響力低下と、代替産業としての出版事業発展を背景とする)ルネサンス期ヴェネツィア商人の手になる「秘密の暴露」までしか遡れませんが、間違いなくその基礎を構築したのは地中海のみならず中華王朝のそれをも含むユーラシア大陸南岸部全域、中央アジア、さらにはアフリカ大陸奥地でさえ闊歩した中世ムスリム商人で、さらなる大源流は天文学/占星術に基づく農業歴起草や測量技術に立脚して当時の灌漑農業を支えていた古代オリエント時代の神殿宗教にまで遡ると目されています。
スムマ(Summa de Arithmetica,1494年) - Wikipedia
とどのつまり大体、ほぼ60進法と同じ由来に辿り着くのですね。政治も科学も経済も全て主教に内包されていた原初の時代に…
【初心者向け】「円そのもの」の近似から派生した角度と経度の概念の起源
