【初心者向け】N進法(N-ary)とp進数(p-adic)

添字化された数列(Indexed Number Sequance)なるもの、それぞれの添字単位(Index Unit)の間を周期単位(Cycle Unit=反復単位)が埋める螺旋構造(Spiral Structure)としてイメージ可能です。つまり射影ピッチ(Projection Pitch)毎に桁上がり(Carry)が起こり次の周回に入るのです。

• 例えば半径R=1で周期単位2πの単位円筒(Unit Cylinder)で考える。
  角速度 - Wikipedia
• 角速度(Angular Velocity)が(半径1と同じ)1Radian/s(ラジアン毎秒)の場合には射影ピッチ=2πとなり、毎秒高さ2πの円筒追加が観測される。
  【初心者向け】物理学における「単位円筒(Unit Cylinder)」の概念について。
  
  
  
  XY軸（円弧）
  
  
  
  ZX軸（Cos波）
  
  
  
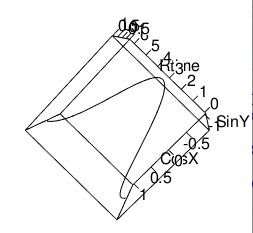
  ZY軸（Sin波）
  
  
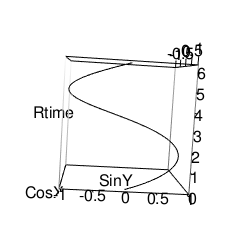
• 角速度が「2πのn倍」Radian/sの場合には射影ピッチ=1となり、毎秒高さ1の円筒追加が観測される。
  

目盛りをどう振るかは観察者の主観に任されています。

• 観察対象は様々な形態における「反復可能単位（周期）」を供給するに過ぎず、選ぶのはあくまで観察者なのである。

今回はこの辺りを詳しく掘り下げてみる事にしましょう。

#N進法(N-ary)とp進数(p-adic)

位取り記数法もしくはもしくはN 進法 - Wikipedia

数の表現方法の一種で、予め定められたN 種類の記号（数字）を列べることによって数を表す方法である。(位取りのことを桁ともいう。)数の表現方法の一種で、予め定められたN 種類の記号（数字）を列べることによって数を表す方法である。(位取りのことを桁ともいう。)

今日の日本において通常使われているのは、 N が十である十進法であるが、コンピューターでは二進法、八進法、十六進法といった「二の冪数」進法が用いられている。用語としては、「十進法」など「N進法」は「N進位取り記数法」を意味する語ではあるが、記数法以外にも「N進（Nで桁上がりする）命数法」という意味や、単に「ある特定の単位から上の単位を作る、冪乗による規則」という意味でも使用される。一方「N進法」はほぼ「base-N positional system/N進位取り記数法」の意味でしか使われない。

p進数

N進表記と関連が深い概念として、素数p毎に定まるp進数というものもある。 別概念ではあるが、両者は非常に関連があり、整数の p進表記を（可算）無限桁の自然数の範囲に拡張したものが p進整数で、さらにそこに有限桁の小数部分を許したものが p進数となる。ただし「無限桁の整数」（の一部は有理数として再解釈できるもののほとんど）は普通の数（実数）とは異なる。

p進数（p-adic number） - Wikipedia

1897年にクルト・ヘンゼルによって導入された、数の体系の一つである。文脈によっては、その体系の個々の数を指して p 進数と呼ぶこともある。

有理数の体系を実数や複素数の体系に拡張するのとは別の方法で各素数 p に対して p 進数の体系が構成される。それらは有理数のつくる空間の局所的な姿を記述していると考えられ、数学の中でも特に数論において重要な役割を果たす。数学のみならず、素粒子物理学の理論などで使われることもある。

「p 進数」とは「2進数」や「3進数」の総称に過ぎないので、文字 p がすでに他の場所で用いられている場合、q 進数や l 進数などと表現されることもある。

なお、自然数や実数を 0 と 1 で表現する方法（2進法）やその結果得られる記号列（2進列）も「2進数」と呼ぶ場合があるが、本項の意味での「2進数」とは異なる。

例えば、お遊びも含め以下の様な展開が考えられる訳です。

#二進数系の世界(2^n族)
イメージ的には「コンピューターが稼働してる環境」？

正方形（Square)
外角の大きさはpi/4=0.7853982ラジアンあるいは180/4=45度、内角の大きさは2pi(4-2)/16=0.7853982ラジアンあるいは180*(4-2)/4=157.5度。

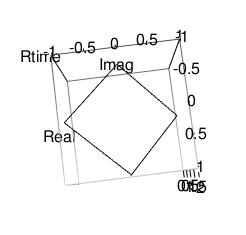
#正方形
library(rgl)
Rtime<-seq(0,2,length=5)
tr01<-c(1,(0+1i),-1,(0-1i),1)
Real<-Re(tr01)
Imag<-Im(tr01)
plot3d(Real,Imag,Rtime,type="l",xlim=c(-1,1),ylim=c(-1,1),zlim=c(0,2))
movie3d(spin3d(axis=c(0,0,1),rpm=5),duration=10,fps=25,movie="~/Desktop/test16")

二進数(正方形)

Three_square_theorem04<-function(x){
c0<-c(0,pi/2,-1*pi,-1*pi/2,0)
c0_cos<-cos(c0)
c0_sin<-sin(c0)
plot(c0_cos,c0_sin,type="l",main="Regular polygon rotation",xlab="Cos(θ)",ylab="Sin(θ)")
text(c0_cos,c0_sin, labels=c("000","010","100","110",""),col=c(rgb(1,0,0),rgb(1,0,0),rgb(1,0,0),rgb(1,0,0),rgb(1,0,0)),cex=c(2,2,2,2,2))
line_scale_01_cos<-seq(cos(c0[1]),cos(c0[2]),length=15)
line_scale_01_sin<-seq(sin(c0[1]),sin(c0[2]),length=15)
line_scale_02_cos<-seq(cos(c0[2]),cos(c0[3]),length=15)
line_scale_02_sin<-seq(sin(c0[2]),sin(c0[3]),length=15)
line_scale_03_cos<-seq(cos(c0[3]),cos(c0[4]),length=15)
line_scale_03_sin<-seq(sin(c0[3]),sin(c0[4]),length=15)
line_scale_04_cos<-seq(cos(c0[4]),cos(c0[1]),length=15)
line_scale_04_sin<-seq(sin(c0[4]),sin(c0[1]),length=15)
text(c(line_scale_01_cos[x],line_scale_02_cos[x],line_scale_03_cos[x],line_scale_04_cos[x]),c(line_scale_01_sin[x],line_scale_02_sin[x],line_scale_03_sin[x],line_scale_04_sin[x]), labels=c("000-001","010-011","100-101","110-111",""),col=c(rgb(0,0,1),rgb(0,0,1),rgb(0,0,1),rgb(0,0,1),rgb(0,0,1)),cex=c(1.5,1.5,1.5,1.5,1.5))
#塗りつぶし
polygon(c(c0_cos[1],line_scale_04_cos[x],line_scale_01_cos[x],c0_cos[1]), #x
c(c0_sin[1],line_scale_04_sin[x],line_scale_01_sin[x],c0_sin[1]), #y
density=c(30), #塗りつぶす濃度
angle=c(45),　 　　　#塗りつぶす斜線の角度
col=rgb(0,1,0)) 　 

#塗りつぶし
polygon(c(c0_cos[2],line_scale_01_cos[x],line_scale_02_cos[x],c0_cos[2]), #x
c(c0_sin[2],line_scale_01_sin[x],line_scale_02_sin[x],c0_sin[2]), #y
density=c(30), #塗りつぶす濃度
angle=c(45),　 　　　#塗りつぶす斜線の角度
col=rgb(0,1,0)) 　 

#塗りつぶし
polygon(c(c0_cos[3],line_scale_02_cos[x],line_scale_03_cos[x],c0_cos[3]), #x
c(c0_sin[3],line_scale_02_sin[x],line_scale_03_sin[x],c0_sin[3]), #y
density=c(30), #塗りつぶす濃度
angle=c(45),　 　　　#塗りつぶす斜線の角度
col=rgb(0,1,0)) 　

#塗りつぶし
polygon(c(c0_cos[4],line_scale_03_cos[x],line_scale_04_cos[x],c0_cos[4]), #x
c(c0_sin[4],line_scale_03_sin[x],line_scale_04_sin[x],c0_sin[4]), #y
density=c(30), #塗りつぶす濃度
angle=c(45),　 　　　#塗りつぶす斜線の角度
col=rgb(0,1,0)) 　

}

#アニメーション
library("animation")
Time_Code=c(1,2,3,4,5,6,7,8,9,10,11,12,13,14,15)
saveGIF({
for (i in Time_Code){
　Three_square_theorem04(i)
}
}, interval = 0.1, movie.name = "TEST04b.gif") 

正八角形（Regular Octagon)
外角の大きさはpi/8=0.3926991ラジアンあるいは180/8=22.5度、内角の大きさは2pi(8-2)/8=4.712389ラジアンあるいは180*(8-2)/8=135度）。

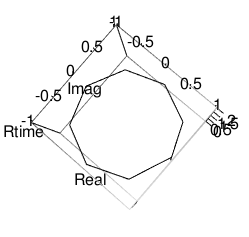
#正８角形
Rtime<-seq(0,2,length=9)
tr01<-exp(seq(0,2*pi,length=9)*(0+1i))
Real<-Re(tr01)
Imag<-Im(tr01)
#plot(Real,Imag,type="l")
plot3d(Real,Imag,Rtime,type="l",xlim=c(-1,1),ylim=c(-1,1),zlim=c(0,2))
movie3d(spin3d(axis=c(0,0,1),rpm=5),duration=10,fps=25,movie="~/Desktop/test08") 

二進数(八角形)

Three_square_theorem08<-function(x){
c0<-seq(0,2*pi,length=9)
c0_cos<-cos(c0)
c0_sin<-sin(c0)
plot(c0_cos,c0_sin,type="l",main="Regular polygon rotation",xlab="Cos(θ)",ylab="Sin(θ)")
text(c0_cos,c0_sin, labels=c("0000","0010","0110","1000","1010","1100","1010","1110",""),col=c(rgb(1,0,0),rgb(1,0,0),rgb(1,0,0),rgb(1,0,0),rgb(1,0,0),rgb(1,0,0),rgb(1,0,0),rgb(1,0,0),rgb(1,0,0)),cex=c(2,2,2,2,2,2,2,2,2))
line_scale_01_cos<-seq(cos(c0[1]),cos(c0[2]),length=15)
line_scale_01_sin<-seq(sin(c0[1]),sin(c0[2]),length=15)
line_scale_02_cos<-seq(cos(c0[2]),cos(c0[3]),length=15)
line_scale_02_sin<-seq(sin(c0[2]),sin(c0[3]),length=15)
line_scale_03_cos<-seq(cos(c0[3]),cos(c0[4]),length=15)
line_scale_03_sin<-seq(sin(c0[3]),sin(c0[4]),length=15)
line_scale_04_cos<-seq(cos(c0[4]),cos(c0[5]),length=15)
line_scale_04_sin<-seq(sin(c0[4]),sin(c0[5]),length=15)
line_scale_05_cos<-seq(cos(c0[5]),cos(c0[6]),length=15)
line_scale_05_sin<-seq(sin(c0[5]),sin(c0[6]),length=15)
line_scale_06_cos<-seq(cos(c0[6]),cos(c0[7]),length=15)
line_scale_06_sin<-seq(sin(c0[6]),sin(c0[7]),length=15)
line_scale_07_cos<-seq(cos(c0[7]),cos(c0[8]),length=15)
line_scale_07_sin<-seq(sin(c0[7]),sin(c0[8]),length=15)
line_scale_08_cos<-seq(cos(c0[8]),cos(c0[1]),length=15)
line_scale_08_sin<-seq(sin(c0[8]),sin(c0[1]),length=15)
text(c(line_scale_01_cos[x],line_scale_02_cos[x],line_scale_03_cos[x],line_scale_04_cos[x],line_scale_05_cos[x],line_scale_06_cos[x],line_scale_07_cos[x],line_scale_08_cos[x]),c(line_scale_01_sin[x],line_scale_02_sin[x],line_scale_03_sin[x],line_scale_04_sin[x],line_scale_05_sin[x],line_scale_06_sin[x],line_scale_07_sin[x],line_scale_08_sin[x]), labels=c("0000-0001","0010-0011","0100-0101","0110-0111","1000-1001","1010-1011","1100-1101","1110-1111",""),col=c(rgb(0,0,1),rgb(0,0,1),rgb(0,0,1),rgb(0,0,1),rgb(0,0,1),rgb(0,0,1),rgb(0,0,1),rgb(0,0,1),rgb(0,0,1)),cex=c(1.5,1.5,1.5,1.5,1.5,1.5,1.5,1.5))
#塗りつぶし
polygon(c(c0_cos[1],line_scale_08_cos[x],line_scale_01_cos[x],c0_cos[1]), #x
c(c0_sin[1],line_scale_08_sin[x],line_scale_01_sin[x],c0_sin[1]), #y
density=c(30), #塗りつぶす濃度
angle=c(45),　 　　　#塗りつぶす斜線の角度
col=rgb(0,1,0)) 　 

#塗りつぶし
polygon(c(c0_cos[2],line_scale_01_cos[x],line_scale_02_cos[x],c0_cos[2]), #x
c(c0_sin[2],line_scale_01_sin[x],line_scale_02_sin[x],c0_sin[2]), #y
density=c(30), #塗りつぶす濃度
angle=c(45),　 　　　#塗りつぶす斜線の角度
col=rgb(0,1,0)) 　 

#塗りつぶし
polygon(c(c0_cos[3],line_scale_02_cos[x],line_scale_03_cos[x],c0_cos[3]), #x
c(c0_sin[3],line_scale_02_sin[x],line_scale_03_sin[x],c0_sin[3]), #y
density=c(30), #塗りつぶす濃度
angle=c(45),　 　　　#塗りつぶす斜線の角度
col=rgb(0,1,0)) 　

#塗りつぶし
polygon(c(c0_cos[4],line_scale_03_cos[x],line_scale_04_cos[x],c0_cos[4]), #x
c(c0_sin[4],line_scale_03_sin[x],line_scale_04_sin[x],c0_sin[4]), #y
density=c(30), #塗りつぶす濃度
angle=c(45),　 　　　#塗りつぶす斜線の角度
col=rgb(0,1,0)) 　

#塗りつぶし
polygon(c(c0_cos[5],line_scale_04_cos[x],line_scale_05_cos[x],c0_cos[5]), #x
c(c0_sin[5],line_scale_04_sin[x],line_scale_05_sin[x],c0_sin[5]), #y
density=c(30), #塗りつぶす濃度
angle=c(45),　 　　　#塗りつぶす斜線の角度
col=rgb(0,1,0)) 　
#塗りつぶし
polygon(c(c0_cos[6],line_scale_05_cos[x],line_scale_06_cos[x],c0_cos[6]), #x
c(c0_sin[6],line_scale_05_sin[x],line_scale_06_sin[x],c0_sin[6]), #y
density=c(30), #塗りつぶす濃度
angle=c(45),　 　　　#塗りつぶす斜線の角度
col=rgb(0,1,0))

#塗りつぶし
polygon(c(c0_cos[7],line_scale_06_cos[x],line_scale_07_cos[x],c0_cos[7]), #x
c(c0_sin[7],line_scale_06_sin[x],line_scale_07_sin[x],c0_sin[7]), #y
density=c(30), #塗りつぶす濃度
angle=c(45),　 　　　#塗りつぶす斜線の角度
col=rgb(0,1,0))

#塗りつぶし
polygon(c(c0_cos[8],line_scale_07_cos[x],line_scale_08_cos[x],c0_cos[8]), #x
c(c0_sin[8],line_scale_07_sin[x],line_scale_08_sin[x],c0_sin[8]), #y
density=c(30), #塗りつぶす濃度
angle=c(45),　 　　　#塗りつぶす斜線の角度
col=rgb(0,1,0))

}

#アニメーション
library("animation")
Time_Code=c(1,2,3,4,5,6,7,8,9,10,11,12,13,14,15)
saveGIF({
for (i in Time_Code){
　Three_square_theorem08(i)
}
}, interval = 0.1, movie.name = "TEST08.gif") 

正16角形（Regular hexagon)
外角の大きさはpi/16=0.1963495ラジアンあるいは180/16=22.5度、内角の大きさは2pi(16-2)/16=5.497787ラジアンあるいは180*(16-2)/16=157.5度

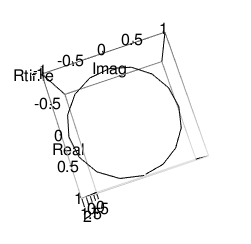
library(rgl)
#正16角形
Rtime<-seq(0,2,length=17)
tr01<-exp(seq(0,2*pi,length=17)*(0+1i))
Real<-Re(tr01)
Imag<-Im(tr01)
#plot(Real,Imag,type="l")
plot3d(Real,Imag,Rtime,type="l",xlim=c(-1,1),ylim=c(-1,1),zlim=c(0,2))
movie3d(spin3d(axis=c(0,0,1),rpm=5),duration=10,fps=25,movie="~/Desktop/test012")

二進数(正16角形)

Three_square_theorem16<-function(x){
c0<-seq(0,2*pi,length=17)
c0_cos<-cos(c0)
c0_sin<-sin(c0)
plot(c0_cos,c0_sin,type="l",main="Regular polygon rotation",xlab="Cos(θ)",ylab="Sin(θ)")
text(c0_cos,c0_sin, labels=c("00000","00010","00100","00110","01000","01010","01100","01110","10000","10010","10100","10110","11000","11010","11100","11110",""),col=c(rgb(1,0,0),rgb(1,0,0),rgb(1,0,0),rgb(1,0,0),rgb(1,0,0),rgb(1,0,0),rgb(1,0,0),rgb(1,0,0),rgb(1,0,0),rgb(1,0,0),rgb(1,0,0),rgb(1,0,0),rgb(1,0,0),rgb(1,0,0),rgb(1,0,0),rgb(1,0,0),rgb(1,0,0)),cex=c(1.5,1.5,1.5,1.5,1.5,1.5,1.5,1.5,1.5,1.5,1.5,1.5,1.5,1.5,1.5,1.5,1.5))
line_scale_01_cos<-seq(cos(c0[1]),cos(c0[2]),length=15)
line_scale_01_sin<-seq(sin(c0[1]),sin(c0[2]),length=15)
line_scale_02_cos<-seq(cos(c0[2]),cos(c0[3]),length=15)
line_scale_02_sin<-seq(sin(c0[2]),sin(c0[3]),length=15)
line_scale_03_cos<-seq(cos(c0[3]),cos(c0[4]),length=15)
line_scale_03_sin<-seq(sin(c0[3]),sin(c0[4]),length=15)
line_scale_04_cos<-seq(cos(c0[4]),cos(c0[5]),length=15)
line_scale_04_sin<-seq(sin(c0[4]),sin(c0[5]),length=15)
line_scale_05_cos<-seq(cos(c0[5]),cos(c0[6]),length=15)
line_scale_05_sin<-seq(sin(c0[5]),sin(c0[6]),length=15)
line_scale_06_cos<-seq(cos(c0[6]),cos(c0[7]),length=15)
line_scale_06_sin<-seq(sin(c0[6]),sin(c0[7]),length=15)
line_scale_07_cos<-seq(cos(c0[7]),cos(c0[8]),length=15)
line_scale_07_sin<-seq(sin(c0[7]),sin(c0[8]),length=15)
line_scale_08_cos<-seq(cos(c0[8]),cos(c0[9]),length=15)
line_scale_08_sin<-seq(sin(c0[8]),sin(c0[9]),length=15)
line_scale_09_cos<-seq(cos(c0[9]),cos(c0[10]),length=15)
line_scale_09_sin<-seq(sin(c0[9]),sin(c0[10]),length=15)
line_scale_10_cos<-seq(cos(c0[10]),cos(c0[11]),length=15)
line_scale_10_sin<-seq(sin(c0[10]),sin(c0[11]),length=15)
line_scale_11_cos<-seq(cos(c0[11]),cos(c0[12]),length=15)
line_scale_11_sin<-seq(sin(c0[11]),sin(c0[12]),length=15)
line_scale_12_cos<-seq(cos(c0[12]),cos(c0[13]),length=15)
line_scale_12_sin<-seq(sin(c0[12]),sin(c0[13]),length=15)
line_scale_13_cos<-seq(cos(c0[13]),cos(c0[14]),length=15)
line_scale_13_sin<-seq(sin(c0[13]),sin(c0[14]),length=15)
line_scale_14_cos<-seq(cos(c0[14]),cos(c0[15]),length=15)
line_scale_14_sin<-seq(sin(c0[14]),sin(c0[15]),length=15)
line_scale_15_cos<-seq(cos(c0[15]),cos(c0[16]),length=15)
line_scale_15_sin<-seq(sin(c0[15]),sin(c0[16]),length=15)
line_scale_16_cos<-seq(cos(c0[16]),cos(c0[1]),length=15)
line_scale_16_sin<-seq(sin(c0[16]),sin(c0[1]),length=15)

text(c(line_scale_01_cos[x],line_scale_02_cos[x],line_scale_03_cos[x],line_scale_04_cos[x],line_scale_05_cos[x],line_scale_06_cos[x],line_scale_07_cos[x],line_scale_08_cos[x],line_scale_09_cos[x],line_scale_10_cos[x],line_scale_11_cos[x],line_scale_12_cos[x],line_scale_13_cos[x],line_scale_14_cos[x],line_scale_15_cos[x],line_scale_16_cos[x]),c(line_scale_01_sin[x],line_scale_02_sin[x],line_scale_03_sin[x],line_scale_04_sin[x],line_scale_05_sin[x],line_scale_06_sin[x],line_scale_07_sin[x],line_scale_08_sin[x],line_scale_09_sin[x],line_scale_10_sin[x],line_scale_11_sin[x],line_scale_12_sin[x],line_scale_13_sin[x],line_scale_14_sin[x],line_scale_15_sin[x],line_scale_16_sin[x]), labels=c("00000-00001","00010-00011","00100-00101","00110-00111","01000-01001","01010-01011","01100-01101","01110-01111","10000-10001","10010-10011","10100-10101","10110-10111","11000-11001","11010-11011","11100-11101","11110-11111",""),col=c(rgb(0,0,1),rgb(0,0,1),rgb(0,0,1),rgb(0,0,1),rgb(0,0,1),rgb(0,0,1),rgb(0,0,1),rgb(0,0,1),rgb(0,0,1),rgb(0,0,1),rgb(0,0,1),rgb(0,0,1),rgb(0,0,1),rgb(0,0,1),rgb(0,0,1),rgb(0,0,1)),cex=c(1.3,1.3,1.3,1.3,1.3,1.3,1.3,1.3,1.3,1.3,1.3,1.3,1.3,1.3,1.3,1.3,1.3))

 #塗りつぶし
polygon(c(c0_cos[1],line_scale_16_cos[x],line_scale_01_cos[x],c0_cos[1]), #x
c(c0_sin[1],line_scale_16_sin[x],line_scale_01_sin[x],c0_sin[1]), #y
density=c(30), #塗りつぶす濃度
angle=c(45),　 　　　#塗りつぶす斜線の角度
col=rgb(0,1,0)) 　 

#塗りつぶし
polygon(c(c0_cos[2],line_scale_01_cos[x],line_scale_02_cos[x],c0_cos[2]), #x
c(c0_sin[2],line_scale_01_sin[x],line_scale_02_sin[x],c0_sin[2]), #y
density=c(30), #塗りつぶす濃度
angle=c(45),　 　　　#塗りつぶす斜線の角度
col=rgb(0,1,0)) 　 

#塗りつぶし
polygon(c(c0_cos[3],line_scale_02_cos[x],line_scale_03_cos[x],c0_cos[3]), #x
c(c0_sin[3],line_scale_02_sin[x],line_scale_03_sin[x],c0_sin[3]), #y
density=c(30), #塗りつぶす濃度
angle=c(45),　 　　　#塗りつぶす斜線の角度
col=rgb(0,1,0)) 　

#塗りつぶし
polygon(c(c0_cos[4],line_scale_03_cos[x],line_scale_04_cos[x],c0_cos[4]), #x
c(c0_sin[4],line_scale_03_sin[x],line_scale_04_sin[x],c0_sin[4]), #y
density=c(30), #塗りつぶす濃度
angle=c(45),　 　　　#塗りつぶす斜線の角度
col=rgb(0,1,0)) 　

#塗りつぶし
polygon(c(c0_cos[5],line_scale_04_cos[x],line_scale_05_cos[x],c0_cos[5]), #x
c(c0_sin[5],line_scale_04_sin[x],line_scale_05_sin[x],c0_sin[5]), #y
density=c(30), #塗りつぶす濃度
angle=c(45),　 　　　#塗りつぶす斜線の角度
col=rgb(0,1,0)) 　
#塗りつぶし
polygon(c(c0_cos[6],line_scale_05_cos[x],line_scale_06_cos[x],c0_cos[6]), #x
c(c0_sin[6],line_scale_05_sin[x],line_scale_06_sin[x],c0_sin[6]), #y
density=c(30), #塗りつぶす濃度
angle=c(45),　 　　　#塗りつぶす斜線の角度
col=rgb(0,1,0))

#塗りつぶし
polygon(c(c0_cos[7],line_scale_06_cos[x],line_scale_07_cos[x],c0_cos[7]), #x
c(c0_sin[7],line_scale_06_sin[x],line_scale_07_sin[x],c0_sin[7]), #y
density=c(30), #塗りつぶす濃度
angle=c(45),　 　　　#塗りつぶす斜線の角度
col=rgb(0,1,0))

#塗りつぶし
polygon(c(c0_cos[8],line_scale_07_cos[x],line_scale_08_cos[x],c0_cos[8]), #x
c(c0_sin[8],line_scale_07_sin[x],line_scale_08_sin[x],c0_sin[8]), #y
density=c(30), #塗りつぶす濃度
angle=c(45),　 　　　#塗りつぶす斜線の角度
col=rgb(0,1,0))
#塗りつぶし
polygon(c(c0_cos[9],line_scale_08_cos[x],line_scale_09_cos[x],c0_cos[9]), #x
c(c0_sin[9],line_scale_08_sin[x],line_scale_09_sin[x],c0_sin[9]), #y
density=c(30), #塗りつぶす濃度
angle=c(45),　 　　　#塗りつぶす斜線の角度
col=rgb(0,1,0))
#塗りつぶし
polygon(c(c0_cos[10],line_scale_09_cos[x],line_scale_10_cos[x],c0_cos[10]), #x
c(c0_sin[10],line_scale_09_sin[x],line_scale_10_sin[x],c0_sin[10]), #y
density=c(30), #塗りつぶす濃度
angle=c(45),　 　　　#塗りつぶす斜線の角度
col=rgb(0,1,0))
#塗りつぶし
polygon(c(c0_cos[11],line_scale_10_cos[x],line_scale_11_cos[x],c0_cos[11]), #x
c(c0_sin[11],line_scale_10_sin[x],line_scale_11_sin[x],c0_sin[11]), #y
density=c(30), #塗りつぶす濃度
angle=c(45),　 　　　#塗りつぶす斜線の角度
col=rgb(0,1,0))

#塗りつぶし
polygon(c(c0_cos[12],line_scale_11_cos[x],line_scale_12_cos[x],c0_cos[12]), #x
c(c0_sin[12],line_scale_11_sin[x],line_scale_12_sin[x],c0_sin[12]), #y
density=c(30), #塗りつぶす濃度
angle=c(45),　 　　　#塗りつぶす斜線の角度
col=rgb(0,1,0)) 
#塗りつぶし
polygon(c(c0_cos[13],line_scale_12_cos[x],line_scale_13_cos[x],c0_cos[13]), #x
c(c0_sin[13],line_scale_12_sin[x],line_scale_13_sin[x],c0_sin[13]), #y
density=c(30), #塗りつぶす濃度
angle=c(45),　 　　　#塗りつぶす斜線の角度
col=rgb(0,1,0)) 
#塗りつぶし
polygon(c(c0_cos[14],line_scale_13_cos[x],line_scale_14_cos[x],c0_cos[14]), #x
c(c0_sin[14],line_scale_13_sin[x],line_scale_14_sin[x],c0_sin[14]), #y
density=c(30), #塗りつぶす濃度
angle=c(45),　 　　　#塗りつぶす斜線の角度
col=rgb(0,1,0)) 
#塗りつぶし
polygon(c(c0_cos[15],line_scale_14_cos[x],line_scale_15_cos[x],c0_cos[15]), #x
c(c0_sin[15],line_scale_14_sin[x],line_scale_15_sin[x],c0_sin[15]), #y
density=c(30), #塗りつぶす濃度
angle=c(45),　 　　　#塗りつぶす斜線の角度
col=rgb(0,1,0)) 
#塗りつぶし
polygon(c(c0_cos[16],line_scale_15_cos[x],line_scale_16_cos[x],c0_cos[16]), #x
c(c0_sin[16],line_scale_15_sin[x],line_scale_16_sin[x],c0_sin[16]), #y
density=c(30), #塗りつぶす濃度
angle=c(45),　 　　　#塗りつぶす斜線の角度
col=rgb(0,1,0)) 

}

#アニメーション
library("animation")
Time_Code=c(1,2,3,4,5,6,7,8,9,10,11,12,13,14,15)
saveGIF({
for (i in Time_Code){
　Three_square_theorem16(i)
}
}, interval = 0.1, movie.name = "TEST016c.gif") 

あまりに味気ないので、補助的な「上級目盛りへの置換」も盛んに行われています。

四進数

Three_square_theorem04<-function(x){
c0<-c(0,pi/2,-1*pi,-1*pi/2,0)
c0_cos<-cos(c0)
c0_sin<-sin(c0)
plot(c0_cos,c0_sin,type="l",main="Regular polygon rotation",xlab="Cos(θ)",ylab="Sin(θ)")
text(c0_cos,c0_sin, labels=c("00","10","20","30",""),col=c(rgb(1,0,0),rgb(1,0,0),rgb(1,0,0),rgb(1,0,0),rgb(1,0,0)),cex=c(2,2,2,2,2))
line_scale_01_cos<-seq(cos(c0[1]),cos(c0[2]),length=15)
line_scale_01_sin<-seq(sin(c0[1]),sin(c0[2]),length=15)
line_scale_02_cos<-seq(cos(c0[2]),cos(c0[3]),length=15)
line_scale_02_sin<-seq(sin(c0[2]),sin(c0[3]),length=15)
line_scale_03_cos<-seq(cos(c0[3]),cos(c0[4]),length=15)
line_scale_03_sin<-seq(sin(c0[3]),sin(c0[4]),length=15)
line_scale_04_cos<-seq(cos(c0[4]),cos(c0[1]),length=15)
line_scale_04_sin<-seq(sin(c0[4]),sin(c0[1]),length=15)
text(c(line_scale_01_cos[x],line_scale_02_cos[x],line_scale_03_cos[x],line_scale_04_cos[x]),c(line_scale_01_sin[x],line_scale_02_sin[x],line_scale_03_sin[x],line_scale_04_sin[x]), labels=c("00-03","10-13","20-23","30-33",""),col=c(rgb(0,0,1),rgb(0,0,1),rgb(0,0,1),rgb(0,0,1),rgb(0,0,1)),cex=c(1.5,1.5,1.5,1.5,1.5))
#塗りつぶし
polygon(c(c0_cos[1],line_scale_04_cos[x],line_scale_01_cos[x],c0_cos[1]), #x
c(c0_sin[1],line_scale_04_sin[x],line_scale_01_sin[x],c0_sin[1]), #y
density=c(30), #塗りつぶす濃度
angle=c(45),　 　　　#塗りつぶす斜線の角度
col=rgb(0,1,0)) 　 

#塗りつぶし
polygon(c(c0_cos[2],line_scale_01_cos[x],line_scale_02_cos[x],c0_cos[2]), #x
c(c0_sin[2],line_scale_01_sin[x],line_scale_02_sin[x],c0_sin[2]), #y
density=c(30), #塗りつぶす濃度
angle=c(45),　 　　　#塗りつぶす斜線の角度
col=rgb(0,1,0)) 　 

#塗りつぶし
polygon(c(c0_cos[3],line_scale_02_cos[x],line_scale_03_cos[x],c0_cos[3]), #x
c(c0_sin[3],line_scale_02_sin[x],line_scale_03_sin[x],c0_sin[3]), #y
density=c(30), #塗りつぶす濃度
angle=c(45),　 　　　#塗りつぶす斜線の角度
col=rgb(0,1,0)) 　

#塗りつぶし
polygon(c(c0_cos[4],line_scale_03_cos[x],line_scale_04_cos[x],c0_cos[4]), #x
c(c0_sin[4],line_scale_03_sin[x],line_scale_04_sin[x],c0_sin[4]), #y
density=c(30), #塗りつぶす濃度
angle=c(45),　 　　　#塗りつぶす斜線の角度
col=rgb(0,1,0)) 　

}

#アニメーション
library("animation")
Time_Code=c(1,2,3,4,5,6,7,8,9,10,11,12,13,14,15)
saveGIF({
for (i in Time_Code){
　Three_square_theorem04(i)
}
}, interval = 0.1, movie.name = "TEST04a.gif") 

八進数

Three_square_theorem08<-function(x){
c0<-seq(0,2*pi,length=9)
c0_cos<-cos(c0)
c0_sin<-sin(c0)
plot(c0_cos,c0_sin,type="l",main="Regular polygon rotation",xlab="Cos(θ)",ylab="Sin(θ)")
text(c0_cos,c0_sin, labels=c("00","10","20","30","40","50","60","70",""),col=c(rgb(1,0,0),rgb(1,0,0),rgb(1,0,0),rgb(1,0,0),rgb(1,0,0),rgb(1,0,0),rgb(1,0,0),rgb(1,0,0),rgb(1,0,0)),cex=c(2,2,2,2,2,2,2,2,2))
line_scale_01_cos<-seq(cos(c0[1]),cos(c0[2]),length=15)
line_scale_01_sin<-seq(sin(c0[1]),sin(c0[2]),length=15)
line_scale_02_cos<-seq(cos(c0[2]),cos(c0[3]),length=15)
line_scale_02_sin<-seq(sin(c0[2]),sin(c0[3]),length=15)
line_scale_03_cos<-seq(cos(c0[3]),cos(c0[4]),length=15)
line_scale_03_sin<-seq(sin(c0[3]),sin(c0[4]),length=15)
line_scale_04_cos<-seq(cos(c0[4]),cos(c0[5]),length=15)
line_scale_04_sin<-seq(sin(c0[4]),sin(c0[5]),length=15)
line_scale_05_cos<-seq(cos(c0[5]),cos(c0[6]),length=15)
line_scale_05_sin<-seq(sin(c0[5]),sin(c0[6]),length=15)
line_scale_06_cos<-seq(cos(c0[6]),cos(c0[7]),length=15)
line_scale_06_sin<-seq(sin(c0[6]),sin(c0[7]),length=15)
line_scale_07_cos<-seq(cos(c0[7]),cos(c0[8]),length=15)
line_scale_07_sin<-seq(sin(c0[7]),sin(c0[8]),length=15)
line_scale_08_cos<-seq(cos(c0[8]),cos(c0[1]),length=15)
line_scale_08_sin<-seq(sin(c0[8]),sin(c0[1]),length=15)
text(c(line_scale_01_cos[x],line_scale_02_cos[x],line_scale_03_cos[x],line_scale_04_cos[x],line_scale_05_cos[x],line_scale_06_cos[x],line_scale_07_cos[x],line_scale_08_cos[x]),c(line_scale_01_sin[x],line_scale_02_sin[x],line_scale_03_sin[x],line_scale_04_sin[x],line_scale_05_sin[x],line_scale_06_sin[x],line_scale_07_sin[x],line_scale_08_sin[x]), labels=c("00-07","10-17","20-27","30-37","40-47","50-57","60-67","70-77",""),col=c(rgb(0,0,1),rgb(0,0,1),rgb(0,0,1),rgb(0,0,1),rgb(0,0,1),rgb(0,0,1),rgb(0,0,1),rgb(0,0,1),rgb(0,0,1)),cex=c(1.5,1.5,1.5,1.5,1.5,1.5,1.5,1.5))
#塗りつぶし
polygon(c(c0_cos[1],line_scale_08_cos[x],line_scale_01_cos[x],c0_cos[1]), #x
c(c0_sin[1],line_scale_08_sin[x],line_scale_01_sin[x],c0_sin[1]), #y
density=c(30), #塗りつぶす濃度
angle=c(45),　 　　　#塗りつぶす斜線の角度
col=rgb(0,1,0)) 　 

#塗りつぶし
polygon(c(c0_cos[2],line_scale_01_cos[x],line_scale_02_cos[x],c0_cos[2]), #x
c(c0_sin[2],line_scale_01_sin[x],line_scale_02_sin[x],c0_sin[2]), #y
density=c(30), #塗りつぶす濃度
angle=c(45),　 　　　#塗りつぶす斜線の角度
col=rgb(0,1,0)) 　 

#塗りつぶし
polygon(c(c0_cos[3],line_scale_02_cos[x],line_scale_03_cos[x],c0_cos[3]), #x
c(c0_sin[3],line_scale_02_sin[x],line_scale_03_sin[x],c0_sin[3]), #y
density=c(30), #塗りつぶす濃度
angle=c(45),　 　　　#塗りつぶす斜線の角度
col=rgb(0,1,0)) 　

#塗りつぶし
polygon(c(c0_cos[4],line_scale_03_cos[x],line_scale_04_cos[x],c0_cos[4]), #x
c(c0_sin[4],line_scale_03_sin[x],line_scale_04_sin[x],c0_sin[4]), #y
density=c(30), #塗りつぶす濃度
angle=c(45),　 　　　#塗りつぶす斜線の角度
col=rgb(0,1,0)) 　

#塗りつぶし
polygon(c(c0_cos[5],line_scale_04_cos[x],line_scale_05_cos[x],c0_cos[5]), #x
c(c0_sin[5],line_scale_04_sin[x],line_scale_05_sin[x],c0_sin[5]), #y
density=c(30), #塗りつぶす濃度
angle=c(45),　 　　　#塗りつぶす斜線の角度
col=rgb(0,1,0)) 　
#塗りつぶし
polygon(c(c0_cos[6],line_scale_05_cos[x],line_scale_06_cos[x],c0_cos[6]), #x
c(c0_sin[6],line_scale_05_sin[x],line_scale_06_sin[x],c0_sin[6]), #y
density=c(30), #塗りつぶす濃度
angle=c(45),　 　　　#塗りつぶす斜線の角度
col=rgb(0,1,0))

#塗りつぶし
polygon(c(c0_cos[7],line_scale_06_cos[x],line_scale_07_cos[x],c0_cos[7]), #x
c(c0_sin[7],line_scale_06_sin[x],line_scale_07_sin[x],c0_sin[7]), #y
density=c(30), #塗りつぶす濃度
angle=c(45),　 　　　#塗りつぶす斜線の角度
col=rgb(0,1,0))

#塗りつぶし
polygon(c(c0_cos[8],line_scale_07_cos[x],line_scale_08_cos[x],c0_cos[8]), #x
c(c0_sin[8],line_scale_07_sin[x],line_scale_08_sin[x],c0_sin[8]), #y
density=c(30), #塗りつぶす濃度
angle=c(45),　 　　　#塗りつぶす斜線の角度
col=rgb(0,1,0))

}

#アニメーション
library("animation")
Time_Code=c(1,2,3,4,5,6,7,8,9,10,11,12,13,14,15)
saveGIF({
for (i in Time_Code){
　Three_square_theorem08(i)
}
}, interval = 0.1, movie.name = "TEST08.gif") 

十六進数

Three_square_theorem16<-function(x){
c0<-seq(0,2*pi,length=17)
c0_cos<-cos(c0)
c0_sin<-sin(c0)
plot(c0_cos,c0_sin,type="l",main="Regular polygon rotation",xlab="Cos(θ)",ylab="Sin(θ)")
text(c0_cos,c0_sin, labels=c("00","10","20","30","40","50","60","70","80","90","a0","b0","c0","d0","e0","f0",""),col=c(rgb(1,0,0),rgb(1,0,0),rgb(1,0,0),rgb(1,0,0),rgb(1,0,0),rgb(1,0,0),rgb(1,0,0),rgb(1,0,0),rgb(1,0,0),rgb(1,0,0),rgb(1,0,0),rgb(1,0,0),rgb(1,0,0),rgb(1,0,0),rgb(1,0,0),rgb(1,0,0),rgb(1,0,0)),cex=c(2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2))
line_scale_01_cos<-seq(cos(c0[1]),cos(c0[2]),length=15)
line_scale_01_sin<-seq(sin(c0[1]),sin(c0[2]),length=15)
line_scale_02_cos<-seq(cos(c0[2]),cos(c0[3]),length=15)
line_scale_02_sin<-seq(sin(c0[2]),sin(c0[3]),length=15)
line_scale_03_cos<-seq(cos(c0[3]),cos(c0[4]),length=15)
line_scale_03_sin<-seq(sin(c0[3]),sin(c0[4]),length=15)
line_scale_04_cos<-seq(cos(c0[4]),cos(c0[5]),length=15)
line_scale_04_sin<-seq(sin(c0[4]),sin(c0[5]),length=15)
line_scale_05_cos<-seq(cos(c0[5]),cos(c0[6]),length=15)
line_scale_05_sin<-seq(sin(c0[5]),sin(c0[6]),length=15)
line_scale_06_cos<-seq(cos(c0[6]),cos(c0[7]),length=15)
line_scale_06_sin<-seq(sin(c0[6]),sin(c0[7]),length=15)
line_scale_07_cos<-seq(cos(c0[7]),cos(c0[8]),length=15)
line_scale_07_sin<-seq(sin(c0[7]),sin(c0[8]),length=15)
line_scale_08_cos<-seq(cos(c0[8]),cos(c0[9]),length=15)
line_scale_08_sin<-seq(sin(c0[8]),sin(c0[9]),length=15)
line_scale_09_cos<-seq(cos(c0[9]),cos(c0[10]),length=15)
line_scale_09_sin<-seq(sin(c0[9]),sin(c0[10]),length=15)
line_scale_10_cos<-seq(cos(c0[10]),cos(c0[11]),length=15)
line_scale_10_sin<-seq(sin(c0[10]),sin(c0[11]),length=15)
line_scale_11_cos<-seq(cos(c0[11]),cos(c0[12]),length=15)
line_scale_11_sin<-seq(sin(c0[11]),sin(c0[12]),length=15)
line_scale_12_cos<-seq(cos(c0[12]),cos(c0[13]),length=15)
line_scale_12_sin<-seq(sin(c0[12]),sin(c0[13]),length=15)
line_scale_13_cos<-seq(cos(c0[13]),cos(c0[14]),length=15)
line_scale_13_sin<-seq(sin(c0[13]),sin(c0[14]),length=15)
line_scale_14_cos<-seq(cos(c0[14]),cos(c0[15]),length=15)
line_scale_14_sin<-seq(sin(c0[14]),sin(c0[15]),length=15)
line_scale_15_cos<-seq(cos(c0[15]),cos(c0[16]),length=15)
line_scale_15_sin<-seq(sin(c0[15]),sin(c0[16]),length=15)
line_scale_16_cos<-seq(cos(c0[16]),cos(c0[1]),length=15)
line_scale_16_sin<-seq(sin(c0[16]),sin(c0[1]),length=15)
 text(c(line_scale_01_cos[x],line_scale_02_cos[x],line_scale_03_cos[x],line_scale_04_cos[x],line_scale_05_cos[x],line_scale_06_cos[x],line_scale_07_cos[x],line_scale_08_cos[x],line_scale_09_cos[x],line_scale_10_cos[x],line_scale_11_cos[x],line_scale_12_cos[x],line_scale_13_cos[x],line_scale_14_cos[x],line_scale_15_cos[x],line_scale_16_cos[x]),c(line_scale_01_sin[x],line_scale_02_sin[x],line_scale_03_sin[x],line_scale_04_sin[x],line_scale_05_sin[x],line_scale_06_sin[x],line_scale_07_sin[x],line_scale_08_sin[x],line_scale_09_sin[x],line_scale_10_sin[x],line_scale_11_sin[x],line_scale_12_sin[x],line_scale_13_sin[x],line_scale_14_sin[x],line_scale_15_sin[x],line_scale_16_sin[x]), labels=c("00-0f","10-1f","20-2f","30-3f","40-4f","50-5f","60-6f","70-7f","80-8f","90-9f","a0-af","b0-bf","c0-cf","d0-df","e0-ef","f0-ff",""),col=c(rgb(0,0,1),rgb(0,0,1),rgb(0,0,1),rgb(0,0,1),rgb(0,0,1),rgb(0,0,1),rgb(0,0,1),rgb(0,0,1),rgb(0,0,1),rgb(0,0,1),rgb(0,0,1),rgb(0,0,1),rgb(0,0,1),rgb(0,0,1),rgb(0,0,1),rgb(0,0,1)),cex=c(1.5,1.5,1.5,1.5,1.5,1.5,1.5,1.5,1.5,1.5,1.5,1.5,1.5,1.5,1.5,1.5))

 #塗りつぶし
polygon(c(c0_cos[1],line_scale_16_cos[x],line_scale_01_cos[x],c0_cos[1]), #x
c(c0_sin[1],line_scale_16_sin[x],line_scale_01_sin[x],c0_sin[1]), #y
density=c(30), #塗りつぶす濃度
angle=c(45),　 　　　#塗りつぶす斜線の角度
col=rgb(0,1,0)) 　 

#塗りつぶし
polygon(c(c0_cos[2],line_scale_01_cos[x],line_scale_02_cos[x],c0_cos[2]), #x
c(c0_sin[2],line_scale_01_sin[x],line_scale_02_sin[x],c0_sin[2]), #y
density=c(30), #塗りつぶす濃度
angle=c(45),　 　　　#塗りつぶす斜線の角度
col=rgb(0,1,0)) 　 

#塗りつぶし
polygon(c(c0_cos[3],line_scale_02_cos[x],line_scale_03_cos[x],c0_cos[3]), #x
c(c0_sin[3],line_scale_02_sin[x],line_scale_03_sin[x],c0_sin[3]), #y
density=c(30), #塗りつぶす濃度
angle=c(45),　 　　　#塗りつぶす斜線の角度
col=rgb(0,1,0)) 　

#塗りつぶし
polygon(c(c0_cos[4],line_scale_03_cos[x],line_scale_04_cos[x],c0_cos[4]), #x
c(c0_sin[4],line_scale_03_sin[x],line_scale_04_sin[x],c0_sin[4]), #y
density=c(30), #塗りつぶす濃度
angle=c(45),　 　　　#塗りつぶす斜線の角度
col=rgb(0,1,0)) 　

#塗りつぶし
polygon(c(c0_cos[5],line_scale_04_cos[x],line_scale_05_cos[x],c0_cos[5]), #x
c(c0_sin[5],line_scale_04_sin[x],line_scale_05_sin[x],c0_sin[5]), #y
density=c(30), #塗りつぶす濃度
angle=c(45),　 　　　#塗りつぶす斜線の角度
col=rgb(0,1,0)) 　
#塗りつぶし
polygon(c(c0_cos[6],line_scale_05_cos[x],line_scale_06_cos[x],c0_cos[6]), #x
c(c0_sin[6],line_scale_05_sin[x],line_scale_06_sin[x],c0_sin[6]), #y
density=c(30), #塗りつぶす濃度
angle=c(45),　 　　　#塗りつぶす斜線の角度
col=rgb(0,1,0))

#塗りつぶし
polygon(c(c0_cos[7],line_scale_06_cos[x],line_scale_07_cos[x],c0_cos[7]), #x
c(c0_sin[7],line_scale_06_sin[x],line_scale_07_sin[x],c0_sin[7]), #y
density=c(30), #塗りつぶす濃度
angle=c(45),　 　　　#塗りつぶす斜線の角度
col=rgb(0,1,0))

#塗りつぶし
polygon(c(c0_cos[8],line_scale_07_cos[x],line_scale_08_cos[x],c0_cos[8]), #x
c(c0_sin[8],line_scale_07_sin[x],line_scale_08_sin[x],c0_sin[8]), #y
density=c(30), #塗りつぶす濃度
angle=c(45),　 　　　#塗りつぶす斜線の角度
col=rgb(0,1,0))
#塗りつぶし
polygon(c(c0_cos[9],line_scale_08_cos[x],line_scale_09_cos[x],c0_cos[9]), #x
c(c0_sin[9],line_scale_08_sin[x],line_scale_09_sin[x],c0_sin[9]), #y
density=c(30), #塗りつぶす濃度
angle=c(45),　 　　　#塗りつぶす斜線の角度
col=rgb(0,1,0))
#塗りつぶし
polygon(c(c0_cos[10],line_scale_09_cos[x],line_scale_10_cos[x],c0_cos[10]), #x
c(c0_sin[10],line_scale_09_sin[x],line_scale_10_sin[x],c0_sin[10]), #y
density=c(30), #塗りつぶす濃度
angle=c(45),　 　　　#塗りつぶす斜線の角度
col=rgb(0,1,0))
#塗りつぶし
polygon(c(c0_cos[11],line_scale_10_cos[x],line_scale_11_cos[x],c0_cos[11]), #x
c(c0_sin[11],line_scale_10_sin[x],line_scale_11_sin[x],c0_sin[11]), #y
density=c(30), #塗りつぶす濃度
angle=c(45),　 　　　#塗りつぶす斜線の角度
col=rgb(0,1,0))

#塗りつぶし
polygon(c(c0_cos[12],line_scale_11_cos[x],line_scale_12_cos[x],c0_cos[12]), #x
c(c0_sin[12],line_scale_11_sin[x],line_scale_12_sin[x],c0_sin[12]), #y
density=c(30), #塗りつぶす濃度
angle=c(45),　 　　　#塗りつぶす斜線の角度
col=rgb(0,1,0)) 
#塗りつぶし
polygon(c(c0_cos[13],line_scale_12_cos[x],line_scale_13_cos[x],c0_cos[13]), #x
c(c0_sin[13],line_scale_12_sin[x],line_scale_13_sin[x],c0_sin[13]), #y
density=c(30), #塗りつぶす濃度
angle=c(45),　 　　　#塗りつぶす斜線の角度
col=rgb(0,1,0)) 
#塗りつぶし
polygon(c(c0_cos[14],line_scale_13_cos[x],line_scale_14_cos[x],c0_cos[14]), #x
c(c0_sin[14],line_scale_13_sin[x],line_scale_14_sin[x],c0_sin[14]), #y
density=c(30), #塗りつぶす濃度
angle=c(45),　 　　　#塗りつぶす斜線の角度
col=rgb(0,1,0)) 
#塗りつぶし
polygon(c(c0_cos[15],line_scale_14_cos[x],line_scale_15_cos[x],c0_cos[15]), #x
c(c0_sin[15],line_scale_14_sin[x],line_scale_15_sin[x],c0_sin[15]), #y
density=c(30), #塗りつぶす濃度
angle=c(45),　 　　　#塗りつぶす斜線の角度
col=rgb(0,1,0)) 
#塗りつぶし
polygon(c(c0_cos[16],line_scale_15_cos[x],line_scale_16_cos[x],c0_cos[16]), #x
c(c0_sin[16],line_scale_15_sin[x],line_scale_16_sin[x],c0_sin[16]), #y
density=c(30), #塗りつぶす濃度
angle=c(45),　 　　　#塗りつぶす斜線の角度
col=rgb(0,1,0)) 

}

#アニメーション
library("animation")
Time_Code=c(1,2,3,4,5,6,7,8,9,10,11,12,13,14,15)
saveGIF({
for (i in Time_Code){
　Three_square_theorem16(i)
}
}, interval = 0.1, movie.name = "TEST016b.gif") 

#三進数系の世界(3^n族)

正三角形（Equilateral Triangle)
外角の大きさはpi/3=1.047198ラジアンあるいは180/pi=60度、内角の大きさは2pi(3-2)/3=2.094395あるいは180*(3-2)/3=60度。

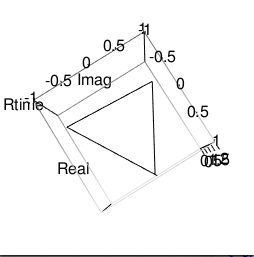
#正三角形
library(rgl)
Rtime<-seq(0,2,length=4)
tr01<-c(1,(-1+sqrt(3)*(0+1i))/2,(-1-sqrt(3)*(0+1i))/2,1)
Real<-Re(tr01)
Imag<-Im(tr01)
#plot(Real,Imag,type="l")
plot3d(Real,Imag,Rtime,type="l",xlim=c(-1,1),ylim=c(-1,1),zlim=c(0,2))
movie3d(spin3d(axis=c(0,0,1),rpm=5),duration=10,fps=25,movie="~/Desktop/test11")

Three_square_theorem03<-function(x){
c0<-c(0,2/3*pi,-2/3*pi,0)
c0_cos<-cos(c0)
c0_sin<-sin(c0)
plot(c0_cos,c0_sin,type="l",xlim=c(-1,1),ylim=c(-1,1),main="Regular polygon rotation",xlab="Cos(θ)",ylab="Sin(θ)")
text(c0_cos,c0_sin, labels=c("00","01","02",""),col=c(rgb(1,0,0),rgb(1,0,0),rgb(1,0,0),rgb(1,0,0)),cex=c(2,2,2,2))
line_scale_01_cos<-seq(cos(c0[1]),cos(c0[2]),length=15)
line_scale_01_sin<-seq(sin(c0[1]),sin(c0[2]),length=15)
line_scale_02_cos<-seq(cos(c0[2]),cos(c0[3]),length=15)
line_scale_02_sin<-seq(sin(c0[2]),sin(c0[3]),length=15)
line_scale_03_cos<-seq(cos(c0[3]),cos(c0[1]),length=15)
line_scale_03_sin<-seq(sin(c0[3]),sin(c0[1]),length=15)
text(c(line_scale_01_cos[x],line_scale_02_cos[x],line_scale_03_cos[x]),c(line_scale_01_sin[x],line_scale_02_sin[x],line_scale_03_sin[x]), labels=c("00-02","10-12","20-22"),col=c(rgb(0,0,1),rgb(0,0,1),rgb(0,0,1)),cex=c(2,2,2))

#塗りつぶし
polygon(c(c0_cos[1],line_scale_03_cos[x],line_scale_01_cos[x],c0_cos[1]), #x
c(c0_sin[1],line_scale_03_sin[x],line_scale_01_sin[x],c0_sin[1]), #y
density=c(30), #塗りつぶす濃度
angle=c(45),　 　　　#塗りつぶす斜線の角度
col=rgb(0,1,0)) 　 

#塗りつぶし
polygon(c(c0_cos[2],line_scale_01_cos[x],line_scale_02_cos[x],c0_cos[2]), #x
c(c0_sin[2],line_scale_01_sin[x],line_scale_02_sin[x],c0_sin[2]), #y
density=c(30), #塗りつぶす濃度
angle=c(45),　 　　　#塗りつぶす斜線の角度
col=rgb(0,1,0)) 　 

#塗りつぶし
polygon(c(c0_cos[3],line_scale_02_cos[x],line_scale_03_cos[x],c0_cos[3]), #x
c(c0_sin[3],line_scale_02_sin[x],line_scale_03_sin[x],c0_sin[3]), #y
density=c(30), #塗りつぶす濃度
angle=c(45),　 　　　#塗りつぶす斜線の角度
col=rgb(0,1,0)) 　

}

#アニメーション
library("animation")
Time_Code=c(1,2,3,4,5,6,7,8,9,10,11,12,13,14,15)
saveGIF({
for (i in Time_Code){
　Three_square_theorem03(i)
}
}, interval = 0.1, movie.name = "TEST003.gif") 

正九角形（Regular Nonagon)
外角の大きさはpi/9=0.3490659ラジアンあるいは180/9=20度、内角の大きさは2pi(9-2)/9=4.886922ラジアンあるいは180*(9-2)/9=140度

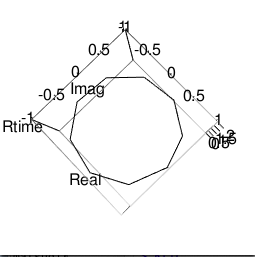
#正９角形
Rtime<-seq(0,2,length=10)
tr01<-exp(seq(0,2*pi,length=10)*(0+1i))
Real<-Re(tr01)
Imag<-Im(tr01)
#plot(Real,Imag,type="l")
plot3d(Real,Imag,Rtime,type="l",xlim=c(-1,1),ylim=c(-1,1),zlim=c(0,2))
movie3d(spin3d(axis=c(0,0,1),rpm=5),duration=10,fps=25,movie="~/Desktop/test09") 

3進法×3桁

Three_square_theorem09<-function(x){
c0<-seq(0,2*pi,length=10)
c0_cos<-cos(c0)
c0_sin<-sin(c0)
plot(c0_cos,c0_sin,type="l",main="Regular polygon rotation",xlab="Cos(θ)",ylab="Sin(θ)")
text(c0_cos,c0_sin, labels=c("000","010","020","100","110","120","200","210","220",""),col=c(rgb(1,0,0),rgb(1,0,0),rgb(1,0,0),rgb(1,0,0),rgb(1,0,0),rgb(1,0,0),rgb(1,0,0),rgb(1,0,0),rgb(1,0,0),rgb(1,0,0)),cex=c(2,2,2,2,2,2,2,2,2,2))
line_scale_01_cos<-seq(cos(c0[1]),cos(c0[2]),length=15)
line_scale_01_sin<-seq(sin(c0[1]),sin(c0[2]),length=15)
line_scale_02_cos<-seq(cos(c0[2]),cos(c0[3]),length=15)
line_scale_02_sin<-seq(sin(c0[2]),sin(c0[3]),length=15)
line_scale_03_cos<-seq(cos(c0[3]),cos(c0[4]),length=15)
line_scale_03_sin<-seq(sin(c0[3]),sin(c0[4]),length=15)
line_scale_04_cos<-seq(cos(c0[4]),cos(c0[5]),length=15)
line_scale_04_sin<-seq(sin(c0[4]),sin(c0[5]),length=15)
line_scale_05_cos<-seq(cos(c0[5]),cos(c0[6]),length=15)
line_scale_05_sin<-seq(sin(c0[5]),sin(c0[6]),length=15)
line_scale_06_cos<-seq(cos(c0[6]),cos(c0[7]),length=15)
line_scale_06_sin<-seq(sin(c0[6]),sin(c0[7]),length=15)
line_scale_07_cos<-seq(cos(c0[7]),cos(c0[8]),length=15)
line_scale_07_sin<-seq(sin(c0[7]),sin(c0[8]),length=15)
line_scale_08_cos<-seq(cos(c0[8]),cos(c0[9]),length=15)
line_scale_08_sin<-seq(sin(c0[8]),sin(c0[9]),length=15)
line_scale_09_cos<-seq(cos(c0[9]),cos(c0[1]),length=15)
line_scale_09_sin<-seq(sin(c0[9]),sin(c0[1]),length=15)
text(c(line_scale_01_cos[x],line_scale_02_cos[x],line_scale_03_cos[x],line_scale_04_cos[x],line_scale_05_cos[x],line_scale_06_cos[x],line_scale_07_cos[x],line_scale_08_cos[x],line_scale_09_cos[x]),c(line_scale_01_sin[x],line_scale_02_sin[x],line_scale_03_sin[x],line_scale_04_sin[x],line_scale_05_sin[x],line_scale_06_sin[x],line_scale_07_sin[x],line_scale_08_sin[x],line_scale_09_sin[x]), labels=c("000-002","010-012","020-022","100-102","110-112","120-122","200-202","210-212","220-222",""),col=c(rgb(0,0,1),rgb(0,0,1),rgb(0,0,1),rgb(0,0,1),rgb(0,0,1),rgb(0,0,1),rgb(0,0,1),rgb(0,0,1),rgb(0,0,1),rgb(0,0,1)),cex=c(1.5,1.5,1.5,1.5,1.5,1.5,1.5,1.5,1.5,1.5))

 #塗りつぶし
polygon(c(c0_cos[1],line_scale_09_cos[x],line_scale_01_cos[x],c0_cos[1]), #x
c(c0_sin[1],line_scale_09_sin[x],line_scale_01_sin[x],c0_sin[1]), #y
density=c(30), #塗りつぶす濃度
angle=c(45),　 　　　#塗りつぶす斜線の角度
col=rgb(0,1,0)) 　 

#塗りつぶし
polygon(c(c0_cos[2],line_scale_01_cos[x],line_scale_02_cos[x],c0_cos[2]), #x
c(c0_sin[2],line_scale_01_sin[x],line_scale_02_sin[x],c0_sin[2]), #y
density=c(30), #塗りつぶす濃度
angle=c(45),　 　　　#塗りつぶす斜線の角度
col=rgb(0,1,0)) 　 

#塗りつぶし
polygon(c(c0_cos[3],line_scale_02_cos[x],line_scale_03_cos[x],c0_cos[3]), #x
c(c0_sin[3],line_scale_02_sin[x],line_scale_03_sin[x],c0_sin[3]), #y
density=c(30), #塗りつぶす濃度
angle=c(45),　 　　　#塗りつぶす斜線の角度
col=rgb(0,1,0)) 　

#塗りつぶし
polygon(c(c0_cos[4],line_scale_03_cos[x],line_scale_04_cos[x],c0_cos[4]), #x
c(c0_sin[4],line_scale_03_sin[x],line_scale_04_sin[x],c0_sin[4]), #y
density=c(30), #塗りつぶす濃度
angle=c(45),　 　　　#塗りつぶす斜線の角度
col=rgb(0,1,0)) 　

#塗りつぶし
polygon(c(c0_cos[5],line_scale_04_cos[x],line_scale_05_cos[x],c0_cos[5]), #x
c(c0_sin[5],line_scale_04_sin[x],line_scale_05_sin[x],c0_sin[5]), #y
density=c(30), #塗りつぶす濃度
angle=c(45),　 　　　#塗りつぶす斜線の角度
col=rgb(0,1,0)) 　
#塗りつぶし
polygon(c(c0_cos[6],line_scale_05_cos[x],line_scale_06_cos[x],c0_cos[6]), #x
c(c0_sin[6],line_scale_05_sin[x],line_scale_06_sin[x],c0_sin[6]), #y
density=c(30), #塗りつぶす濃度
angle=c(45),　 　　　#塗りつぶす斜線の角度
col=rgb(0,1,0))

#塗りつぶし
polygon(c(c0_cos[7],line_scale_06_cos[x],line_scale_07_cos[x],c0_cos[7]), #x
c(c0_sin[7],line_scale_06_sin[x],line_scale_07_sin[x],c0_sin[7]), #y
density=c(30), #塗りつぶす濃度
angle=c(45),　 　　　#塗りつぶす斜線の角度
col=rgb(0,1,0))

#塗りつぶし
polygon(c(c0_cos[8],line_scale_07_cos[x],line_scale_08_cos[x],c0_cos[8]), #x
c(c0_sin[8],line_scale_07_sin[x],line_scale_08_sin[x],c0_sin[8]), #y
density=c(30), #塗りつぶす濃度
angle=c(45),　 　　　#塗りつぶす斜線の角度
col=rgb(0,1,0))
#塗りつぶし
polygon(c(c0_cos[9],line_scale_08_cos[x],line_scale_09_cos[x],c0_cos[9]), #x
c(c0_sin[9],line_scale_08_sin[x],line_scale_09_sin[x],c0_sin[9]), #y
density=c(30), #塗りつぶす濃度
angle=c(45),　 　　　#塗りつぶす斜線の角度
col=rgb(0,1,0))

}

#アニメーション
library("animation")
Time_Code=c(1,2,3,4,5,6,7,8,9,10,11,12,13,14,15)
saveGIF({
for (i in Time_Code){
　Three_square_theorem09(i)
}
}, interval = 0.1, movie.name = "TEST009.gif") 

#10進数の世界(2^n5^m族)
厳密にいうと素数ベースではないが、多くの人間に最も親しまれている表示方法？

正10角形（Regular Decagon)
外角の大きさはpi/10=0.3141593ラジアンあるいは180/10=18度、内角の大きさは2pi(10-2)/10=5.026548ラジアンあるいは180*(10-2)/10=144度

#正10角形
Rtime<-seq(0,2,length=11)
tr01<-exp(seq(0,2*pi,length=11)*(0+1i))
Real<-Re(tr01)
Imag<-Im(tr01)
#plot(Real,Imag,type="l")
plot3d(Real,Imag,Rtime,type="l",xlim=c(-1,1),ylim=c(-1,1),zlim=c(0,2))
movie3d(spin3d(axis=c(0,0,1),rpm=6),duration=10,fps=25,movie="~/Desktop/test011")

10進数、小数点なし

Three_square_theorem10<-function(x){
c0<-seq(0,2*pi,length=11)
c0_cos<-cos(c0)
c0_sin<-sin(c0)
plot(c0_cos,c0_sin,type="l",main="Regular polygon rotation",xlab="Cos(θ)",ylab="Sin(θ)")
text(c0_cos,c0_sin, labels=c("00","10","20","30","40","50","60","70","80","90",""),col=c(rgb(1,0,0),rgb(1,0,0),rgb(1,0,0),rgb(1,0,0),rgb(1,0,0),rgb(1,0,0),rgb(1,0,0),rgb(1,0,0),rgb(1,0,0),rgb(1,0,0),rgb(1,0,0)),cex=c(2,2,2,2,2,2,2,2,2,2,2))
line_scale_01_cos<-seq(cos(c0[1]),cos(c0[2]),length=15)
line_scale_01_sin<-seq(sin(c0[1]),sin(c0[2]),length=15)
line_scale_02_cos<-seq(cos(c0[2]),cos(c0[3]),length=15)
line_scale_02_sin<-seq(sin(c0[2]),sin(c0[3]),length=15)
line_scale_03_cos<-seq(cos(c0[3]),cos(c0[4]),length=15)
line_scale_03_sin<-seq(sin(c0[3]),sin(c0[4]),length=15)
line_scale_04_cos<-seq(cos(c0[4]),cos(c0[5]),length=15)
line_scale_04_sin<-seq(sin(c0[4]),sin(c0[5]),length=15)
line_scale_05_cos<-seq(cos(c0[5]),cos(c0[6]),length=15)
line_scale_05_sin<-seq(sin(c0[5]),sin(c0[6]),length=15)
line_scale_06_cos<-seq(cos(c0[6]),cos(c0[7]),length=15)
line_scale_06_sin<-seq(sin(c0[6]),sin(c0[7]),length=15)
line_scale_07_cos<-seq(cos(c0[7]),cos(c0[8]),length=15)
line_scale_07_sin<-seq(sin(c0[7]),sin(c0[8]),length=15)
line_scale_08_cos<-seq(cos(c0[8]),cos(c0[9]),length=15)
line_scale_08_sin<-seq(sin(c0[8]),sin(c0[9]),length=15)
line_scale_09_cos<-seq(cos(c0[9]),cos(c0[10]),length=15)
line_scale_09_sin<-seq(sin(c0[9]),sin(c0[10]),length=15)
line_scale_10_cos<-seq(cos(c0[10]),cos(c0[1]),length=15)
line_scale_10_sin<-seq(sin(c0[10]),sin(c0[1]),length=15)
text(c(line_scale_01_cos[x],line_scale_02_cos[x],line_scale_03_cos[x],line_scale_04_cos[x],line_scale_05_cos[x],line_scale_06_cos[x],line_scale_07_cos[x],line_scale_08_cos[x],line_scale_09_cos[x],line_scale_10_cos[x]),c(line_scale_01_sin[x],line_scale_02_sin[x],line_scale_03_sin[x],line_scale_04_sin[x],line_scale_05_sin[x],line_scale_06_sin[x],line_scale_07_sin[x],line_scale_08_sin[x],line_scale_09_sin[x],line_scale_10_sin[x]), labels=c("00-09","10-19","20-29","30-39","40-49","50-59","60-69","70-79","80-89","90-99",""),col=c(rgb(0,0,1),rgb(0,0,1),rgb(0,0,1),rgb(0,0,1),rgb(0,0,1),rgb(0,0,1),rgb(0,0,1),rgb(0,0,1),rgb(0,0,1),rgb(0,0,1),rgb(0,0,1)),cex=c(1.5,1.5,1.5,1.5,1.5,1.5,1.5,1.5,1.5,1.5))

#塗りつぶし
polygon(c(c0_cos[1],line_scale_10_cos[x],line_scale_01_cos[x],c0_cos[1]), #x
c(c0_sin[1],line_scale_10_sin[x],line_scale_01_sin[x],c0_sin[1]), #y
density=c(30), #塗りつぶす濃度
angle=c(45),　 　　　#塗りつぶす斜線の角度
col=rgb(0,1,0)) 　 

#塗りつぶし
polygon(c(c0_cos[2],line_scale_01_cos[x],line_scale_02_cos[x],c0_cos[2]), #x
c(c0_sin[2],line_scale_01_sin[x],line_scale_02_sin[x],c0_sin[2]), #y
density=c(30), #塗りつぶす濃度
angle=c(45),　 　　　#塗りつぶす斜線の角度
col=rgb(0,1,0)) 　 

#塗りつぶし
polygon(c(c0_cos[3],line_scale_02_cos[x],line_scale_03_cos[x],c0_cos[3]), #x
c(c0_sin[3],line_scale_02_sin[x],line_scale_03_sin[x],c0_sin[3]), #y
density=c(30), #塗りつぶす濃度
angle=c(45),　 　　　#塗りつぶす斜線の角度
col=rgb(0,1,0)) 　

#塗りつぶし
polygon(c(c0_cos[4],line_scale_03_cos[x],line_scale_04_cos[x],c0_cos[4]), #x
c(c0_sin[4],line_scale_03_sin[x],line_scale_04_sin[x],c0_sin[4]), #y
density=c(30), #塗りつぶす濃度
angle=c(45),　 　　　#塗りつぶす斜線の角度
col=rgb(0,1,0)) 　

#塗りつぶし
polygon(c(c0_cos[5],line_scale_04_cos[x],line_scale_05_cos[x],c0_cos[5]), #x
c(c0_sin[5],line_scale_04_sin[x],line_scale_05_sin[x],c0_sin[5]), #y
density=c(30), #塗りつぶす濃度
angle=c(45),　 　　　#塗りつぶす斜線の角度
col=rgb(0,1,0)) 　
#塗りつぶし
polygon(c(c0_cos[6],line_scale_05_cos[x],line_scale_06_cos[x],c0_cos[6]), #x
c(c0_sin[6],line_scale_05_sin[x],line_scale_06_sin[x],c0_sin[6]), #y
density=c(30), #塗りつぶす濃度
angle=c(45),　 　　　#塗りつぶす斜線の角度
col=rgb(0,1,0))

#塗りつぶし
polygon(c(c0_cos[7],line_scale_06_cos[x],line_scale_07_cos[x],c0_cos[7]), #x
c(c0_sin[7],line_scale_06_sin[x],line_scale_07_sin[x],c0_sin[7]), #y
density=c(30), #塗りつぶす濃度
angle=c(45),　 　　　#塗りつぶす斜線の角度
col=rgb(0,1,0))

#塗りつぶし
polygon(c(c0_cos[8],line_scale_07_cos[x],line_scale_08_cos[x],c0_cos[8]), #x
c(c0_sin[8],line_scale_07_sin[x],line_scale_08_sin[x],c0_sin[8]), #y
density=c(30), #塗りつぶす濃度
angle=c(45),　 　　　#塗りつぶす斜線の角度
col=rgb(0,1,0))
#塗りつぶし
polygon(c(c0_cos[9],line_scale_08_cos[x],line_scale_09_cos[x],c0_cos[9]), #x
c(c0_sin[9],line_scale_08_sin[x],line_scale_09_sin[x],c0_sin[9]), #y
density=c(30), #塗りつぶす濃度
angle=c(45),　 　　　#塗りつぶす斜線の角度
col=rgb(0,1,0))
#塗りつぶし
polygon(c(c0_cos[10],line_scale_09_cos[x],line_scale_10_cos[x],c0_cos[10]), #x
c(c0_sin[10],line_scale_09_sin[x],line_scale_10_sin[x],c0_sin[10]), #y
density=c(30), #塗りつぶす濃度
angle=c(45),　 　　　#塗りつぶす斜線の角度
col=rgb(0,1,0))

}

#アニメーション
library("animation")
Time_Code=c(1,2,3,4,5,6,7,8,9,10,11,12,13,14,15)
saveGIF({
for (i in Time_Code){
　Three_square_theorem10(i)
}
}, interval = 0.1, movie.name = "TEST010a.gif")  

10進数、小数点あり

Three_square_theorem10<-function(x){
c0<-seq(0,2*pi,length=11)
c0_cos<-cos(c0)
c0_sin<-sin(c0)
plot(c0_cos,c0_sin,type="l",main="Regular polygon rotation",xlab="Cos(θ)",ylab="Sin(θ)")
text(c0_cos,c0_sin, labels=c("0.0","0.1","0.2","0.3","0.4","0.5","0.6","0.7","0.8","0.9",""),col=c(rgb(1,0,0),rgb(1,0,0),rgb(1,0,0),rgb(1,0,0),rgb(1,0,0),rgb(1,0,0),rgb(1,0,0),rgb(1,0,0),rgb(1,0,0),rgb(1,0,0),rgb(1,0,0)),cex=c(2,2,2,2,2,2,2,2,2,2,2))
line_scale_01_cos<-seq(cos(c0[1]),cos(c0[2]),length=15)
line_scale_01_sin<-seq(sin(c0[1]),sin(c0[2]),length=15)
line_scale_02_cos<-seq(cos(c0[2]),cos(c0[3]),length=15)
line_scale_02_sin<-seq(sin(c0[2]),sin(c0[3]),length=15)
line_scale_03_cos<-seq(cos(c0[3]),cos(c0[4]),length=15)
line_scale_03_sin<-seq(sin(c0[3]),sin(c0[4]),length=15)
line_scale_04_cos<-seq(cos(c0[4]),cos(c0[5]),length=15)
line_scale_04_sin<-seq(sin(c0[4]),sin(c0[5]),length=15)
line_scale_05_cos<-seq(cos(c0[5]),cos(c0[6]),length=15)
line_scale_05_sin<-seq(sin(c0[5]),sin(c0[6]),length=15)
line_scale_06_cos<-seq(cos(c0[6]),cos(c0[7]),length=15)
line_scale_06_sin<-seq(sin(c0[6]),sin(c0[7]),length=15)
line_scale_07_cos<-seq(cos(c0[7]),cos(c0[8]),length=15)
line_scale_07_sin<-seq(sin(c0[7]),sin(c0[8]),length=15)
line_scale_08_cos<-seq(cos(c0[8]),cos(c0[9]),length=15)
line_scale_08_sin<-seq(sin(c0[8]),sin(c0[9]),length=15)
line_scale_09_cos<-seq(cos(c0[9]),cos(c0[10]),length=15)
line_scale_09_sin<-seq(sin(c0[9]),sin(c0[10]),length=15)
line_scale_10_cos<-seq(cos(c0[10]),cos(c0[1]),length=15)
line_scale_10_sin<-seq(sin(c0[10]),sin(c0[1]),length=15)
text(c(line_scale_01_cos[x],line_scale_02_cos[x],line_scale_03_cos[x],line_scale_04_cos[x],line_scale_05_cos[x],line_scale_06_cos[x],line_scale_07_cos[x],line_scale_08_cos[x],line_scale_09_cos[x],line_scale_10_cos[x]),c(line_scale_01_sin[x],line_scale_02_sin[x],line_scale_03_sin[x],line_scale_04_sin[x],line_scale_05_sin[x],line_scale_06_sin[x],line_scale_07_sin[x],line_scale_08_sin[x],line_scale_09_sin[x],line_scale_10_sin[x]), labels=c("0.00-0.09","0.10-0.19","0.20-0.29","0.30-0.39","0.40-0.49","0.50-0.59","0.60-0.69","0.70-0.79","0.80-0.89","0.90-0.99",""),col=c(rgb(0,0,1),rgb(0,0,1),rgb(0,0,1),rgb(0,0,1),rgb(0,0,1),rgb(0,0,1),rgb(0,0,1),rgb(0,0,1),rgb(0,0,1),rgb(0,0,1),rgb(0,0,1)),cex=c(1.5,1.5,1.5,1.5,1.5,1.5,1.5,1.5,1.5,1.5,1.5))

#塗りつぶし
polygon(c(c0_cos[1],line_scale_10_cos[x],line_scale_01_cos[x],c0_cos[1]), #x
c(c0_sin[1],line_scale_10_sin[x],line_scale_01_sin[x],c0_sin[1]), #y
density=c(30), #塗りつぶす濃度
angle=c(45),　 　　　#塗りつぶす斜線の角度
col=rgb(0,1,0)) 　 

#塗りつぶし
polygon(c(c0_cos[2],line_scale_01_cos[x],line_scale_02_cos[x],c0_cos[2]), #x
c(c0_sin[2],line_scale_01_sin[x],line_scale_02_sin[x],c0_sin[2]), #y
density=c(30), #塗りつぶす濃度
angle=c(45),　 　　　#塗りつぶす斜線の角度
col=rgb(0,1,0)) 　 

#塗りつぶし
polygon(c(c0_cos[3],line_scale_02_cos[x],line_scale_03_cos[x],c0_cos[3]), #x
c(c0_sin[3],line_scale_02_sin[x],line_scale_03_sin[x],c0_sin[3]), #y
density=c(30), #塗りつぶす濃度
angle=c(45),　 　　　#塗りつぶす斜線の角度
col=rgb(0,1,0)) 　

#塗りつぶし
polygon(c(c0_cos[4],line_scale_03_cos[x],line_scale_04_cos[x],c0_cos[4]), #x
c(c0_sin[4],line_scale_03_sin[x],line_scale_04_sin[x],c0_sin[4]), #y
density=c(30), #塗りつぶす濃度
angle=c(45),　 　　　#塗りつぶす斜線の角度
col=rgb(0,1,0)) 　

#塗りつぶし
polygon(c(c0_cos[5],line_scale_04_cos[x],line_scale_05_cos[x],c0_cos[5]), #x
c(c0_sin[5],line_scale_04_sin[x],line_scale_05_sin[x],c0_sin[5]), #y
density=c(30), #塗りつぶす濃度
angle=c(45),　 　　　#塗りつぶす斜線の角度
col=rgb(0,1,0)) 　
#塗りつぶし
polygon(c(c0_cos[6],line_scale_05_cos[x],line_scale_06_cos[x],c0_cos[6]), #x
c(c0_sin[6],line_scale_05_sin[x],line_scale_06_sin[x],c0_sin[6]), #y
density=c(30), #塗りつぶす濃度
angle=c(45),　 　　　#塗りつぶす斜線の角度
col=rgb(0,1,0))

#塗りつぶし
polygon(c(c0_cos[7],line_scale_06_cos[x],line_scale_07_cos[x],c0_cos[7]), #x
c(c0_sin[7],line_scale_06_sin[x],line_scale_07_sin[x],c0_sin[7]), #y
density=c(30), #塗りつぶす濃度
angle=c(45),　 　　　#塗りつぶす斜線の角度
col=rgb(0,1,0))

#塗りつぶし
polygon(c(c0_cos[8],line_scale_07_cos[x],line_scale_08_cos[x],c0_cos[8]), #x
c(c0_sin[8],line_scale_07_sin[x],line_scale_08_sin[x],c0_sin[8]), #y
density=c(30), #塗りつぶす濃度
angle=c(45),　 　　　#塗りつぶす斜線の角度
col=rgb(0,1,0))
#塗りつぶし
polygon(c(c0_cos[9],line_scale_08_cos[x],line_scale_09_cos[x],c0_cos[9]), #x
c(c0_sin[9],line_scale_08_sin[x],line_scale_09_sin[x],c0_sin[9]), #y
density=c(30), #塗りつぶす濃度
angle=c(45),　 　　　#塗りつぶす斜線の角度
col=rgb(0,1,0))
#塗りつぶし
polygon(c(c0_cos[10],line_scale_09_cos[x],line_scale_10_cos[x],c0_cos[10]), #x
c(c0_sin[10],line_scale_09_sin[x],line_scale_10_sin[x],c0_sin[10]), #y
density=c(30), #塗りつぶす濃度
angle=c(45),　 　　　#塗りつぶす斜線の角度
col=rgb(0,1,0))

}

#アニメーション
library("animation")
Time_Code=c(1,2,3,4,5,6,7,8,9,10,11,12,13,14,15)
saveGIF({
for (i in Time_Code){
　Three_square_theorem10(i)
}
}, interval = 0.1, movie.name = "TEST010b.gif")  

正五角形（Regular Pentagon
外角の大きさはpi/5=0.6283185ラジアンあるいは180/5=36度、内角の大きさは2pi(5-2)/5=3.769911ラジアンあるいは180*(5-2)/5=108度

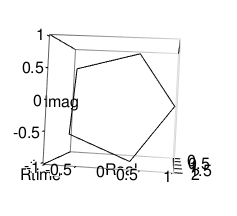
#正５角形
library(rgl)
Rtime<-seq(0,2,length=6)
tr01<-c(1,(-1+sqrt(5)+(0+1i)*sqrt(10+2*sqrt(5)))/4,(-1-sqrt(5)+(0+1i)*sqrt(10-2*sqrt(5)))/4,(-1-sqrt(5)-(0+1i)*sqrt(10-2*sqrt(5)))/4,(-1+sqrt(5)-(0+1i)*sqrt(10+2*sqrt(5)))/4,1)
Real<-Re(tr01)
Imag<-Im(tr01)
#plot(Real,Imag,type="l")
plot3d(Real,Imag,Rtime,type="l",xlim=c(-1,1),ylim=c(-1,1),zlim=c(0,2))
movie3d(spin3d(axis=c(0,0,1),rpm=5),duration=10,fps=25,movie="~/Desktop/test13") 

Three_square_theorem05<-function(x){
c0<-seq(0,2*pi,length=6)
c0_cos<-cos(c0)
c0_sin<-sin(c0)
plot(c0_cos,c0_sin,type="l",main="Regular polygon rotation",xlab="Cos(θ)",ylab="Sin(θ)")
text(c0_cos,c0_sin, labels=c("a","b","c","d","e",""),col=c(rgb(1,0,0),rgb(1,0,0),rgb(1,0,0),rgb(1,0,0),rgb(1,0,0),rgb(1,0,0)),cex=c(2,2,2,2,2,2))
line_scale_01_cos<-seq(cos(c0[1]),cos(c0[2]),length=15)
line_scale_01_sin<-seq(sin(c0[1]),sin(c0[2]),length=15)
line_scale_02_cos<-seq(cos(c0[2]),cos(c0[3]),length=15)
line_scale_02_sin<-seq(sin(c0[2]),sin(c0[3]),length=15)
line_scale_03_cos<-seq(cos(c0[3]),cos(c0[4]),length=15)
line_scale_03_sin<-seq(sin(c0[3]),sin(c0[4]),length=15)
line_scale_04_cos<-seq(cos(c0[4]),cos(c0[5]),length=15)
line_scale_04_sin<-seq(sin(c0[4]),sin(c0[5]),length=15)
line_scale_05_cos<-seq(cos(c0[5]),cos(c0[1]),length=15)
line_scale_05_sin<-seq(sin(c0[5]),sin(c0[1]),length=15)
text(c(line_scale_01_cos[x],line_scale_02_cos[x],line_scale_03_cos[x],line_scale_04_cos[x],line_scale_05_cos[x]),c(line_scale_01_sin[x],line_scale_02_sin[x],line_scale_03_sin[x],line_scale_04_sin[x],line_scale_05_sin[x]), labels=c("ab","bc","cd","de","ea",""),col=c(rgb(0,0,1),rgb(0,0,1),rgb(0,0,1),rgb(0,0,1),rgb(0,0,1),rgb(0,0,1)),cex=c(2,2,2,2,2,2))

#塗りつぶし
polygon(c(c0_cos[1],line_scale_05_cos[x],line_scale_01_cos[x],c0_cos[1]), #x
c(c0_sin[1],line_scale_05_sin[x],line_scale_01_sin[x],c0_sin[1]), #y
density=c(30), #塗りつぶす濃度
angle=c(45),　 　　　#塗りつぶす斜線の角度
col=rgb(0,1,0)) 　 

#塗りつぶし
polygon(c(c0_cos[2],line_scale_01_cos[x],line_scale_02_cos[x],c0_cos[2]), #x
c(c0_sin[2],line_scale_01_sin[x],line_scale_02_sin[x],c0_sin[2]), #y
density=c(30), #塗りつぶす濃度
angle=c(45),　 　　　#塗りつぶす斜線の角度
col=rgb(0,1,0)) 　 

#塗りつぶし
polygon(c(c0_cos[3],line_scale_02_cos[x],line_scale_03_cos[x],c0_cos[3]), #x
c(c0_sin[3],line_scale_02_sin[x],line_scale_03_sin[x],c0_sin[3]), #y
density=c(30), #塗りつぶす濃度
angle=c(45),　 　　　#塗りつぶす斜線の角度
col=rgb(0,1,0)) 　

#塗りつぶし
polygon(c(c0_cos[4],line_scale_03_cos[x],line_scale_04_cos[x],c0_cos[4]), #x
c(c0_sin[4],line_scale_03_sin[x],line_scale_04_sin[x],c0_sin[4]), #y
density=c(30), #塗りつぶす濃度
angle=c(45),　 　　　#塗りつぶす斜線の角度
col=rgb(0,1,0)) 　

#塗りつぶし
polygon(c(c0_cos[5],line_scale_04_cos[x],line_scale_05_cos[x],c0_cos[5]), #x
c(c0_sin[5],line_scale_04_sin[x],line_scale_05_sin[x],c0_sin[5]), #y
density=c(30), #塗りつぶす濃度
angle=c(45),　 　　　#塗りつぶす斜線の角度
col=rgb(0,1,0)) 　
}

#アニメーション
library("animation")
Time_Code=c(1,2,3,4,5,6,7,8,9,10,11,12,13,14,15)
saveGIF({
for (i in Time_Code){
　Three_square_theorem05(i)
}
}, interval = 0.1, movie.name = "TEST005.gif") 

#12進数の世界(2^n3^m族)
やはり厳密にいうと素数ベースではないが、例えば音楽理論の世界。****（Just Intonation）と平均律（Equal Temperament）のズレなんて問題も抱える。
平均律と純正律って？

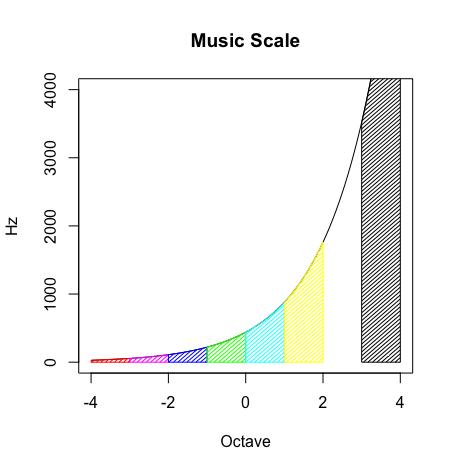
f1<-function(x){440*2^x}
plot(f1,xlim=c(-4,4),ylim=c(0,4000),type="l",col=rgb(0,0,0), main="Music Scale",xlab="Octave",ylab="Hz")

#第一区間(2^-4(27.5Hz)~2^-3(55.0Hz))
tc <- round(seq(-4,-3,length=10)) #0から1までを10等分
tcvals <- f1(tc) #それぞれの縦軸の値
polygon(c(-4,tc,-3), #x
c(0,tcvals,0), #y
density=c(30), #塗りつぶす濃度
angle=c(45),　 　　　#塗りつぶす斜線の角度
col=rgb(1,0,0)) 　#塗りつぶす色

#第2区間(2^-3(55.0Hz)~2^-2(110Hz))
tc <- seq(-3, -2, length=10) #1から2までを10等分
tcvals <- f1(tc) #それぞれの縦軸の値
polygon(c(-3,tc,-2), #x
c(0,tcvals,0), #y
density=c(30), #塗りつぶす濃度
angle=c(45),　 　　　#塗りつぶす斜線の角度
col=rgb(1,0,1)) 　#塗りつぶす色

#第3区間(2^-2(110Hz)~2^-1(220Hz))
tc <- seq(-2, -1, length=10) #3から8までを10等分
tcvals <- f1(tc) #それぞれの縦軸の値
polygon(c(-2,tc,-1), #x
c(0,tcvals,0), #y
density=c(30), #塗りつぶす濃度
angle=c(45),　 　　　#塗りつぶす斜線の角度
col=rgb(0,0,1)) 　#塗りつぶす色

#第4区間(2^-1(220Hz)~2^0（440Hz）)
tc <- seq(-1, 0, length=10) #8から16までを10等分
tcvals <- f1(tc) #それぞれの縦軸の値
polygon(c(-1,tc,0), #x
c(0,tcvals,0), #y
density=c(30), #塗りつぶす濃度
angle=c(45),　 　　　#塗りつぶす斜線の角度
col=rgb(0,1,0)) 　#塗りつぶす色

#第5区間(2^0(440Hz)〜2^1(880Hz))
tc <- seq(0, 1, length=10) #16から32までを10等分
tcvals <- f1(tc) #それぞれの縦軸の値
polygon(c(0,tc,1), #x
c(0,tcvals,0), #y
density=c(30), #塗りつぶす濃度
angle=c(45),　 　　　#塗りつぶす斜線の角度
col=rgb(0,1,1)) 　#塗りつぶす色

#第6区間(2^2(1760Hz)~2^3(1760Hz))
tc <- seq(1, 2, length=10) #32から64までを10等分
tcvals <- f1(tc) #それぞれの縦軸の値
polygon(c(1,tc,2), #x
c(0,tcvals,0), #y
density=c(30), #塗りつぶす濃度
angle=c(45),　 　　　#塗りつぶす斜線の角度
col=rgb(1,1,0)) 　#塗りつぶす色

#第8区間(2^3(3520Hz)~2^4(4186Hz))
tc <- seq(3, 4, length=10) #32から64までを10等分
tcvals <- f1(tc) #それぞれの縦軸の値
polygon(c(3,tc,4), #x
c(0,tcvals,0), #y
density=c(30), #塗りつぶす濃度
angle=c(45),　 　　　#塗りつぶす斜線の角度
col=rgb(0,0,0)) 　#塗りつぶす色

	American_and_British	German	Italian	French	Japanese
1	C	C	Do	Do(Ut)	ｲ(I)
2	C#=D♭	Cis=Des	Do#=Re♭	Do(Ut)dièse=Re bémol	嬰ｲ(I)=変ﾛ(Ro)
3	D	D	Re	Re	ﾛ(Ro)
4	D#=E♭	Dis=Ees	Re#=Mi♭	Re dièse=Mi bémol	嬰ﾛ(Ro)=変ﾊ(Ha)
5	E	E	Mi	Mi	ﾊ(Ha)
6	E#=F	Eis=Fes	Mi#=Fa♭	Mi dièse=Fa bémol	嬰ﾊ(Ha)=変ﾆ(Ni)
7	F	F	Fa	Fa	ﾆ(Ni)
8	G	G	So	So	ﾎ(Ho)
9	G#=A♭	Gis=Aes	So#=Ra♭	So dièse=Ra bémol	嬰ﾎ(Ho)=変ﾍ(He)
10	A	A	Ra	Ra	ﾍ(He)
11	A#=B♭	Ais=Hes	Ra#=Si♭	Ra dièse=Si bémol	嬰ﾍ(He)=変ﾄ(To)
12	B	H	Si	Si	ﾄ(To)

#世界各国の音階表示
american_and_british<-c("C","C#=D♭","D","D#=E♭","E","E#=F","F","G","G#=A♭","A","A#=B♭","B")
german<-c("C","Cis=Des","D","Dis=Ees","E","Eis=Fes","F","G","Gis=Aes","A","Ais=Hes","H")
italian<-c("Do","Do#=Re♭","Re","Re#=Mi♭","Mi","Mi#=Fa♭","Fa","So","So#=Ra♭","Ra","Ra#=Si♭","Si")
french<-c("Do(Ut)","Do(Ut)dièse=Re bémol","Re","Re dièse=Mi bémol","Mi","Mi dièse=Fa bémol","Fa","So","So dièse=Ra bémol","Ra","Ra dièse=Si bémol","Si")
japanese<-c("ｲ(I)","嬰ｲ(I)=変ﾛ(Ro)","ﾛ(Ro)","嬰ﾛ(Ro)=変ﾊ(Ha)","ﾊ(Ha)","嬰ﾊ(Ha)=変ﾆ(Ni)","ﾆ(Ni)","ﾎ(Ho)","嬰ﾎ(Ho)=変ﾍ(He)","ﾍ(He)","嬰ﾍ(He)=変ﾄ(To)","ﾄ(To)")
Music_scales<-data.frame(American_and_British=american_and_british, German=german,Italian=italian,French=french,Japanese=japanese)
library(xtable)
print(xtable(Music_scales), type = "html")

人間はある周波数[Hz]の音を聞いていたとき、その２倍の周波数[Hz]の音を聞くと音の高さが２倍になったように感じます。言い換えると、周波数の対数を取ったものを横軸とし、縦軸に人間が感じる音の高さをプロットすると直線になるのです。これは精神物理学者が実験で確かめた人間の特性で心理学者ヴエーバ・フェヒナの法則（Weber–Fechner law）と呼ばれています。

ヴェーバー‐フェヒナーの法則 - Wikipedia

エルンスト・ヴェーバー（Ernst Heinrich Weber、1795年〜1878年）は、1834年に錘を持ち上げる実験を行い、錘の重さの変化を感じ取る感覚は、何g増えたかといった差ではなく、何倍になったかという比に依存していることを「Zusätze zur Lehre vom Bau und von der Verrichtung der Geschlechtsorgane（1846年）」や「Die Lehre vom Tastsinn und Gemeingefühl（『触覚と一般感覚』1851年）」で発表。

それによれば刺激の弁別閾（threshold、丁度可知差異：気づくことができる最小の刺激差）は、基準となる基礎刺激の強度に比例する。

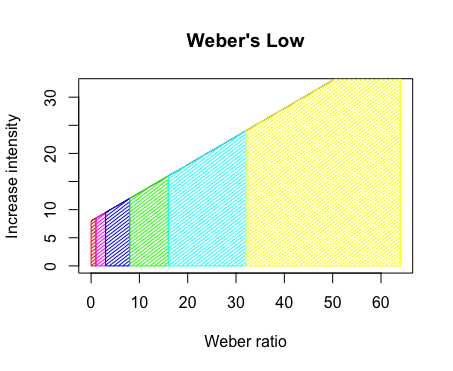
はじめに加えられる基礎刺激量の強度をRとし、これに対応する識別閾値をΔRとすると、Rの値にかかわらずΔR/R=constant（定数）が成り立つ。この一定の値をヴェーバー比（Weber ratio）という。たとえば音の強さについては 11分の1，圧覚では7分の1になる。

f0<-function(x){(1/2)*x+8}
plot(f0,xlim=c(0,64),ylim=c(0,32),type="l",col=rgb(0,0,0), main="Weber's Low",xlab="Background Intencity",ylab="Increase intensity") 

#第一区間(0-1)
tc <- seq(0, 1, length=10) #0から1までを10等分
tcvals <- f0(tc) #それぞれの縦軸の値
polygon(c(0,tc,1), #x
c(0,tcvals,0), #y
density=c(30), #塗りつぶす濃度
angle=c(45),　 　　　#塗りつぶす斜線の角度
col=rgb(1,0,0)) 　#塗りつぶす色

#第2区間(1-3)
tc <- seq(1, 3, length=10) #1から2までを10等分
tcvals <- f0(tc) #それぞれの縦軸の値
polygon(c(1,tc,3), #x
c(0,tcvals,0), #y
density=c(30), #塗りつぶす濃度
angle=c(45),　 　　　#塗りつぶす斜線の角度
col=rgb(1,0,1)) 　#塗りつぶす色

#第3区間(3-8)
tc <- seq(3, 8, length=10) #3から8までを10等分
tcvals <- f0(tc) #それぞれの縦軸の値
polygon(c(3,tc,8), #x
c(0,tcvals,0), #y
density=c(30), #塗りつぶす濃度
angle=c(45),　 　　　#塗りつぶす斜線の角度
col=rgb(0,0,1)) 　#塗りつぶす色
#第4区間(8-16)
tc <- seq(8, 16, length=10) #8から16までを10等分
tcvals <- f0(tc) #それぞれの縦軸の値
polygon(c(8,tc,16), #x
c(0,tcvals,0), #y
density=c(30), #塗りつぶす濃度
angle=c(45),　 　　　#塗りつぶす斜線の角度
col=rgb(0,1,0)) 　#塗りつぶす色

#第5区間(16-32)
tc <- seq(16, 32, length=10) #16から32までを10等分
tcvals <- f0(tc) #それぞれの縦軸の値
polygon(c(16,tc,32), #x
c(0,tcvals,0), #y
density=c(30), #塗りつぶす濃度
angle=c(45),　 　　　#塗りつぶす斜線の角度
col=rgb(0,1,1)) 　#塗りつぶす色
#第6区間(32-64)
tc <- seq(32, 64, length=10) #32から64までを10等分
tcvals <- f0(tc) #それぞれの縦軸の値
polygon(c(32,tc,64), #x
c(0,tcvals,0), #y
density=c(30), #塗りつぶす濃度
angle=c(45),　 　　　#塗りつぶす斜線の角度
col=rgb(1,1,0)) 　#塗りつぶす色

ヴェーバーの弟子でその研究を発展させ精神物理学という学問を創始し、実験心理学の成立に大きな影響を与えたグスタフ・フェヒナー（Gustav Theodor Fechner、1801年〜1887年）は、ヴェーバーの法則の式を積分することにより、以下の対数法則を導き出した。実はここでΔRをdRとして積分することは若干の飛躍があり、厳密な計算ではなく近似である。

#汎用計算機代数ソフトウェアYacas使用
library(Ryacas)
yacas("Integrate(x) a/x")
expression(a * log(x))

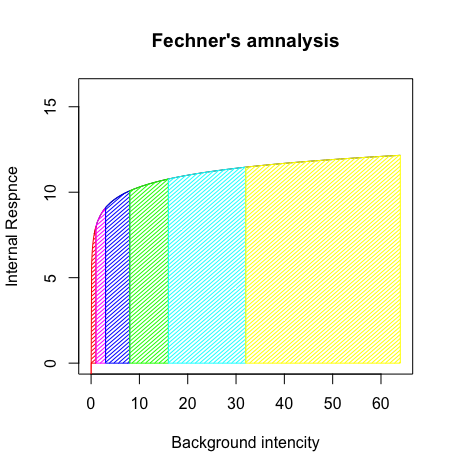
刺激量の強度R が変化する時、これに対応する感覚量E はE=C*log(R)（ここでCは定数）の関係となる。つまり心理的な感覚量は、刺激の強度ではなく、その対数に比例して知覚される。フェヒナーの法則と呼ばれることも多いが、ヴェーバーの法則から導出したことからヴェーバー・フェヒナーの法則とも呼ばれる。たとえば、100の刺激が倍に増加して200になるときの感覚量と、200の刺激が倍に増加して400になるときの感覚量の変化は等しい。

f1<-function(x){log(x)+8}
plot(f1,xlim=c(0,64),ylim=c(0,16),type="l",col=rgb(0,0,0), main="Fechner's amnalysis",xlab="Background intencity",ylab="Internal Respnce") 

#第一区間(0-1)
tc <- seq(0.0001, 1, length=10) #0から1までを10等分
tcvals <- f1(tc) #それぞれの縦軸の値
polygon(c(0.0001,tc,1), #x
c(0.0001,tcvals,0), #y
density=c(30), #塗りつぶす濃度
angle=c(45),　 　　　#塗りつぶす斜線の角度
col=rgb(1,0,0)) 　#塗りつぶす色

#第2区間(1-3)
tc <- seq(1, 3, length=10) #1から2までを10等分
tcvals <- f1(tc) #それぞれの縦軸の値
polygon(c(1,tc,3), #x
c(0,tcvals,0), #y
density=c(30), #塗りつぶす濃度
angle=c(45),　 　　　#塗りつぶす斜線の角度
col=rgb(1,0,1)) 　#塗りつぶす色

#第3区間(3-8)
tc <- seq(3, 8, length=10) #3から8までを10等分
tcvals <- f1(tc) #それぞれの縦軸の値
polygon(c(3,tc,8), #x
c(0,tcvals,0), #y
density=c(30), #塗りつぶす濃度
angle=c(45),　 　　　#塗りつぶす斜線の角度
col=rgb(0,0,1)) 　#塗りつぶす色
#第4区間(8-16)
tc <- seq(8, 16, length=10) #8から16までを10等分
tcvals <- f1(tc) #それぞれの縦軸の値
polygon(c(8,tc,16), #x
c(0,tcvals,0), #y
density=c(30), #塗りつぶす濃度
angle=c(45),　 　　　#塗りつぶす斜線の角度
col=rgb(0,1,0)) 　#塗りつぶす色

#第5区間(16-32)
tc <- seq(16, 32, length=10) #16から32までを10等分
tcvals <- f1(tc) #それぞれの縦軸の値
polygon(c(16,tc,32), #x
c(0,tcvals,0), #y
density=c(30), #塗りつぶす濃度
angle=c(45),　 　　　#塗りつぶす斜線の角度
col=rgb(0,1,1)) 　#塗りつぶす色
#第6区間(32-64)
tc <- seq(32, 64, length=10) #32から64までを10等分
tcvals <- f1(tc) #それぞれの縦軸の値
polygon(c(32,tc,64), #x
c(0,tcvals,0), #y
density=c(30), #塗りつぶす濃度
angle=c(45),　 　　　#塗りつぶす斜線の角度
col=rgb(1,1,0)) 　#塗りつぶす色

正十二角形(Regular Dodecagon)
外角の大きさはpi/12=0.2617994ラジアンあるいは180/12=15度、内角の大きさは2pi(12-2)/12=5.235988ラジアンあるいは180*(12-2)/12=150度

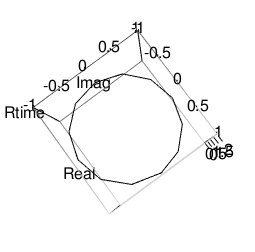
Three_square_theorem12<-function(x){
c0<-seq(0,2*pi,length=13)
c0_cos<-cos(c0)
c0_sin<-sin(c0)
plot(c0_cos,c0_sin,type="l",main="Regular polygon rotation",xlab="Cos(θ)",ylab="Sin(θ)")
text(c0_cos,c0_sin, labels=c("C","C#","D","D#","E","E#=F","G","G#=Ab","A","A#=Bb","B","C#=Ab",""),col=c(rgb(1,0,0),rgb(1,0,0),rgb(1,0,0),rgb(1,0,0),rgb(1,0,0),rgb(1,0,0),rgb(1,0,0),rgb(1,0,0),rgb(1,0,0),rgb(1,0,0),rgb(1,0,0),rgb(1,0,0),rgb(1,0,0)),cex=c(2,2,2,2,2,2,2,2,2,2,2,2,2))
line_scale_01_cos<-seq(cos(c0[1]),cos(c0[2]),length=15)
line_scale_01_sin<-seq(sin(c0[1]),sin(c0[2]),length=15)
line_scale_02_cos<-seq(cos(c0[2]),cos(c0[3]),length=15)
line_scale_02_sin<-seq(sin(c0[2]),sin(c0[3]),length=15)
line_scale_03_cos<-seq(cos(c0[3]),cos(c0[4]),length=15)
line_scale_03_sin<-seq(sin(c0[3]),sin(c0[4]),length=15)
line_scale_04_cos<-seq(cos(c0[4]),cos(c0[5]),length=15)
line_scale_04_sin<-seq(sin(c0[4]),sin(c0[5]),length=15)
line_scale_05_cos<-seq(cos(c0[5]),cos(c0[6]),length=15)
line_scale_05_sin<-seq(sin(c0[5]),sin(c0[6]),length=15)
line_scale_06_cos<-seq(cos(c0[6]),cos(c0[7]),length=15)
line_scale_06_sin<-seq(sin(c0[6]),sin(c0[7]),length=15)
line_scale_07_cos<-seq(cos(c0[7]),cos(c0[8]),length=15)
line_scale_07_sin<-seq(sin(c0[7]),sin(c0[8]),length=15)
line_scale_08_cos<-seq(cos(c0[8]),cos(c0[9]),length=15)
line_scale_08_sin<-seq(sin(c0[8]),sin(c0[9]),length=15)
line_scale_09_cos<-seq(cos(c0[9]),cos(c0[10]),length=15)
line_scale_09_sin<-seq(sin(c0[9]),sin(c0[10]),length=15)
line_scale_10_cos<-seq(cos(c0[10]),cos(c0[11]),length=15)
line_scale_10_sin<-seq(sin(c0[10]),sin(c0[11]),length=15)
line_scale_11_cos<-seq(cos(c0[11]),cos(c0[12]),length=15)
line_scale_11_sin<-seq(sin(c0[11]),sin(c0[12]),length=15)
line_scale_12_cos<-seq(cos(c0[12]),cos(c0[1]),length=15)
line_scale_12_sin<-seq(sin(c0[12]),sin(c0[1]),length=15)

 text(c(line_scale_01_cos[x],line_scale_02_cos[x],line_scale_03_cos[x],line_scale_04_cos[x],line_scale_05_cos[x],line_scale_06_cos[x],line_scale_07_cos[x],line_scale_08_cos[x],line_scale_09_cos[x],line_scale_10_cos[x],line_scale_11_cos[x],line_scale_12_cos[x]),c(line_scale_01_sin[x],line_scale_02_sin[x],line_scale_03_sin[x],line_scale_04_sin[x],line_scale_05_sin[x],line_scale_06_sin[x],line_scale_07_sin[x],line_scale_08_sin[x],line_scale_09_sin[x],line_scale_10_sin[x],line_scale_11_sin[x],line_scale_12_sin[x]), labels=c("C-C#","C#-D","D-D#","D#-E","E-E#/F","E#/F-G","G-G#/Ab","G#/Ab-A","A-A#/Bb","A#/Bb-B","B-C#/Ab","C#=Ab-C",""),col=c(rgb(0,0,1),rgb(0,0,1),rgb(0,0,1),rgb(0,0,1),rgb(0,0,1),rgb(0,0,1),rgb(0,0,1),rgb(0,0,1),rgb(0,0,1),rgb(0,0,1),rgb(0,0,1),rgb(0,0,1),rgb(0,0,1)),cex=c(1.5,1.5,1.5,1.5,1.5,1.5,1.5,1.5,1.5,1.5,1.5,1.5))

 #塗りつぶし
polygon(c(c0_cos[1],line_scale_12_cos[x],line_scale_01_cos[x],c0_cos[1]), #x
c(c0_sin[1],line_scale_12_sin[x],line_scale_01_sin[x],c0_sin[1]), #y
density=c(30), #塗りつぶす濃度
angle=c(45),　 　　　#塗りつぶす斜線の角度
col=rgb(0,1,0)) 　 

#塗りつぶし
polygon(c(c0_cos[2],line_scale_01_cos[x],line_scale_02_cos[x],c0_cos[2]), #x
c(c0_sin[2],line_scale_01_sin[x],line_scale_02_sin[x],c0_sin[2]), #y
density=c(30), #塗りつぶす濃度
angle=c(45),　 　　　#塗りつぶす斜線の角度
col=rgb(0,1,0)) 　 

#塗りつぶし
polygon(c(c0_cos[3],line_scale_02_cos[x],line_scale_03_cos[x],c0_cos[3]), #x
c(c0_sin[3],line_scale_02_sin[x],line_scale_03_sin[x],c0_sin[3]), #y
density=c(30), #塗りつぶす濃度
angle=c(45),　 　　　#塗りつぶす斜線の角度
col=rgb(0,1,0)) 　

#塗りつぶし
polygon(c(c0_cos[4],line_scale_03_cos[x],line_scale_04_cos[x],c0_cos[4]), #x
c(c0_sin[4],line_scale_03_sin[x],line_scale_04_sin[x],c0_sin[4]), #y
density=c(30), #塗りつぶす濃度
angle=c(45),　 　　　#塗りつぶす斜線の角度
col=rgb(0,1,0)) 　

#塗りつぶし
polygon(c(c0_cos[5],line_scale_04_cos[x],line_scale_05_cos[x],c0_cos[5]), #x
c(c0_sin[5],line_scale_04_sin[x],line_scale_05_sin[x],c0_sin[5]), #y
density=c(30), #塗りつぶす濃度
angle=c(45),　 　　　#塗りつぶす斜線の角度
col=rgb(0,1,0)) 　
#塗りつぶし
polygon(c(c0_cos[6],line_scale_05_cos[x],line_scale_06_cos[x],c0_cos[6]), #x
c(c0_sin[6],line_scale_05_sin[x],line_scale_06_sin[x],c0_sin[6]), #y
density=c(30), #塗りつぶす濃度
angle=c(45),　 　　　#塗りつぶす斜線の角度
col=rgb(0,1,0))

#塗りつぶし
polygon(c(c0_cos[7],line_scale_06_cos[x],line_scale_07_cos[x],c0_cos[7]), #x
c(c0_sin[7],line_scale_06_sin[x],line_scale_07_sin[x],c0_sin[7]), #y
density=c(30), #塗りつぶす濃度
angle=c(45),　 　　　#塗りつぶす斜線の角度
col=rgb(0,1,0))

#塗りつぶし
polygon(c(c0_cos[8],line_scale_07_cos[x],line_scale_08_cos[x],c0_cos[8]), #x
c(c0_sin[8],line_scale_07_sin[x],line_scale_08_sin[x],c0_sin[8]), #y
density=c(30), #塗りつぶす濃度
angle=c(45),　 　　　#塗りつぶす斜線の角度
col=rgb(0,1,0))
#塗りつぶし
polygon(c(c0_cos[9],line_scale_08_cos[x],line_scale_09_cos[x],c0_cos[9]), #x
c(c0_sin[9],line_scale_08_sin[x],line_scale_09_sin[x],c0_sin[9]), #y
density=c(30), #塗りつぶす濃度
angle=c(45),　 　　　#塗りつぶす斜線の角度
col=rgb(0,1,0))
#塗りつぶし
polygon(c(c0_cos[10],line_scale_09_cos[x],line_scale_10_cos[x],c0_cos[10]), #x
c(c0_sin[10],line_scale_09_sin[x],line_scale_10_sin[x],c0_sin[10]), #y
density=c(30), #塗りつぶす濃度
angle=c(45),　 　　　#塗りつぶす斜線の角度
col=rgb(0,1,0))
#塗りつぶし
polygon(c(c0_cos[11],line_scale_10_cos[x],line_scale_11_cos[x],c0_cos[11]), #x
c(c0_sin[11],line_scale_10_sin[x],line_scale_11_sin[x],c0_sin[11]), #y
density=c(30), #塗りつぶす濃度
angle=c(45),　 　　　#塗りつぶす斜線の角度
col=rgb(0,1,0))

#塗りつぶし
polygon(c(c0_cos[12],line_scale_11_cos[x],line_scale_12_cos[x],c0_cos[12]), #x
c(c0_sin[12],line_scale_11_sin[x],line_scale_12_sin[x],c0_sin[12]), #y
density=c(30), #塗りつぶす濃度
angle=c(45),　 　　　#塗りつぶす斜線の角度
col=rgb(0,1,0)) 

}

#アニメーション
library("animation")
Time_Code=c(1,2,3,4,5,6,7,8,9,10,11,12,13,14,15)
saveGIF({
for (i in Time_Code){
　Three_square_theorem12(i)
}
}, interval = 0.1, movie.name = "TEST012h.gif") 

正六角形(Regular Hexagon)
外角の大きさはpi/6=0.5235988ラジアンあるいは180/6=30度、内角の大きさは2pi(6-2)/6=4.18879ラジアンあるいは180*(6-2)/6=120度

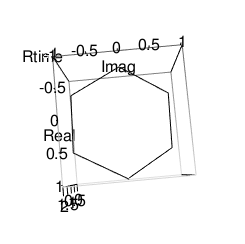
統計言語Rによる作図例
#正６角形
library(rgl)
Rtime<-seq(0,2,length=7)
tr01<-c(1,(1+sqrt(3)*(0+1i))/2,(-1+sqrt(3)*(0+1i))/2,-1,(-1-sqrt(3)*(0+1i))/2,(1-sqrt(3)*(0+1i))/2,1)
Real<-Re(tr01)
Imag<-Im(tr01)
#plot(Real,Imag,type="l")
plot3d(Real,Imag,Rtime,type="l",xlim=c(-1,1),ylim=c(-1,1),zlim=c(0,2))
movie3d(spin3d(axis=c(0,0,1),rpm=5),duration=10,fps=25,movie="~/Desktop/test13")

Three_square_theorem06<-function(x){
c0<-seq(0,2*pi,length=7)
c0_cos<-cos(c0)
c0_sin<-sin(c0)
plot(c0_cos,c0_sin,type="l",main="Regular polygon rotation",xlab="Cos(θ)",ylab="Sin(θ)")
text(c0_cos,c0_sin, labels=c("a","b","c","d","e","f",""),col=c(rgb(1,0,0),rgb(1,0,0),rgb(1,0,0),rgb(1,0,0),rgb(1,0,0),rgb(1,0,0),rgb(1,0,0)),cex=c(2,2,2,2,2,2,2))
line_scale_01_cos<-seq(cos(c0[1]),cos(c0[2]),length=15)
line_scale_01_sin<-seq(sin(c0[1]),sin(c0[2]),length=15)
line_scale_02_cos<-seq(cos(c0[2]),cos(c0[3]),length=15)
line_scale_02_sin<-seq(sin(c0[2]),sin(c0[3]),length=15)
line_scale_03_cos<-seq(cos(c0[3]),cos(c0[4]),length=15)
line_scale_03_sin<-seq(sin(c0[3]),sin(c0[4]),length=15)
line_scale_04_cos<-seq(cos(c0[4]),cos(c0[5]),length=15)
line_scale_04_sin<-seq(sin(c0[4]),sin(c0[5]),length=15)
line_scale_05_cos<-seq(cos(c0[5]),cos(c0[6]),length=15)
line_scale_05_sin<-seq(sin(c0[5]),sin(c0[6]),length=15)
line_scale_06_cos<-seq(cos(c0[6]),cos(c0[1]),length=15)
line_scale_06_sin<-seq(sin(c0[6]),sin(c0[1]),length=15)
text(c(line_scale_01_cos[x],line_scale_02_cos[x],line_scale_03_cos[x],line_scale_04_cos[x],line_scale_05_cos[x],line_scale_06_cos[x]),c(line_scale_01_sin[x],line_scale_02_sin[x],line_scale_03_sin[x],line_scale_04_sin[x],line_scale_05_sin[x],line_scale_06_sin[x]), labels=c("ab","bc","cd","de","ef","fa",""),col=c(rgb(0,0,1),rgb(0,0,1),rgb(0,0,1),rgb(0,0,1),rgb(0,0,1),rgb(0,0,1),rgb(0,0,1)),cex=c(2,2,2,2,2,2,2))

#塗りつぶし
polygon(c(c0_cos[1],line_scale_06_cos[x],line_scale_01_cos[x],c0_cos[1]), #x
c(c0_sin[1],line_scale_06_sin[x],line_scale_01_sin[x],c0_sin[1]), #y
density=c(30), #塗りつぶす濃度
angle=c(45),　 　　　#塗りつぶす斜線の角度
col=rgb(0,1,0)) 　 

#塗りつぶし
polygon(c(c0_cos[2],line_scale_01_cos[x],line_scale_02_cos[x],c0_cos[2]), #x
c(c0_sin[2],line_scale_01_sin[x],line_scale_02_sin[x],c0_sin[2]), #y
density=c(30), #塗りつぶす濃度
angle=c(45),　 　　　#塗りつぶす斜線の角度
col=rgb(0,1,0)) 　 

#塗りつぶし
polygon(c(c0_cos[3],line_scale_02_cos[x],line_scale_03_cos[x],c0_cos[3]), #x
c(c0_sin[3],line_scale_02_sin[x],line_scale_03_sin[x],c0_sin[3]), #y
density=c(30), #塗りつぶす濃度
angle=c(45),　 　　　#塗りつぶす斜線の角度
col=rgb(0,1,0)) 　

#塗りつぶし
polygon(c(c0_cos[4],line_scale_03_cos[x],line_scale_04_cos[x],c0_cos[4]), #x
c(c0_sin[4],line_scale_03_sin[x],line_scale_04_sin[x],c0_sin[4]), #y
density=c(30), #塗りつぶす濃度
angle=c(45),　 　　　#塗りつぶす斜線の角度
col=rgb(0,1,0)) 　

#塗りつぶし
polygon(c(c0_cos[5],line_scale_04_cos[x],line_scale_05_cos[x],c0_cos[5]), #x
c(c0_sin[5],line_scale_04_sin[x],line_scale_05_sin[x],c0_sin[5]), #y
density=c(30), #塗りつぶす濃度
angle=c(45),　 　　　#塗りつぶす斜線の角度
col=rgb(0,1,0)) 　
#塗りつぶし
polygon(c(c0_cos[6],line_scale_05_cos[x],line_scale_06_cos[x],c0_cos[6]), #x
c(c0_sin[6],line_scale_05_sin[x],line_scale_06_sin[x],c0_sin[6]), #y
density=c(30), #塗りつぶす濃度
angle=c(45),　 　　　#塗りつぶす斜線の角度
col=rgb(0,1,0))

}

#アニメーション
library("animation")
Time_Code=c(1,2,3,4,5,6,7,8,9,10,11,12,13,14,15)
saveGIF({
for (i in Time_Code){
　Three_square_theorem06(i)
}
}, interval = 0.1, movie.name = "TEST06.gif") 

とりあえず、以下続報。