今回の投稿の出発点はこれ。
【初心者向け】「円そのもの」の近似から派生した角度概念の起源

人類は如何にして三角関数に到達したかについて、物理学の領域にはまた独自の「神話」が存在するのです。
最初の出発点は等速円運動。
円運動(circular motion) - Wikipedia
回転運動を回転面上の観測者が真横から見ると物体は単振動しているように見える。あるいは、物体のx座標とy座標は互いに位相が90度=π/2ずれた単振動を行っている。
振動運動では回転速度のことを周波数または振動数と呼ぶ。
①まず「あらゆる運動の原型の一つ」たる等速円運動(Constant Velocity Circular Motion)を想定する。回転運動を互いに直交するx軸側とy軸側からそれぞれ観測(observe)すると、同じ波形が互いに位相が90度=π/2ずれた単振動(simple vibration)が二つ得られる。これが(x軸からの観測結果に由来する)余弦波(Cosin wave)と(y軸からの観測結果に由来する)正弦波(Sine wave)の起源となる。
XY軸(円弧)

# CosSin=Cos波とSin波の検出
# Radian=角度(60分割)
CosSin<-function(Radian){
c0<-seq(0,2*pi,length=60)
cx<-cos(c0)
cy<-sin(c0)
plot(cx,cy,asp=1,type="l",col=rgb(0,1,0),main="Constant Velocity Circular Motion",xlab="cos(θ)",ylab="sin(θ)")
# 塗りつぶし(円)
polygon(cx, #x
cy, #y
density=c(30), #塗りつぶす濃度
angle=c(45), #塗りつぶす斜線の角度
col=c(200,200,200)) #塗りつぶす色
text(cx[Radian],cy[Radian],"%",col=rgb(1,0,0))
# 補助線
segments(cx[Radian],cy[Radian],0,0,col=rgb(1,0,0))
# Cos
segments(-1,1,1,1,col=rgb(0,0,0))
segments(cx[Radian],cy[Radian],cx[Radian],1,col=rgb(0,0,0))
segments(0,1,cx[Radian],1,col=rgb(0,1,1),lwd =4)
# Sin
segments(-1,1,-1,-1,col=rgb(0,0,0))
segments(cx[Radian],cy[Radian],-1,cy[Radian],col=rgb(0,0,0))
segments(-1,0,-1,cy[Radian],col=rgb(0,0,1),lwd =4)
# 凡例
legend("bottomright", legend=c("side=2π/1τ","radius=1"), lty=c(1,1), col=c(rgb(0,1,0),rgb(1,0,0)))
}
# アニメーション
library("animation")
Time_Code=seq(1,59, length=30)
saveGIF({
for (i in Time_Code){
CosSin(i)
}
}, interval = 0.1, movie.name = "CosSin01.gif")
CosCos<-function(Radian){
cx<-seq(0,2*pi,length=60)
cy<-cos(c0)
plot(cx,cy,type="l",col=rgb(0,1,0),ylim=c(-1,1),main="Cosine wave",xlab="cos(θ)",ylab="t(Radian/s)")
# 塗りつぶし(Cos波)
polygon(c(0,cx,2*pi), #x
c(0,cy,0), #y
density=c(30), #塗りつぶす濃度
angle=c(45), #塗りつぶす斜線の角度
col=c(200,200,200)) #塗りつぶす色
text(cx[Radian],cy[Radian],"%",col=rgb(1,0,0))
# 補助線
segments(0,-1,0,1,col=rgb(0,0,0))
segments(cx[Radian],cy[Radian],0,cy[Radian],col=rgb(0,0,0))
segments(0,0,0,cy[Radian],col=rgb(0,1,1),lwd =4)
}
# アニメーション
library("animation")
Time_Code=seq(1,59, length=30)
saveGIF({
for (i in Time_Code){
CosCos(i)
}
}, interval = 0.1, movie.name = "CosCos01.gif")
SinSin<-function(Radian){
cx<-seq(0,2*pi,length=60)
cy<-sin(c0)
plot(cx,cy,type="l",col=rgb(0,0,1),ylim=c(-1,1),main="Sine wave",xlab="cos(θ)",ylab="t(Radian/s)")
# 塗りつぶし(Cos波)
polygon(c(0,cx,2*pi), #x
c(0,cy,0), #y
density=c(30), #塗りつぶす濃度
angle=c(45), #塗りつぶす斜線の角度
col=c(200,200,200)) #塗りつぶす色
# 補助線
text(cx[Radian],cy[Radian],"%",col=rgb(1,0,0))
segments(0,-1,0,1,col=rgb(0,0,0))
segments(cx[Radian],cy[Radian],0,cy[Radian],col=rgb(0,0,0))
segments(0,0,0,cy[Radian],col=rgb(0,1,1),lwd =4)
}
# アニメーション
library("animation")
Time_Code=seq(1,59, length=30)
saveGIF({
for (i in Time_Code){
SinSin(i)
}
}, interval = 0.1, movie.name = "SinSin01.gif")
そして単位円筒(Unit Cylinder)概念の登場
私達は概ね物体の運動を「位置の変化」と認識しているが、この表現は不正確で「位置が時間経過とともに変化してる」と表現すべきなのである。
とどのつまり、私達は「時間経過」を暗黙の了解としながら「位置の変化」を認知した時点で初めて運動なる物理現象を認識した事になる。
この様に物理学的アプローチにおいては(数学における)角度θの概念が角速度(Angular velocity、単位Radian/S)または周波数(frequency、単位Hz)として検出されるので、最終的に構成されるのも「(空間概念としてのみ意識される)単位円(Unit Circle、半径1)」ではなく「(空間として認識されるZ軸と時間経過として意識されるt軸が可換性を有する)単位円筒(Unit Cylinder、半径1、周期2π)」となります。

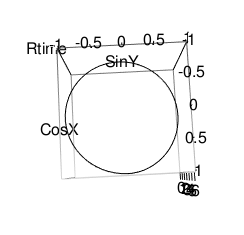
XY軸(円弧)
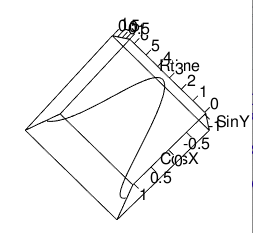
ZX軸(Cos波)
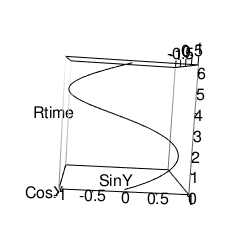
ZY軸(Sin波)
library(rgl)
Rtime<-seq(0,2*pi,length=60)
CosX<-cos(Rtime)
SinY<-sin(Rtime)
plot3d(CosX,SinY,Rtime,type="l",xlim=c(-1,1),ylim=c(-1,1),zlim=c(0,2*pi))
movie3d(spin3d(axis=c(0,0,1),rpm=5),duration=10,fps=25,movie="~/Desktop/test01")
-
物理学の世界においては、この考え方こそが単位球面(Unit Sphere)概念の出発点となる。
【初心者向け】「単位円筒」から「単位球面」へ
- 一方、数学の世界では「時間経過概念の存在しない」独特の「正面図/側面図」概念が育まれた。
【初心者向け】誤差関数(ERF)と相補誤差関数 (ERFC)。

これを「裏面まで見通せるブラックホール視点」として一つのアニメーションに統合する事も可能だが、人間の視覚は「余分に表示されている部分」をあっけなく誤差として切り捨ててしまうのである。
とりあえず以下続報・・・


