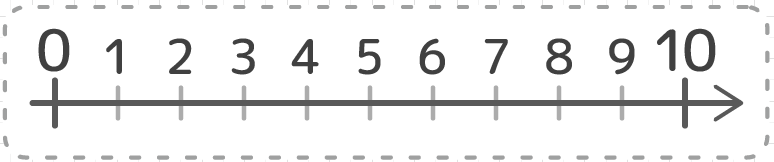
ある意味数直線(Number Line)、すなわち自然数(Natural Number)や整数(Integer Number)が何か規定する等差数列(Arithmetic Progression)あるいは算術数列(Arithmetic Sequence)の導入(Introduction)こそが加算直積可能世界(The Countable and Productable Sets)の出発点といえましょう。
[等差数列あるいは算術数列 - Wikipedia]
(https://ja.wikipedia.org/wiki/%E7%AD%89%E5%B7%AE%E6%95%B0%E5%88%97)
等差数列(Arithmetic Progression)または算術数列(Arithmetic Sequence) の定義。
- 与えられた区間(Interval)において、任意の項(Any Term)の添字(index)nに拠らず、隣接する二項の差(difference)が全て等しい数列(Sequence of Numbers with Common Difference)をいう。
- 各項に共通(Common) するその一定の差の事を公差(Common Difference)といい、公差dはその数列a[1],a[2],a[3],a[4]…a[n](nは項(term)の総数sum)における各項の添字(Index)nを用いてd:=a[n+1]-a[n]なる形で取り出すことができる。
- なので等差数列の各項は初項aと公比rとその数列における各項の添字nを用いてa[1]+(n-1)*dと表せる。かかるn番目の項a[n]の値をその等比数列における一般項(General Term)という。
- すなわち一般に第n項a[n]と第m項a[m]の関係はa[n]=a[m]+(n-m)dとなる。例えばa[n]=3, 5, 7…∞なる片側無限数列(one-sided infinite sequence)(a[n])(n=1~∞)は、各項が直前の項に2を加えたものになっているから、初項3、公比2の片側無限等差数列(One-Sided Arithmetic Sequence)であり、その7番目の項の値は15となる。
# 等比数列=初項*公差^(数列の項数-1)
ap01<-function(x,y,z){x+y*(z-1)}
# 初項3,公比2,項数3の場合
ap01(3,2,7)
[1] 15
c0<-ap01(3,2,c(1,2,3))
c0
[1] 3 5 7
# 公差の検出=数列[N+1]-数列[N]
c0[1+1]-c0[1]
[1] 2
c0[2+1]-c0[2]
[1] 2
# 公差の「逆数」検出=数列[N]-数列[N+1]
c0[1]-c0[1+1]
[1] -2
c0[2]-c0[2+1]
[1] -2
# 各項における係数と値の関係a[n]=a[m]*r^(n-m)
c0[1]
[1] 3
c0[2]
[1] 5
c0[3]
[1] 7
# 逐次計算結果
1+2*(1-0)
[1] 3
3+2*(2-1)
[1] 5
5+2*(3-2)
[1] 7
特に初項a,公差0の等差数列は初項a,公比1の等比数列(Geometric Progression)ないしは幾何数列(Geometric Sequence)のそれと重なります。
# 初項a=1の時
ap01(1,0,c(1:7))
[1] 1 1 1 1 1 1 1
# 初項a=7の時
ap01(7,0,c(1:7))
[1] 7 7 7 7 7 7 7
有限算術数列(Finite arithmetic sequence)の総和(sum)としての算術級数 (Arithmetic Series) と算術平均(Arithmetic Mean)」。
両側とも閉じて有限個の項しか持たない閉区間(Closed Interval)の算術数列を有限算術数列(Finite Arithmetic Sequence)と呼び、初等数学でいうところの等差数列は概ねこれを指します。そして有限算術数列の和を算術級数 (Arithmetic Series) というのです。
①まず有限算術数列(Finite arithmetic Sequence)の総和(sum)S(1~n)[係数n]=初項a+a[1]+a[2]+a[3]…a[n]における公差dを巡る計算順序を入れ替えて以下の式を構成する。
- 式A…S(1~n)[n]=a+(a+1d)+(a+2d)+(a+3*d)…(a+(n-1)*d)
- 式B…S(1~n)[n]=a[n]+(a[n]-1d)+(a+2d)+(a+3*d)…(a+(n-1)*d)
②この2式を両辺で項ごとに足し合わせる。
- 左辺…2*S(1~n)[n]
- 右辺…各項で公差dを含む成分がすべて相殺されて初項a[1]と末項a[n]の和だけが残り、これがn項続く。
- 従って答えは_2S[n] = n(a[1] + a[n])_。
- 両辺を2で割れば_S[n]=n(a[1]+a[n])/2=n(2*a[1]+(n-1)d)/2_。
# 有限算術数列c0(n=1~100)の生成
c0=c(1:100)
c0
[1] 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38
[39] 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76
[77] 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100
# 係数nの確認
length(c0)
[1] 100
# 初項a[1]の確認
c0[1]
[1] 1
# 末項a[n]の確認
c0[length(c0)]
[1] 100
# 総和(sum)の計算(公差1のケース)
c0[length(c0)]*(2*c0[1]+(length(c0)-1)*1)/2
[1] 5050
100*(2*1+(100-1)*1)/2
[1] 5050
100*101/2
[1] 5050
# sum関数による答え合わせ
sum(c0)
[1] 5050
# 算術平均(arithmetic mean)S[n]/nの計算
(c0[1]+c0[length(c0)])/2
[1] 50.5
# mean関数による答え合わせ
mean(c0)
[1] 50.5
自然数(Natural)、整数(Integer)、偶数(Even)、奇数(Odd)、そして片側無限算術数列(One-Sided Infinite Arithmetic Sequence)と両側無限算術数列(Two-Sided Infinite Arithmetic Sequence)。
上掲の表現(Explession)を用いると、以下の単調数列(Monotonic Sequence)が自明の場合(Torivial Case)としてそれぞれこの様に表現されます。
- 自然数(Natural)N[n]={1,2,3…,1+(n-1)*1}…区間1~無限大Inf、初項1、公差1、一般項1+(n-1)*1
- 整数(Integer)Z[n]={0-(n-1)*1,…,-3,-2,-1,0,1,2,3,…1+(n-1)*1}…区間無限小-Inf~0~無限大Inf、初項0、公差±1、一般項0±(n-1)*1
- 偶数(Even)e[n]={-2n,…-6,-4,-2,0,2,4,6,…2n}…区間無限小-Inf~0~無限大Inf、初項0、公差±2、一般項±2n
- 奇数(Odd)o[n]={2n-1,…-5,-3,-1,1,3,5,…2n+1}…区間無限小-Inf~0~無限大Inf、初項0、公差±2、一般項±2n±1
自然数の様に片側の端点(End Point)のみが無限大Infもしくは無限小-Infに開き(open)、もう片側が閉じた(closed)半開区間(Semi-Open Interval)で仕切られた算術数列を片側無限算術数列(One-Sided Infinite Arithmetic Sequence)、整数や偶数や奇数の様に初項0を中心に無限大Infと無限小-Infに挟まれた開区間(Open Interval)で仕切られた算術数列を両側無限算術数列(Two-Sided Infinite Arithmetic Sequence)と呼びますが、その振る舞いは公差dの符号の向き(Sign direction)によって定まるのです。
- dの符号が正(plus)ならば、その数列の項(term)は増加数列(Increasing Sequence)を構成し無限大Infに発散(divergence)する。
- dの符号が負(minus)ならば、その数列の項(term)は減少数列(Decreasing Sequence)を構成し無限小-Infに発散(divergence)する。
ところで コンピューター言語は原則として無限大Infや無限小-Infを直接は扱ません(例外的に扱う場合も、概ね図示は困難)。そこでここでは数直線(Number Line)上の-5~0~5近辺を区間(Interval)と定めての実装を試みる事にします。
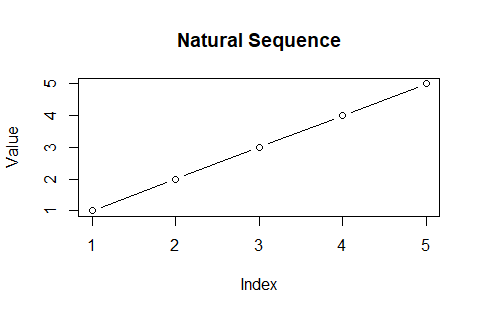
①自然数列(Natural Sequence)N[n]={1,2,3…,1+(n-1)*1}(ただしnは0以上の整数)…数列(sequence)a[m]の順番(order)=添字(Index)mがそれ自身、すなわち自然数集合(set of natulal numbers)Nによって与えられ、その範囲では添字とその値(Value)が一致する。
# 代数ライブラリYACASを用いた表現。
library(Ryacas)
yacas("Table(n,n,1,5,1)")
Yacas vector:
[1] 1 2 3 4 5
# 標準搭載関数seqを用いた表現
c0<-seq(1L,5L,by=1L)
c0
[1] 1 2 3 4 5
表の出力
library(xtable)
N0<- data.frame(Index=c0, Value=c0)
print(xtable(N0),type="html")
| Index | Value | |
|---|---|---|
| 1 | 1 | 1 |
| 2 | 2 | 2 |
| 3 | 3 | 3 |
| 4 | 4 | 4 |
| 5 | 5 | 5 |
plot(N0$Index,N0$Value,type="b",main="Natural Sequence",xlab="Index",ylab="Value")
②整数数列(Integer Sequance)Z[n]={0-(n-1)*1,…,-3,-2,-1,0,1,2,3,…1+(n-1)*1}(ただしnは0以上の整数)…自然数集合Nを添字として用い続ける場合、0や負数概念の導入によって順番と係数が一致しなくなる。ただし概ね同時に添字も整数集合(set of ineger numbers)にバージョンアップされ、その範囲で添字とその値が一致する。
# 代数ライブラリYACASを用いた表現。
library(Ryacas)
yacas("Table(n,n,-5,5,1)")
Yacas vector:
[1] -5 -4 -3 -2 -1 0 1 2 3 4 5
# 標準搭載関数seqを用いた表現
c0<-seq(-5L,5L,by=1L)
c0
[1] -5 -4 -3 -2 -1 0 1 2 3 4 5
表の出力
library(xtable)
Z0<- data.frame(Index=c0, Value=c0)
print(xtable(Z0),type="html")
| Index | Value | |
|---|---|---|
| 1 | -5.00 | -5.00 |
| 2 | -4.00 | -4.00 |
| 3 | -3.00 | -3.00 |
| 4 | -2.00 | -2.00 |
| 5 | -1.00 | -1.00 |
| 6 | 0.00 | 0.00 |
| 7 | 1.00 | 1.00 |
| 8 | 2.00 | 2.00 |
| 9 | 3.00 | 3.00 |
| 10 | 4.00 | 4.00 |
| 11 | 5.00 | 5.00 |
plot(Z0$Index,Z0$Value,type="b",main="Integer sequence",xlab="Index",ylab="Value")
abline(h = 0,col=c(200,200,200))
abline(v = 0,col=c(200,200,200))
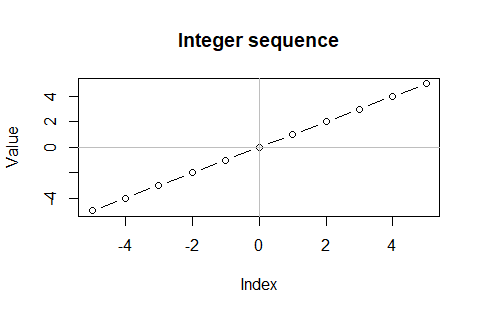
つまり自然数列は整数列の真部分集合(Proper Subset)として存在する。
【初心者向け】集合論①部分集合(subset)と真部分集合(proper subset)について。
③偶数列(Even Sequance)e[n]={-2n,…-6,-4,-2,0,2,4,6,…2n}…「-5~0~5近辺」なる曖昧表現を用いたのはこのケースを想定したから。
# 代数ライブラリYACASを用いた表現。
library(Ryacas)
yacas("Table(n,n,-6,6,2)")
Yacas vector:
[1] -6 -4 -2 0 2 4 6
# 標準搭載関数seqを用いた表現
c0<-seq(-6L,6L,by=2L)
c0
[1] -6 -4 -2 0 2 4 6
表の出力
library(xtable)
Even0<- data.frame(Index=c0, Value=c0)
print(xtable(Even0),type="html")
| Index | Value | |
|---|---|---|
| 1 | -6 | -6 |
| 2 | -4 | -4 |
| 3 | -2 | -2 |
| 4 | 0 | 0 |
| 5 | 2 | 2 |
| 6 | 4 | 4 |
| 7 | 6 | 6 |
plot(Even0$Index,Even0$Value,type="b",main="Even sequence",xlab="Index",ylab="Value")
abline(h = 0,col=c(200,200,200))
abline(v = 0,col=c(200,200,200))
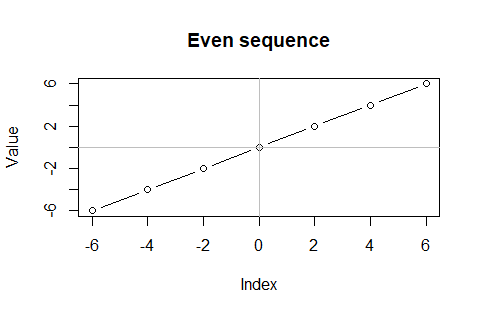
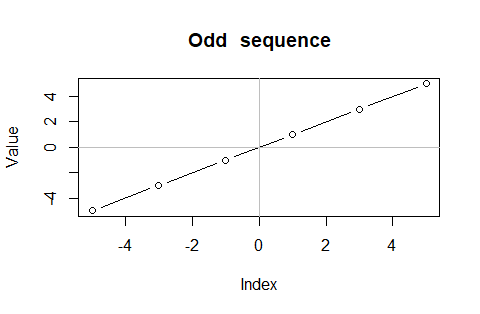
④奇数列(Odd Sequance)o[n]={2n-1,…-5,-3,-1,1,3,5,…2n+1}…偶数列の一般項2nに対し、奇数列の一般項は2n±1という関係。
# 代数ライブラリYACASを用いた表現。
library(Ryacas)
yacas("Table(n,n,-5,5,2)")
Yacas vector:
[1] -5 -3 -1 1 3 5
# 標準搭載関数seqを用いた表現
c0<-seq(-5L,5L,by=2L)
c0
[1] -5 -3 -1 1 3 5
表の出力
library(xtable)
Odd0<- data.frame(Index=c0, Value=c0)
print(xtable(Odd0),type="html")
| Index | Value | |
|---|---|---|
| 1 | -5 | -5 |
| 2 | -3 | -3 |
| 3 | -1 | -1 |
| 4 | 1 | 1 |
| 5 | 3 | 3 |
| 6 | 5 | 5 |
plot(Odd0$Index,Odd0$Value,type="b",main="Odd sequence",xlab="Index",ylab="Value")
abline(h = 0,col=c(200,200,200))
abline(v = 0,col=c(200,200,200))
つまり偶数列と奇数列は整数列の真部分集合(Proper Subset)として存在する。
【初心者向け】集合論①部分集合(subset)と真部分集合(proper subset)について。
片側無限数列(One-Sided Infinite Sequence)の発散(divergence)
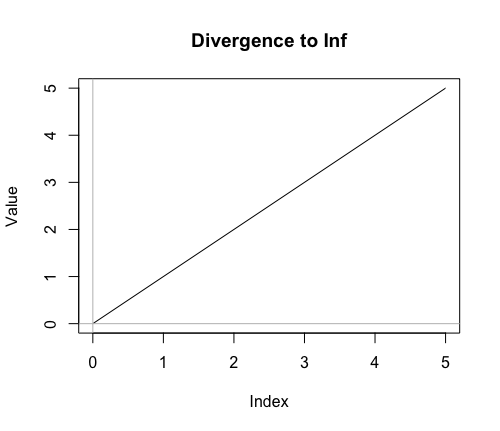
公差dの符号が正(plus)ならば、その数列の項(term)は片側無限増加数列(One-side Infinity Increasing Sequence)を構成し無限大Infに発散する。
c0<-seq(0,5,by=1)
PD0<- data.frame(Index=c0, Value=c0)
plot(PD0$Index,PD0$Value,type="l",main="Divergence to Inf",xlab="Index",ylab="Value")
abline(h = 0,col=c(200,200,200))
abline(v = 0,col=c(200,200,200))
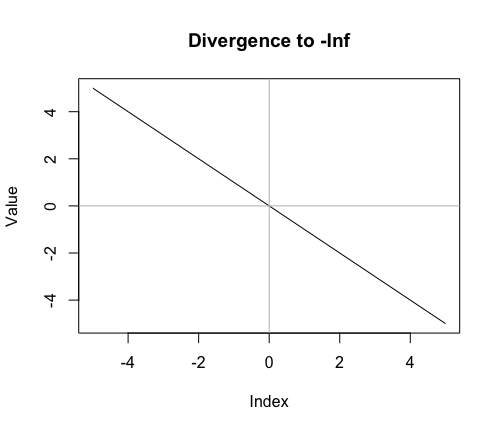
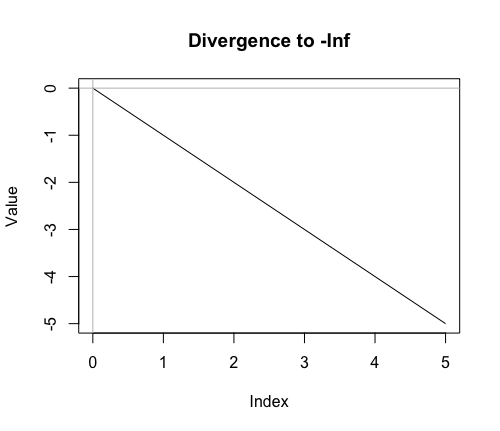
公差dの符号が負(plus)ならば、その数列の項(term)は片側無限減少数列(One-side Infinity Decreasing Sequence)を構成し無限小-Infに発散する。
c0<-seq(0,5,by=1)
PD0<- data.frame(Index=c0, Value=-c0)
plot(PD0$Index,PD0$Value,type="l",main="Divergence to -Inf",xlab="Index",ylab="Value")
abline(h = 0,col=c(200,200,200))
abline(v = 0,col=c(200,200,200))
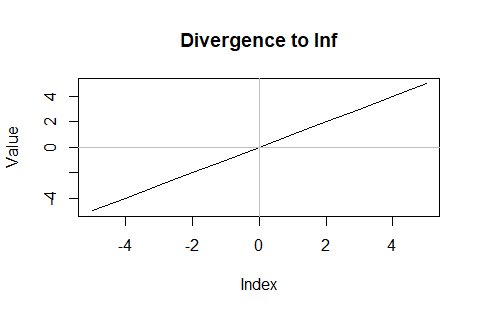
両側無限増加数列(Two-Sided Infinite Decreasing Sequence)の発散(divergence)
それぞれ0を初項とする公差マイナスの片側無限増加数列(One-side Infinite Increasing Sequence)(範囲-Inf~0)と公差の値は同じで符号が逆の片側無限減少数列(One-side Infinite Decreasing Sequence)(範囲0~Inf)のセット(Set)。
c0<-seq(-5,5,by=1)
PD0<- data.frame(Index=c0, Value=c0)
plot(PD0$Index,PD0$Value,type="l",main="Divergence to Inf",xlab="Index",ylab="Value")
abline(h = 0,col=c(200,200,200))
abline(v = 0,col=c(200,200,200))
両側無限減少数列(Two-Sided Infinite Decreasing Sequence)の発散(divergence)
それぞれ0を初項とする公差プラスの片側無限減少数列(One-side Infinite Decreasing Sequence)(範囲-Inf~0)と公差の値は同じで符号が逆の片側無限減少数列(One-side Infinite Decreasing Sequence)(範囲0~Inf)のセット(Set)。
ただし、統計言語Rの標準関数Seq(St(始点),Ed(終点),by=Def(公差))には以下の制約があります。
- Def(公差)の値がマイナスを取れない。
- Def(公差)=0がエラーとならないのはSt(始点)=Ed(終点)の場合のみ。
従って与えられた条件をそのままの形では実装出来ません。
cx<-c(-5:5)
cy<-c(5:-5)
ND0<- data.frame(Index=cx, Value=cy)
plot(ND0$Index,ND0$Value,type="l",main="Divergence to -Inf",xlab="Index",ylab="Value")
abline(h = 0,col=c(200,200,200))
abline(v = 0,col=c(200,200,200))
直交座標系(Rectangular Coordinate System / Orthogonal Coordinate System)への道
互いに直交する座標軸を指定することによって定まる直交座標系を興成する各座標軸がしばしば半直線(Half Straight Line)として扱われるのは、この様に等しく0を原点とし、発散の向きのみが逆の片側無限数列のセットと考えた方が何かと都合が良いからです。
受験問題で延々と有限算術数列(Finite arithmetic sequence)に取り組まされてきたせいですっかり見逃してしまっていましたが、実は一番の勘所はここだったとも。
【Rで球面幾何学】等差数列(算術数列)②数直線(Number Line)概念から同心円集合(Concentric Set)概念へ