【初心者向け】複素共役（Complex Conjugate）のアニメーション表示について。

(2020年11月21日)Rによる投稿。
掲題の複素共役（複素共軛, Complex Conjugate）のアニメーション表示については、以前の投稿でこう実装した事もあります。

#RD=2角形（Regular Digon）
#Radian=角度（60分割）
RD<-function(Radian){
cx<-seq(-1,1,length=60)
f0<-function(x) sqrt(1-x^2)
cy<-f0(cx)
plot(cx,cy,asp=1,type="l",col=rgb(0,1,0),xlim=c(-1,1),ylim=c(-1,1),main="Complex Conjugate",xlab="X",ylab="sqrt(1-X^2) & -sqrt(1-X^2)")

par(new=T)#上書き指定

plot(cx,-1*cy,asp=1,type="l",col=rgb(1,0,0),xlim=c(-1,1),ylim=c(-1,1),main="",xlab="",ylab="")

#緯度(latitude)の描写
lat<-seq(-1,1,length=9)

for(i in lat){
segments(i,f0(i),i,-f0(i),col=c(200,200,200))
}

#経度（Longitude）の描写
lon<-seq(-pi/2,pi/2,length=9)
for(i in lon){

par(new=T)#上書き指定

plot(cx,sin(i)*cy,asp=1,type="l",col=c(200,200,200),xlim=c(-1,1),ylim=c(-1,1),main="",xlab="",ylab="")
}
#塗りつぶし

p_max<-15
p0<-seq(pi,0,length=p_max)
px_Hi<-rev(cos(p0))
px_Low<-rev(cos(p0*-1))
py_Hi<-rev(sin(p0))
py_Low<-rev(sin(p0*-1))

#左側インジケータ描画（緑）
polygon(c(px_Hi[1:Radian],px_Low[Radian:1]), #x
c(py_Hi[1:Radian],py_Low[Radian:1]), #y
density=c(30), #塗りつぶす濃度
angle=c(45),　 　　　#塗りつぶす斜線の角度
col=rgb(0,1,0)) 　#塗りつぶす色
#右側インジケータ描画（赤）
polygon(c(px_Hi[p_max:Radian],px_Low[Radian:p_max]), #x
c(py_Hi[p_max:Radian],py_Low[Radian:p_max]), #y
density=c(30), #塗りつぶす濃度
angle=c(45),　 　　　#塗りつぶす斜線の角度
col=rgb(1,0,0)) 　#塗りつぶす色
}
#アニメーション
library("animation")
Time_Code=c(1:15,14:1)
saveGIF({
for (i in Time_Code){
　RD(i)
}
}, interval = 0.1, movie.name = "RD01.gif")

しかしながら以下の投稿によって「観測者問題(ある種の錯視問題)」が浮上してきたので再チャレンジの必要が生じてしまったのです。
【初心者向け】「観測者問題」のあっけない解決方法? - Qiita

x軸に沿った展開。

要するにCos(θ)+Sin(θ)iの場合ですね。まずはアニメーションさせる関数を準備します。

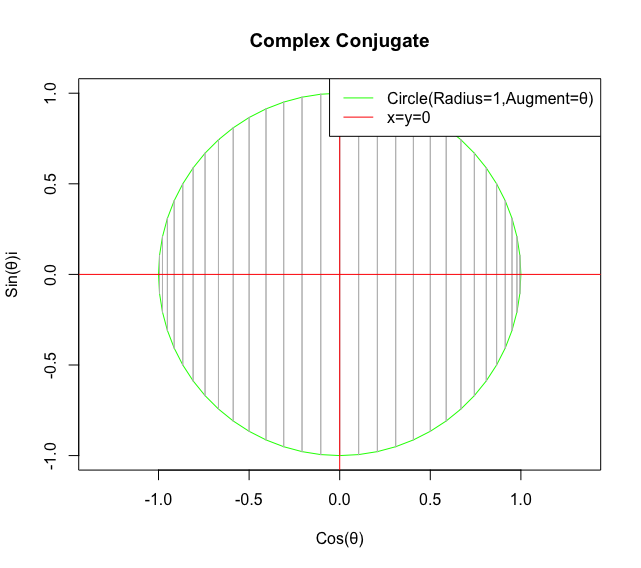
conjugate00<-function(inbetween){

c0<-seq(0,pi*2,length=61)
cx<-cos(c0)
cy<-sin(c0)

plot(cx,cy,type="l",xlim=c(-1,1),asp=1,ylim=c(-1,1),main="Complex Conjugate",xlab="Cos(θ)",ylab="Sin(θ)i", col=rgb(0,1,0))

#複素共役を結ぶ補助線(座標の半分しか使わない)
segments(cos(c0[2:30]+inbetween),sin(c0[2:30]+inbetween),cos(c0[2:30]+inbetween),-sin(c0[2:30]+inbetween),col=c(200,200,200,200))

abline(h=0,col=rgb(1,0,0))
abline(v=0,col=rgb(1,0,0))

# 凡例を書き添える 。
legend("topright", legend=c("Circle(Radius=1,Augment=θ)","x=y=0"), lty =c(1,1),col=c(rgb(0,1,0),rgb(1,0,0)))
}

conjugate00(0)

アニメーション化(x=+1→-1、中割り二枚)

#アニメーション
library("animation")
Time_Code=c(0,pi/90,pi*2/90,0,pi/90,pi*2/90,0,pi/90,pi*2/90,0,pi/90,pi*2/90)

saveGIF({
for (i in Time_Code){
　conjugate00(i)
}
}, interval = 0.1, movie.name = "conjugateX_forward.gif")

アニメーション化(-1→+1、中割り二枚)

#アニメーション
library("animation")
Time_Code=c(0,2*pi/90,pi/90,0,2*pi/90,pi/90,0,2*pi/90,pi/90,0,2*pi/90,pi/90)
saveGIF({
for (i in Time_Code){
　conjugate00(i)
}
}, interval = 0.1, movie.name = "conjugateX_back.gif")

アニメーション化(どちらにも見える、中割り一枚)

#アニメーション
library("animation")
Time_Code=c(0,pi/60,0,pi/60,0,pi/60,0,pi/60)
saveGIF({
for (i in Time_Code){
　conjugate00(i)
}
}, interval = 0.1, movie.name = "conjugateX_even.gif")

そもそも複素共役には「回転の向き」についての情報が欠落してますから、最後の見え方こそが正解なんですね。

y軸に沿った展開。

今度はSin(θ)+Cos(θ)iの場合ですね。やはりアニメーションさせる関数を準備します。

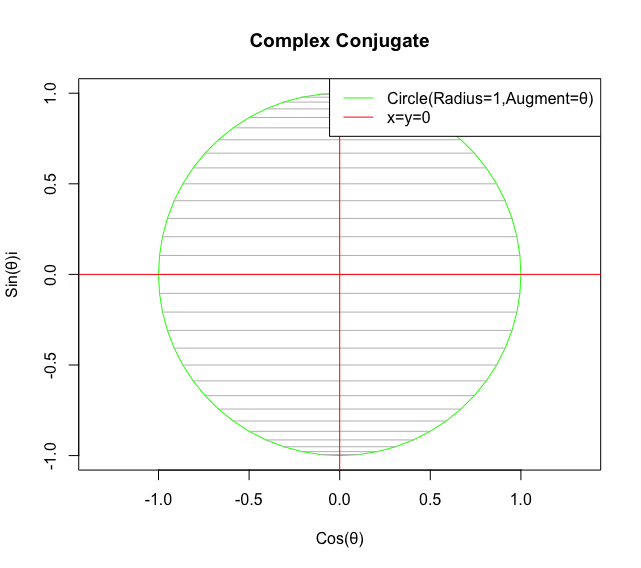
conjugate01<-function(inbetween){

c0<-seq(0,pi*2,length=61)
c1<-seq(pi/2,2*pi+pi/2,length=61)
cx<-cos(c0)
cy<-sin(c0)

plot(cx,cy,type="l",xlim=c(-1,1),asp=1,ylim=c(-1,1),main="Complex Conjugate",xlab="Cos(θ)",ylab="Sin(θ)i", col=rgb(0,1,0))

#複素共役を結ぶ補助線(座標の半分しか使わない)

segments(cos(c1[2:30]+inbetween),sin(c1[2:30]+inbetween),-cos(c1[2:30]+inbetween),sin(c1[2:30]+inbetween),col=c(200,200,200,200))

abline(h=0,col=rgb(1,0,0))
abline(v=0,col=rgb(1,0,0))

# 凡例を書き添える 。
legend("topright", legend=c("Circle(Radius=1,Augment=θ)","x=y=0"), lty =c(1,1),col=c(rgb(0,1,0),rgb(1,0,0)))
}

conjugate01(0)

アニメーション化(y=+1→-1、中割り二枚)

#アニメーション
library("animation")
Time_Code=c(0,pi/90,2*pi/90,0,pi/90,2*pi/90,0,pi/90,2*pi/90,0,pi/90,2*pi/90)
saveGIF({
for (i in Time_Code){
　conjugate01(i)
}
}, interval = 0.1, movie.name = "conjugateY_back.gif")

アニメーション化(y=-1→+1、中割り二枚)

#アニメーション
library("animation")
Time_Code=c(0,2*pi/90,pi/90,0,2*pi/90,pi/90,0,2*pi/90,pi/90,0,2*pi/90,pi/90)

saveGIF({
for (i in Time_Code){
　conjugate01(i)
}
}, interval = 0.1, movie.name = "conjugateY_forward.gif")

アニメーション化(どちらにも見える、中割り一枚)

#アニメーション
library("animation")
Time_Code=c(0,pi/60,0,pi/60,0,pi/60,0,pi/60)
saveGIF({
for (i in Time_Code){
　conjugate01(i)
}
}, interval = 0.1, movie.name = "conjugateY_even.gif")

そう、複素共役は別に軸線に縛られた概念ではないのです。我々が概ね数直線(Number Line)とイメージしている概念の正体が、実は同心円集合(Concentric Circle Set)/同心球面集合(Homocentric Sphere Set)に過ぎない様に…


直線y=0を軸線に選ぶとxの値が+1から-1(-1から+1)にかけて推移するのに対して、yの値は決して0以下(0以上)にならない。見え方としては反時計回り。

これは円関数集合(Circle Function Set)でいうとCos(θ)+Sin(θ)iに該当する。

直線x=0を軸線に選ぶとyの値が+1から-1(-1から+1)にかけて推移するのに対して、xの値は決して0以下(0以上)にならない。見え方としては時計回り。

これは円関数集合(Circle Function Set)でいうとSin(θ)+Cos(θ)iに該当する。

という事は…

そして僕は途方に暮れる。

それでは同時に再生してみましょう。アニメーションさせる関数は以下。

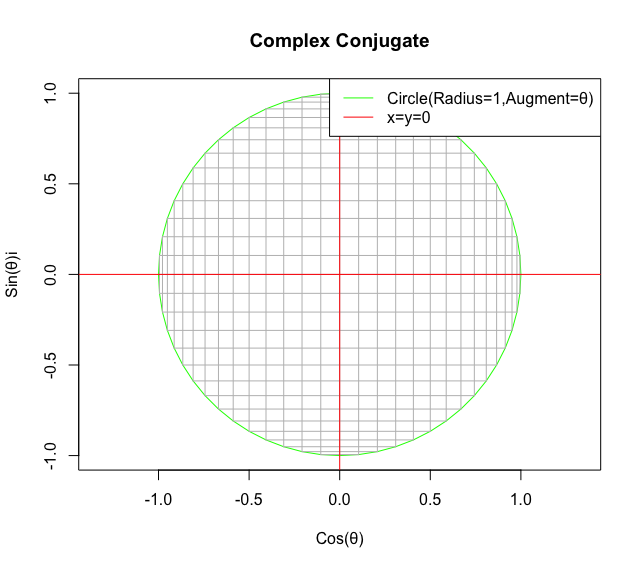
conjugate02<-function(inbetween){

c0<-seq(0,pi*2,length=61)

c1<-seq(pi/2,2*pi+pi/2,length=61)
cx<-cos(c0)
cy<-sin(c0)

plot(cx,cy,type="l",xlim=c(-1,1),asp=1,ylim=c(-1,1),main="Complex Conjugate",xlab="Cos(θ)",ylab="Sin(θ)i", col=rgb(0,1,0))

#複素共役を結ぶ補助線(座標の半分しか使わない)
segments(cos(c0[2:30]+inbetween),sin(c0[2:30]+inbetween),cos(c0[2:30]+inbetween),-sin(c0[2:30]+inbetween),col=c(200,200,200,200))

segments(cos(c1[2:30]+inbetween),sin(c1[2:30]+inbetween),-cos(c1[2:30]+inbetween),sin(c1[2:30]+inbetween),col=c(200,200,200,200))

abline(h=0,col=rgb(1,0,0))
abline(v=0,col=rgb(1,0,0))

# 凡例を書き添える 。
legend("topright", legend=c("Circle(Radius=1,Augment=θ)","x=y=0"), lty =c(1,1),col=c(rgb(0,1,0),rgb(1,0,0)))
}

conjugate02(0)

アニメーション化(x=y=+1→-1、中割り二枚)

#アニメーション
library("animation")
Time_Code=c(0,pi/90,2*pi/90,0,pi/90,2*pi/90,0,pi/90,2*pi/90,0,pi/90,2*pi/90)
saveGIF({
for (i in Time_Code){
　conjugate02(i)
}
}, interval = 0.1, movie.name = "conjugateXY_back.gif")

アニメーション化(x=y=-1→+1、中割り二枚)

#アニメーション
library("animation")
Time_Code=c(0,2*pi/90,pi/90,0,2*pi/90,pi/90,0,2*pi/90,pi/90,0,2*pi/90,pi/90)

saveGIF({
for (i in Time_Code){
　conjugate02(i)
}
}, interval = 0.1, movie.name = "conjugateXY_forward.gif")

アニメーション化(どちらにも見える、中割り一枚)

#アニメーション
library("animation")
Time_Code=c(0,pi/60,0,pi/60,0,pi/60,0,pi/60)
saveGIF({
for (i in Time_Code){
　conjugate02(i)
}
}, interval = 0.1, movie.name = "conjugateXY_even.gif")

なんじゃこりゃ〜!!(by 松田優作)
ジーパン刑事の「殉職シーン」は上下白のジーパンスタイル　セリフはすべてアドリブだった

• 目を凝らせば確かに「x軸に沿った展開」と「y軸に沿った展開」を抽出して目で追う事が出来る。
• だが本能が、これがあるべき「x軸に沿った展開」と「y軸に沿った展開」の合成結果ではないと必死に告げてくる。違和感が…違和感が仕事をする!!

「違和感仕事しろ」とは【ピクシブ百科事典】
そう、人間がつい期待してしまうのは、上掲図を「側面図」と見立てた場合の「正面図」に当たる何か。例えばこんな感じの…
【初心者向け】誤差関数(ERF=Error Function)と相補誤差関数 (ERFC=Complementary Error Function)。
アニメーション化(x=y=0→±1、中割り二枚)

アニメーション化(x=y=±1→0、中割り二枚)

アニメーション化(どちらにも見える、中割り一枚)

こういう見え方も存在します。辺縁部が観測原点(Observation Origin)を北極(Arctic)に置いた場合の南極(Antarctic)に該当する、すなわち重力レンズ効果で裏側まで見通せるブラックホールの見え方。ただし「裏側の景色(The Other Side of the World)」は事象の地平線(Event Horizon)に近過ぎてすっかり潰れてしまっているので「誤差(Error)」として視界から切り捨てられてしまうのです。
重力レンズ - Wikipedia
重力レンズとは

アニメーション化(x=y=0→±1、中割り二枚)

アニメーション化(x=y=±1→0、中割り二枚)

アニメーション化(どちらにも見える、中割り一枚)

何故教えてくれなかったんだ、ガウス!!
【無限遠点を巡る数理】無限遠点としての正規分布と分散概念の歴史 - Qiita

pythonによる実装

(2021年03月20日)Python部分の追加。
無駄に早いぞ、Python!!

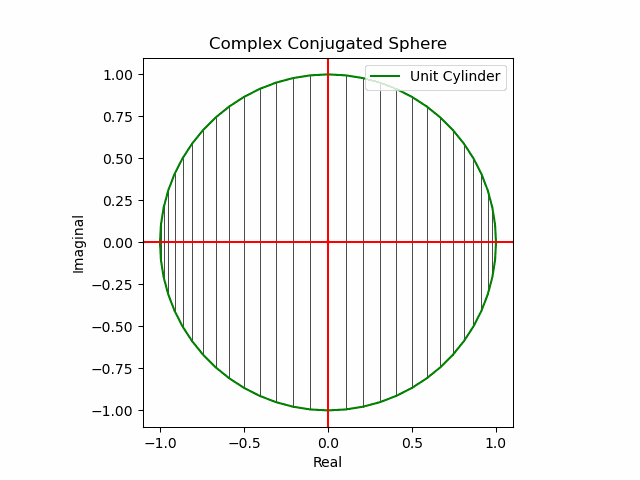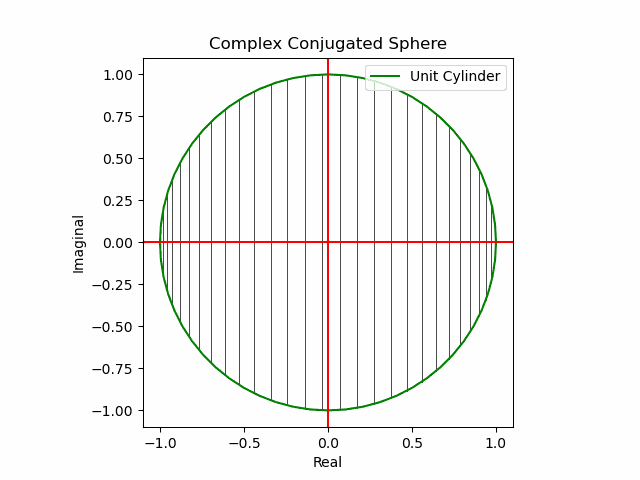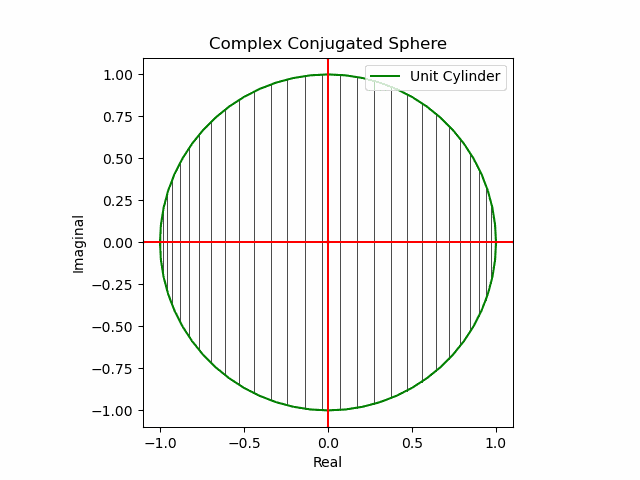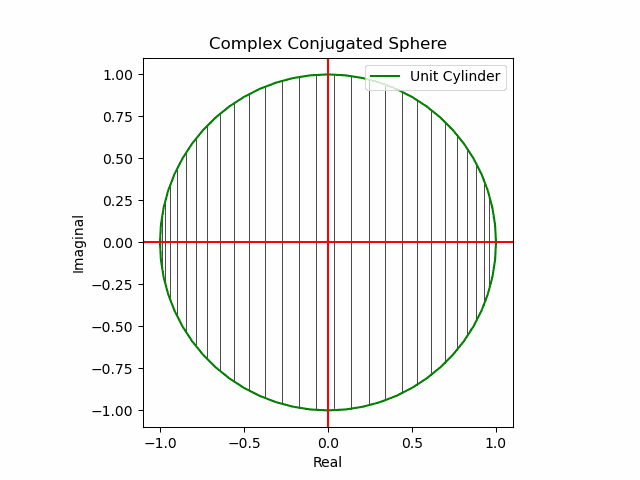
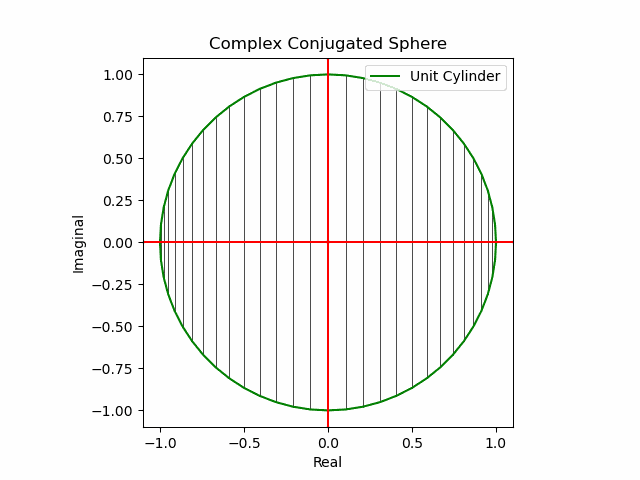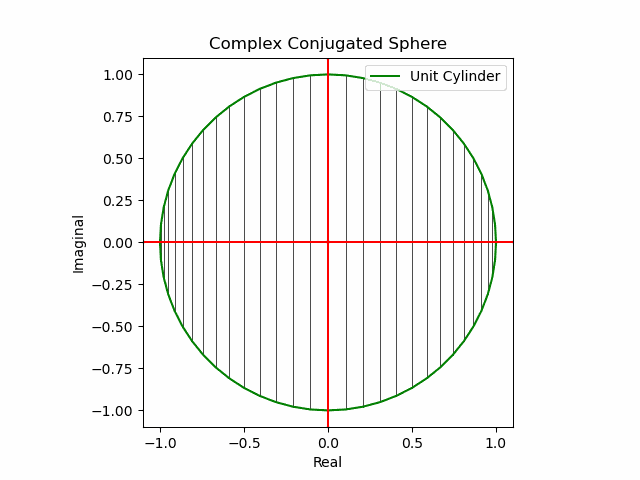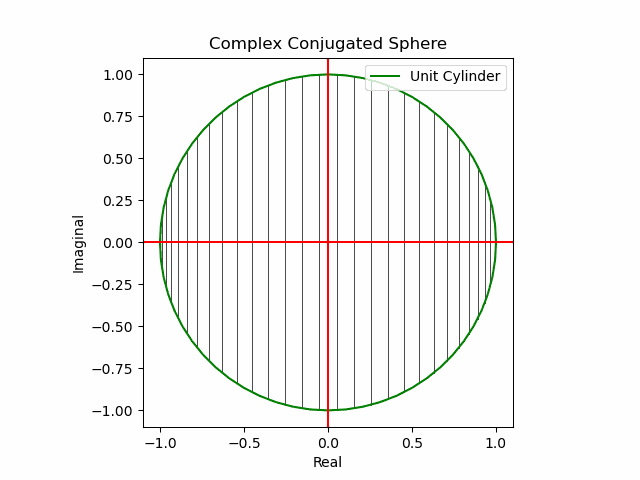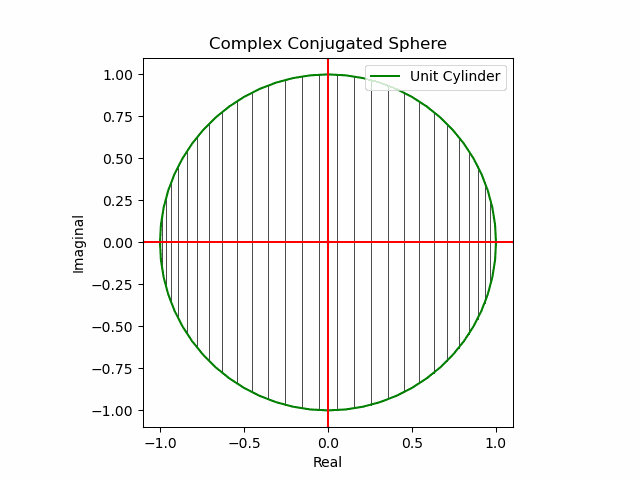
x軸に沿った展開(関数基本部)。

import math as m
import cmath as c
import numpy as num
import matplotlib.pyplot as plt
import matplotlib.animation as animation

#単位円データ作成
c0=num.linspace(0,2*m.pi,61,endpoint = True)
s0=[]
for nm in range(len(c0)):
    s0.append(complex(m.cos(c0[nm]),m.sin(c0[nm])))
s1=num.array(s0)

#複素共役データ作成

#描画準備
plt.style.use('default')
fig = plt.figure(111)

#関数定義
def Complex_Conjugated_Sphere(n):
    plt.cla()
    #共益線描画
    for nm in range(2,30):
        plt.plot([m.cos(c0[nm]+Time_code[n]),m.cos(c0[nm]+Time_code[n])],[m.sin(c0[nm]+Time_code[n]),-m.sin(c0[nm]+Time_code[n])],color="black",lw=0.5);    
    #円周描画
    plt.plot(s1.real,s1.imag,color="green", label="Unit Cylinder")

    plt.ylim([-1.1,1.1])
    plt.xlim([-1.1,1.1])
    plt.title("Complex Conjugated Sphere")
    plt.xlabel("Real")
    plt.ylabel("Imaginal")
    ax = fig.add_subplot()
    ax.set_aspect('equal', adjustable='box')
    ax.legend(loc='upper right')
    #補助線描画
    plt.axvline(0, 0, 1,color="red")
    plt.axhline(0, 0, 1,color="red")

アニメーション化(y=+1→-1、中割り二枚)

Time_code=[0,m.pi/90,2*m.pi/90,0,m.pi/90,2*m.pi/90,0,m.pi/90,2*m.pi/90,0,m.pi/90,2*m.pi/90]
ani = animation.FuncAnimation(fig, Complex_Conjugated_Sphere, interval=50,frames=len(Time_code))
ani.save("output112.gif", writer="pillow")

アニメーション化(x=y=-1→+1、中割り二枚)

Time_code=[0,2*m.pi/90,m.pi/90,0,2*m.pi/90,m.pi/90,0,2*m.pi/90,m.pi/90,0,2*m.pi/90,m.pi/90]
ani = animation.FuncAnimation(fig, Complex_Conjugated_Sphere, interval=50,frames=len(Time_code))
ani.save("output113.gif", writer="pillow")

アニメーション化(どちらにも見える、中割り一枚)

Time_code=[0,m.pi/60,0,m.pi/60,0,m.pi/60,0,m.pi/60]
ani = animation.FuncAnimation(fig, Complex_Conjugated_Sphere, interval=50,frames=len(Time_code))
ani.save("output111.gif", writer="pillow")

Y軸に沿った展開(関数基本部)。

import math as m
import cmath as c
import numpy as num
import matplotlib.pyplot as plt
import matplotlib.animation as animation

#単位円データ作成
c0a=num.linspace(0,2*m.pi,61,endpoint = True)
c0=num.concatenate([c0a[15:45],c0a[46:60],c0a[0:16]])
s0=[]
for nm in range(len(c0)):
    s0.append(complex(m.cos(c0[nm]),m.sin(c0[nm])))
s1=num.array(s0)

#複素共役データ作成

#描画準備
plt.style.use('default')
fig = plt.figure(111)

#関数定義
def Complex_Conjugated_Sphere(n):
    plt.cla()
    #共益線描画
    for nm in range(2,30):
        plt.plot([m.cos(c0[nm]+Time_code[n]),-m.cos(c0[nm]+Time_code[n])],[m.sin(c0[nm]+Time_code[n]),m.sin(c0[nm]+Time_code[n])],color="black",lw=0.5);    
    #円周描画
    plt.plot(s1.real,s1.imag,color="green", label="Unit Cylinder")

    plt.ylim([-1.1,1.1])
    plt.xlim([-1.1,1.1])
    plt.title("Complex Conjugated Sphere")
    plt.xlabel("Real")
    plt.ylabel("Imaginal")
    ax = fig.add_subplot()
    ax.set_aspect('equal', adjustable='box')
    ax.legend(loc='upper right')
    #補助線描画
    plt.axvline(0, 0, 1,color="red")
    plt.axhline(0, 0, 1,color="red")

アニメーション化(y=+1→-1、中割り二枚)

Time_code=[0,m.pi/90,2*m.pi/90,0,m.pi/90,2*m.pi/90,0,m.pi/90,2*m.pi/90,0,m.pi/90,2*m.pi/90]
ani = animation.FuncAnimation(fig, Complex_Conjugated_Sphere, interval=50,frames=len(Time_code))
ani.save("output116.gif", writer="pillow")

アニメーション化(x=y=-1→+1、中割り二枚)

Time_code=[0,2*m.pi/90,m.pi/90,0,2*m.pi/90,m.pi/90,0,2*m.pi/90,m.pi/90,0,2*m.pi/90,m.pi/90]
ani = animation.FuncAnimation(fig, Complex_Conjugated_Sphere, interval=50,frames=len(Time_code))
ani.save("output116.gif", writer="pillow")

アニメーション化(どちらにも見える、中割り一枚)

Time_code=[0,m.pi/60,0,m.pi/60,0,m.pi/60,0,m.pi/60]
ani = animation.FuncAnimation(fig, Complex_Conjugated_Sphere, interval=50,frames=len(Time_code))
ani.save("output114.gif", writer="pillow")

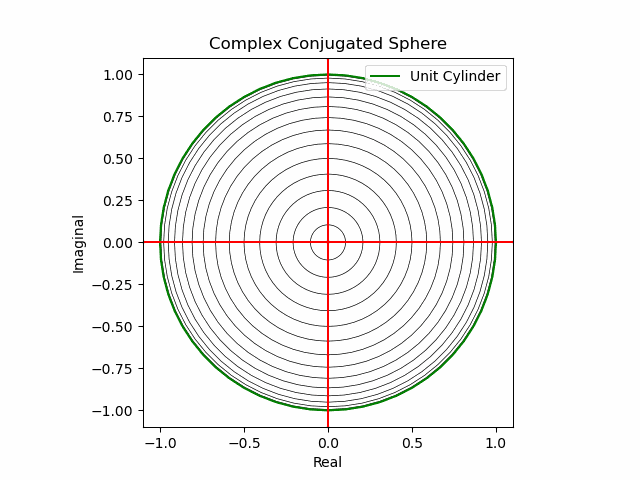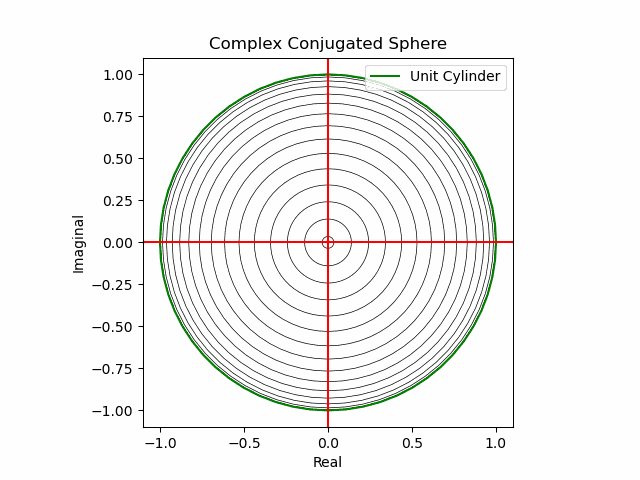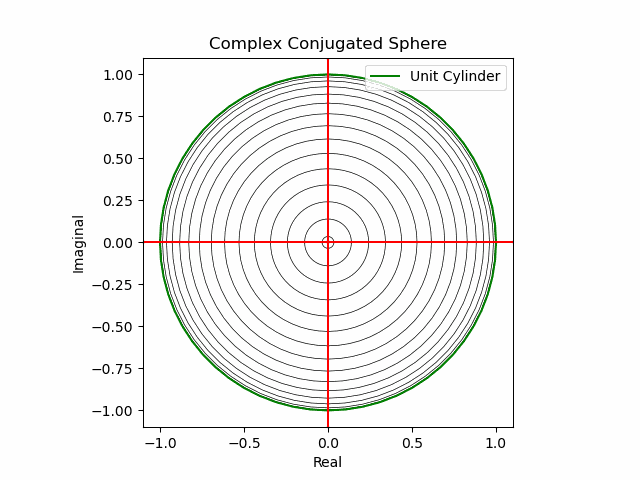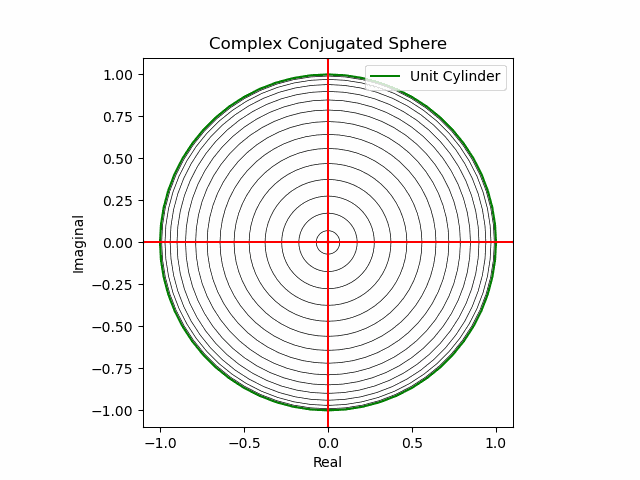
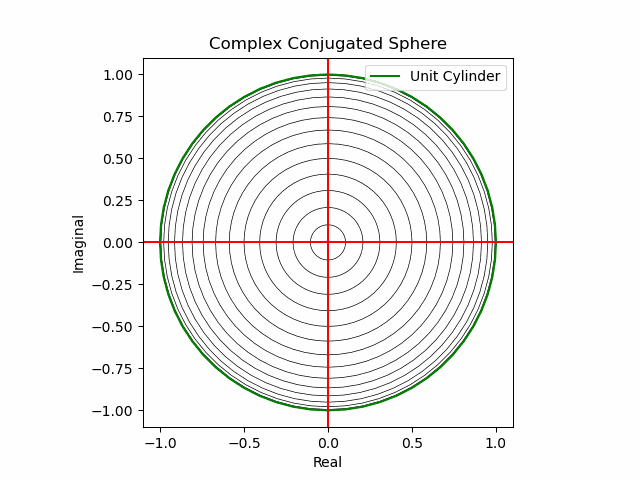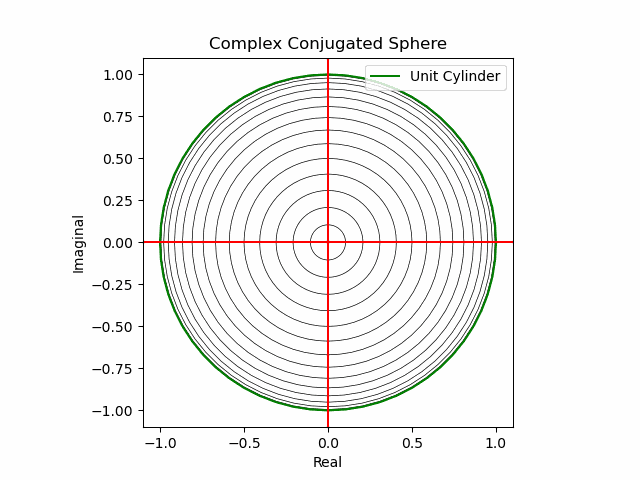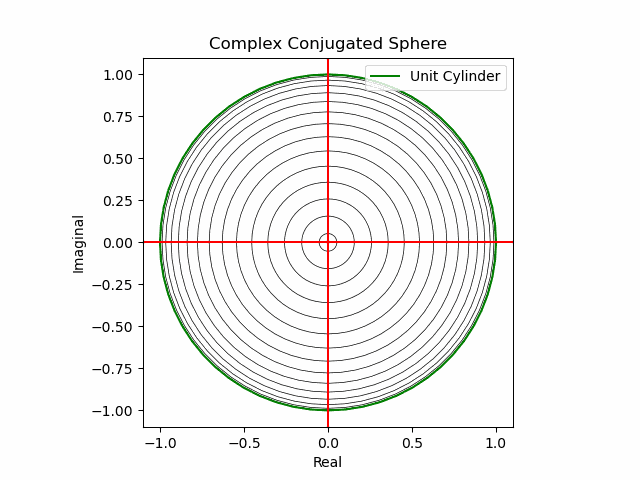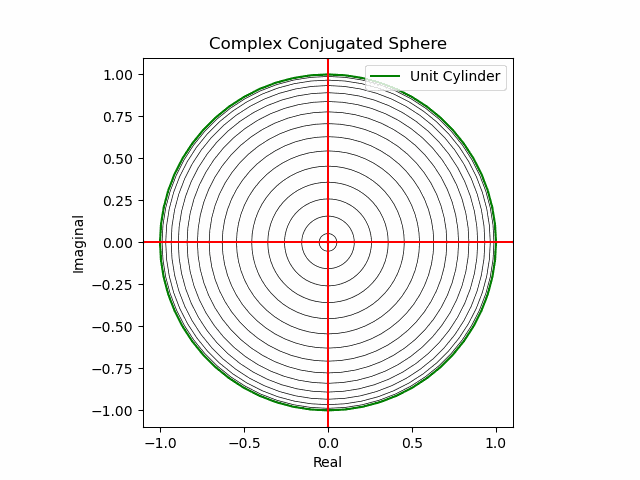
XY軸に沿った同心円展開(関数基本部)。

import math as m
import cmath as c
import numpy as num
import matplotlib.pyplot as plt
import matplotlib.animation as animation

#単位円データ作成
c0=num.linspace(0,2*m.pi,61,endpoint = True)
s0=[]
for nm in range(len(c0)):
    s0.append(complex(m.cos(c0[nm]),m.sin(c0[nm])))
s1=num.array(s0)

#複素共役データ作成

#描画準備
plt.style.use('default')
fig = plt.figure(111)

#関数定義
def sin_scale(x):
    return ((0+1j)**(2*x)).imag
def Complex_Conjugated_Sphere(n):
    plt.cla()
    #共益線描画
    z0=num.linspace(0,1/2,16)
    for nm in z0:
        plt.plot(s1.real*sin_scale(nm+Time_code[n]),s1.imag*sin_scale(nm+Time_code[n]),color="black",lw=0.5);    
    #円周描画
    plt.plot(s1.real,s1.imag,color="green", label="Unit Cylinder")

    plt.ylim([-1.1,1.1])
    plt.xlim([-1.1,1.1])
    plt.title("Complex Conjugated Sphere")
    plt.xlabel("Real")
    plt.ylabel("Imaginal")
    ax = fig.add_subplot()
    ax.set_aspect('equal', adjustable='box')
    ax.legend(loc='upper right')
    #補助線描画
    plt.axvline(0, 0, 1,color="red")
    plt.axhline(0, 0, 1,color="red")

アニメーション化(内側→外側、中割り二枚)

Time_code=[0,1/90,2/90,0,1/90,2/90,0,1/90,2/90,0,1/90,2/90]
ani = animation.FuncAnimation(fig, Complex_Conjugated_Sphere, interval=50,frames=len(Time_code))
ani.save("output122.gif", writer="pillow")

アニメーション化(外側→内側、中割り二枚)

Time_code=[0,2/90,1/90,0,2/90,1/90,0,2/90,1/90,0,2/90,1/90]
ani = animation.FuncAnimation(fig, Complex_Conjugated_Sphere, interval=50,frames=len(Time_code))
ani.save("output123.gif", writer="pillow")

アニメーション化(どちらにも見える、中割り一枚)

Time_code=[0,1/60,0,1/60,0,1/60,0,1/60,0,1/60,0,1/60]
ani = animation.FuncAnimation(fig, Complex_Conjugated_Sphere, interval=50,frames=len(Time_code))
ani.save("output121.gif", writer="pillow")

そんな感じで以下続報…