(2021年02月27日)投稿
(2021年04月13日)pythonによる実装の追記。
以下は下記の概念のささやかなサブセット(部分集合)とも思えるのですが、現代数学の用語は難し過ぎてまるで頭に入ってきません。
完全加法族 - Wikipedia
実数の集合論の基礎の基礎
なので今はある種の作業仮説として自分なりの言葉でまとめ、それを独自の方法で発展させていくしかありません。もしかしたら最終的には既存の数理のどれかに発展的解消を遂げるのかもしれませんが、少なくともその段階に到達するまでは迂闊に特定の既存概念によって強引な説明をつける事は避けたいのです。
実数族(Real Famiry)の定義。
とりあえず「(特定の数直線=座標軸上に存在し得る)あらゆる数」を元(Elemennt)と置く。逆を言えば、この条件を満たさないのが虚数集合(Imaginal Set)という事になる。
1.整数族(Integer Famiry)の定義。
整数集合(Integer Set)=小数点以下を含まず離散的に存在する整数の両側無限数列(Both Sides Infinity Sequance)を元(Element)とする。これに下属する(部分集合として成立する)演算結果集合(Operation Result Set)は、それぞれ以下の等差数列(Arithmetic Progression)表現(Explession)によって表される。
1.1.自然数集合(Natulal Set)の定義
演算結果集合としては区間:1~無限大$\infty$、初項1、公差1、一般項1+n(n-1)の片側無限数列(One Side Infinity Sequance)を構成する。
N_n(n=1→\infty)=(1+0=1,1+1=2,1+1×2=3,…,1+n(n-1),…,\infty)
Rによる実装例
natural<-function(x) 1+(x-1)*1
c0<-1:9
# 結果
> c0
[1] 1 2 3 4 5 6 7 8 9
> natural(c0)
[1] 1 2 3 4 5 6 7 8 9
pythonによる実装例
import numpy as np
def Natural(x):
return 1+(x-1)*1
c0=np.arange(1,10,1)
print(c0)
print(Natural(c0))
# 出力結果
[1 2 3 4 5 6 7 8 9]
[1 2 3 4 5 6 7 8 9]
- 漸化式(Recurrence Relation=再帰関係式)で考える場合は以下。
N_n(n=1→\infty)=(1,1+1=2,(1+1)+1=3,…,\infty)
Rによる実装例
natural<-function(x,n){
if (x==0) return(n)
else x=x1;n=n+1;print(paste("x=",x,"n=",n));return(Recall(x,n))}
# 出力結果
> natural(5,0)
[1] "x= 4 n= 1"
[1] "x= 3 n= 2"
[1] "x= 2 n= 3"
[1] "x= 1 n= 4"
[1] "x= 0 n= 5"
[1] 5
Pythonによる実装例
import numpy as np
def natural(x,n):
if x==0: return n
else:
x=x-1
n=n+1
print('x:{0}, n:{1}'.format(x, n))
return natural(x,n)
print(natural(5,0))
# 出力結果
x:4, n:1
x:3, n:2
x:2, n:3
x:1, n:4
x:0, n:5
5
- その演算は結合法則(a+b)+c=a+(b+c)を満たし、加算方向には閉じているものの、減算方向には閉じてない(計算結果が集合範囲外の0以下にはみ出し得る)さらには単位元も逆元も持たない為、群の定義は満たさない。
- 整数同様、最も代表的な添字集合(Indexed Set)の一つであり、増減を測る際の周期単位(Unit Cycle)の倍数たる周回数(Number of laps)の表示にも使われる。
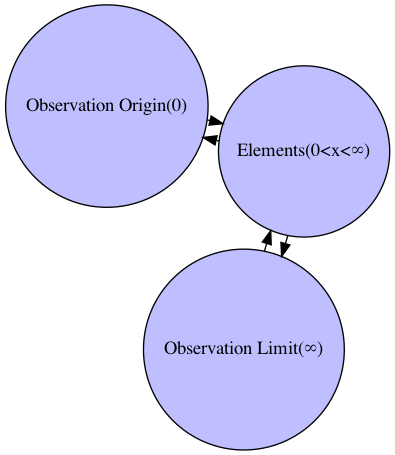
一般的に数直線としてイメージされるが、実際には同心円や同心球面を構成している。このイメージがきっちり出来ていれば「どうして自然数には逆元が存在しないか」悩む事はない。また自然数を(それ自体は観測不可能な)観測原点(Observation Origin)0と可算範囲を超える観測限界(Observation Limit)Inf(inity)を結ぶ観測線と考えると「どうして自然数には単位元が存在しないか」も自明の場合(Trival Case)として考えられる様になる。
Rによる「同心円状態」の実装例
【Rで球面幾何学】等差数列(算術数列)②数直線概念から同心円集合概念へ

OIAS01<-function(index){
# 同心円の描画
c0=seq(0,2*pi,length=60)
cmp0<-complex(mod=1,arg=c0)
cx=Re(cmp0)
cy=Im(cmp0)
plot(cx,cy,asp=1,type="l",xlim=c(-3,3),ylim=c(-3,3),main="One-sided Infinite Arithmetic Sequence",xlab="",ylab="")
par(new=T)#上書き
plot(cx*2,cy*2,asp=1,type="l",xlim=c(-3,3),ylim=c(-3,3),main="",xlab="",ylab="")
par(new=T)#上書き
plot(cx*3,cy*3,asp=1,type="l",xlim=c(-3,3),ylim=c(-3,3),main="",xlab="",ylab="")
par(new=T)#上書き
plot(cx*4,cy*4,asp=1,type="l",xlim=c(-3,3),ylim=c(-3,3),main="",xlab="",ylab="")
par(new=T)#上書き
plot(cx*5,cy*5,asp=1,type="l",xlim=c(-3,3),ylim=c(-3,3),main="",xlab="",ylab="")
# 同心円領域の塗り潰し(x=1)
polygon(cx, #x
cy, #y
density=c(50), #塗りつぶす濃度
angle=c(45), #塗りつぶす斜線の角度
col=c(200,200,200)) #塗りつぶす色
# 同心円領域の塗り潰し(x=2)
polygon(cx*2, #x
cy*2, #y
density=c(40), #塗りつぶす濃度
angle=c(45), #塗りつぶす斜線の角度
col=c(200,200,200)) #塗りつぶす色
# 同心円領域の塗り潰し(x=3)
polygon(cx*3, #x
cy*3, #y
density=c(30), #塗りつぶす濃度
angle=c(45), #塗りつぶす斜線の角度
col=c(200,200,200)) #塗りつぶす色
# 同心円領域の塗り潰し(x=3)
polygon(cx*4, #x
cy*4, #y
density=c(20), #塗りつぶす濃度
angle=c(45), #塗りつぶす斜線の角度
col=c(200,200,200)) #塗りつぶす色
# 同心円領域の塗り潰し(x=3)
polygon(cx*5, #x
cy*5, #y
density=c(10), #塗りつぶす濃度
angle=c(45), #塗りつぶす斜線の角度
col=c(200,200,200)) #塗りつぶす色
abline(h = 0,col=c(200,200,200))
abline(v = 0,col=c(200,200,200))
segments(0,0,5,0,col=rgb(0,1,0))
par(new=T)#上書き
ax=c(0,cx[index]*1,cx[index]*2,cx[index]*3,cx[index]*4,cx[index]*5)
ay=c(0,cy[index]*1,cy[index]*2,cy[index]*3,cy[index]*4,cy[index]*5)
plot(ax,ay,asp=1,type="o",xlim=c(-3,3),ylim=c(-3,3),col=rgb(0,0,1),main="",xlab="",ylab="")
}
# アニメーション動作設定
Time_Code<-seq(1,59,by=2)
# アニメーション
library("animation")
saveGIF({
for (i in Time_Code){
OIAS01(i)
}
}, interval = 0.1, movie.name = "OIAS03.gif")
Rによる「同心球面状態」の実装例
【初心者向け】「単位円筒」から「単位球面」へ

library(rgl)
radians<-seq(0,60*pi,length=3000)
f0<-function(x){exp(x*(0+1i))}
Real<-Re(f0(radians))
Imaginal<-Im(f0(radians))
Rtime<-seq(-1,1,length=3000)
# 工夫
f1<-function(x){sqrt(1-x^2)}
c0<-seq(-1,1,length=3000)
c1<-f1(c0)
# > plot(c0,c1,type="l",xlim=c(-1,1),ylim=c(0,1))
Real_c<-Real*c1
Imaginal_c<-Imaginal*c1
plot3d(Real_c,Imaginal_c,Rtime,type="l",xlim=c(-1,1),ylim=c(-1,1),zlim=c(-1,1),xlab="",ylab="",zlab="",col=c(200,200,200))
# 観測原点**(Observation Origin)
texts3d(0,0,0,texts="OO(0,0,0)",col=rgb(0,0,0),adj=1.0)
# 原蹠(PorTal)
portal_i<-0
portal_j<-0
portal_k<-1
portal_text=paste0("Rad(",portal_i,",",portal_j,",",portal_k,")")
# 原蹠表示
texts3d(portal_i,portal_j,portal_k,texts=portal_text,col=rgb(0,0,1),adj=1.0)
# 立方対角線(Cubic Diagonal)
lines3d(c(portal_i,0),c(portal_j,0),c(portal_k,0),col=rgb(0,0,1),lwd=2)
# アニメーション
movie3d(spin3d(axis=c(0,0,1),rpm=5),duration=10,fps=25,movie="~/Desktop/Sphere01f")
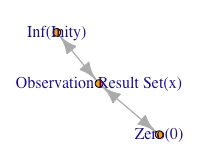
「観測原点(Observation Origin)0 - 観測結果集合(Observation Result Set)- 観測限界(Observation Limit)」の関係の図式化。
Rによる実装
library(igraph)
par(mfrow=c(1,2),mar=c(3,3,3,3))
gd<-graph(c(
"Zero(0)","Observation Result Set(x)",
"Observation Result Set(x)","Zero(0)",
"Observation Result Set(x)","Inf(Inity)",
"Inf(Inity)","Observation Result Set(x)"
))
plot(gd,layout=layout.fruchterman.reingold)
pythonによる実装
【Python演算処理】NetworkXライブラリを導入する。
1.2.加法整数群(Additive Integer Group)
演算結果集合としては区間:無限小$-\infty$~0~無限大$+\infty$、初項0、公差±1、一般項0±(n-1)1の両側無限数列(Both Sides Infinity Set)を構成する。
Z_n(n=-\infty→0→+\infty)=(-\infty,…,1-4(1)=-3,1-3(1)=-2,1-2(1)=-1,n-n=0,1+0=1,1+1=2,1+2(1)+1=3,…,1+n(n-1),…,\infty)
Rによる実装例
# 演算内容そのものは自然数と同じ。
natural<-function(x) 1+(x-1)*1
c0<--5:5
# 結果
c0
natural(c0)
# 結果
> c0
[1] -5 -4 -3 -2 -1 0 1 2 3 4 5
> natural(c0)
[1] -5 -4 -3 -2 -1 0 1 2 3 4 5
pythonによる実装例
# 演算内容そのものは自然数と同じ。
import numpy as np
def Natural(x):
return 1+(x-1)*1
c0=np.arange(-5,5,1)
print(c0)
print(Natural(c0))
# 出力結果
[-5 -4 -3 -2 -1 0 1 2 3 4]
[-5 -4 -3 -2 -1 0 1 2 3 4]
- その演算は加減算の範囲で閉じており、加法単位元と逆元を備え、かつ結合則(a+b)+c=a+(b+c)を満たす(元と単位元と逆元が同じ等差数列上に連続する)。
- 自然数同様、最も代表的な添字集合(Indexed Set)の一つであり、増減を測る際の周期単位(Unit Cycle)の倍数たる周回数(Number of laps)の表示にも使われる。
要するに群論(Group Theory)的に言うと「自然数集合に単位元と逆元の概念を追加したもの」という事になる。
【初心者向け】群論概念(Group Theory Concept)①基本定義
library(rgl)
f0<-function(x){exp(x*(0+1i))}
# 円筒描画
radians<-seq(0,120*pi,length=5000)
Real<-Re(f0(radians))
Imaginal<-Im(f0(radians))
Rtime<-seq(0,2,length=3000)
plot3d(Real,Imaginal,Rtime,type="l",xlim=c(-1,1),ylim=c(-1,1),zlim=c(0,2),xlab="",ylab="",zlab="",col=c(200,200,200))
# 無限円(Infinity Circle)の描画
radians0<-seq(0,2*pi,length=60)
Real0<-Re(f0(radians0))
Imaginal0<-Im(f0(radians0))
Rtime0<-numeric(60)
lines3d(Real0,Imaginal0,Rtime0,col=rgb(0,1,0),lwd=2)
lines3d(Real0,Imaginal0,Rtime0+1,col=rgb(0,1,0),lwd=2)
lines3d(Real0,Imaginal0,Rtime0+2,col=rgb(0,1,0),lwd=2)
# 観測原点**(Observation Origin)
texts3d(1,0,0,texts="OO(1,0,0)",col=rgb(0,0,0),adj=1.0)
# 座標「1」表示
texts3d(1,0,1,texts="(1,0,1)",col=rgb(0,0,1),adj=1.0)
# 座標「2」表示
texts3d(1,0,2,texts="(1,0,2)",col=rgb(0,0,1),adj=1.0)
# 数直線(Line)
lines3d(c(1,1),c(0,0),c(0,2),col=rgb(0,0,1),lwd=2)
movie3d(spin3d(axis=c(0,0,1),rpm=5),duration=10,fps=25,movie="~/Desktop/sylinder08")
pythonによる「自然数集合」実装例
【Python演算処理】単位円筒(Unit Cylinder)の描画

library(rgl)
f0<-function(x){exp(x*(0+1i))}
# 円筒描画
radians<-seq(0,120*pi,length=5000)
Real<-Re(f0(radians))
Imaginal<-Im(f0(radians))
Rtime<-seq(-2,0,length=3000)
plot3d(Real,Imaginal,Rtime,type="l",xlim=c(-1,1),ylim=c(-1,1),zlim=c(-2,0),xlab="",ylab="",zlab="",col=c(200,200,200))
# 無限円(Infinity Circle)の描画
radians0<-seq(0,2*pi,length=60)
Real0<-Re(f0(radians0))
Imaginal0<-Im(f0(radians0))
Rtime0<-numeric(60)
lines3d(Real0,Imaginal0,Rtime0,col=rgb(0,1,0),lwd=2)
lines3d(Real0,Imaginal0,Rtime0-1,col=rgb(0,1,0),lwd=2)
lines3d(Real0,Imaginal0,Rtime0-2,col=rgb(0,1,0),lwd=2)
# 観測原点**(Observation Origin)
texts3d(1,0,0,texts="OO(0,0,0)",col=rgb(0,0,0),adj=1.0)
# 座標「1」表示
texts3d(1,0,-1,texts="(0,0,-1)",col=rgb(1,0,0),adj=1.0)
# 座標「2」表示
texts3d(1,0,-2,texts="(0,0,-2)",col=rgb(1,0,0),adj=1.0)
# 数直線(Line)
lines3d(c(1,1),c(0,0),c(0,-2),col=rgb(1,0,0),lwd=2)
movie3d(spin3d(axis=c(0,0,1),rpm=5),duration=10,fps=25,movie="~/Desktop/sylinder10")
pythonによる「逆元」実装例
【Python演算処理】単位円筒(Unit Cylinder)の描画

library(rgl)
f0<-function(x){exp(x*(0+1i))}
# 円筒描画
radians<-seq(0,120*pi,length=5000)
Real<-Re(f0(radians))
Imaginal<-Im(f0(radians))
Rtime<-seq(-1,1,length=3000)
plot3d(Real,Imaginal,Rtime,type="l",xlim=c(-1,1),ylim=c(-1,1),zlim=c(-1,1),xlab="",ylab="",zlab="",col=c(200,200,200))
# 無限円(Infinity Circle)の描画
radians0<-seq(0,2*pi,length=60)
Real0<-Re(f0(radians0))
Imaginal0<-Im(f0(radians0))
Rtime0<-numeric(60)
lines3d(Real0,Imaginal0,Rtime0,col=rgb(0,1,0),lwd=2)
lines3d(Real0,Imaginal0,Rtime0+1,col=rgb(0,1,0),lwd=2)
lines3d(Real0,Imaginal0,Rtime0-1,col=rgb(0,1,0),lwd=2)
# 観測原点**(Observation Origin)
texts3d(1,0,0,texts="OO(0,0,0)",col=rgb(0,0,0),adj=1.0)
# 座標「1」表示
texts3d(1,0,1,texts="(0,0,1)",col=rgb(0,0,1),adj=1.0)
# 座標「2」表示
texts3d(1,0,-1,texts="(0,0,-1)",col=rgb(1,0,0),adj=1.0)
# 数直線(Line)
lines3d(c(1,1),c(0,0),c(0,1),col=rgb(0,0,1),lwd=2)
lines3d(c(1,1),c(0,0),c(0,-1),col=rgb(1,0,0),lwd=2)
movie3d(spin3d(axis=c(0,0,1),rpm=5),duration=10,fps=25,movie="~/Desktop/sylinder13")
pythonによる「加法整数群」実装例
【Python演算処理】単位円筒(Unit Cylinder)の描画

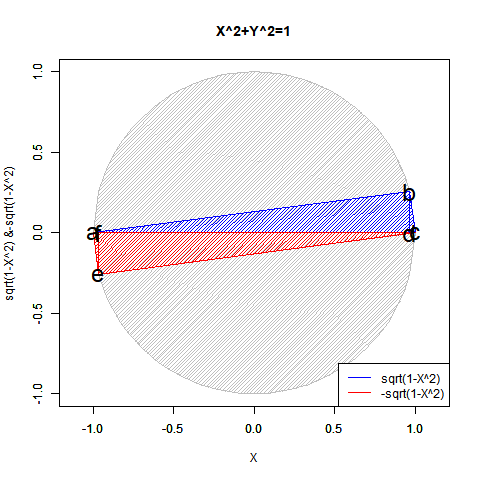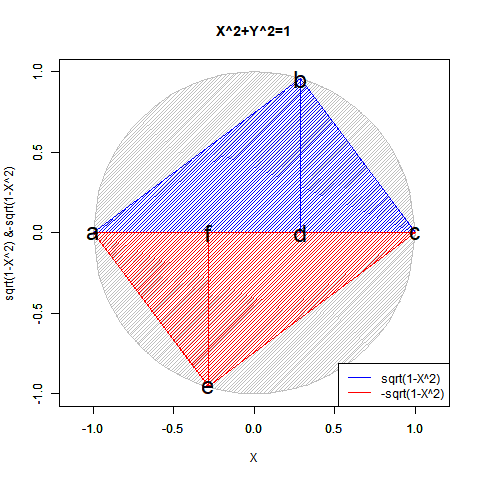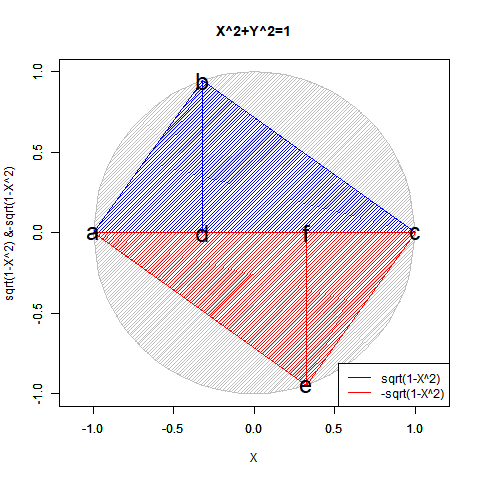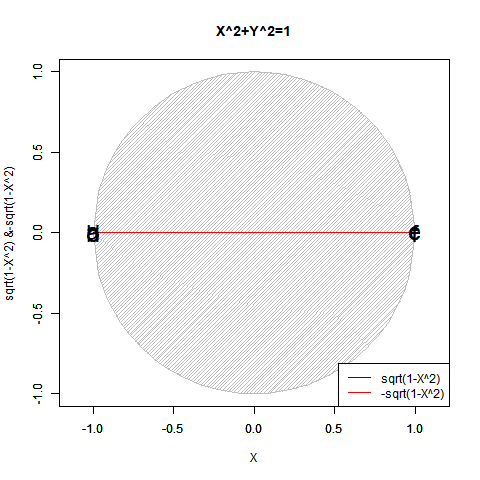
この時観測原点(Observation Origin)0が可算範囲に加わると同時に観測限界(Observation Limit)Inf(inity)の概念が無限小-Inf(inity)と無限大+Inf(inity)に二分されるイメージが重要。「どうして単位円描画関数y=±sqrt(1-x^2)/x=±sqrt(1-y^2)のそれぞれの関数は半円ずつしか描かないか」にも関わってくる話である。
【Rで球面幾何学】「半円しか描けなかった」世界の思い出?
CFD<-function(Radian){
cx<-seq(-1,1,length=60)
f0<-function(x) sqrt(1-x^2)
cy<-f0(cx)
plot(cx,cy,asp=1,type="l",xlim=c(-1,1),ylim=c(-1,1),main="X^2+Y^2=1",xlab="X",ylab="sqrt(1-X^2) &-sqrt(1-X^2) ")
par(new=T)#上書き指定
plot(cx,-1*cy,asp=1,type="l",xlim=c(-1,1),ylim=c(-1,1),main="",xlab="",ylab="")
# 塗りつぶし(上背景)
polygon(cx, #x
cy, #y
density=c(30), #塗りつぶす濃度
angle=c(45), #塗りつぶす斜線の角度
col=c(200,200,200)) #塗りつぶす色
# 塗りつぶし(下背景)
polygon(cx, #x
-cy, #y
density=c(30), #塗りつぶす濃度
angle=c(45), #塗りつぶす斜線の角度
col=c(200,200,200)) #塗りつぶす色
# 塗りつぶし(上三角)
polygon(c(-1,cx[Radian],1), #x
c(0,cy[Radian],0), #y
density=c(30), #塗りつぶす濃度
angle=c(45), #塗りつぶす斜線の角度
col=rgb(0,0,1)) #塗りつぶす色
# 塗りつぶし(下三角)
cx1<-rev(cx)
cy1<-rev(cy)*-1
polygon(c(1,cx1[Radian],-1), #x
c(0,cy1[Radian],0), #y
density=c(30), #塗りつぶす濃度
angle=c(45), #塗りつぶす斜線の角度
col=rgb(1,0,0)) #塗りつぶす色
# 線追加(三角)
segments(cx[Radian],cy[Radian],cx[Radian],0,col=rgb(0,0,1))
segments(cx1[Radian],cy1[Radian],cx1[Radian],0,col=rgb(1,0,0))
# 文字追加
text(c(-1,cx[Radian],1,cx[Radian],-cx[Radian],-cx[Radian]),c(0,cy[Radian],0,0,-cy[Radian],0), labels=c("a","b","c","d","e","f"),col=c(rgb(0,0,0),rgb(0,0,0),rgb(0,0,0),rgb(0,0,0),rgb(0,0,0)),cex=c(2,2,2,2,2,2))
# 凡例
legend("bottomright", legend=c("sqrt(1-X^2)","-sqrt(1-X^2)"), lty=c(1,1), col=c(rgb(0,0,1),rgb(1,0,0)))
}
# アニメーション
library("animation")
Time_Code=rev(seq(1,59, length=30))
saveGIF({
for (i in Time_Code){
CFD(i)
}
}, interval = 0.1, loop=TRUE, movie.name = "CFD01.gif")
# CFD90Sift=Circle Function Double 90Sift
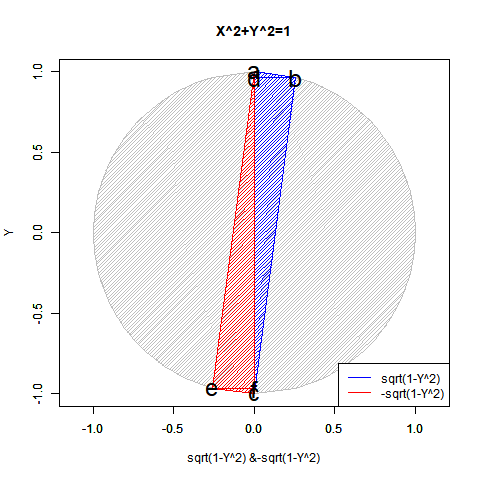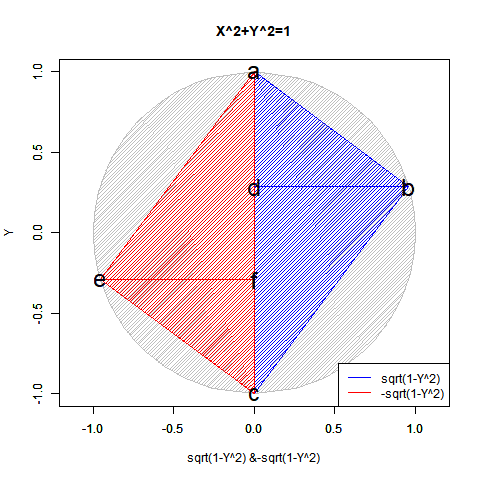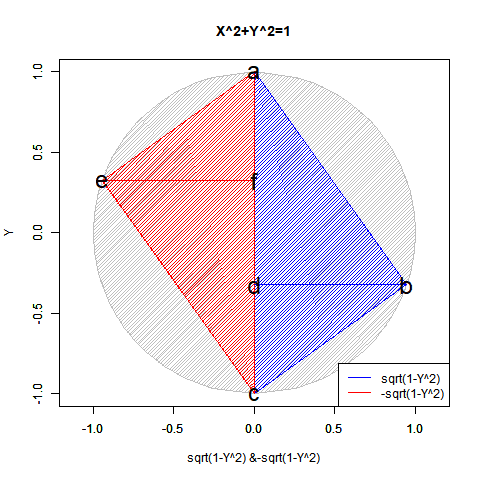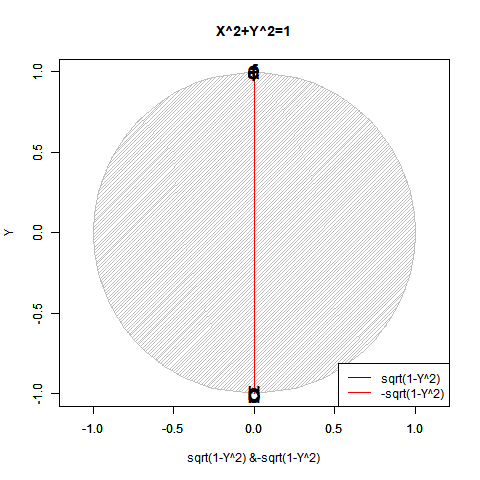
CFD90Sift<-function(Radian){
cx<-seq(-1,1,length=60)
f0<-function(x) sqrt(1-x^2)
cy<-f0(cx)
plot(cy,cx,asp=1,type="l",xlim=c(-1,1),ylim=c(-1,1),main="X^2+Y^2=1",xlab="sqrt(1-Y^2) &-sqrt(1-Y^2)",ylab="Y")
par(new=T)#上書き指定
plot(cy*-1,cx,asp=1,type="l",xlim=c(-1,1),ylim=c(-1,1),main="",xlab="",ylab="")
# 塗りつぶし(上背景)
polygon(cy, #x
cx, #y
density=c(30), #塗りつぶす濃度
angle=c(45), #塗りつぶす斜線の角度
col=c(200,200,200)) #塗りつぶす色
# 塗りつぶし(下背景)
polygon(-cy, #x
cx, #y
density=c(30), #塗りつぶす濃度
angle=c(45), #塗りつぶす斜線の角度
col=c(200,200,200)) #塗りつぶす色
# 塗りつぶし(上三角)
polygon(c(0,cy[Radian],0), #x
c(-1,cx[Radian],1), #y
density=c(30), #塗りつぶす濃度
angle=c(45), #塗りつぶす斜線の角度
col=rgb(0,0,1)) #塗りつぶす色
# 塗りつぶし(下三角)
cx1<-rev(cx)
cy1<-rev(cy)*-1
polygon(c(0,cy1[Radian],0), #x
c(1,cx1[Radian],-1), #y
density=c(30), #塗りつぶす濃度
angle=c(45), #塗りつぶす斜線の角度
col=rgb(1,0,0)) #塗りつぶす色
# 線追加(三角)
segments(cy[Radian],cx[Radian],0,cx[Radian],col=rgb(0,0,1))
segments(cy1[Radian],cx1[Radian],0,cx1[Radian],col=rgb(1,0,0))
# 文字追加
text(c(0,cy[Radian],0,0,-cy[Radian],0),c(1,cx[Radian],-1,cx[Radian],-cx[Radian],-cx[Radian]), labels=c("a","b","c","d","e","f"),col=c(rgb(0,0,0),rgb(0,0,0),rgb(0,0,0),rgb(0,0,0),rgb(0,0,0)),cex=c(2,2,2,2,2,2))
# 凡例
legend("bottomright", legend=c("sqrt(1-Y^2)","-sqrt(1-Y^2)"), lty=c(1,1), col=c(rgb(0,0,1),rgb(1,0,0)))
}
# アニメーション
library("animation")
Time_Code=rev(seq(1,59, length=30))
saveGIF({
for (i in Time_Code){
CFD90Sift(i)
}
}, interval = 0.1, movie.name = "CFD90Sift02.gif")
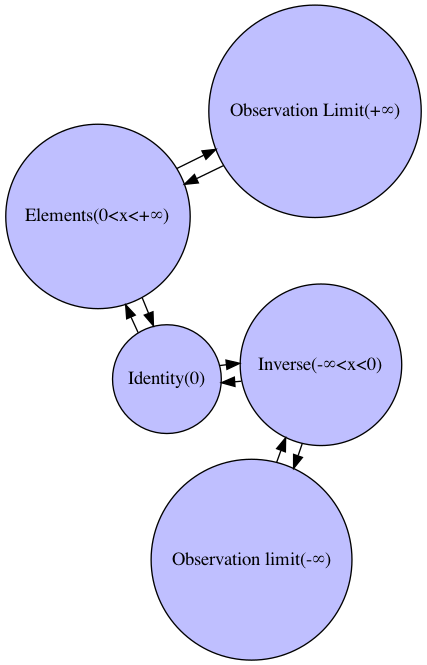
「無限小-Inf(inity) - 観測結果集合(-)(Observation Result Set) - 演算原点0 - 観測結果集合(+)(Observation Result Set) - 無限大+Inf(inity)」の関係の図式化。観測結果集合から導出した加法単位元0の概念を導入した事により(それ自体は観測不可能な)観測原点が座標上から消える。この効果は演算結果集合の演算結果が観測結果集合と一致する限り持続する。
library(igraph)
gd<-graph(edges=c("Zero(0)","Element(g)","Element(g)","Zero(0)","Element(g)","Inf(inity)","Inf(inity)","Element(g)","Zero(0)","Inverse(-g)","Inverse(-g)","Zero(0)","Inverse(-g)","-Inf(inity)","-Inf(inity)","Inverse(-g)"))
plot(gd,layout=layout.fruchterman.reingold)
pythonによる「加法整数族」の表現
【Python演算処理】NetworkXライブラリを導入する。
かかる「加法整数群」の概念を出発点として「偶数群」と「奇数集合」の概念が派生する。
群論はこの辺りも極めて抽象的な表現で語るが、現時点の私には理解出来ない。
置換の符号 - Wikipedia
高校数学の美しい物語 置換と偶置換・奇置換に関する基礎的なこと
偶数群(Even Group)
演算結果集合としては区間:無限小$-\infty$~0~無限大$+\infty$、初項0、公差±2、一般項±2nの両側無限数列を構成する。
Even_n(n=-\infty→0→+\infty)=(-\infty,…,-2n,…,-2×2=-4,-2×1=-2,-2×0=0,-2×1=2,-2×2=4,…,2n,…,+\infty)
Rによる実装例
natural<-function(x) 2*x
c0<--5:5
# 結果
> c0
[1] -5 -4 -3 -2 -1 0 1 2 3 4 5
> natural(c0)
[1] -10 -8 -6 -4 -2 0 2 4 6 8 10
pythonによる実装例
import numpy as np
def Natural(x):
return 2*x
c0=np.arange(1,10,1)
print(c0)
print(Natural(c0))
# 出力結果
[1 2 3 4 5 6 7 8 9]
[ 2 4 6 8 10 12 14 16 18]
- その演算は加減算の範囲で閉じており(偶数+偶数=偶数、偶数-偶数=偶数)、加法単位元と逆元を備え、かつ結合則(a+b)+c=a+(b+c)を満たす(元と単位元と逆元が同じ等差数列上に連続する)ので群の成立条件を満たす。
奇数集合(Odd Set)
演算結果集合としては区間:無限小$-\infty$~0~無限大$+\infty$、初項1、公差±2、一般項±2n+1の両側無限数列を構成する。
Odd_n(n=-\infty→0→+\infty)=(-\infty,…,-2n+1,…,-2×2+1=-3,-2×1+1=-1,2×0+1=1,2×1+1=3,…,2n+1,…,+\infty)
あるいは
Odd_n(n=-\infty→0→+\infty)=(-\infty,…,-2n-1,…,-2×2-1=-5,-2×1-1=-3,2×0-1=-1,2×1-1=1,2×2-1=3,…,2n+1,…,+\infty)
Rによる「y=2x+1」実装例
natural<-function(x) 2*x+1
c0<--5:5
# 結果
> c0
[1] -5 -4 -3 -2 -1 0 1 2 3 4 5
> natural(c0)
[1] -9 -7 -5 -3 -1 1 3 5 7 9 11
Rによる「y=2x-1」実装例
natural<-function(x) 2*x-1
c0<--5:5
c0
natural(c0)
# 結果
> c0
[1] -5 -4 -3 -2 -1 0 1 2 3 4 5
> natural(c0)
[1] -11 -9 -7 -5 -3 -1 1 3 5 7 9
pythonによる「y=2x+1」実装例
import numpy as np
def Natural(x):
return 2*x+1
c0=np.arange(-5,5,1)
print(c0)
print(Natural(c0))
# 出力結果
[-5 -4 -3 -2 -1 0 1 2 3 4]
[-9 -7 -5 -3 -1 1 3 5 7 9]
pythonによる「y=2x-1」実装例
import numpy as np
def Natural(x):
return 2*x-1
c0=np.arange(-5,5,1)
print(c0)
print(Natural(c0))
# 出力結果
[-5 -4 -3 -2 -1 0 1 2 3 4]
[-11 -9 -7 -5 -3 -1 1 3 5 7]
- その演算は逆元を備え、結合則(a+b)+c=a+(b+c)も満たすものの、加法単位元0は集合範囲外で演算結果も閉じてない(奇数+奇数=偶数、奇数-奇数=偶数)。ゆえに群の成立条件を満たさない。
- 関数における奇関数も(その対称性ゆえにそれを備えない偶関数と異なり)逆関数を備え常に一対で現れる。また幾何学における(対蹠間を結ぶ直線が引けない)奇数角形の多角形もまた(それぞれ片側の対蹠にのみ接する)一対として現れる。かかる「偶数の対称性」と「奇数の双極性」の対比は、あらゆる分野に偏在する普遍的概念だったりする。
この事を関数に表すとどうなるか。この疑問こそが交代級数(Alternating series)概念の出発点となる。
偶奇性(Parity)と交代級数(Alternating series)概念の起源。
1のn乗の答えは全て1であり、-1のn乗の答えは1と-1の間を往復する。後者を特に交代級数(Alternating series)といい、その合計が0になる事で知られる。
【数理考古学】解析学史に「虚数概念」をもたらした交代級数(Alternating Series)
\begin{align}
1^n(n=-\infty→0→+\infty)=(…,1,1,1,…)\\
-1^n(n=-\infty→0→+\infty)=(…,-1,1,-1,…)
\end{align}
あれ? もしかしたら交代級数における「合計したら0になる」考え方って偶奇の概念だけでなくコーシーの積分定理の出発点でもある?
コーシーの積分定理 - Wikipedia
かかる全体像を把握するにはいわゆるオイラーの等式(Euler's identity)$e^{πi}=-1$の世界観、すなわち虚数(Imaginal)$i^2=-1$および複素数(Complex)$α+βi$の概念導入による単位円筒(Unit Cylinder)のイメージ構築が欠かせない。整数すなわち周回数(Rap)を実軸(Real Axis)と置くと、これを法とする剰余類(Residue Class)すなわち1周未満の(小数点下の)軌跡は全て虚軸(Imaginal Axis)へと追いやられてしまう訳である。とはいえ…
剰余類 - Wikipedia
剰余類 [物理のかぎしっぽ]
import math as m
import cmath as c
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.animation as animation
# 単位円データ作成
c0=np.linspace(-m.pi,m.pi,61,endpoint = True)
s0=[]
for num in range(len(c0)):
s0.append(complex(m.cos(c0[num]),m.sin(c0[num])))
s1=np.array(s0)
plt.style.use('default')
fig = plt.figure(111)
# 関数定義
def unit_circle(n):
plt.cla()
#スポーク線描画
for num in range(len(s1)):
plt.plot([0,s1[num].real],[0,s1[num].imag],color="gray",lw=0.5);
#円周描画
plt.plot(s1.real,s1.imag,color="green", label="Unit Cylinder")
plt.plot([1,1],[-2,2],color="blue", label="X=1")
plt.plot([-1,-1],[-2,2],color="red", label="X=-1")
plt.ylim([-1.1,1.1])
plt.xlim([-1.1,1.1])
plt.title("Unit Circle")
plt.xlabel("Real")
plt.ylabel("Imaginal")
ax = fig.add_subplot()
ax.set_aspect('equal', adjustable='box')
ax.legend(loc='upper right')
#補助線描画
plt.axvline(0, 0, 1,color="black")
plt.axhline(0, 0, 1,color="black")
#移動線描画
if s1[n].real < 0:
col="red"
else:
col="blue"
plt.plot([0,s1[n].real],[0,s1[n].imag],color=col,lw=1)
ani = animation.FuncAnimation(fig, unit_circle, interval=50,frames=len(s1))
ani.save("output09.gif", writer="pillow")
複素関数論においては、かかる無限周期運動を積分する為に(その周期を代表する)分枝点(Branch)を設定して周回数を数える(分枝切断=Branch Cut)。この考え方を援用するなら-1のn乗は複素関数(0±1i)^2x、それが描く円と数直線の2つの接点x=±1は分枝点、整数集合とは「分枝切断の結果、数えられる様になった周回数」に他ならない事になる。
i^x=-1\\
-1^x=i^2x=(0±1i)^{2x}
pythonによる単位円筒の垂直展開例示①「分枝切断概念」の導入

%matplotlib nbagg
import math as m
import cmath as c
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
# 単位円データ作成
c0=np.linspace(-m.pi,m.pi,61,endpoint = True)
s0=[]
for num in range(len(c0)):
s0.append(complex(m.cos(c0[num]),m.sin(c0[num])))
s1=np.array(s0)
z0=np.linspace(-1,1,61,endpoint = True)
# グラフ表示
plt.style.use('default')
fig = plt.figure()
ax = Axes3D(fig)
# 関数定義
def unit_cylinder(n):
plt.cla()
#スポーク線描画
ax.plot([0,-1],[0,0],[-1,-1],color="red",lw=1)
ax.plot([0,0],[0,0],[-1,0],color="red",lw=1)
ax.plot([0,0],[0,0],[0,1],color="blue",lw=1)
ax.plot([0,-1],[0,0],[1,1],color="blue",lw=1)
for num in range(len(s1)):
ax.plot([0,s1[num].real],[0,s1[num].imag],[z0[num],z0[num]],color="gray",lw=0.5);
ax.plot(s1.real,s1.imag,z0,color="green")
ax.set_ylim([-1.1,1.1])
ax.set_xlim([-1.1,1.1])
ax.set_zlim([-1.1,1.1])
ax.set_title("Unit Cylinder")
ax.set_xlabel("Real")
ax.set_ylabel("Imaginal")
ax.set_zlabel("Cycle")
#動線描画
if s1[n].imag < 0:
col="red"
else:
col="blue"
ax.plot([0,s1[n].real],[0,s1[n].imag],[z0[n],z0[n]],color=col,lw=1);
ani = animation.FuncAnimation(fig, unit_cylinder, interval=50,frames=len(s1))
ani.save("output12.gif", writer="pillow")
pythonによる単位円筒の垂直展開例示②水平展開との重ね合わせ。
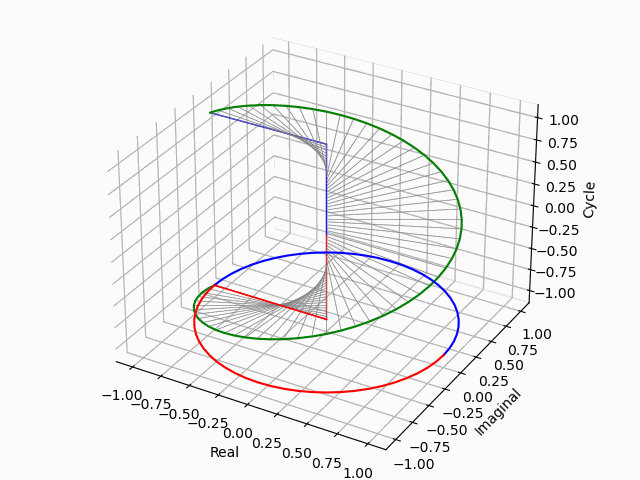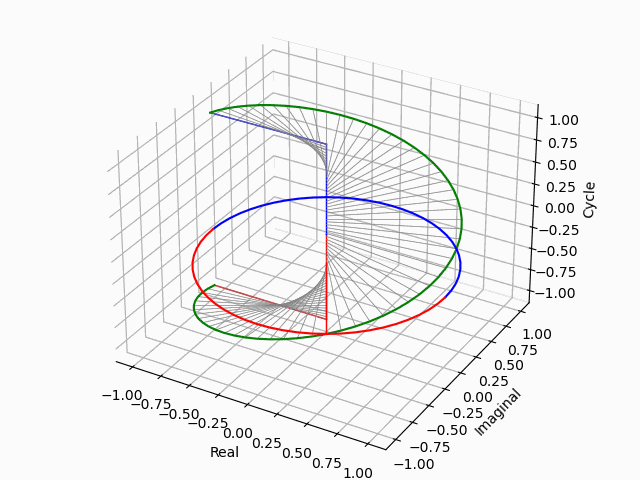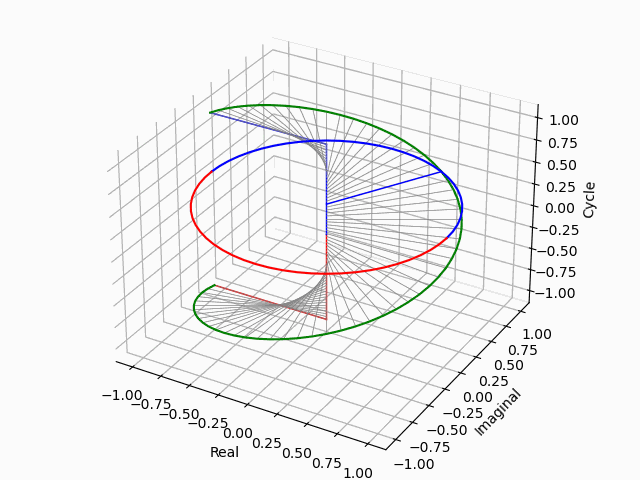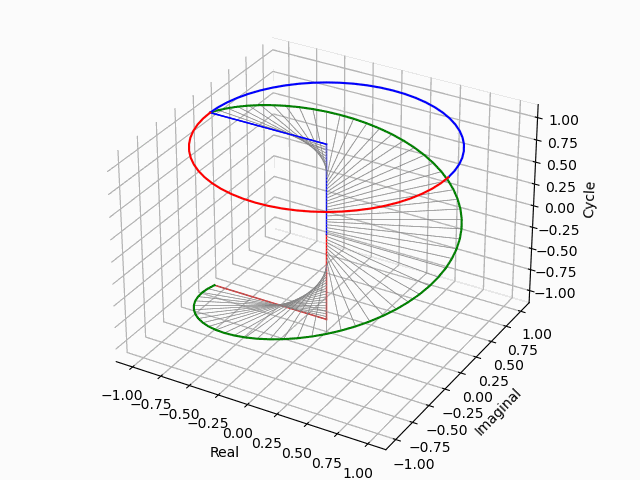
%matplotlib nbagg
import math as m
import cmath as c
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
import matplotlib.animation as animation
# 単位円データ作成
c0=np.linspace(-m.pi,m.pi,61,endpoint = True)
s0=[]
for num in range(len(c0)):
s0.append(complex(m.cos(c0[num]),m.sin(c0[num])))
s1=np.array(s0)
z0=np.linspace(-1,1,61,endpoint = True)
# 単位円(-)データ作成
c1=np.linspace(-m.pi,0,31,endpoint = True)
s2=[]
for num in range(len(c1)):
s2.append(complex(m.cos(c1[num]),m.sin(c1[num])))
shm=np.array(s2)
z1=np.repeat(0,31)
# 単位円(+)データ作成
c2=np.linspace(0,m.pi,31,endpoint = True)
s3=[]
for num in range(len(c2)):
s3.append(complex(m.cos(c2[num]),m.sin(c2[num])))
shp=np.array(s3)
# グラフ表示
plt.style.use('default')
fig = plt.figure()
ax = Axes3D(fig)
# 関数定義
def unit_cylinder(n):
plt.cla()
#スポーク線描画
ax.plot([0,-1],[0,0],[-1,-1],color="red",lw=1)
ax.plot([0,0],[0,0],[-1,0],color="red",lw=1)
ax.plot([0,0],[0,0],[0,1],color="blue",lw=1)
ax.plot([0,-1],[0,0],[1,1],color="blue",lw=1)
for num in range(len(s1)):
ax.plot([0,s1[num].real],[0,s1[num].imag],[z0[num],z0[num]],color="gray",lw=0.5);
ax.plot(s1.real,s1.imag,z0,color="green")
ax.set_ylim([-1.1,1.1])
ax.set_xlim([-1.1,1.1])
ax.set_zlim([-1.1,1.1])
ax.set_title("Unit Cylinder")
ax.set_xlabel("Real")
ax.set_ylabel("Imaginal")
ax.set_zlabel("Cycle")
#動線描画
if s1[n].imag < 0:
col="red"
else:
col="blue"
ax.plot([0,s1[n].real],[0,s1[n].imag],[z0[n],z0[n]],color=col,lw=1)
z1=np.repeat(z0[n],31)
ax.plot(shp.real,shp.imag,z1,color="blue")
ax.plot(shm.real,shm.imag,z1,color="red")
ani = animation.FuncAnimation(fig, unit_cylinder, interval=50,frames=len(s1))
ani.save("output13.gif", writer="pillow")
見ての通り話はそれだけに留まらない。-1と1の距離は2であり(自明の場合として、半径1の円の直径は2となる)、このままでは2単位の目盛りしか切れないのである。それで偶奇性(Parity)概念の導入が必須となる。
# CVCM=等速円運動(Constant Velocity Circular Motion)
# Radian=角度(60分割)
CVCM<-function(Radian){
c0<-seq(0,2*pi,length=60)
# 大円
cx<-cos(c0)
cy<-sin(c0)
# 小円(奇数系)1個目
s1cx<-cos(c0)/2+cx[Radian]/2
s1cy<-sin(c0)/2+cy[Radian]/2
# 小円(奇数系)2個目
s2cx<-cos(c0)/2+cx[Radian]+cx[Radian]/2
s2cy<-sin(c0)/2+cy[Radian]+cy[Radian]/2
# 小円(偶数系)1個目
s1cx0<-cos(c0)/2
s1cy0<-sin(c0)/2
# 小円(偶数系)2個目
s2cx0<-cos(c0)/2-cx[Radian]
s2cy0<-sin(c0)/2-cy[Radian]
# 円描画
plot(cx,cy,asp=1,type="l",col=rgb(0,0,0),main="Even & Odd Circles",xlab="cos(θ)",ylab="sin(θ)")
# 塗りつぶし(円全体)
polygon(cx, #x
cy, #y
density=c(30), #塗りつぶす濃度
angle=c(45), #塗りつぶす斜線の角度
col=c(200,200,200)) #塗りつぶす色
# 塗りつぶし(奇数系小円1)
polygon(s1cx, #x
s1cy, #y
density=c(30), #塗りつぶす濃度
angle=c(45), #塗りつぶす斜線の角度
col=rgb(1,0,0)) #塗りつぶす色
# 塗りつぶし(奇数系小円2)
polygon(s2cx, #x
s2cy, #y
density=c(30), #塗りつぶす濃度
angle=c(45), #塗りつぶす斜線の角度
col=rgb(1,0,0)) #塗りつぶす色
# 塗りつぶし(偶数系小円1)
polygon(s1cx0, #x
s1cy0, #y
density=c(40), #塗りつぶす濃度
angle=c(45), #塗りつぶす斜線の角度
col=rgb(0,0,1)) #塗りつぶす色
# 塗りつぶし(偶数系小円2)
polygon(s2cx0, #x
s2cy0, #y
density=c(40), #塗りつぶす濃度
angle=c(45), #塗りつぶす斜線の角度
col=rgb(0,0,1)) #塗りつぶす色
text(0,0,"(0,0,0,…)",col=rgb(0,0,0))
text(cx[Radian],cy[Radian],"(1,1,1,…)",col=rgb(0,0,0))
text(cx[Radian]/2,cy[Radian]/2,"(1/2,1/2,1/2,…)",col=rgb(0,0,0))
# 対蹠の設定
segments(cx[Radian],cy[Radian],cx[Radian]/2,cy[Radian]/2,col=rgb(1,0,0))
segments(cx[Radian]/2,cy[Radian]/2,0,0,col=rgb(0,0,1))
# lines(s1cx,s1cy,col=rgb(0,1,0))
# lines(s1cx0,s1cy0,col=rgb(1,0,1))
# 凡例
legend("bottomright", legend=c("Even Circles","Odd Circles"), lty=c(1,1), col=c(rgb(0,0,1),rgb(1,0,0)))
}
# アニメーション
library("animation")
Time_Code=seq(1,59, length=30)
saveGIF({
for (i in Time_Code){
CVCM(i)
}
}, interval = 0.1, movie.name = "CVCM05.gif")
Int01<-function(Rad){
cx00<-seq(-3,3,length=61)
f0<-function(x) 1^x
cy00<-f0(cx00)
s00<-complex(re=cx00,im=cy00)
plot(s00,type="l",xlim=c(-2,2),ylim=c(-2,2),main="(0+1i)^ax(a= 0→1)",xlab="Real",ylab="Imaginal",col=rgb(0,1,0))
# -1^x=(0±1i)^2x(i^2=-1)
par(new=T)#上書き
c01<-seq(-1,1,length=61)
f0<-function(x) (0+1i)^(x*Rad)
s01<-f0(cx00)
plot(s01,type="l",xlim=c(-2,2),ylim=c(-2,2),main="",xlab="",ylab="",col=rgb(0,0,1))
par(new=T)#上書き
plot(s01+1,type="l",xlim=c(-2,2),ylim=c(-2,2),main="",xlab="",ylab="",col=rgb(1,0,0))
par(new=T)#上書き
plot(s01-1,type="l",xlim=c(-2,2),ylim=c(-2,2),main="",xlab="",ylab="",col=rgb(1,0,0))
par(new=T)#上書き
plot(s01+2,type="l",xlim=c(-2,2),ylim=c(-2,2),main="",xlab="",ylab="",col=rgb(0,0,1))
par(new=T)#上書き
plot(s01-2,type="l",xlim=c(-2,2),ylim=c(-2,2),main="",xlab="",ylab="",col=rgb(0,0,1))
abline(h=0,col=c(200,200,200))
abline(v=0,col=c(200,200,200))
abline(v=1,col=c(200,200,200))
abline(v=2,col=c(200,200,200))
abline(v=-1,col=c(200,200,200))
abline(v=-2,col=c(200,200,200))
even01<-paste("y=(0+1i)^",Rad,"x(Even)")
odd01<-paste("y=(0+1i)^",Rad,"x(Odd)")
legend("bottomleft", legend=c("y=1^x",even01,odd01), lty =c(1,1,1),col=c(rgb(0,1,0),rgb(0,0,1),rgb(1,0,0)))
}
# アニメーション動作設定
Time_Code<-seq(0,1,length=11)
# アニメーション
library("animation")
saveGIF({
for (i in Time_Code){
Int01(i)
}
}, interval = 0.1, movie.name = "Int04.gif")
Int01<-function(Rad){
cx00<-seq(-3,3,length=61)
f0<-function(x) 1^x
cy00<-f0(cx00)
s00<-complex(re=cx00,im=cy00)
plot(s00,type="l",xlim=c(-2,2),ylim=c(-2,2),main="-(0+1i)^ax(a= 0→1)",xlab="Real",ylab="Imaginal",col=rgb(0,1,0))
# -1^x=(0±1i)^2x(i^2=-1)
par(new=T)#上書き
c01<-seq(-1,1,length=61)
f0<-function(x) -(0+1i)^(x*Rad)
s01<-f0(cx00)
plot(s01,type="l",xlim=c(-2,2),ylim=c(-2,2),main="",xlab="",ylab="",col=rgb(0,0,1))
par(new=T)#上書き
plot(s01+1,type="l",xlim=c(-2,2),ylim=c(-2,2),main="",xlab="",ylab="",col=rgb(1,0,0))
par(new=T)#上書き
plot(s01-1,type="l",xlim=c(-2,2),ylim=c(-2,2),main="",xlab="",ylab="",col=rgb(1,0,0))
par(new=T)#上書き
plot(s01+2,type="l",xlim=c(-2,2),ylim=c(-2,2),main="",xlab="",ylab="",col=rgb(0,0,1))
par(new=T)#上書き
plot(s01-2,type="l",xlim=c(-2,2),ylim=c(-2,2),main="",xlab="",ylab="",col=rgb(0,0,1))
abline(h=0,col=c(200,200,200))
abline(v=0,col=c(200,200,200))
abline(v=1,col=c(200,200,200))
abline(v=2,col=c(200,200,200))
abline(v=-1,col=c(200,200,200))
abline(v=-2,col=c(200,200,200))
even01<-paste("y=-(0+1i)^",Rad,"x(Even)")
odd01<-paste("y=-(0+1i)^",Rad,"x(Odd)")
legend("bottomleft", legend=c("y=1^x",even01,odd01), lty =c(1,1,1),col=c(rgb(0,1,0),rgb(0,0,1),rgb(1,0,0)))
}
# アニメーション動作設定
Time_Code<-seq(0,1,length=11)
# アニメーション
library("animation")
saveGIF({
for (i in Time_Code){
Int01(i)
}
}, interval = 0.1, movie.name = "Int06.gif")
実軸(Real Axis)を成立させる為の虚軸(Imaginal Axis)の設定方法は((それこそ「補助線」に過ぎないので)何パターンでも思い付くが、そのどのケースにおいても位相幾何学的(Topological)に(交代級数の概念に対応させる為、一般の複素関数論には登場しない)「一つの円上に分枝点を2つ置く」独特の射影を含まねばならない。その結果、上掲で説明した様な偶奇性(Parity)の概念導入や「単価関数としては半円しか描けなくなる」問題に加え、以下の様な特徴が付加される。
[【初心者向け】偶奇性概念と共役関係概念の連続性について。]
(https://qiita.com/ochimusha01/items/cca87fc1fe1294ae6b20)
-
複素共益(Complex Conjugate)の概念の導入。
【初心者向け】複素共役(Complex Conjugate)のアニメーション表示について。


- 球面座標系を二つの角度$θ,φ$で表そうとする時、全周分必要なのは片方だけで、もう片方は半周分だけで済む(例:経度と緯度の関係)。

実はこの考え方の背後にはトーラス(Torus)の概念が実存する。
【Python演算処理】単位球面を巡る数理②そして単位トーラスへ


- 周回数が偶数倍(整数倍)系の時に2倍系、奇数倍(1/2倍)系の時にπ倍系で値を返すΓ関数(階乗の概念を複素数全体に拡張した特殊関数)導入による円概念(直径,円の周長と面積,球の表面積と球体積)の数理的統合
【Python演算処理】半径・直径・円周長・円の面積・球の表面積・球の体積の計算上の往復
【Python演算処理】階乗と順列と組み合わせ
【Python演算処理】「N次球概念導入による円/球関係の数理の統合」?
ところでこの「円を二分する一対の分枝点」は、球面座標系では北極と南極の概念に対応する訳だが、対蹠(Antipodes)と呼ばれ多角形/多面体を扱う幾何学でも重要な役割を果たす。何しろこの2点を結んだ直線は必ず中心を通るし、その長さは直径(Diameter)に対応するし、さらに球面上の任意の第三点を追加して成立する三角形は全て直角三角形となるのである(ターレスの定理)。「補助線」としての複素数次元はこうした「まだその次元の実数軸の説明に組み込まれていない数理集合」の組み合わせによって出来ている訳である。
整数族(Integer Famiry)の実数への漸近戦略。
整数族は十進法(Decimal System)、すなわち10を法とする剰余類(Cosets)を周期単位(Unit Cycle)とし、さらにこれを周回数(Number of laps)の倍数で示す表表示形式を入れ子状態にした桁上がり法の導入によって2桁以上や少数点下の数字も示せる。この考え方は理論的には任意の整数を法とする有理数集合(Rational Set)にも適用可能であり、さらには演算に必要とされる精度さえ満たしていれば、(円周率πやネイピア数eの様な)無理数(Irrational number)を有理数の一種として擬似的に扱う事さえ可能とする。
Rによる10進数処理/数列化
# 0以上の整数のみを数列化対象とする場合
dc01<-c()
mydecimal <- function(n,dc01) {
if (n<10) return(c(n,dc01))
else dc01<-c(n%%10,dc01);return(Recall(trunc(n/10),dc01))
}
mydecimal(12345,dc01)
[1] 1 2 3 4 5
# 少数点下は求めたい桁数+1を与え、計算の後に同数で割る、
# すると計算対象外となった残りが「残余項」となる。
mydecimal(123.456*100,dc01)
[1] 1.0 2.0 3.0 4.0 5.6
Pythonによる10進数処理/数列化
# 0以上の整数のみを数列化対象とする場合
import math as m
dc02=[]
def mydecimal(n,dc02):
if n < 10:
dc02.insert(0,n);
return dc02
else:
dc02.insert(0,n%10)
return(mydecimal(m.floor(n/10),dc02))
print(mydecimal(12345,dc02))
# 少数点下は求めたい桁数+1を与え、計算の後に同数で割る、
# すると計算対象外となった残りが「残余項」となる。
dc02=[]
mydecimal(123.456*100,dc02)
print(dc02)
# 処理結果
[1, 2, 3, 4, 5]
[1, 2, 3, 4, 5.600000000000364]
かかる思考様式を近世から近代にかけて整備してきた数学者達は、同時に物理学者や天文学者である事が多く「演算結果と観測結果を可能な限り一致させる近似技術」の開発に血道を上げてきた。
-
テイラー級数(Taylor Series,1715年)/マクローリン級数(McLaughlin Series,18世紀)/ローラン級数(Laurent Series,1843年)、フーリエ級数(FT=Fourier Transform,1807年~1812年)などに見受けられる「計算可能な範囲まで計算し、残りの残余項を誤差として示す」漸近戦略。
【数理考古学】オイラーの公式を導出したマクローリン級数の限界?
ローラン級数(Laurent Series)のテイラー展開を試す。
【初心者向け】フーリエ解析(Fourier Analysis)を可視化する。 - ヤコブ・ベルヌーイが主著「推測法(Ars Conjectandi, Opus Posthumum, 1713)」の中でベルヌーイ試行(「成功か失敗か」「表か裏か」「勝ちか負けか」と2種類の結果しか得られない実験/試行)や、二項分布(Binomial Distribution、ベルヌーイ試行が生み出す独特の確率分布)や大数の弱法則(Weak Law of Large Numbers)に言及した事から始まり、ガウスが誤差関数(ERF=Error Function)や相補誤差関数 (ERFC=Complementary Error Function)を発表(1809年)した事で新局面を迎えた確率論の世界。
【初心者向け】誤差関数(ERF=Error Function)と相補誤差関数 (ERFC=Complementary Error Function)。
ここ数年取り組んできた「数についての考え方の総まとめ」その1。そんな感じで以下続報…