(2021年3月29日)pythonによる投稿。
(2021年4月12日)回転方向を反時計回りで統一。
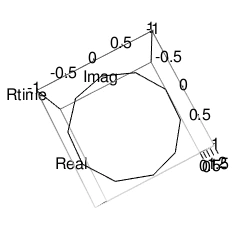
これまでの投稿内容から浮かび上がってきた単位円筒(Unit Cylinder)の概念についてまとめておきたいと思います。
単位円筒(Unit Cylinder)の定義
【初心者向け】N進法(N-ary)とp進数(p-adic) - Qiita
整数の除法に由来する商群(Factor Group)によって実数概念(Real Concept)を規定する場合を考える。ここでいう商群とは例えば10を法とする(任意の整数を10で割った結果得られる)10種類の剰余$G/N_{10}=(0,1,2,3,4,5,6,7,8,9)$を元とする集合で、この場合10段階を1周期とする10進法(Decimal System)に対応する。よく知られている様に周期数(Rap Set=周回集合)と段階数(Index Set=添字集合)を無限に入れ子状態にし続ける事により、その範囲内において任意の実数を表す事ができる。
商群 - Wikipedia演算上それは(1の冪根の演算結果集合たるガウス巡回群によって得られる)高さ(垂直方面の分割数)と辺数(水平方面の分割数)を同じくする多角形螺旋状1次元座標系(Polygonal Spiral One-dimensional Coordinate System)とイメージされる。
【初心者向け】挟み撃ち定理による円周率πの近似
これを単位円筒(Unit Cylinder)と設定し、周期数(周回集合)や段階数(添字集合)として加法整数群を与える場合を検討していく形となります。
加法整数群(Additive Integer Group)
【初心者向け】群論概念(Group Theory Concept)①基本定義
Z_n(n=-\infty→-1→0→1→+\infty)\\=(-\infty,…,-3,-2,-1,0,1,2,3,…,+\infty)
群論(Group Theory)における基本中の基本ですが、単位円筒概念導入に合わせた再定義が必要となるのです。
自然数集合(Natulal Set)の準備
まず元(Element) として自然数集合(Natulal Set)、すなわち初項(First Term)$α=1$,公差(Common Difference)$d=1$,一般項(General Term)$α+(n-1)d$の等差数列(Arithmetic Sequence=算術数列)を準備します。
N_n(n=1→\infty)\\
=(1+(1-1)×1=1,1+(2-1)×1=2,1+(3-1)×1=3,…,1+(\infty-1)×1=\infty)\\
=(1,2,3,…,Inf(inity))
以下の様に再帰的に考える事も出来ます。
N_n(n=1→\infty)\\
=(1,1+1=2,(1+1)+1=3,…,\infty+1=\infty)\\
=(1,2,3,…,Inf(inity))
どちらの場合も範囲に加法単位元(Additive Identity)0を加えても添字範囲が拡張されるだけで演算の連続性(Operation Continuity)そのものは維持され(結合法則((Associative Law))の成立)、演算結果(Operation Result)も閉じています(整数以外の数が登場する余地がない)。

%matplotlib nbagg
import math as m
import cmath as c
import numpy as num
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
import matplotlib.animation as animation
# 円柱データ作成
c0=num.linspace(0,m.pi*120,1201,endpoint = True)
s0=[]
for nm in range(len(c0)):
s0.append(complex(m.cos(c0[nm]),m.sin(c0[nm])))
s1=num.array(s0)
z0=num.linspace(0,2,1201,endpoint = True)
# 単位円データ作成
u0=num.linspace(0,m.pi*2,61,endpoint = True)
u1=[]
for nm in range(len(u0)):
u1.append(complex(m.cos(u0[nm]),m.sin(u0[nm])))
uc=num.array(u1)
uz0=num.repeat(0,61)
uz1=num.repeat(1,61)
uz2=num.repeat(2,61)
# グラフ表示
plt.style.use('default')
fig = plt.figure()
ax = Axes3D(fig)
# 関数定義
def unit_cylinder(n):
plt.cla()
#円柱描画
ax.plot(s1.real,s1.imag,z0,color="gray",lw=0.5)
#スポーク描画
#for num in range(len(uc)):
# ax.plot([0,uc[num].real],[0,uc[num].imag],[0,0],color="gray",lw=0.5)
#for num in range(len(uc)):
# ax.plot([0,uc[num].real],[0,uc[num].imag],[1,1],color="gray",lw=0.5)
for num in range(len(uc)):
ax.plot([0,uc[num].real],[0,uc[num].imag],[0,0],color="olivedrab",lw=0.5)
#単位円描画
ax.plot(uc.real,uc.imag,uz0,color="green",lw=1)
ax.plot(uc.real,uc.imag,uz1,color="blue",lw=1)
ax.plot(uc.real,uc.imag,uz2,color="blue",lw=1)
#実数線追加
ax.plot([1,1],[0,0],[0,2],color="blue",lw=1)
ax.plot([0,1],[0,0],[0,0],color="black",lw=1)
ax.plot([0,1],[0,0],[1,1],color="blue",lw=1)
ax.plot([0,1],[0,0],[2,2],color="blue",lw=1)
ax.plot([0,0],[0,0],[0,2],color="black",lw=1)
#諸元追加
ax.set_ylim([-1.1,1.1])
ax.set_xlim([-1.1,1.1])
ax.set_zlim([0.1,2.1])
ax.set_title("Unit Cylinder")
ax.set_xlabel("Real")
ax.set_ylabel("Imaginal")
ax.set_zlabel("Cycle")
# グラフを回転
ax.view_init(elev=45, azim=Time_code[n])
Time_code0=num.arange(0,360,6)
Time_code=Time_code0[::-1]
# unit_cylinder(len(s1))
# plt.show()
ani = animation.FuncAnimation(fig, unit_cylinder, interval=50,frames=len(Time_code))
ani.save("output500.gif", writer="pillow")
逆元(Inverse Element)の準備
上掲の拡張自然数集合(?)$N_n(n=0→\infty)(0,1,2,3,…,\infty)$について逆元(Inverse Element)$-N_n(n=-\infty→0)=(-\infty,…,-3,-2,-1,0)$を準備します。この場合も「結合法則成立による演算の連続性の担保」は成立し、演算結果も閉じています。

%matplotlib nbagg
import math as m
import cmath as c
import numpy as num
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
import matplotlib.animation as animation
# 円柱データ作成
c0=num.linspace(0,m.pi*120,1201,endpoint = True)
s0=[]
for nm in range(len(c0)):
s0.append(complex(m.cos(c0[nm]),m.sin(c0[nm])))
s1=num.array(s0)
z0=num.linspace(-2,0,1201,endpoint = True)
# 単位円データ作成
u0=num.linspace(0,m.pi*2,61,endpoint = True)
u1=[]
for nm in range(len(u0)):
u1.append(complex(m.cos(u0[nm]),m.sin(u0[nm])))
uc=num.array(u1)
uz0=num.repeat(-2,61)
uz1=num.repeat(-1,61)
uz2=num.repeat(0,61)
# グラフ表示
plt.style.use('default')
fig = plt.figure()
ax = Axes3D(fig)
# 関数定義
def unit_cylinder(n):
plt.cla()
#円柱描画
ax.plot(s1.real,s1.imag,z0,color="gray",lw=0.5)
#スポーク描画
#for num in range(len(uc)):
# ax.plot([0,uc[num].real],[0,uc[num].imag],[0,0],color="gray",lw=0.5)
#for num in range(len(uc)):
# ax.plot([0,uc[num].real],[0,uc[num].imag],[1,1],color="gray",lw=0.5)
for num in range(len(uc)):
ax.plot([0,uc[num].real],[0,uc[num].imag],[0,0],color="olivedrab",lw=0.5)
#単位円描画
ax.plot(uc.real,uc.imag,uz0,color="red",lw=1)
ax.plot(uc.real,uc.imag,uz1,color="red",lw=1)
ax.plot(uc.real,uc.imag,uz2,color="green",lw=1)
#実数線追加
ax.plot([0,0],[0,0],[-2,0],color="black",lw=1)
ax.plot([0,1],[0,0],[-0,0],color="black",lw=1)
ax.plot([0,1],[0,0],[-1,-1],color="red",lw=1)
ax.plot([0,1],[0,0],[-2,-2],color="red",lw=1)
ax.plot([1,1],[0,0],[-2,0],color="red",lw=1)
#諸元追加
ax.set_ylim([-1.1,1.1])
ax.set_xlim([-1.1,1.1])
ax.set_zlim([-2.1,0.1])
ax.set_title("Unit Cylinder")
ax.set_xlabel("Real")
ax.set_ylabel("Imaginal")
ax.set_zlabel("Cycle")
# グラフを回転
ax.view_init(elev=45, azim=Time_code[n])
Time_code0=num.arange(0,360,6)
Time_code=Time_code0[::-1]
# unit_cylinder(len(s1))
# plt.show()
ani = animation.FuncAnimation(fig, unit_cylinder, interval=50,frames=len(Time_code))
ani.save("output401.gif", writer="pillow")
元と逆元の合成
上掲二つの演算結果集合(Operation Result Set)を一つの集合に射影(Projection)した積(Product)が加法整数群となります。この場合も「結合法則成立による演算の連続性の担保」は成立し、演算結果も閉じています。

%matplotlib nbagg
import math as m
import cmath as c
import numpy as num
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
import matplotlib.animation as animation
# 円柱データ作成
c0=num.linspace(0,m.pi*120,1201,endpoint = True)
s0=[]
for nm in range(len(c0)):
s0.append(complex(m.cos(c0[nm]),m.sin(c0[nm])))
s1=num.array(s0)
z0=num.linspace(-1,1,1201,endpoint = True)
# 単位円データ作成
u0=num.linspace(0,m.pi*2,61,endpoint = True)
u1=[]
for nm in range(len(u0)):
u1.append(complex(m.cos(u0[nm]),m.sin(u0[nm])))
uc=num.array(u1)
uz0=num.repeat(-1,61)
uz1=num.repeat(-0,61)
uz2=num.repeat(1,61)
# グラフ表示
plt.style.use('default')
fig = plt.figure()
ax = Axes3D(fig)
# 関数定義
def unit_cylinder(n):
plt.cla()
#円柱描画
ax.plot(s1.real,s1.imag,z0,color="gray",lw=0.5)
#スポーク描画
#for num in range(len(uc)):
# ax.plot([0,uc[num].real],[0,uc[num].imag],[0,0],color="gray",lw=0.5)
#for num in range(len(uc)):
# ax.plot([0,uc[num].real],[0,uc[num].imag],[1,1],color="gray",lw=0.5)
for num in range(len(uc)):
ax.plot([0,uc[num].real],[0,uc[num].imag],[0,0],color="olivedrab",lw=0.5)
#単位円描画
ax.plot(uc.real,uc.imag,uz0,color="red",lw=1)
ax.plot(uc.real,uc.imag,uz1,color="green",lw=1)
ax.plot(uc.real,uc.imag,uz2,color="blue",lw=1)
#実数線追加
ax.plot([0,0],[0,0],[-1,1],color="black",lw=1)
ax.plot([0,1],[0,0],[-1,-1],color="red",lw=1)
ax.plot([0,1],[0,0],[0,0],color="black",lw=1)
ax.plot([0,1],[0,0],[1,1],color="blue",lw=1)
ax.plot([1,1],[0,0],[-1,0],color="red",lw=1)
ax.plot([1,1],[0,0],[0,1],color="blue",lw=1)
#諸元追加
ax.set_ylim([-1.1,1.1])
ax.set_xlim([-1.1,1.1])
ax.set_zlim([-1.1,1.1])
ax.set_title("Unit Cylinder")
ax.set_xlabel("Real")
ax.set_ylabel("Imaginal")
ax.set_zlabel("Cycle")
# グラフを回転
ax.view_init(elev=45, azim=Time_code[n])
Time_code0=num.arange(0,360,6)
Time_code=Time_code0[::-1]
# unit_cylinder(len(s1))
# plt.show()
ani = animation.FuncAnimation(fig, unit_cylinder, interval=50,frames=len(Time_code))
ani.save("output502.gif", writer="pillow")
偶数群(Even Group)と奇数集合(Odd Set)
単位円筒で考える以上、ここでいわゆる「ピッチ問題」を検討しない訳にはいきません。
ピッチ1(周期1)の場合の増減
以下の無限級数に対応。ここでは仮にラップ級数(Rap Series)と呼ぶ。加法整数群の増減幅を1に定める案外重要な演算(Opreation)。
1^n(n=-\infty→+\infty)=(1,…,1,1,1,…,1)
%matplotlib nbagg
import math as m
import cmath as c
import numpy as num
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
import matplotlib.animation as animation
# 円柱データ作成
c0=num.linspace(0,m.pi*4,121,endpoint = True)
s0=[]
for nm in range(len(c0)):
s0.append(complex(m.cos(c0[nm]),m.sin(c0[nm])))
s1=num.array(s0)
z0=num.linspace(-1,1,121,endpoint = True)
# 単位円データ作成
u0=num.linspace(0,m.pi*2,61,endpoint = True)
u1=[]
for nm in range(len(u0)):
u1.append(complex(m.cos(u0[nm]),m.sin(u0[nm])))
uc=num.array(u1)
uz0=num.repeat(-1,61)
uz1=num.repeat(-0,61)
uz2=num.repeat(1,61)
# グラフ表示
plt.style.use('default')
fig = plt.figure()
ax = Axes3D(fig)
# 関数定義
def unit_cylinder(n):
plt.cla()
#円柱描画
ax.plot(s1.real,s1.imag,z0,color="black",lw=0.5)
#スポーク描画
for nm in range(len(s1)):
ax.plot([0,s1[nm].real],[0,s1[nm].imag],z0[nm],color="gray",lw=0.5)
#単位円描画
ax.plot(uc.real,uc.imag,uz0,color="red",lw=1)
ax.plot(uc.real,uc.imag,uz1,color="green",lw=1)
ax.plot(uc.real,uc.imag,uz2,color="blue",lw=1)
#実数線追加
ax.plot([0,0],[0,0],[-1,1],color="black",lw=1)
ax.plot([0,1],[0,0],[-1,-1],color="red",lw=1)
ax.plot([0,1],[0,0],[0,0],color="green",lw=1)
ax.plot([0,1],[0,0],[1,1],color="blue",lw=1)
ax.plot([1,1],[0,0],[-1,0],color="red",lw=1)
ax.plot([1,1],[0,0],[0,1],color="blue",lw=1)
#諸元追加
ax.set_ylim([-1.1,1.1])
ax.set_xlim([-1.1,1.1])
ax.set_zlim([-1.1,1.1])
ax.set_title("Unit Cylinder")
ax.set_xlabel("Real")
ax.set_ylabel("Imaginal")
ax.set_zlabel("Cycle")
# グラフを回転
ax.view_init(elev=10, azim=Time_code[n])
Time_code0=num.arange(0,360,6)
Time_code=Time_code0[::-1]
# unit_cylinder(len(s1))
# plt.show()
ani = animation.FuncAnimation(fig, unit_cylinder, interval=50,frames=len(Time_code))
ani.save("output503.gif", writer="pillow")
その水平位置からの観測結果(互いに直交する周期1の$\cos(θ)$波と$\sin(θ)$波の検出)

$\cos(θ)$波
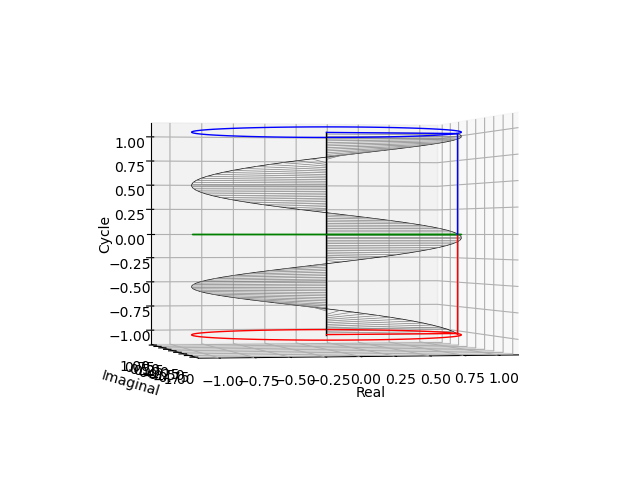
$\sin(θ)$波
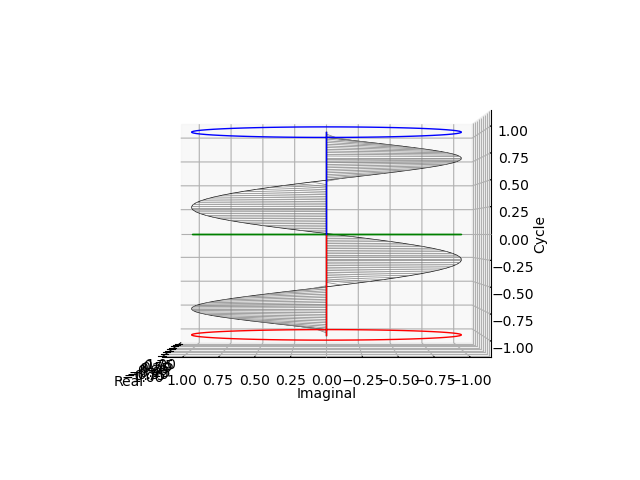
%matplotlib nbagg
import math as m
import cmath as c
import numpy as num
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
import matplotlib.animation as animation
# 円柱データ作成
c0=num.linspace(0,m.pi*4,121,endpoint = True)
s0=[]
for nm in range(len(c0)):
s0.append(complex(m.cos(c0[nm]),m.sin(c0[nm])))
s1=num.array(s0)
z0=num.linspace(-1,1,121,endpoint = True)
# 単位円データ作成
u0=num.linspace(0,m.pi*2,61,endpoint = True)
u1=[]
for nm in range(len(u0)):
u1.append(complex(m.cos(u0[nm]),m.sin(u0[nm])))
uc=num.array(u1)
uz0=num.repeat(-1,61)
uz1=num.repeat(-0,61)
uz2=num.repeat(1,61)
# グラフ表示
plt.style.use('default')
fig = plt.figure()
ax = Axes3D(fig)
# 関数定義
def unit_cylinder(n):
plt.cla()
#円柱描画
ax.plot(s1.real,s1.imag,z0,color="black",lw=0.5)
#スポーク描画
for nm in range(len(s1)):
ax.plot([0,s1[nm].real],[0,s1[nm].imag],z0[nm],color="gray",lw=0.5)
#単位円描画
ax.plot(uc.real,uc.imag,uz0,color="red",lw=1)
ax.plot(uc.real,uc.imag,uz1,color="green",lw=1)
ax.plot(uc.real,uc.imag,uz2,color="blue",lw=1)
#実数線追加
ax.plot([0,0],[0,0],[-1,1],color="black",lw=1)
ax.plot([0,1],[0,0],[-1,-1],color="red",lw=1)
ax.plot([0,1],[0,0],[0,0],color="green",lw=1)
ax.plot([0,1],[0,0],[1,1],color="blue",lw=1)
ax.plot([1,1],[0,0],[-1,0],color="red",lw=1)
ax.plot([1,1],[0,0],[0,1],color="blue",lw=1)
#諸元追加
ax.set_ylim([-1.1,1.1])
ax.set_xlim([-1.1,1.1])
ax.set_zlim([-1.1,1.1])
ax.set_title("Unit Cylinder")
ax.set_xlabel("Real")
ax.set_ylabel("Imaginal")
ax.set_zlabel("Cycle")
# グラフを回転
ax.view_init(elev=0, azim=Time_code[n])
Time_code0=num.arange(0,360,6)
Time_code=Time_code0[::-1]
# unit_cylinder(len(s1))
# plt.show()
ani = animation.FuncAnimation(fig, unit_cylinder, interval=50,frames=len(Time_code))
ani.save("output504.gif", writer="pillow")
一見単純極まりない数理に見えますが、ここから突如としてガンマ関数(Γ Function)の概念が派生するから要注意です。
【Python演算処理】階乗と順列と組み合わせ
【Python演算処理】「N次球概念導入による円/球関係の数理の統合」?
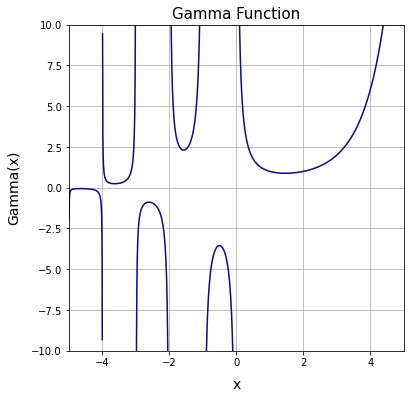
ピッチ1/2(周期2)の場合の増減
交代級数(Alternating Series)概念に対応。
-1^n(n=-\infty→+\infty)=(-1,…,1,-1,1,…,-1)
%matplotlib nbagg
import math as m
import cmath as c
import numpy as num
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
import matplotlib.animation as animation
# 円柱データ作成
c0=num.linspace(0,m.pi*2,121,endpoint = True)
s0=[]
for nm in range(len(c0)):
s0.append(complex(m.cos(c0[nm]),m.sin(c0[nm])))
s1=num.array(s0)
z0=num.linspace(-1,1,121,endpoint = True)
# 単位円データ作成
u0=num.linspace(0,m.pi*2,61,endpoint = True)
u1=[]
for nm in range(len(u0)):
u1.append(complex(m.cos(u0[nm]),m.sin(u0[nm])))
uc=num.array(u1)
uz0=num.repeat(-1,61)
uz1=num.repeat(-0,61)
uz2=num.repeat(1,61)
# グラフ表示
plt.style.use('default')
fig = plt.figure()
ax = Axes3D(fig)
# 関数定義
def unit_cylinder(n):
plt.cla()
#円柱描画
ax.plot(s1.real,s1.imag,z0,color="black",lw=0.5)
#スポーク描画
for nm in range(len(s1)):
ax.plot([0,s1[nm].real],[0,s1[nm].imag],z0[nm],color="gray",lw=0.5)
#単位円描画
ax.plot(uc.real,uc.imag,uz0,color="red",lw=1)
ax.plot(uc.real,uc.imag,uz1,color="green",lw=1)
ax.plot(uc.real,uc.imag,uz2,color="blue",lw=1)
#実数線追加
ax.plot([0,0],[0,0],[-1,1],color="black",lw=1)
ax.plot([0,1],[0,0],[-1,-1],color="red",lw=1)
ax.plot([0,-1],[0,0],[0,0],color="green",lw=1)
ax.plot([0,1],[0,0],[1,1],color="blue",lw=1)
ax.plot([1,1],[0,0],[-1,0],color="red",lw=1)
ax.plot([1,1],[0,0],[0,1],color="blue",lw=1)
#諸元追加
ax.set_ylim([-1.1,1.1])
ax.set_xlim([-1.1,1.1])
ax.set_zlim([-1.1,1.1])
ax.set_title("Unit Cylinder")
ax.set_xlabel("Real")
ax.set_ylabel("Imaginal")
ax.set_zlabel("Cycle")
# グラフを回転
ax.view_init(elev=10, azim=Time_code[n])
Time_code0=num.arange(0,360,6)
Time_code=Time_code0[::-1]
# unit_cylinder(len(s1))
# plt.show()
ani = animation.FuncAnimation(fig, unit_cylinder, interval=50,frames=len(Time_code))
ani.save("output505.gif", writer="pillow")
その水平位置からの観測(互いに直交する周期2の$\cos(θ)$波と$\sin(θ)$波の検出)

$\cos(θ)$波
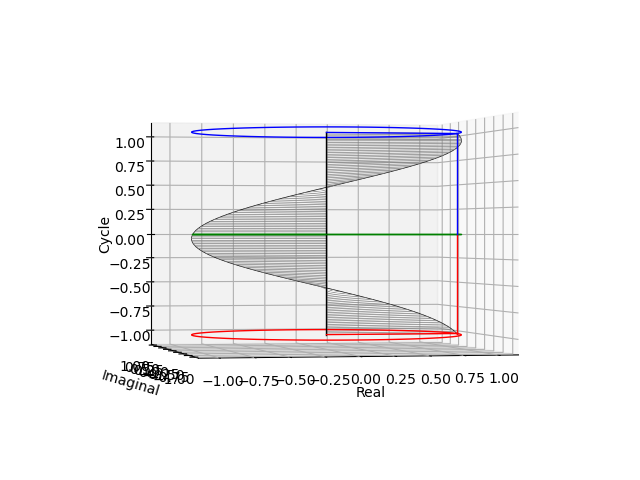
$\sin(θ)$波
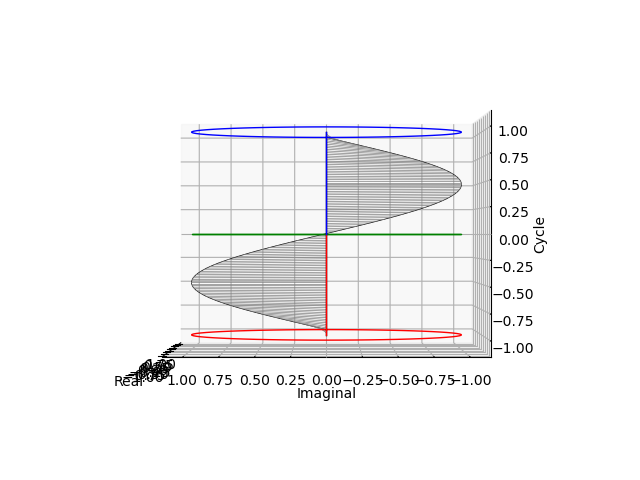
%matplotlib nbagg
import math as m
import cmath as c
import numpy as num
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
import matplotlib.animation as animation
# 円柱データ作成
c0=num.linspace(0,m.pi*2,121,endpoint = True)
s0=[]
for nm in range(len(c0)):
s0.append(complex(m.cos(c0[nm]),m.sin(c0[nm])))
s1=num.array(s0)
z0=num.linspace(-1,1,121,endpoint = True)
# 単位円データ作成
u0=num.linspace(0,m.pi*2,61,endpoint = True)
u1=[]
for nm in range(len(u0)):
u1.append(complex(m.cos(u0[nm]),m.sin(u0[nm])))
uc=num.array(u1)
uz0=num.repeat(-1,61)
uz1=num.repeat(-0,61)
uz2=num.repeat(1,61)
# グラフ表示
plt.style.use('default')
fig = plt.figure()
ax = Axes3D(fig)
# 関数定義
def unit_cylinder(n):
plt.cla()
#円柱描画
ax.plot(s1.real,s1.imag,z0,color="black",lw=0.5)
#スポーク描画
for nm in range(len(s1)):
ax.plot([0,s1[nm].real],[0,s1[nm].imag],z0[nm],color="gray",lw=0.5)
#単位円描画
ax.plot(uc.real,uc.imag,uz0,color="red",lw=1)
ax.plot(uc.real,uc.imag,uz1,color="green",lw=1)
ax.plot(uc.real,uc.imag,uz2,color="blue",lw=1)
#実数線追加
ax.plot([0,0],[0,0],[-1,1],color="black",lw=1)
ax.plot([0,1],[0,0],[-1,-1],color="red",lw=1)
ax.plot([0,-1],[0,0],[0,0],color="green",lw=1)
ax.plot([0,1],[0,0],[1,1],color="blue",lw=1)
ax.plot([1,1],[0,0],[-1,0],color="red",lw=1)
ax.plot([1,1],[0,0],[0,1],color="blue",lw=1)
#諸元追加
ax.set_ylim([-1.1,1.1])
ax.set_xlim([-1.1,1.1])
ax.set_zlim([-1.1,1.1])
ax.set_title("Unit Cylinder")
ax.set_xlabel("Real")
ax.set_ylabel("Imaginal")
ax.set_zlabel("Cycle")
# グラフを回転
ax.view_init(elev=0, azim=Time_code[n])
Time_code0=num.arange(0,360,6)
Time_code=Time_code0[::-1]
# unit_cylinder(len(s1))
# plt.show()
ani = animation.FuncAnimation(fig, unit_cylinder, interval=50,frames=len(Time_code))
ani.save("output506.gif", writer="pillow")
周期1でとった場合にΓ関数導入が自明の場合として導入されてくる様に、周期2でとった場合には偶数群(Even Group)と奇数集合(Odd Set)の概念導入が不可避となります。
【数理考古学】とある実数列の規定例①等差数列から加法整数群へ
実軸(Real Axis)を成立させる為の虚軸(Imaginal Axis)の設定方法自体は(それこそ「補助線」に過ぎないので)どの様な形にも設定可能なのですが、どの場合でも全体を周期2の単位円筒2セットで表す偶奇性(Parity)概念の導入だけは避けられないのです。
Rによる「偶奇性導入による整数表現」実装例(-方向)

Rによる「偶奇性導入による整数表現」実装例(+方向)

偶数群(Even Group)
演算結果集合としては区間:無限小$-\infty$~0~無限大$+\infty$、初項0、公差±2、一般項±2nの両側無限数列を構成する。
Even_n(n=-\infty→0→+\infty)=(-\infty,…,-2n,…,-2×2=-4,-2×1=-2,-2×0=0,-2×1=2,-2×2=4,…,2n,…,+\infty)
- その演算は加減算の範囲で閉じており(偶数+偶数=偶数、偶数-偶数=偶数)、加法単位元と逆元を備え、かつ結合則(a+b)+c=a+(b+c)を満たす(元と単位元と逆元が同じ等差数列上に連続する)ので群の成立条件を満たす。
奇数集合(Odd Set)
演算結果集合としては区間:無限小$-\infty$~0~無限大$+\infty$、初項1、公差±2、一般項±2n+1の両側無限数列を構成する。
Odd_n(n=-\infty→0→+\infty)=(-\infty,…,-2n+1,…,-2×2+1=-3,-2×1+1=-1,2×0+1=1,2×1+1=3,…,2n+1,…,+\infty)
あるいは
Odd_n(n=-\infty→0→+\infty)=(-\infty,…,-2n-1,…,-2×2-1=-5,-2×1-1=-3,2×0-1=-1,2×1-1=1,2×2-1=3,…,2n+1,…,+\infty)
- その演算は逆元を備え、結合則(a+b)+c=a+(b+c)も満たすものの、加法単位元0は集合範囲外で演算結果も閉じてない(奇数+奇数=偶数、奇数-奇数=偶数)。ゆえに群の成立条件を満たさない。
- 関数における奇関数も(その対称性ゆえにそれを備えない偶関数と異なり)逆関数を備え常に一対で現れる。また幾何学における(対蹠間を結ぶ直線が引けない)奇数角形の多角形もまた(それぞれ片側の対蹠にのみ接する)一対として現れる。この様に「偶数の対称性」と「奇数の双極性」の対比は(それぞれ形を変えながら)あらゆる分野に普遍的に現れる。
とりあえず実用レベルでは「単位円筒には大まかに分けて(偶奇の概念の導入方法がそれぞれこの様に異なる)2種類あって状況に応じた使い分けが必要」程度の認識で構わないでしょう。実際、それまで数学史や物理学史の世界は(ほとんど無意識のうちに自明の理っぽく)この辺りを巧みに使い分けてきた訳で「ここを曖昧にしたままではコンピューター上で走らない」現実に直面して初めて問題の重要性を直視した側面すらある訳です。
固有ベクトル(Eigenvector)/固有値(Eigenvalue)概念の萌芽。
後者の場合はCos(θ)の増減に注目するなら、こうも図示可能だったりします。

%matplotlib nbagg
import math as m
import cmath as c
import numpy as num
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
import matplotlib.animation as animation
# 円柱データ作成
c0=num.linspace(0,m.pi*4,121,endpoint = True)
s0=[]
for nm in range(len(c0)):
s0.append(complex(m.cos(c0[nm]),m.sin(c0[nm])))
s1=num.array(s0)
z0=num.linspace(-1,1,121,endpoint = True)
# 単位円データ作成
u0=num.linspace(0,m.pi*2,61,endpoint = True)
u1=[]
for nm in range(len(u0)):
u1.append(complex(m.cos(u0[nm]),m.sin(u0[nm])))
uc=num.array(u1)
uz0=num.repeat(-1,61)
uz1=num.repeat(-0,61)
uz2=num.repeat(1,61)
# グラフ表示
plt.style.use('default')
fig = plt.figure()
ax = Axes3D(fig)
# 関数定義
def unit_cylinder(n):
plt.cla()
#円柱描画
ax.plot(s1.real,s1.imag,s1.real,color="black",lw=0.5)
#スポーク描画
for nm in range(len(s1)):
ax.plot([s1[nm].real,s1[nm].real],[s1[nm].imag,s1[nm].imag],[s1[nm].real,0],color="gray",lw=0.5)
#単位円描画
ax.plot(uc.real,uc.imag,uz0,color="red",lw=1)
ax.plot(uc.real,uc.imag,uz1,color="green",lw=1)
ax.plot(uc.real,uc.imag,uz2,color="blue",lw=1)
#実数線追加
ax.plot([0,0],[0,0],[-1,1],color="black",lw=1)
ax.plot([0,-1],[0,0],[-1,-1],color="red",lw=1)
ax.plot([0,1],[0,0],[0,0],color="green",lw=1)
ax.plot([0,1],[0,0],[1,1],color="blue",lw=1)
ax.plot([-1,-1],[0,0],[-1,0],color="red",lw=1)
ax.plot([1,1],[0,0],[0,1],color="blue",lw=1)
#諸元追加
ax.set_ylim([-1.1,1.1])
ax.set_xlim([-1.1,1.1])
ax.set_zlim([-1.1,1.1])
ax.set_title("Unit Cylinder")
ax.set_xlabel("Real")
ax.set_ylabel("Imaginal")
ax.set_zlabel("Cycle")
# グラフを回転
ax.view_init(elev=0, azim=Time_code[n])
Time_code0=num.arange(0,360,6)
Time_code=Time_code0[::-1]
# unit_cylinder(len(s1))
# plt.show()
ani = animation.FuncAnimation(fig, unit_cylinder, interval=50,frames=len(Time_code))
ani.save("output507.gif", writer="pillow")
まずは以下の数理との関連に興味が湧きます。
-
一次関数(Linear Function)$y= \pm x$や$y= \pm |x|$を回転軸とする確率楕円の世界。上掲の「Cos(θ)回転概念」の上位互換で「2本目/3本目の実数軸導入による円錐的空間展開」を基調とする「デカルト座標系(Cartesian Coordinate System)」への拡張が視野に入ってくる(あくまで「上位互換」なので、偶奇性概念との関連も出てくる。)。
【初心者向け】方形描画関数①三角関数との関係。



- 平面上は$\cos(θ)$のサイクルを適用した楕円の高さの増減によってシミュレーション可能な球面座標上の回転の世界。実軸wと互いに(少なくとも一つのベクトルがそれ以外のベクトルの線形結合によって表される)線形従属(linearly Dependent)関係にあるi,j,kの4軸によって構成される四元数(Quaternion)の座標系へと繋がっていく。
線形独立性とは? 線形従属性とは?
【Rで球面幾何学】ジンバルロック(?)やリサージュ曲線(?)との邂逅。

- 三次元デカルト座標系の展開が3対6個の円錐の幾何学的イメージを基調とする様に、四元数の展開は(任意の球表面上における対蹠=立方対角線の両端を出発点とする)立方体の幾何学的イメージを基調とする。
【初心者向け】線形関数や絶対値関数
【オイラーの多面体定理と正多面体】正方形における平方対角線と立方体における立方対角線の関係について。

そう、どの場合も原則として(立体空間上の円弧の回転操作を側面から観察した)平面空間における楕円の変形過程が「直交する2軸の値の増減の連動」と見て取れるのが特徴で、線形代数(linear Algebra)の世界においては、おそらくここでいう「直交する2軸」が「固有ベクトル(Eigenvector)」、「(連動して変動する)2軸の値」が「固有値(Eigenvalue)」の概念で掌握される展開を迎えると思われます(不勉強につき断言までは出来ない)。
線形代数の基礎 第12回 - 固有値・固有ベクトル - Qiita
線形代数の基礎 第13回 - 対角化 - Qiita
ただし単位円筒の世界はあくまで(z軸の値を「xy面上の演算結果に特定の形で紐付けられた」単純形でのみ認識する)実軸(Real Axis)1本のみが実在し、他の座標軸全てを(なまじこれと直交し、線形独立を果たしているが故に任意の設定が導入可能な)虚軸(Imaginal Axis)に追いやる一次元的世界観に過ぎず、こうした考え方の導入は(座標系全体の基本設定に影響を与えない)オプションの一つとしか捉えられない訳です(逆をいえば、だからこそデカルト座標系と四元数座標系の導入がチャンポンに並列的に考えられたりもする)。しばしば世間は「虚数は実在するか?」といった話題で盛り上がりますが、こう考えてしまうと残念ながらその話題自体には別に深淵な哲学的意味合いは内在してないと断言せざるを得ません。そう、あくまでどこまでがその座標系の実数軸に標準的に組み込まれ、どこからが虚数軸としてその外側に置かれるかは全て「観測側が自ら設けた認識上の限界設定」に依存しているに過ぎないのです。深淵な哲学的意味合いに飢えているなら、むしろ「その峻別は観察対象を説明する上で本当に適切か」についてこだわり抜くべきでしょう。
線形代数6|線形独立のイメージと線形独立性とランクの関係
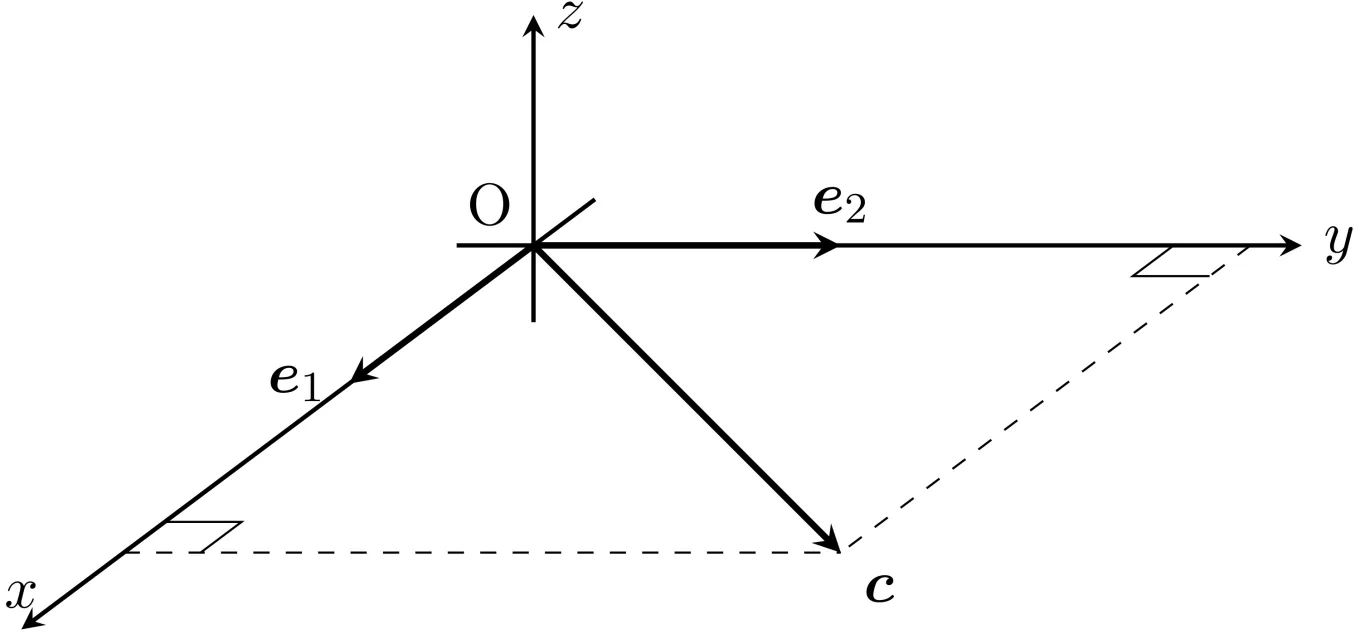
離心率(Eccentricity)概念との関連性の萌芽
ついでに上掲の「cos(θ)回転図」について「円が垂直に立つ」の極限状態を想定してみます。円筒系座標系(Cylinder Coordinate System)を球面系座標系(Spherical Coordinate System)に拡張する際に必ず通らねばならない重要な関門の一つとなるのです。
- 理論上、Z軸に位置する一対の「対蹠円」の半径を$1→0$、中心からの距離(絶対値)を$1→\infty$に近づける形で近似される(到達は不可能)。

- 究極的にはZ軸を均等尺から円尺に推移させる形で対応される。

どうやら(実際にはそこに真円が置けないとされる一方、反対側の極限状態として放物線や双曲線が出現する)離心率の数理と何か関係がありそうだ?(不勉強につき断言までは出来ない)
【無限遠点を巡る数理】離心率①二次曲線(楕円,放物線,双曲線)の極座標表示からの出発。
この問題については知識が全然足りていないので、今の私には全く論じる事が出来ません。そもそも取っ掛かりが全然見つからなくて絶賛放置中…
最後に(To be continued=以下続報)
数年がかりで試行錯誤しながら理解を進めてきましたが、全体像を俯瞰するとたったこれだけの事に過ぎないんですね。以降も逐次追記していきます。