本稿は、線形代数を独学でやり直し勉強した時のメモです。せっかくなのでアウトプットしようと思って書き始めました。詳しくは第1回の説明をご参照ください。
今回は、固有値・固有ベクトルの応用として、対角化の説明をしたいと思います。まずは対角化とはどういうものかを説明した後に、対角化の何が便利なのかを説明します。その後、対角の意味を図解して考えてみます。
1. 対角化とは何か
ある$n \times n$の正方行列$A$について、以下を考えます。
$$
\begin{array}{cll}
P &=& (\mathbf{p}_1, \mathbf{p}_2,\cdots,\mathbf{p}_n) &:& 固有ベクトルを横に並べた行列 \
\
\Lambda &=&
\left(
\begin{matrix}
\lambda_1 & & \
& \ddots && \
& & \lambda_n
\end{matrix}
\right) &:& 固有値を対角成分に並べた対角行列
\end{array}
$$
ここで、細かいことは考えず、$A$や$P$は正則であり、固有値・固有ベクトルはそれぞれ$n$個あるとしておきます(厳密でなくてすみませんが)。
このとき、固有値・固有ベクトルの定義から、
$$
AP = P\Lambda \tag{1}
$$
が成り立ちます。(後ほど2次元の例で確かめまてみます)。(1)の両辺に左から$P^{-1}$をかけると、
$$
P^{-1}AP=\Lambda \tag{2}
$$
となります。このように、行列$A$に対して、左側と右側からそれぞれ$P^{-1}$と$P$をかけることで、固有値を対角成分とする対角行列を作ることを、対角化と言います。
1.1. 2次元の例で(1)式を確かめてみる
$$
\begin{array}{cll}
P &=& (\mathbf{p}_1, \mathbf{p}_2) \
\
\Lambda &=& \left(
\begin{matrix}
\lambda_1 & \
& \lambda_2
\end{matrix}
\right)
\end{array}
$$
とすると、
$$
\begin{array}{cll}
AP &=& A(\mathbf{p}_1, \mathbf{p}_2) \
&=& (A\mathbf{p}_1, A\mathbf{p}_2)
\end{array}
$$
$$
\begin{array}{cll}
P\Lambda &=& (\mathbf{p}_1, \mathbf{p}_2)
\left(
\begin{matrix}
\lambda_1 & \
& \lambda_2
\end{matrix}
\right) \
&=& (\lambda_1 \mathbf{p}_1 + 0 \times \mathbf{p}_2, 0 \times \mathbf{p}_1 + \lambda_2 \mathbf{p}_2) \
&=& (\lambda_1 \mathbf{p}_1, \lambda_2 \mathbf{p}_2)
\end{array}
$$
ここで、$\lambda_i, \mathbf{p}_i$はそれぞれ$A$の固有値、固有ベクトルなので、
$$
\begin{array}{ccc}
A\mathbf{p}_1 &=& \lambda_1 \mathbf{p}_1 \
A\mathbf{p}_2 &=& \lambda_2 \mathbf{p}_2
\end{array}
$$
以上から、$AP = P\Lambda$が確かめられた。
2. 対角化の何がよいのか?
次に、対角化を使うと問題が簡単になる例として、$A$の$m$乗($A^m$)を求めることを考えてみます。(なお、次回に、もう1つの例として、楕円を回転させて簡単にする例を示してみる予定です。)
まず、対角化の式(2)の両辺を$m$乗すると、
$$
(P^{-1}AP)^m = \Lambda^m
$$
左辺を展開してみると、
$$
P^{-1}APP^{-1}AP\cdots P^{-1}AP = \Lambda^m
$$
(左辺には$P^{-1}AP$が$m$個並んでいる)。隣り合った$P$と$P^{-1}$は相殺されるので、
$$
PAA\cdots AP = \Lambda^m
$$
$A$をまとめると、結局、
$$
P^{-1}A^m P = \Lambda^m \tag{3}
$$
となります。(3)の両辺に左と右からそれぞれ$P$, $P^{-1}$をかけると、
$$
A^m = P \Lambda^m P^{-1} \tag{4}
$$
となります。ここで、$\Lambda$は対角行列なので、$\Lambda^m$は簡単に求まり、
$$
\Lambda^m =
\left(
\begin{matrix}
\lambda_1^m & & \
& \ddots & \
& & \lambda_n^m
\end{matrix}
\right)
$$
(4)式より、これに、両側からそれぞれ$P$と$P^{-1}$をかけることで$A^m$も簡単に求まることになります。
以上から、$A^m$を求めるときに、1回ずつ$A$をかけるという行列の計算をせず、成分毎の$m$乗を求められることになり、計算の見通しもとてもよくなりますし、計算量も減るということになります。
3. 座標についてのおさらい
次に、図を用いて対角化の意味を考えてみます。まず結論を簡単に書きますと、対角化とは、解きたい問題の見通しがよくなる方向(具体的には固有ベクトルの方向)に座標の取り方を変えているだけなのです。以下、このことを説明していきたいと思いますが、まずが、前提知識として、座標についてのおさらいから考えてみます。
3.1. 座標とは相対的なもの
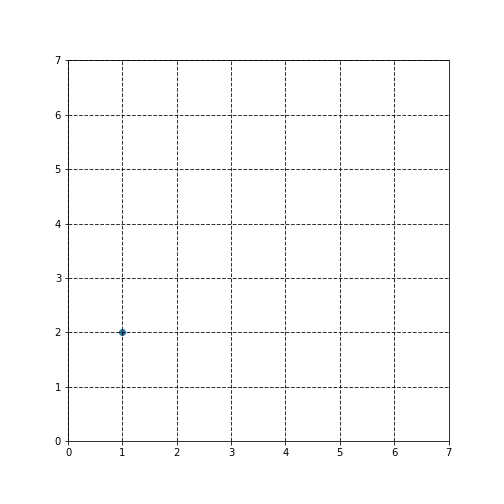
以下の図にあるような、2次元上の点を考えてみます。
この点の座標はいくつでしょうか?
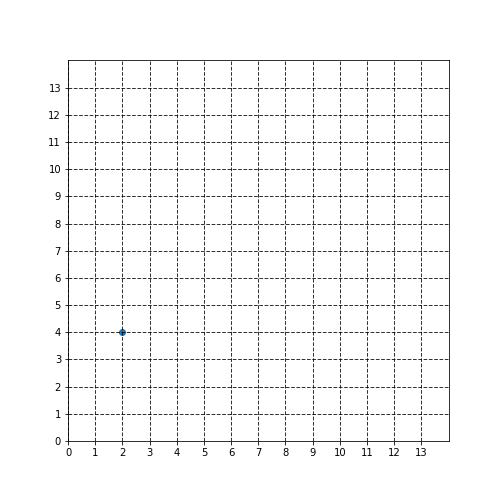
$(1,2)$ですね。本当にそうでしょうか?下図の点の位置は先ほどの図の点の位置と同じですが、この図でみると座標は$(2,4)$になっていますね。
このように、よく考えると、座標というのは相対的なもので、目盛りの取り方次第でどうにでも取れるのです。まあ、100cm=1mは、単位次第で1とも取れるし100とも取れるという話と同じで、当たり前といえば当たり前ですね。今後、この目盛りの取り方のことを座標系と呼ぶことにします。
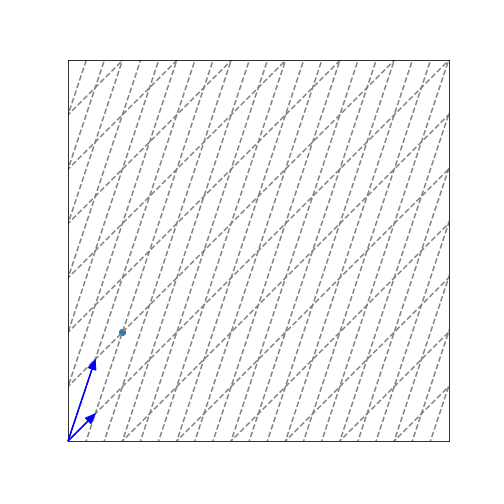
さらに、目盛りを以下のように斜めに取ってみるとどうでしょうか?(下図の点の位置もこれまでの図の点の位置と同じです。)
この目盛りを用いた座標系で考えると、この点は、$(1,1)$と見ることもできますね。(それぞれの矢印の方向に1単位ずつ進んでいる点と見なすことができるため。)
このように、目盛りは必ずしも直角に交わるように取らなければならないというわけではなく、自由自在に決めることができるのです!そして、この目盛り(軸)のことを、基底と呼ぶのでした。この辺の話は、第3回で説明していますので、そちらもご参照いただけましたらと思います。
3.2. 座標を変換してみる
次に、基底の取り方を変えた時に、座標がどのように変換されるかを考えてみます。例えば、3.1節の一番上の図の座標系での座標$(1,2)$と一番下の図の座標系での座標$(1,1)$の間には、どのような関係が成り立っているのでしょうか?
第3回でもご説明している通り、2次元上の点が、通常の座標系(つまり、正規直交基底$\mathbf{e}_1=(1,0)^t$と$\mathbf{e}_2=(0,1)^t$を用いた座標系)で$(x_1, x_2)$と表されている時、この点の位置$\mathbf{z}$は、$\mathbf{e}_1, \mathbf{e}_2$を用いて、
$$
\mathbf{z}=x_1 \mathbf{e}_1 + x_2 \mathbf{e}_2 \tag{5}
$$
と表すことができます。
また、同様に、$\mathbf{p}_1$、$\mathbf{p}_2$を基底とした座標系で、この点が$(y_1, y_2)$と表されている時は、この点の位置$\mathbf{z}$は、$\mathbf{p}_1$、$\mathbf{p}_2$を用いて、
$$
\mathbf{z}=y_1 \mathbf{p}_1 + y_2 \mathbf{p}_2 \tag{6}
$$
と表すことができます。(先ほどの例では、$\mathbf{p}_1$、$\mathbf{p}_2$はそれぞれ、図上の青色の2本の矢印に対応し、座標は$(1,1)$に対応していることになります。)
次に、
$$
\begin{array}{cll}
E &=& (\mathbf{e}_1, \mathbf{e}_2) \
&=& \left(
\begin{matrix}
1 & 0 \
0 & 1
\end{matrix}
\right) \
\mathbf{x} &=& \left(
\begin{matrix}
x_1 \
x_2
\end{matrix}
\right)
\end{array}
$$
とすると、(5)式は、
$$
\mathbf{z} = E \mathbf{x} \tag{7}
$$
と表すことができます。(単に行列の表現に書き換えただけです。行列の計算については第4回もご参照ください。)
また、同様に、
$$
\begin{array}{cll}
P &=& (\mathbf{p}_1, \mathbf{p}_2) \
\mathbf{y} &=& \left(
\begin{matrix}
y_1 \
y_2
\end{matrix}
\right)
\end{array}
$$
とすると、(6)式は、
$$
\mathbf{z} = P \mathbf{y} \tag{8}
$$
とおくことができます。
ここで、(7)式と(8)式は同じ点$\mathbf{z}$を表しているので、
$$
P \mathbf{y} = E \mathbf{x}
$$
成り立ちます。ここで、$E$は単位行列なので、
$$
P \mathbf{y} = \mathbf{x} \tag{9}
$$
さらに、(9)式の両辺に左から$P$の逆行列$P^{-1}$をかけると、
$$
\mathbf{y} = P^{-1} \mathbf{x} \tag{10}
$$
となります。
以上から、
-
正規直交基底による座標系での座標$\mathbf{x}=(x_1, x_2)^t$を、基底$P=(\mathbf{p}_1, \mathbf{p}_2)$による座標系での座標$\mathbf{y}=(y_1, y_2)^t$に変換する時は、(10)式のように$\mathbf{x}$に$P^{-1}$をかけることにより変換できる。
-
逆に、基底$P=(\mathbf{p}_1, \mathbf{p}_2)$にによる座標系での座標$\mathbf{y}=(y_1, y_2)^t$を正規直交基底による座標系での座標$\mathbf{x}=(x_1, x_2)^t$に変換する時は、(9)式のように、$\mathbf{y}$に$P$をかけることにより変換できる。
ということになります。
4. 対角化の意味を図示してみる
さて、では次に、2節の話に戻り、例として、$\mathbf{x}=(1,2)^t$に左から順次、以下の行列$A$をかけることを考えてみます。(つまり$A^{m}\mathbf{x}$を計算してみるということです。)
$$
A=
\left(
\begin{matrix}
3 & 1 \
1 & 3
\end{matrix}
\right)
$$
4.1. もともとの座標系(正規直交座標)で表現した場合
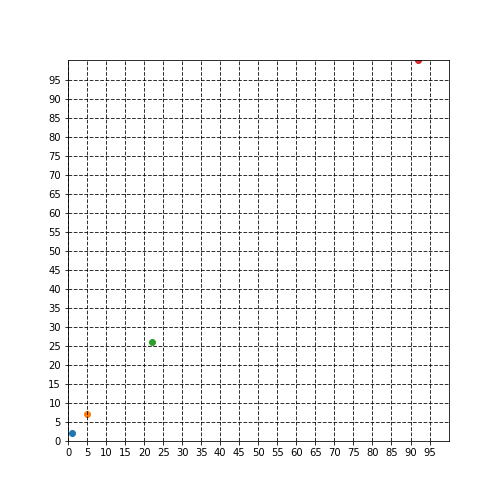
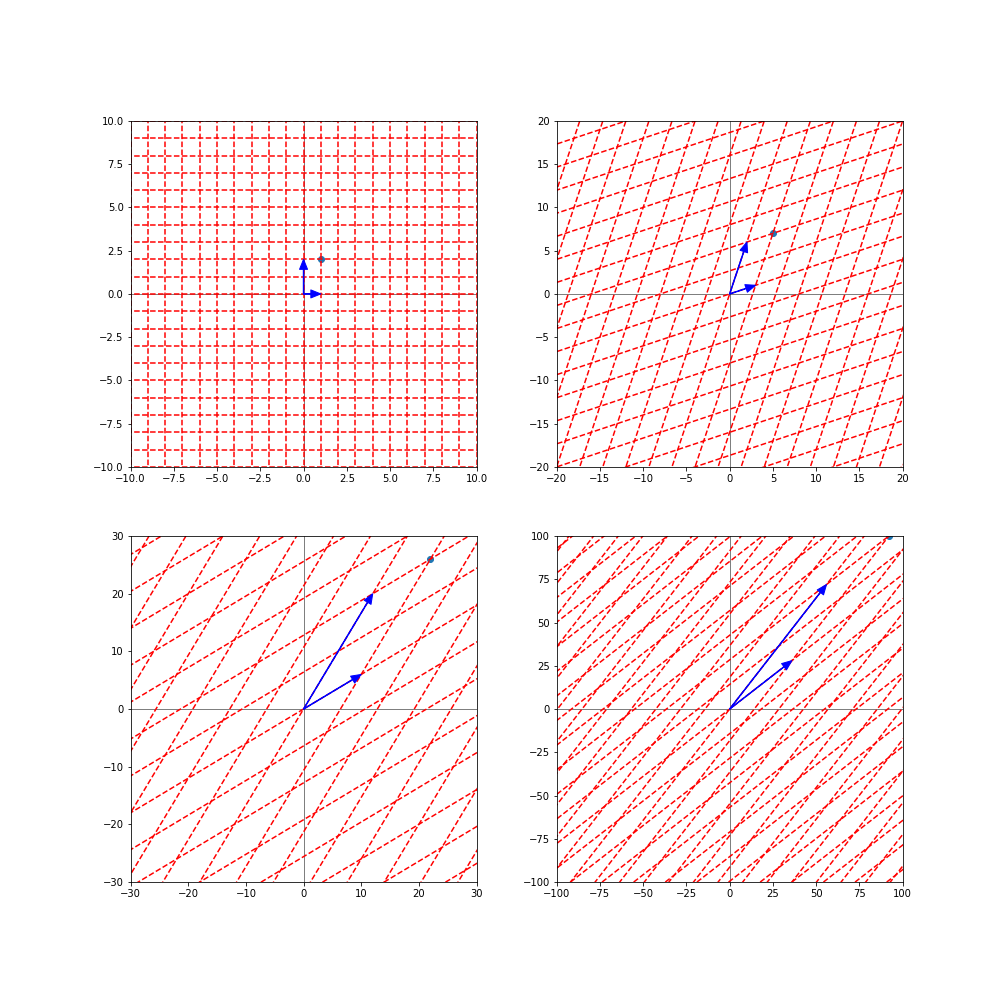
$A$から$A^{4}$までをかけた様子を図示したものが以下になります。もともとの点$\mathbf{x}=(1,2)^t$が青の点で、これに順次$A$をかけた点がそれぞれ、$(5,7)^t$(オレンジ色点), $(22, 26)^t$(緑色点), $(92,100)^t$(赤色点)になっています。
これだけですとよく分からないので、$A$により正規直交基底がどのように変換されるかも合わせて図示すると以下のようになります。
$A$による変換(左から$A$をかけること)により、正規直交基底がだんだん歪んでいってますね。また、これに伴い、元々の正規直交基底を用いて表されていた点$(1,2)$が、新しい歪ん基底を用いても$(1,2)$と表されていることが分かります。
つまり、もともとの点$(1,2)$は、$A$をかけることにより、正規直交基底を用いた座標系での座標の表現では、$(5,7)$, $(22, 26)$, $(92,100)$と変化していきますが、見方を変えて、$A$により変換された新しい基底を用いた座標系での座標の表現では、常に$(1,2)$のままということになります。
なるほどそういうことかという気もしますが、一方で、これですと、今一つ、結局、もともとの点がどのように変換されていっているのかがよく分かりません。
4.2. Aの固有ベクトルを基底とした座標系で表現した場合
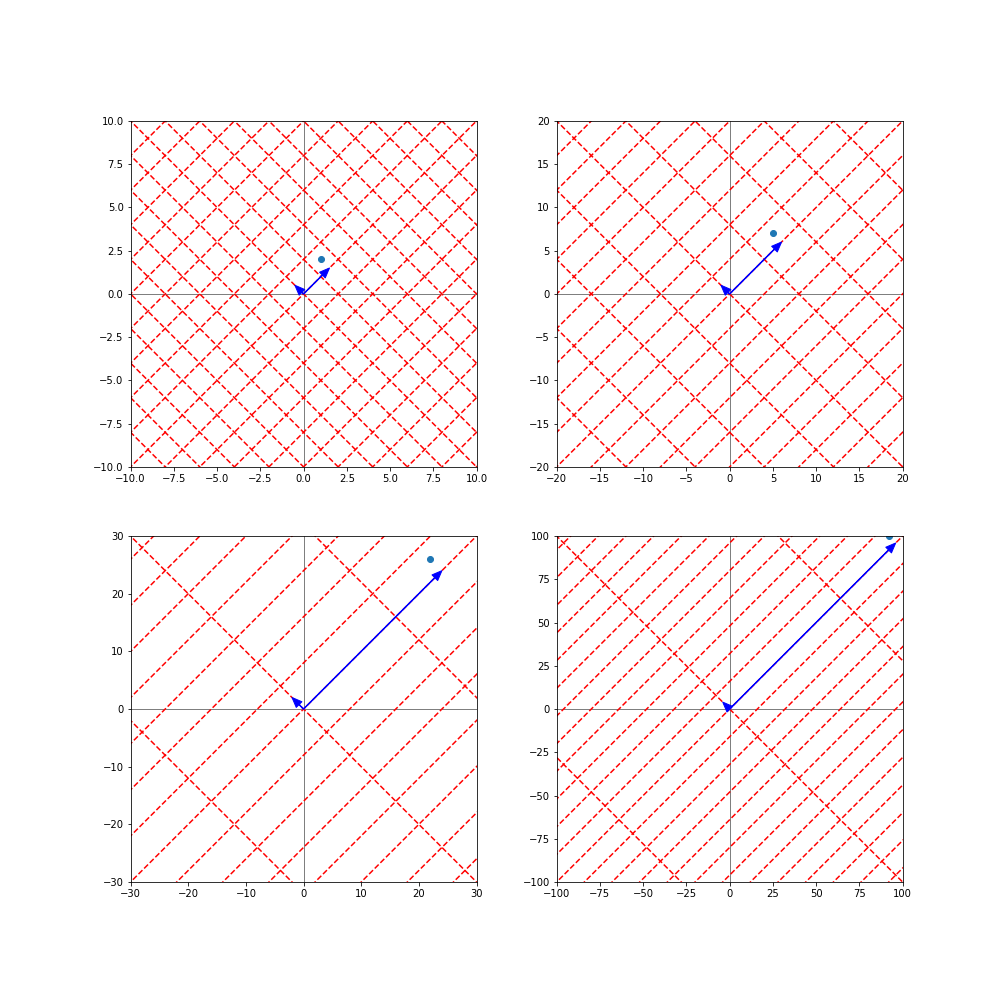
ということで、次に、固有ベクトルを基底とした座標系で考えてみます。先ほどの例と同様に、$A$から$A^{4}$までをかけた様子を図示したものが以下になります。(ここで、各点の位置自体は、座標系の取り方に依存せず、4.1節の図と同じ位置であることにご注意ください。)
この座標系で見た時には、この点の座標は、$(1.5, 0.5)$であり、4.1節の例と同様、$A$をかけることで、基底自体が伸縮していますが、この座標は$(1.5, 0.5)$で変わっていないことが分かります。また、4.1節の時と異なり、今回は、$A$による変換により、基底の方向は変わらず長さのみが変わっていることが分かります。(これは、固有ベクトルを基底に取ったことを考えると、当たり前ではあります。詳細は前回のご説明もご参照ください。)
4.3. Aの固有ベクトルを基底とし、かつ、Aによる変換前後で基底は固定と解釈する
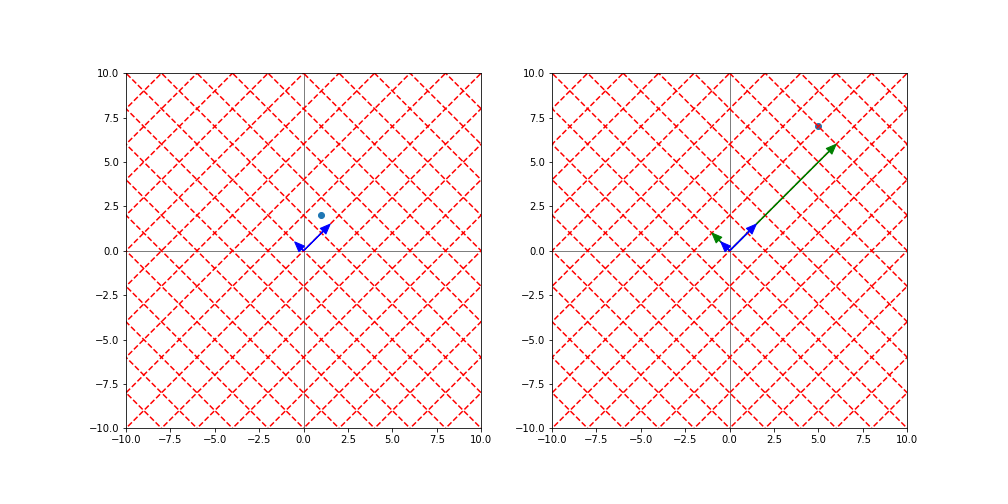
次に、上記と同様に、固有ベクトルを基底とした座標系を考えますが、$A$による変換により基底が変換されるのではなく、この座標系で表現された座標の点の位置が変わると解釈してみます。つまり、下図のように、$A$による変換前後(右図と左図)で、基底は不変(両者とも青色矢印)で、点の座標が緑色矢印のように伸縮したとみなしてみます。
このとき、元の点の(この座標系での)座標を$(x_1, x_2)$, Aの固有ベクトルを$\mathbf{p}_1, \mathbf{p}_2$, 対応する固有値を$\lambda_1, \lambda_2$、変換後の点を$\mathbf{y}$とすると、
$$
\begin{array}{cll}
\mathbf{y}
&=& A(x_1 \mathbf{p}_1+x_2 \mathbf{p}_2) \
&=& x_1 A \mathbf{p}_1+x_2 A \mathbf{p}_2 \
&=& x_1 \lambda_1 \mathbf{p}_1+x_2 \lambda_2 \mathbf{p}_2 \
&=& (x_1 \lambda_1) \mathbf{p}_1+(x_2 \lambda_2) \mathbf{p}_2 \
\end{array}
$$
となるため、変換後の(この座標系での)座標は$(x_1 \lambda_1, x_2 \lambda_2)$となり、結局、固有ベクトルを基底とした座標系で考えた場合は、$A$による変換は、各座標にそれぞれ対応した固有値をかけることに対応するということになります。
これはつまり、固有ベクトルを基底とした座標系で表した時に、元の点を$\mathbf{x}$, $A$による変換後の点を$\mathbf{y}$とすると、
$$
\mathbf{y} =
\left(
\begin{matrix}
\lambda_1 & \
& \lambda_2
\end{matrix}
\right)
\mathbf{x} \tag{11}
$$
と表せるということを意味しています。
5. 結局、対角化は何をやっているのか?
3節、4節をまとめると、結局、対角化とは、以下を行っていることになります。
- (10)式により、もともとの正規直交基底による座標系を、固有ベクトルを基底とした座標系による座標表現に変換。
- 1により変換後の座標系で$A^{m}$を計算する。この時、(11)式により、$A^{m}$の計算は、単に各方向毎に対応する固有値倍することにより簡単に計算できる。
- (9)式により、もともとの正規直交基底による座標系による座標表現に戻す。
また、(10), (11), (9)式より、上記の各計算は、具体的には左から行列を掛けていることなので、これらをまとめると、
$$
P \Lambda^{m} P^{-1} \tag{12}
$$
となります。ここで、
$$
\Lambda =
\left(
\begin{matrix}
\lambda_1 & \
& \lambda_2
\end{matrix}
\right)
$$
とおきました。
2節でご説明した(4)式は(12)式と同じであり、結局、(4)式は、上記手順1〜3を表現した式になっていることなのです。
6. まとめ
すみませんが、うまく説明できなかったかも知れませんが、この記事を読んでいただいた方が、対角化というのは、要は、(固有ベクトルの方向に)座標系を置き換えることにより、行列の計算を各成分毎の計算に分離しているということをご理解いただけると嬉しいです。疑問点・ご質問等ありましたらコメントをいただけると記事の改善に活かせると思いますのでありがたいです。
次回は、もう1つ対角化の応用例をご説明する予定です。