本稿は、線形代数を独学でやり直し勉強した時のメモです。せっかくなのでアウトプットしようと思って書き始めました。詳しくは第1回の説明をご参照ください。
今回は固有値・固有ベクトルについて説明します。固有値・固有ベクトルや次回ご説明予定の対角化は、線形代数のクライマックスであり、とても面白いところだと思います。
今回の記事では、まずは固有値・固有ベクトルの定義と意味について考えてみます。その後、固有値・固有ベクトルの算出方法についてご説明します。また、次回に、固有値・固有ベクトルの応用例として、対角化についてご説明をしたいと思います。今回と次回の説明により、固有値・固有ベクトルの凄さを理解していただけるのではないかと期待しています。
ちなみに、簡単に次回の予告だけしておきますと、実は、対角化は、単に同じ対象に対して見方を変えているだけ(座標の取り方を変えているだけ)なのです。つまり、一見複雑そうな対象に対して、対象のもの自体はなんら変更をせず、計算をしやすいように見方を変えているだけなのです。個人的には、このことがクリアに理解できた時の感動はとても大きかったです。
1. 固有値・固有ベクトルの定義
ある行列に対して、以下を満たす定数$\lambda$と、$\mathbf{0}$でないベクトル$\mathbf{x}$のことを、それぞれ固有値・固有ベクトルと言います。
$$
A \mathbf{x} = \lambda \mathbf{x} \tag{1}
$$
2. 固有値・固有ベクトルの意味
次に、固有値・固有ベクトルの意味について考えてみます。(1)式は、
- 左辺は、固有ベクトル$\mathbf{x}$に行列$A$を掛けている
- 右辺は、固有ベクトル$\mathbf{x}$に定数(固有値)$\lambda$を掛けている。つまり、$\mathbf{x}$の向きは変えずに、長さだけを変えている。
ということになります。このことから、固有値・固有ベクトルの意味は、固有ベクトルに行列$A$を掛けて変換しても、固有ベクトルの方向は変わらずに、大きさだけ「固有値倍」されるということになります。
言葉だけですとイメージが沸きにくいと思いますので、具体例で図示してみます。以下行列$A$の固有値・固有ベクトルを考えてみることにします。
$$
A=
\left(
\begin{matrix}
1 & 0.2 \
0.2 & 1
\end{matrix}
\right)
$$
まず、行列$A$の固有値・固有ベクトルを計算すると、以下のようになります。(固有値・固有ベクトルの求め方はこの後、3節でご説明します。)
- 固有ベクトル:
$$
\mathbf{x}_1=
\left(
\begin{matrix}
1 \
1
\end{matrix}
\right)
$$
$$
\mathbf{x}_2=
\left(
\begin{matrix}
1 \
-1
\end{matrix}
\right)
$$
- 固有値:
$$
\lambda_1 = 1.2, \lambda_2 = 0.8
$$
下図は、(上記の固有ベクトルを含む)いろいろなベクトルに対して、次々と(左から)$A$を掛けてみるとどうなるかを図示したものです。(もしアニメーションしなかったらリロードしてみて下さい)。
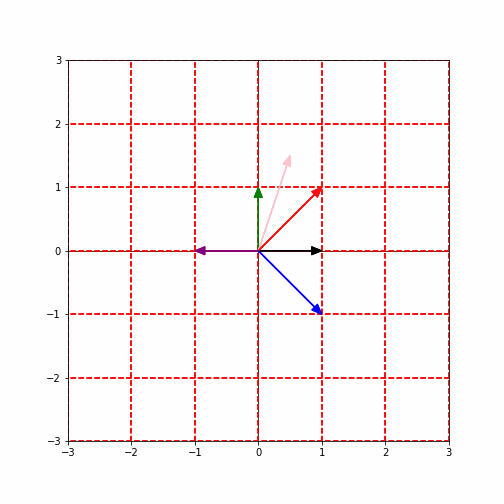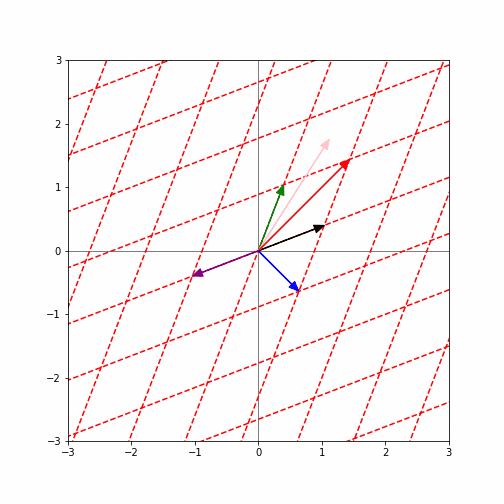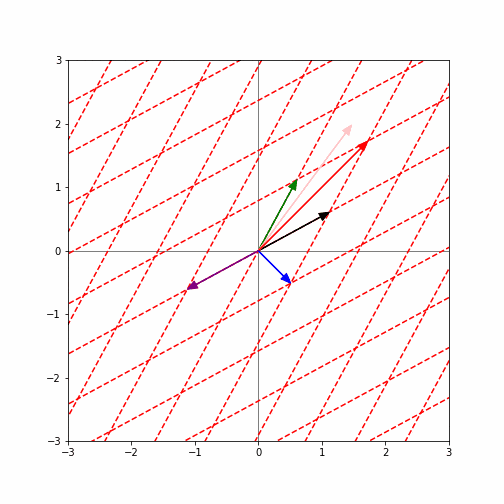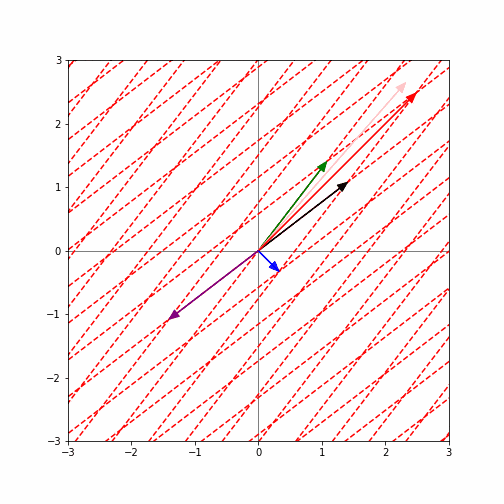
ここで、青と赤の矢印で示したベクトルに注目してみて下さい。他のベクトルは方向がどんどん変わってしまっていますが、青と赤のベクトルは方向が変わらず、長さだけが変わっていることが分かると思います。(赤ベクトルはどんどん長くなっており、青ベクトルはどんどん短くなっている)。実はこれらが、上記で求めた行列$A$の固有ベクトルなのです。そして、それぞれが、対応する固有値倍になっているのです。(つまり、赤ベクトルは1.2倍、青矢印は0.8倍されている。)
つまり、固有ベクトルとは、行列$A$をかけることにより向きが変わらず、長さだけが変わるベクトルであると言えます。また、その時に長さが何倍になるかが、対応する固有値ということになります。
んー、そんなの当たり前じゃないかって思われる方もいらっしゃるかも知れませんが、実は、これがすごい威力を発揮するのです!(ということで、この辺は次回にご説明予定です。)
3. 固有値・固有ベクトルの計算方法
次に、固有値・固有ベクトルの算出方法についてご説明します。固有値・固有ベクトルは高校の数学でも出てくる(※)ので、この辺はご存知の方も多いと思いますが、実は、個人的には、高校の時に最初に固有値・固有ベクトルの算出方法を習った時には、とてもモヤモヤするものがありました。私のモヤモヤと同じモヤモヤを感じてる方もいらっしゃるかも知れないので、この記事では、このモヤモヤについてもご説明をしたいと思います。
(※)実は今は高校では出てこないかも知れません。。
3.1. 固有値・固有ベクトルの算出方法 →固有方程式を解く
では、何はともあれ、固有値・固有ベクトルの算出方法です。固有値・固有ベクトルは(1)式を満たす$x$, $\lambda$のことですので、(1)式の右辺を左辺に移項すると、
$$
A \mathbf{x} = \lambda \mathbf{x}
$$$$
\Leftrightarrow A\mathbf{x} - \lambda \mathbf{x} = \mathbf{0}
$$$$
\Leftrightarrow (A- \lambda I) \mathbf{x} = \mathbf{0} \tag{2}
$$
ここで、$\mathbf{x}$は$\mathbf{0}$でないと仮定しているので、(2)式が成り立つためには行列$(A-\lambda I)$はランクが落ちていなければなりません(フルランクではだめということです)。このため、$(A-\lambda I)$の行列式は$0$でなければなりません。つまり、
$$
|A-\lambda I|=0 \tag{3}
$$
が成り立たなければ、(2)が成立することはできません。ちなみに、式(3)のことを固有方程式と言います。
ここで、いきなり行列式が出てきたと戸惑った方もいらっしゃったかも知れませんが、実は、フルランクではないときには行列式は0になります。なぜならば、「フルランクでないときは次元がつぶれる。次元がつぶれるときは行列式は0だから」です。この辺の理解が曖昧な場合は、前回までのご説明を復習してみていただけましたらと思います。
また、詳細は後述しますが、式(3)は式(2)を満たすための必要条件であり、必要十分条件ではありません。(この辺が高校生の時に私がモヤモヤしていたところです。)
ということで、式(3)を解くことで、$\lambda$を求めることができます。行列式の解き方については、第7回や第8回をご参照ください。
次に、上記手順で$\lambda$が求まったら、式(2)に$\lambda$を代入し、式(2)を$\mathbf{x}$について解くことで$\mathbf{x}$を求めることができます。以上で、めでたく$\lambda$と$\mathbf{x}$を求めることができました。この後、$2 \times 2$の行列の例も書きましたので、そちらもご参照いただけましたと思います。
3.2. 「λが固有方程式を満たす、かつ、xが固有ベクトルの条件を満たす」ことが(2)が成り立つための必要十分条件
**(2021/12/1修正)**今更ですが、いただいたコメント等をもとに本節の件名を変更しました。結論としては以下の本文の内容自体はあっていると自分では思っています。まずは固有値だけ求めるところがポイントだと思います。ご異論がある方はコメントいただけましたらと思います。
ここで、高校生の頃の私(だいぶ昔)は、なんとなく、**「え、けど、固有方程式(3)が0だからと言って、(2)式が成り立たない場合もあるんじゃないの??」**とモヤモヤしました。
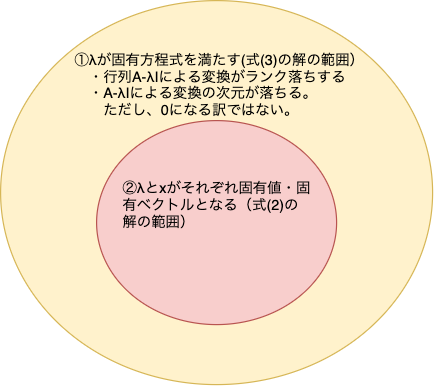
実は、このモヤモヤはその通りで、行列$A-\lambda I$がフルランクじゃ無いってことは、例えば3次元(立体)が2次元(平面)になるってことですが、平面になったからと言って、必ずしもこの行列による変換先のベクトルは$\mathbf{0}$にはならないですよね。なので、実は、固有方程式の解は、(2)式を満たすための必要条件というだけであって、必要十分条件では無いのです。図で書くと以下のようになります。
まとめると、固有値・固有ベクトルは、以下の流れで行っているということになります。
- まず、固有方程式(3)の解を求めることで、$\lambda$の候補の当たりをつける。(上図のオレンジ色の範囲を求める)
- 次に、1で求めた$\lambda$を使って固有ベクトル$\mathbf{x}$をもとめる。(上記赤色の範囲を求める)
- 結果的に、1、2で求めた$\lambda$, $\mathbf{x}$は、固有値・固有ベクトルになっている。
3.3. サイズ2x2の行列による具体例
では、次に、例として、具体的に、以下の$2 \times 2$行列の行列$A$の固有値・固有ベクトルを求めてみます。
$$
A =
\left(
\begin{matrix}
3 & 1 \
1 & 3
\end{matrix}
\right)
$$
まず、固有方程式を解きます。
$$
\begin{align}
& \big| A-\lambda I \big| = 0 \
\Leftrightarrow &
\left|
\begin{matrix}
\left(
\begin{matrix}
3 & 1 \
1 & 3
\end{matrix}
\right) -
\left(
\begin{matrix}
\lambda & 0 \
0 & \lambda
\end{matrix}
\right)
\end{matrix}
\right| = 0 \
\Leftrightarrow &
\left|
\begin{matrix}
3-\lambda & 1 \
1 & 3-\lambda \
\end{matrix}
\right| = 0
\end{align}
$$
$2 \times 2$行列の場合は、行列式は$ad-bc=0$で求まるので、
$$
\begin{align}
& (3-\lambda)^2-1 = 0 \
\Leftrightarrow & 9-6\lambda + \lambda^2-1 = 0 \
\Leftrightarrow & \lambda^2-6\lambda+8=0 \
\Leftrightarrow & (\lambda-2)(\lambda-4)=0
\end{align}
$$
よって、$\lambda=2, 4$となります。
次に、$\lambda=2$, $\lambda=4$それぞれの場合について、
$$
A\mathbf{x}=\lambda\mathbf{x}
$$
を満たす$\mathbf{x}=(x_{1}, x_{2})^t$を求めます。まず、$\lambda=2$の時は、
$$
\left(
\begin{matrix}
3 & 1 \
1 & 3
\end{matrix}
\right)
\mathbf{x} = 2 \mathbf{x}
$$
よって、
$$
\begin{align}
3 x_{1} + x_{2} &= 2 x_{1} \
x_{1} + 3 x_{2} &= 2 x_{2}
\end{align}
$$
上記2つの式は、結果的にはどちらも以下の形に変形できます。
$$
x_{2} = -x_{1}
$$
よって、固有値$\lambda=2$に対応する固有ベクトルは、
$$
\mathbf{x} = \left(
\begin{matrix}
1 \
-1
\end{matrix}
\right)
$$
となります。ここで注意ですが、実は、上記から分かるように、1つの固有値に対応する固有ベクトルは一意には定まりません。例えば、
$$
\mathbf{x} = \left(
\begin{matrix}
2 \
-2
\end{matrix}
\right)
$$
も同様に、$\lambda=2$に対応した固有ベクトルになります。これは、実際に$A\mathbf{x}=\lambda \mathbf{x}$に代入して成り立つことで確かめることができます。
同様に、$\lambda=4$の時の固有ベクトルは
$$
\mathbf{x} = \left(
\begin{matrix}
1 \
1
\end{matrix}
\right)
$$
と求めることができます。(計算方法は同様なので省略します。)
4. まとめ
今回は固有値・固有ベクトルについてご説明しました。2節で書いた固有値・固有ベクトルの意味は、当たり前のように思われるかも知れませんが、とても重要です。何回もくどくてすみませんが、次回ご説明予定の「対角化」により、その威力がよく理解できると思います。
また、3節では固有値・固有ベクトルの計算方法についてご説明しました。これまでの行列式や逆行列と同様、実務上は、固有値・固有ベクトルを実際に手計算で計算する機会はとても少ないと思います。ただ、3節で書いた、必要条件・十分条件・必要十分条件を意識することは、一般的に、数学を理解するためにはとても重要だと思います。