本稿は、線形代数を独学でやり直し勉強した時のメモです。せっかくなのでアウトプットしようと思って書き始めました。詳しくは第1回の説明をご参照ください。今回は、行列式の説明の2回目です。
今回の内容ですが、まず、前回、行列式の定義について曖昧にしか書きませんでしたが、さすがに、正しい定義くらい触れておいたほうがいい気がしてきたので、行列式の正式な定義について少し書きたいと思います。ただし、定義はぱっと見意味不明だと思いますので、ここの部分は読み流していただいてもいいと思います。次に、行列式を算出するために必要な行列式の性質について、いくつかご説明したいと思います。最後に、行列式の算出方法の流れについての説明をします。具体的な計算例と補足は次回にご説明したいと思います。
実際の応用では、行列式の計算はライブラリにやらせてしまうと思いますが、数学への苦手意識を克服する意味でも、一度くらいは勉強しておくのがいいのではないかと個人的には思っています。また、実際には行列式の算出自体はしないにしても、今回ご説明する行列式の説明は、ベクトルや行列についての理解を深めるためにも有益なものであると思います。
1. 行列式の定義
では、まずは、行列式の正式な定義です。ただし、先ほども書きましたとおり、定義はよ〜く解読しないと意味不明ですので、よく分からない場合は気にしないで読み飛ばすことをお勧めします。
行列式の定義
行列式の定義は以下のとおりです。ただし、くどいですが、嫌になる前に初めに書きますが、以下こねこねと定義を書きますが、一言で書くとこの定義は、行列式を行列$A$による体積変換倍率を表すように(前回ご説明のように)定義し、成分に書き下すと結果的にこのような定義になったと解釈できます。(正確には、この後2.2でご説明する、負号も考慮した体積です)。ですので、この定義自体はあまり深入りはする必要はないものだと思います。
$A=(a_{ij})$を$n \times n$の行列とすると、$A$の行列式は$|A|$は以下で定義される。
$$
|A| = \sum_{\sigma \in S_n} sgn(\sigma)
a_{1\sigma(1)}
a_{2\sigma(2)}
a_{3\sigma(3)}
\cdots
a_{n\sigma(n)}
$$
ただし、$\sum_{\sigma \in S_n}$は、「$n$次置換全体について和をとる」という意味である。
ちなみに、$sgn()$は$()$内の値の負号をとったもの(例えば、$()$内が5だったら1, $()$内が-10だったら-1)を表します。
上記の定義を大雑把に解読してみますと、
- $a_{1\sigma(1)} a_{2\sigma(2)} a_{3\sigma(3)}
\cdots a_{n\sigma(n)}$ : 行列の各行のどこかの成分(どこかの列のもの)をすべて掛け合わせたもの。 - $sgn(\sigma)$ : 組み合わせにより、負号を適当に変えている。
- $\sum_{\sigma \in S_n}$ : これらについて、「$n$次置換全体について和をとって」いる。(全てのパターンについての合計をとっている)
ということになります。なんとなく、2次元の時の(高校で習う)定義のように、行列の斜めの成分同士の掛け算を適当に足し引きしてるっぽいですね。また、繰り返しになりますが、体積を具体的に計算するように定義するとこのようになるということですね。はい、では、これ以上深入りはせず、一旦次に進みましょう。
2. 行列式の性質
次に、行列式を計算するために必要な、行列式の性質をいくつかご紹介します。
2.1. 【性質1】列を入れ替えると行列式の負号は反転する
前回説明しましたとおり、
$$
\begin{align}
A &=(\mathbf{a}_1 , \mathbf{a}_2) \
&=
\left(
\begin{matrix}
a & b\
c & d
\end{matrix}
\right)
\end{align}
$$
とすると、$A$の行列式$|A|$は、
$$
|A| = ad - bc
$$
となります。一方、このとき、
$$
\begin{align}
B &=(\mathbf{a}_2 , \mathbf{a}_1) \
&=
\left(
\begin{matrix}
b & a\
d & c
\end{matrix}
\right)
\end{align}
$$
の行列式$|B|$は、
$$
\begin{align}
|B| &= bc - ad \
&= -(ad - bc) \
&=-|A|
\end{align}
$$
となります。つまり、行列式には、$\mathbf{a}_1$と$\mathbf{a}_2$の順番を入れ替えると、行列式の負号が反転するという性質があります。このことは、行列式の正式な定義に$sgn(\sigma)$があることからも想像できると思います。
例として、
$$
A=\left(
\begin{matrix}
\sqrt{2}/2 & -\sqrt{2}/2 \
\sqrt{2}/2 & \sqrt{2}/2
\end{matrix}
\right)
$$
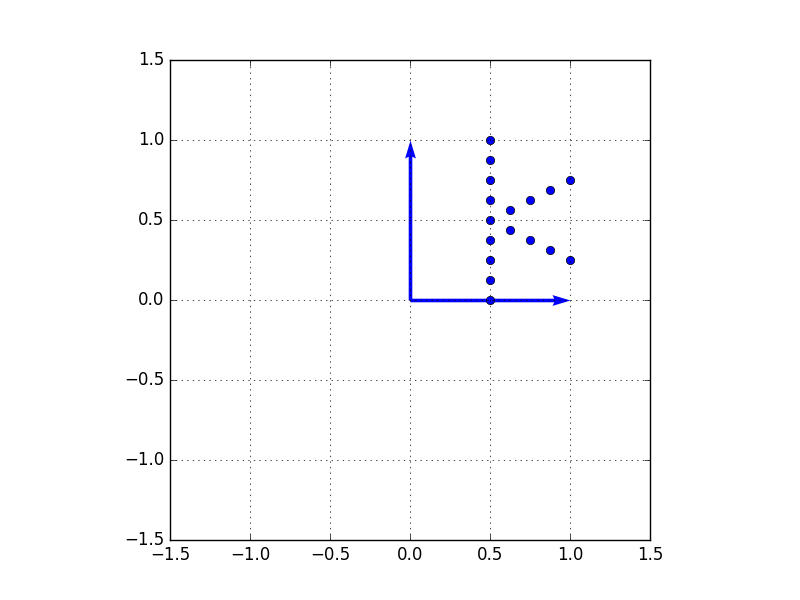
による変換を考えてみます。これは、全体の面積を変えず、全体を45度回転させる変換となります。実際、行列式を求めてみると、
$$
\begin{align}
\sqrt{2}/2 \times \sqrt{2}/2 - \sqrt{2}/2 \times (-\sqrt{2}/2)
&= 2/4 + 2/4 \\
&= 1
\end{align}
$$
となります。ここで、変換前後の様子を観察するため、平面上に適当に点をプロットさせてみると以下のようになります。(特に意味はないですが、「k」という文字をプロットしてみました。)
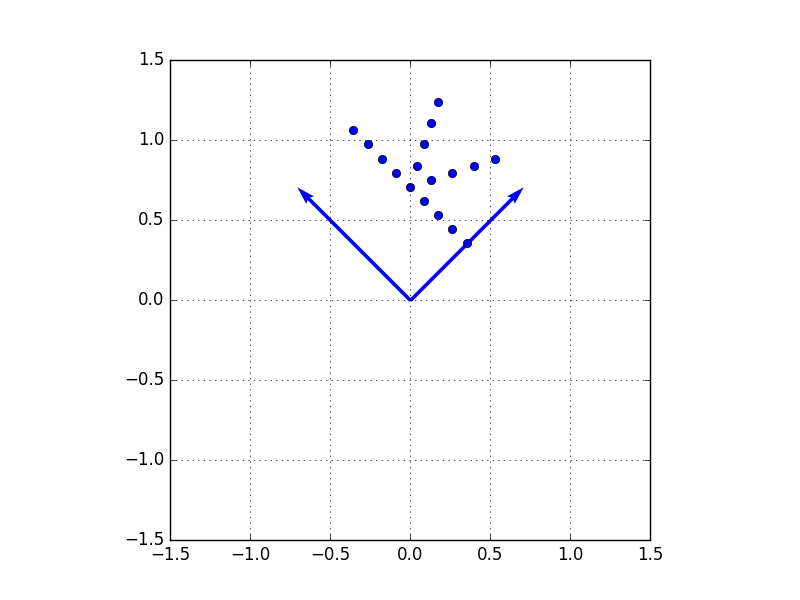
次に、この行列の1列目と2列目を入れ替えた行列
$$
A'=\left(
\begin{matrix}
-\sqrt{2}/2 & \sqrt{2}/2 \
\sqrt{2}/2 & \sqrt{2}/2
\end{matrix}
\right)
$$
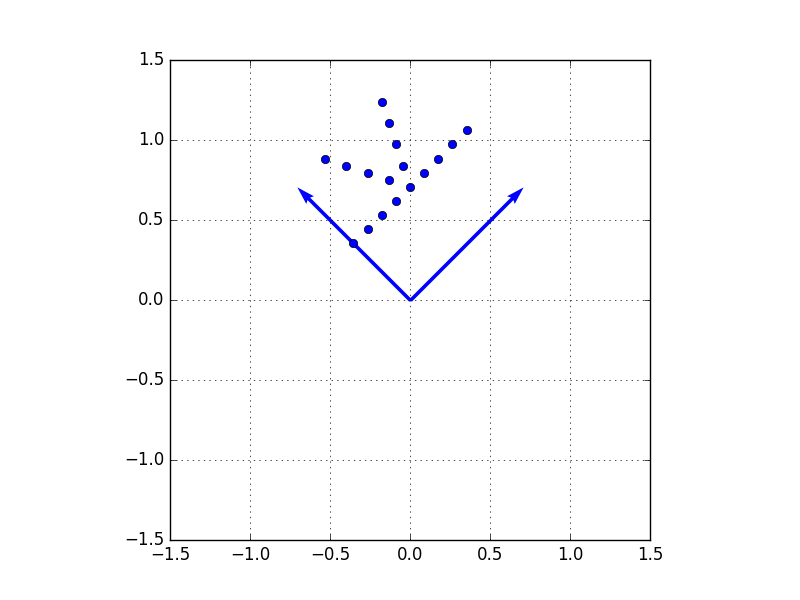
による変換を考えてみましょう。この行列による変換は、以下図のとおり、先ほどの行列と同様に面積は変えずに45度回転する変換となっていますが、「k」の文字が逆さになっていることがわかります。
また、この行列の行列式を計算してみると、
$$
\begin{align}
(-\sqrt{2}/2) \times \sqrt{2}/2 - \sqrt{2}/2 \times \sqrt{2}/2
&= -2/4 - 2/4 \\
&= -1
\end{align}
$$
となります。つまり、行列式の絶対値は変わりませんが、負号が反対になっています。
以上から、行列式の列を入れ替えると、変換後の図形が反転し、かつ、行列式の負号も反転することが分かります。つまり、行列式は、変換後の図形の向きも考慮した体積を表していると言えるのです。つまり、行列による変換の向きが行列式の負号として現れているのです。
2.2. 【性質2】ある列の定数倍を別の列に加えても行列式の値は不変
言葉で書くと分かりにくいですが、例えば、2次元の行列$A$と、行列$A$の1列目の定数倍を2列目に加えた行列$B$を考えます。つまり、
$$
A=
\left(
\begin{matrix}
a & b \
c & d \
\end{matrix}
\right)
$$
$$
B=
\left(
\begin{matrix}
a & b+\alpha a \
c & d+\alpha c \
\end{matrix}
\right)
$$
ここで、$\alpha$は任意の定数とします。このとき、実は、$A$と$B$の行列式は等しくなります。つまり、行列のある列の定数倍を他の列に加えても、行列式の値は変わらないのです。
では、なぜ行列式はこのような性質を持つか、これまで何回か出てきた具体例で考えてみましょう。
まず、次の行列を考えます。
$$
\begin{align}
A &=
\left(
\begin{matrix}
2 & 1 \
1 & 4
\end{matrix}
\right) \
&=
\left(
\begin{matrix}
\mathbf{a} & \mathbf{b}
\end{matrix}
\right)
\end{align}
$$
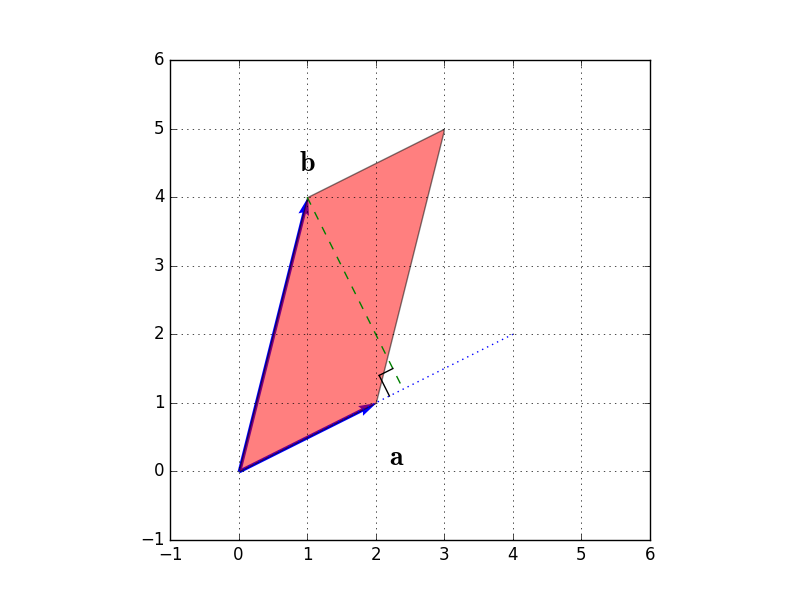
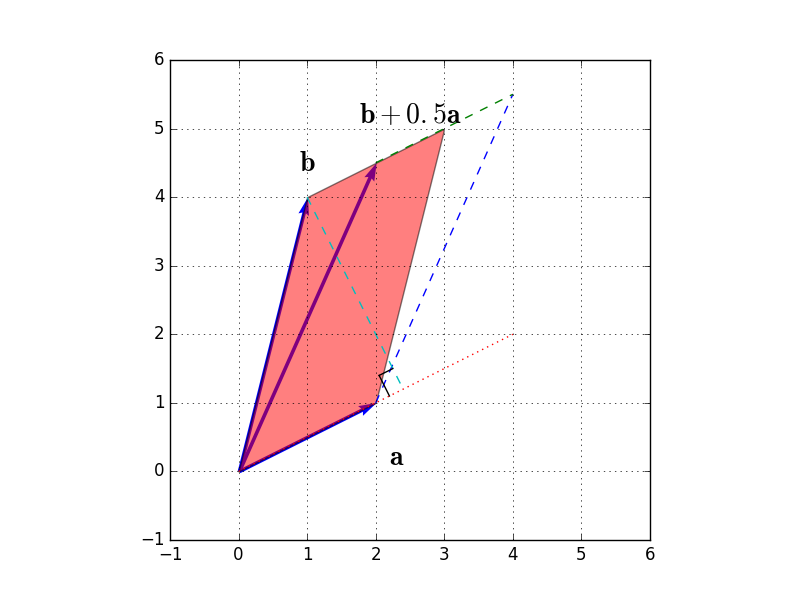
この行列の行列式は、前回ご説明しました通り、以下図の赤塗りした平行四辺形の面積になります。
次に、この行列の1列目の0.5倍を2列目に加えた、以下行列を考えます。
$$
\begin{align}
B &=
\left(
\begin{matrix}
\mathbf{a} & \mathbf{b} + 0.5 \times \mathbf{a}
\end{matrix}
\right) \
&=
\left(
\begin{matrix}
2 & 1 + 0.5 \times 2 \
1 & 4 + 0.5 \times 1
\end{matrix}
\right)
\end{align}
$$
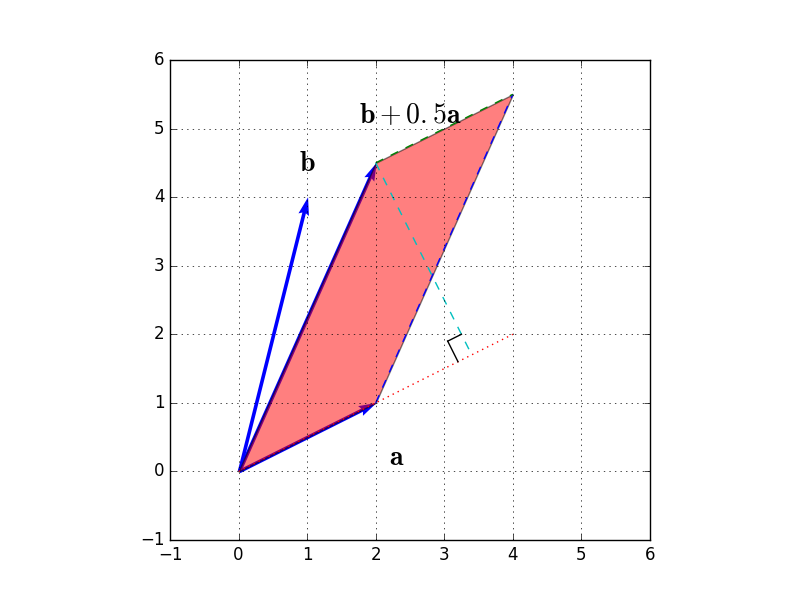
この行列による変換を図示すると、以下図のようになります。(紫色の矢印が、$\mathbf{b} + 0.5 \times \mathbf{a}$(つまり、$\mathbf{e}_2 = (0,1)^t$の変換先)を表しています。)
ここで、この行列の行列式は、以下図の赤塗り部分の平行四辺形の面積となりますが、行列$A$の行列式を表す平行四辺形とよく見比べてみると、実は底辺も高さも同じであることが分かります。
以上から、行列$A$の行列式と行列$B$の行列式は等しい(つまり、$|A|=|B|$)であることが分かります。
また、ここでは、2次元の例で説明しましたが、3次元の場合でも同様に考えれば、ある列の定数倍を他の列に加えても行列式の値は変わらないという性質があることが分かります。さらに、いつものように、2次元、3次元のときのイメージをそのまま$n$次元で考えてみると想像できると思いますが、一般的に$n$次元の行列についても同一の性質が成り立つのです。
2.3. 【性質3】対角行列の行列式は、対角成分をかけたものになる
次に、対角行列の行列式について考えてみます。例として、3次元の行列
$$
\begin{align}
A &=
\left(
\begin{matrix}
a & 0 & 0 \
0 & b & 0 \
0 & 0 & c \
\end{matrix}
\right) \
&=
\left(
\begin{matrix}
\mathbf{a} & \mathbf{b} & \mathbf{c}
\end{matrix}
\right)
\end{align}
$$
の行列式を考えてみます。
前回ご説明したとおり、行列の各列は、それぞれ、正規直交基底$\mathbf{e}_{i}$の変換先を表していました(詳細は前回のご説明をご参照ください)。つまり、この例では、正規直交基底$\mathbf{e}_1 = (1, 0, 0)^t$、$\mathbf{e}_1 = (0, 1, 0)^t$、$\mathbf{e}_1 = (0, 0, 1)^t$は、それぞれ、この行列により、以下のベクトルに変換されることが分かります。
$$
\mathbf{a} =
\left(
\begin{matrix}
a \
0 \
0
\end{matrix}
\right)
$$
$$
\mathbf{b} =
\left(
\begin{matrix}
0 \
b \
0
\end{matrix}
\right)
$$
$$
\mathbf{c} =
\left(
\begin{matrix}
0 \
0 \
c
\end{matrix}
\right)
$$
ここで、よく考えると、これらのベクトルは、単に、$x$, $y$, $z$軸方向の長さがそれぞれ$a$, $b$, $c$の立方体ですので、これらのベクトルで囲まれる領域の体積(=行列$A$の行列式)は$a \times b \times c$であることが分かります。つまり、対角行列の行列式は、単に対角成分の掛け算をすれば求まるのです。
2.4. 【性質4】上三角行列の行列式は対角成分をかけたものになる
次に、上三角行列
$$
A=\left(
\begin{matrix}
a_{11} && a_{12} && a_{13} \
0 && a_{22} && a_{23} \
0 && 0 && a_{33}
\end{matrix}
\right)
$$
の行列式を考えてみます。実は、こちらも簡単で、行列式は、単に、各対角成分の積になります。つまり、この例ですと、
$$
|A|=a_{11} \times a_{22} \times a_{33}
$$
となります。
これは、【性質2】と【性質3】(対角行列の行列式)からすぐに示すことができます。具体的には、まず、$A$の1列目の$-a_{12} / a_{11}$倍を2列目に加えた行列を$A'$とすると、
$$
A'=\left(
\begin{matrix}
a_{11} && 0 && a_{13} \
0 && a_{22} && a_{23} \
0 && 0 && a_{33}
\end{matrix}
\right)
$$
となりますが、【性質2】により、行列式の値は変わらず、
$$
|A| = |A'|
$$
となります。
次に、$A'$の1列目の$-_{13} / a_{11}$倍と、2列目の$-a_{23} / a_{22}$倍を3列目に加えた行列を$A''$とすると、同様に、
$$
A''=\left(
\begin{matrix}
a_{11} && 0 && 0 \
0 && a_{22} && 0 \
0 && 0 && a_{33}
\end{matrix}
\right)
$$
となりますが、行列式の値は変わらず、
$$
|A''| = |A'| = |A|
$$
となります。ここで、$A''$は対角行列なので、以上から、
$$
|A| = |A'| = |A''|=a_{11} \times a_{22} \times a_{33}
$$
であることが分かります。
2.5. 【性質5】ある列の要素が1要素以外は0の場合の行列式
次のような、先頭の列は1番の上の要素以外は0である行列の行列式を考えてみます。
$$
A=\left(
\begin{matrix}
a_{11} && a_{12} && \cdots && a_{1n} \
0 && && && \
\vdots && && B && \
0 && && &&
\end{matrix}
\right)
$$
このような行列の行列式は、実は、
$$
|A|=a_{11} \times |B|
$$
で求めることができます。つまり、このような行列の行列式は、一番左上の数字(上記例の場合$a_{11}$)と、1行目・1列目を除いた行列(上記例の場合、行列$B$)の行列式の掛け算で求めることができます。
では、また具体例で考えてみましょう。3次元の行列
$$
A=\left(
\begin{matrix}
a_{11} && a_{12} && a_{13} \
0 && a_{22} && a_{23} \
0 && a_{32} && a_{33}
\end{matrix}
\right)
$$
を考えます。まず、【性質2】を利用して、この行列の1列目の$-a_{12}/a_{11}$倍と$-a_{13}/a_{11}$倍をそれぞれ2列目と3列目に掛けると、行列$A$は、行列式の値を変化させずに、
$$
A=\left(
\begin{matrix}
a_{11} && 0 && 0 \
0 && a_{22} && a_{23} \
0 && a_{32} && a_{33}
\end{matrix}
\right)
$$
と変形することができます(先ほどの上三角行列のときと同様)。
ここで、これまで同様、この行列により、$\mathbf{e}_1 = (1,0,0)^t$, $\mathbf{e}_2 = (0,1,0)^t$, $\mathbf{e}_3 = (0,0,1)^t$はそれぞれ、以下ベクトルに変換されます。
$$
\mathbf{a} =
\left(
\begin{matrix}
a_{11} \
0 \
0
\end{matrix}
\right)
$$
$$
\mathbf{b} =
\left(
\begin{matrix}
0 \
a_{22} \
a_{32}
\end{matrix}
\right)
$$
$$
\mathbf{c} =
\left(
\begin{matrix}
0 \
a_{23} \
a_{33}
\end{matrix}
\right)
$$
例えば、
$$
A=\left(
\begin{matrix}
3 && 0 && 0 \
0 && 2 && 1 \
0 && 1 && 4
\end{matrix}
\right)
$$
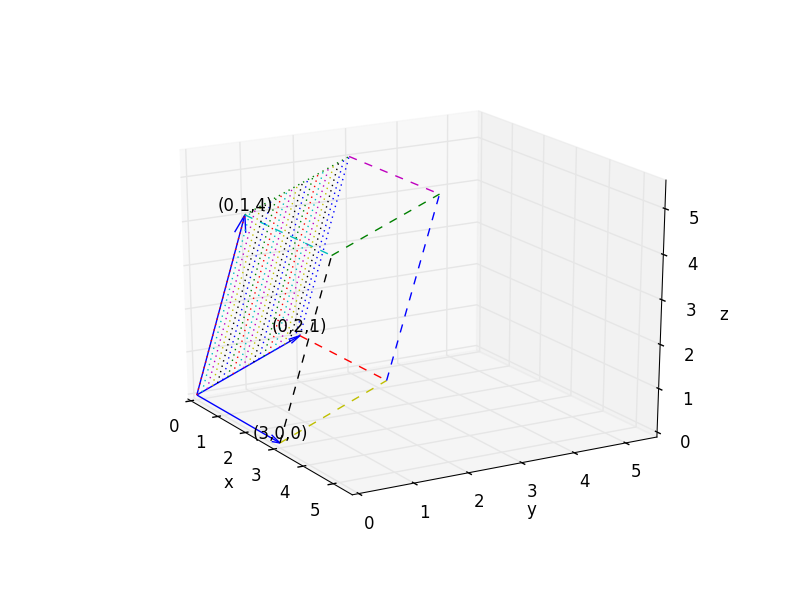
の場合にこの様子を図で表すと、以下のようになります。
図をよく眺めると分かるように、$y-z$平面方向は、それぞれ、
$$
\begin{align}
\mathbf{b}' &=
\left(
\begin{matrix}
a_{22} \
a_{32}
\end{matrix}
\right) \
&=
\left(
\begin{matrix}
2 \
1
\end{matrix}
\right)
\end{align}
$$
$$
\begin{align}
\mathbf{c}' &=
\left(
\begin{matrix}
a_{23} \
a_{33}
\end{matrix}
\right) \
&=
\left(
\begin{matrix}
1 \
4
\end{matrix}
\right)
\end{align}
$$
で表させるベクトルに変換されるとともに、$x$方向は、
$$
\begin{align}
\mathbf{a} &=
\left(
\begin{matrix}
a_{11} \
0 \
0
\end{matrix}
\right) \
&=
\left(
\begin{matrix}
3 \
0 \
0
\end{matrix}
\right)
\end{align}
$$
で表されるベクトルに変換されていることが分かります。(分かりにくいかもしれませんが、ここでは、$\mathbf{b}$と$\mathbf{c}$は3次元ベクトルですが、$y-z$平面上のベクトルは2次元なので、一応区別するためにそれぞれ$\mathbf{b}'$, $\mathbf{c}'$としました)。つまり、この行列による拡大率を表す体積は、底辺が$\mathbf{b}'$と$\mathbf{c}'$で囲まれた平行四辺形(図の網掛け部分)で、高さが$\mathbf{a}$(上記例では3)の四角柱の体積となるということです。
ここで、図の網掛け部分の行列式は、2次元の行列式ですので、すぐに求められて、
$$
a_{22} a_{33} - a_{32} a_{23}
$$
となりますので、結論として、求める行列式は、
$$
\begin{align}
|A| &= a_{11} \times (a_{22} a_{33} - a_{32} a_{23}) \
&= a_{11} \times |B|
\end{align}
$$
となるのです。
3. 行列式の計算方法の流れ
以上で、行列式を計算するために必要な性質が出揃いましたので、最後に、行列式の計算方法の流れについてご説明したいと思います。なお、説明が少し長くなってきたので、具体例は次回にご説明しようと思います。
行列式の計算方法の流れですが、要は、【性質1】や【性質2】を駆使して、列の入れ替えや列同士の足し算を行い、求めたい行列を【性質5】の形に変形し、最終的には2次元の行列式を求める形にして計算をすればよいのです。つまり、$n$次元(=サイズが$n \times n$)の行列の行列式を計算する手順は、具体的には以下流れになります。
- 【性質2】でご説明したように、ある列の定数倍を別の列にかけることで、求めたい行列を、【性質5】の形に変形する。このとき、【性質2】より、行列式の値は変わらない。
- 手順1できれいにならない場合は、適宜、各列の入れ替えを行う。このとき、【性質1】より、行列式の負号が反転する。
- 【性質5】の形になったら、1行目1列目を除いた$n-1$次元の行列(2.5の例では行列$B$)について、同様に1,2のて順を繰り返す。
- 最終的に、右下の行列(2.5の例の行列$B$)を2次元($2 \times 2$)になるまで、上記1〜3の手順を繰り返す。
- 手順4で残った2次元の行列は、高校のときに学習した2次元の行列の行列式の計算($ad-bc$)により計算する。
4. まとめ
いかがでしたでしょうか? 個人的には、今回の内容についても、やはり、線形代数は2次元、3次元のイメージをそのまま$n$次元に拡張しているものだということを意識することが重要なのではないかと思っています。具体的には、
- 行列式の定義は、小難しく書いてますが、要は、2次元の面積、3次元の体積を$n$次元に拡張もの。このときに、$n$次元での体積の計算方法がたまたま、今回ご説明した定義のような式になる。
- 行列式の計算方法や、そのときに使う行列式の性質も、行列式の上記定義方法のため、2次元や3次元の図でイメージできる性質をそのまま使うことができる。
ということなんだと思っています。ということで、今回ご説明しました【性質1】〜【性質5】は、2次元、3次元でイメージすると当たり前とも思えることですが、よく理解しておくことが重要なのではないかと思います。(数学科の中では超基本的なことなんでしょうけど、ちょっと数学の抽象化の威力を垣間見ることができる気がします。)