すみません、ぼーっとしたら1年近く時間が空いてしまいました。本稿は、線形代数を独学でやり直し勉強した時のメモです。せっかくなのでアウトプットしようと思って書き始めました。詳しくは第1回の説明をご参照ください。
今回は行列式についての説明をします。まず最初に、前回(1年前ですが、、)説明しそびれたことで、行列式の意味を理解するためにも必要となる「行列の各列の意味」について説明をし、その後、行列式の定義・計算方法について説明したいと思います。
1. 行列の各列の意味
これまでも何度か出てきたように、行列の各列を区切った縦ベクトルを考えてみます。具体的には、ある行列$A$について、
$$
A=
\left(
\begin{matrix}
\mathbf{a}_1 & \cdots & \mathbf{a}_n
\end{matrix}
\right)
$$
とします。この時、各列を表す$\mathbf{a}_i$は、実は、$n$次元空間の正規直交基底$\mathbf{e}_i$の$A$による変換先のベクトルを表しているのです。
文だけでは分かりにくいかもしれないので、2次元の例で考えてみましょう。いま、行列$A$を、
$$
\begin{align}
A &=
\left(
\begin{matrix}
2 & 1 \
1 & 4
\end{matrix}
\right) \
&=
\left(
\begin{matrix}
\mathbf{a}_1 & \mathbf{a}_2
\end{matrix}
\right)
\end{align}
$$
とし、2次元空間の正規直交基底$\mathbf{e_1}=(1,0)^t$, $\mathbf{e_2}=(0,1)^t$がこの行列によりどのように変換されるかを考えてみます。これは具体的に計算してみるとすぐにわかり、
$$
\begin{align}
A \mathbf{e}_1 &=
\left(
\begin{matrix}
2 & 1\
1 & 4
\end{matrix}
\right)
\left(
\begin{matrix}
1 \
0
\end{matrix}
\right) \
&= \left(
\begin{matrix}
2 \
1
\end{matrix}
\right) \
&= \mathbf{a}_1
\end{align}
$$
$$
\begin{align}
A\mathbf{e}_2 &=
\left(
\begin{matrix}
2 & 1\
1 & 4
\end{matrix}
\right)
\left(
\begin{matrix}
0 \
1
\end{matrix}
\right) \
&= \left(
\begin{matrix}
1 \
4
\end{matrix}
\right) \
&= \mathbf{a}_2
\end{align}
$$
となります。つまり、$\mathbf{a_1}$, $\mathbf{a_2}$は、それぞれ正規直交基底$\mathbf{e_1}$, $\mathbf{e_2}$の変換先を表しているのです。少し計算すればすぐにわかることなのですが、この性質もとても便利ですので、ぜひ覚えておくことをお勧めします。
また、この性質により、2次元空間上の任意の点$\mathbf{x} = (x_1, x_2)^t$は、この行列$A$により、$x_1 \mathbf{a_1} + x_2 \mathbf{a_2}$に変換されることが分かります。例えば、前回までに見てきたとおり、$\mathbf{x} = (1,2)^t$は、基底を用いて以下のように表せます。
$$
\begin{align}
\left(
\begin{matrix}
1 \
2
\end{matrix}
\right)
&=
1 \mathbf{e_1} + 2 \mathbf{e_2} \
&=
1
\left(
\begin{matrix}
1 \
0
\end{matrix}
\right)
+
2
\left(
\begin{matrix}
0 \
1
\end{matrix}
\right)
\end{align}
$$
よって、$\mathbf{x} = (1,2)^t$は行列$A$により以下のように変換されることが分かります。
$$
\begin{align}
1
\left(
\begin{matrix}
2 \
1
\end{matrix}
\right)
+
2
\left(
\begin{matrix}
1 \
4
\end{matrix}
\right)
&=
\left(
\begin{matrix}
4 \
9
\end{matrix}
\right)
\end{align}
$$
この変換を図で表すと以下のようになります。
- 変換前
- 行列$A$による変換後
行列$A$により、$x$軸、$y$軸がそれぞれ$(2,1)^t$,$(1,4)^t$へ変換される。また、これに伴い、$(1,2)^t$は、$(4,9)^t$へ変換される。
2. 行列式
2.1. 行列式の表記方法
では、次に、今回の本題である行列式の説明に移りたいと思います。
まずは、何はともあれ、行列式の表記方法をご説明します。数学でよくあることですが、実は、行列式は何通りかの表記方法がありますが、よく使われる表記方法として、行列$A$の行列式は以下のように表されます。
$$|A| \
detA
$$
2.1. 行列式の定義
次に、行列式の定義です。行列$A$の行列式は、この行列による変換の倍率を表します。(これが行列式の定義と言っていいと思います。)
例として、先ほどの行列
$$
A=\left(
\begin{matrix}
2 & 1 \
1 & 4
\end{matrix}
\right)
$$
による変換を考えてみます。
以下図のとおり、正規直交規定$\mathbf{e}_1=(1,0)^t$と$\mathbf{e}_2=(0,1)^t$に囲まれた領域(下図の赤塗り部分)の面積は、当たり前ですが、$1 \times 1 = 1$となります。
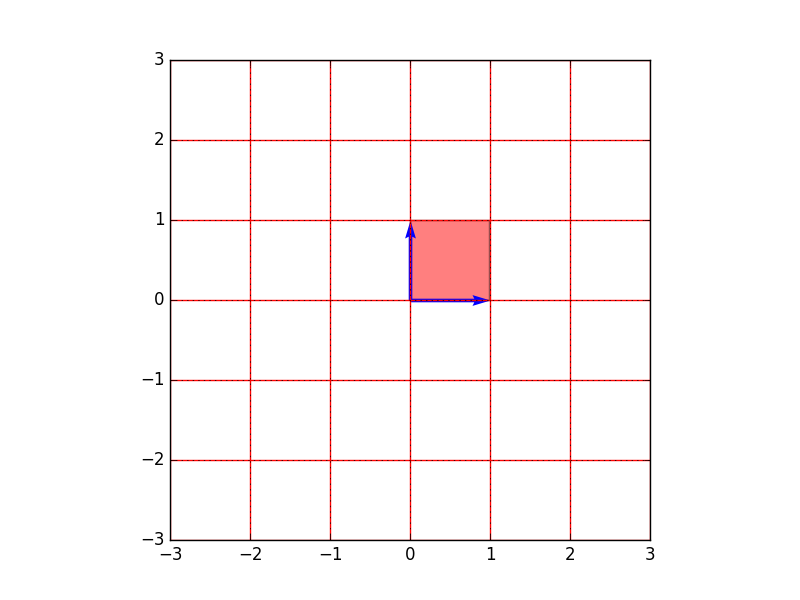
先ほどもご説明したとおり、$\mathbf{e}_1$と$\mathbf{e}_2$に囲まれた領域は、行列$A$により、下図のとおり、$\mathbf{a}_1=(2,1)^t$と$\mathbf{a}_2=(1,4)^t$に囲まれた領域(赤塗り部分)に変換されますが、この赤塗り部分の面積が、$A$の行列式になります。

ここで、念のため補足しますと、上記のとおり、もともとは面積1だった領域が、この変換により、上図の赤塗り部分の領域に変換されたということになりますので、この変換による倍率=変換後の領域の面積ということになります。
また、3次元の場合も同様に、行列による変換の倍率(=正規直交規定に囲まれた体積1の領域の変換先の領域の体積)のことを行列式と定義します。
さらに、$n$次元の場合も同様で、行列による変換の倍率(正規直交規定に囲まれた領域の変換後の領域の体積)のことを行列式と定義します。(くどいようですが、第1回で書きましたとおり、$n$次元は人間にはイメージできませんので、$n$次元は、3次元に落としてイメージします。このため、$n$次元の領域のことも「体積」と呼びます。)
2.3. 行列式の計算方法(2次元の場合)
次に、高校で習った2次元の行列の行列式の計算方法を確認し、行列式の結果が、上記説明の通り、変換後の領域の面積と等しくなっていることを確認してみたいと思います。なお、3次元以上の行列についての行列式の計算方法については次回に説明をしたいと思います。
高校の数学の復習となりますが、2次元の行列
$$
A=\left(
\begin{matrix}
a & b \
c & d
\end{matrix}
\right)
$$
についての行列式の値$|A|$は、
$$
|A| = ad - cb
$$
となります。
次に、ベクトル$\mathbf{r}_1=(a,c)^t$と$\mathbf{r}_2=(b,d)^t$に囲まれた平行四辺形領域の面積を計算してみます。いろいろと計算方法はあると思いますが、ここでは、$\mathbf{r}_1$と$\mathbf{r}_2$のなす角度を$\theta$とし、平行四辺形の面積を計算してみたいと思います(下図ご参照)。
まず、それぞれの変の長さを求めると、
$$
\begin{align}
|\mathbf{r}_1| &=\sqrt{a^2 + c^2} \
|\mathbf{r}_2| &=\sqrt{b^2 + d^2}
\end{align}
$$
次に、$\mathbf{r}_1$と$\mathbf{r}_2$の内積を考えると、
$$
\begin{align}
\mathbf{r}_1 \cdot \mathbf{r}_2
&= |\mathbf{r}_1||\mathbf{r}_2|\cos \theta \
&= ab + cd
\end{align}
$$
よって、平行四辺形の面積$S$は、
$$
\begin{align}
S &= |\mathbf{r}_1||\mathbf{r}_2|\sin \theta \
&= |\mathbf{r}_1||\mathbf{r}_2|\sqrt{1-\cos^2 \theta } \
&= |\mathbf{r}_1||\mathbf{r}_2|\sqrt{1-\frac{(\mathbf{r}_1 \cdot \mathbf{r}_2)^2}{|\mathbf{r}_1|^2|\mathbf{r}_2|^2}} \
&= |\mathbf{r}_1||\mathbf{r}_2|
\sqrt{\frac{|\mathbf{r}_1|^2|\mathbf{r}_2|^2-(\mathbf{r}_1 \cdot \mathbf{r}_2)^2}{|\mathbf{r}_1|^2|\mathbf{r}_2|^2}} \
&= \sqrt{|\mathbf{r}_1|^2|\mathbf{r}_2|^2-(\mathbf{r}_1 \cdot \mathbf{r}_2)^2} \
&= \sqrt{(a^2 + c^2)(b^2 + d^2) - (ab + cd)^2} \
&= \sqrt{a^2b^2+a^2d^2+c^2b^2+c^2d^2-a^2b^2-2abcd-c^2d^2} \
&= \sqrt{(ad-cb)^2} \
&= ad-cb
\end{align}
$$
以上から、行列式の値と平行四辺形の面積が等しいことが確かめられました。
3. 行列式はなぜ重要か?
最後に、少し本題からは逸れるところもありますが、行列式がどのような場面で使われて、なぜ重要なのかということを説明しておきたいと思います。
正則性
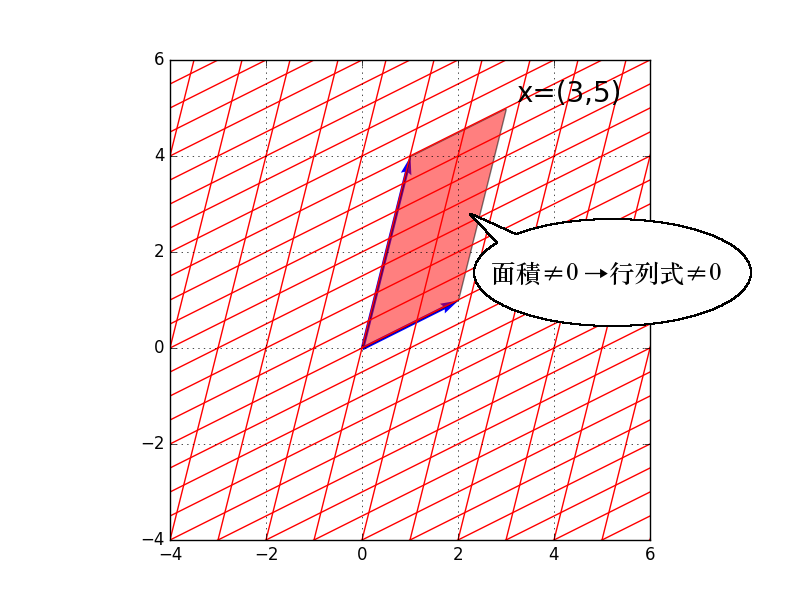
詳細は別の回に説明したいと思いますが、行列$A$により、$n$次元から$n$次元(例えば3次元から3次元)に変換がされるとき、行列$A$は正則であると言います。行列$A$が$n$次元から、より低い次元(例えば3次元から2次元)に変換されるとき、行列$A$は正則でないと言います。行列$A$が正則であるとき、変換後の領域の体積(面積)は0ではありません(つまり行列式≠0)。しかし、行列$A$が正則でないときは、変換後の領域の体積(面積)は0(つまり、行列式=0)になってしまいます。例えば、下図の通り、2次元から2次元への変換の場合は、変換後の面積は0ではないため、行列式も0ではありませんが、2次元から1次元への変換の場合は、変換後の領域は「線」になってしまうので、この領域の面積は0、行列式も0になります。
上記理由から、行列式は、行列が正則であるかどうかを確認するために用いることができるのです。ちなみに、正則性がなぜ重要かと言いますと、正則なときは逆行列が存在する、つまり、可逆性があるからです。この辺は逆行列のご説明の際に詳しく書きたいと思います。
- 2次元から2次元への変換
- 2次元から1次元への変換
一次関数との対比
第5回でご説明したとおり、行列は一次関数を一般化したものと考えることができるのでした。つまり、$\mathbf{y} = A \mathbf{x}$は、$y=ax$を一般化したものと考えることができます。ところで、$y=ax$により、$y$は$x$の$a$倍になります。つまり、$y=ax$は$x$を$a$倍する変換と考えることができます。とすると、同様に$\mathbf{y} = A \mathbf{x}$は$\mathbf{x}$を何倍にする変換なのか?と考えたくなると思いませんか?この変換倍率が$A$の行列式なのです。
ヤコビアン
※本稿の主題ではないので、分かりにくかったら読み飛ばしてください。また、説明が雑になってしまったため、誤りがありましたらご指摘いただけましたらと思います。
第1回でご説明したとおり、線形代数の大きな目的の1つとして、曲線も拡大すれば直線の集まりと見ることができるため、線形代数は曲線の近似手段として使われるとお伝えしました。詳細は省略しますが、このような解釈から、行列式は、重積分(2変数以上の積分)について変数変換をする際の拡大率として使うことができます。このような行列式のことをヤコビアンと言います。要はヤコビアンという行列式を使うと、変数変換が出来て、重積分が解けるようになるということです。(ちなみに、細かい話ですが、実際には上記「近似」は、実は、極限を取ると近似ではなく答えそのものになります。このため線形を扱う道具である行列式を、非線形な関数を扱う解析で使うことができているという理解です。)
多次元正規分布
※こちらも本稿の主題ではないので、適宜読み飛ばしてください。
確率統計で超重要な、1変数(1次元)の正規分布の分布関数は以下のように定義されます。
$$
N(\mu, \sigma^2) =
\frac{1}{(2\pi\sigma^2)^{1/2}}
\exp \Big(-\frac{1}{2\sigma^2}(x-\mu)^2\Big)
$$
ここで、$\mu$は正規分布の平均、$\sigma$は分散を表すパラメータです(細かいことは省略)。
これを多次元(多変数)に拡張し、$N$次元の正規分布の分布関数は以下のように定義されます。
$$
N(\mathbf{\mu}, \Sigma) =
\frac{1}{(2\pi)^{N/2}} \frac{1}{|\Sigma|^{1/2}}
\Big( -\frac{1}{2}(\mathbf{x}-\mathbf{\mu})^T \Sigma ^{-1} (\mathbf{x} - \mathbf{\mu})\Big)
$$
ここで、$\mathbf{\mu}$は平均を表すパラメータ(ベクトル)、$\Sigma$は、分散共分散行列です。また、$\Sigma^{-1}$は、$\Sigma$の逆行列を表します(逆行列については別の回で説明予定です。)
上記見比べると、両者は形が非常によく似ていることがわかります。このように、多次元の正規分布は、ベクトルと行列・行列式を表すと、1次元の正規分布と非常によく似た形で表すことができ、その表現の中の一部として行列式が出てくるのです。
私の理解では、行列式は、上記例のように、多次元のものを考えた際に多くの箇所で出現してしまうので、好む好まざるに関わらず、そもそも避けては通れないものなのではないかと思うのです。(たぶん、本当は、賢い数学者の方々にとっては逆で、行列は1次関数を抽象化したものなので、1次関数のときと同様に倍率を考えてみればいい。とすると、行列式が出てくるんじゃないか?と予想して式を導いているのではないかと思います。)
4. まとめ
今回の結論としては以下のとおり。
- 行列式は、行列の変換倍率を表す。
- たしかに、行列による変換後の領域の面積を計算してみると、高校のときに習った行列式の計算結果と一致している。
- 好む好まざるに関わらず、行列式は数学や工学のいろいろなところで出てくるので、避けては通れない。
次回は、(ライブラリを使えば普通は計算できるので、応用上あまり使うことがない気がするので)あまり気が進みませんが、行列式の計算方法について説明したいと思います。