本稿は、線形代数を独学でやり直し勉強した時のメモです。せっかくなのでアウトプットしようと思って書き始めました。詳しくは第1回の説明をご参照ください。
今回は前回に引き続き行列についての説明をします。前回は行列の計算方法を中心に書きましたが、今回は行列の意味(特に、行列をかける意味)についてご説明します。
1. 行列を掛ける⇔線形写像
まず結論から書きますと、**「行列を掛ける操作⇔線形写像」**となります。いきなり言われると難しそうに思う方がいらっしゃるかもしれませんが、線形写像というのは、簡単に言うと、1次関数$y=ax$を一般化したもののことです。つまり、行列を掛ける操作は、1次関数を多次元に一般化したものと言うことができます。(第1回でご説明しましたとおり、数学の目的の1つは、なんでも一般化・抽象化することなので、この目的に沿って一般化したものと思います。)
1.1. 線形写像とは?
次に、線形写像の意味についてご説明します。まず、写像というのは、簡単に言うと関数のことです。平たく言うと、$y=f(x)$の$f$のことを写像と言います。また、すべての$x$について、$f$が次の性質を満たすとき、 $f$を線形写像と言います。
- $f(x+y)=f(x)+f(y)$
- $f(cx)=cf(x)$
繰り返しになりますが、これは、1次関数(原点を通る直線の式)$f(x)=ax$を一般化したものと言えます。実際、 $f(x)=ax$は、以下のとおり上記性質を満たすため、線形写像です。
\begin{align}
f(x+y) &= a(x+y) \\
&= ax + ay \\
&= f(x)+f(y)
\end{align}
\begin{align}
f(cx) &= a \times (c x) \\
&= cax \\
&= cf(x)
\end{align}
1.2. 行列を掛ける操作⇔線形写像となることの確認
まず、少し話が逸れますが、一般的に、数学で、同値(必要十分条件、矢印で書くと"$\Leftrightarrow$")であることを証明・説明するときは、十分条件であること("$\Rightarrow$"方向)と、必要条件であること("$\Leftarrow$"方向)の両方向の証明・説明をする必要があります。(これは、数学では非常によく出てくるパターンですので、よく理解しておく必要があります。ちなみに、方程式を解く場合や、式の展開の時等は、あまり意識していないと思いますが、たまたま両方向の証明が同時にできているだけなのです。このことは、機会があれば別途ご説明できればと思っています。)
ちなみに、この後の説明は少しごちゃごちゃしていると感じるかもしれません。まずはイメージを理解したいという方は先に2に進んだ方がいいかもしれません。
1.1.1. 行列を掛ける操作⇒線形写像となることの確認
ということで、まずは、"$\Rightarrow$"方向の確認です。つまり、『行列を掛ける操作はすべて、線形写像となっている』ということが、ここで確認したいことです。前回書かなかったかも知れませんが、実はこれは行列の掛け算の性質そのものです。実際、行列とベクトルの積の定義から、任意のベクトル$\mathbf{x}$、$\mathbf{y}$、任意の定数$c$と行列$A$について、
\begin{align}
A(\mathbf{x} + \mathbf{y}) &= A\mathbf{x}+A\mathbf{y} \\
A(c\mathbf{x}) &= cA\mathbf{x}
\end{align}
が成り立ちます。(すみませんが省略しますが、定義に代入してみればすぐにわかります)。以上から、行列を掛ける操作は線形写像であること("$\Rightarrow$"方向)は確認できました。
1.1.2.線形写像⇒行列を掛ける操作となることの確認
次に、"$\Leftarrow$"方向の確認(線形写像⇒行列を掛ける操作となること)の確認です。もう少し分かりやすく書くと、『すべての線形写像は、「行列を掛ける」という操作で表せる』ということが、ここで確認したいこととなります。
今、ある線形写像$f$を考えます。まず、任意の$n$次元ベクトル$\mathbf{x}=(x_1, \cdots, x_n)$について、正規直行基底(第3回をご参照)を$\mathbf{e}_i, i=1, \cdots, n$とすると、$\mathbf{x}$は以下のように表せます。
\mathbf{x}=x_1 \mathbf{e}_1 + \cdots + x_n \mathbf{e}_n
ちなみに、くどいかもしれませんが、念のため書きますと、$\mathbf{e}_i (i=1 \cdots n)$は以下の通りです。
\begin{align}
\mathbf{e}_1 &= (1, 0, \cdots, 0)^t \\
\mathbf{e}_2 &= (0, 1, \cdots, 0)^t \\
&\vdots \\
\mathbf{e}_n &= (0, 0, \cdots, 1)^t
\end{align}
ここで、$\mathbf{a}_i = f(\mathbf{e}_i)$とすると、
\begin{align}
f(\mathbf{x}) &= f(x_1 \mathbf{e}_1 + x_2 \mathbf{e}_2 + \cdots + x_n \mathbf{e}_n) \\
&= f(x_1 \mathbf{e}_1) + f(x_2 \mathbf{e}_2) + \cdots + f(x_n \mathbf{e}_n) \\
&= x_1 f(\mathbf{e}_1) + x_2 f(\mathbf{e}_2) + \cdots + x_n f(\mathbf{e}_n) \\
&= x_1 \mathbf{a}_1 + x_2 \mathbf{a}_2 + \cdots + x_n \mathbf{a}_n \\
&= \left(
\begin{matrix}
\mathbf{a}_1 , \mathbf{a}_2 , \cdots , \mathbf{a}_n
\end{matrix}
\right) \mathbf{x} \\
&= A \mathbf{x}
\end{align}
上式で、
- 2行目,3行目は、$f$が線形写像であることから、それぞれ、線形写像の性質$f(x+y) = f(x)+f(y)$, $f(cx)=cf(x)$から成り立ちます。
- 5行目は、行列とベクトルの掛け算の性質(第4回の『4.5.2 基本的な計算パターンのまとめ』の4番目の・をご参照)から成り立ちます。
- 6行目は、$A=(\mathbf{a}_1, \cdots, \mathbf{a} _n)$とおきました。
以上より、任意のベクトル$\mathbf{x}$に対しての線形写像$f$は、行列を掛ける操作として表すことができました。(正確には、線形写像 $f$は、各正規直行基底$\mathbf{e}_i$の$f$による写像$\mathbf{a}_i$を縦に並べて作った行列 $A$を掛けるという操作によって表すことができたということです)。これで、『すべての線形写像は、「行列を掛ける」という操作で表せる』ことが確認できました。
以上より、『行列を掛ける操作⇔線形写像となることの確認』が確認できました。
2020年5月追記:
続きの記事を書こうと思って読み返してみましたが、ちょっと分かりにくかったと思いましたので追記です。上記の説明中、$f(\mathbf{x})$は関数です。($\mathbf{x}$の値に応じて$f(\mathbf{x})$の値が変わるもの)。一方、$\mathbf{a}_{i}=f(\mathbf{e}_{i})$は、$f(\mathbf{x})$に具体的な値(定数)${\mathbf{e}_i}$を代入して求まる定数です。
上記で言いたいことは、要は、線形写像$f(\mathbf{x})$は、$\mathbf{x}$に『定数$\mathbf{a}_i$を横に並べて作った行列$A$』を掛けたもので表せるということになります。
2. 線形写像(1次関数の一般化)の意味
次に、線形写像(1次関数の一般化)の意味についてもう少し詳しく考えてみます。
2.1. 1次関数の意味
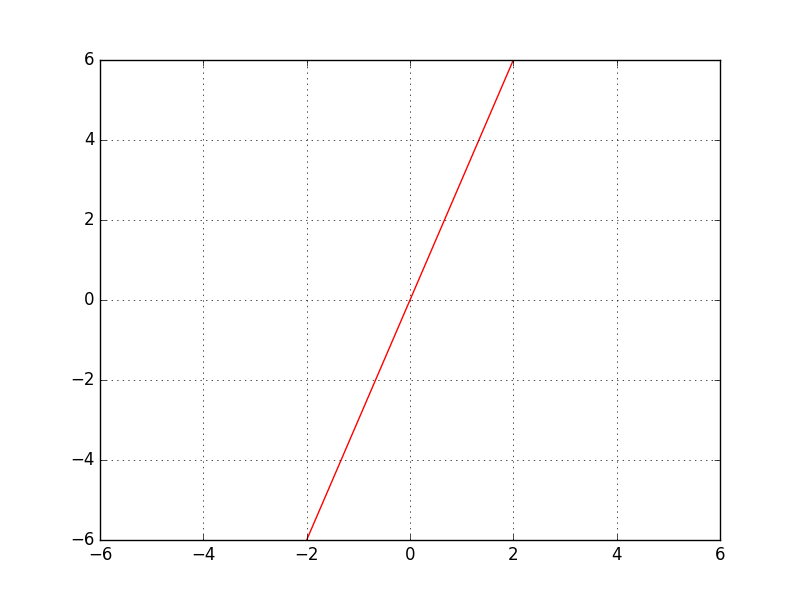
ほとんど中学校の数学の復習のような感じになりますが、まずは、$y=ax$の意味について考えてみます。当たり前ですが、$y=ax$は、ある$x$が入力として与えられると、その数を$a$倍する関数です。つまり、**$x$の値を拡大したり縮小したりしています($a>1$の場合は伸ばし、$a<1$の場合は縮める)**。例えば、$a=3$の場合、以下の表・図のように、$x$の値によって、その3倍の値を返す関数です。(グラフを描くまでもないことかも知れませんが。)
| x | y |
|---|---|
| -1 | -3 |
| 0 | 0 |
| 1 | 3 |
| 2 | 6 |
2.2. 線形写像の意味
では、1次関数を一般化した、線形写像(=ベクトルに行列を掛けたもの)の意味はどのようなものになるでしょうか?
まず、簡単な例として、以下の$2 \times 2$の行列を考えてみます。
A=\left(
\begin{matrix}
5 & 0 \\
0 & 3
\end{matrix}
\right)
いま、正規直行基底
\begin{align}
\mathbf{e}_1 &=
\left(
\begin{matrix}
1 \\
0
\end{matrix}
\right) \\
\mathbf{e}_2 &=
\left(
\begin{matrix}
0 \\
1
\end{matrix}
\right)
\end{align}
は、この行列 $A$により、それぞれ、
\begin{align}
A\mathbf{e}_1 &=
\left(
\begin{matrix}
5 & 0 \\
0 & 3
\end{matrix}
\right)
\left(
\begin{matrix}
1 \\
0
\end{matrix}
\right) \\
&=
\left(
\begin{matrix}
5 \\
0
\end{matrix}
\right)
\end{align}
\begin{align}
A\mathbf{e}_2 &=
\left(
\begin{matrix}
5 & 0 \\
0 & 3
\end{matrix}
\right)
\left(
\begin{matrix}
0 \\
1
\end{matrix}
\right) \\
&=
\left(
\begin{matrix}
0 \\
3
\end{matrix}
\right)
\end{align}
のように変換されます。
また、任意のベクトル$\mathbf{x} = (x_1, x_2)^t$は、
\mathbf{x} = x_1 \mathbf{e}_1 + x_2 \mathbf{e}_2
と表されるので、この$\mathbf{x}$は、$A$により、以下のように変換されます。
\begin{align}
A \mathbf{x} &= A (x_1 \mathbf{e}_1 + x_2 \mathbf{e}_2) \\
&= x_1 A \mathbf{e}_1 + x_2 A \mathbf{e}_2 \\
&=
x_1
\left(
\begin{matrix}
5 \\
0
\end{matrix}
\right)
+
x_2
\left(
\begin{matrix}
0 \\
3
\end{matrix}
\right) \\
&=
\left(
\begin{matrix}
5 x_1 \\
3 x_2
\end{matrix}
\right)
\end{align}
つまり、この行列$A$により、2次元空間上の任意のベクトルは、$x$方向に5倍、$y$方向に3倍引き延ばされることになります。(1次関数が2次元のベクトルに対して一般化されています。)
例えば、以下図のとおり、$\mathbf{x}=(1,2)^t$は、この変換により、$x$方向に5倍、$y$方向に3倍されます。
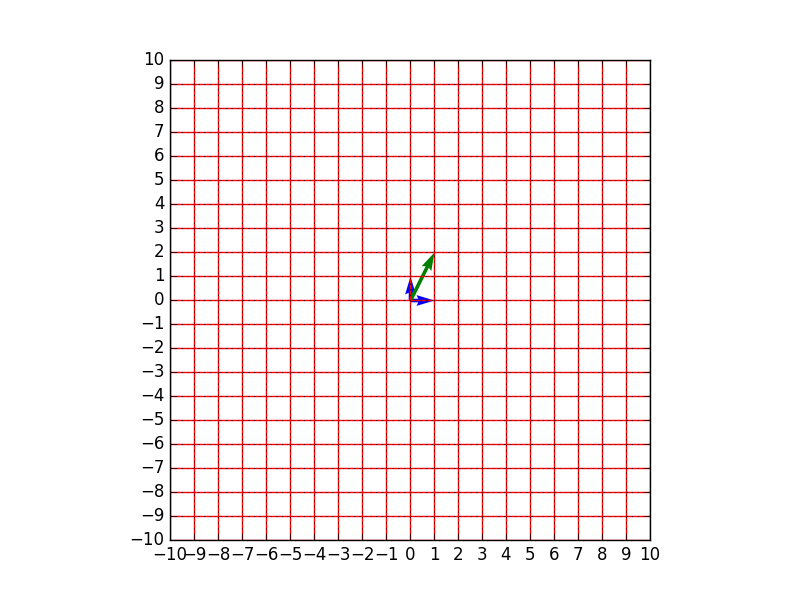
- 変換前のベクトル$\mathbf{x} = (1,2)^t$ (青矢印が基底、緑矢印がベクトル$x$)
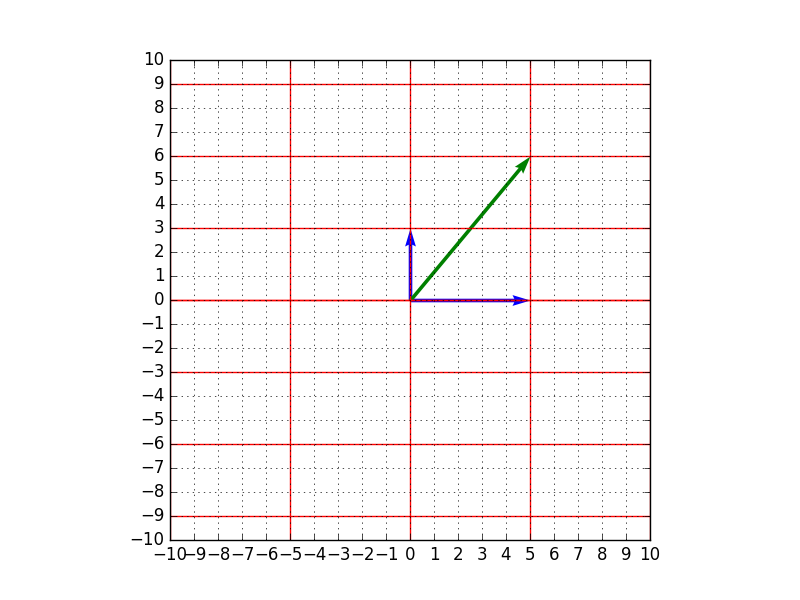
- $A$による変換後のベクトル$A \mathbf{x} = (5,6)^t$ (青矢印が基底、緑矢印がベクトル$A \mathbf{x}$)
→$x$軸が全体的に5倍に、$y$軸方向が全体的に3倍に伸びています。
次に、以下の行列を考えてみます。(第3回でご説明した基底を用いた例を示すため、このように複雑な数字になっています。)
A = \left(
\begin{matrix}
\frac{13}{7} & \frac{2}{7} \\
-\frac{4}{7} & \frac{22}{7}
\end{matrix}
\right)
考え方は先ほどの例と同様ですが、今度は、正規直行基底ではなく、以下の基底(第3回の例でご説明した基底)について考えてみると、
\begin{align}
\mathbf{b}_1 &=
\left(
\begin{matrix}
2 \\
1
\end{matrix}
\right) \\
\mathbf{b}_2 &=
\left(
\begin{matrix}
1 \\
4
\end{matrix}
\right)
\end{align}
これらは、行列$A$により、それぞれ以下のように変換されます。
\begin{align}
A\mathbf{b}_1 &=
\left(
\begin{matrix}
\frac{13}{7} & \frac{2}{7} \\
-\frac{4}{7} & \frac{22}{7}
\end{matrix}
\right)
\left(
\begin{matrix}
2 \\
1
\end{matrix}
\right) \\
&=
\left(
\begin{matrix}
4 \\
2
\end{matrix}
\right) \\
&=
2 \mathbf{b}_1
\end{align}
\begin{align}
A\mathbf{b}_2 &=
\left(
\begin{matrix}
\frac{13}{7} & \frac{2}{7} \\
-\frac{4}{7} & \frac{22}{7}
\end{matrix}
\right)
\left(
\begin{matrix}
1 \\
4
\end{matrix}
\right) \\
&=
\left(
\begin{matrix}
3 \\
12
\end{matrix}
\right) \\
&= 3 \mathbf{b}_2
\end{align}
つまり、行列$A$により、基底$\mathbf{b}_1$、基底$\mathbf{b}_2$はそれぞれ、2倍、3倍に拡大されます。
また、先ほどの例と同様、任意のベクトル$\mathbf{x}$は、基底$\mathbf{b}_1, \mathbf{b}_2$によって
\mathbf{x} = x_1 \mathbf{b}_1 + x_2 \mathbf{b}_2
と表されます。(ただし、先ほどの例とは違い、$\mathbf{x}$は$(x_1, x_2)^t$ではありません。なぜなら、$\mathbf{b}_1, \mathbf{b}_2$が正規直行基底ではないからです。よく分からなくなってきた方は第3回をご参照ください。それでもよくわからない方がいらっしゃいましたら、補足の説明を考えたいと思います。)
上記より、この$\mathbf{x}$は、$A$により以下のように変換されます。
\begin{align}
A \mathbf{x} &= A (x_1 \mathbf{b}_1 + x_2 \mathbf{b}_2) \\
&= x_1 A \mathbf{b}_1 + x_2 A \mathbf{b}_2 \\
&= 2 x_1 \mathbf{b}_1 + 3 x_2 \mathbf{b}_2
\end{align}
以上より、変換後のベクトル$A\mathbf{x}$は、元の基底を2倍、3倍したベクトル$2\mathbf{b} _1$と$3 \mathbf{b} _2$を用いて表されることが分かります。
つまり、元のベクトル$\mathbf{x}$は、$\mathbf{b}_1$方向に2倍、$\mathbf{b}_2$方向に3倍されているのです。
例えば、$\mathbf{x}=(5, 6)^t$を考えると、
\begin{align}
\mathbf{x} &=
\left(
\begin{matrix}
5 \\
6
\end{matrix}
\right) \\
&= 2
\left(
\begin{matrix}
2 \\
1
\end{matrix}
\right)
+ 1
\left(
\begin{matrix}
1 \\
4
\end{matrix}
\right) \\
&= 2 \mathbf{b}_1 + 1 \mathbf{b}_2
\end{align}
なので、
\begin{align}
A \mathbf{x} &= 2 \times 2 \mathbf{b}_1 + 1 \times 3 \mathbf{b}_2 \\
&=
\left(
\begin{matrix}
11 \\
16
\end{matrix}
\right)
\end{align}
となります。これを図で表すと以下のようになります。
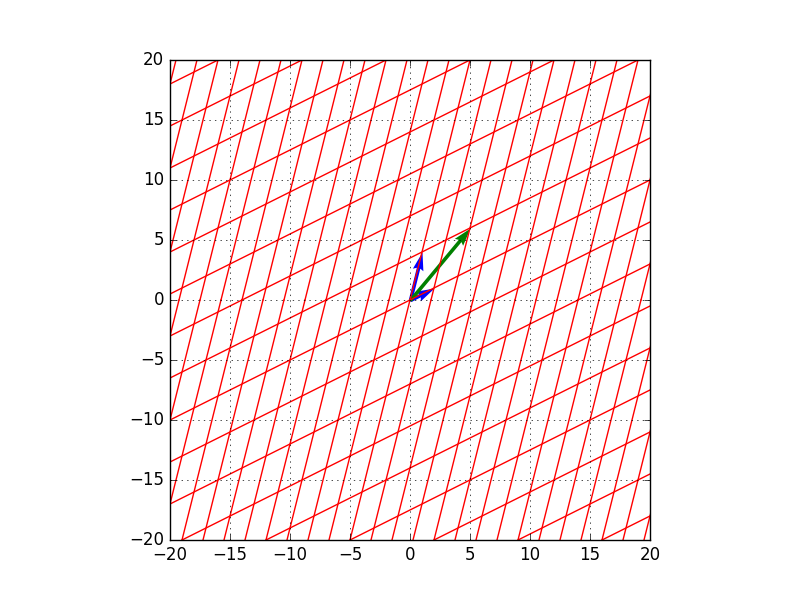
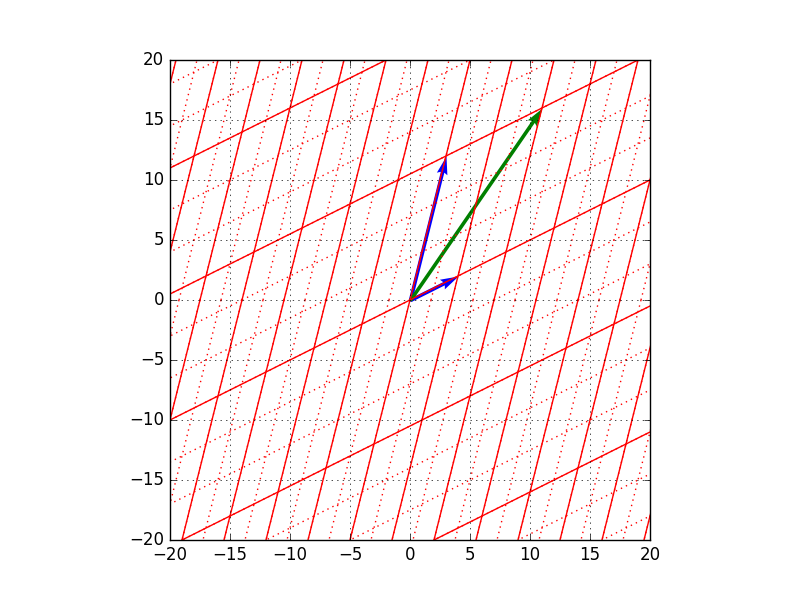
- 変換前のベクトル$\mathbf{x} = (5,6)^t$ (青矢印が基底、緑矢印がベクトル$x$)
- $A$による変換後のベクトル$A \mathbf{x} = (11,16)^t$ (青矢印が基底、緑矢印がベクトル$A \mathbf{x}$)
→$\mathbf{b}_1$方向に全体的に2倍に、$\mathbf{b}_2$方向に全体的に3倍に伸びています。
以上のように、この例でも、行列$A$を掛けるという操作は、ある特別な方向(基底$\mathbf{b}_1$、$\mathbf{b}_2$方向)に拡大するという、1次関数を一般化した形になっています。このように、線形写像は、一次関数を一般化したものとして、特定の軸の方向に拡大・縮小をする変換となるのです。
2.3. 補足
ちなみに、補足として、少しだけ固有値・固有ベクトルについて触れておきます。(固有値・固有ベクトルの詳細は別の回でご説明予定です。)
実は、先ほどの例は、$A$が、基底$\mathbf{b}_1$、$\mathbf{b}_2$方向に拡大・縮小するようになるような例をうまく作ったものです。逆に、第3回でもご説明した通り、基底は無数のパターンを選ぶことができるので、ある行列$A$が与えらえた時に、その行列によって、拡大・縮小する軸の組み合わせ(基底)を選択することで、上記の例のように、行列の操作を簡単に表現することができるのです。この基底の組みが、実は固有ベクトルで、それぞれの軸の拡大率(先ほどの例では、2倍と3倍)が、固有値なのです。
3.まとめ
今回のまとめです。
- 行列の掛け算は、一次関数を一般化したものであり、「線形写像」を表したものである。
- これは、具体的には、ベクトルを特定の方向に拡大・縮小したものである。
- ちなみに、特定の軸は固有ベクトルであり、それぞれの拡大率は固有値である(詳細は別の回でご説明予定)。
- 今回は2次元の例でご説明しましたが、3次元も同様。
どうだったでしょうか? 私は、大学数学の最初の挫折ポイントの一つである線形代数が、実は中学生で習う1次関数を単に一般化しただけだったというのは、とても新鮮に思いました。1次関数を一般化しただけの線形代数が、大学以降の理工学の各分野で重要な役割を果たしている理由をつらつらと考えてしまいましたが、たぶん、第1回でも書きましたとおり、非線形な挙動も局所的には線形(1次関数)に近似できることと、たくさんの数をベクトルとしてひとまとまりで考えることが多いからなんだろうな〜と思いました。
以上、分かりにくいところがありましたらお気軽にご指摘いただけましたらと思います(反応は遅いかもしれませんが)。次回は行列式について説明予定です。