本稿は、線形代数を独学でやり直し勉強した時のメモです。せっかくなのでアウトプットしようと思って書き始めました。詳しくは第1回の説明をご参照ください。
1. (前回の復習)ベクトルの足し算
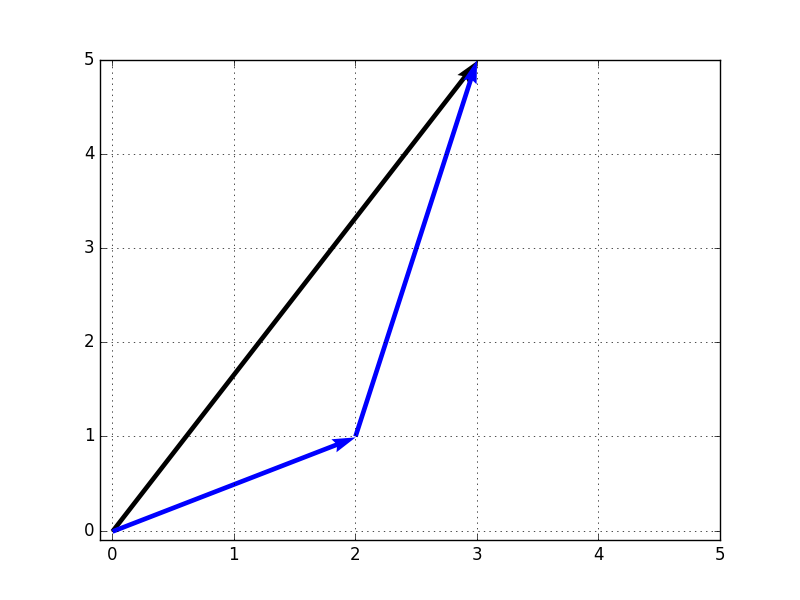
まずは前回の復習兼補足です。前回の説明の通り、ベクトルは矢印で表せますが、ベクトルの足し算は、2つの矢印をつなぎ合わせたものとして表せます。例えば、
\begin{align}
\left(
\begin{matrix}
3\\\
5
\end{matrix}
\right)
&=
\left(
\begin{matrix}
2\\\
1
\end{matrix}
\right)
+
\left(
\begin{matrix}
1\\\
4
\end{matrix}
\right)
\end{align}
ですが、これは図で表すと以下の通りとなります。
2. 基底
次に、今回の本題の基底の説明です。
2.1 基底の意味・目的
まず、読むのが嫌になる前に、基底の意味と目的を私なりに書きますと、基底は、表現しようとする空間(例えば平面)全体を表す枠組み(グリッド)の元になるもののようなイメージになると思います。このため、基底から、対象となる空間全体を把握することができるため、基底は線形代数の重要な要素なのではないかと思っています。
2.2 基底の定義
次に、基底の定義です。基底とは、足し算と定数倍で、考えようとしている空間(例えば2次元だったら平面、3次元だった空間)上のすべての点をくまなく表現することができ、かつ、表現の仕方が重複しないようなベクトルの組のことを言います。実は、方向の違う$n$個の$n$次元ベクトルの組はすべて基底となるので、基底は無数に存在することになります。例えば、方向の違う2個の2次元ベクトルの組はすべて2次元空間(平面)上の基底となります。
2.3 2次元の基底の例
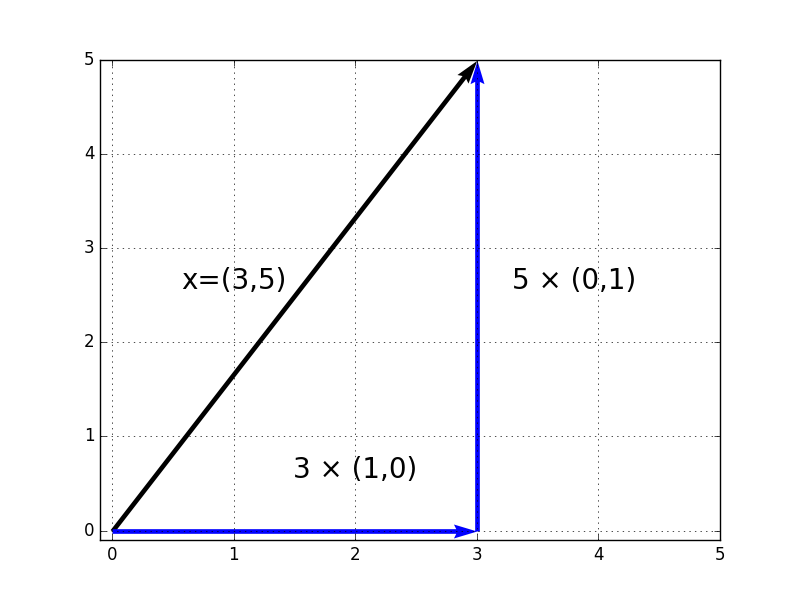
$e_1=(1,0)^t$,$e_2=(0,1)^t$という2つのベクトルの組は2次元の基底です。なぜならば、平面上の任意の点を足し算と定数倍で一通りで表すことができるからです。例えば、$(3,5)^t$は、$e_1$と$e_2$の足し算と定数倍で以下のように表すことができます。
\begin{align}
\left(
\begin{matrix}
3\\\
5
\end{matrix}
\right)
&=3
\left(
\begin{matrix}
1\\\
0
\end{matrix}
\right)
+5
\left(
\begin{matrix}
0\\\
1
\end{matrix}
\right)\\\
&=
3 \mathbf{e}_1 + 5 \mathbf{e}_2
\end{align}
図で表現すると以下の通りです。
同様に、平面上の任意の点$(x,y$)は以下のように表すことができます。
\begin{align}
\left(
\begin{matrix}
x\\\
y
\end{matrix}
\right)
&=x
\left(
\begin{matrix}
1\\\
0
\end{matrix}
\right)
+y
\left(
\begin{matrix}
0\\\
1
\end{matrix}
\right)\\\
&=
x \mathbf{e}_1 + y \mathbf{e}_2
\end{align}
また、$(x,y)$は、$e_1$と$e_2$を用いて、上記の表し方でしか表すことができません。(上式の右辺の$x$と$y$の部分に$x$、$y$以外の数が入ると、左辺と等しくなりません)。
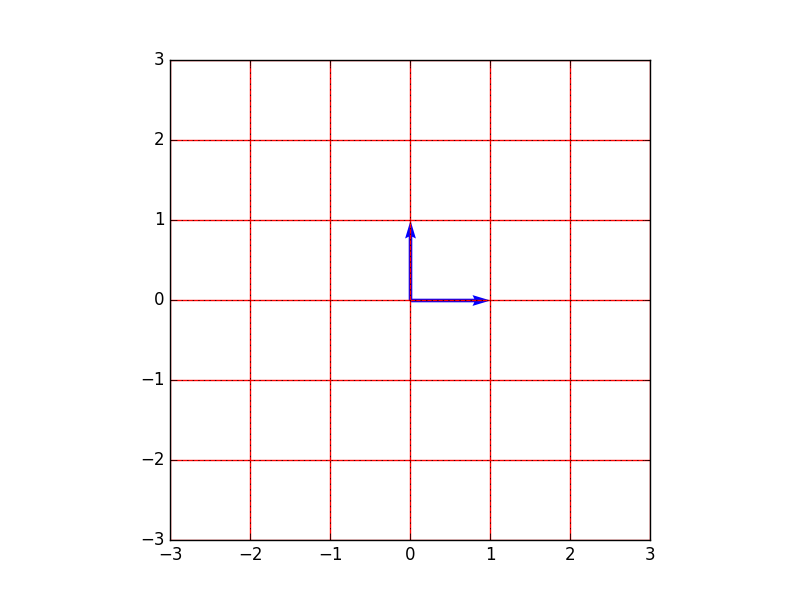
ちなみに、まだ厳密な定義はまだ説明してませんが、$e_1$と$e_2$は図からも明らかなように、長さが1で、直交している(直角に交わっている)ので、$正規直交基底$と言います。
上の例は当たり前のような感じもしますが、実は、2次元上の、向きの違う2つの矢印は組はすべて基底となります。
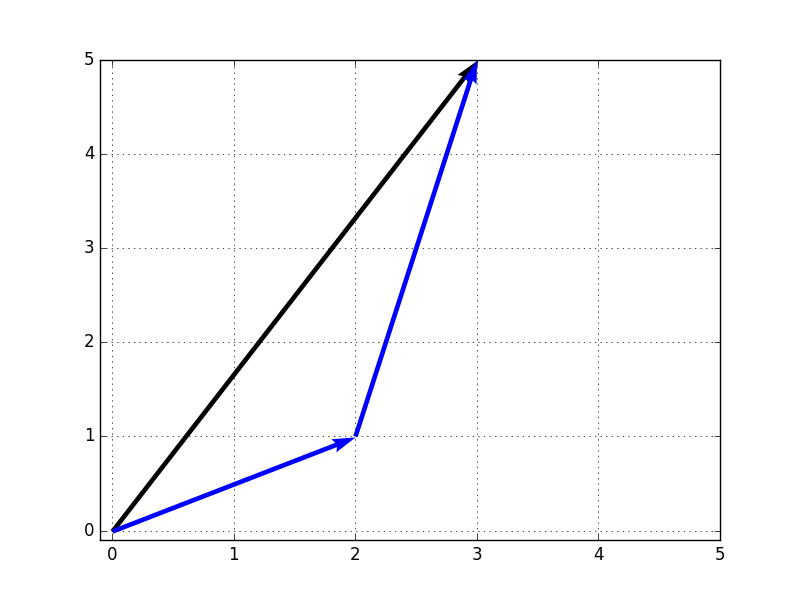
例えば、2次元上のベクトルの組$(2,1)^t$,$(1,4)^t$は基底です。例えば、$(3,5)^t$は本ページの一番最初のベクトルの足し算の例のように、
\begin{align}
\left(
\begin{matrix}
3\\\
5
\end{matrix}
\right)
&=1
\left(
\begin{matrix}
2\\\
1
\end{matrix}
\right)
+1
\left(
\begin{matrix}
1\\\
4
\end{matrix}
\right)
\end{align}
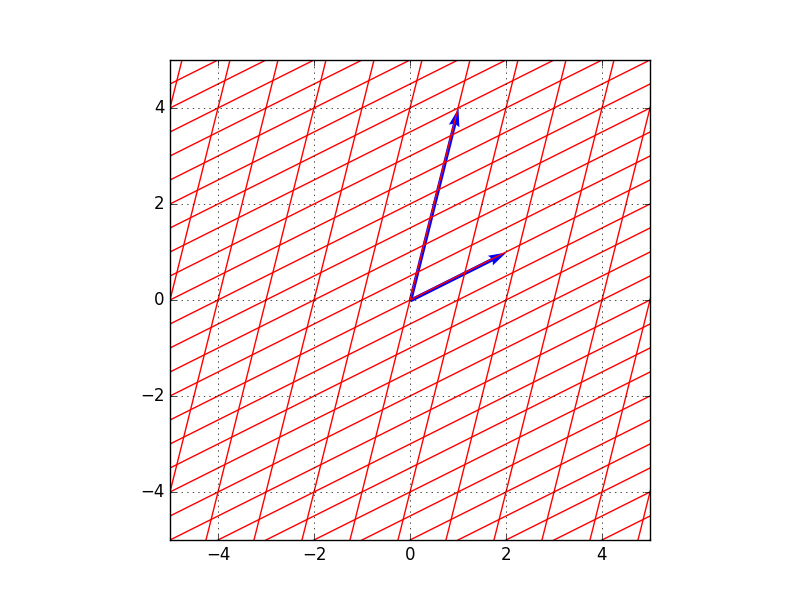
です。図で表すと以下のようになります。
以下の図のように、基底は、考えようとしている空間上をくまなく表す網目(グリッド)の元となる構成要素と言えます。
- 基底$(1,0)^t$と$(0,1)^t$のイメージ →これらの組み合わせ(足し算と定数倍)で、平面上のすべての点を表すことができる。
- 基底$(2,1)^t$と$(1,4)^t$のイメージ →これらの組み合わせ(足し算と定数倍)で、平面上のすべての点を表すことができる。
2つのベクトルの向きが同じだったらどうなるか
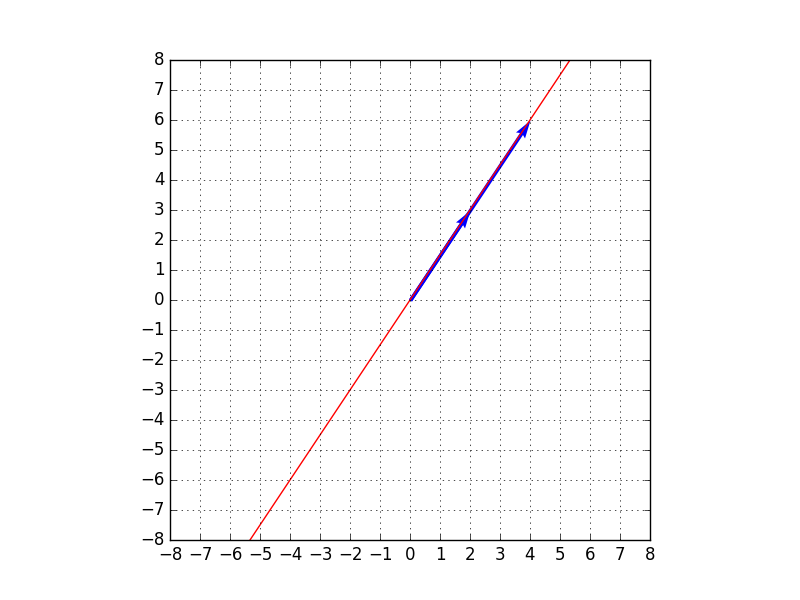
この場合は、平面上をくまなく表すことができないので、基底にはなりません。例えば、$(2,3)^t$と$(4,6)^t$は向きが同じのため、これらのベクトルの足し算と定数倍では、次の図のイメージのように、直線しか表すことができず、基底とはなれません。
- 基底$(2,3)^t$と$(4,6)^t$のイメージ →これらの組み合わせ(足し算と定数倍)では、ベクトル$(2,3)^t$の延長上の直線上の点しか表すことができない。
3本のベクトルの組は2次元平面上の基底となるか?
なれません。2次元平面上の基底を構成するベクトルの本数は必ず2本となります。なぜなら、そもそも、先ほどまでの説明のとおり、2本の向きの違う2つのベクトルの足し算と定数倍で、平面上のすべての点は表すことができるので、3本のベクトルの組があった場合は、そのうちの2本のベクトルの足し算と定数倍で、平面上のすべての点を表すことができてしまい、同じ点を複数の方法で表すことができてしまうからです。
例えば、$\mathbf{a}$,$\mathbf{b}$,$\mathbf{c}$という3本のベクトルがあった場合、ある点$\mathbf{x} = (x,y)^t$は、以下2通りで表すことができてしまうということです。(ベクトルの前の係数($x_a$等)は適当に決めただけですので気にしないでください。)
\mathbf{x} = x_a \mathbf{a} + x_{b1} \mathbf{b} \\\
\mathbf{x} = x_{b2} \mathbf{b} + x_c \mathbf{c}
一般的に、$n$次元空間上の基底は、必ず$n$本のベクトルの組から構成されます。
2.4 3次元以上の場合
- 3次元以上の場合も、考え方は2次元の場合と全く同じです。3次元だったら、3次元空間上の向きが異なる3本のベクトルの組が基底となります。また、$n$次元だったら、向きの異なる$n$本のベクトルの組が基底となります。
- 3次元でしたら、2次元と同じように、図を書いてイメージを湧かせることは可能だと思います。(説明用に書いてみようとしましたが、分かりにくくなってしまったので頓挫しました。)
- 何度も同じことですみませんが、$n$次元の場合は図でイメージを描くことはできません。ただし、イメージできないところで2次元の上記説明と全く同じことが起きていると理解しておけば、今後の勉強を進める上で全く問題はありません。
- また、話がこんがらがりそうなので流していただいて結構ですが、逆に、実は先に次元ありきではなく、基底を構成するベクトルの本数=次元と定義をしていたと思います。
3. まとめ
- n次元空間上の基底は、向きが異なるn本のベクトルの組のことをいう。
- 向きが異なるベクトルの組ならばなんでもいいので、基底は何通りも存在する。
- 基底は、その空間を表す枠組み(グリッド)のようなものとイメージしておけばよい。
とりあえず基底のイメージを理解しておきたいというかたは、上記理解しておけば十分だと思います。線形代数の教科書では、上記イメージが本当に$n$次元でも成り立っているかを確認するために、こねこねと説明をしているということになりますので、厳密な説明を確認しておきたいという場合は、上記イメージを持ちつつ、教科書の説明や式を追っていってもらえればよいかと思います。
以上でイメージは伝わりましたでしょうか?説明しようとするとなかなか難しいですね。ご質問等ありましたらお気軽にどうぞ。(反応が遅い場合でもご勘弁ください。また、数学科の皆様はお手柔らかにお願いします。)
4. 次回の予定
次回は行列についての説明を書きたいと思います。