Go to Qiita Advent Calendar 2024 Top
LoginSignup
0
0

Delete article

Deleted articles cannot be recovered.

Draft of this article would be also deleted.

Are you sure you want to delete this article?

More than 3 years have passed since last update.

@ochimusha01(yasunori matuki)

【数理考古学】離心率①二次曲線（楕円，放物線，双曲線）の極座標表示からの出発。

Last updated at Posted at 2021-02-13
  • (2021年02月14日)Rによる初投稿
  • (2021年04月26日)Texを導入
  • (2021年07月02日)「pytonの場合」を導入

とりあえず離心率εを媒介変数とする離心率関数$\frac{1}{1+ε\cos(θ)}(θ=-π→π)$を動かしてみました。極座標系(Polar Coordinates System)なので絶対値(Module)=上掲式、角度(Argment)θ=-π→πの範囲の複素数表現(Complex Expression)を合成したPlotとなります。
二次曲線（楕円，放物線，双曲線）の極座標表示 | 高校数学の美しい物語
image.gif

Eccentricity01<-function(x){
c0<-seq(-pi,pi,length=60) 
f0<-function(x)1/(1+x*cos(c0))
s0<-complex(mod=f0(x),arg=c0)
plot(s0,type="b",asp=1,xlim=c(-10,20),ylim=c(-5,5),main="Eccentricity",xlab="Real",ylab="Imaginal",col=rgb(0,1,0))
abline(h=0,col=rgb(1,0,0))
abline(v=0,col=rgb(1,0,0))
legend("topright", legend=paste("1/(1+",x,"*cos(θ))"),lty=1,col=rgb(0,1,0))
}

library("animation")
Time_Code=seq(0,5,length=51)
saveGIF({
for (i in Time_Code){
　　Eccentricity01(i)
}
}, interval = 0.1, movie.name = "Eccentricity01.gif")
  • 離心率ε=0の時に半径1の単位円$y=±\sqrt{1-x^2}$(楕円方程式$\frac{x^2}{a^2}+\frac{y^2}{b^2}-1=0$においてa=b=1の場合)
    image.png
  • 離心率0<ε<1の時に**楕円**$y=\sqrt{b^2(1-\frac{x^2}{a^2})}$
    image.png
  • 離心率ε=1の時に放物線を横にした$y=\frac{1}{2}±\sqrt{x}$
    image.png
  • 離心率ε>1の時に双曲線$y=\sqrt{b^2(\frac{x^2}{a^2}-1)}$
    image.png

    image.png

そして離心率εが無限大$\infty$に近くにつれY軸上の原点{0,0}へと収束していきます。
image.gif

Eccentricity02<-function(x){
c0<-seq(-pi,pi,length=60) 
f0<-function(x)1/(1+x*cos(c0))
s0<-complex(mod=f0(x),arg=c0)
plot(s0,type="b",asp=1,xlim=c(-3,3),ylim=c(-3,3),main="Eccentricity",xlab="Real",ylab="Imaginal",col=rgb(0,1,0))
abline(h=0,col=rgb(1,0,0))
abline(v=0,col=rgb(1,0,0))
legend("topright", legend=paste("1/(1+",x,"*cos(θ))"),lty=1,col=rgb(0,1,0))
}

library("animation")
Time_Code=seq(2,100,length=99)
saveGIF({
for (i in Time_Code){
　　Eccentricity02(i)
}
}, interval = 0.1, movie.name = "Eccentricity02.gif")

ところで上掲の引用サイトには重要な指摘が抜けてますね。
二次曲線（楕円，放物線，双曲線）の極座標表示 | 高校数学の美しい物語

式r=l/(1+εcosθ)と式r=−l1−εcosθは同じ曲線を表すことに注意する（1におけるθ=αの点と2におけるθ=α+πの点は一致する）。

要するに両者は「複素共役の関係にある」という事です。それも水平方向に展開する半径1の単位円に対して垂直方向の!!
image.gif

Eccentricity01<-function(x){
c0<-seq(-pi,pi,length=60) 
f0<-function(x)1/(1-x*cos(c0))
s0<-complex(mod=f0(x),arg=c0)
plot(s0,type="b",asp=1,xlim=c(-20,10),ylim=c(-5,5),main="Eccentricity",xlab="Real",ylab="Imaginal",col=rgb(0,1,0))
abline(h=0,col=rgb(1,0,0))
abline(v=0,col=rgb(1,0,0))
legend("topright", legend=paste("1/(1+",x,"*cos(θ))"),lty=1,col=rgb(0,1,0))
}

library("animation")
Time_Code=seq(0,5,length=51)
saveGIF({
for (i in Time_Code){
　　Eccentricity01(i)
}
}, interval = 0.1, movie.name = "Eccentricity03.gif")

同時表示
image.gif

Eccentricity01<-function(x){
c0<-seq(-pi,pi,length=60) 
f0<-function(x)1/(1+x*cos(c0))
s0<-complex(mod=f0(x),arg=c0)
plot(s0,type="b",asp=1,xlim=c(-20,20),ylim=c(-5,5),main="Eccentricity",xlab="Real",ylab="Imaginal",col=rgb(0,0,1))
par(new=T) 
f0<-function(x)1/(1-x*cos(c0))
s0<-complex(mod=f0(x),arg=c0)
plot(s0,type="b",asp=1,xlim=c(-20,20),ylim=c(-5,5),main="",xlab="",ylab="",col=rgb(1,0,0))
abline(h=0,col=rgb(1,0,0))
abline(v=0,col=rgb(1,0,0))
legend("topright", legend=paste("1/(1+",x,"*cos(θ))"),lty=1,col=rgb(0,1,0))
}

library("animation")
Time_Code=seq(0,5,length=51)
saveGIF({
for (i in Time_Code){
　　Eccentricity01(i)
}
}, interval = 0.1, movie.name = "Eccentricity04.gif")

これはどういう事でしょう？　ヒントは二次形式の扱いにあるのかもしれません。
2 次形式の標準化

ここで得られた「(水平方向の複素共役に直交する)垂直方向の複素共役」なる概念も視野に加えてこれまでの投稿内容の整理を試みます。

  • 片側無限数列(One Side Inf(inity) Sequance)に由来する同心円集合(Concentric Circle Set)/同心球面集合(Concentric Sphere Set)によって構成される極座標系に対数尺(範囲1→0、すなわちexp(-x)の範囲)へと射影された原点0から無限遠点Inf(inity)までの範囲を半径(Radius)として与えると「(単位円の縁が単位円の縁に重なるので)重力レンズ効果によって裏面まで写り込んだブラックホールの景色(ただし人間の視覚は裏面部分を誤差として切り捨ててしまうので、全体として球面に見える)」あるいは「底面を単位円とする高さ無限大の円錐」が現れる。
    【Rで球面幾何学】等差数列(算術数列)②数直線概念から同心円集合概念へ
    image.gif
    image.gif
    【初心者向け】誤差関数(ERF)と相補誤差関数 (ERFC)。
    image.gif

  • 無限遠点Inf(inity)を無限小-Infと無限大Infに分割する両側無限数列(Both Side Inf(inity) Sequance)の概念を直径(Diameter)に採用した極座標系は自明の場合(Trivial Case)として対蹠(Antipodes)と共役(Conjugate)の概念を獲得するが、この時「縦方向/垂直方向」すなわち実数軸(Real Axis)に直交する虚数軸(Imaginal Axis)も(底面の半径範囲が0から1にかけての)無限円錐でいうところの中央(高さ1/2)、半径1(直径2)の単位球面でいうところのCos(π/2)=90度の箇所で2分割される(要するに線上だと2分割、平面だと2×2で4分割、立体だと2×2×2で8分割される訳である。これがオイラーのφ関数でいうところの「素数族2^n概念の導入」?)。
    【初心者向け】複素共役のアニメーション表示について。
    image.gif

    image.gif

    image.gif

  • ここで実軸(Real Axis)と虚軸(Imaginal Axis)の関係について改めてまとめておこう。例えばオイラーの多面体定理(Euler's Polyhedron Theorem)を満たす正多面体(Regular Polyhedron)しか実在し得ない幾何学空間においてはプラトン立体(Euler's Polyhedron Theorem)すなわち正四面体(Tetrahedron)、正六面体(Cube)、正八面体(Octahedron)、正十二面体（Dodecahedron）、正二十面体(Icosahedron)の５種類しか実軸(Real Axis)上に現れ得ないが、その遷移過程の全体像をオイラーのφ関数に従って「素数族2^n,3^n,2^n3^m…概念の追加」という形で説明しようとすると、どうしても中間に「両者を結ぶ補助線が引ける空間」を想定しなければならなくなる。さらにいうならその過程では「対蹠間の実軸が通ってない」**奇数系**(2n+1角形)の**多角形**を(それぞれの対蹠を始点とする)**共役関係**にある一対として扱う必要が出てくる。
    [【オイラーの多面体定理と正多面体】とある「球面幾何学」の出発点…](https://qiita.com/ochimusha01/items/5f8dbf33bac5b7227a11)
    この考え方を一般の座標系に適用したのが「0-0.5**次元**(実軸0本)」「1-1.5**次元**(実軸1本)」「2-2.5**次元**(実軸2本)」「3-3.5**次元**(実軸3本)」なる思考様式となる。かかる「補助線空間」をまとめて「**虚数軸**」と呼ぶなら、その**虚数空間**自体は「実軸上に表せない任意の次元数の座標の集合」なので自明の場合として次元数を数えられない。要するに私の投稿の主題たる「(それ自体は観測不能な観測原点0と観測原点Inf(inity)の間に観測結果集合が分布する)**認識可能範囲外を跋扈する絶対他者の領域**」に半分足を突っ込んでいる事になる。
    【無限遠点を巡る数理】等差数列と等比数列①関数列との関係は？

ここで「1-1.5次元(実軸1本)」「2-2.5次元(実軸2本)」「3-3.5次元(実軸3本)」を峻別するのはオイラー標数(Eulerian Characteristic)となります。
【数理考古学】オイラー定数(Eulerian Constant)の求め方

  • 立体上におけるオイラー標数=2は「偶数系立体(Even-numbered Solid)=正多面体(Platonic solid=プラトン立体)でいうと正六面体(Cube),正八面体(Regular Octahedron),正12面体(Regular Dodecahedron),正20面体(Regular Icosahedron)」における(凸型正多面体の場合は単一となるその立体の)外接球面上の対蹠(Antipodes)の対、「奇数系立体(Even-numbered Solid)=正多面体でいうと正四面体(Regular Tetrahedron)」における(それぞれの対蹠を始点とし、特定の面を終点とする展開の対における)始点と終面に該当する。オイラーの多面体定理の証明を通じて得られるこのイメージは、関数における(逆関数を持たない)偶関数(Even Function)と(常に逆関数と一対で現れる)奇関数(Odd Function)の関係に対応する。
    オイラーの多面体定理の証明
    偶関数と奇関数の意味，性質などまとめ
  • 一方、 平面上におけるオイラー標数=1と線上におけるオイラー標数=0は多辺形(Polylateral)/多角形(Polygon）の面数を表裏2面と数えるか(xyz座標系が実軸と認識される世界)、片側1面と数えるか(xy座標系が実軸と認識される世界)輪郭線のみに着目して0面と数えるか(数直線の様にスカラー量の増減のみが実軸と認識される世界)に由来し、この選択こそがまさにそれぞれ2.0-2,5次元と3.0-3.5次元、1.0-1,5次元と2.0-2.5次元の境界線となる。
    オイラー数と曲面
  • ちなみに(線上もしくは平面上の)多角形において頂点数と辺数は必ず等しくなるが、オイラーの公式(Eulerian Formula)e^θi=cos(θ)+sin(θi)など(1の冪根に由来する)ガウスの巡回群を用いた計算ではこれに(始点と重なる終点、あるいは終点と重なる始点となる)原点1を加える。例えば統計言語Rにおける(円の近似たる)60角形の表現はc<-seq(-pi,pi,length=61),x<-cos(c),y<-sin(c)となる。
    1の冪根 - Wikipedia
    【無限遠点を巡る数理】オイラーの公式と等比数列③Cos波とSin波の正体？

新しい展開に合わせてこの辺りの表現もさらに厳密化していかなければいけなさそうですが、とりあえずはこうも考えられる様になった事が重要です。

  • この座標系において中央の単位円を1→±1/2の方向に回転させると**楕円**が現れ、丁度1/2(90度)の時点でその縁が無限遠点に到達して半分が「前後の周期に押し出された」放物線が現れる。
  • そしてさらに±1/2→0の方向に回転を続けると漸近線をy=ax/y=-axとする双曲線が原点{0,0}に向けて収束していく。

以前から「無限遠点を視野に入れると円、楕円、放物線、双曲線が単一の球面座標系上で表現可能になる」という話自体は伝え聞いていましたが、どうやらここでいう球面は(半径1の単位円の中心と垂直に交わる対蹠のうち、片方が無限遠点、もう片方が0となる)リーマン球面だった様です。
【無限遠点を巡る数理】等差数列と等比数列②基底関数(Basis Function)概念の導入
image.gif
image.gif

#pythonの場合
「叩けよ、さらば開かん」で、挑戦したら割とあっけなく移植に成功してしまいました。inf出まくるのに、幸いアニメーションの障害にはならず…

image.gif

import numpy as np
import cmath as c
import matplotlib.pyplot as plt
import matplotlib.animation as animation

#figure()でグラフを表示する領域をつくり，figというオブジェクトにする．
plt.style.use('default')
fig = plt.figure()
ax = fig.add_subplot(111,aspect='equal')

#1周分の角度
θ=np.linspace(0,np.pi*2,61,endpoint = True)

#ε(離心率)
ε=np.linspace(0,5,51,endpoint = True)

#描画関数
def Eccentricity01(n): 
    plt.cla()
    fp0=[]
    for nm in range(len(θ)):
        fp0.append(c.rect(1/(1+ε[n]*np.cos(θ[nm])),θ[nm]))
    xyp=np.array(fp0)
    fm0=[]
    for nm in range(len(θ)):
        fm0.append(c.rect(1/(1-ε[n]*np.cos(θ[nm])),θ[nm]))
    xym=np.array(fm0)
    #描画
    plt.plot(xyp.real,xyp.imag,color="blue",marker="o",lw=1)
    plt.plot(xym.real,xym.imag,color="red",marker="o",lw=1)
    plt.axvline(0, 0, 1,color="black",lw=0.5)
    plt.axhline(0, 0, 1,color="black",lw=0.5)
    plt.xlim([-20,20])
    plt.ylim([-20,20])
    plt.xlabel("Real")
    plt.ylabel("Imaginal")
    plt.title("Eccentricity")
    
#Eccentricity01(10)
#plt.show()

ani = animation.FuncAnimation(fig, Eccentricity01, interval=100,frames=len(ε))
ani.save("Ecc002.gif", writer="pillow")

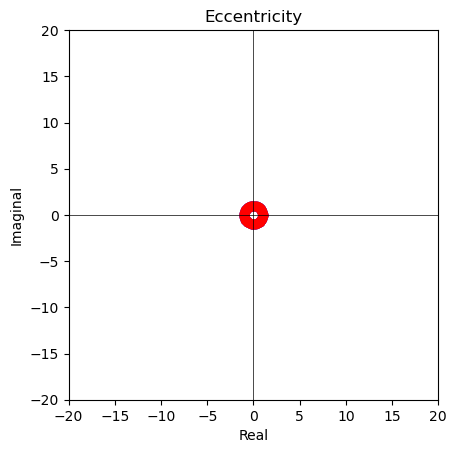
離心率0($\frac{1}{1±0cos(θ)}$)=半径1の単位円$e^{iθ},e^{-iθ}$の場合
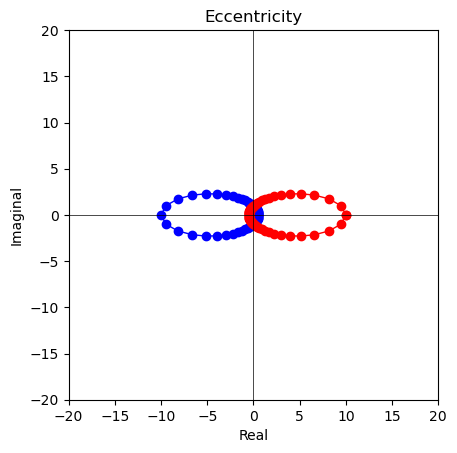
image.png
離心率0<ε<1=楕円の場合
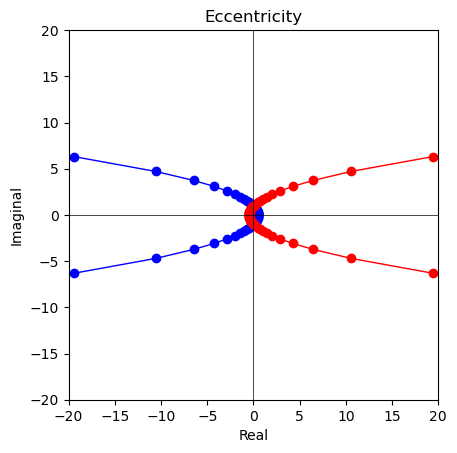
image.png
離心率1($\frac{1}{1±1cos(θ)}$)=放物線$y=\sqrt{\frac{1}{2}-x},\sqrt{\frac{1}{2}+x}$の場合

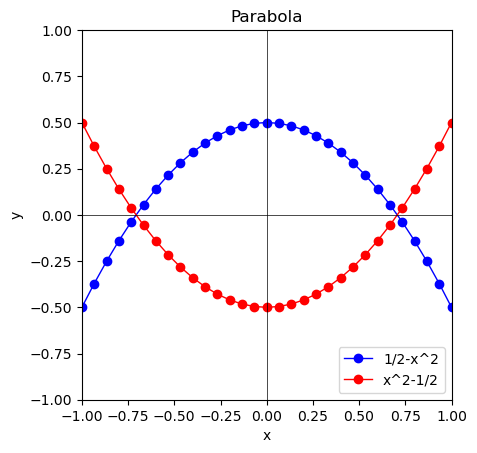
image.png

  • これを90度反時計まわりに回転させると(xとyを入れ替えると)放物線$y=\frac{1}{2}-x^2,x^2-\frac{1}{2}$となる。
import sympy as sp
x,y = sp.symbols('x,y')

ap=sp.Eq(y,sp.sqrt(1/2-x))
am=sp.Eq(y,sp.sqrt(1/2+x))
bp=sp.solve(ap,x)
bm=sp.solve(am,x)

sp.init_printing()
display(ap) 
print(sp.latex(ap))
display(bp) 
print(sp.latex(bp))
display(am) 
print(sp.latex(am))
display(bm) 
print(sp.latex(bm))

y = \sqrt{0.5 - x}→x=0.5 - y^{2}\\
y = \sqrt{x + 0.5}→x=y^{2} - 0.5

image.png

import numpy as np
import cmath as c
import matplotlib.pyplot as plt
import matplotlib.animation as animation

#figure()でグラフを表示する領域をつくり，figというオブジェクトにする．
plt.style.use('default')
fig = plt.figure()
ax = fig.add_subplot(111,aspect='equal')

#双曲線計算
x=np.linspace(-1,1,31,endpoint = True)
y=1/2-x**2

#描画関数
def parabola01(n): 
    plt.cla()
    #描画
    plt.plot(x,y,color="blue",marker="o",lw=1,label="1/2-x^2")
    plt.plot(x,-y,color="red",marker="o",lw=1,label="x^2-1/2")
    plt.axvline(0, 0, 1,color="black",lw=0.5)
    plt.axhline(0, 0, 1,color="black",lw=0.5)
    plt.xlim([-1,1])
    plt.ylim([-1,1])
    plt.xlabel("x")
    plt.ylabel("y")
    plt.title("Parabola")
    ax.legend(loc='lower right')
    
parabola01(0)
plt.show()

離心率ε>1=双曲線の場合
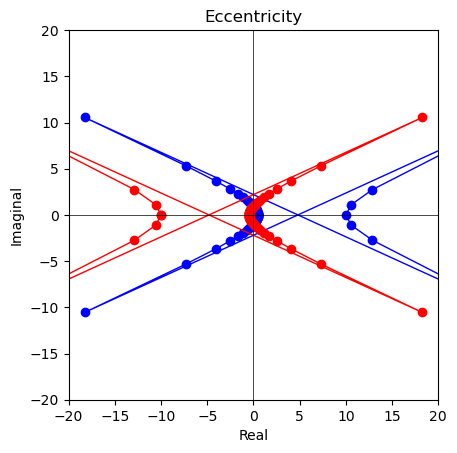
image.png
こうしてリーマン座標系(Riemann Coordinate System)なる新たな概念が浮上し「1次元/1.5次元が2次元/2.5次元に拡張される瞬間」を捉えられそうな感触が得られた時点で、以下続報…

0
0
0

Register as a new user and use Qiita more conveniently

  1. You get articles that match your needs
  2. You can efficiently read back useful information
  3. You can use dark theme
What you can do with signing up
Sign upLogin
0
0

Delete article

Deleted articles cannot be recovered.

Draft of this article would be also deleted.

Are you sure you want to delete this article?