(2021.1.15)Rによる投稿
(2021.3.19)Tex導入
以前の投稿では複素数列SVoI(Simple Vibration of Imaginal=虚数単振動)Αn(n=1⇄-1)と複素関数e^iθの関係を探るうちに虚数共役(Imaginary Conjugate)に対応する実数共役(Real Conjugate)の概念に邂逅しました。元来は二つ合わせて複素共役(Complex Conjugate)概念の筈ですが、コンピューターの挙動に怪しい箇所が…
【無限遠点を巡る数理】オイラーの公式と等比数列①その根本的差異について。

さすが複素関数分野の独習には参考書導入が不可欠です。
高校数学でわかる複素関数 微分からコーシー積分、留数定理まで (ブルーバックス) | 竹内淳 | 数学 | Kindleストア | Amazon
①オイラーの公式を用いるとコサイン波$\cos(θ)$とサイン波$\sin(θ)$を$e^{θi}$と$e^{-θi}$で表せます。
e^{θi}=\cos(θ)+\sin(θ)i(2-0)\\
e^{-θi}=\cos(-θ)+\sin(-θ)i=\cos(-θ)-\sin(θ)i…(2-1)
②コサイン波$\cos(θ)$の場合は…
e^{θi}+e^{-θi}=2\cos(θ)=\frac{e^{θi}+e^{-θi}}{2}…(2-2)
③サイン波の場合は(2-0)式より(2-1)式を引いて2iで割ります。
\frac{e^{θi}-e^{-θi}}{2i}…(2-3)
④複素数の極形式も次の様に指数関数で表せます。
a+bi=r(\cos(θ)+\sin(θi))=re^{iθ}
⑤また複素共役は以下となります。
a-bi=r(cos(θ)-sin(θi))=re^{-iθ}
⑥ピタゴラスの定理はこう表されます。
cos(θ)^2+sin(θ)^2\\
=\frac{e^{2θ}+2(e^{iθ}×e^{-iθ})+e^{-2θ}}{4}-\frac{e^{2θ}-2(e^{iθ}×e^{-iθ})+e^{-2θ}}{4}\\
=\frac{4(e^{iθ}×e^{-iθ})}{4}=1
この自明の場合(Trival Case)の連続による立板に水を流す様な流暢な説明こそが専門家による整理され尽くした解説の魅力ですね。どうやら「対称的なものと交代的(反対称的)なものに分解するための恒等式」$x=\frac{x+y}{2}+\frac{x-y}{2}$と密接な関係にある様です。というより、むしろ逆に上掲の場合こそがこの概念の出発点とも?
行列・関数・多項式に共通する有名な性質 | 高校数学の美しい物語
①任意の行列は対称行列と交代行列の和に分解可能である。
A=\frac{A+At}{2}+\frac{A-At}{2}
②任意の関数は偶関数と奇関数の和に分解可能である。
f(x)=\frac{f(x)+f(-x)}{2}+\frac{f(x)-f(-x)}{2}
③任意の2変数関数は対称式と交代式(反対称式)の和に分解可能である。
f(x,y)=\frac{f(x,y)+f(y,x)}{2}+\frac{f(x)-f(y,x)}{2}
この考え方を援用すれば、指数関数e^xも,偶関数と奇関数の和で表せます。
e^x=\frac{e^x+e^−x}{2}+\frac{e^x−e^−x}{2}
実は右辺の偶関数部分はカテナリー(懸垂線)と呼ばれる有名な曲線です。偶関数の部分は$cosh(x)$、奇関数の部分は$sinh(x)$とも表され,双曲線関数とも呼ばれます。
cx0<-seq(-2,2,length=41)
f0<-function(x) {(exp(x)+exp(-x))/2+(exp(x)-exp(-x))/2}
cy0<-f0(cx0)
plot(cx0,cy0,type="l",xlim=c(-2,2),ylim=c(-4,4),main="exp(x)=(exp(x)+exp(-x))/2+(exp(x)-exp(-x))/2",xlab="X",ylab="Y",col=rgb(0,1,0))
par(new=T)
f1<-function(x) {(exp(x)+exp(-x))/2}
cy1<-f1(cx0)
plot(cx0,cy1,type="l",xlim=c(-2,2),ylim=c(-4,4),main="",xlab="",ylab="",col=rgb(0,0,1))
par(new=T)
f2<-function(x) {(exp(x)-exp(-x))/2}
cy2<-f2(cx0)
plot(cx0,cy2,type="l",xlim=c(-2,2),ylim=c(-4,4),main="",xlab="",ylab="",col=rgb(1,0,0))
abline(h=0,col=c(200,200,200))
abline(v=0,col=c(200,200,200))
legend("bottomright", legend=c("y=exp(x)=coshx+sinhx","coshx=(exp(x)+exp(-x))/2","sinhx=(exp(x)-exp(-x))/2"), lty =c(1,1,1),col=c(rgb(0,1,0),rgb(0,0,1),rgb(1,0,0)))
さらには、以下の関数の挙動も取り込んでいかないといけません。
【Rで球面幾何学】そもそも複素数Xi(x*(0+1i))はどう振る舞う?
実数関数$y=(1+0i)X^n$の場合(第一象限の虚数部が動かない)

複素関数$y=(0+1i)X^n$の場合(実数部と虚数部の交代が起こる)

実数関数$y=\log(n,(1+0i)x)$の場合(第一象限の虚数部が動かない)

複素関数$y=\log(n,(0+1i)x)$の場合(実数部と虚数部の交代が起こる)

なるほど、これまで実数共役(Real Conjugate)の概念を私の視野から隠してきたのは、この「第一象限の実数関数では虚数部が動かない(第四象限の動きも異なる。第二象限と第三象限の動きは同じ)」なる振る舞いだったのです。そして指数関数Y=X^Nの実数部の挙動はマクローリン級数(McLaughlin Series)による近似過程そのままです。
【Rで球面幾何学】オイラーの公式を導出したマクローリン級数の限界?

さて、こうした話は何処へ収束(Convergence)していくのでしょう?
そもそも(0±1i)を掛けるとは?
とりあえず上掲式が処理過程でどう見えるかプログラムでも確認していきましょう。まずはガウス平面(Gaussian plane) 上で(0±1i)を掛ける事にどういう意味があるか確かめる必要がありますね。
複素平面(Complex Plane) - Wikipedia
複素数z=x+iyを直交座標(x,y)に対応させた直交座標平面のことである。複素数の実部を表す軸を実軸(Real Axis=実数直線)、虚部を表す軸を虚軸(Imaginary Axis)という。
1811年頃にガウスによって導入されたため、ガウス平面(Gaussian plane)とも呼ばれる。一方、それに先立つ1806年にJean-Robert Argandも同様の手法を用いたため、アルガン図(Argand Diagram)とも呼ばれている。さらに、それ以前の1797年のCaspar Wesselの書簡にも登場している。このように複素数の幾何的表示はガウス以前にも知られていたが、今日用いられているような形式で複素平面を論じたのはガウスである。三者の名前をとってガウス・アルガン平面、ガウス・ウェッセル平面などとも言われる。
英称Complex Planeの訳として複素平面と呼ぶことも少なくなく、大学以上の数学書では『複素平面』または『ガウス平面』の方が〔複素数平面よりも〕圧倒的に主流であるとの見解がある。しかし、接頭辞「複素—」を「係数体を複素数体とする」という意味に解釈すると、複素数を成分とする「平面」という意味になり、C^2(実部と虚部に分けた実4次元線形空間=二次元複素解析空間)を指すので、文脈によってどちらを指しているかは注意が必要である。日本の高等学校の学習指導要領では現在は「複素数平面」が用いられている。
これ自体は簡単。ガウス平面上において座標を実部中心に±90度回転させるのです。

rol01<-function(Rad){
# Imaginal
i0<-rev(seq(-1,1,length=21))
# (0+1i)→(0-1i)
s0<-complex(re=0,im=i0)
s1<-s0*(0+1i)
s2<-s0*(0-1i)
plot(s0,type="b",xlim=c(-1,1),ylim=c(-1,1),main="(0+1i)×(0±1i)",xlab="Real",ylab="Imaginal",col=rgb(0,1,0))
par(new=T)
plot(s1,type="b",xlim=c(-1,1),ylim=c(-1,1),main="",xlab="",ylab="",col=rgb(0,1,0))
segments(Re(s0[1]),Im(s0[1]),Re(s0[Rad]),Im(s0[Rad]),col=rgb(0,0,0))
segments(Re(s1[1]),Im(s1[1]),Re(s1[Rad]),Im(s1[Rad]),col=rgb(0,0,1))
segments(Re(s2[1]),Im(s2[1]),Re(s2[Rad]),Im(s2[Rad]),col=rgb(1,0,0))
legend("bottomleft",legend=c("s=(0+1i)→(0-1i)","s×(0+1i)","s×(0-1i)"),lty=c(1,1,1),col=c(rgb(0,0,0),rgb(0,0,1),rgb(1,0,0)))
}
# アニメーション表示
library("animation")
Time_Code=c(1:21)
saveGIF({
for (i in Time_Code){
rol01(i)
}
}, interval = 0.1, movie.name = "rol01.gif")
Cos波の正体?
まずはCos波の計算過程を式そのままに図示してみると、ただでさえ距離が足りてない上(端が欠ける)、e^θi+e^-θiに対して「中心{0,1},半径2の円弧のcos(θ)」を、(e^θi+e^-θi)/2に対して「中心{0,1/2},半径1の円弧のcos(θ)」を返してきます。
cos01<-function(Rad){
# Imaginal
i0<-seq(-1,1,length=21)
# (0-1i)→(0+1i)
Imaginal<-complex(re=0,im=i0)
s0<-exp(Imaginal)+Conj(exp(Imaginal))
plot(s0,type="b",xlim=c(0,2),ylim=c(-1/2,1/2),main="e^θi+e^-θi",xlab="Real",ylab="Imaginal",col=rgb(0,1,0))
segments(Re(s0[1]),Im(s0[1]),Re(s0[Rad]),Im(s0[Rad]),col=rgb(1,0,0))
legend("bottomleft", legend="e^θi+e^-θi", lty =1,col=rgb(0,1,0))
}
# アニメーション表示
library("animation")
Time_Code=c(1:21)
saveGIF({
for (i in Time_Code){
cos01(i)
}
}, interval = 0.1, movie.name = "Cos01.gif")
cos01<-function(Rad){
# Imaginal
i0<-seq(-1,1,length=21)
# (0-1i)→(0+1i)
Imaginal<-complex(re=0,im=i0)
s0<-(exp(Imaginal)+Conj(exp(Imaginal)))/2
plot(s0,type="b",xlim=c(0,2),ylim=c(-1/2,1/2),main="(e^θi+e^-θi)/2",xlab="Real",ylab="Imaginal",col=rgb(0,1,0))
segments(Re(s0[1]),Im(s0[1]),Re(s0[Rad]),Im(s0[Rad]),col=rgb(1,0,0))
legend("bottomleft", legend="(e^θi+e^-θi)/2", lty =1,col=rgb(0,1,0))
}
# アニメーション表示
library("animation")
Time_Code=c(1:21)
saveGIF({
for (i in Time_Code){
cos01(i)
}
}, interval = 0.1, movie.name = "Cos02.gif")
添字にπ/2を掛ける事によって初めて見慣れた円状分布(Circular Distribution)が現れるのです。
cos01<-function(Rad){
# Imaginal
i0<-rev(seq(-1,1,length=21))
# (0-1i)→(0+1i)
Imaginal<-complex(re=0,im=i0)
s0<-exp(Imaginal*pi/2)+Conj(exp(Imaginal*pi/2))
plot(s0,type="b",xlim=c(0,2),ylim=c(-1/2,1/2),main="e^(θi×π/2)+e^(-θi×π/2)",xlab="Real",ylab="Imaginal",col=rgb(0,1,0))
segments(Re(s0[1]),Im(s0[1]),Re(s0[Rad]),Im(s0[Rad]),col=rgb(1,0,0))
legend("bottomleft", legend="e^(θi×π/2)+e^(-θi×π/2)", lty =1,col=rgb(0,1,0))
}
# アニメーション表示
library("animation")
Time_Code=c(1:21)
saveGIF({
for (i in Time_Code){
cos01(i)
}
}, interval = 0.1, movie.name = "Cos11.gif")
cos01<-function(Rad){
# Imaginal
i0<-rev(seq(-1,1,length=21))
# (0-1i)→(0+1i)
Imaginal<-complex(re=0,im=i0)
s0<-(exp(Imaginal*pi/2)+Conj(exp(Imaginal*pi/2)))/2
plot(s0,type="b",xlim=c(0,2),ylim=c(-1/2,1/2),main="(e^(θii×π/2)+e^(-θii×π/2))/2",xlab="Real",ylab="Imaginal",col=rgb(0,1,0))
segments(Re(s0[1]),Im(s0[1]),Re(s0[Rad]),Im(s0[Rad]),col=rgb(1,0,0))
legend("bottomleft", legend="(e^(θii×π/2)+e^(-θii×π/2))/2", lty =1,col=rgb(0,1,0))
}
# アニメーション表示
library("animation")
Time_Code=c(1:21)
saveGIF({
for (i in Time_Code){
cos01(i)
}
}, interval = 0.1, movie.name = "Cos12.gif")
Sin波の正体?
Sin波の場合もやはり、計算過程を式そのままに図示すると距離が足りていません(端が欠ける)。
sin01<-function(Rad){
# Imaginal
i0<-rev(seq(-1,1,length=21))
# (0-1i)→(0+1i)
Imaginal<-complex(re=0,im=i0)
s0<-exp(Imaginal)-Conj(exp(Imaginal))
plot(s0,type="b",xlim=c(-2,2),ylim=c(-2,2),main="e^θi-e^-θi",xlab="Real",ylab="Imaginal",col=rgb(0,1,0))
segments(Re(s0[1]),Im(s0[1]),Re(s0[Rad]),Im(s0[Rad]),col=rgb(1,0,0))
legend("bottomleft", legend="e^θi-e^-θi", lty =1,col=rgb(0,1,0))
}
# アニメーション表示
library("animation")
Time_Code=c(1:21)
saveGIF({
for (i in Time_Code){
sin01(i)
}
}, interval = 0.1, movie.name = "Sin01.gif")
sin01<-function(Rad){
# Imaginal
i0<-seq(-1,1,length=21)
# (0-1i)→(0+1i)
Imaginal<-complex(re=0,im=i0)
s0<-(exp(Imaginal)-Conj(exp(Imaginal)))/(2*(0+1i))
plot(s0,type="b",xlim=c(-1,1),ylim=c(-1/2,1/2),main="(e^θi+e^-θi)/2i",xlab="Real",ylab="Imaginal",col=rgb(0,1,0))
segments(Re(s0[1]),Im(s0[1]),Re(s0[Rad]),Im(s0[Rad]),col=rgb(1,0,0))
legend("bottomleft", legend="(e^θi-e^-θi)/2i", lty =1,col=rgb(0,1,0))
}
# アニメーション表示
library("animation")
Time_Code=c(1:21)
saveGIF({
for (i in Time_Code){
sin01(i)
}
}, interval = 0.1, movie.name = "Sin04.gif")
やはりこちらも添字にπ/2を掛ける事によって初めて見慣れた円状分布(Circular Distribution)が現れるのです。
sin01<-function(Rad){
# Imaginal
i0<-rev(seq(-1,1,length=21))
# (0-1i)→(0+1i)
Imaginal<-complex(re=0,im=i0)
s0<-exp(Imaginal*pi/2)-Conj(exp(Imaginal*pi/2))
plot(s0,type="b",xlim=c(-2,2),ylim=c(-2,2),main="e^(θi×π/2)-e^(-θi×π/2)",xlab="Real",ylab="Imaginal",col=rgb(0,1,0))
segments(Re(s0[1]),Im(s0[1]),Re(s0[Rad]),Im(s0[Rad]),col=rgb(1,0,0))
legend("bottomleft", legend="e^(θi×π/2)-e^(-θi×π/2)", lty =1,col=rgb(0,1,0))
}
# アニメーション表示
library("animation")
Time_Code=c(1:21)
saveGIF({
for (i in Time_Code){
sin01(i)
}
}, interval = 0.1, movie.name = "Sin11.gif")
(e^(θi×π/2)-e^(-θi×π/2))/(2*(0±1i))

sin01<-function(Rad){
# Imaginal
i0<-rev(seq(-1,1,length=21))
# (0-1i)→(0+1i)
Imaginal<-complex(re=0,im=i0)
s0<-(exp(Imaginal*pi/2)-Conj(exp(Imaginal*pi/2)))/(2*(0+1i))
plot(s0,type="b",xlim=c(-1,1),ylim=c(-1/2,1/2),main="(e^(θii×π/2)-e^(-θii×π/2))/2(2*(0±1i))",xlab="Real",ylab="Imaginal",col=rgb(0,1,0))
segments(Re(s0[1]),Im(s0[1]),Re(s0[Rad]),Im(s0[Rad]),col=rgb(1,0,0))
legend("bottomleft", legend="(e^(θi×π/2)-e^(-θi×π/2))/(2*(0±1i))", lty =1,col=rgb(0,1,0))
}
# アニメーション表示
library("animation")
Time_Code=c(1:21)
saveGIF({
for (i in Time_Code){
sin01(i)
}
}, interval = 0.1, movie.name = "Sin12.gif")
オイラーの定理e^πi=cos(θ)+sin(θ)iから円状分布(Circular Distribution)の世界へ
どうやら四元数計算で外積や内積だけ抽出する演算と関係ありそうです。
四元数を作ろう
とはいえ、こうして得られた円状分布(Circular Distribution)は、cos(θ)の場合に0→1→0、sin(θ)の場合に-1→0→1と推移してしまいます(見慣れたcos(θ)/sin(θ)の振る舞いだと第四象限から第二象限に掛けての振る舞い)、とはいえ両波形は位相が90度(π/2ラジアン)ズレてさえいればセットで無限周期で円を描き続けるので、どうとでも調整が効く次第。
- cos(θ)=±(1-abs(sin(θ))
- sin(θ)=±(1-abs(cos(θ))
こういう対応関係も利用可能です。
【初心者向け】方形描画関数①三角関数との関係。
むしろ気になるのは、これだけ選択肢があり、かつ明らかに語源的には正弦波(Sine Wave)あっての余弦波(Cosine Wave)だったにも関わらず、歴史的にはいつの間にか立場が逆転しまった流れ。
- 最初の契機として想定されるのが、マクローリン級数による近似を出発点としてのオイラーの定理e^πi=cos(θ)+sin(θ)iの発見。以降cos(θ)は偶関数、sin(θ)は奇関数の代表例と目されていくが、マクローリン級数による近似ではまず偶関数が最初に現れるのである。
【Rで球面幾何学】オイラーの公式を導出したマクローリン級数の限界? - 次の重要な契機として想定されるのがガウス平面(Gaussian Plane)の制定で、この時点までに既に完全に(Cos(θ)によって表される)X軸上の実数部が主、(Sin(θ)iによって表される)Y軸上の虚数部が従として動くイメージが樹立していたと想定される。
複素平面 - Wikipedia
脱線が過ぎました。それはそれとして、透視図法に対応する自然指数関数(Natural Exponential function)や自然対数関数(Natural Logarithmic function)の概念、すなわち「xy=1(面積)となる数列の積の極限」がピタゴラスの定理(Pythagorean Theorem)z^2=sqrt(x^2+y^2)と関係してくるのが、なんとも不思議な感じがします。
【無限遠点を巡る数理】オイラーの公式と等比数列②線形性ならぬ円形性について
さらに奇異に感じるのが「X軸が奇数系でY軸が偶数系」の以下の方眼。

c0<-seq(-pi,pi,length=61)
cx<-cos(c0)
cy<-sin(c0)
plot(cx,cy,type="l",asp=1,xlim=c(-1,1),ylim=c(-1,1),main="Cos(θ) & Sin(θ)",xlab="Cos(θ)",ylab="Sin(θ)",col=rgb(0,1,0))
c2<-seq(-pi,pi,length=31)
for (i in c2){
abline(h=sin(i),col=c(200,200,200))
}
for (i in c2){
abline(v=cos(i),col=c(200,200,200))
}
c1<-c(3/4,1/2,1/4)
for (i in c1){
par(new=T)
plot(cx*i,cy*i,type="l",asp=1,xlim=c(-1,1),ylim=c(-1,1),main="",xlab="",ylab="",col=rgb(0,1,0))
}
c3<-c(cos(c2[3]),cos(c2[5]),cos(c2[7]),cos(c2[9]))
for (i in c3){
par(new=T)
plot(cx*i,cy*i,type="l",asp=1,xlim=c(-1,1),ylim=c(-1,1),main="",xlab="",ylab="",col=rgb(1,1,0))
}
abline(h=0,col=rgb(1,0,0))
abline(v=0,col=rgb(1,0,0))
legend("bottomleft", legend=c("1,4/3,cos(π/3)=1/2,4/1","cos(π*14/15),cos(π*12/15),cos(π*6/15),cos(π*7/15)"), cex=0.75,lty =c(1,1),col=c(rgb(0,1,0),rgb(1,1,0)))
で、とっさに思いついたのが(しばらく前から使い始めた、角度の概念を放棄した)円状対数尺(Circular Logarithmic Scale)だったという次第。要するに共役(Conjugate)概念の全周化…もはやCos(θ)とSin(θ)を区別する必要がありません。
【初心者向け】複素共役のアニメーション表示について。



どうやらe^xが幾ら微分しても、幾ら積分してもe^xのままである事と何か関係がありそうです。
【無限遠点を巡る数理】オイラーの公式と等比数列④「中学生には難しいが高校生なら気付くレベル」?
e^{x}\frac{d^n}{dθ^n}=(e^{x},e^{x},e^{x},…)\\
\int \int \int … \int e^{x}(dθ)=(e^{x},e^{x},e^{x},…)
python導入による全体像のまとめ。
Rの場合(2021年1月15日時点での挑戦)
【無限遠点を巡る数理】オイラーの公式と等比数列③Cos波とSin波の正体?
$i_n$を複素数座標系(Real,Imaginal)上における(0,-1)から(0,1)にかけて連続する数列と想定すると$\pm e^{\frac{πi_n}{2}}$の結果は以下となる。
i_{n}(n=-1→1)=(0,…,0)\\
\pm e^{\frac{πi_n}{2}}= \pm π

これが共役関係で、$i_n × \pm i$は数列$i_n$を±90度($\frac{π}{2}$)回転させる。

この基本に従うと$\cos(θ)$や$\sin(θ)$の導出過程は以下となる。
I_{n}(n=-π→+π)=(-π,…,+π)\\
i_n=I_{n}×i\\
\cos(θ)=\frac{e^{+i_{n}}+e^{-i_{n}}}{2}
①共益関係から、$e^{+θi}+e^{-θi}$に該当する演算で「2倍の横棒」が出来る。

②この「2倍の横棒」を2で割って平均を求めると$\cos(θ)$になる。

I_{n}(n=-π→+π)=(-π,…,+π)\\
i_n=I_{n}×i\\
\sin(θ)=\frac{e^{+i_{n}}-e^{-i_{n}}}{2i}
①共役関係から、$e^{+θi}-e^{-θi}$に該当する演算で「2倍の縦棒」が出来る。

②この「2倍の縦棒」を2で割って平均を求め、90度回転させると$\sin(θ)$となる。

画像の処理ではは$\cos(θ)$と$\sin(θ)$の内容が逆転しています。実際にはこの処理をさらに90度回転させてイメージしないといけません。
pythonの場合((2021年3月19日時点の再挑戦))
等速円運動についての物理学と数学の立場の違い?
上掲の過程をより厳密に見ていこう。

import math as m
import cmath as c
import numpy as num
from matplotlib import pyplot as plt
# 単位円データ作成
zp=num.linspace(1,-1,31,endpoint = True)*(0+1j)
p0=[]
for nm in range(len(zp)):
p0.append(c.exp(zp[nm]*m.pi/2))
p1=num.array(p0)
# 共役複素数列(-)
m1=-p1
# グラフ表示準備
plt.style.use('default')
fig = plt.figure()
plt.plot(zp.real,zp.imag,color="green",marker=".", label="SV(1→-1)")
plt.plot(p1.real,p1.imag,color="blue",marker=".", label="e^iπ")
plt.plot(m1.real,m1.imag,color="red",marker=".", label="e^-iπ")
plt.ylim([-1.1,1.1])
plt.xlim([-1.1,1.1])
plt.title("Conjugate Complex")
plt.xlabel("Real")
plt.ylabel("Imaginal")
ax = fig.add_subplot(111)
ax.set_aspect('equal', adjustable='box')
ax.legend(loc='lower right')
plt.show()
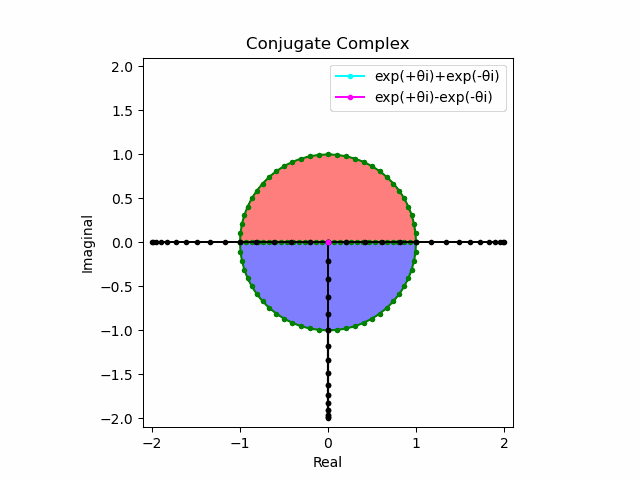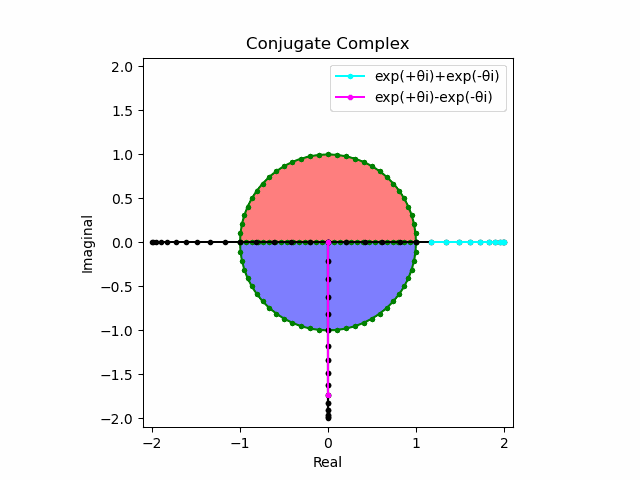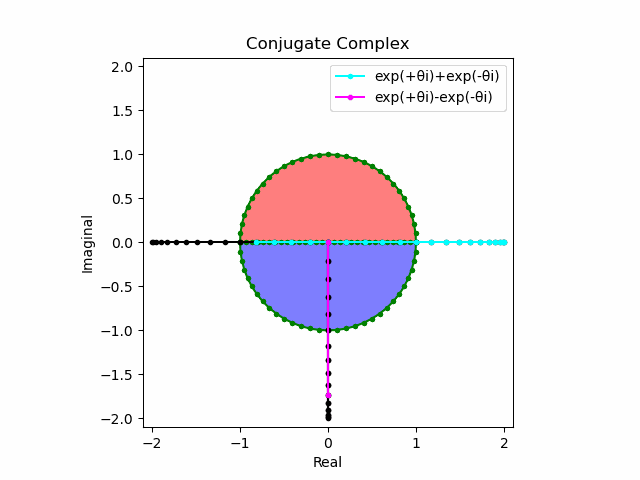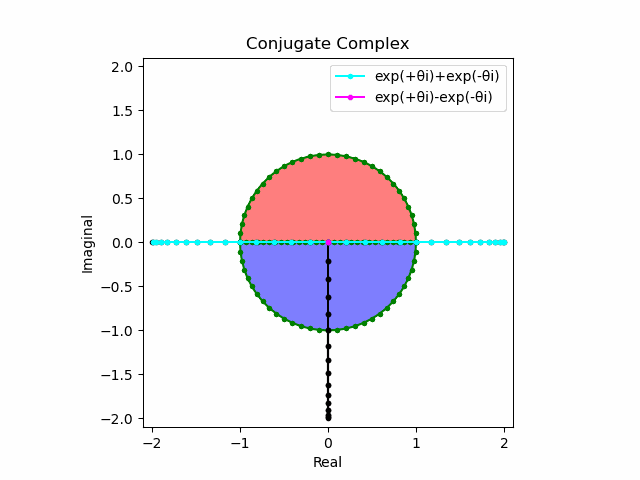
$θ_n(n=1→-1)$と置いた場合、 $e^{θ_nπi}$と$e^{-θ_nπi}$が共役関係を構成する。$(n=1→-1)$の条件を満たすのは$θ_n*(0-1i)$の位相。
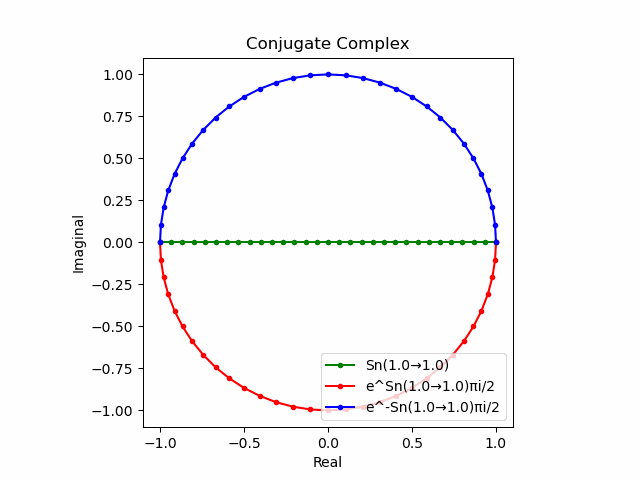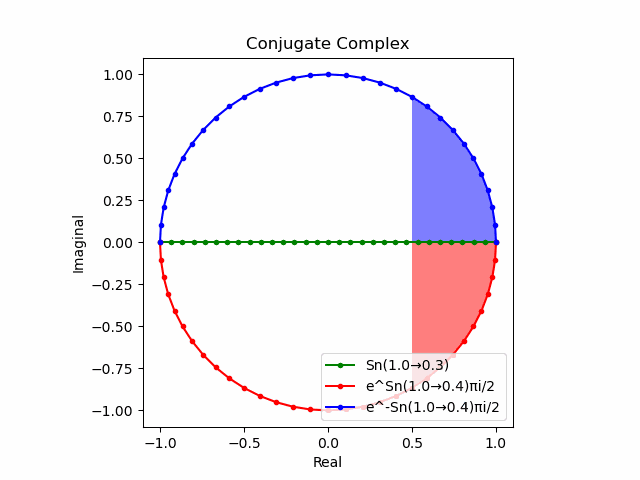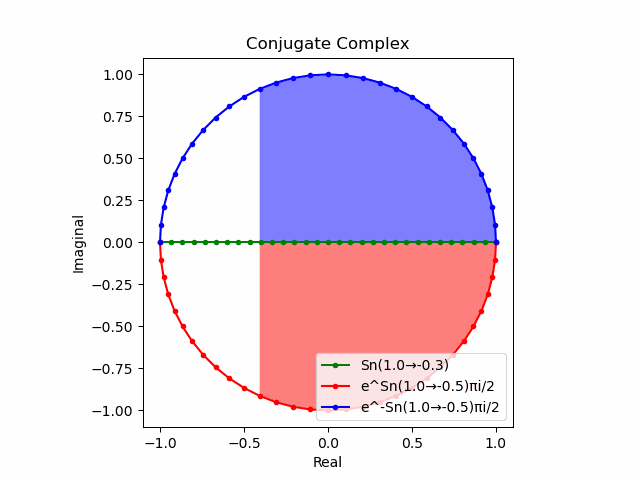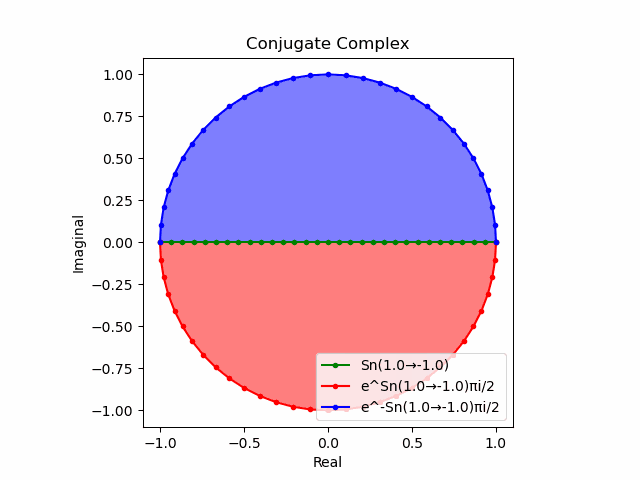
そして$e^{θ_nπi}+e^{-θ_nπi}$は幅2倍の横棒、$e^{θ_nπi}-e^{-θ_nπi}$は高さ2倍の縦棒となる。
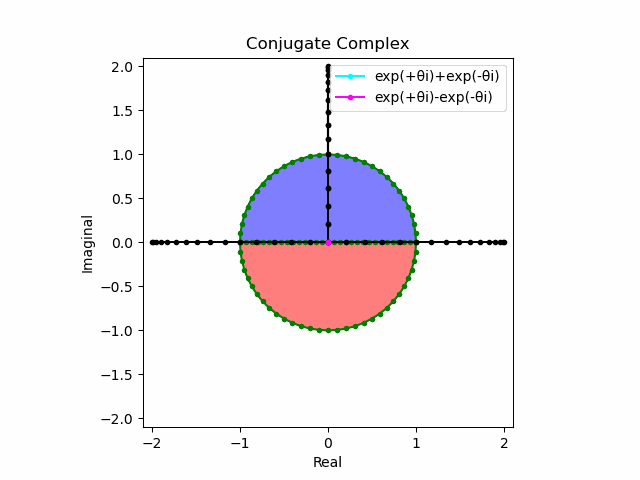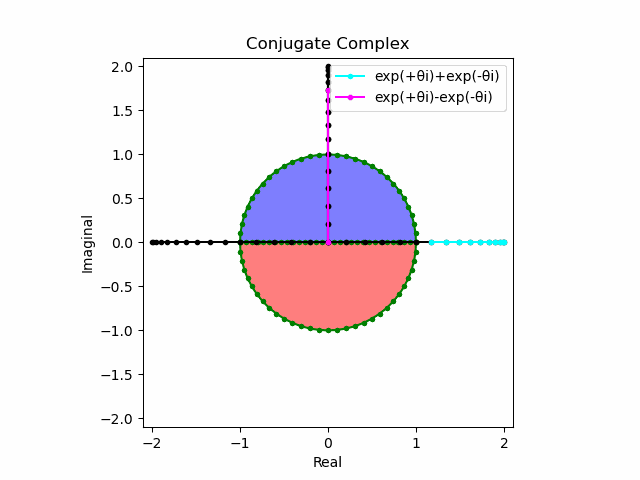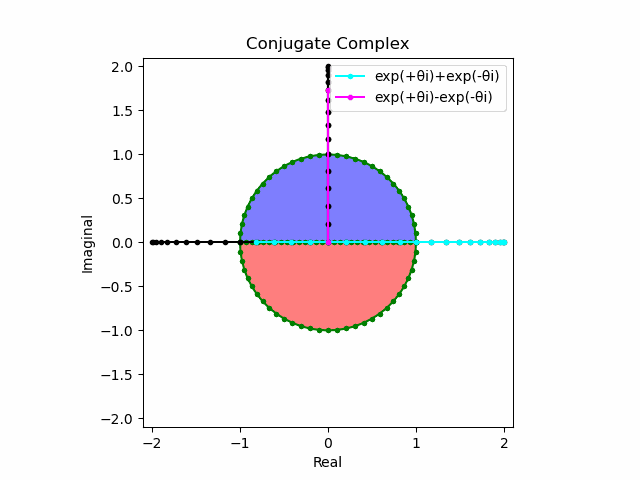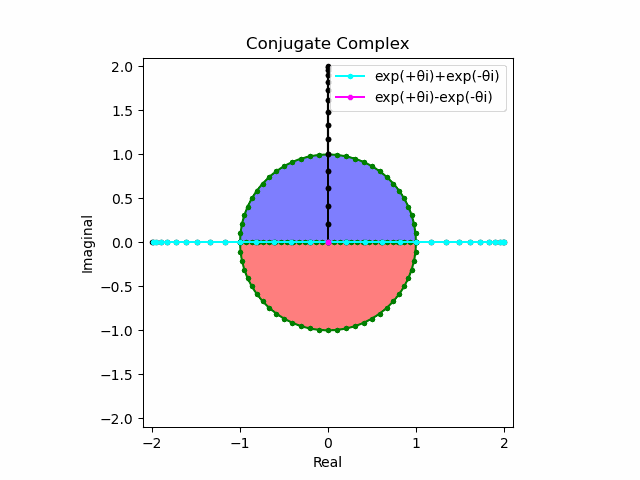
import math as m
import cmath as c
import numpy as num
from matplotlib import pyplot as plt
import matplotlib.animation as animation
# 単位円データ作成
z=num.linspace(1,-1,31,endpoint = True)*(1+0j)
zp=z*(0-1j)
p0=[]
for nm in range(len(zp)):
p0.append(c.exp(zp[nm]*m.pi/2)*(0+1j))
p1=num.array(p0)
# 共役複素数列(-)
m1=-p1[::-1]
lx=p1+m1
ly=p1-m1
# グラフ表示準備
plt.style.use('default')
fig = plt.figure()
# 関数定義
def Conjugate_Complex(n):
plt.cla()
plt.plot(z.real,z.imag,color="green", marker=".")
plt.plot(p1.real,p1.imag,color="green", marker=".")
plt.plot(m1.real,m1.imag,color="green", marker=".")
plt.fill_between(p1.real,p1.imag,facecolor='blue',alpha=0.5)
plt.fill_between(m1.real,m1.imag,facecolor='red',alpha=0.5)
plt.plot(lx.real,lx.imag,color="black", marker=".")
plt.plot(ly.real,ly.imag,color="black", marker=".")
plt.ylim([-2.1,2.1])
plt.xlim([-2.1,2.1])
plt.title("Conjugate Complex")
plt.xlabel("Real")
plt.ylabel("Imaginal")
ax = fig.add_subplot(111)
ax.set_aspect('equal', adjustable='box')
#exp(+θi)±exp(-θi)
plt.plot(lx[0:n].real,lx[0:n].imag,color="cyan", marker=".", label="exp(+θi)+exp(-θi)")
plt.plot([0,ly[n].real],[0,ly[n].imag],color="magenta", marker=".", label="exp(+θi)-exp(-θi)")
ax.legend(loc='upper right')
ani = animation.FuncAnimation(fig, Conjugate_Complex, interval=50,frames=len(z))
ani.save("output91.gif", writer="pillow")
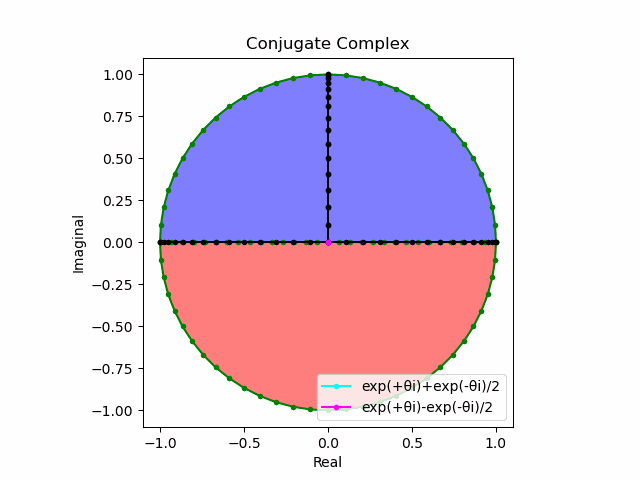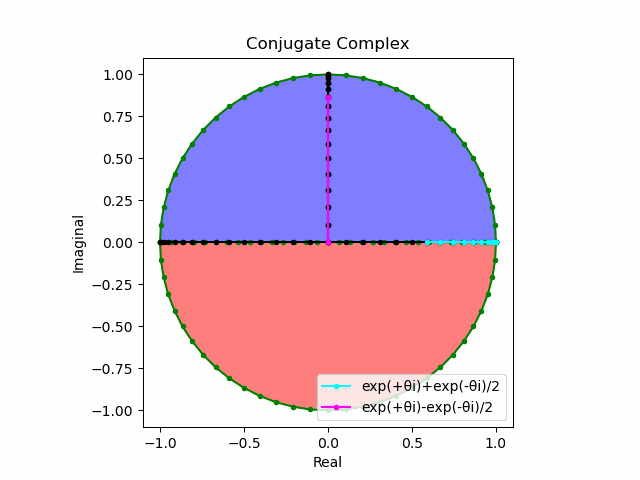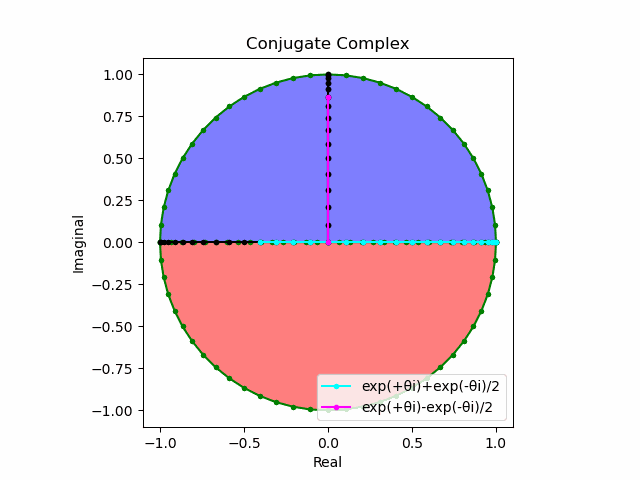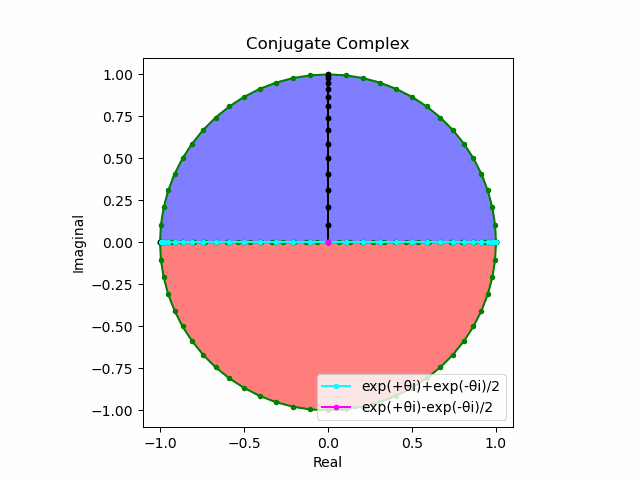
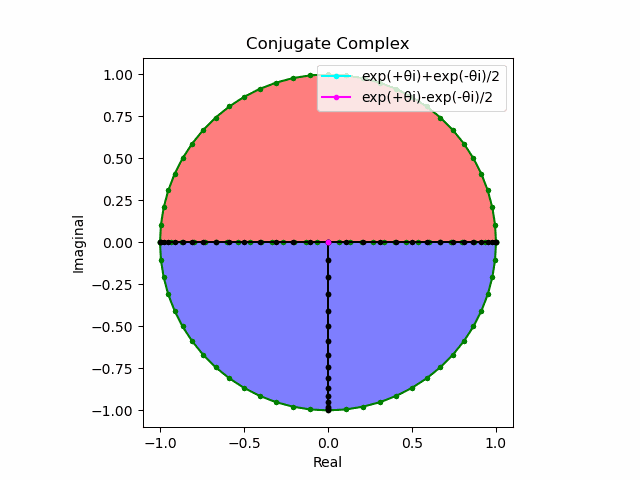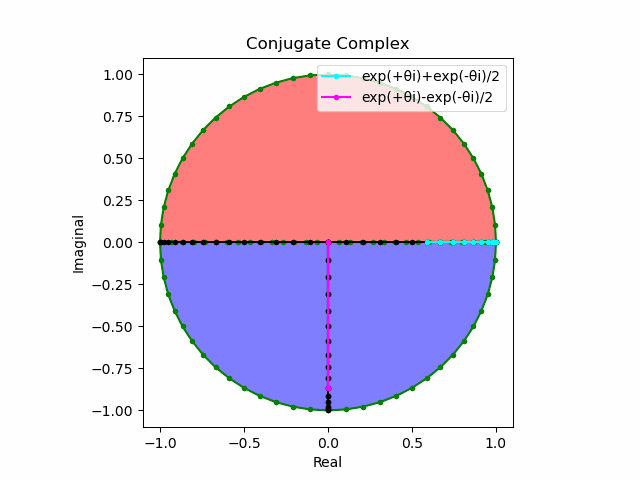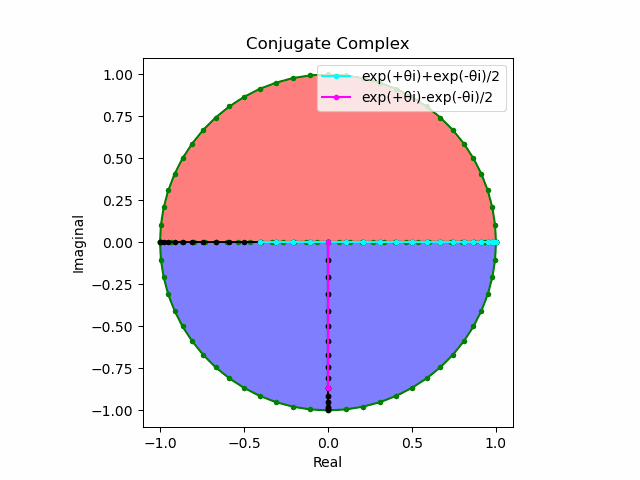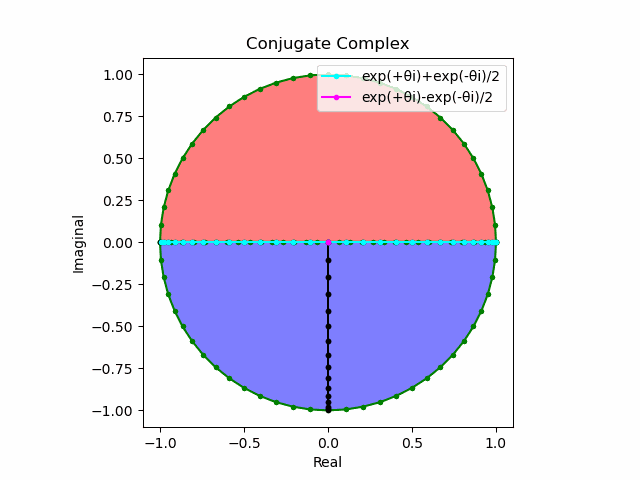
これを2で割って平均を求めると幅も高さも1に戻る。$\cos(θ)$の導出式は$\frac{e^{θ_nπi}+e^{-θ_nπi}}{2}$なのでこちらの答えはこの時点で得られる。
import math as m
import cmath as c
import numpy as num
from matplotlib import pyplot as plt
import matplotlib.animation as animation
# 単位円データ作成
z=num.linspace(1,-1,31,endpoint = True)*(1+0j)
zp=z*(0-1j)
p0=[]
for nm in range(len(zp)):
p0.append(c.exp(zp[nm]*m.pi/2)*(0+1j))
p1=num.array(p0)
# 共役複素数列(-)
m1=-p1[::-1]
lx=(p1+m1)/2
ly=(p1-m1)/2
# グラフ表示準備
plt.style.use('default')
fig = plt.figure()
# 関数定義
def Conjugate_Complex(n):
plt.cla()
plt.plot(z.real,z.imag,color="green", marker=".")
plt.plot(p1.real,p1.imag,color="green", marker=".")
plt.plot(m1.real,m1.imag,color="green", marker=".")
plt.fill_between(p1.real,p1.imag,facecolor='blue',alpha=0.5)
plt.fill_between(m1.real,m1.imag,facecolor='red',alpha=0.5)
plt.plot(lx.real,lx.imag,color="black", marker=".")
plt.plot(ly.real,ly.imag,color="black", marker=".")
plt.ylim([-1.1,1.1])
plt.xlim([-1.1,1.1])
plt.title("Conjugate Complex")
plt.xlabel("Real")
plt.ylabel("Imaginal")
ax = fig.add_subplot(111)
ax.set_aspect('equal', adjustable='box')
#exp(+θi)±exp(-θi)
plt.plot(lx[0:n].real,lx[0:n].imag,color="cyan", marker=".", label="exp(+θi)+exp(-θi)/2")
plt.plot([0,ly[n].real],[0,ly[n].imag],color="magenta", marker=".", label="exp(+θi)-exp(-θi)/2")
ax.legend(loc='lower right')
ani = animation.FuncAnimation(fig, Conjugate_Complex, interval=50,frames=len(z))
ani.save("output93.gif", writer="pillow")
そしてさらにこれを+90度($+\frac{π}{2}$ラジアン)回転させた$\frac{e^{+θ_n πi}-e^{-θ_nπi}}{2(0+1i)}$の結果が$\sin(0→π)$と一致する。
import math as m
import cmath as c
import numpy as num
from matplotlib import pyplot as plt
import matplotlib.animation as animation
# 単位円データ作成
z=num.linspace(1,-1,31,endpoint = True)*(1+0j)
zp=z*(0+1j)
p0=[]
for nm in range(len(zp)):
p0.append(c.exp(zp[nm]*m.pi/2)*(0+1j))
p1=num.array(p0)
# 共役複素数列(-)
m1=-p1[::-1]
lx=(p1+m1)/2
ly1=(p1-m1)/2
ly2=(p1-m1)/(2*(0+1j))
u0=num.linspace(m.pi,0,31,endpoint = True)
u1=[]
for nm in range(len(u0)):
u1.append(m.sin(u0[nm]))
u2=num.array(u1)
print("Imaginal of $\frac{exp(+θ_nπ(0+1i))-exp(-θ_nπ(0+1i)))}{2}$=",num.round(ly1.imag,8))
print("Real of $\frac{exp(+θ_nπ(0+1i))-exp(-θ_nπ(0+1i))}{2*(0-1i)}=",num.round(ly2.real,8))
print("$\sin(0→π)$=",num.round(u2,8))
Imaginal of $\frac{exp(+θ_nπ(0+1i))-exp(-θ_nπ(0+1i)))}{2}$
[0. 0.10452846 0.20791169 0.30901699 0.40673664 0.5
0.58778525 0.66913061 0.74314483 0.80901699 0.8660254 0.91354546
0.95105652 0.9781476 0.9945219 1. 0.9945219 0.9781476
0.95105652 0.91354546 0.8660254 0.80901699 0.74314483 0.66913061
0.58778525 0.5 0.40673664 0.30901699 0.20791169 0.10452846
0. ]
Real of $\frac{exp(+θ_nπ(0+1i))-exp(-θ_nπ(0+1i))}{2*(0+1i)}$
[0. 0.10452846 0.20791169 0.30901699 0.40673664 0.5
0.58778525 0.66913061 0.74314483 0.80901699 0.8660254 0.91354546
0.95105652 0.9781476 0.9945219 1. 0.9945219 0.9781476
0.95105652 0.91354546 0.8660254 0.80901699 0.74314483 0.66913061
0.58778525 0.5 0.40673664 0.30901699 0.20791169 0.10452846
0. ]
$\sin(0→π)$
[0. 0.10452846 0.20791169 0.30901699 0.40673664 0.5
0.58778525 0.66913061 0.74314483 0.80901699 0.8660254 0.91354546
0.95105652 0.9781476 0.9945219 1. 0.9945219 0.9781476
0.95105652 0.91354546 0.8660254 0.80901699 0.74314483 0.66913061
0.58778525 0.5 0.40673664 0.30901699 0.20791169 0.10452846
0. ]
かかる共役関係は$-e^{θ_nπi}$と$-e^{-θ_nπi}$の場合も維持され、この場合$(n=1→-1)$の条件が継承されるのは$θ_n*(0+1i)$の位相となる。
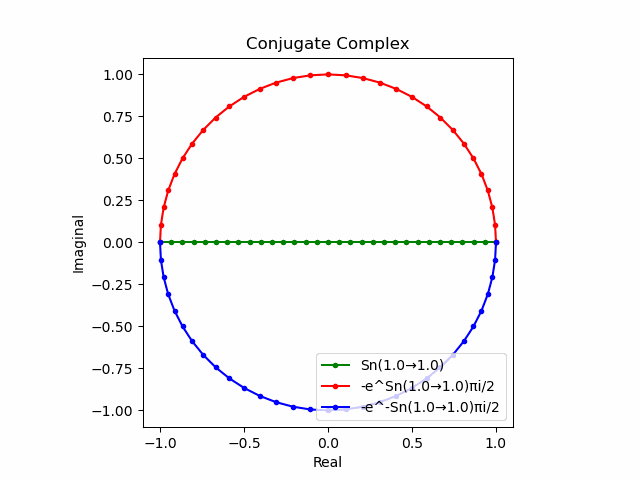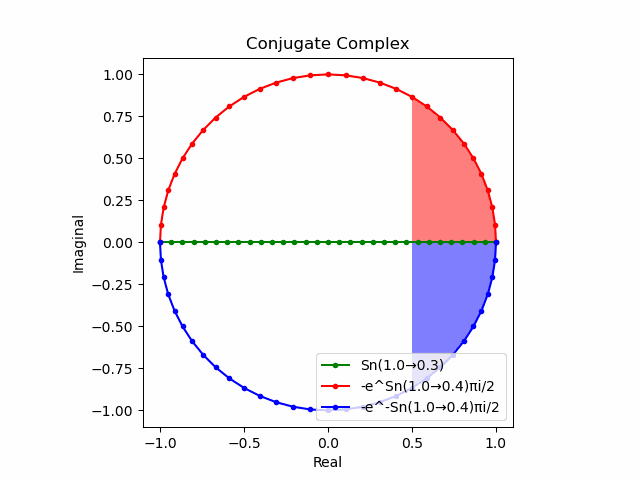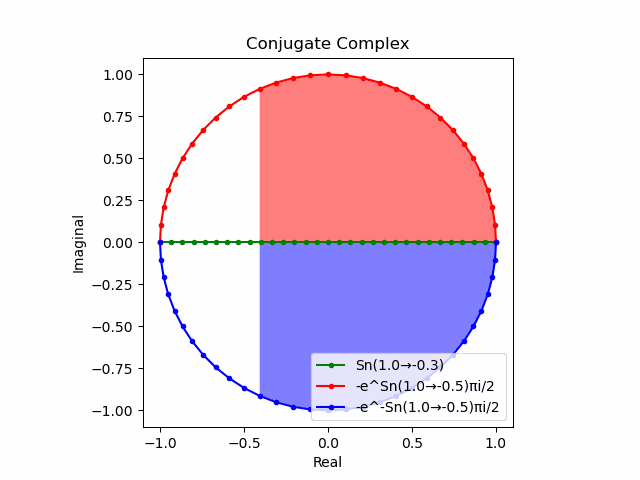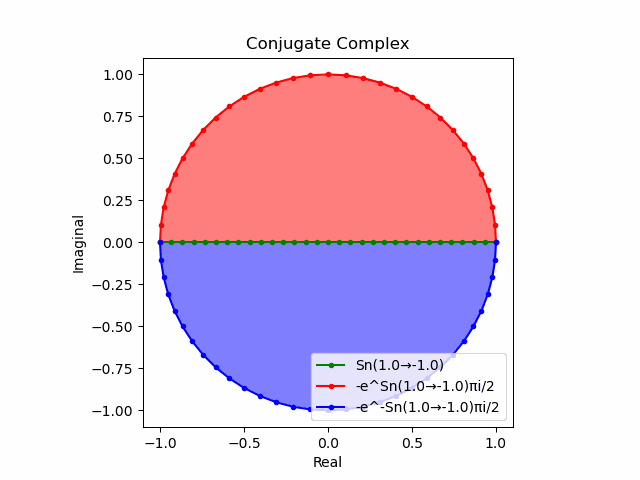
この場合ももちろん$-(e^{θ_nπi}+e^{-θ_nπi})$は幅2倍の横棒、$e^{-θ_nπi}-e^{+θ_nπi}$は高さ2倍の縦棒となる。
import math as m
import cmath as c
import numpy as num
from matplotlib import pyplot as plt
import matplotlib.animation as animation
# 単位円データ作成
z=num.linspace(1,-1,31,endpoint = True)*(1+0j)
zp=z*(0+1j)
p0=[]
for nm in range(len(zp)):
p0.append(-c.exp(zp[nm]*m.pi/2)*(0+1j))
p1=num.array(p0)
# 共役複素数列(-)
m1=-p1[::-1]
lx=p1+m1
ly=p1-m1
# グラフ表示準備
plt.style.use('default')
fig = plt.figure()
# 関数定義
def Conjugate_Complex(n):
plt.cla()
plt.plot(z.real,z.imag,color="green", marker=".")
plt.plot(p1.real,p1.imag,color="green", marker=".")
plt.plot(m1.real,m1.imag,color="green", marker=".")
plt.fill_between(p1.real,p1.imag,facecolor='blue',alpha=0.5)
plt.fill_between(m1.real,m1.imag,facecolor='red',alpha=0.5)
plt.plot(lx.real,lx.imag,color="black", marker=".")
plt.plot(ly.real,ly.imag,color="black", marker=".")
plt.ylim([-2.1,2.1])
plt.xlim([-2.1,2.1])
plt.title("Conjugate Complex")
plt.xlabel("Real")
plt.ylabel("Imaginal")
ax = fig.add_subplot(111)
ax.set_aspect('equal', adjustable='box')
#exp(+θi)±exp(-θi)
plt.plot(lx[0:n].real,lx[0:n].imag,color="cyan", marker=".", label="exp(+θi)+exp(-θi)")
plt.plot([0,ly[n].real],[0,ly[n].imag],color="magenta", marker=".", label="exp(+θi)-exp(-θi)")
ax.legend(loc='upper right')
ani = animation.FuncAnimation(fig, Conjugate_Complex, interval=50,frames=len(z))
ani.save("output94.gif", writer="pillow")
2で割って平均を求めた結果が幅も高さも1に戻るのも同じ。$\cos(θ)$の導出式は$\frac{e^{θ_nπi}+e^{-θ_nπi}}{2}$なのでこちらの答えはこの時点で得られる。符号が逆だが結果は同じ。そう、$\cos(θ)$は「回転の方向がない(逆関数を備えない)」偶関数なのである。
import math as m
import cmath as c
import numpy as num
from matplotlib import pyplot as plt
import matplotlib.animation as animation
# 単位円データ作成
z=num.linspace(1,-1,31,endpoint = True)*(1+0j)
zp=z*(0+1j)
p0=[]
for nm in range(len(zp)):
p0.append(-c.exp(zp[nm]*m.pi/2)*(0+1j))
p1=num.array(p0)
# 共役複素数列(-)
m1=-p1[::-1]
lx=(p1+m1)/2
ly=(p1-m1)/2
# グラフ表示準備
plt.style.use('default')
fig = plt.figure()
# 関数定義
def Conjugate_Complex(n):
plt.cla()
plt.plot(z.real,z.imag,color="green", marker=".")
plt.plot(p1.real,p1.imag,color="green", marker=".")
plt.plot(m1.real,m1.imag,color="green", marker=".")
plt.fill_between(p1.real,p1.imag,facecolor='blue',alpha=0.5)
plt.fill_between(m1.real,m1.imag,facecolor='red',alpha=0.5)
plt.plot(lx.real,lx.imag,color="black", marker=".")
plt.plot(ly.real,ly.imag,color="black", marker=".")
plt.ylim([-1.1,1.1])
plt.xlim([-1.1,1.1])
plt.title("Conjugate Complex")
plt.xlabel("Real")
plt.ylabel("Imaginal")
ax = fig.add_subplot(111)
ax.set_aspect('equal', adjustable='box')
#exp(+θi)±exp(-θi)
plt.plot(lx[0:n].real,lx[0:n].imag,color="cyan", marker=".", label="exp(+θi)+exp(-θi)/2")
plt.plot([0,ly[n].real],[0,ly[n].imag],color="magenta", marker=".", label="exp(+θi)-exp(-θi)/2")
ax.legend(loc='upper right')
ani = animation.FuncAnimation(fig, Conjugate_Complex, interval=50,frames=len(z))
ani.save("output95.gif", writer="pillow")
この場合には-90度($\frac{π}{2}$ラジアン)回転させた$\frac{e^{-θ_n πi}-e^{+θ_nπi}}{2(0-1i)}$の結果が$\sin(0→π)$と一致する。そう、$\sin(θ)$は「回転の方向がある(逆関数を備える)」奇関数なのである。
import math as m
import cmath as c
import numpy as num
from matplotlib import pyplot as plt
import matplotlib.animation as animation
# 単位円データ作成
z=num.linspace(1,-1,31,endpoint = True)*(1+0j)
zp=z*(0+1j)
p0=[]
for nm in range(len(zp)):
p0.append(-c.exp(zp[nm]*m.pi/2)*(0+1j))
p1=num.array(p0)
# 共役複素数列(-)
m1=-p1[::-1]
lx=(p1+m1)/2
ly1=(p1-m1)/2
ly2=(p1-m1)/(2*(0-1j))
u0=num.linspace(m.pi,0,31,endpoint = True)
u1=[]
for nm in range(len(u0)):
u1.append(m.sin(u0[nm]))
u2=num.array(u1)
print("Imaginal of $\frac{exp(-θ_nπ(0+1i))-exp(+θ_nπ(0+1i)))}{2}$=",num.round(ly1.imag,8))
print("Real of $\frac{exp(-θ_nπ(0+1i))-exp(+θ_nπ(0+1i))}{2*(0-1i)}=",num.round(ly2.real,8))
print("$\sin(0→π)$=",num.round(u2,8))
Imaginal of $\frac{exp(-θ_nπ(0+1i))-exp(+θ_nπ(0+1i)))}{2}$
[-0. -0.10452846 -0.20791169 -0.30901699 -0.40673664 -0.5
-0.58778525 -0.66913061 -0.74314483 -0.80901699 -0.8660254 -0.91354546
-0.95105652 -0.9781476 -0.9945219 -1. -0.9945219 -0.9781476
-0.95105652 -0.91354546 -0.8660254 -0.80901699 -0.74314483 -0.66913061
-0.58778525 -0.5 -0.40673664 -0.30901699 -0.20791169 -0.10452846
-0. ]
Real of $\frac{exp(-θ_nπ(0+1i))-exp(+θ_nπ(0+1i))}{2*(0-1i)}$
[0. 0.10452846 0.20791169 0.30901699 0.40673664 0.5
0.58778525 0.66913061 0.74314483 0.80901699 0.8660254 0.91354546
0.95105652 0.9781476 0.9945219 1. 0.9945219 0.9781476
0.95105652 0.91354546 0.8660254 0.80901699 0.74314483 0.66913061
0.58778525 0.5 0.40673664 0.30901699 0.20791169 0.10452846
0. ]
$\sin(0→π)$
[0. 0.10452846 0.20791169 0.30901699 0.40673664 0.5
0.58778525 0.66913061 0.74314483 0.80901699 0.8660254 0.91354546
0.95105652 0.9781476 0.9945219 1. 0.9945219 0.9781476
0.95105652 0.91354546 0.8660254 0.80901699 0.74314483 0.66913061
0.58778525 0.5 0.40673664 0.30901699 0.20791169 0.10452846
0. ]
そんな感じで以下続報…







