【無限遠点を巡る数理】オイラーの公式と等比数列①その根本的差異について。

正直、この「発見」の余波が続いています。おそらく専門家のとっては「ああ、あれね」レベルの話と頭では分かってるんですが…
【無限遠点を巡る数理】オイラー座標系②複素等比数列による整数概念の再構築。

とにかく最大の違いはオイラーの公式exp(±1)^θiの描画する円を構成するCos波とSin波が2π周期なのに対し、等比数列-1^x=(0±1i)^2xの描画する円を構成するCos波とSin波が2周期だという事。

c0=seq(-pi,pi,length=61)
f0<-function(x)exp(1)^(x*(0+1i))
s0=f0(c0)
plot(s0,type="l",xlim=c(-pi,pi),ylim=c(-pi,pi),main="exp(1)^(x*(0+1i))",xlab="Real",ylab="Imaginal",col=rgb(0,1,0))
par(new=T)
plot(c0,Re(s0),type="l",xlim=c(-pi,pi),ylim=c(-pi,pi),main="",xlab="",ylab="",col=rgb(0,0,1))
par(new=T)
plot(c0,Im(s0),type="l",xlim=c(-pi,pi),ylim=c(-pi,pi),main="",xlab="",ylab="",col=rgb(1,0,0))
legend("bottomleft", legend=c("Circle","Cosine Wave","Sine Wave"), lty =c(1,1,1),col=c(rgb(0,1,0),rgb(0,0,1),rgb(1,0,0)))

c0=seq(-pi,pi,length=61)
f0<-function(x)exp(1)^(x*(0+1i))
s0=f0(c0)
plot(s0,type="l",xlim=c(-pi,pi),ylim=c(-pi,pi),main="exp(1)^(x*(0-1i))",xlab="Real",ylab="Imaginal",col=rgb(0,1,0))
par(new=T)
plot(c0,Re(s0),type="l",xlim=c(-pi,pi),ylim=c(-pi,pi),main="",xlab="",ylab="",col=rgb(0,0,1))
par(new=T)
plot(c0,Im(s0),type="l",xlim=c(-pi,pi),ylim=c(-pi,pi),main="",xlab="",ylab="",col=rgb(1,0,0))
legend("bottomleft", legend=c("Circle","Cosine Wave","Sine Wave"), lty =c(1,1,1),col=c(rgb(0,1,0),rgb(0,0,1),rgb(1,0,0)))

c10<-seq(-1,1,length=41)
f0<-function(x)(0+1i)^(2*x)
s0=f0(c10) 
plot(s0,type="l",xlim=c(-1,1),ylim=c(-1,1),main="(0+1i)^2x",xlab="Real",ylab="Imaginal",col=rgb(0,1,0))

par(new=T)
plot(c10,Re(s0),type="l",xlim=c(-1,1),ylim=c(-1,1),main="",xlab="",ylab="",col=rgb(0,0,1))
par(new=T)
plot(c10,Im(s0),type="l",xlim=c(-1,1),ylim=c(-1,1),main="",xlab="",ylab="",col=rgb(1,0,0))
legend("bottomleft", legend=c("Circle","Cosine Wave","Sine Wave"), lty =c(1,1,1),col=c(rgb(0,1,0),rgb(0,0,1),rgb(1,0,0)))

c10<-seq(-1,1,length=41)
f0<-function(x)(0-1i)^(2*x)
s0=f0(c10) 
plot(s0,type="l",xlim=c(-1,1),ylim=c(-1,1),main="(0-1i)^2x",xlab="Real",ylab="Imaginal",col=rgb(0,1,0))

par(new=T)
plot(c10,Re(s0),type="l",xlim=c(-1,1),ylim=c(-1,1),main="",xlab="",ylab="",col=rgb(0,0,1))
par(new=T)
plot(c10,Im(s0),type="l",xlim=c(-1,1),ylim=c(-1,1),main="",xlab="",ylab="",col=rgb(1,0,0))
legend("bottomleft", legend=c("Circle","Cosine Wave","Sine Wave"), lty =c(1,1,1),col=c(rgb(0,1,0),rgb(0,0,1),rgb(1,0,0)))

そしてオイラーの公式exp(±1)^θi自体について、これまでの投稿ではこう指摘しています。

• 円分布自体の生成に関わっているのはi=(0±1i)^2の部分。これ以外の複素数は無限に拡散してしまうか0に収束してしまう。
  【無限遠点を巡る数理】オイラー座標系②複素等比数列による整数概念の再構築。
• 複素関数(0±1i)^2xのxには単位円のSVoR(Simple vibration on Radius)(-1→0→1)が入る。これを2で割ってπを掛ける事でSin波やCos波への対応を準備しているものと推測される。見え方としては「半径をπ/2倍する」イメージ?
  【初心者向け】指数・対数関数の発見とそれ以降の発展について。
• 自然指数関数e^x自体の機能はY軸{-Inf,0,Inf}の{0,1,Inf}への射影のみ。
  【初心者向け】指数・対数関数の発見とそれ以降の発展について。

このうち複素関数(0±1i)^2xについての情報が決定的に不足している訳です。そして最初に気になるのが以下の対比。

#オイラーの公式「exp(±1)^θi」の場合。
【Rで球面幾何学】指数関数や対数関数における「ネイピア数周期」の意味について。
オイラーの公式exp(±1)^θiでは、-π/2~π/2を範囲として与えられた場合、および根がexp(1/2)の時に半円しか描画されません(片道)。

Src01<-function(Rad){
c0=rev(seq(-pi/2,pi/2,length=61))
f0<-function(x)exp(1)^(x*(0+1i))
f1<-function(x)exp(1)^(x*(0-1i))
s0=f0(c0)
s1=f1(c0)
plot(s0,type="l",xlim=c(-1,1),ylim=c(-1,1),main="exp^(x*(0±1i))",xlab="Real",ylab="Imaginal",col=rgb(0,0,1))
segments(0,0,Re(s0[Rad]),Im(s0[Rad]),col=rgb(0,1,0))
segments(0,0,Re(s1[Rad]),Im(s1[Rad]),col=rgb(1,0,0))
crc01<-paste("exp(1)^(x*(0+1i) Rad=",Rad)
crc02<-paste("exp(1)^(x*(0-1i) Rad=",Rad)
legend("bottomleft", legend=c(crc01,crc02), lty =c(1,1),col=c(rgb(0,1,0),rgb(1,0,0)))
}

#アニメーション
library("animation")
Time_Code=seq(1,59, length=30)
saveGIF({
for (i in Time_Code){
　Src01(i)
}
}, interval = 0.1, movie.name = "Src10.gif")

Src01<-function(Rad){
c0=seq(-pi,pi,length=61)
f0<-function(x)exp(1/2)^(x*(0+1i))
f1<-function(x)exp(1/2)^(x*(0-1i))
s0=f0(c0)
s1=f1(c0)
plot(s0,type="l",xlim=c(-1,1),ylim=c(-1,1),main="exp(1/2)^(x*(0+1i))",xlab="Real",ylab="Imaginal",col=rgb(0,0,1))
segments(0,0,Re(s0[Rad]),Im(s0[Rad]),col=rgb(0,1,0))
segments(0,0,Re(s1[Rad]),Im(s1[Rad]),col=rgb(1,0,0))
crc01<-paste("exp(1/2)^(x*(0+1i) Rad=",Rad)
crc02<-paste("exp(1/2)^(x*(0+1i) Rad=",Rad)
legend("bottomleft", legend=c(crc01,crc02), lty =c(1,1),col=c(rgb(0,1,0),rgb(1,0,0)))
}

#アニメーション
library("animation")
Time_Code=seq(1,59, length=30)
saveGIF({
for (i in Time_Code){
　Src01(i)
}
}, interval = 0.1, movie.name = "Src11.gif")

それではexp(1/2)^θiに-2π~2πを範囲として与えるとどうなるかというと、ちゃんと丁度1周してしまうのです。

Src01<-function(Rad){
c0=rev(seq(-2*pi,2*pi,length=61))
f0<-function(x)exp(1/2)^(x*(0+1i))
f1<-function(x)exp(1/2)^(x*(0-1i))
s0=f0(c0)
s1=f1(c0)
plot(s0,type="l",xlim=c(-1,1),ylim=c(-1,1),main="exp^(x*(0±1i))",xlab="Real",ylab="Imaginal",col=rgb(0,0,1))
segments(0,0,Re(s0[Rad]),Im(s0[Rad]),col=rgb(0,1,0))
segments(0,0,Re(s1[Rad]),Im(s1[Rad]),col=rgb(1,0,0))
crc01<-paste("exp(1)^(x*(0+1i) Rad=",Rad)
crc02<-paste("exp(1)^(x*(0-1i) Rad=",Rad)
legend("bottomleft", legend=c(crc01,crc02), lty =c(1,1),col=c(rgb(0,1,0),rgb(1,0,0)))
}

#アニメーション
library("animation")
Time_Code=seq(1,59, length=30)
saveGIF({
for (i in Time_Code){
　Src01(i)
}
}, interval = 0.1, movie.name = "Src15.gif")

根の値がexp(1)以下またはexp(-1)の場合はこれを繰り返します。

• おそらくこれはリーマン面(Riemann Surface)に対応する。
  リーマン面 - Wikipedia

#等比数列「-1^x=(0±1i)^2x」の場合。
一方、等比数列-1^xはi^2=-1なので自明の場合(Trivial Case)として(0±1i)^2xとなり、-1→1の範囲を与えられた関数(0±1i)^xは半円しか描画しません(片道)。

Src01<-function(Rad){
c0=rev(seq(-1,1,length=61))
f0<-function(x)(0+1i)^x
f1<-function(x)(0-1i)^x
s0=f0(c0)
s1=f1(c0)
plot(s0,type="l",xlim=c(-1,1),ylim=c(-1,1),main="(0+1i)^x",xlab="Real",ylab="Imaginal",col=rgb(0,0,1))
segments(0,0,Re(s0[Rad]),Im(s0[Rad]),col=rgb(0,1,0))
segments(0,0,Re(s1[Rad]),Im(s1[Rad]),col=rgb(1,0,0))
crc01<-paste("(0+1i)^x Rad=",Rad)
crc02<-paste("(0^-1i)^x Rad=",Rad)
legend("bottomleft", legend=c(crc01,crc02), lty =c(1,1),col=c(rgb(0,1,0),rgb(1,0,0)))
}

#アニメーション
library("animation")
Time_Code=seq(1,59, length=30)
saveGIF({
for (i in Time_Code){
Src01(i)
}
}, interval = 0.1, movie.name = "Src07.gif")

①二倍の振幅範囲(1→-1→1)を与えても半円の範囲を往復するのみ。

Src01<-function(Rad){
c01=seq(-1,1,length=21)
c02=rev(c01)
c10<-c(c02,c01[2:21])
f0<-function(x)(0+1i)^x
f1<-function(x)(0-1i)^x
s0=f0(c10)
s1=f1(c10) 
plot(s0,type="l",xlim=c(-1,1),ylim=c(-1,1),main="(0+1i)^x",xlab="Real",ylab="Imaginal",col=rgb(0,0,1))
segments(0,0,Re(s0[Rad]),Im(s0[Rad]),col=rgb(0,1,0))
segments(0,0,Re(s1[Rad]),Im(s1[Rad]),col=rgb(1,0,0))
crc01<-paste("(0+1i)^x Rad=",Rad)
crc02<-paste("(0^-1i)^x Rad=",Rad)
legend("bottomleft", legend=c(crc01,crc02), lty =c(1,1),col=c(rgb(0,1,0),rgb(1,0,0)))
}

#アニメーション
library("animation")
Time_Code=seq(1,40, length=40)
saveGIF({
for (i in Time_Code){
　Src01(i)
}
}, interval = 0.1, movie.name = "Src08.gif")

②等比数列(0±1i)^axのaの値を1/2にすると(添字なので1/8になりそうだが)素直に1/4になってその範囲を往復する。

Src01<-function(Rad){
c01=seq(-1,1,length=21)
c02=rev(c01)
c10<-rev(c(c02,c01[2:21]))
f0<-function(x)(0+1i)^(x/2)
f1<-function(x)(0-1i)^(x/2)
s0=f0(c10)
s1=f1(c10) 
plot(s0,type="l",xlim=c(-1,1),ylim=c(-1,1),main="(0+1i)^(x/2)",xlab="Real",ylab="Imaginal",col=rgb(0,0,1))
segments(0,0,Re(s0[Rad]),Im(s0[Rad]),col=rgb(0,1,0))
segments(0,0,Re(s1[Rad]),Im(s1[Rad]),col=rgb(1,0,0))
crc01<-paste("(0+1i)^x Rad=",Rad)
crc02<-paste("(0^-1i)^x Rad=",Rad)
legend("bottomleft", legend=c(crc01,crc02), lty =c(1,1),col=c(rgb(0,1,0),rgb(1,0,0)))
}

#アニメーション
library("animation")
Time_Code=seq(1,40, length=40)
saveGIF({
for (i in Time_Code){
　Src01(i)
}
}, interval = 0.1, movie.name = "Src09.gif")

③円を完全に描くのは等比数列(0±1i)^2xで1~-1の範囲を与えられた場合。

Src10<-function(Rad){
c10<-seq(-1,1,length=41)
f0<-function(x)(0+1i)^(2*x)
f1<-function(x)(0-1i)^(2*x)
s0=f0(c10)
s1=f1(c10) 
plot(s0,type="l",xlim=c(-1,1),ylim=c(-1,1),main="(0+1i)^2x",xlab="Real",ylab="Imaginal",col=rgb(0,0,1))
segments(0,0,Re(s0[Rad]),Im(s0[Rad]),col=rgb(0,1,0))
segments(0,0,Re(s1[Rad]),Im(s1[Rad]),col=rgb(1,0,0))
crc01<-paste("(0+1i)^2x Rad=",Rad)
crc02<-paste("(0^-1i)^2x Rad=",Rad)
legend("bottomleft", legend=c(crc01,crc02), lty =c(1,1),col=c(rgb(0,1,0),rgb(1,0,0)))
}

#アニメーション
library("animation")
Time_Code=seq(1,40, length=40)
saveGIF({
for (i in Time_Code){
　Src10(i)
}
}, interval = 0.1, movie.name = "Src14.gif")

④距離が半分に思えるが1→-1→1→-1を範囲として与えると何故かピッチが半分になってしまう(この場合、40角形から20角形に劣化)。距離をいくら増やしても状況は同じ。また距離をいくら増やしても1回転しかしない(いや、正確には(0+1i)と(0-1i)の値が入れ替わる？)。

Src10<-function(Rad){
c01=seq(-1,1,length=21)
c02=rev(c01)
c10<-c(c02,c01[2:21],c02[2:21],c01[2:21])
f0<-function(x)(0+1i)^(2*x)
f1<-function(x)(0-1i)^(2*x)
s0=f0(c10)
s1=f1(c10) 
plot(s0,type="l",xlim=c(-1,1),ylim=c(-1,1),main="(0+1i)^2x",xlab="Real",ylab="Imaginal",col=rgb(0,0,1))
segments(0,0,Re(s0[Rad]),Im(s0[Rad]),col=rgb(0,1,0))
segments(0,0,Re(s1[Rad]),Im(s1[Rad]),col=rgb(1,0,0))
crc01<-paste("(0+1i)^2x Rad=",Rad)
crc02<-paste("(0^-1i)^2x Rad=",Rad)
legend("bottomleft", legend=c(crc01,crc02), lty =c(1,1),col=c(rgb(0,1,0),rgb(1,0,0)))
}

#アニメーション
library("animation")
Time_Code=seq(1,40, length=40)
saveGIF({
for (i in Time_Code){
　Src10(i)
}
}, interval = 0.1, movie.name = "Src13.gif")

#結局、どういう事？
完全に行き詰まってしまった時点で新しい知見を得たのです。
偏微分方程式の初期値問題 - 理学のキーワード - 東京大学 大学院理学系研究科・理学部

自然現象を記述する偏微分方程式に対して，現象を記述するのは方程式そのものではなくその解である。

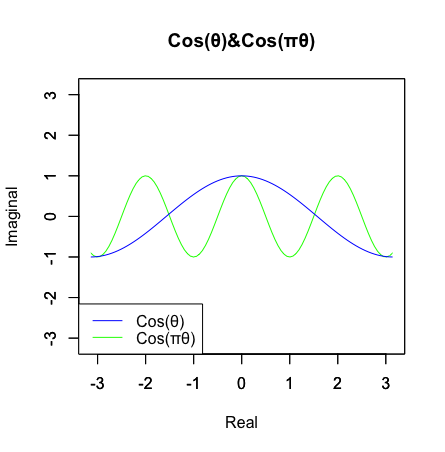
そう、注目すべきはオイラーの公式exp(±1)^θ(0±1i)と複素等比数列-1^x=(0±1i)^2xの特徴比較でなく、それぞれの出力結果がCos(θ)+Sin(θ)iである事とCos(πθ)+Sin(πθ)iである事の摺り合わせだったのです。

f0<-function(x)cos(x*pi)
plot(f0,xlim=c(-pi,pi),ylim=c(-pi,pi),main="Cos(θ)&Cos(πθ)",xlab="Real",ylab="Imaginal",col=rgb(0,1,0))
par(new=T)
plot(cos,xlim=c(-pi,pi),ylim=c(-pi,pi),main="",xlab="",ylab="",col=rgb(0,0,1))
legend("bottomleft", legend=c("Cos(θ)","Cos(πθ)"), lty =c(1,1),col=c(rgb(0,0,1),rgb(0,1,0)))

f0<-function(x)sin(x*pi)
f1<-function(x)-sin(x*pi)
plot(f0,xlim=c(-pi,pi),ylim=c(-pi,pi),main="Sin(θ)&Sin(πθ)&-Sin(πθ)",xlab="Real",ylab="Imaginal",col=rgb(0,1,0))
par(new=T)
plot(f1,xlim=c(-pi,pi),ylim=c(-pi,pi),main="",xlab="",ylab="",col=rgb(1,0,0))
par(new=T)
plot(sin,xlim=c(-pi,pi),ylim=c(-pi,pi),main="",xlab="",ylab="",col=rgb(0,0,1))
legend("bottomleft", legend=c("Sin(θ)","Sin(πθ)","-Sin(πθ)"), lty =c(1,1,1),col=c(rgb(0,0,1),rgb(0,1,0),rgb(1,0,0)))

式に従えば(0±1i)にπを掛けています。

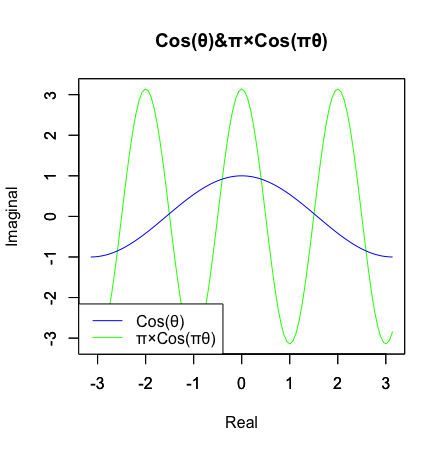
f0<-function(x)pi*cos(x*pi)
plot(f0,xlim=c(-pi,pi),ylim=c(-pi,pi),main="Cos(θ)&π×Cos(πθ)",xlab="Real",ylab="Imaginal",col=rgb(0,1,0))
par(new=T)
plot(cos,xlim=c(-pi,pi),ylim=c(-pi,pi),main="",xlab="",ylab="",col=rgb(0,0,1))
legend("bottomleft", legend=c("Cos(θ)","π×Cos(πθ)"), lty =c(1,1),col=c(rgb(0,0,1),rgb(0,1,0)))

考えてみれば当たり前の話なのですが、Sin(θ)と-Sin(θ)が別波形である事によって「回転の向き」が生じるのです。だからここでは両波形を見ていかないといけません。

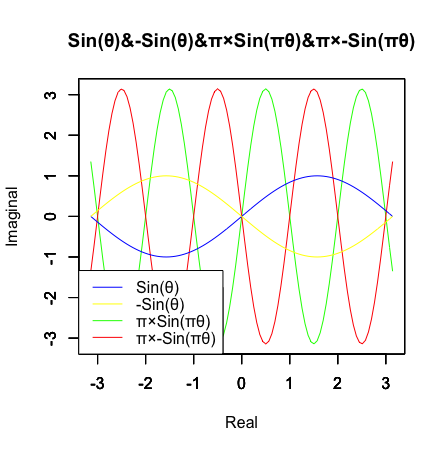
f0<-function(x)pi*sin(x*pi)
f1<-function(x)pi*-sin(x*pi)
plot(f0,xlim=c(-pi,pi),ylim=c(-pi,pi),main="Sin(θ)&-Sin(θ)&π×Sin(πθ)&π×-Sin(πθ)",xlab="Real",ylab="Imaginal",col=rgb(0,1,0))
par(new=T)
plot(f1,xlim=c(-pi,pi),ylim=c(-pi,pi),main="",xlab="",ylab="",col=rgb(1,0,0))
par(new=T)
plot(sin,xlim=c(-pi,pi),ylim=c(-pi,pi),main="",xlab="",ylab="",col=rgb(0,0,1))
legend("bottomleft", legend=c("Sin(θ)","π×Sin(πθ)","π×-Sin(πθ)"), lty =c(1,1,1),col=c(rgb(0,0,1),rgb(0,1,0),rgb(1,0,0),rgb(1,1,0)))
par(new=T)
f2<-function(x)-sin(x)
plot(f2,xlim=c(-pi,pi),ylim=c(-pi,pi),main="",xlab="",ylab="",col=rgb(1,1,0))
legend("bottomleft", legend=c("Sin(θ)","-Sin(θ)","π×Sin(πθ)","π×-Sin(πθ)"), lty =c(1,1,1,1),col=c(rgb(0,0,1),rgb(1,1,0),rgb(0,1,0),rgb(1,0,0)))

合算するとこう見えます(Plot関数は複素数関数を引数としても実数部しかPlotしないのでデータを渡し複素数集合を引数とする必要がある)。Cos(θ)+Sin(θ×(0+1i))とCos(θ)+Sin(θ×(0-1i))、π×(0+1i)^θとπ×(0-1i)^θは描画方向が逆なだけで同じ円を描くので重なって見える訳ですね。

c0<-seq(-pi,pi,length=61)
c1<-seq(-1,1,length=61)
f0<-function(x)complex(re=cos(x), im=sin(x))
f1<-function(x)pi*(0+1i)^(2*x)
s0<-f0(c0)
s1<-f1(c1)
plot(s0,type="l",asp=1,xlim=c(-pi,pi),ylim=c(-pi,pi),main="Cos(θ)+Sin(θ)i&π×(0+1i)^θ",xlab="Real",ylab="Imaginal",col=rgb(0,0,1))
par(new=T)
plot(s1,type="l",asp=1,xlim=c(-pi,pi),ylim=c(-pi,pi),main="",xlab="",ylab="",col=rgb(0,1,0))
abline(h=0,col=c(200,200,200))
abline(v=0,col=c(200,200,200))
segments(0,-pi,0,pi,col=rgb(1,1,0))
legend("bottomleft", legend=c("Cos(θ)+Sin(θ×(0±1i))","π×(0±1i)^θ","π×(0±1i)"), lty =c(1,1,1),col=c(rgb(0,0,1),rgb(0,1,0),rgb(1,1,0)))

あれ？　もしかしたらここは逆に考えないといけない？ 複素数を自然指数関数(Natural Exponential Function)の添字に与えるという事は、その実数部が示唆するX軸と虚数部が示唆するY軸に同時に対数尺を与える事。そしてオイラーの公式を素直に解釈すると与えられる対象はθ(-π→π)×(0±1i)…

c0<-seq(-pi,pi,length=61)
s1<-(0+1i)*c0
s0<-exp^s1
plot(s1,type="l",asp=1,xlim=c(-pi,pi),ylim=c(-pi,pi),main="θ(-π→π)×(0±1i)&exp(1)^(θ×(0±1i))",xlab="Real",ylab="Imaginal",col=rgb(1,1,0))
par(new=T)
plot(s0,type="l",asp=1,xlim=c(-pi,pi),ylim=c(-pi,pi),main="",xlab="",ylab="",col=rgb(0,1,0))
par(new=T)
plot(c0,Re(s0),type="l",asp=1,xlim=c(-pi,pi),ylim=c(-pi,pi),main="",xlab="",ylab="",col=rgb(0,0,1))
par(new=T)
plot(c0,Im(s0),type="l",asp=1,xlim=c(-pi,pi),ylim=c(-pi,pi),main="",xlab="",ylab="",col=rgb(1,0,0))
legend("bottomleft", legend=c("exp(1)^(θ×(0±1i))","θ×(0±1i)","Cos(θ)","Sin(θ)"), lty =c(1,1),col=c(rgb(0,1,0),rgb(1,1,0),rgb(0,0,1),rgb(1,0,0)))

つまり実はオイラーの公式はSVoI(Simple Vibration on Imaginal,複素数0+1iと0+1iの等速往復)を共有しつつ複素等差数列(0±1i)^2xも-1→1の範囲を与えれば円を描く事と式上の直接の関係はなかったのです(直接π倍して対数尺で潰していた)。もちろん同じ数理を利用はしてるのでしょうが…ああ、早くこういう事が式を見ただけで閃く様になりたいです。

と思ったら(何せ(0±1i)^2axはa=1の時しか丁度1周分の円を描かないので)どうやらあくまで「複素数列i((0±1i)⇄(0∓1i))が演算±exp(i×π/2)を経て半円2つを重ね1周分の円を描く」とか、そういう風に考えねばならない様です。

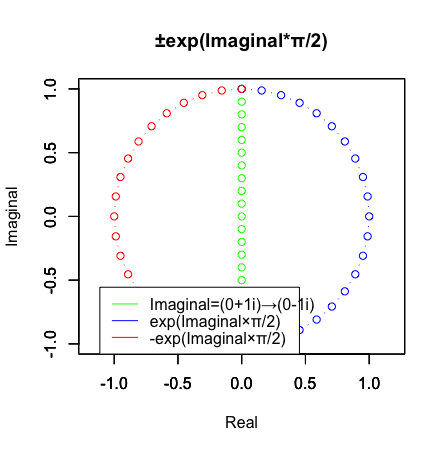
#Imaginal
i0<-seq(-1,1,length=21)
#(0+1i)→(0-1i)
Imaginal<-complex(re=0,im=rev(i0))
plot(Imaginal,type="b",asp=1,xlim=c(-1,1),ylim=c(-1,1),main="±exp(Imaginal*π/2)",xlab="Real",ylab="Imaginal",col=rgb(0,1,0))
par(new=T)
plot(exp(Imaginal*pi/2),asp=1,type="b",xlim=c(-1,1),ylim=c(-1,1),main="",xlab="",ylab="",col=rgb(0,0,1))
par(new=T)
plot(-exp(Imaginal*pi/2),type="b",asp=1,xlim=c(-1,1),ylim=c(-1,1),main="",xlab="",ylab="",col=rgb(1,0,0))
legend("bottomleft", legend=c("Imaginal=(0+1i)→(0-1i)","exp(Imaginal×π/2)","-exp(Imaginal×π/2)"), lty =c(1,1,1),col=c(rgb(0,1,0),rgb(0,0,1),rgb(1,0,0)))

これでも「半分は逆から描く」ズルをしています。

> Imaginal
 [1] 0+1.0i 0+0.9i 0+0.8i 0+0.7i 0+0.6i 0+0.5i 0+0.4i 0+0.3i
 [9] 0+0.2i 0+0.1i 0+0.0i 0-0.1i 0-0.2i 0-0.3i 0-0.4i 0-0.5i
[17] 0-0.6i 0-0.7i 0-0.8i 0-0.9i 0-1.0i
> exp(Imaginal*pi/2)
 [1] 0.0000000+1.0000000i 0.1564345+0.9876883i
 [3] 0.3090170+0.9510565i 0.4539905+0.8910065i
 [5] 0.5877853+0.8090170i 0.7071068+0.7071068i
 [7] 0.8090170+0.5877853i 0.8910065+0.4539905i
 [9] 0.9510565+0.3090170i 0.9876883+0.1564345i
[11] 1.0000000+0.0000000i 0.9876883-0.1564345i
[13] 0.9510565-0.3090170i 0.8910065-0.4539905i
[15] 0.8090170-0.5877853i 0.7071068-0.7071068i
[17] 0.5877853-0.8090170i 0.4539905-0.8910065i
[19] 0.3090170-0.9510565i 0.1564345-0.9876883i
[21] 0.0000000-1.0000000i
> -exp(Imaginal*pi/2)
 [1]  0.0000000-1.0000000i -0.1564345-0.9876883i
 [3] -0.3090170-0.9510565i -0.4539905-0.8910065i
 [5] -0.5877853-0.8090170i -0.7071068-0.7071068i
 [7] -0.8090170-0.5877853i -0.8910065-0.4539905i
 [9] -0.9510565-0.3090170i -0.9876883-0.1564345i
[11] -1.0000000+0.0000000i -0.9876883+0.1564345i
[13] -0.9510565+0.3090170i -0.8910065+0.4539905i
[15] -0.8090170+0.5877853i -0.7071068+0.7071068i
[17] -0.5877853+0.8090170i -0.4539905+0.8910065i
[19] -0.3090170+0.9510565i -0.1564345+0.9876883i
[21]  0.0000000+1.0000000i 

考えてみれば当たり前の話ですが、共役複素数を求める演算(統計言語RだとConj(i))を導入してもこの問題は解決しません(やはり逆から描くだけ)。

> Imaginal
 [1] 0+1.0i 0+0.9i 0+0.8i 0+0.7i 0+0.6i 0+0.5i 0+0.4i 0+0.3i
 [9] 0+0.2i 0+0.1i 0+0.0i 0-0.1i 0-0.2i 0-0.3i 0-0.4i 0-0.5i
[17] 0-0.6i 0-0.7i 0-0.8i 0-0.9i 0-1.0i
> Conj(Imaginal)
 [1] 0-1.0i 0-0.9i 0-0.8i 0-0.7i 0-0.6i 0-0.5i 0-0.4i 0-0.3i
 [9] 0-0.2i 0-0.1i 0+0.0i 0+0.1i 0+0.2i 0+0.3i 0+0.4i 0+0.5i
[17] 0+0.6i 0+0.7i 0+0.8i 0+0.9i 0+1.0i
> exp(Conj(Imaginal)/2*pi)
 [1] 0.0000000-1.0000000i 0.1564345-0.9876883i
 [3] 0.3090170-0.9510565i 0.4539905-0.8910065i
 [5] 0.5877853-0.8090170i 0.7071068-0.7071068i
 [7] 0.8090170-0.5877853i 0.8910065-0.4539905i
 [9] 0.9510565-0.3090170i 0.9876883-0.1564345i
[11] 1.0000000+0.0000000i 0.9876883+0.1564345i
[13] 0.9510565+0.3090170i 0.8910065+0.4539905i
[15] 0.8090170+0.5877853i 0.7071068+0.7071068i
[17] 0.5877853+0.8090170i 0.4539905+0.8910065i
[19] 0.3090170+0.9510565i 0.1564345+0.9876883i
[21] 0.0000000+1.0000000i

• あくまでY軸上のSVoI(Simple Vibration of Imaginal=虚数単振動)とX軸上のSVoR(Simple Vibration of Real=実数単振動)が対応しているイメージ、すなわち(1+0i)~(-1+0i)と(-1+0i)~(1+0i)が虚数共役(Imaginary Conjugate)ならぬ実数共役(Real Conjugate)の関係にあるという意識が重要なのですね。「人間の脳」なる粗雑な代数構造を許容するハード上ではexp(iθ)やexp(-iθ)のイメージが多少曖昧でも問題は生じませんが、コンピューター上で走るプログラムはこう厳格に意識しないとちゃんと動作してくれないのです。しかもこの場合、どう考えてもコンピューターの方が正しい…そういえばこの数理自体は演算(a×exp)^aθiのaの値を-1~0~1の範囲で動かした以下の投稿の時点で既に明らかになっていたのですね。完全に見逃してました。
  【Rで球面幾何学】指数関数や対数関数における「ネイピア数周期」の意味について。
  
  
  

そういえば「πiの棒」はオイラーの公式のもう一つの形(1±πi/N)^Nにも登場しますね。こちらは河童巻き状に側面から巻き付くイメージ。
【Rで球面幾何学】「世界で一番美しい公式」オイラーの等式の罠？



零元を有し、スカラー倍で増減し、かつ線状なので|x+y|=|x|+|y|が成立する為、これもノルム(Norm)成立条件を満たす距離関数(Metric Function)の一種と考えられます。
【初心者向け】方形描画関数②距離空間との関係。 - Qiita

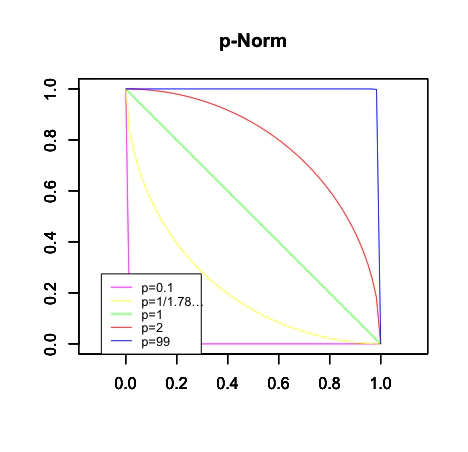
そして1次元ベクトル上の外積(Outer Product)は常に0なので、この場合の外積も0と考えます。「半径rをスカラー積(内積)、残りをベクトル積(外積)と考える」思考様式の導入…
【Rで球面幾何学】そもそも「内積」とは「外積」とは何か？ - Qiita

ところで試行錯誤の過程で思いついた「exp(1)^πiのマクローリン展開」。あれ？　よく見るとこのCos波とSin波は…
【Rで球面幾何学】オイラーの公式を導出したマクローリン級数の限界？

Macrolin_expansion_exp<-function(x,s0){

#グラフのスケール決定
Graph_scale_x<-c(-6,6)
Graph_scale_y<-c(-1,6)
#関数と凡例の決定
switch(x,
"0"= f0<-function(x) {x/x},
"1"= f0<-function(x) {1+x},
"2"= f0<-function(x) {1+x+x^2/2},
"3"= f0<-function(x) {1+x+x^2/2+x^3/6},
"4"= f0<-function(x) {1+x+x^2/2+x^3/6+x^4/24},
"5"= f0<-function(x) {1 + x + x^2/2 + x^3/6+ x^4/24+ x^5/120},
"6"= f0<-function(x) {1 + x + x^2/2 + x^3/6+ x^4/24+ x^5/120+ x^6/720},
"7"= f0<-function(x) {1 + x + x^2/2 + x^3/6+ x^4/24+ x^5/120+ x^6/720+ x^7/5040},
"8"= f0<-function(x) {1 + x + x^2/2 + x^3/6+ x^4/24+ x^5/120+ x^6/720+ x^7/5040+ x^8/40320},
"9"= f0<-function(x) {1 + x + x^2/2 + x^3/6+ x^4/24 + x^5/120 + x^6/720 + x^7/5040 + x^8/40320 + x^9/362880 }
)

switch(x,
"0"=text<-c("1"),
"1"=text<-c("1+x"),
"2"=text<-c("1+x+x^2/2!"),
"3"=text<-c("1+x+x^2/2!+x^3/3!"),
"4"=text<-c("1+x+x^2/2!+x^3/3!+x^4/4!"),
"5"=text<-c("1+x+x^2/2!+x^3/3!+x^4/4!+x^5/5!"),
"6"=text<-c("1+x+x^2/2!+x^3/3!+x^4/4!+x^5/5!+x^6/6!"),
"7"=text<-c("1+x+x^2/2!+x^3/3!+x^4/4!+x^5/5!+x^6/6!+x^7/7!"),
"8"=text<-c("1+x+x^2/2!+x^3/3!+x^4/4!+x^5/5!+x^6/6!+x^7/7!+x^8/8!"),
"9"=text<-c("1+x+x^2/2!+x^3/3!+x^4/4!+x^5/5!+x^6/6!+x^7/7!+x^8/8!+x^9/9!")
)

s1<-f0(s0)
plot(s1,type="l",asp=1,xlim=c(-pi,pi),ylim=c(-pi,pi),main="Macrolin Expansion of EXP(1)^πi",xlab="Real",ylab="Imaginal",col=rgb(0,0,1))
par(new=T)
plot(c1,Re(s1),type="l",asp=1,xlim=c(-pi,pi),ylim=c(-pi,pi),main="",xlab="",ylab="",col=rgb(0,1,0))
par(new=T)
plot(c1,Im(s1),type="l",asp=1,xlim=c(-pi,pi),ylim=c(-pi,pi),main="",xlab="",ylab="",col=rgb(1,0,0))

legend("bottomleft", legend=c("e^πi","Cos(θ)","Sin(θ)",text),lty=c(1,1,1,1),col=c(rgb(0,1,0),rgb(0,0,1),rgb(1,0,0),rgb(0,0,0)))
}

#アニメーション描画

library("animation")

c0<-seq(-pi,pi,length=61)
s0<-(0+1i)*c0

Time_Code=c("0","0","0","1","1","1","2","2","2","3","3","3","4","4","4","5","5","5","6","6","6","7","7","7","8","8","8","9","9","9")
saveGIF({
for (i in Time_Code){
　　Macrolin_expansion_exp(i,s0)
}
}, interval = 0.1, movie.name = "TEST02.gif")

これではむしろ物理学的観察結果から導出される「2π長(-π→π)をX軸のCos(θ)とY軸のSin(θ)に与える円の描き方」との間に互換性がない事になってしまう？ いやむしろ「半径rをスカラー積(内積)、残りをベクトル積(外積)と考える」思考様式の導入によって数学的円把握と物理的円把握が統合されるとも考えられそうです。
【初心者向け】物理学における「単位円筒(Unit Cylinder)」の概念について。
XY軸（円弧）

XZ軸（Cos波）

YZ軸（Sin波）

数学はそれ自体の魅力に加え、こういう「未知の対象に出会した時の対処方法」を磨く面白さがあります。解決に向けて地道な努力を続けていくうちに精神的に鍛えられるというか…そんな感じで以下続報…