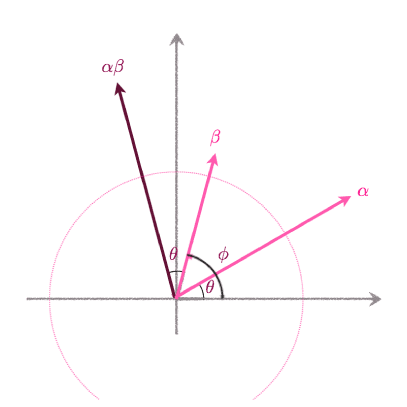ウィリアム・ローワン・ハミルトン(William Rowan Hamilton、1805年〜1865年)は、どうやっても三元数が安定した数理にまとまらない事に気付いて四元数への移行を決断したとされています。
四元数を発見法的に導く
Hamiltonはどうしても第4番目の元kがあることを認めなければならなかった。すなわち、一般の”三元数”の積を考えれば”三元数”の中にはなかった第4番目の元kが必然的に出てくるのだから、”三元数”の積は”三元数”としては表せない(数学的にいえば閉じていない)。したがって、”三元数”を”三元数”の範囲で合理的に定義することはできない。
ここで鍵となるのが内積(Inner Product)=スカラー積(Scalar Product)と外積(Outer Product)=ベクトル積(Vector Product)の概念。まずは算出方法について確認しておきましょう。それ自体はRだけでなく、多くのコンピューター言語の標準ライブラリーに含まれてますね。
R による行列の演算
>a0 <- matrix(c(0,0,1,2), nrow = 2, ncol = 2)
>b0 <- matrix(c(0,0,3,4), nrow = 2, ncol = 2)
# 内積計算関数
> crossprod(a0,b0)
[,1] [,2]
[1,] 0 0
[2,] 0 11
# 内積の手計算結果
>(a0[1,2]-a0[1,1])*(b0[1,2]-b0[1,1])+(a0[2,2]-a0[2,1])*(b0[2,2]-b0[2,1])
[1] 11
# 外積計算関数の計算結果
> outer(a0,b0)
, , 1, 1
[,1] [,2]
[1,] 0 0
[2,] 0 0
, , 2, 1
[,1] [,2]
[1,] 0 0
[2,] 0 0
, , 1, 2
[,1] [,2]
[1,] 0 3
[2,] 0 6
, , 2, 2
[,1] [,2]
[1,] 0 4
[2,] 0 8
# 外積関連数値の手計算結果
> (a0[1,2]-a0[1,1])*(b0[1,2]-b0[1,1])
[1] 3
> (a0[2,2]-a0[2,1])*(b0[1,2]-b0[1,1])
[1] 6
>(a0[1,2]-a0[1,1])*(b0[2,2]-b0[2,1])
[1] 4
>(a0[2,2]-a0[2,1])*(b0[2,2]-b0[2,1])
[1] 8
2つのベクトルからスカラーを与える二項演算である内積に対して外積とも呼ばれるが、英語でOuter Productは直積を意味するので注意を要する。
(半径1の)単位円(Unit Circle)/単位球面(Unit Sphere)上や極座標系(Polar Coordinate System)の振る舞いに限定して考えると内容はもっと整理され、分かりやすく単純化されますが、困った事にここで異なる2つの考え方が浮上してきてしまうのです。
単位円上での平面展開では内積がCos(θ)、外積がSin(θ)となる。
ゲームが作れるようになるまでがんばる日記:2次元での内積と外積
二次元上の内積は(X軸に沿った)スカラー値となる
a・b=|a||b|cosθ=axbx+ayby
二次元上の外積は(Y軸に沿った)スカラー値となる
a×b=|a||b|sinθ=axby-aybx
従って演算対象のベクトルが両方とも長さ1の単位ベクトルにおいては(すなわち半径1の単位円上の振る舞いにおいては)内積はCos(θ)、外積はSin(θ)と一致する。
この概念(Concept)自体は自明の場合(Trivial Case)として扱って差し支えない様に思われます。

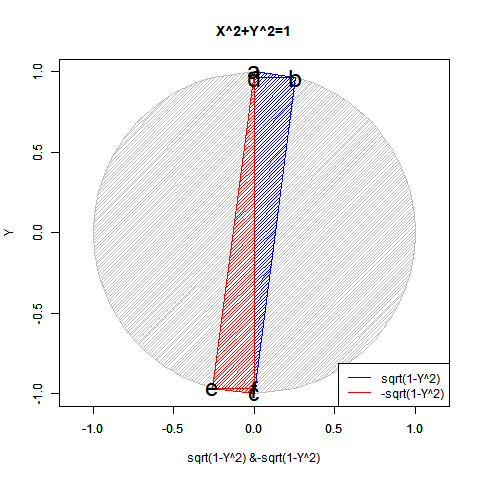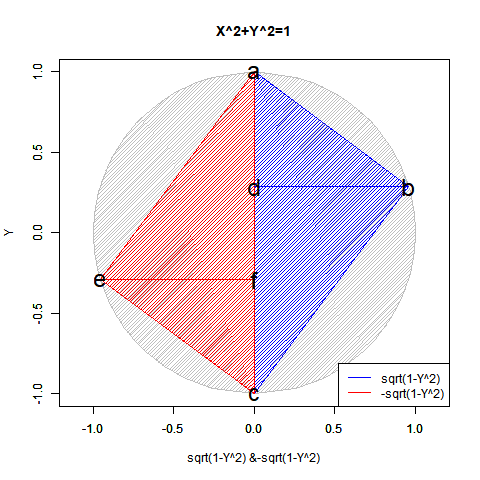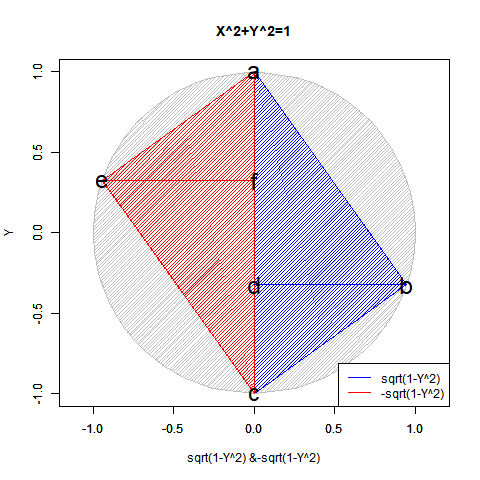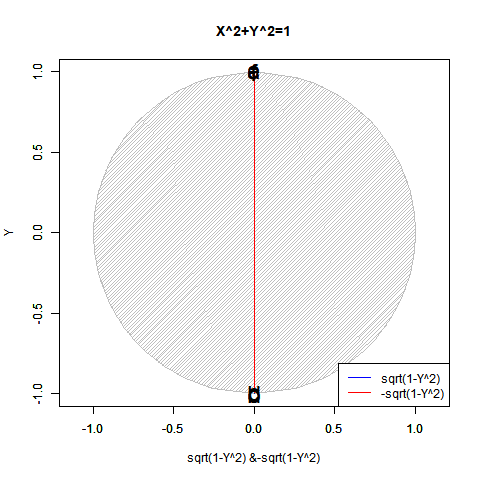
# 複素平面(球面)
Complex_plane<-function(x){
ifelse*1
theta <- c(seq(0, pi, length=180),seq(-pi, 0, length=180))
dr<-seq(0,2*pi,length=360)
theta00<- seq(1, -1, length=360)
theta01 <- c(theta[x:360],theta[1:x-1])
theta_cos<-cos(theta01)
theta_sin<-sin(theta01)
plot(cos(theta), sin(theta), xlim=c(-1,1), ylim=c(-1,1), type="l", main="Correlation coefficient",xlab="Real Expanse", ylab="Imaginal Expanse")
par(new=T)#上書き指定
plot(theta_cos,theta00,xlim=c(-1,1), ylim=c(-1,1), type="l",col=rgb(0,1,0),main="",xlab="", ylab="")
# cos(x)を塗りつぶす
polygon(theta_cos, #x
theta00, #y
density=c(30), #塗りつぶす濃度
angle=c(45), #塗りつぶす斜線の角度
col=rgb(0,1,0)) #塗りつぶす色
# sin(x)を塗りつぶす
polygon(theta00, #x
theta_sin, #y
density=c(30), #塗りつぶす濃度
angle=c(45), #塗りつぶす斜線の角度
col=rgb(0,0,1)) #塗りつぶす色
# 線を引く
segments(cos(dr[x]),sin(dr[x]),0,0,rgb(0,0,0))
# Cosθ+Sinθを塗りつぶす
polygon(c(0,cos(dr[x]),cos(dr[x]),0,0), #x
c(0,0,sin(dr[x]),sin(dr[x]),0), #y
density=c(30), #塗りつぶす濃度
angle=c(45),#塗りつぶす斜線の角度
col=rgb(1,0,0))#塗りつぶす色
# 凡例
# legend("bottomleft", legend=c("cos","sin", "cosθ & sinθ"), lty=c(1,1,1),col =c(rgb(0,1,0),rgb(0,0,1),rgb(0,1,1))
}
# アニメーションさせてみる。
library("animation")
Time_Code=c(1,15,30,45,60,75,90,105,120,135,150,165,180,195,210,225,240,255,270,285,300,315,330,345)
saveGIF({
for (i in Time_Code){
Complex_plane(i)
}
}, interval = 0.1, movie.name = "TEST001.gif")
問題はそれが自然に内積や外積の概念まで敷衍(Enlarge)可能かどうかなのですね。何故なら以下の様な概念もまた自明の場合と思えてならないからなのです。
1次元ベクトル上の外積は常に0となる。
複素数a+ibのaをスカラー部, ibをベクトル部とみなせば,一次元ベクトルの外積を定義できそうです.
(b1*i)(b2*i)
=b1*b2*i^2)
# ところで複素数においては以下が成立する。
bdi^2=-b1*b2 #i^2=-1
四元数や八元数のときと同様,マイナス付き内積のようなスカラー項で出てきましたが,右辺にベクトル部は出てきません.つまり,一次元ベクトルの外積は常に0なのです.何も面白くない結果だと思うかも知れませんが『一次元ベクトルの外積は常に0である』と定義できた ことが,何よりも嬉しいことです.
ここでさらに気になるのが三角関数を巡る以下の概念上の混乱。
①三次元上の直交座標系や極座標形で考えると、三角関数の正体は(外積=Z軸の値が0となる)X軸の値(Cos(φ))とY軸の値(Sin(φ))の関数である(-π<φ<π)。これにさらにZ軸上の角度θ(-π/2<=θ<=π/2)の変化を加えても(緯度に直交する)断面積の縮尺が変わるに過ぎない。すなわち「半径rをスカラー積、残りをベクトル積と考える事も出来る」という事。

円弧における極座標系
- x=r*cos(φ)
- y=r*sin(φ)
球面上における極座標系
- x=r*cos(φ)*sin(θ)
- y=r*sin(φ)*sin(θ)
- z=r*cos(θ)
【初心者向け】物理学における「単位円筒(Unit Cylinder)」の概念について。
XY軸(円弧)

XZ軸(Cos波)

YZ軸(Sin波)

【初心者向け】「単位円筒」から「単位球面」へ

これはある種の対蹠点効果(Antipodal effect)、すなわち関数-1^x=i^2xの実数部変動に対応した共役複素数(Conjugate Complex Number)の値の変動が全て揃っている為、断面の実数軸に対する直交性が保たれ続けるせいである。
対蹠点効果?|JE6RIJの気まぐれ無線日記-アメブロ
フォークランドに-5dB ~ 対蹠点(たいせきてん)効果か?
CQ ham radio-アマチュア無線の専門誌-CQ出版
対蹠点効果
地球上における一点に対して,正反対側の位置を対蹠点(対蹠とは足の裏の意味)という.これら2地点間の短波通信では,地球上において最も遠距離であるにもかかわらず,電波伝搬の大圏コースが無数にあるため電界強度が大きくなり,強力に電波が届く.
【Rで球面幾何学】オイラーの多面体定理(Euler's Polyhedron Theorem)と平面充填(Tiling)の連続性について。

また縦角θ(-π/2<=θ<=π/2)の変動範囲制限により、元来共役複素数の変動には「元蹠から対蹠に向かう方向性」と「対蹠から元蹠に向かう方向性」の2種類がある現実も巧妙に隠されている。
【初心者向け】三角関数と指数・対数関数の「巡回性」について。
オイラー角と異なり四元数にジンバルロックの概念が存在しないのは、実はこの「角度制限」のせいとも? まぁ正体は単なる1次元ベクトルなので実際には何の制限も加えず何回転させても問題が生じる事はなく、その辺りがCGや宇宙船/ドローンの制御に向いてる理由とも。
【Rで球面幾何学】ジンバルロック(?)やリサージュ曲線(?)との邂逅。


いずれにせよこうした妥協の積み重ねが人類にもたらした最大の恩恵、それこそがまさに大航海時代から産業革命の時代にかけて地図製作者達の経験と知識の集積空間として重宝された(座標を緯度±180度と経度±90度の組み合わせで表す)地球儀の概念だったのである。
【初心者向け】半径・直径・円周長・円の面積・球の表面積・球の体積の計算上の往復

②それが純粋な複素平面上の数理であるにも関わらず、「1の冪乗の巡回性」についても多くの人間が「正多角形の作図から定規やコンパスを追い出した便利なアルゴリズム」程度にしか意識しておらず、実際プログラム上も三角関数の概念さえ把握してれば誰でも使えるc0=seq(-pi,pi,length=NoS);cx=cos(c0);cy=sin(c0)(NoS(Number of Sides)=描く多角形の辺数+巡回を完成させる為の1)の構文さえ覚えていれば虚数だの複素数だのを意識する必要がない。
【初心者向け】挟み撃ち定理(Squeeze Theorem)による円周率πの近似

③まぁ概ねこうした隠蔽工作の裏にはしばしば(虚数や複素数の概念に触れただけで物議を醸した時代にあえてそれに触れないまま基礎を完成させ、しかもこっそり広める事に成功した)ガウス(Johann Carl Friedrich Gauß/Carolus Fridericus Gauss、1777年〜1855年)渾身の方便が隠されてる。だがもちろん、虚数や複素数の概念にはさらなる発展の余地があって四元数の概念に到達したハミルトンにとっては全然それだけで十分でなく、だからあえてあんな大騒動を引き起こす道を選んだともいえる。
1.1.7 ベクトルの概念に関する簡単な歴史
そう、数理間の齟齬自体というより、かかる軋轢を避け続ける顕密体制めいた概念運用こそが数学史上様々な弊害を引き起こしてきたといえましょう。ここでもある意味「ガウス渾身の方便」こそが、さらにその先に進もうとしたハミルトンのハードルを致命的なまでに引き揚げてしまった側面が確実に見て取れるのです。しかもこの論争で最終勝者となったのはハミルトンの四元数自体ではなく(やはり原則として虚数や複素数の概念に触れる必要がなく、まさにその事が論争上の勝因となった)ベクトル演算や線形代数学だった訳です。そもそもハミルトンが到達した「複素数の新側面」とは一体どういう内容だったのでしょうか? 話はまずそこまで遡らないといけません。
複素数同士の掛け算と、その概念の四元数への適用
# 二元数(複素数)同士の掛算。
(a+bi)(c+di)
=a(c+di)+bi(c+di)
=ac+adi+bci+bdi^2
# ところで複素数においては以下が成立する。
bdi^2=-bd #i^2=-1
# 従って計算結果は以下となる。
=(ac-bd)+(ad+bc)i
# このうち(ac-bd)の部分がスカラー積=内積。
# このうち(ad+bc)の部分がベクトル積=外積。
α=a+ibとβ=c+idの積を計算すると、
αβ=(a+ib)(c+id)=(ac–bd)+i(ad+bc)
となります。
θ=arg(α),ϕ=arg(β)
と置いて、このかけ算を極座標表示
α=|α|(cosθ+isinθ)
β=|β|(cosϕ+isinϕ)
で表すと、
αβ=(|α|(cosθ+isinθ))(|β|(cosϕ+isinϕ))
=|α||β|((cosθcosϕ–sinθsinϕ)+i(cosθsinϕ+sinθcosϕ))
=|α||β|(cos(θ+ϕ)+isin(θ+ϕ))
となります。最後の等号は、cosとsinの和の公式によって導かれます。従って、複素数のかけ算は、2つの複素数の絶対値を掛け合わせて、偏角を足したものになります。この様に、一見複雑そうな複素数のかけ算も、幾何学的な見方をすると、より見やすい意味を持つことが分かります。
ここでサラリと加法定理(Trigonometric Addition Formulas)が投入されてますね。しかもそれがcosとsinの和の公式導入でオイラーの公式(Euler's Formula)右辺に変換されてます。
【初心者向け】「加法定理の幾何学的証明」に挑戦。
加法定理、この球面幾何学シリーズ(Spherical Geometry Series)では、ピタゴラスの定理やタレスの定理に匹敵する参照数。実はこの辺りこそが三角関数の肝だった?
【初心者向け】ピタゴラスの定理あるいは三平方の定理からの出発
ところで平方ピタゴラスの定理a^2=b^2+c^2は一般の2項展開(Binomial Expansion)(a±b)^2では扱い切れません。
その証明には「角度が90度(π/2ラジアン)という特別条件」あるいは「複素平面(Complex Plane)における単位円上の操作、すなわち虚数i^2=-1の概念の導入と共益複素数(Conjugate Complex Number)の相互打ち消し作用」を必要とするのです。
【初心者向け】三角関数と指数・対数関数の「巡回性」について。
頭蹠(Portal)と対蹠(Antipodal)を結ぶ直径2を斜辺とする円弧上の三角関数x=cos(φ),y=sin(φ)において、曲がる角度の直角性は正弦定理(Law of Sines)A/sin(a)=B/sin(b)=C/sin(c)=2Rの特殊型たるタレスの定理(Thales' Theorem)「直径に対する円周角は直角である」が保証します。
そしていよいよ四元数同士の掛算の話に…・
# 四元数同士の掛算。
(ai+bj+ck)(di+ej+fk)
=ai(di+ej+fk)+bj(di+ej+fk)+cj(di+ej+fk)
=adi^2+aeij+afik+bdji+bej^2+bfjk+cdki+cekj+cfk^2
# ところで四元数では以下が成立する
adi^2=-ad #i^2=-1
aeij=aek #ij=k
afik=-afj #ik=-j
bdji=-bdk #ji=-k
bej^2=-be #j^2=-1
bfjk=bfi #jk=i
cdki=cdj #ki=j
cekj=-cei #kj=-i
cfk^2=-cf #k^2=-1
=−1*(ad+be+cf)+(bf−ce)i+(cd−af)j+(ae−bd)k
# このうち(ad+be+cf)の部分がスカラー積=内積。
# このうち(bf−ce)i+(cd−af)j+(ae−bd)kの部分がベクトル積=外積。
内積がマイナスになっている点については、四元数が先にあって内積の概念が確立されたため、初期の内積は四元数と同じ符号で扱われていたそうです。符号にマイナスが付かないように修正したクリフォード代数というものがあります。
そう、先に内積(Inner Product)や外積(Outer Product)の概念が実存し、それに立脚して四元数の概念が樹立された訳ではなく、真逆に四元数におけるこのスカラー積(Scalar Product)やベクトル積(Vector Product)の概念から(あえて虚数や複素数の特徴に立ち入らず扱いやすい部分だけを抽出した)内積や外積の定義が生み出され普及したのです。ここは絶対に履き違えてはいけません。
現時点における球面幾何学(Spherical Geometry)での立場からの解釈
それにつけてもピタゴラスの定理、座標系ごとに全く異なる振る舞いを見せるのですね。
- 極座標系…座標単位となるベクトル積は「中心からの距離1」と角度の概念のみで構成される単位円弧/単位球面。これに半径r=スカラー積が対応する(まさしく原点1点のみでしか固定されていないのでスカラー積に比例する同心円集合を構成する数直線の世界)。
- 直交座標系…座標単位となるベクトル積は「(x軸、Y軸、Z軸などに沿って伸ばされる)1辺の長さ1」が固定される一方、対角線が2次元では平方対角線(Square diagonal)sqrt(2),3次元では立方対角線(Cube Diagonal)sqrt(3)と変化していく単位方眼(Square Grid)/単位立方眼(Cube Grid)。X軸やY軸やZ軸ごとにそれぞれにスカラー積が設定可能(統計計算や人工知能最適化の分野における主要調整対象)。
そして今回の球面幾何学シリーズで主に扱う対蹠座標系(Antipordal Coordinate System)。座標単位となるベクトル積は原蹠と対蹠の座標が固定された単位球面。以下の「球表面上の任意の点を結んで何回曲がって原蹠から対蹠(あるいは対蹠から原蹠)に到達する可能性がある経路全ての集合」であり、条件を満たした部分だけその形で顕現すると考えます。要するに原蹠と対蹠を結ぶ直径、およびそれが浮かび上がらせる単位球面上の任意の頂点のみが「実」。むしろそれを結ぶ辺や面こそが「虚」という極めて量子力学的な系なのです。
①「原蹠から出発して対蹠に到達しない」あるいは「対蹠から出発して原蹠に到達しない」1頂点操作…まさしく円周角(Circumference Angle)の振る舞い。円弧そのもの(Circle itself)の特徴に従って「角度0度(0ラジアン)あるいは角度180度(πラジアン)の場合の無限小(1/Inf)」を最小値、「角度90度(π/2ラジアン)の場合の直径2」を最大値とする。パスカルの三角形1段目「1」に対応。断面0枚。
【Rで球面幾何学】単位円と単位球②円周角(Circumference Angle)とは何か?

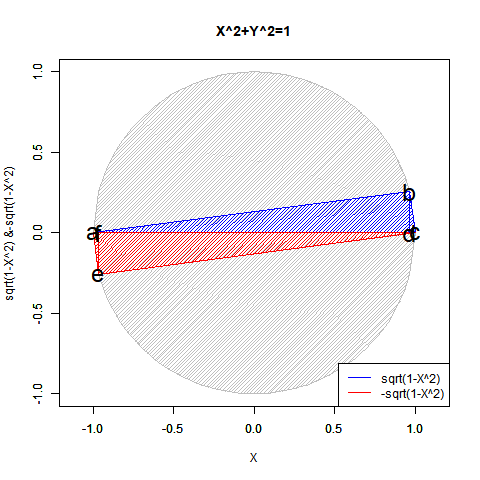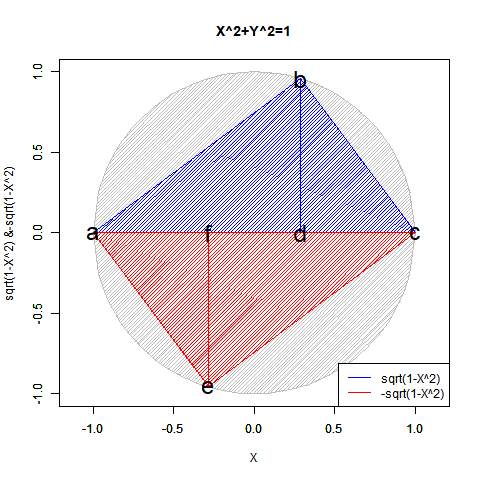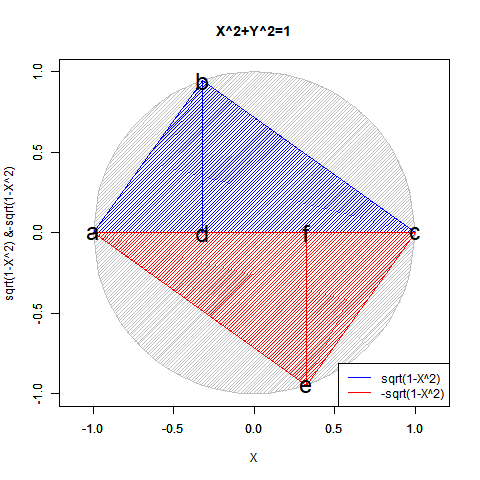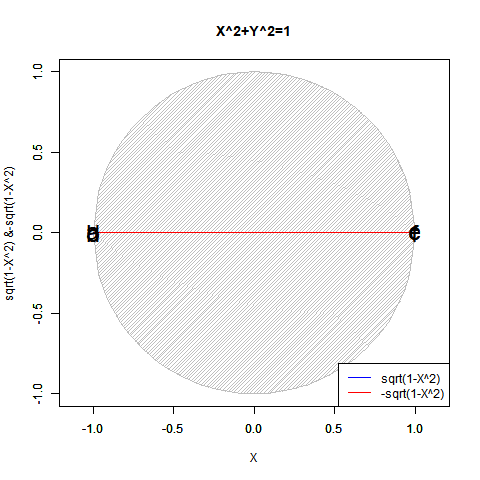
②「原蹠と対蹠の間を往復する」2頂点操作…関数1^x=i^2xの振る舞いそのもので、その値は0を中心に-1と1すなわち単位円上におけるCos(θ)の計算結果となる。既にこの段階で(頂点数が一つ上の)③の操作可能性が内包されていると考えるとCos(θ)+Sin(θ)iの公式が成立。稼働範囲の目安は片道2(一巡4で、その過程で4回円を描く)。パスカルの三角形2段目「1,1」に対応。断面0/1枚。
【Rで球面幾何学】オイラーの多面体定理(Euler's Polyhedron Theorem)と平面充填(Tiling)の連続性について。

③「原蹠から対蹠、あるいは対蹠から原蹠を1回直角に曲がって結ぶ(3回直角に曲がると現点に戻る)」3頂点操作…タレスの定理に従って直径を斜辺とする直角三角形を描く。四元数におけるi^2=-1,j^2=-1,k^2=-1はそれぞれ残りの要素の一つが同値で最後の要素が0の特殊状態と考える。稼働範囲の目安は片道sqrt(2)*2(一巡4sqrt(2))。パスカルの三角形3段目「1,2,1」に対応。断面1枚。
【初心者向け】三角関数と指数・対数関数の「巡回性」について。


またこの可能性が文字通り四方八方で同時顕現したのが正八面体といえそうなのである。
【Rで球面幾何学】正四面体と正六面体と正八面体の連続性と「テトラパックの思わぬ正体」について。
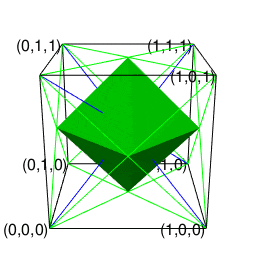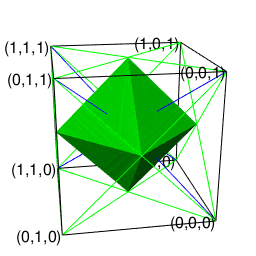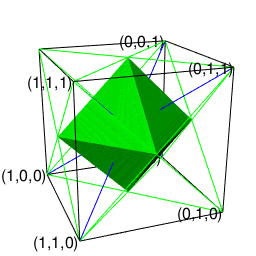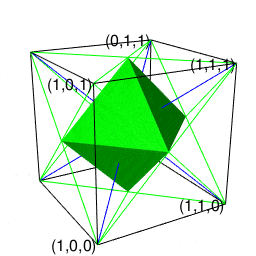
それは「ただの三角形」が「奇数系図形」四面体一対の状態を経て「ただの六角形」に至る三角形的展開の一環として現れる。
【Rで球面幾何学】正四面体(Tetrahedron)と正六面体(Cube)と正八面体(Octahedron)と正二十面体(Icosahedron)の狭間。そして正十二面体(Dodecahedron)との関係について。
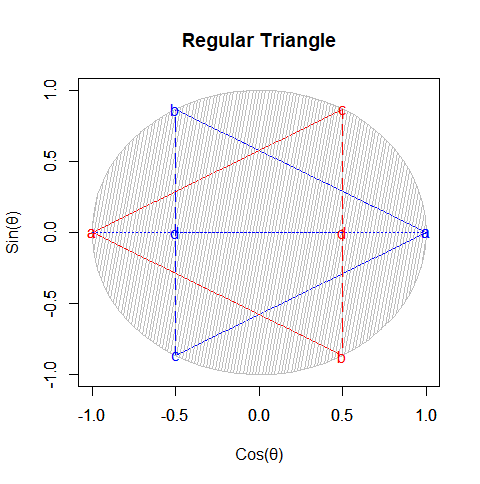

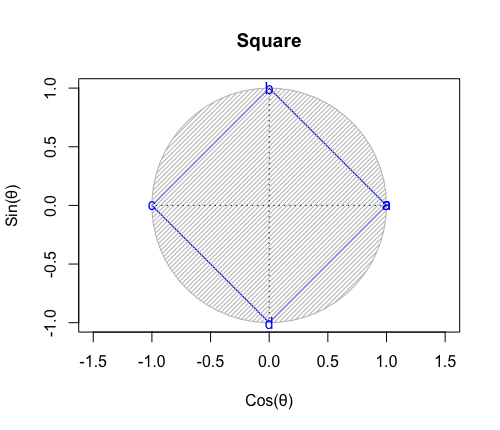
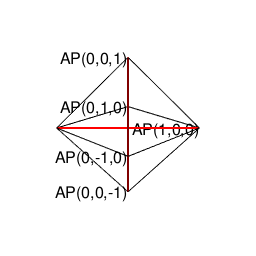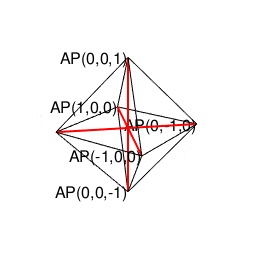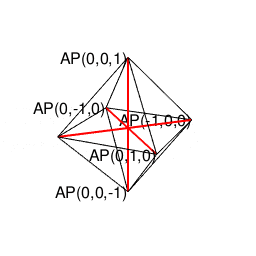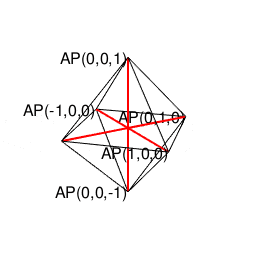
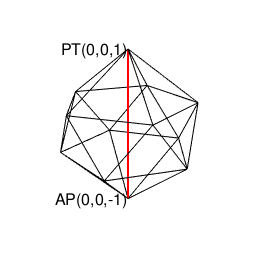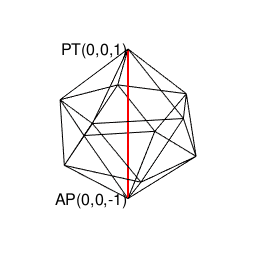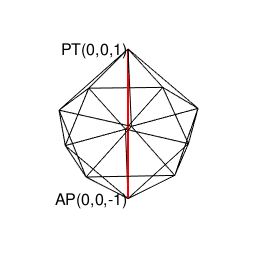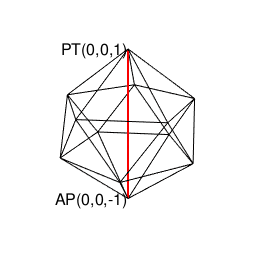
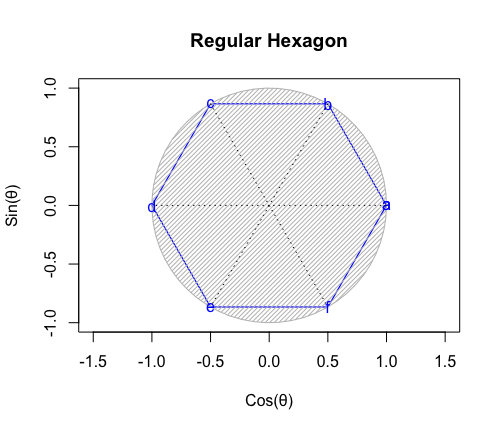
④「原蹠から対蹠、あるいは対蹠から原蹠を2回直角に曲がって結ぶ(5回直角に曲がると現点に戻る)」4頂点操作…まさしく正六面体/立方体の表面経路そのもの。四元数ijk=-1にij=k,jk=i,ki=jの系統と真逆のji=-k,kj=-i,ik=-jの系統の計算式が併存するのは、ここで見られる「(「右手の法則」「左手の法則」)的な意味合いで)左右に1回ずつ曲がらないと目標地点に到達出来ない構造」と密接な関係にあると推察される。稼働範囲の目安は片道2/sqrt(3)*3(一巡12/sqrt(3))。パスカルの三角形4段目「1,3,3,1」に対応。断面2枚。
【Rで球面幾何学】正方形における平方対角線(Square diagonal)と立方体における立方対角線(Cubic diagonal)の関係について。
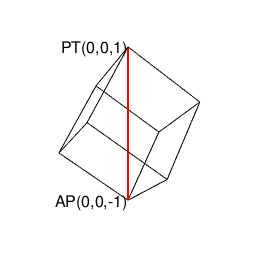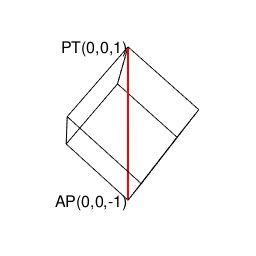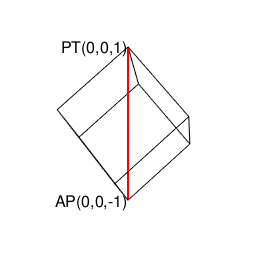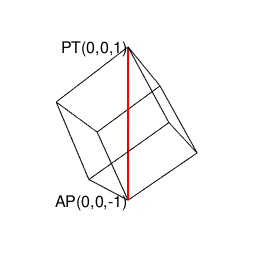
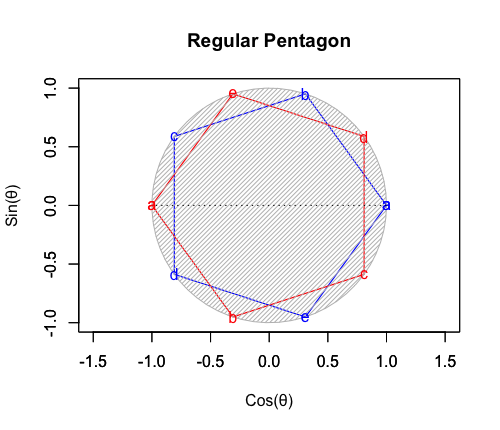
⑤「原蹠から対蹠、あるいは対蹠から原蹠を3回曲がって結ぶ(7回曲がると現点に戻る)5頂点操作」…ある意味、その特徴が正十二面体に部分的に顕現しているとも見て取れる。だとすれば、そこに見て取れる「(「右手の法則」「左手の法則」的な意味合いで)左右に2回ずつ曲がらないと(最短距離で)目標地点に到達出来ない構造」を継承してる可能性が高まるが、如何せん既に曲がる角度が直角でなく、断面も正多角形でなく、「迂回路」が存在するなど色々と顕現上の限界を呈している。またそもそも六元数(スカラー積+ベクトル積5次元)は安定した数理を構築しない事で知られる。断面3枚。
【Rで球面幾何学】正12面体(Regular Dodecahedron)の作図について。
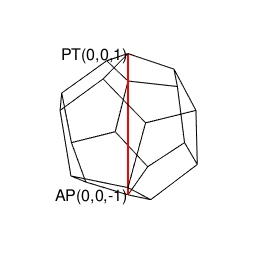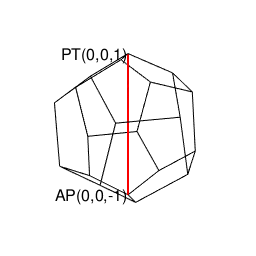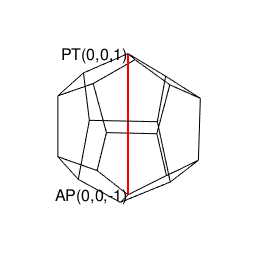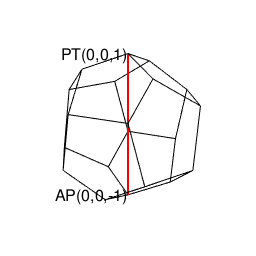
⑥「原蹠から対蹠、あるいは対蹠から原蹠を4回曲がって結ぶ(9回曲がると現点に戻る)6頂点操作」…ここまでの推察結果を統合すると(「右手の法則」「左手の法則」的意味合いで)原蹠から対蹠、あるいは対蹠から原蹠を左右2回ずつ曲がって目標地点に到達する構造」を八元数(スカラー積+ベクトル積7次元)も継承している可能性が高まるが、如何せんオイラーの多面体定理(Euler's Polyhedron Theorem)を満たして顕現可能な限界を超越しており三次元空間上にそのイメージを思い描く事自体が不可能。断面4枚。

七次元の外積 [物理のかぎしっぽ]
全体像がこうだと考えれば「各操作系によって(「右手の法則」「左手の法則」的意味合いで)左右に曲がる数が定まっている」事と「1次元ベクトル積の連続操作の最後の回は常にベクトル積の演算結果が0になる=目標地点に到達したと目される」事が矛盾なく連続的に扱える様になるんですよね。すると既存の「内積」や「外積」の概念との関係は一体どうなってしまうの?
ベクトルの内積(スカラー積)と外積(ベクトル積)の成分表示
こうして疑問が山積みになった辺りで以下続報…