【オイラーの多面体定理と正多面体】正四面体(Tetrahedron)と正六面体(Cube)と正八面体(Octahedron)と正二十面体(Icosahedron)の狭間。そして正十二面体（Dodecahedron）との関係について。

【Rで球面幾何学】そもそも「内積(Inner Product)」とは「外積(Outer Product)」とは何か？

今回の球面幾何学シリーズ(Spherical Geometry Series)で主に扱う対蹠座標系(Antipordal Coordinate System)は座標単位となるベクトル積は原蹠と対蹠の座標が固定された単位球面。要するに原蹠と対蹠を結ぶ直径、およびそれが浮かび上がらせる単位球面上の任意の頂点のみが「実」。むしろそれを結ぶ辺や面こそが「虚」という極めて量子力学的な系なのです。

さて、どういう事なんでしょう？　ここでは三角形を巡る位相転換過程(Phase Shift Process)の追跡を通じてその謎に迫ってみたいと思います。

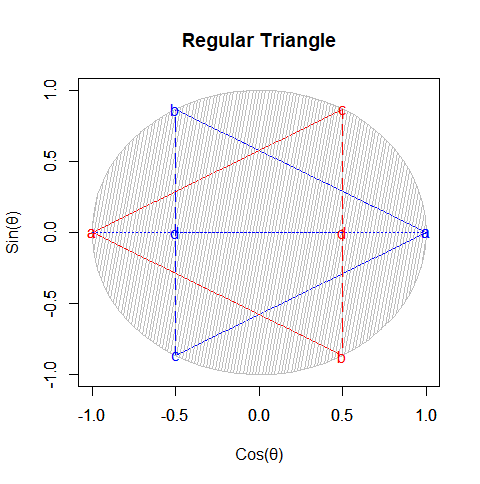
#出発点としてのただの正三角形(Equilateral Triangle)
正三角形は「面を起点に単一図形で平面充填(Tiring)可能な」正平面充填形(Equilateral Triangle) の一つなので、これは立派な「安定型」の一つといえましょう（そして平面図形的展開においては、起点としての原蹠か対蹠のみが重要で反対側の頂点との関係性は問われない）。

library(rgl)
#分割数Nod(Number of divide)=3
NoD<-3
#円周分割数列(Sequence of Divided Circumference)
SoDC<-seq(0,2*pi,length=NoD+1)

#原蹠(PorTal)
portal_i<-0
portal_j<-0
portal_k<-1
portal_text=paste0("PT(",portal_i,",",portal_j,",",portal_k,")")

#原蹠表示
texts3d(portal_i,portal_j,portal_k,texts=portal_text,col=rgb(0,0,0),adj=1.0)

#対蹠(AntiPordal)
antipordal_i<-0
antipordal_j<-0
antipordal_k<--1
antipordal_text=paste0("AP(",antipordal_i,",",antipordal_j,",",antipordal_k,")" main="Cross section for ")

#対蹠表示
texts3d(antipordal_i,antipordal_j,antipordal_k,texts=antipordal_text,col=rgb(0,0,0),adj=1.0)

#立方対角線(Cubic Diagonal)
lines3d(c(portal_i,antipordal_i),c(portal_j,antipordal_j),c(portal_k,antipordal_k),col=rgb(1,0,0),lwd=2)

#正三角形描画
mx<-cos(SoDC)*sin(pi/3)
my<-sin(SoDC)*sin(pi/3)

lines3d(c(mx[1],mx[2]),c(my[1],my[2]),c(0,0),col=rgb(0,0,0),lwd=1)
lines3d(c(mx[2],mx[3]),c(my[2],my[3]),c(0,0),col=rgb(0,0,0),lwd=1)
lines3d(c(mx[3],mx[1]),c(my[3],my[1]),c(0,0),col=rgb(0,0,0),lwd=1)

#アニメーション
movie3d(spin3d(axis=c(0,0,1),rpm=5),duration=10,fps=25,movie="~/Desktop/Tetrahedron15")

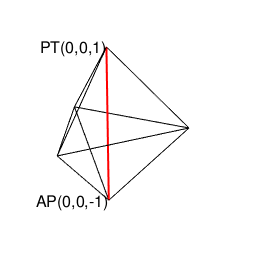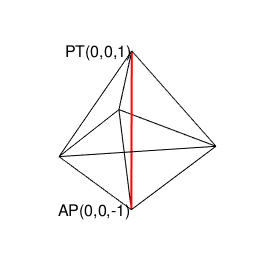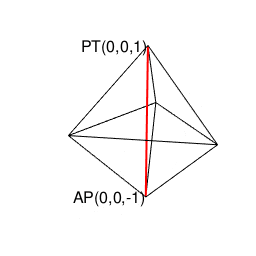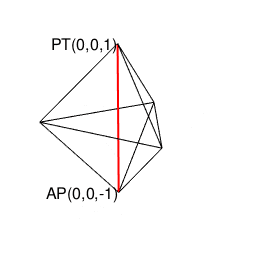
①ここで現れる正三角形(Equilateral Triangle)は奇数形図形なのでそれぞれ原蹠から出発し対蹠に届いてない状態の一対として顕現。
【Rで球面幾何学】正四面体と正六面体と正八面体の連続性と「テトラパックの思わぬ正体」について。

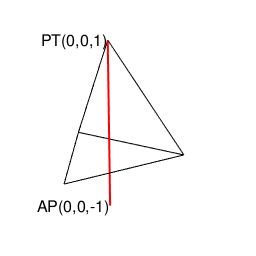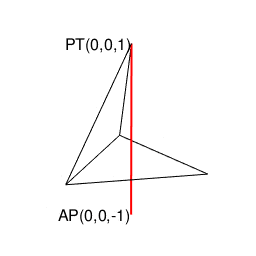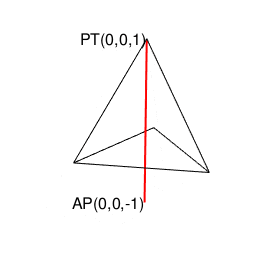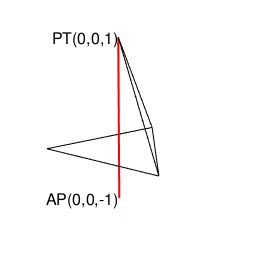
#正四面体(Regular Tetrahedron)の導入(Introduction)
この座標系においては頂点のみが「(球表面上に存在する)実(Reality)」であり、辺も面も「(球表面外に仮想として存在するだけの)虚(Imaginary)」に過ぎないので、正三角形のみが顕現している状態に頂点が一つ追加されるとたちまち四面体が顕現します(要するに三角形が二枚とか三枚の状態が実質上存在しない)。中でも最も安定してるのが(全ての辺と面が同型の)正四面体が安定型なのでその代表格と目される次第。

library(rgl)
#分割数Nod(Number of divide)=3
NoD<-3
#円周分割数列(Sequence of Divided Circumference)
SoDC<-seq(0,2*pi,length=NoD+1)

#原蹠(PorTal)
portal_i<-0
portal_j<-0
portal_k<-1
portal_text=paste0("PT(",portal_i,",",portal_j,",",portal_k,")")

#原蹠表示
texts3d(portal_i,portal_j,portal_k,texts=portal_text,col=rgb(0,0,0),adj=1.0)

#対蹠(AntiPordal)
antipordal_i<-0
antipordal_j<-0
antipordal_k<--1
antipordal_text=paste0("AP(",antipordal_i,",",antipordal_j,",",antipordal_k,")" main="Cross section for ")

#対蹠表示
texts3d(antipordal_i,antipordal_j,antipordal_k,texts=antipordal_text,col=rgb(0,0,0),adj=1.0)

#立方対角線(Cubic Diagonal)
lines3d(c(portal_i,antipordal_i),c(portal_j,antipordal_j),c(portal_k,antipordal_k),col=rgb(1,0,0),lwd=2)

#正四面体描画
mx<-cos(SoDC)*sin(pi/3)
my<-sin(SoDC)*sin(pi/3)

lines3d(c(portal_i,mx[1]),c(portal_j,my[1]),c(portal_k,-1/3),col=rgb(0,0,0),lwd=1)
lines3d(c(portal_i,mx[2]),c(portal_j,my[2]),c(portal_k,-1/3),col=rgb(0,0,0),lwd=1)
lines3d(c(portal_i,mx[3]),c(portal_j,my[3]),c(portal_k,-1/3),col=rgb(0,0,0),lwd=1)

lines3d(c(mx[1],mx[2]),c(my[1],my[2]),c(-1/3,-1/3),col=rgb(0,0,0),lwd=1)
lines3d(c(mx[2],mx[3]),c(my[2],my[3]),c(-1/3,-1/3),col=rgb(0,0,0),lwd=1)
lines3d(c(mx[3],mx[1]),c(my[3],my[1]),c(-1/3,-1/3),col=rgb(0,0,0),lwd=1)

#アニメーション
movie3d(spin3d(axis=c(0,0,1),rpm=5),duration=10,fps=25,movie="~/Desktop/Tetrahedron05")

②全体像を俯瞰すると「(外接円上に全ての頂点が存在する)正三角形(Equilateral triangles)２枚の間の補完操作(Completion Operation)によって生じる」という考え方も出来る(とりあえず不可逆的過程と考える)。

library(rgl)
#分割数Nod(Number of divide)=3
NoD<-3
#円周分割数列(Sequence of Divided Circumference)
SoDC<-seq(0,2*pi,length=NoD+1)

#原蹠(PorTal)
portal_i<-0
portal_j<-0
portal_k<-1
portal_text=paste0("PT(",portal_i,",",portal_j,",",portal_k,")")

#原蹠表示
texts3d(portal_i,portal_j,portal_k,texts=portal_text,col=rgb(0,0,0),adj=1.0)

#対蹠(AntiPordal)
antipordal_i<-0
antipordal_j<-0
antipordal_k<--1
antipordal_text=paste0("AP(",antipordal_i,",",antipordal_j,",",antipordal_k,")" main="Cross section for ")

#対蹠表示
texts3d(antipordal_i,antipordal_j,antipordal_k,texts=antipordal_text,col=rgb(0,0,0),adj=1.0)

#立方対角線(Cubic Diagonal)
lines3d(c(portal_i,antipordal_i),c(portal_j,antipordal_j),c(portal_k,antipordal_k),col=rgb(1,0,0),lwd=2)

#正三角形描画
mx<-cos(SoDC)*sin(pi/3)
my<-sin(SoDC)*sin(pi/3)

#正四面体描画
mx<-cos(SoDC)*sin(pi/3)
my<-sin(SoDC)*sin(pi/3)

lines3d(c(portal_i,mx[1]),c(portal_j,my[1]),c(portal_k,-1/3),col=rgb(0,0,0),lwd=1)
lines3d(c(portal_i,mx[2]),c(portal_j,my[2]),c(portal_k,-1/3),col=rgb(0,0,0),lwd=1)
#lines3d(c(portal_i,mx[3]),c(portal_j,my[3]),c(portal_k,-1/3),col=rgb(0,0,0),lwd=1)

lines3d(c(mx[1],mx[2]),c(my[1],my[2]),c(-1/3,-1/3),col=rgb(0,0,0),lwd=1)
lines3d(c(mx[2],mx[3]),c(my[2],my[3]),c(-1/3,-1/3),col=rgb(0,0,0),lwd=1)
lines3d(c(mx[3],mx[1]),c(my[3],my[1]),c(-1/3,-1/3),col=rgb(0,0,0),lwd=1)

#アニメーション
movie3d(spin3d(axis=c(0,0,1),rpm=5),duration=10,fps=25,movie="~/Desktop/Pretetrahedron01")

③正四面体は（特定の辺数が伸びる）頂点と（同数の辺数を備える）面を交換する双対変換(Dual Transformation)操作の結果が同じ正四面体となる自己双対(Self Dual)図形でもあり、これにより原蹠を起点とする正四面体と対蹠を起点とする正四面体の峻別がさらに困難となる。

library(rgl)
#分割数Nod(Number of divide)=3
NoD<-3
#円周分割数列(Sequence of Divided Circumference)
SoDC<-seq(0,2*pi,length=NoD+1)

#原蹠(PorTal)
portal_i<-0
portal_j<-0
portal_k<-1
portal_text=paste0("PT(",portal_i,",",portal_j,",",portal_k,")")

#原蹠表示
texts3d(portal_i,portal_j,portal_k,texts=portal_text,col=rgb(0,0,0),adj=1.0)

#対蹠(AntiPordal)
antipordal_i<-0
antipordal_j<-0
antipordal_k<--1
antipordal_text=paste0("AP(",antipordal_i,",",antipordal_j,",",antipordal_k,")" main="Cross section for ")

#対蹠表示
texts3d(antipordal_i,antipordal_j,antipordal_k,texts=antipordal_text,col=rgb(0,0,0),adj=1.0)

#立方対角線(Cubic Diagonal)
lines3d(c(portal_i,antipordal_i),c(portal_j,antipordal_j),c(portal_k,antipordal_k),col=rgb(1,0,0),lwd=2)

#正四面体描画
mx<-cos(SoDC)*sin(pi/3)
my<-sin(SoDC)*sin(pi/3)

lines3d(c(antipordal_i,mx[1]),c(antipordal_j,my[1]),c(antipordal_k,1/3),col=rgb(0,0,0),lwd=1)
lines3d(c(antipordal_i,mx[2]),c(antipordal_j,my[2]),c(antipordal_k,1/3),col=rgb(0,0,0),lwd=1)
lines3d(c(antipordal_i,mx[3]),c(antipordal_j,my[3]),c(antipordal_k,1/3),col=rgb(0,0,0),lwd=1)

lines3d(c(mx[1],mx[2]),c(my[1],my[2]),c(1/3,1/3),col=rgb(0,0,0),lwd=1)
lines3d(c(mx[2],mx[3]),c(my[2],my[3]),c(1/3,1/3),col=rgb(0,0,0),lwd=1)
lines3d(c(mx[3],mx[1]),c(my[3],my[1]),c(1/3,1/3),col=rgb(0,0,0),lwd=1)

#アニメーション
movie3d(spin3d(axis=c(0,0,1),rpm=5),duration=10,fps=25,movie="~/Desktop/Tetrahedron06")

④正多面体唯一の奇数系として「(原蹠と対蹠を直接結ばない図形が)二つ対で観測される」のが当然視される状況下にある。単位円上の共益複素数が２つセットで観測される事などとも密接に関係してくる展開。
【Rで球面幾何学】正四面体と正六面体と正八面体の連続性と「テトラパックの思わぬ正体」について。

⑤そして、かかる状況下において突如として三次元存在条件を満たした（断面を一つでなく二つ備えた)立方体が顕現してくる訳である。
【Rで球面幾何学】正方形における平方対角線(Square diagonal)と立方体における立方対角線(Cubic diagonal)の関係について。

⑥さらには断面を三つ備えた正十二面体も正四面体を第一層とする形で構成される。
【Rで球面幾何学】正六面体と正十二面体の間の往復(「屋根掛け法」とは何か？)

⑦こうした「2個か1個か」問題は、さらに「(正方形とその縦方向と横方向の180度回転しか存在しない)クラインの四元群(Klein's Quaternion Qroup)」問題まで巻き込む展開を迎える。
【Rで球面幾何学】平方眼と立方眼の小宇宙(Square & Cube Grid Set)について。

例えばこの数理体系においてはp^2=q^2=r^2=eとされるが、さてその時到達するeは出発点たる原蹠なのだろうか？　それとも対蹠なのだろうか？
クラインの四元群

	e	p	q	r
e	e	p	q	r
p	p	e	r	q
q	q	r	e	p
r	r	q	p	e

• 操作"e"…何もしない(何もしなかったのと同様の結果)。
• 操作"p"…X軸に沿って180度裏返す(その操作が行われたのと同様の結果)。
• 操作"q"…Y軸に沿って180度裏返す(その操作が行われたのと同様の結果)。
• 操作"r"…Z軸に沿って180度裏返す(その操作が行われたのと同様の結果)。

library(rgl)
#分割数Nod(Number of divide)=3
NoD<-3
#円周分割数列(Sequence of Divided Circumference)
SoDC<-seq(0,2*pi,length=NoD+1)

#原蹠(PorTal)
portal_i<-0
portal_j<-0
portal_k<-1
portal_text=paste0("PT(",portal_i,",",portal_j,",",portal_k,")")

#原蹠表示
texts3d(portal_i,portal_j,portal_k,texts=portal_text,col=rgb(0,0,0),adj=1.0)

#対蹠(AntiPordal)
antipordal_i<-0
antipordal_j<-0
antipordal_k<--1
antipordal_text=paste0("AP(",antipordal_i,",",antipordal_j,",",antipordal_k,")" main="Cross section for ")

#対蹠表示
texts3d(antipordal_i,antipordal_j,antipordal_k,texts=antipordal_text,col=rgb(0,0,0),adj=1.0)

#立方対角線(Cubic Diagonal)
lines3d(c(portal_i,antipordal_i),c(portal_j,antipordal_j),c(portal_k,antipordal_k),col=rgb(1,0,0),lwd=2)

#正四面体描画
mx<-cos(SoDC)
my<-sin(SoDC)

lines3d(c(portal_i,mx[1]),c(portal_j,my[1]),c(portal_k,0),col=rgb(0,0,0),lwd=1)
lines3d(c(portal_i,mx[2]),c(portal_j,my[2]),c(portal_k,0),col=rgb(0,0,0),lwd=1)
lines3d(c(portal_i,mx[3]),c(portal_j,my[3]),c(portal_k,0),col=rgb(0,0,0),lwd=1)

lines3d(c(mx[1],mx[2]),c(my[1],my[2]),c(0,0),col=rgb(0,0,0),lwd=1)
lines3d(c(mx[2],mx[3]),c(my[2],my[3]),c(0,0),col=rgb(0,0,0),lwd=1)
lines3d(c(mx[3],mx[1]),c(my[3],my[1]),c(0,0),col=rgb(0,0,0),lwd=1)

lines3d(c(mx[1],antipordal_i),c(my[1],antipordal_j),c(0,antipordal_k),col=rgb(0,0,0),lwd=1)
lines3d(c(mx[2],antipordal_i),c(my[2],antipordal_j),c(0,antipordal_k),col=rgb(0,0,0),lwd=1)
lines3d(c(mx[3],antipordal_i),c(my[3],antipordal_j),c(0,antipordal_k),col=rgb(0,0,0),lwd=1)

#アニメーション
movie3d(spin3d(axis=c(0,0,1),rpm=5),duration=10,fps=25,movie="~/Desktop/Tetrahedron07")

#正八面体(Regular Octahedron)の導入(Introduction)
断面上にあと１個頂点を追加すると原蹠から対蹠に直角に１回曲がって到達する経路を三方向から備えた偶数系の図形が顕現します。

library(rgl)
#分割数Nod(Number of divide)=4
NoD<-4
#円周分割数列(Sequence of Divided Circumference)
SoDC<-seq(0,2*pi,length=NoD+1)

#原蹠(PorTal)
portal_i<-0
portal_j<-0
portal_k<-1
portal_text=paste0("AP(",portal_i,",",portal_j,",",portal_k,")")

#原蹠表示
texts3d(portal_i,portal_j,portal_k,texts=portal_text,col=rgb(0,0,0),adj=1.0)

#対蹠(AntiPordal)
antipordal_i<-0
antipordal_j<-0
antipordal_k<--1
antipordal_text=paste0("AP(",antipordal_i,",",antipordal_j,",",antipordal_k,")")

#対蹠表示
texts3d(antipordal_i,antipordal_j,antipordal_k,texts=antipordal_text,col=rgb(0,0,0),adj=1.0)

#立方対角線(Cubic Diagonal)
lines3d(c(portal_i,antipordal_i),c(portal_j,antipordal_j),c(portal_k,antipordal_k),col=rgb(1,0,0),lwd=2)

#正八面体描画
mx<-cos(SoDC)
my<-sin(SoDC)

lines3d(c(portal_i,mx[1]),c(portal_j,my[1]),c(portal_k,0),col=rgb(0,0,0),lwd=1)
lines3d(c(portal_i,mx[2]),c(portal_j,my[2]),c(portal_k,0),col=rgb(0,0,0),lwd=1)
lines3d(c(portal_i,mx[3]),c(portal_j,my[3]),c(portal_k,0),col=rgb(0,0,0),lwd=1)
lines3d(c(portal_i,mx[4]),c(portal_j,my[4]),c(portal_k,0),col=rgb(0,0,0),lwd=1)

lines3d(c(mx[1],mx[2]),c(my[1],my[2]),c(0,0),col=rgb(0,0,0),lwd=1)
lines3d(c(mx[2],mx[3]),c(my[2],my[3]),c(0,0),col=rgb(0,0,0),lwd=1)
lines3d(c(mx[3],mx[4]),c(my[3],my[4]),c(0,0),col=rgb(0,0,0),lwd=1)
lines3d(c(mx[4],mx[1]),c(my[4],my[1]),c(0,0),col=rgb(0,0,0),lwd=1)

lines3d(c(mx[1],antipordal_i),c(my[1],antipordal_j),c(0,antipordal_k),col=rgb(0,0,0),lwd=1)
lines3d(c(mx[2],antipordal_i),c(my[2],antipordal_j),c(0,antipordal_k),col=rgb(0,0,0),lwd=1)
lines3d(c(mx[3],antipordal_i),c(my[3],antipordal_j),c(0,antipordal_k),col=rgb(0,0,0),lwd=1)
lines3d(c(mx[4],antipordal_i),c(my[4],antipordal_j),c(0,antipordal_k),col=rgb(0,0,0),lwd=1)

#追加立方対角線(Cubic Diagonal)

ap11_text=paste0("AP(",round(mx[1]),",",round(my[1]),",","0",")")
texts3d(mx[1],my[1],0,texts=ap11_text,col=rgb(0,0,0),adj=1.0)
ap12_text=paste0("AP(",round(mx[3]),",",round(my[3]),",","0",")")
texts3d(mx[3],my[3],0,texts=ap12_text,col=rgb(0,0,0),adj=1.0)
lines3d(c(mx[1],mx[3]),c(my[1],my[3]),c(0,0),col=rgb(1,0,0),lwd=2)

ap21_text=paste0("AP(",round(mx[2]),",",round(my[2]),",","0",")")
texts3d(mx[2],my[2],0,texts=ap21_text,col=rgb(0,0,0),adj=1.0)
ap22_text=paste0("AP(",round(mx[4]),",",round(my[4]),",","0",")")
texts3d(mx[4],my[4],0,texts=ap22_text,col=rgb(0,0,0),adj=1.0)
lines3d(c(mx[2],mx[4]),c(my[2],my[4]),c(0,0),col=rgb(1,0,0),lwd=2)

#アニメーション
movie3d(spin3d(axis=c(0,0,1),rpm=5),duration=10,fps=25,movie="~/Desktop/Octahedron02")

①ここで現れる正方形(Square)は偶数形図形なので単独で顕現。それ自体が対蹠間を結ぶ線を２本備えている。

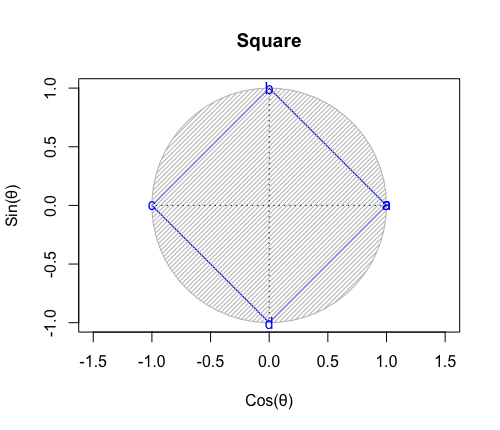
#分割数Nod(Number of divide)=4

NoD<-4
#円周分割数列(Sequence of Divided Circumference)
SoDC<-seq(0,2*pi,length=NoD+1)
#円周上の四角形の頂点を集める。
cx_nomal=cos(SoDC)
cy_nomal=sin(SoDC)

#グラフ描画
plot(cx_nomal,cy_nomal,asp=1,col=rgb(0,0,1),type="l",xlim=c(-1,1),ylim=c(-1,1),main="Square",xlab="Cos(θ)",ylab="Sin(θ)",lwd=1.2)

#背景円の塗り潰し
Circumference<-seq(0,2*pi,length=60)
cx_circle=cos(Circumference)
cy_circle=sin(Circumference)
polygon(cx_circle, #x
cy_circle, #y
density=c(30), #塗りつぶす濃度
angle=c(45),　 　　　#塗りつぶす斜線の角度
col=c(200,200,200)) 　#塗りつぶす色

#文字追加
text(cx_nomal,cy_nomal, labels=c("a","b","c","d"),col=rgb(0,0,1))

#補助線
segments(1,0,-1,0,lty=3,col=rgb(0,0,0))
segments(0,1,0,-1,lty=3,col=rgb(0,0,0))

②正八面体は正四面体の補完を受けて空間充填する(両者の間にはこれ以外にももっと様々な関係が潜在していそうである)。また正八面体は立方体と双対の関係にあるがこの操作の結果現れる立方体は(正四面体２つが直接融合して生まれる「四元数的」立方体と異なり)全ての辺がX軸、Y軸、Z軸に沿うか平方対角線を成す形で顕現する。
【Rで球面幾何学】正四面体と正六面体と正八面体の連続性と「テトラパックの思わぬ正体」について。

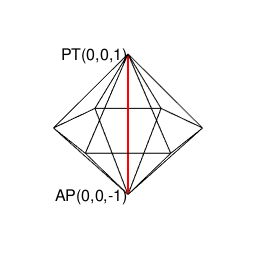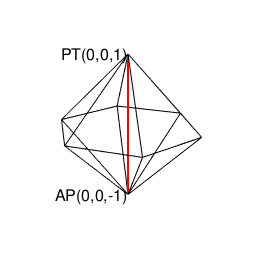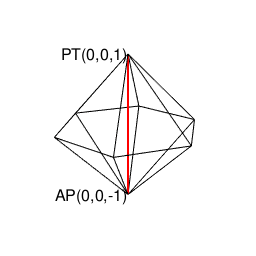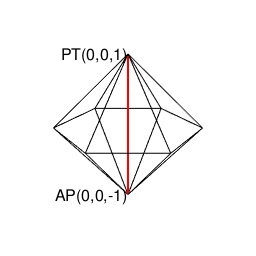
#正二十面体(Regular Icosahedron)の頭蹠(Portal)
(既に頭蹠と対蹠を結ぶ線が1本通っているので)断面上にあと１個頂点を追加しても図形全体が奇数系に戻る事はありません。

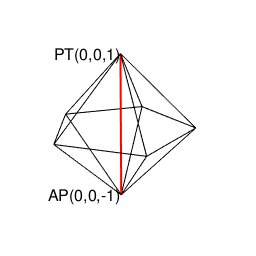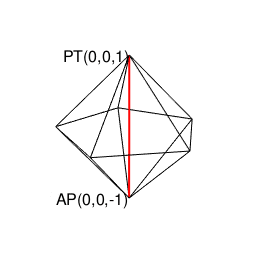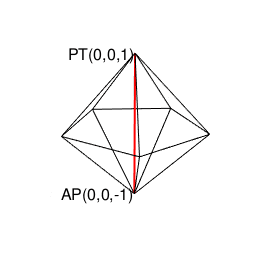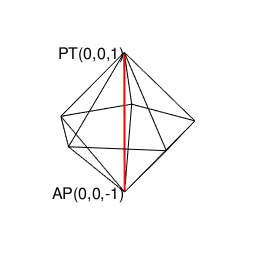
library(rgl)
#分割数Nod(Number of divide)=5
NoD<-5
#円周分割数列(Sequence of Divided Circumference)
SoDC<-seq(0,2*pi,length=NoD+1)

#原蹠(PorTal)
portal_i<-0
portal_j<-0
portal_k<-1
portal_text=paste0("PT(",portal_i,",",portal_j,",",portal_k,")")

#原蹠表示
texts3d(portal_i,portal_j,portal_k,texts=portal_text,col=rgb(0,0,0),adj=1.0)

#対蹠(AntiPordal)
antipordal_i<-0
antipordal_j<-0
antipordal_k<--1
antipordal_text=paste0("AP(",antipordal_i,",",antipordal_j,",",antipordal_k,")" main="Cross section for ")

#対蹠表示
texts3d(antipordal_i,antipordal_j,antipordal_k,texts=antipordal_text,col=rgb(0,0,0),adj=1.0)

#立方対角線(Cubic Diagonal)
lines3d(c(portal_i,antipordal_i),c(portal_j,antipordal_j),c(portal_k,antipordal_k),col=rgb(1,0,0),lwd=2)

#正四面体描画
mx<-cos(SoDC)
my<-sin(SoDC)

lines3d(c(portal_i,mx[1]),c(portal_j,my[1]),c(portal_k,0),col=rgb(0,0,0),lwd=1)
lines3d(c(portal_i,mx[2]),c(portal_j,my[2]),c(portal_k,0),col=rgb(0,0,0),lwd=1)
lines3d(c(portal_i,mx[3]),c(portal_j,my[3]),c(portal_k,0),col=rgb(0,0,0),lwd=1)
lines3d(c(portal_i,mx[4]),c(portal_j,my[4]),c(portal_k,0),col=rgb(0,0,0),lwd=1)
lines3d(c(portal_i,mx[5]),c(portal_j,my[5]),c(portal_k,0),col=rgb(0,0,0),lwd=1)

lines3d(c(mx[1],mx[2]),c(my[1],my[2]),c(0,0),col=rgb(0,0,0),lwd=1)
lines3d(c(mx[2],mx[3]),c(my[2],my[3]),c(0,0),col=rgb(0,0,0),lwd=1)
lines3d(c(mx[3],mx[4]),c(my[3],my[4]),c(0,0),col=rgb(0,0,0),lwd=1)
lines3d(c(mx[4],mx[5]),c(my[4],my[5]),c(0,0),col=rgb(0,0,0),lwd=1)
lines3d(c(mx[5],mx[1]),c(my[5],my[1]),c(0,0),col=rgb(0,0,0),lwd=1)

lines3d(c(mx[1],antipordal_i),c(my[1],antipordal_j),c(0,antipordal_k),col=rgb(0,0,0),lwd=1)
lines3d(c(mx[2],antipordal_i),c(my[2],antipordal_j),c(0,antipordal_k),col=rgb(0,0,0),lwd=1)
lines3d(c(mx[3],antipordal_i),c(my[3],antipordal_j),c(0,antipordal_k),col=rgb(0,0,0),lwd=1)
lines3d(c(mx[4],antipordal_i),c(my[4],antipordal_j),c(0,antipordal_k),col=rgb(0,0,0),lwd=1)
lines3d(c(mx[5],antipordal_i),c(my[5],antipordal_j),c(0,antipordal_k),col=rgb(0,0,0),lwd=1)

#アニメーション
movie3d(spin3d(axis=c(0,0,1),rpm=5),duration=10,fps=25,movie="~/Desktop/Octahedron01")

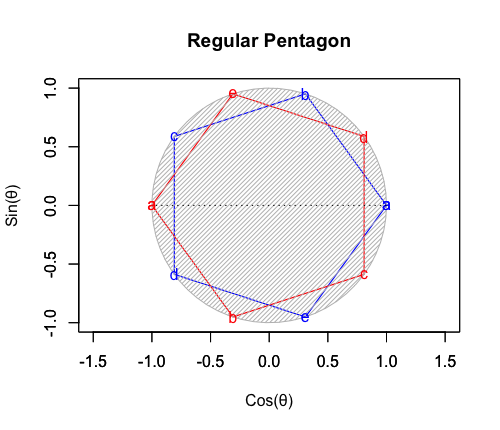
①ここで現れる正五角形(Regular Pentagon)は奇数形図形なのでそれぞれ原蹠から出発し対蹠に届いてない状態の一対として顕現。

#分割数Nod(Number of divide)=5

NoD<-5
#円周分割数列(Sequence of Divided Circumference)
SoDC<-seq(0,2*pi,length=NoD+1)
#円周上の五角形の頂点を集める。
cx_nomal=cos(SoDC)
cy_nomal=sin(SoDC)
cx_reverse=cos(SoDC+pi)
cy_reverse=sin(SoDC+pi)
#グラフ描画
plot(cx_nomal,cy_nomal,asp=1,col=rgb(0,0,1),type="l",xlim=c(-1,1),ylim=c(-1,1),main="Regular Pentagon",xlab="Cos(θ)",ylab="Sin(θ)",lwd=1.2)
par(new=T)
plot(cx_reverse,cy_reverse,asp=1,col=rgb(1,0,0),type="l",xlim=c(-1,1),ylim=c(-1,1),main="",xlab="",ylab="",lwd=1.2)
#背景円の塗り潰し
Circumference<-seq(0,2*pi,length=60)
cx_circle=cos(Circumference)
cy_circle=sin(Circumference)
polygon(cx_circle, #x
cy_circle, #y
density=c(30), #塗りつぶす濃度
angle=c(45),　 　　　#塗りつぶす斜線の角度
col=c(200,200,200)) 　#塗りつぶす色

#文字追加
text(cx_nomal,cy_nomal, labels=c("a","b","c","d","e"),col=rgb(0,0,1))
text(cx_reverse,cy_reverse, labels=c("a","b","c","d","e"),col=rgb(1,0,0))
#補助線
segments(1,0,-1,0,lty=3,col=rgb(0,0,0))

②この形はオイラーの多面体定理(Euler's Polyhedron Theorem)Vertex(頂点数)-Edge(辺数)+Face(面数)=2展開上における「(立方体同様に断面を２つ備える)正二十面体形成の頭蹠」となる。
【Rで球面幾何学】オイラーの多面体定理(Euler's Polyhedron Theorem)と平面充填(Tiling)の連続性について。

オイラーの多面体定理の証明方法…ある頂点か面を選んで始端とし、これに隣接する面を段階的に除去していくと最後にただ一つの終端として頂点か面が残る。要するに2とは最後に残る始端と終端の事である。

逆をいえば、ある頂点か面を選んで始端とし、これから出発する辺や面を段階的に積み上げていって最後にただ一つの終端に到達すればそこに多角形が顕現する事になる。

【Rで球面幾何学】正20面体(Regular Icosahedron)の作図について。

#到達点としてのただの正六角形(Regular Hexagon)
断面上にあと一個頂点を追加しても、やはり意味ある立体図形には発展しません。ただし…

library(rgl)
#分割数Nod(Number of divide)=6
NoD<-6
#円周分割数列(Sequence of Divided Circumference)
SoDC<-seq(0,2*pi,length=NoD+1)

#原蹠(PorTal)
portal_i<-0
portal_j<-0
portal_k<-1
portal_text=paste0("PT(",portal_i,",",portal_j,",",portal_k,")")

#原蹠表示
texts3d(portal_i,portal_j,portal_k,texts=portal_text,col=rgb(0,0,0),adj=1.0)

#対蹠(AntiPordal)
antipordal_i<-0
antipordal_j<-0
antipordal_k<--1
antipordal_text=paste0("AP(",antipordal_i,",",antipordal_j,",",antipordal_k,")" main="Cross section for ")

#対蹠表示
texts3d(antipordal_i,antipordal_j,antipordal_k,texts=antipordal_text,col=rgb(0,0,0),adj=1.0)

#立方対角線(Cubic Diagonal)
lines3d(c(portal_i,antipordal_i),c(portal_j,antipordal_j),c(portal_k,antipordal_k),col=rgb(1,0,0),lwd=2)

#正四面体描画
mx<-cos(SoDC)
my<-sin(SoDC)

lines3d(c(portal_i,mx[1]),c(portal_j,my[1]),c(portal_k,0),col=rgb(0,0,0),lwd=1)
lines3d(c(portal_i,mx[2]),c(portal_j,my[2]),c(portal_k,0),col=rgb(0,0,0),lwd=1)
lines3d(c(portal_i,mx[3]),c(portal_j,my[3]),c(portal_k,0),col=rgb(0,0,0),lwd=1)
lines3d(c(portal_i,mx[4]),c(portal_j,my[4]),c(portal_k,0),col=rgb(0,0,0),lwd=1)
lines3d(c(portal_i,mx[5]),c(portal_j,my[5]),c(portal_k,0),col=rgb(0,0,0),lwd=1)
lines3d(c(portal_i,mx[6]),c(portal_j,my[6]),c(portal_k,0),col=rgb(0,0,0),lwd=1)

lines3d(c(mx[1],mx[2]),c(my[1],my[2]),c(0,0),col=rgb(0,0,0),lwd=1)
lines3d(c(mx[2],mx[3]),c(my[2],my[3]),c(0,0),col=rgb(0,0,0),lwd=1)
lines3d(c(mx[3],mx[4]),c(my[3],my[4]),c(0,0),col=rgb(0,0,0),lwd=1)
lines3d(c(mx[4],mx[5]),c(my[4],my[5]),c(0,0),col=rgb(0,0,0),lwd=1)
lines3d(c(mx[5],mx[6]),c(my[5],my[6]),c(0,0),col=rgb(0,0,0),lwd=1)
lines3d(c(mx[6],mx[1]),c(my[6],my[1]),c(0,0),col=rgb(0,0,0),lwd=1)

lines3d(c(mx[1],antipordal_i),c(my[1],antipordal_j),c(0,antipordal_k),col=rgb(0,0,0),lwd=1)
lines3d(c(mx[2],antipordal_i),c(my[2],antipordal_j),c(0,antipordal_k),col=rgb(0,0,0),lwd=1)
lines3d(c(mx[3],antipordal_i),c(my[3],antipordal_j),c(0,antipordal_k),col=rgb(0,0,0),lwd=1)
lines3d(c(mx[4],antipordal_i),c(my[4],antipordal_j),c(0,antipordal_k),col=rgb(0,0,0),lwd=1)
lines3d(c(mx[5],antipordal_i),c(my[5],antipordal_j),c(0,antipordal_k),col=rgb(0,0,0),lwd=1)
lines3d(c(mx[6],antipordal_i),c(my[6],antipordal_j),c(0,antipordal_k),col=rgb(0,0,0),lwd=1)

#アニメーション
movie3d(spin3d(axis=c(0,0,1),rpm=5),duration=10,fps=25,movie="~/Desktop/Tetrahedron13")

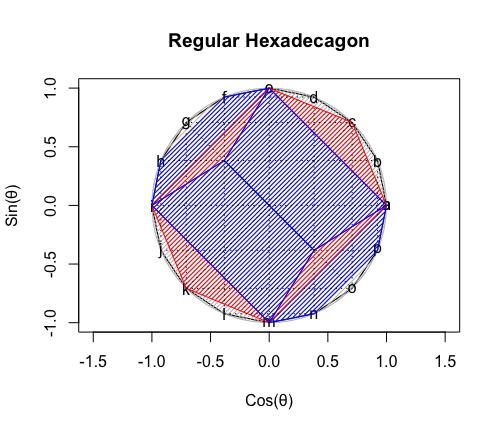
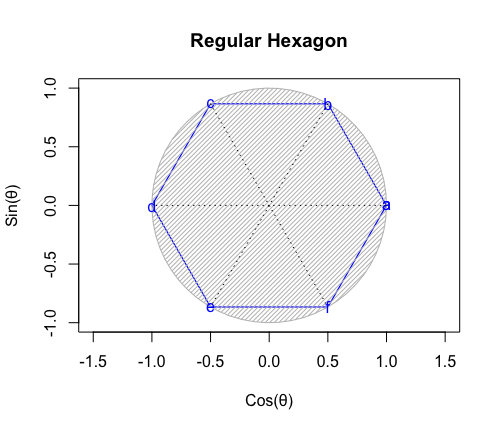
①ここで現れる正六角形(Regular Hexagon)は偶数系図形なので単独で顕現。それ自体が対蹠間を結ぶ線を3本備える。

#分割数Nod(Number of divide)=6
NoD<-6
#円周分割数列(Sequence of Divided Circumference)
SoDC<-seq(0,2*pi,length=NoD+1)
#円周上の四角形の頂点を集める。
cx_nomal=cos(SoDC)
cy_nomal=sin(SoDC)

#グラフ描画
plot(cx_nomal,cy_nomal,asp=1,col=rgb(0,0,1),type="l",xlim=c(-1,1),ylim=c(-1,1),main="Regular Hexagon",xlab="Cos(θ)",ylab="Sin(θ)",lwd=1.2)

#背景円の塗り潰し
Circumference<-seq(0,2*pi,length=60)
cx_circle=cos(Circumference)
cy_circle=sin(Circumference)
polygon(cx_circle, #x
cy_circle, #y
density=c(30), #塗りつぶす濃度
angle=c(45),　 　　　#塗りつぶす斜線の角度
col=c(200,200,200)) 　#塗りつぶす色

#文字追加
text(cx_nomal,cy_nomal, labels=c("a","b","c","d","e","f"),col=rgb(0,0,1))

#補助線
segments(1,0,-1,0,lty=3,col=rgb(0,0,0))
segments(cx_nomal[2],cy_nomal[2],cx_nomal[5],cy_nomal[5],lty=3,col=rgb(0,0,0))
segments(cx_nomal[3],cy_nomal[3],cx_nomal[6],cy_nomal[6],lty=3,col=rgb(0,0,0))

②実際にはむしろ、内角を合わせると丁度360度(2πラジアン)となる正三角形六個の組み合わせの顕現によって「原蹠=対蹠」の図式が成立する事は、両者の峻別を出発点とする球面幾何学(Spherical geometry)が末端、すなわちある種の極限状態に到達したと考えるべきかもしれない。なので以降のこの系の断面への頂点追加はもはや立体的展開を伴わなくなる訳である。

library(rgl)
#分割数Nod(Number of divide)=6
NoD<-6
#円周分割数列(Sequence of Divided Circumference)
SoDC<-seq(0,2*pi,length=NoD+1)

#原蹠(PorTal)
portal_i<-0
portal_j<-0
portal_k<-1
portal_text=paste0("PT(",portal_i,",",portal_j,",",portal_k,")")

#原蹠表示
texts3d(portal_i,portal_j,portal_k,texts=portal_text,col=rgb(0,0,0),adj=1.0)

#対蹠(AntiPordal)
antipordal_i<-0
antipordal_j<-0
antipordal_k<--1
antipordal_text=paste0("AP(",antipordal_i,",",antipordal_j,",",antipordal_k,")" main="Cross section for ")

#対蹠表示
texts3d(antipordal_i,antipordal_j,antipordal_k,texts=antipordal_text,col=rgb(0,0,0),adj=1.0)

#立方対角線(Cubic Diagonal)
lines3d(c(portal_i,antipordal_i),c(portal_j,antipordal_j),c(portal_k,antipordal_k),col=rgb(1,0,0),lwd=2)

#正四面体描画
mx<-cos(SoDC)
my<-sin(SoDC)

lines3d(c(portal_i,mx[1]),c(portal_j,my[1]),c(0,0),col=rgb(0,0,0),lwd=1)
lines3d(c(portal_i,mx[2]),c(portal_j,my[2]),c(0,0),col=rgb(0,0,0),lwd=1)
lines3d(c(portal_i,mx[3]),c(portal_j,my[3]),c(0,0),col=rgb(0,0,0),lwd=1)
lines3d(c(portal_i,mx[4]),c(portal_j,my[4]),c(0,0),col=rgb(0,0,0),lwd=1)
lines3d(c(portal_i,mx[5]),c(portal_j,my[5]),c(0,0),col=rgb(0,0,0),lwd=1)
lines3d(c(portal_i,mx[6]),c(portal_j,my[6]),c(0,0),col=rgb(0,0,0),lwd=1)

lines3d(c(mx[1],mx[2]),c(my[1],my[2]),c(0,0),col=rgb(0,0,0),lwd=1)
lines3d(c(mx[2],mx[3]),c(my[2],my[3]),c(0,0),col=rgb(0,0,0),lwd=1)
lines3d(c(mx[3],mx[4]),c(my[3],my[4]),c(0,0),col=rgb(0,0,0),lwd=1)
lines3d(c(mx[4],mx[5]),c(my[4],my[5]),c(0,0),col=rgb(0,0,0),lwd=1)
lines3d(c(mx[5],mx[6]),c(my[5],my[6]),c(0,0),col=rgb(0,0,0),lwd=1)
lines3d(c(mx[6],mx[1]),c(my[6],my[1]),c(0,0),col=rgb(0,0,0),lwd=1)

#アニメーション
movie3d(spin3d(axis=c(0,0,1),rpm=5),duration=10,fps=25,movie="~/Desktop/Tetrahedron14")

とりあえずは以下続報…