【オイラーの多面体定理と正多面体】正方形における平方対角線(Square diagonal)と立方体における立方対角線(Cubic diagonal)の関係について。

【Rで球面幾何学】単位円と単位球①「半径１」と「直径２」の関係について。

真円の円弧(Circular Arc of True Circle)/真球の表面(Sphere Surface of True Sphere)上においては任意の原蹠(Portal)と対蹠(Antipodal)を結ぶ直線距離、すなわち直径(Diameter))が全て等しくなる。

そしてその円弧/球面上の直径は、これに内接する正方形の平方対角線(Square diagonal)/立方体の立方対角線(Cubic diagonal)と一致するのです。

①まずは1辺を1と置くN次元方眼(n-grid)上に直径２の単位球面に内接する、すなわち立方対角線の長さが２の立方体を作図する。ここではZ軸を計算の基準に選んだが、X軸やY軸を選んでも同じ結果となるのは言うまでもない。

library(rgl)

#原蹠(PorTal)
portal_i<-0
portal_j<-0
portal_k<-1
portal_text=paste0("PT(",portal_i,",",portal_j,",",portal_k,")")

#原蹠表示
texts3d(portal_i,portal_j,portal_k,texts=portal_text,col=rgb(0,0,0),adj=1.0)

#対蹠(AntiPordal)
antipordal_i<-0
antipordal_j<-0
antipordal_k<--1
antipordal_text=paste0("AP(",antipordal_i,",",antipordal_j,",",antipordal_k,")")

#対蹠表示
texts3d(antipordal_i,antipordal_j,antipordal_k,texts=antipordal_text,col=rgb(0,0,0),adj=1.0)

#立方対角線(Cubic Diagonal)
lines3d(c(portal_i,antipordal_i),c(portal_j,antipordal_j),c(portal_k,antipordal_k),col=rgb(1,0,0),lwd=2)

#立方体におけるxy軸上の経度(LoNgitude)座標
LN0=sin(pi/3)
c0<-seq(0,2*pi,length=4)
LN01_cos<-cos(c0)*LN0
LN01_sin<-sin(c0)*LN0
LN02_cos<-cos(c0+pi)*LN0
LN02_sin<-sin(c0+pi)*LN0

#立方体におけるz軸上の緯度(LaTitude)座標
LT0=1/3
AP01=LT0
AP02=-LT0

#立方体描写(原蹠から最初の隣点)
lines3d(c(portal_i,LN01_cos[1]),c(portal_j,LN01_sin[1]),c(portal_k,AP01),col=rgb(0,0,0),lwd=1)
lines3d(c(portal_i,LN01_cos[2]),c(portal_j,LN01_sin[2]),c(portal_k,AP01),col=rgb(0,0,0),lwd=1)
lines3d(c(portal_i,LN01_cos[3]),c(portal_j,LN01_sin[3]),c(portal_k,AP01),col=rgb(0,0,0),lwd=1)

#立方体描写(原蹠から最初の隣点)
lines3d(c(antipordal_i,LN02_cos[1]),c(antipordal_j,LN02_sin[1]),c(antipordal_k,AP02),col=rgb(0,0,0),lwd=1)
lines3d(c(antipordal_i,LN02_cos[2]),c(antipordal_j,LN02_sin[2]),c(antipordal_k,AP02),col=rgb(0,0,0),lwd=1)
lines3d(c(antipordal_i,LN02_cos[3]),c(antipordal_j,LN02_sin[3]),c(antipordal_k,AP02),col=rgb(0,0,0),lwd=1)

#立方体描写(中線の結合)
lines3d(c(LN01_cos[1],LN02_cos[3],LN01_cos[2],LN02_cos[1],LN01_cos[3],LN02_cos[2],LN01_cos[1]),c(LN01_sin[1],LN02_sin[3],LN01_sin[2],LN02_sin[1],LN01_sin[3],LN02_sin[2],LN01_sin[1]),c(AP01,AP02,AP01,AP02,AP01,AP02,AP01),col=rgb(0,0,0),lwd=1)

#アニメーション
movie3d(spin3d(axis=c(0,0,1),rpm=5),duration=10,fps=25,movie="~/Desktop/square002")

ちなみ立方体には立方体角線=対蹠のセットが他に３個あり、どれを選んでも同じ結果となります。

library(rgl)

#原蹠(PorTal)
portal_i<-0
portal_j<-0
portal_k<-1
portal_text=paste0("PT(",portal_i,",",portal_j,",",portal_k,")")

#原蹠表示
texts3d(portal_i,portal_j,portal_k,texts=portal_text,col=rgb(0,0,0),adj=1.0)

#対蹠(AntiPordal)
antipordal_i<-0
antipordal_j<-0
antipordal_k<--1
antipordal_text=paste0("AP(",antipordal_i,",",antipordal_j,",",antipordal_k,")")

#対蹠表示
texts3d(antipordal_i,antipordal_j,antipordal_k,texts=antipordal_text,col=rgb(0,0,0),adj=1.0)

#立方対角線(Cubic Diagonal)
lines3d(c(portal_i,antipordal_i),c(portal_j,antipordal_j),c(portal_k,antipordal_k),col=rgb(1,0,0),lwd=2)

#立方体におけるxy軸上の経度(LoNgitude)座標
LN0=sin(pi/3)
c0<-seq(0,2*pi,length=4)
LN01_cos<-cos(c0)*LN0
LN01_sin<-sin(c0)*LN0
LN02_cos<-cos(c0+pi)*LN0
LN02_sin<-sin(c0+pi)*LN0

#立方体におけるz軸上の緯度(LaTitude)座標
LT0=1/3
AP01=LT0
AP02=-LT0

#立方体描写(原蹠から最初の隣点)
lines3d(c(portal_i,LN01_cos[1]),c(portal_j,LN01_sin[1]),c(portal_k,AP01),col=rgb(0,0,0),lwd=1)
lines3d(c(portal_i,LN01_cos[2]),c(portal_j,LN01_sin[2]),c(portal_k,AP01),col=rgb(0,0,0),lwd=1)
lines3d(c(portal_i,LN01_cos[3]),c(portal_j,LN01_sin[3]),c(portal_k,AP01),col=rgb(0,0,0),lwd=1)

#立方体描写(対蹠から最初の隣点)
lines3d(c(antipordal_i,LN02_cos[1]),c(antipordal_j,LN02_sin[1]),c(antipordal_k,AP02),col=rgb(0,0,0),lwd=1)
lines3d(c(antipordal_i,LN02_cos[2]),c(antipordal_j,LN02_sin[2]),c(antipordal_k,AP02),col=rgb(0,0,0),lwd=1)
lines3d(c(antipordal_i,LN02_cos[3]),c(antipordal_j,LN02_sin[3]),c(antipordal_k,AP02),col=rgb(0,0,0),lwd=1)

#立方体描写(中線の結合)
lines3d(c(LN01_cos[1],LN02_cos[3],LN01_cos[2],LN02_cos[1],LN01_cos[3],LN02_cos[2],LN01_cos[1]),c(LN01_sin[1],LN02_sin[3],LN01_sin[2],LN02_sin[1],LN01_sin[3],LN02_sin[2],LN01_sin[1]),c(AP01,AP02,AP01,AP02,AP01,AP02,AP01),col=rgb(0,0,0),lwd=1)

#追加立方対角線
lines3d(c(LN01_cos[1],LN02_cos[1]),c(LN01_sin[1],LN02_sin[1]),c(AP01,AP02),col=rgb(0,1,0),lwd=1)
lines3d(c(LN01_cos[2],LN02_cos[2]),c(LN01_sin[2],LN02_sin[2]),c(AP01,AP02),col=rgb(0,1,0),lwd=1)
lines3d(c(LN01_cos[3],LN02_cos[3]),c(LN01_sin[3],LN02_sin[3]),c(AP01,AP02),col=rgb(0,1,0),lwd=1)

#アニメーション
movie3d(spin3d(axis=c(0,0,1),rpm=5),duration=10,fps=25,movie="~/Desktop/square004")

②次にピタゴラスの定理(Pythagorean theorem)の平方展開形sqrt(x^2+y^2)=1を用いて原蹠から出発する3枚の正方形の平方対角線を求めると、その立方体の表面に「三辺比1:1:sqrt(2)の二等辺直角三角形」が３枚現れる。その角度比は45度(π/8ラジアン):45度(π/8ラジアン):90度(π/4ラジアン)。

library(rgl)

#原蹠(PorTal)
portal_i<-0
portal_j<-0
portal_k<-1
portal_text=paste0("PT(",portal_i,",",portal_j,",",portal_k,")")

#原蹠表示
texts3d(portal_i,portal_j,portal_k,texts=portal_text,col=rgb(0,0,0),adj=1.0)

#対蹠(AntiPordal)
antipordal_i<-0
antipordal_j<-0
antipordal_k<--1
antipordal_text=paste0("AP(",antipordal_i,",",antipordal_j,",",antipordal_k,")")

#対蹠表示
texts3d(antipordal_i,antipordal_j,antipordal_k,texts=antipordal_text,col=rgb(0,0,0),adj=1.0)

#立方対角線(Cubic Diagonal)
lines3d(c(portal_i,antipordal_i),c(portal_j,antipordal_j),c(portal_k,antipordal_k),col=rgb(1,0,0),lwd=2)

#立方体におけるxy軸上の経度(LoNgitude)座標
LN0=sin(pi/3)
c0<-seq(0,2*pi,length=4)
LN01_cos<-cos(c0)*LN0
LN01_sin<-sin(c0)*LN0
LN02_cos<-cos(c0+pi)*LN0
LN02_sin<-sin(c0+pi)*LN0

#立方体におけるz軸上の緯度(LaTitude)座標
LT0=1/3
AP01=LT0
AP02=-LT0

#立方体描写(原蹠から最初の隣点)
lines3d(c(portal_i,LN01_cos[1]),c(portal_j,LN01_sin[1]),c(portal_k,AP01),col=rgb(0,0,0),lwd=1)
lines3d(c(portal_i,LN01_cos[2]),c(portal_j,LN01_sin[2]),c(portal_k,AP01),col=rgb(0,0,0),lwd=1)
lines3d(c(portal_i,LN01_cos[3]),c(portal_j,LN01_sin[3]),c(portal_k,AP01),col=rgb(0,0,0),lwd=1)

#立方体描写(原蹠から最初の隣点)
lines3d(c(antipordal_i,LN02_cos[1]),c(antipordal_j,LN02_sin[1]),c(antipordal_k,AP02),col=rgb(0,0,0),lwd=1)
lines3d(c(antipordal_i,LN02_cos[2]),c(antipordal_j,LN02_sin[2]),c(antipordal_k,AP02),col=rgb(0,0,0),lwd=1)
lines3d(c(antipordal_i,LN02_cos[3]),c(antipordal_j,LN02_sin[3]),c(antipordal_k,AP02),col=rgb(0,0,0),lwd=1)

#立方体描写(中線の結合)
lines3d(c(LN01_cos[1],LN02_cos[3],LN01_cos[2],LN02_cos[1],LN01_cos[3],LN02_cos[2],LN01_cos[1]),c(LN01_sin[1],LN02_sin[3],LN01_sin[2],LN02_sin[1],LN01_sin[3],LN02_sin[2],LN01_sin[1]),c(AP01,AP02,AP01,AP02,AP01,AP02,AP01),col=rgb(0,0,0),lwd=1)

#平方対角線を斜線として備える二等辺三角形(１枚目)
x1<-c(portal_i, LN01_cos[1], LN02_cos[2])
y1<-c(portal_j, LN01_sin[1], LN02_sin[2])
z1<-c(portal_k,AP01,AP02)
triangles3d(x1,y1,z1,color=rgb(0,0,1))

#平方対角線を斜線として備える二等辺三角形(2枚目)
x1<-c(portal_i, LN01_cos[2], LN02_cos[3])
y1<-c(portal_j, LN01_sin[2], LN02_sin[3])
z1<-c(portal_k,AP01,AP02)
triangles3d(x1,y1,z1,color=rgb(0,0,1))

#平方対角線を斜線として備える二等辺三角形(3枚目)
x1<-c(portal_i, LN01_cos[3], LN02_cos[1])
y1<-c(portal_j, LN01_sin[3], LN02_sin[1])
z1<-c(portal_k,AP01,AP02)
triangles3d(x1,y1,z1,color=rgb(0,0,1))

#アニメーション
movie3d(spin3d(axis=c(0,0,1),rpm=5),duration=10,fps=25,movie="~/Desktop/square005")

③こうして求めた立方体の表面上の正方形の平方対角線と対蹠に到達する残り１辺の間にさらにピタゴラスの定理(Pythagorean theorem)の平方展開形sqrt(x^2+y^2)=1を用いて正方形の平方対角線を算出すると、今度は「三辺比1:sqrt(2):sqrt(3)の直角三角形」がさらに３枚現れる。

library(rgl)

#原蹠(PorTal)
portal_i<-0
portal_j<-0
portal_k<-1
portal_text=paste0("PT(",portal_i,",",portal_j,",",portal_k,")")

#原蹠表示
texts3d(portal_i,portal_j,portal_k,texts=portal_text,col=rgb(0,0,0),adj=1.0)

#対蹠(AntiPordal)
antipordal_i<-0
antipordal_j<-0
antipordal_k<--1
antipordal_text=paste0("AP(",antipordal_i,",",antipordal_j,",",antipordal_k,")")

#対蹠表示
texts3d(antipordal_i,antipordal_j,antipordal_k,texts=antipordal_text,col=rgb(0,0,0),adj=1.0)

#立方対角線(Cubic Diagonal)
lines3d(c(portal_i,antipordal_i),c(portal_j,antipordal_j),c(portal_k,antipordal_k),col=rgb(1,0,0),lwd=2)

#立方体におけるxy軸上の経度(LoNgitude)座標
LN0=sin(pi/3)
c0<-seq(0,2*pi,length=4)
LN01_cos<-cos(c0)*LN0
LN01_sin<-sin(c0)*LN0
LN02_cos<-cos(c0+pi)*LN0
LN02_sin<-sin(c0+pi)*LN0

#立方体におけるz軸上の緯度(LaTitude)座標
LT0=1/3
AP01=LT0
AP02=-LT0

#立方体描写(原蹠から最初の隣点)
lines3d(c(portal_i,LN01_cos[1]),c(portal_j,LN01_sin[1]),c(portal_k,AP01),col=rgb(0,0,0),lwd=1)
lines3d(c(portal_i,LN01_cos[2]),c(portal_j,LN01_sin[2]),c(portal_k,AP01),col=rgb(0,0,0),lwd=1)
lines3d(c(portal_i,LN01_cos[3]),c(portal_j,LN01_sin[3]),c(portal_k,AP01),col=rgb(0,0,0),lwd=1)

#立方体描写(原蹠から最初の隣点)
lines3d(c(antipordal_i,LN02_cos[1]),c(antipordal_j,LN02_sin[1]),c(antipordal_k,AP02),col=rgb(0,0,0),lwd=1)
lines3d(c(antipordal_i,LN02_cos[2]),c(antipordal_j,LN02_sin[2]),c(antipordal_k,AP02),col=rgb(0,0,0),lwd=1)
lines3d(c(antipordal_i,LN02_cos[3]),c(antipordal_j,LN02_sin[3]),c(antipordal_k,AP02),col=rgb(0,0,0),lwd=1)

#立方体描写(中線の結合)
lines3d(c(LN01_cos[1],LN02_cos[3],LN01_cos[2],LN02_cos[1],LN01_cos[3],LN02_cos[2],LN01_cos[1]),c(LN01_sin[1],LN02_sin[3],LN01_sin[2],LN02_sin[1],LN01_sin[3],LN02_sin[2],LN01_sin[1]),c(AP01,AP02,AP01,AP02,AP01,AP02,AP01),col=rgb(0,0,0),lwd=1)

#平方対角線を斜線として備える二等辺三角形(1枚目)
x1<-c(portal_i, LN01_cos[1], LN02_cos[2])
y1<-c(portal_j, LN01_sin[1], LN02_sin[2])
z1<-c(portal_k,AP01,AP02)
triangles3d(x1,y1,z1,color=rgb(0,0,1))

#平方対角線を斜線として備える二等辺三角形(2枚目)
x1<-c(portal_i, LN01_cos[2], LN02_cos[3])
y1<-c(portal_j, LN01_sin[2], LN02_sin[3])
z1<-c(portal_k,AP01,AP02)
triangles3d(x1,y1,z1,color=rgb(0,0,1))

#平方対角線を斜線として備える二等辺三角形(3枚目)
x1<-c(portal_i, LN01_cos[3], LN02_cos[1])
y1<-c(portal_j, LN01_sin[3], LN02_sin[1])
z1<-c(portal_k,AP01,AP02)
triangles3d(x1,y1,z1,color=rgb(0,0,1))

#立方対角線を斜線として備える直角三角形（１枚目）
x2<-c(portal_i, LN02_cos[2],antipordal_i)
y2<-c(portal_j, LN02_sin[2],antipordal_j)
z2<-c(portal_k, AP02, antipordal_k)
triangles3d(x2,y2,z2,color=rgb(1,0,0))

#立方対角線を斜線として備える直角三角形（２枚目）
x2<-c(portal_i, LN02_cos[3],antipordal_i)
y2<-c(portal_j, LN02_sin[3],antipordal_j)
z2<-c(portal_k, AP02, antipordal_k)
triangles3d(x2,y2,z2,color=rgb(1,0,0))

#立方対角線を斜線として備える直角三角形（３枚目）
x2<-c(portal_i, LN02_cos[1],antipordal_i)
y2<-c(portal_j, LN02_sin[1],antipordal_j)
z2<-c(portal_k, AP02, antipordal_k)
triangles3d(x2,y2,z2,color=rgb(1,0,0))

#アニメーション
movie3d(spin3d(axis=c(0,0,1),rpm=5),duration=10,fps=25,movie="~/Desktop/square006")

④ちなみに「三辺比1:1:sqrt(2)の二等辺直角三角形」と「三辺比1:sqrt(2):sqrt(3)の直角三角形」を検出する順番は逆でも構わないが、この操作をプログラムで実装するに当たっては「出発点としての原蹠」と「到達点としての対蹠」の設定(この場合、Z軸を巡る操作)に可換性が存在しない点に注意を払わねばならない。

library(rgl)

#原蹠(PorTal)
portal_i<-0
portal_j<-0
portal_k<-1
portal_text=paste0("PT(",portal_i,",",portal_j,",",portal_k,")")

#原蹠表示
texts3d(portal_i,portal_j,portal_k,texts=portal_text,col=rgb(0,0,0),adj=1.0)

#対蹠(AntiPordal)
antipordal_i<-0
antipordal_j<-0
antipordal_k<--1
antipordal_text=paste0("AP(",antipordal_i,",",antipordal_j,",",antipordal_k,")")

#対蹠表示
texts3d(antipordal_i,antipordal_j,antipordal_k,texts=antipordal_text,col=rgb(0,0,0),adj=1.0)

#立方対角線(Cubic Diagonal)
lines3d(c(portal_i,antipordal_i),c(portal_j,antipordal_j),c(portal_k,antipordal_k),col=rgb(1,0,0),lwd=2)

#立方体におけるxy軸上の経度(LoNgitude)座標
LN0=sin(pi/3)
c0<-seq(0,2*pi,length=4)
LN01_cos<-cos(c0)*LN0
LN01_sin<-sin(c0)*LN0
LN02_cos<-cos(c0+pi)*LN0
LN02_sin<-sin(c0+pi)*LN0

#立方体におけるz軸上の緯度(LaTitude)座標
LT0=1/3
AP01=LT0
AP02=-LT0

#立方体描写(原蹠から最初の隣点)
lines3d(c(portal_i,LN01_cos[1]),c(portal_j,LN01_sin[1]),c(portal_k,AP01),col=rgb(0,0,0),lwd=1)
lines3d(c(portal_i,LN01_cos[2]),c(portal_j,LN01_sin[2]),c(portal_k,AP01),col=rgb(0,0,0),lwd=1)
lines3d(c(portal_i,LN01_cos[3]),c(portal_j,LN01_sin[3]),c(portal_k,AP01),col=rgb(0,0,0),lwd=1)

#立方体描写(原蹠から最初の隣点)
lines3d(c(antipordal_i,LN02_cos[1]),c(antipordal_j,LN02_sin[1]),c(antipordal_k,AP02),col=rgb(0,0,0),lwd=1)
lines3d(c(antipordal_i,LN02_cos[2]),c(antipordal_j,LN02_sin[2]),c(antipordal_k,AP02),col=rgb(0,0,0),lwd=1)
lines3d(c(antipordal_i,LN02_cos[3]),c(antipordal_j,LN02_sin[3]),c(antipordal_k,AP02),col=rgb(0,0,0),lwd=1)

#立方体描写(中線の結合)
lines3d(c(LN01_cos[1],LN02_cos[3],LN01_cos[2],LN02_cos[1],LN01_cos[3],LN02_cos[2],LN01_cos[1]),c(LN01_sin[1],LN02_sin[3],LN01_sin[2],LN02_sin[1],LN01_sin[3],LN02_sin[2],LN01_sin[1]),c(AP01,AP02,AP01,AP02,AP01,AP02,AP01),col=rgb(0,0,0),lwd=1)

#立方対角線を斜線として備える直角三角形（１枚目）
x2<-c(portal_i, LN01_cos[2],antipordal_i)
y2<-c(portal_j, LN01_sin[2],antipordal_j)
z2<-c(portal_k, AP01, antipordal_k)
triangles3d(x2,y2,z2,color=rgb(1,0,0))

#立方対角線を斜線として備える直角三角形（２枚目）
x2<-c(portal_i, LN01_cos[3],antipordal_i)
y2<-c(portal_j, LN01_sin[3],antipordal_j)
z2<-c(portal_k, AP01, antipordal_k)
triangles3d(x2,y2,z2,color=rgb(1,0,0))

#立方対角線を斜線として備える直角三角形（３枚目）
x2<-c(portal_i, LN01_cos[1],antipordal_i)
y2<-c(portal_j, LN01_sin[1],antipordal_j)
z2<-c(portal_k, AP01, antipordal_k)
triangles3d(x2,y2,z2,color=rgb(1,0,0))

#平方対角線を斜線として備える二等辺三角形(1枚目)
x1<-c(antipordal_i, LN02_cos[1], LN01_cos[2])
y1<-c(antipordal_j, LN02_sin[1], LN01_sin[2])
z1<-c(antipordal_k, AP02, AP01)
triangles3d(x1,y1,z1,color=rgb(0,0,1))

#平方対角線を斜線として備える二等辺三角形(2枚目)
x1<-c(antipordal_i, LN02_cos[2], LN01_cos[3])
y1<-c(antipordal_j, LN02_sin[2], LN01_sin[3])
z1<-c(antipordal_k, AP02, AP01)
triangles3d(x1,y1,z1,color=rgb(0,0,1))

#平方対角線を斜線として備える二等辺三角形(3枚目)
x1<-c(antipordal_i, LN02_cos[3], LN01_cos[1])
y1<-c(antipordal_j, LN02_sin[3], LN01_sin[1])
z1<-c(antipordal_k,AP02,AP01)
triangles3d(x1,y1,z1,color=rgb(0,0,1))

#アニメーション
movie3d(spin3d(axis=c(0,0,1),rpm=5),duration=10,fps=25,movie="~/Desktop/square008")

⑤さらに「三辺比1:1:sqrt(2)の二等辺直角三角形」と「三辺比1:sqrt(2):sqrt(3)の直角三角形」を検出する向きを逆にしても構わないが、この操作をプログラムで実装するに当たっては「各三角形を検出する順序」の設定(この場合、X-Y面を巡る操作)に可換性が存在しない点に注意を払わねばならない。

library(rgl)

#原蹠(PorTal)
portal_i<-0
portal_j<-0
portal_k<-1
portal_text=paste0("PT(",portal_i,",",portal_j,",",portal_k,")")

#原蹠表示
texts3d(portal_i,portal_j,portal_k,texts=portal_text,col=rgb(0,0,0),adj=1.0)

#対蹠(AntiPordal)
antipordal_i<-0
antipordal_j<-0
antipordal_k<--1
antipordal_text=paste0("AP(",antipordal_i,",",antipordal_j,",",antipordal_k,")")

#対蹠表示
texts3d(antipordal_i,antipordal_j,antipordal_k,texts=antipordal_text,col=rgb(0,0,0),adj=1.0)

#立方対角線(Cubic Diagonal)
lines3d(c(portal_i,antipordal_i),c(portal_j,antipordal_j),c(portal_k,antipordal_k),col=rgb(1,0,0),lwd=2)

#立方体におけるxy軸上の経度(LoNgitude)座標
LN0=sin(pi/3)
c0<-seq(0,2*pi,length=4)
LN01_cos<-cos(c0)*LN0
LN01_sin<-sin(c0)*LN0
LN02_cos<-cos(c0+pi)*LN0
LN02_sin<-sin(c0+pi)*LN0

#立方体におけるz軸上の緯度(LaTitude)座標
LT0=1/3
AP01=LT0
AP02=-LT0

#立方体描写(原蹠から最初の隣点)
lines3d(c(portal_i,LN01_cos[1]),c(portal_j,LN01_sin[1]),c(portal_k,AP01),col=rgb(0,0,0),lwd=1)
lines3d(c(portal_i,LN01_cos[2]),c(portal_j,LN01_sin[2]),c(portal_k,AP01),col=rgb(0,0,0),lwd=1)
lines3d(c(portal_i,LN01_cos[3]),c(portal_j,LN01_sin[3]),c(portal_k,AP01),col=rgb(0,0,0),lwd=1)

#立方体描写(原蹠から最初の隣点)
lines3d(c(antipordal_i,LN02_cos[1]),c(antipordal_j,LN02_sin[1]),c(antipordal_k,AP02),col=rgb(0,0,0),lwd=1)
lines3d(c(antipordal_i,LN02_cos[2]),c(antipordal_j,LN02_sin[2]),c(antipordal_k,AP02),col=rgb(0,0,0),lwd=1)
lines3d(c(antipordal_i,LN02_cos[3]),c(antipordal_j,LN02_sin[3]),c(antipordal_k,AP02),col=rgb(0,0,0),lwd=1)

#立方体描写(中線の結合)
lines3d(c(LN01_cos[1],LN02_cos[3],LN01_cos[2],LN02_cos[1],LN01_cos[3],LN02_cos[2],LN01_cos[1]),c(LN01_sin[1],LN02_sin[3],LN01_sin[2],LN02_sin[1],LN01_sin[3],LN02_sin[2],LN01_sin[1]),c(AP01,AP02,AP01,AP02,AP01,AP02,AP01),col=rgb(0,0,0),lwd=1)

#平方対角線を斜線として備える二等辺三角形(1枚目)
x1<-c(portal_i, LN01_cos[2], LN02_cos[1])
y1<-c(portal_j, LN01_sin[2], LN02_sin[1])
z1<-c(portal_k,AP01,AP02)
triangles3d(x1,y1,z1,color=rgb(0,0,1))

#平方対角線を斜線として備える二等辺三角形(2枚目)
x1<-c(portal_i, LN01_cos[3], LN02_cos[2])
y1<-c(portal_j, LN01_sin[3], LN02_sin[2])
z1<-c(portal_k,AP01,AP02)
triangles3d(x1,y1,z1,color=rgb(0,0,1))

#平方対角線を斜線として備える二等辺三角形(3枚目)
x1<-c(portal_i, LN01_cos[1], LN02_cos[3])
y1<-c(portal_j, LN01_sin[1], LN02_sin[3])
z1<-c(portal_k,AP01,AP02)
triangles3d(x1,y1,z1,color=rgb(0,0,1))

#立方対角線を斜線として備える直角三角形（１枚目）
x2<-c(portal_i, LN02_cos[3],antipordal_i)
y2<-c(portal_j, LN02_sin[3],antipordal_j)
z2<-c(portal_k, AP02, antipordal_k)
triangles3d(x2,y2,z2,color=rgb(1,0,0))

#立方対角線を斜線として備える直角三角形（２枚目）
x2<-c(portal_i, LN02_cos[2],antipordal_i)
y2<-c(portal_j, LN02_sin[2],antipordal_j)
z2<-c(portal_k, AP02, antipordal_k)
triangles3d(x2,y2,z2,color=rgb(1,0,0))

#立方対角線を斜線として備える直角三角形（３枚目）
x2<-c(portal_i, LN02_cos[1],antipordal_i)
y2<-c(portal_j, LN02_sin[1],antipordal_j)
z2<-c(portal_k, AP02, antipordal_k)
triangles3d(x2,y2,z2,color=rgb(1,0,0))

#アニメーション
movie3d(spin3d(axis=c(0,0,1),rpm=5),duration=10,fps=25,movie="~/Desktop/square009")

⑥「球内を２回直角に曲がって原蹠と対蹠を結ぶ」内接立方体の空間操作(Spatial operations, 原蹠と対蹠の設置はX軸、Y軸、Z軸全てで可換)では「三辺比1:1:sqrt(2)の二等辺直角三角形」と「三辺比1:sqrt(2):sqrt(3)の直角三角形」を検出する順番において原蹠と対蹠の可換性が存在しないのは、それが奇数系(Odd=2n+1 System)に分類される三次元操作系(3D operation system)だからで操作が２回あるから。「円内を1回直角に曲がって原蹠と対蹠を結ぶ」偶数系(Even=2N System)に分類される二次元操作系(2D operation system)においては操作が１回しか存在せず、この問題は発生しない。
【Rで球面幾何学】「半円しか描けなかった」世界の思い出？

⑦また内接立方体の空間操作において「各三角形を検出する順序」の設定(原蹠と対蹠をZ軸に設定した場合のX-Y面を巡る操作、原蹠と対蹠をX軸に設定した場合のY-Z面を巡る操作、原蹠と対蹠をY軸に設定した場合のX-Z面を巡る操作)に可換性が存在しないのは、このプログラムが対象円に内接する正多角形の各頂点の座標計算にガウスが発見した「1の冪根の巡回性」を用いているからである。これは「球内を1回も曲がらず直線で原蹠と対蹠を結ぶ」一次元操作系(1D operation system)に分類されるが、かかる次元においては「符号の向きが存在しない」奇数系(Odd=2n+1 System)と「符号の向きが存在する」偶数系(Even System)が併存し、後者の制約を受けるので、符号の向きが逆になると、結果も逆になる。
1の冪根 - Wikipedia
【Rで球面幾何学】等差数列(算術数列)②数直線(Number Line)概念から同心円集合(Concentric Set)概念へ
一次元操作系における「奇数系」の振る舞い

一次元操作系における「偶数系(y=f(x)系統)」の振る舞い

一次元操作系における「偶数系(x=f(y)系統)」の振る舞い

ところで「三辺比1:sqrt(2):sqrt(3)の直角三角形」の角度比はどうなっているのでしょう？ それについて考え始めると、いきなり三角関数表の限界を問う内容に突入してしまいます。
三角関数表
上掲プログラムではとりあえず「立方対角線を立方眼の軸に合わせた図形はどの方角から観察しても正六角形となるのが自明の理である」なる立場を貫いてcos(θ)=1/3(≃0.333…)という計算結果を採択ししました。一方、実際の数学史上においてはこの角度θは概ね正五角形の性質記述で登場するcos(72度=2π/5ラジアン)=sin(18度=π/10ラジアン)=(sqrt(5)-1)/4≃0.3090175…で近似されてきたのです。
cos72度、sin18度の2通りの求め方

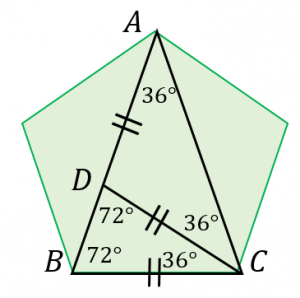
まさにここで正五角形(Pentagon)の概念が乱入してくる訳ですね。これはこれでまぁ、それなりに良いアイディアであったとはいえましょう。人類は10進法とか大好きですし…
正五角形というだけで 分かる角度は…

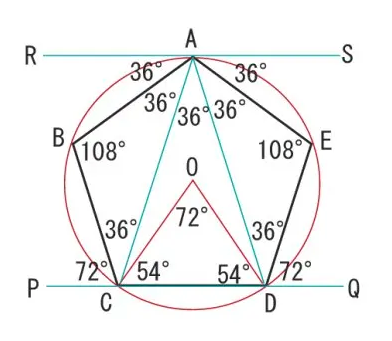
難解で知られるハミルトンの四元数(Hamilton's Quaternion)概念の中核をなす幾何学概念の一つ。
【Rで球面幾何学】ハミルトンの四元数(Quaternion)は何を表しているのか？

	i	j	k
i	-1	-k	j
j	k	-1	-i
k	-j	i	-1

それにも関わらず、日常生活の中に思わぬ形で浸透していた？
【Rで球面幾何学】正四面体と正六面体と正八面体の連続性と「テトラパックの思わぬ正体」について。