【Pythonで球面幾何学】ハミルトンの四元数(Hamilton's Quaternion)は何を表しているのか？

(2020年04月18日)Rによる投稿
(2021年03月26日)tex,pythonを導入した追記

アイルランドの数学者ウィリアム・ローワン・ハミルトン(William Rowan Hamilton, 1805年~1865年)は、1843年に四元数(Quaternion)の概念に到達した時「既存の数理より、こう考えた方が余程自然だ」と直感したそうです。

i^2=j^2=k^2=ijk=-1\\
ij=k,jk=i,ki=j\\
ji=-k,kj=-i,ik=-j

Rの場合

	i	j	k
i	-1	-k	j
j	k	-1	-i
k	-j	i	-1

#三角比(Triangle Ratio)一覧

ijk<-c("-1","k","-j")
jki<-c("-k","-1","i")
kij<-c("j","-i","-1")
TR01<- data.frame(i=ijk,j=jki,k=kij)

colnames(TR01)<-c("i","j","k")
rownames(TR01)<-c("i","j","k")
library(xtable)
print(xtable(TR01),type="html")

pythonの場合

'

	i	j	k
i	-1	-k	j
j	k	-1	-i
k	-j	i	-1

'

import pandas as pnds

Quarterlion=[["-1","-k","j"],["k","-1","-i"],["-j","i","-1"]]
elements=["i","j","k"]

df1 = pnds.DataFrame(Quarterlion,columns=elements,index=elements)
df2=df1.to_html()
df2.replace('\n', '')

【python】listから表を作成する方法（表作成の基本操作・行列名の変更）
Pandas: DataFrame.to_csv() の改行コードを制御
Python の Pandas で HTML 出力した時に改行したい。
Pythonで改行コードLF「\n」を削除する

四元数を用いた画像表現

以下で定義した描画関数から出発します。
【Rで球面幾何学】ジンバルロック(?)やリサージュ曲線(?)との邂逅。

import math as m
import cmath as c
import numpy as num
from matplotlib import pyplot as plt
import matplotlib.animation as animation

#複素円データ作成(外周データを兼ねる)
c0=num.linspace(0,2*m.pi,61,endpoint = True)
c1=[]
for nm in range(len(c0)):
    c1.append(complex(m.cos(c0[nm]),m.sin(c0[nm])))
c2=num.array(c1)

#回転テーブル(Rotation Ratio Table)作成
RRTa=num.linspace(0,2*m.pi,61,endpoint = True)
RRTb=[]
for nm in range(len(RRTa)):
    RRTb.append(m.cos(RRTa[nm]))
RRT=num.array(RRTb)

#対蹠線テーブル(AntiPodes Table)作成
APTa=num.linspace(0,2*m.pi,61,endpoint = True)
APTb=[]
for nm in range(len(APTa)):
    APTb.append(m.sin(APTa[nm]))
APT=num.array(APTb)

#単位円データ作成
z=num.linspace(1,-1,31,endpoint = True)*(1+0j)
zp=z*(0+1j)
p0=[]
for nm in range(len(zp)):
    p0.append(c.exp(zp[nm]*m.pi/2)*(0-1j))
p1=num.array(p0)
#共役複素数列(-)
m1=-p1[::-1]

#グラフ表示準備
plt.style.use('default')
fig = plt.figure()

#関数定義
def Circle_Rotation(ind):
    plt.cla()
    n=TC_wi[ind]
    m=TC_jk[ind]
    #座標変換(jk)
    p2=[]
    for nm in range(len(p1)):
        p2.append(complex(p1[nm].real,p1[nm].imag*RRT[m]))
    p3=num.array(p2)
    m2=[]
    for nm in range(len(m1)):
        m2.append(complex(m1[nm].real,m1[nm].imag*RRT[m]))
    m3=num.array(m2)
    c3=[]
    for nm in range(len(c2)):
        c3.append(complex(c2[nm].real,c2[nm].imag*RRT[m]))
    c4=num.array(c3)
    apt1=complex(0,APT[m])
    #座標変換(wi)
    z2=[]
    for nm in range(len(z)):
        z2.append(z[nm]*c2[n])
    z3=num.array(z2)
    p4=[]
    for nm in range(len(p3)):
        p4.append(p3[nm]*c2[n])
    p5=num.array(p4)
    m4=[]
    for nm in range(len(m3)):
        m4.append(m3[nm]*c2[n])
    m5=num.array(m4)
    c5=[]
    for nm in range(len(c4)):
        c5.append(c4[nm]*c2[n])
    c6=num.array(c5)
    apt2=apt1*c2[n]
    #スポーク描画
    for nm in range(len(c2)):
        plt.plot([0,c6[nm].real],[0,c6[nm].imag],color="gray",lw=0.5);

    #円描画
    plt.plot(c2.real,c2.imag,color="black")
    plt.plot(z3.real,z3.imag,color="green", marker=".")
    plt.plot([0,apt2.real],[0,apt2.imag],color="green", marker="x")
    plt.plot(p5.real,p5.imag,color="red", marker=".")
    plt.plot(m5.real,m5.imag,color="blue", marker=".")
    plt.ylim([-1.1,1.1])
    plt.xlim([-1.1,1.1])
    plt.title("Conjugate Complex")
    plt.xlabel("Real")
    plt.ylabel("Imaginal")
    ax = fig.add_subplot(111)
    ax.set_aspect('equal', adjustable='box')
    #塗りつぶし
    p6=num.concatenate([p5,z3])
    m6=num.concatenate([m5,z3])
    plt.fill(p6.real,p6.imag,facecolor="red",alpha=0.5)
    plt.fill(m6.real,m6.imag,facecolor="blue",alpha=0.5)

問題の本質はデカルト座標系における「右上が＋方向(左下が-方向)」と考える伝統と、(その影響を受けた)複素平面における$(0+1i)^2=(0-1i)^2=-1$と考える伝統とその規約に従わない極座標系の振る舞いの衝突にあり、その矛盾が「3番目の複素数」kについて考えた時に噴出してくる点にあります。

i^2=j^2=k^2=^1

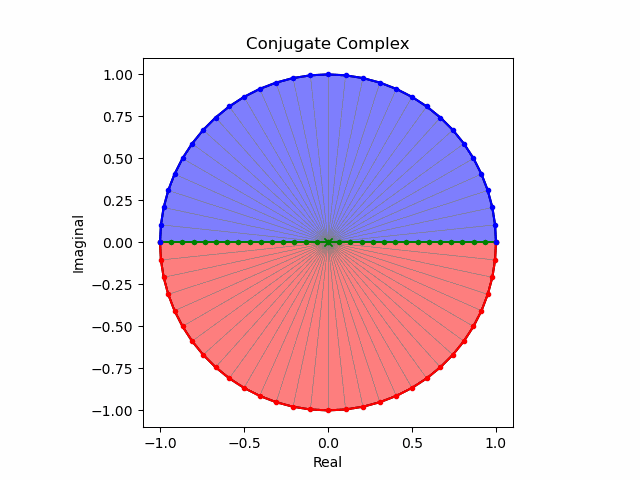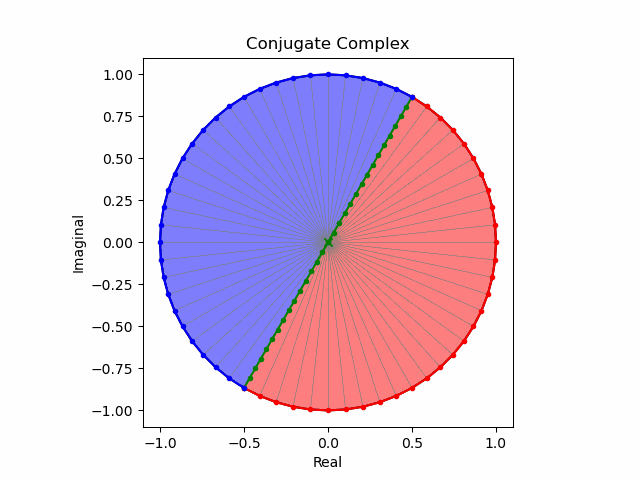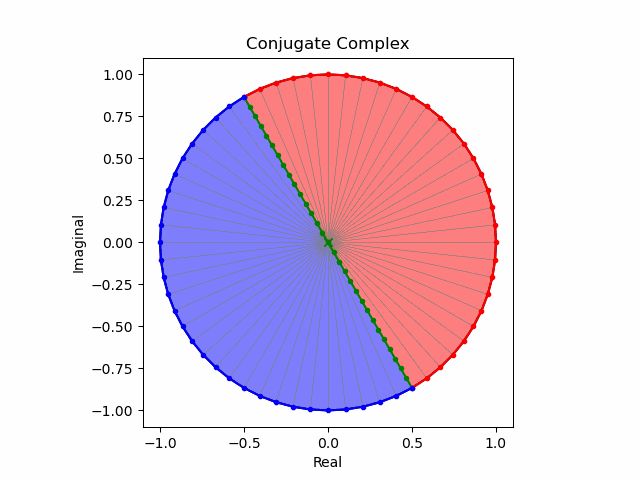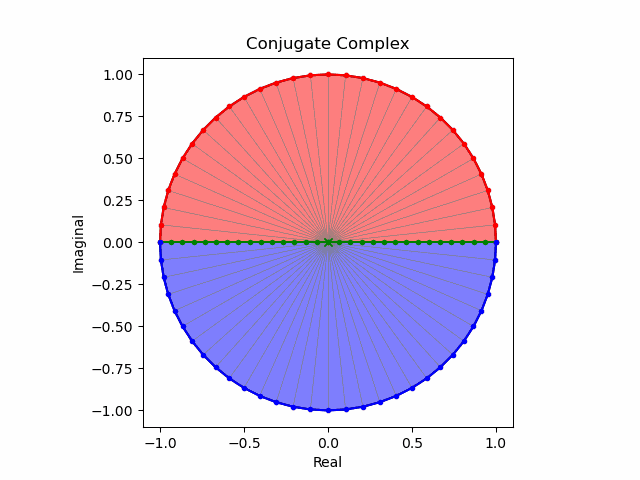
iもjもkも90度方向に2回回せば正反対を向く(それぞれ開始位置と終了位置が異なる事に注意)。伝統的複素数の規約から共役の結果も同じとなる。

i^2=-1

$i^2=(0+1i)^2=-1$(Z軸を中心とするXY面上における正方向への半回転)。$+x→-x$。

#タイムコード(Time Code) 
TC_jk=num.arange(0,31)
TC_wi=num.repeat(0,31)

ani = animation.FuncAnimation(fig, Circle_Rotation, interval=100,frames=31)
ani.save("output201.gif", writer="pillow")

その共役$(0-1i)^2=-1$

#タイムコード(Time Code) 
TC_0=num.arange(31,61)
TC_wi=TC_0[::-1]
TC_jk=num.repeat(0,30)

ani = animation.FuncAnimation(fig, Circle_Rotation, interval=100,frames=30)
ani.save("output210.gif", writer="pillow")

j^2=-1

$j^2=(0+1j)^2=-1$(X軸を中心とするYZ面上における正方向への半回転)。インジケーターの先端が$+z→-y$に推移。

#タイムコード(Time Code) 
TC_jk=num.arange(0,31)
TC_wi=num.repeat(0,31)

ani = animation.FuncAnimation(fig, Circle_Rotation, interval=100,frames=31)
ani.save("output201.gif", writer="pillow")

その共役$(0-1j)^2=-1$

#タイムコード(Time Code) 
TC_0=num.arange(31,61)
TC_jk=TC_0[::-1]
TC_wi=num.repeat(0,30)

ani = animation.FuncAnimation(fig, Circle_Rotation, interval=100,frames=30)
ani.save("output211.gif", writer="pillow")

k^2=-1

$k^2=-1$(X軸を中心とするYZ面上における正方向への半回転)。やはりインジケーターの先端が$+z→-y$に推移。

$k=(0+1i)(0-1j)$と考える場合
$k^2=(0+1k)^2=-1$

#タイムコード(Time Code) 
TC_jk=num.arange(0,31)
TC_wi=num.repeat(45,31)

ani = animation.FuncAnimation(fig, Circle_Rotation, interval=100,frames=31)
ani.save("output202.gif", writer="pillow")

その共役$(0-1k)^2=-1$

#タイムコード(Time Code) 
TC_0=num.arange(31,61)
TC_jk=TC_0[::-1]
TC_wi=num.repeat(45,30)

ani = animation.FuncAnimation(fig, Circle_Rotation, interval=100,frames=30)
ani.save("output212.gif", writer="pillow")

$k=(0+1i)(0+1j)$と考える場合
$k^2=(0+1k)^2=-1$

#タイムコード(Time Code) 
TC_jk=num.arange(0,31)
TC_wi=num.repeat(15,31)

ani = animation.FuncAnimation(fig, Circle_Rotation, interval=100,frames=31)
ani.save("output203.gif", writer="pillow")

その共役$(0-1k)^2=-1$

#タイムコード(Time Code) 
TC_0=num.arange(31,61)
TC_jk=TC_0[::-1]
TC_wi=num.repeat(15,30)

ani = animation.FuncAnimation(fig, Circle_Rotation, interval=100,frames=30)
ani.save("output213.gif", writer="pillow")

なぜ$k=(0+1i)(0-1j)$を「正方向」、$k=(0+1i)(0+1j)$を「負方向」と考えるかというとデカルト座標系の伝統に従って「右上が+方向である」と考えたがる人類の勝手な都合としか言い様がありません。

ij=k,jk=i,ki=j / ji=-k,kj=-i,ik=-j

かくして$ij=k,ji=-k$が成立し、それぞれの記号が入れ替え可能なので$ij=k,jk=i,ki=j$および$ji=-k,kj=-i,ik=-j$と一般化されるのです。

ij=k,ijk=-1 / ji=-k,ji-k=-1

ij=kの場合

#タイムコード(Time Code) 
TC_wi01=num.arange(0,15)
TC_wi02=num.repeat(15,15)
TC_wi=num.concatenate((TC_wi01,TC_wi02))

TC_jk01=num.repeat(0,15)
TC_jk02=num.arange(0,15)
TC_jk=num.concatenate((TC_jk01,TC_jk02))

ani = animation.FuncAnimation(fig, Circle_Rotation, interval=100,frames=30)
ani.save("output220.gif", writer="pillow")

ijk=-1の場合

#タイムコード(Time Code) 
TC_wi01=num.arange(0,15)
TC_wi02=num.repeat(15,15)
TC_wi03=num.arange(16,31)
TC_wi=num.concatenate((TC_wi01,TC_wi02,TC_wi03))

TC_jk01=num.repeat(0,15)
TC_jk02=num.arange(0,15)
TC_jk03=TC_jk02[::-1]
TC_jk=num.concatenate((TC_jk01,TC_jk02,TC_jk03))

ani = animation.FuncAnimation(fig, Circle_Rotation, interval=100,frames=45)
ani.save("output221.gif", writer="pillow")

ji=-kの場合

#タイムコード(Time Code) 

TC_wi01=num.repeat(0,15)
TC_wi02=num.arange(0,16)
TC_wi=num.concatenate((TC_wi01,TC_wi02))

TC_jk01=num.arange(0,15)
TC_jk02=num.repeat(15,16)
TC_jk=num.concatenate((TC_jk01,TC_jk02))

ani = animation.FuncAnimation(fig, Circle_Rotation, interval=100,frames=31)
ani.save("output230.gif", writer="pillow")

ji-k=-1の場合
iを戻す場合

#タイムコード(Time Code) 
TC_wi01=num.repeat(0,15)
TC_wi02=num.arange(0,16)
TC_wi03=TC_wi02[::-1]
TC_wi=num.concatenate((TC_wi01,TC_wi02,TC_wi03))

TC_jk01=num.arange(0,15)
TC_jk02=num.repeat(15,16)
TC_jk03=num.arange(16,32)
TC_jk=num.concatenate((TC_jk01,TC_jk02,TC_jk03))

ani = animation.FuncAnimation(fig, Circle_Rotation, interval=100,frames=46)
ani.save("output233.gif", writer="pillow")

jを戻す場合

#タイムコード(Time Code) 
TC_wi01=num.repeat(0,15)
TC_wi02=num.arange(0,16)
TC_wi03=num.repeat(16,32)
TC_wi=num.concatenate((TC_wi01,TC_wi02,TC_wi03))

TC_jk01=num.arange(0,15)
TC_jk02=num.repeat(15,16)
TC_jk03=TC_jk01[::-1]
TC_jk=num.concatenate((TC_jk01,TC_jk02,TC_jk03))

ani = animation.FuncAnimation(fig, Circle_Rotation, interval=100,frames=46)
ani.save("output235.gif", writer="pillow")

jk=i,jki=-1 / kj=-i,kj-i=-1

jk=iの場合

#タイムコード(Time Code) 
TC_wi01=num.repeat(0,15)
TC_wi02=num.arange(0,16)
TC_wi=num.concatenate((TC_wi01,TC_wi02))

TC_jk01=num.arange(0,16)
TC_jk02=TC_jk01[::-1]
TC_jk=num.concatenate((TC_jk01,TC_jk02))

ani = animation.FuncAnimation(fig, Circle_Rotation, interval=100,frames=31)
ani.save("output222.gif", writer="pillow")

jki=-1の場合

#タイムコード(Time Code) 
TC_wi01=num.repeat(0,15)
TC_wi02=num.arange(0,15)
TC_wi03=num.arange(16,32)
TC_wi=num.concatenate((TC_wi01,TC_wi02,TC_wi03))

TC_jk01=num.arange(0,15)
TC_jk02=TC_jk01[::-1]
TC_jk03=num.repeat(0,16)
TC_jk=num.concatenate((TC_jk01,TC_jk02,TC_jk03))

ani = animation.FuncAnimation(fig, Circle_Rotation, interval=100,frames=45)
ani.save("output223.gif", writer="pillow")

kj=-iの場合

#タイムコード(Time Code) 
TC_wi01=num.arange(0,15)
TC_wi02=num.repeat(15,16)
TC_wi=num.concatenate((TC_wi01,TC_wi02))
print(len(TC_wi))

TC_jk01=num.arange(0,15)
TC_jk02=num.arange(15,31)
TC_jk=num.concatenate((TC_jk01,TC_jk02))
print(len(TC_jk))

ani = animation.FuncAnimation(fig, Circle_Rotation, interval=100,frames=31)
ani.save("output236.gif", writer="pillow")

kj-i=-1の場合

#タイムコード(Time Code) 
TC_wi01=num.arange(0,15)
TC_wi02=num.repeat(15,16)
TC_wi03=TC_wi01[::-1]
TC_wi=num.concatenate((TC_wi01,TC_wi02,TC_wi03))

TC_jk01=num.arange(0,15)
TC_jk02=num.arange(15,31)
TC_jk03=num.repeat(31,16)
TC_jk=num.concatenate((TC_jk01,TC_jk02,TC_jk03))

ani = animation.FuncAnimation(fig, Circle_Rotation, interval=100,frames=45)
ani.save("output237.gif", writer="pillow")

ki=j,kij=-1 / ik=-j,ik-j=-1

ki=jの場合

#タイムコード(Time Code) 
TC_wi01=num.arange(0,15)
TC_wi02=num.arange(16,31)
TC_wi=num.concatenate((TC_wi01,TC_wi02))
#print(len(TC_wi))

TC_jk01=num.arange(45,60)
TC_jk02=num.repeat(45,45)
TC_jk=num.concatenate((TC_jk01[::-1],TC_jk02))
#print(len(TC_jk))

ani = animation.FuncAnimation(fig, Circle_Rotation, interval=100,frames=30)
ani.save("output226.gif", writer="pillow")

kij=-1の場合

#タイムコード(Time Code) 
TC_wi01=num.arange(0,15)
TC_wi02=num.arange(16,31)
TC_wi03=num.repeat(31,15)
TC_wi=num.concatenate((TC_wi01,TC_wi02,TC_wi03))

TC_jk01=num.arange(45,60)
TC_jk02=num.repeat(45,45)
TC_jk=num.concatenate((TC_jk01[::-1],TC_jk02,TC_jk01))

ani = animation.FuncAnimation(fig, Circle_Rotation, interval=100,frames=45)
ani.save("output227.gif", writer="pillow")

ik=-jの場合

#タイムコード(Time Code) 
TC_wi01=num.arange(0,15)
TC_wi02=num.arange(15,31)
TC_wi=num.concatenate((TC_wi01,TC_wi02))
#print(len(TC_wi))

TC_jk01=num.repeat(0,15)
TC_jk02=num.arange(45,61)
TC_jk=num.concatenate((TC_jk01,TC_jk02[::-1]))
#print(len(TC_jk))

ani = animation.FuncAnimation(fig, Circle_Rotation, interval=100,frames=31)
ani.save("output238.gif", writer="pillow")

ik-j=-1の場合

#タイムコード(Time Code) 
TC_wi01=num.arange(0,15)
TC_wi02=num.arange(15,30)
TC_wi03=num.repeat(30,16)
TC_wi=num.concatenate((TC_wi01,TC_wi02,TC_wi03))
print(len(TC_wi))

TC_jk01=num.repeat(0,16)
TC_jk02=num.arange(45,60)
TC_jk=num.concatenate((TC_jk01[::-1],TC_jk02[::-1],TC_jk02))
print(len(TC_jk))

ani = animation.FuncAnimation(fig, Circle_Rotation, interval=100,frames=45)
ani.save("output240.gif", writer="pillow")

実は四元数の設定には無数のバリエーションが存在します。
四元数を作ろう
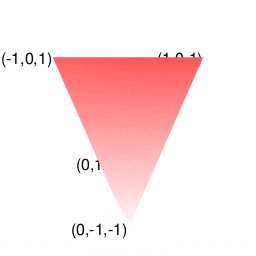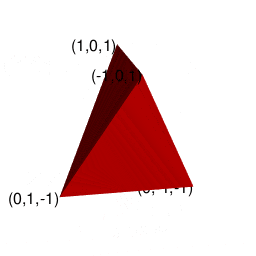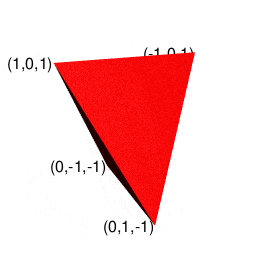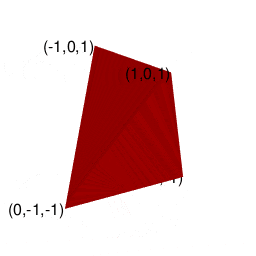
そのうち一般に知られているのは球面幾何学上における「対蹠間を2回直角に曲がって結ぶ経路がそれぞれ反対方向に曲がる」制約に従ったバージョンとなります(この制約を守らないと隣接する球面座標系への「乗り換え」が起こってしまう)。位相幾何学的には「2つの対蹠と球表面の頂点6個が興成する立方体」と重なります。

なお、こうした剛体の有限回転(回転の大きさが無視できない回転)の制約を乗り越える方法として以下も提案されています。
無限小回転1
無限小回転2

その幾何学的側面

ここでいう幾何学的側面については、以下の投稿をまとめる過程でその一環に触れる事になりました。
【Rで球面幾何学】正方形における平方対角線(Square diagonal)と立方体における立方対角線(Cubic diagonal)の関係について。
①まずは基本から。

1. i^2とはjかkの値が0で、残りがiと等価の特殊状況を指す(次元系の１レベルダウン)。さらに残りのjかkの値も0なら、答えは自明的にiとなり(次元系の2レベルダウン)、単なる直径、すなわちその円弧/球表面上に検出された任意の原蹠と対蹠のセットを結ぶ直線上に位置する任意の点の振る舞いに過ぎなくなる。
2. j^2とはiかkの値が0で、残りがjと等価の特殊状況を指す(次元系の１レベルダウン)。さらに残りのiかkの値も0なら、答えは自明的にjとなり(次元系の2レベルダウン)、単なる直径、すなわちその円弧/球表面上に検出された任意の原蹠と対蹠のセットを結ぶ直線上に位置する任意の点の振る舞いに過ぎなくなる。
3. k^2とはiかjの値が0で、残りがkと等価の特殊状況を指す(次元系の１レベルダウン)。さらに残りのiかjの値も0なら、答えは自明的にkとなり(次元系の2レベルダウン)、単なる直径、すなわちその円弧/球表面上に検出された任意の原蹠と対蹠のセットを結ぶ直線上に位置する任意の点の振る舞いに過ぎなくなる。

似た記述の繰り返しとなるのは、これがijk座標系をxyz座標系に射影(Projection)する問題に過ぎないからである(すなわちi=x,j=y,k=zと置いても、i=y,j=z,k=xと置いても、i=z,j=x,k=yと置いても操作内容自体に何ら影響が及ばない)。
射影 (集合論) - Wikipedia
かかる状況を可換(Commutative)という。
可換(カカン)とは - コトバンク
しかも単独射影に過ぎないから直積(Direct Product)の概念はまだ導入(Introduction)は必要とされない。

②そしてijkは「球面上に位置する原蹠と対蹠の間を2回直角に曲がって結ぶ３次元系の空間処理」に該当する。

1. もしi=0なら、必要とされる空間処理はjとkを巡る「円弧上に位置する原蹠と対蹠の間を1回直角に曲がって結ぶ2次元処理」にレベルダウンする。そしてさらにj=0の時のkを巡る空間処理、k=0の時のjを巡る空間処理は「円弧上に位置する原蹠と対蹠の間を1回も曲がらず直線で結ぶ1次元処理」にレベルダウンする。
2. もしj=0なら、必要とされる空間処理はiとkを巡る「円弧上に位置する原蹠と対蹠の間を1回直角に曲がって結ぶ2次元処理」にレベルダウンする。そしてさらにi=0の時のkを巡る空間処理、k=0の時のiを巡る空間処理は「円弧上に位置する原蹠と対蹠の間を1回も曲がらず直線で結ぶ1次元処理」にレベルダウンする。
3. もしk=0なら、必要とされる空間処理はiとkを巡る「円弧上に位置する原蹠と対蹠の間を1回直角に曲がって結ぶ2次元処理」にレベルダウンする。そしてさらにi=0の時のjを巡る空間処理、j=0の時のiを巡る空間処理は「円弧上に位置する原蹠と対蹠の間を1回も曲がらず直線で結ぶ1次元処理」にレベルダウンする。

このijk座標系のxyz座標系への単独射影操作も、それ自体は可換であり、かつやはりまだ直積の概念の導入は必要とされない。

③ところで「球面上に位置する原蹠と対蹠の間を2回直角に曲がって結ぶ３次元系の空間処理」をピタゴラスの平方定理の2回適用の形で遂行しようとすると可換性が破れる。まず

A=\sqrt{i^2+j^2}\\
\sqrt{A^2+k^2}

と計算する場合と、真逆に

A=\sqrt{k^2+2^2}\\
\sqrt{A^2+i^2}

と計算する場合では、途中で通る経路が重ならないのである。


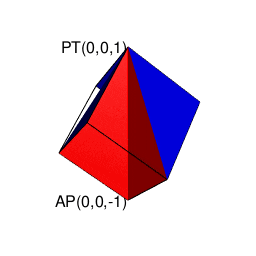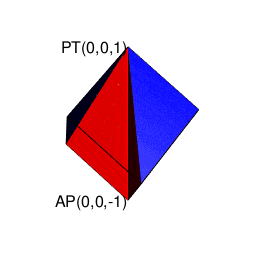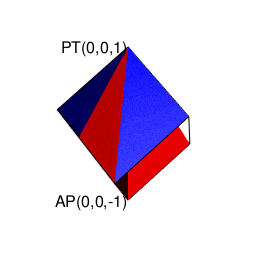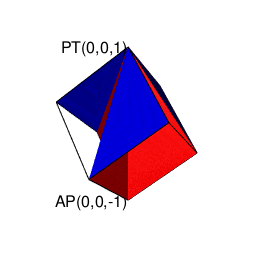
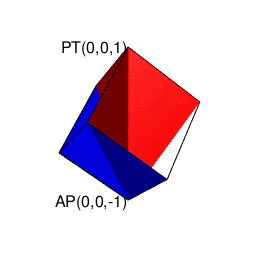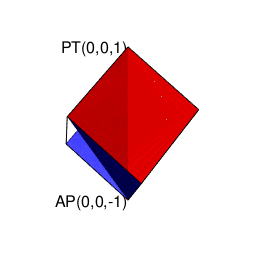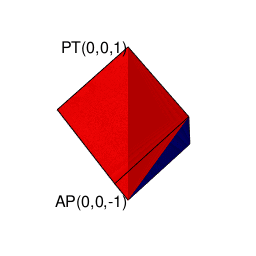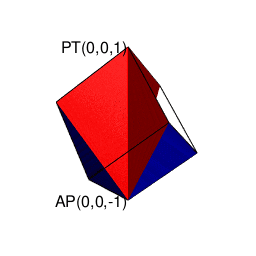
これは「円弧上に位置する原蹠と対蹠の間を1回も曲がらず直線で結ぶ1次元処理」において既に「原蹠から対蹠に向かうルート」と「対蹠から原蹠に向かうルート」の２つが存在する事に由来する。

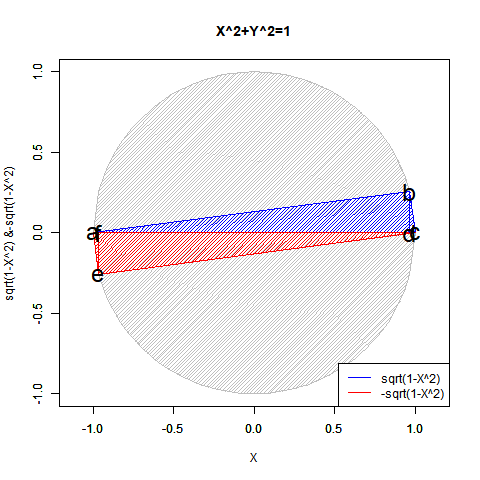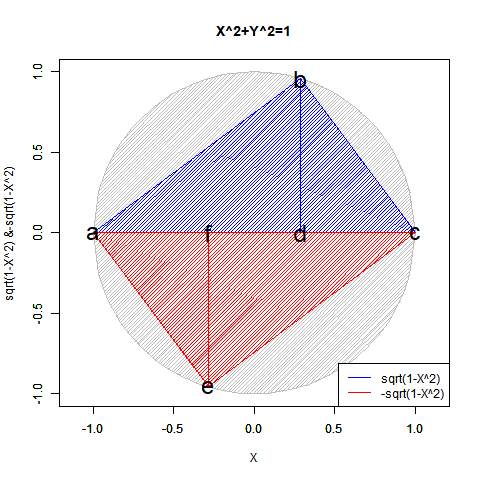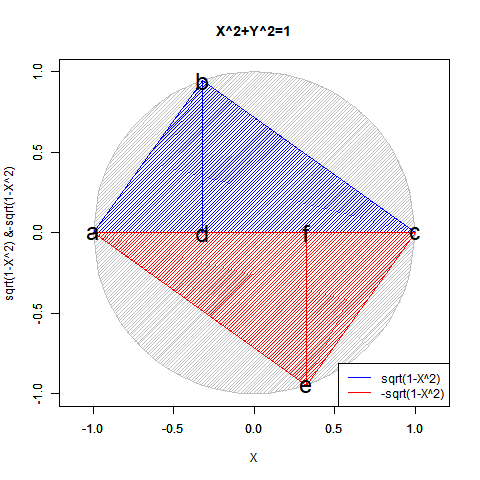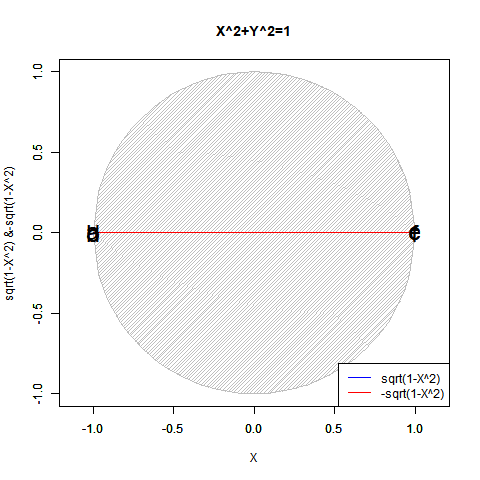
④そしてさらに計算結果にij=k,jk=i,ki=jの系列とji=-k,kj=-i,ik=-jの系列が存在するのは、例えば今回のプログラム実装に即した形で説明すると対象円に内接する正多角形の頂点座標計算にガウスが発見した「1の冪根の巡回性」を用いており、各頂点の検出順序がその値の符号によって逆転するからである。


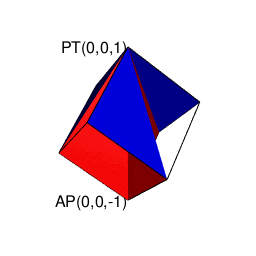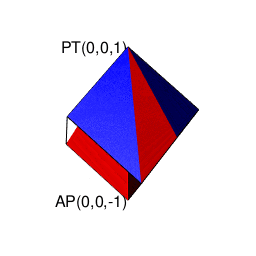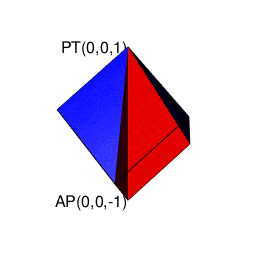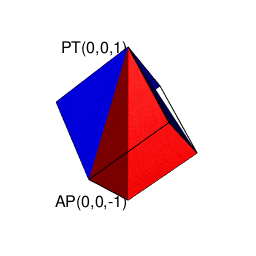
そう、極座表系(Polar Coordinate System)においては「円弧上に位置する原蹠と対蹠の間を1回も曲がらず直線で結ぶ1次元処理」が「円弧上に位置する原蹠と対蹠の間を1回直角に曲がって結ぶ2次元処理」を経て「球面上に位置する原蹠と対蹠の間を2回直角に曲がって結ぶ３次元系の空間処理」へと拡張される(あるいは逆に0入力によって次元数がレベルダウンする)のが自然な姿なのです。そして直交座標系（Rectangular Coordinate System/Orthogonal Coordinate System）の振る舞いとの最大の相違点はピタゴラスの定理から自明的に導かれる以下。

1. 円弧/球面上の任意の原蹠と対蹠のセットを１回も曲がらず結ぶ直線距離(つまり直径)は常に2。つまり2回分4進むと１周して原蹠に戻ってくる。
2. 円弧上の任意の原蹠と対蹠のセットを１回直角に曲がって辿り着くルートの最大距離はsqrt(2)２回分(2sqrt(2))。つまり4回分4sqrt(2)進むと１周して原蹠に戻ってくる。
3. 球面上の任意の原蹠と対蹠のセットを２回直角に曲がって辿り着くルートの最大距離は2/sqrt(3)3回分(6sqrt(3))。つまり6回分12/sqrt(3)進むと１周して原蹠に戻ってくる。
4. こうしたイメージの連続で我々は観念上「球面上の任意の原蹠と対蹠のセットを3以上回直角に曲がって辿り着くルート」も想定可能だが、その掌握はもはや直感的空間把握能力の限度を超えている。

古代より知られ、誰でも知り尽くしている筈のピタゴラスの定理は、こんな思わぬ秘密を隠し持ってきたのですね。かかるパラダイムシフトが確認された時点で、以下続報…

【追記】思わぬ形で思わぬ部分が日常生活の中に浸透していた事を発見…そうか、中身の液体との接触面積も、従って廃棄重量も最小になるのが嬉しい？
【Rで球面幾何学】正四面体と正六面体と正八面体の連続性と「テトラパックの思わぬ正体」について。