【オイラーの多面体定理と正多面体】正四面体と正六面体と正八面体の連続性と「テトラパックの思わぬ正体」について。

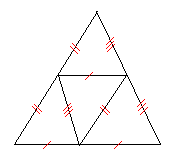
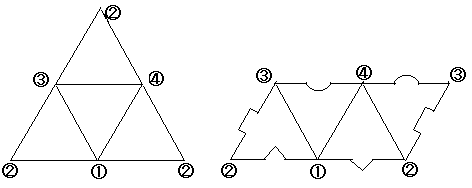
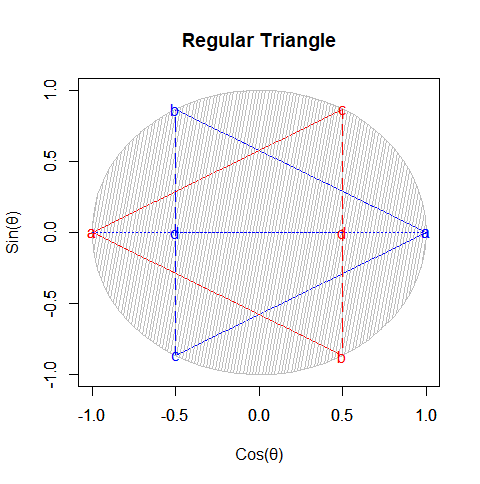
まずは基本中の基本から。正三角形(Reguler Triangle)は三辺比2:1:sqrt(3)の直角三角形(Right Triangle)２つから構成されています。

#分割数Nod(Number of divide)=3

NoD<-3
#円周分割数列(Sequence of Divided Circumference)
SoDC<-seq(0,2*pi,length=NoD+1)
#円周上の三角形の頂点を集める。
cx_nomal=cos(SoDC)
cy_nomal=sin(SoDC)
cx_reverse=cos(SoDC+pi)
cy_reverse=sin(SoDC+pi)
#グラフ描画
plot(cx_nomal,cy_nomal,col=rgb(0,0,1),type="l",xlim=c(-1,1),ylim=c(-1,1),main="Regular Triangle",xlab="Cos(θ)",ylab="Sin(θ)",lwd=1.2)
par(new=T)
plot(cx_reverse,cy_reverse,col=rgb(1,0,0),type="l",xlim=c(-1,1),ylim=c(-1,1),main="",xlab="",ylab="",lwd=1.2)
#背景円の塗り潰し
Circumference<-seq(0,2*pi,length=60)
cx_circle=cos(Circumference)
cy_circle=sin(Circumference)
polygon(cx_circle, #x
cy_circle, #y
density=c(30), #塗りつぶす濃度
angle=c(45),　 　　　#塗りつぶす斜線の角度
col=c(200,200,200)) 　#塗りつぶす色

#文字追加
text(cx_nomal,cy_nomal, labels=c("a","b","c"),col=rgb(0,0,1))
text(cx_reverse,cy_reverse, labels=c("a","b","c"),col=rgb(1,0,0))
#補助線と補助文字追加
segments(1,0,-1,0,lty=3,col=rgb(0,0,0))
text(cx_nomal[2],0, labels=c("d"),col=rgb(0,0,1))
text(cx_reverse[2],0, labels=c("d"),col=rgb(1,0,0))

	ac	ad	cd
1	sqrt(3)	2	1
2	1	2/sqrt(3)	1/sqrt(3)
3	1/2	1/sqrt(3)	1/(2*sqrt(3))

 #三角比(Triangle Ratio)一覧

angle_ac<-c("sqrt(3)","1","1/2")
angle_ad<-c("2","2/sqrt(3)","1/sqrt(3)")
angle_cd<-c("1","1/sqrt(3)","1/(2*sqrt(3))")

library(xtable)
TR01<- data.frame(ac=angle_ac,ad=angle_ad,cd=angle_cd)
print(xtable(TR01),type="html")

それでは「騙し絵版画家」エッシャー（Maurits Cornelis Escher, 1898年～1972年）も注目した以下の立体図形の組み合わせ方について考えてみましょう。

正三角形(Regular Triangle)にはその角度(60度=2/3πラジアン)の和が360度(2πラジアン)となる組み合わせ（6個）がある上、４個の組み合わせが自己相似形となる為、正方形や正六角形(実体として正三角形を6個集めたもの)同様に単独で平面充填(Tiling)性を備える正平面充填形 (Regular Tessellation)に分類されます。
大人になってからの再学習:平面充当
平面充填 - Wikipedia
その延長線上で一見、正四面体(Regular Tetrahedron)もまた空間充当（Space-filling）性を備えているかの様に見えるのですが…

library(rgl)
#分割数Nod(Number of divide)=3
NoD<-3
#円周分割数列(Sequence of Divided Circumference)
SoDC<-seq(0,2*pi,length=NoD+1)
#座標起点
texts3d(-1,0,0,texts=c("(-1,0,0)"),col=rgb(1,0,0),adj=1.0)
texts3d(1,0,0,texts=c("(1,0,0)"),col=rgb(0,0,1),adj=1.0)
#-1を起点(start point)とする正四面体（Normal(Regular)Tetrahedron）
my<-cos(SoDC)
mz<-sin(SoDC)
mx<-c(1/3,1/3,1/3,1/3)
triangles3d(c(-1,mx[2:3]),c(0,my[2:3]),c(0,mz[2:3]),col=rgb(1,0,0),lwd=1)
triangles3d(c(mx[1],-1,mx[3]),c(my[1],0,my[3]),c(mz[1],0,mz[3]),col=rgb(1,0,0),lwd=1)
triangles3d(c(mx[1:2],-1),c(my[1:2],0),c(mz[1:2],0),col=rgb(1,0,0),lwd=1)
triangles3d(mx[1:3],my[1:3],mz[1:3],col=rgb(1,0,0),lwd=1)
#1を起点(start point)とする逆正四面体（Reverse(Regular)Tetrahedron）
py<-cos(SoDC+pi)
pz<-sin(SoDC+pi)
px<-c(-1/3,-1/3,-1/3,-1/3)
triangles3d(c(1,px[2:3]),c(0,py[2:3]),c(0,pz[2:3]),col=rgb(0,0,1),lwd=1)
triangles3d(c(px[1],1,px[3]),c(py[1],0,py[3]),c(pz[1],0,pz[3]),col=rgb(0,0,1),lwd=1)
triangles3d(c(px[1:2],1),c(py[1:2],0),c(pz[1:2],0),col=rgb(0,0,1),lwd=1)
triangles3d(px[1:3],py[1:3],pz[1:3],col=rgb(0,0,1),lwd=1)

#アニメーション
movie3d(spin3d(axis=c(0,0,1),rpm=5),duration=10,fps=25,movie="C:/Users/81806/Desktop/Markdown/Tetrahedron03")

透視図化すると胡麻化してる箇所が浮かび上がってきます。要するに隠された内部でこっそり誤魔化しが発生してるんですね。

library(rgl)
#分割数Nod(Number of divide)=3
NoD<-3
#円周分割数列(Sequence of Divided Circumference)
SoDC<-seq(0,2*pi,length=NoD+1)
#座標起点
texts3d(-1,0,0,texts=c("(-1,0,0)"),col=rgb(1,0,0),adj=1.0)
texts3d(1,0,0,texts=c("(1,0,0)"),col=rgb(0,0,1),adj=1.0)
#texts3d(-5/3,0,0,texts=c("(-5/3,0,0)"),col=rgb(0,0,1),adj=1.0)
#texts3d(5/3,0,0,texts=c("(5/3,0,0)"),col=rgb(1,0,0),adj=1.0)
#-1を起点(start point)とする正四面体（Normal(Regular)Tetrahedron）
my<-cos(SoDC)
mz<-sin(SoDC)
mx<-c(1/3,1/3,1/3,1/3)
lines3d(c(-1,mx[1]),c(0,my[1]),c(0,mz[1]),col=rgb(1,0,0),lwd=1)
lines3d(c(-1,mx[2]),c(0,my[2]),c(0,mz[2]),col=rgb(1,0,0),lwd=1)
lines3d(c(-1,mx[3]),c(0,my[3]),c(0,mz[3]),col=rgb(1,0,0),lwd=1)
triangles3d(mx[1:3],my[1:3],mz[1:3],col=rgb(1,0,0),lwd=1)
#lines3d(c(mx[1],mx[2]),c(my[1],my[2]),c(mz[1],mz[2]),col=rgb(1,0,0),lwd=1)
#lines3d(c(mx[2],mx[3]),c(my[2],my[3]),c(mz[2],mz[3]),col=rgb(1,0,0),lwd=1)
#lines3d(c(mx[3],mx[1]),c(my[3],my[1]),c(mz[3],mz[1]),col=rgb(1,0,0),lwd=1)
#lines3d(c(5/3,mx[1]),c(0,my[1]),c(0,mz[1]),col=rgb(1,0,0),lwd=1)
#lines3d(c(5/3,mx[2]),c(0,my[2]),c(0,mz[2]),col=rgb(1,0,0),lwd=1)
#lines3d(c(5/3,mx[3]),c(0,my[3]),c(0,mz[3]),col=rgb(1,0,0),lwd=1)

#1を起点(start point)とする逆正四面体（Reverse(Regular)Tetrahedron）
py<-cos(SoDC+pi)
pz<-sin(SoDC+pi)
px<-c(-1/3,-1/3,-1/3,-1/3)
lines3d(c(1,px[1]),c(0,py[1]),c(0,pz[1]),col=rgb(0,0,1),lwd=1)
lines3d(c(1,px[2]),c(0,py[2]),c(0,pz[2]),col=rgb(0,0,1),lwd=1)
lines3d(c(1,px[3]),c(0,py[3]),c(0,pz[3]),col=rgb(0,0,1),lwd=1)
triangles3d(px[1:3],py[1:3],pz[1:3],col=rgb(0,0,1),lwd=1)
#lines3d(c(px[1],px[2]),c(py[1],py[2]),c(pz[1],pz[2]),col=rgb(1,0,0),lwd=1)
#lines3d(c(px[2],px[3]),c(py[2],py[3]),c(pz[2],pz[3]),col=rgb(1,0,0),lwd=1)
#lines3d(c(px[3],px[1]),c(py[3],py[1]),c(pz[3],pz[1]),col=rgb(1,0,0),lwd=1)
#lines3d(c(-5/3,px[1]),c(0,py[1]),c(0,pz[1]),col=rgb(1,0,0),lwd=1)
#lines3d(c(-5/3,px[2]),c(0,py[2]),c(0,pz[2]),col=rgb(1,0,0),lwd=1)
#lines3d(c(-5/3,px[3]),c(0,py[3]),c(0,pz[3]),col=rgb(1,0,0),lwd=1)

#アニメーション
movie3d(spin3d(axis=c(0,0,1),rpm=5),duration=10,fps=25,movie="C:/Users/81806/Desktop/Markdown/Tetrahedron01")

2個連ねるとさらに周期のズレが明瞭に見て取れます。

library(rgl)
#分割数Nod(Number of divide)=3
NoD<-3
#円周分割数列(Sequence of Divided Circumference)
SoDC<-seq(0,2*pi,length=NoD+1)
#座標起点
texts3d(-1,0,0,texts=c("(-1,0,0)"),col=rgb(1,0,0),adj=1.0)
texts3d(1,0,0,texts=c("(1,0,0)"),col=rgb(0,0,1),adj=1.0)
texts3d(-5/3,0,0,texts=c("(-5/3,0,0)"),col=rgb(0,0,1),adj=1.0)
texts3d(5/3,0,0,texts=c("(5/3,0,0)"),col=rgb(1,0,0),adj=1.0)
#-1を起点(start point)とする正四面体（Normal(Regular)Tetrahedron）
my<-cos(SoDC)
mz<-sin(SoDC)
mx<-c(1/3,1/3,1/3,1/3)
lines3d(c(-1,mx[1]),c(0,my[1]),c(0,mz[1]),col=rgb(1,0,0),lwd=1)
lines3d(c(-1,mx[2]),c(0,my[2]),c(0,mz[2]),col=rgb(1,0,0),lwd=1)
lines3d(c(-1,mx[3]),c(0,my[3]),c(0,mz[3]),col=rgb(1,0,0),lwd=1)
triangles3d(mx[1:3],my[1:3],mz[1:3],col=rgb(1,0,0),lwd=1)
#lines3d(c(mx[1],mx[2]),c(my[1],my[2]),c(mz[1],mz[2]),col=rgb(1,0,0),lwd=1)
#lines3d(c(mx[2],mx[3]),c(my[2],my[3]),c(mz[2],mz[3]),col=rgb(1,0,0),lwd=1)
#lines3d(c(mx[3],mx[1]),c(my[3],my[1]),c(mz[3],mz[1]),col=rgb(1,0,0),lwd=1)
lines3d(c(5/3,mx[1]),c(0,my[1]),c(0,mz[1]),col=rgb(1,0,0),lwd=1)
lines3d(c(5/3,mx[2]),c(0,my[2]),c(0,mz[2]),col=rgb(1,0,0),lwd=1)
lines3d(c(5/3,mx[3]),c(0,my[3]),c(0,mz[3]),col=rgb(1,0,0),lwd=1)

#1を起点(start point)とする逆正四面体（Reverse(Regular)Tetrahedron）
py<-cos(SoDC+pi)
pz<-sin(SoDC+pi)
px<-c(-1/3,-1/3,-1/3,-1/3)
lines3d(c(1,px[1]),c(0,py[1]),c(0,pz[1]),col=rgb(0,0,1),lwd=1)
lines3d(c(1,px[2]),c(0,py[2]),c(0,pz[2]),col=rgb(0,0,1),lwd=1)
lines3d(c(1,px[3]),c(0,py[3]),c(0,pz[3]),col=rgb(0,0,1),lwd=1)
triangles3d(px[1:3],py[1:3],pz[1:3],col=rgb(0,0,1),lwd=1)
#lines3d(c(px[1],px[2]),c(py[1],py[2]),c(pz[1],pz[2]),col=rgb(1,0,0),lwd=1)
#lines3d(c(px[2],px[3]),c(py[2],py[3]),c(pz[2],pz[3]),col=rgb(1,0,0),lwd=1)
#lines3d(c(px[3],px[1]),c(py[3],py[1]),c(pz[3],pz[1]),col=rgb(1,0,0),lwd=1)

lines3d(c(-5/3,px[1]),c(0,py[1]),c(0,pz[1]),col=rgb(0,0,1),lwd=1)
lines3d(c(-5/3,px[2]),c(0,py[2]),c(0,pz[2]),col=rgb(0,0,1),lwd=1)
lines3d(c(-5/3,px[3]),c(0,py[3]),c(0,pz[3]),col=rgb(0,0,1),lwd=1)

#アニメーション
movie3d(spin3d(axis=c(0,0,1),rpm=5),duration=10,fps=25,movie="C:/Users/81806/Desktop/Markdown/Tetrahedron02")

空間充填立体

T：三角形を２倍に拡大すると面積は４倍になります。図で示すと一目瞭然です。

つまり真ん中の三角形が中点連結定理(midpoint(connector)theorem)で合同となり、相似比1:2だから面積比1^2:2^2=1:4となるからです。では、立体だったらどうでしょう。正四面体(Regular Tetrahedron)で考えてみましょう。正四面体の各辺を２倍にします。同じ大きさの正四面体を何個か作り並べてみます。体積比1^3:2^3=1:8)ですから8個の正四面体が入るはずです。

写真のように正四面体を３個並べて真ん中に4個目を置いてみます。この上に正四面体のせようとしても上手くいきません。正四面体を隙間無く充填することはできないのです。そこで、真ん中の正四面体を取り、代わりにどんな立体が入るのか考えてみましょう…そうです、ずばり正八面体(Regular Octahedron)です。

正四面体 - Wikipedia

4枚の合同な正三角形を面とする四面体で、対角線が存在しない。
①面数4、辺数6、頂点数4。あらゆる多面体で最少の数であり、またパスカルの三角形第5段2～4番目の数字と重なる。
【初心者向け】パスカルの三角形と二項定理または二項展開
②頂点形状は正三角形であり、辺3本と正三角形3枚が集まるが、こちらはパスカルの三角形第4段2、3番目の数字と重なる。
【初心者向け】パスカルの三角形と二項定理または二項展開

③立方体(Regular Hexahedron) (±1, ±1, ±1)の4つの頂点(1,1,1),(1,-1,-1),(-1,1,-1),(-1,-1,1) を結べば正四面体になる。
正六面体 - Wikipedia

④正四面体の辺の中点を結べば、正八面体(Regular Octahedron)になる。このとき4個の正四面体ができる。逆に正八面体の互い違いの4面を延長すると、正四面体になる。正四面体単独での空間充填は出来ないが、正八面体と組み合わせた空間充填は可能である。
正八面体 - Wikipedia

展開図は2通りあり、一方は正三角形、もう一方は平行四辺形になる。

自らと双対(dual, duality)である（自己双対多面体）。

作図過程は以下。
まず立方体における平行対角線と立方対角線に注目する。

library(rgl)
#頂点座標=8個
texts3d(0,0,0,texts=c("(0,0,0)"),col=rgb(0,0,0),adj=1.0)
texts3d(1,0,0,texts=c("(1,0,0)"),col=rgb(0,0,0),adj=1.0)
texts3d(0,1,0,texts=c("(0,1,0)"),col=rgb(0,0,0),adj=1.0)
texts3d(1,1,0,texts=c("(1,1,0)"),col=rgb(0,0,0),adj=1.0)
texts3d(0,0,1,texts=c("(0,0,1)"),col=rgb(0,0,0),adj=1.0)
texts3d(1,0,1,texts=c("(1,0,1)"),col=rgb(0,0,0),adj=1.0)
texts3d(0,1,1,texts=c("(0,1,1)"),col=rgb(0,0,0),adj=1.0)
texts3d(1,1,1,texts=c("(1,1,1)"),col=rgb(0,0,0),adj=1.0)
#正六面体(Square)本体=6面

lines3d(c(0,1,1,0,0),c(0,0,1,1,0),c(0,0,0,0,0),col=rgb(0,0,0),lwd=1)
lines3d(c(0,1,1,0,0),c(0,0,1,1,0),c(1,1,1,1,1),col=rgb(0,0,0),lwd=1)
lines3d(c(0,0),c(0,0),c(0,1),col=rgb(0,0,0),lwd=1)
lines3d(c(1,1),c(0,0),c(0,1),col=rgb(0,0,0),lwd=1)
lines3d(c(0,0),c(1,1),c(0,1),col=rgb(0,0,0),lwd=1)
lines3d(c(1,1),c(1,1),c(0,1),col=rgb(0,0,0),lwd=1)

#平方対角線(長さsqrt(2))=6面*2=12本
lines3d(c(0,1),c(0,1),c(0,0),col=rgb(0,1,0),lwd=1)
lines3d(c(0,1),c(1,0),c(0,0),col=rgb(0,1,0),lwd=1)
lines3d(c(0,1),c(0,1),c(1,1),col=rgb(0,1,0),lwd=1)
lines3d(c(0,0),c(0,1),c(0,1),col=rgb(0,1,0),lwd=1)
lines3d(c(0,1),c(1,0),c(1,1),col=rgb(0,1,0),lwd=1)
lines3d(c(0,0),c(0,1),c(1,0),col=rgb(0,1,0),lwd=1)
lines3d(c(0,1),c(0,0),c(0,1),col=rgb(0,1,0),lwd=1)
lines3d(c(0,1),c(0,0),c(1,0),col=rgb(0,1,0),lwd=1)
lines3d(c(1,1),c(0,1),c(1,0),col=rgb(0,1,0),lwd=1)
lines3d(c(1,1),c(0,1),c(0,1),col=rgb(0,1,0),lwd=1)
lines3d(c(0,1),c(1,1),c(1,0),col=rgb(0,1,0),lwd=1)
lines3d(c(0,1),c(1,1),c(0,1),col=rgb(0,1,0),lwd=1)

#立方対角線(長さsqrt(3))=3本

lines3d(c(0,1),c(0,1),c(0,1),col=rgb(0,0,1),lwd=1)
lines3d(c(0,1),c(1,0),c(1,0),col=rgb(0,0,1),lwd=1)
lines3d(c(0,1),c(0,1),c(1,0),col=rgb(0,0,1),lwd=1)

#アニメーション
movie3d(spin3d(axis=c(0,0,1),rpm=5),duration=10,fps=25,movie="C:/Users/81806/Desktop/Markdown/square001") 

平方対角線同士を結ぶと２つの正四面体が現れる。

library(rgl)
#頂点座標=8個
texts3d(0,0,0,texts=c("(0,0,0)"),col=rgb(0,0,0),adj=1.0)
texts3d(1,0,0,texts=c("(1,0,0)"),col=rgb(0,0,0),adj=1.0)
texts3d(0,1,0,texts=c("(0,1,0)"),col=rgb(0,0,0),adj=1.0)
texts3d(1,1,0,texts=c("(1,1,0)"),col=rgb(0,0,0),adj=1.0)
texts3d(0,0,1,texts=c("(0,0,1)"),col=rgb(0,0,0),adj=1.0)
texts3d(1,0,1,texts=c("(1,0,1)"),col=rgb(0,0,0),adj=1.0)
texts3d(0,1,1,texts=c("(0,1,1)"),col=rgb(0,0,0),adj=1.0)
texts3d(1,1,1,texts=c("(1,1,1)"),col=rgb(0,0,0),adj=1.0)
#正六面体(Square)本体=6面

lines3d(c(0,1,1,0,0),c(0,0,1,1,0),c(0,0,0,0,0),col=rgb(0,0,0),lwd=1)
lines3d(c(0,1,1,0,0),c(0,0,1,1,0),c(1,1,1,1,1),col=rgb(0,0,0),lwd=1)
lines3d(c(0,0),c(0,0),c(0,1),col=rgb(0,0,0),lwd=1)
lines3d(c(1,1),c(0,0),c(0,1),col=rgb(0,0,0),lwd=1)
lines3d(c(0,0),c(1,1),c(0,1),col=rgb(0,0,0),lwd=1)
lines3d(c(1,1),c(1,1),c(0,1),col=rgb(0,0,0),lwd=1)

#平方対角線(長さsqrt(2))=6面*2=12本
lines3d(c(0,1),c(0,1),c(0,0),col=rgb(0,1,0),lwd=1)
lines3d(c(0,1),c(1,0),c(0,0),col=rgb(0,1,0),lwd=1)
lines3d(c(0,1),c(0,1),c(1,1),col=rgb(0,1,0),lwd=1)
lines3d(c(0,0),c(0,1),c(0,1),col=rgb(0,1,0),lwd=1)
lines3d(c(0,1),c(1,0),c(1,1),col=rgb(0,1,0),lwd=1)
lines3d(c(0,0),c(0,1),c(1,0),col=rgb(0,1,0),lwd=1)
lines3d(c(0,1),c(0,0),c(0,1),col=rgb(0,1,0),lwd=1)
lines3d(c(0,1),c(0,0),c(1,0),col=rgb(0,1,0),lwd=1)
lines3d(c(1,1),c(0,1),c(1,0),col=rgb(0,1,0),lwd=1)
lines3d(c(1,1),c(0,1),c(0,1),col=rgb(0,1,0),lwd=1)
lines3d(c(0,1),c(1,1),c(1,0),col=rgb(0,1,0),lwd=1)
lines3d(c(0,1),c(1,1),c(0,1),col=rgb(0,1,0),lwd=1)

#立方対角線(長さsqrt(3))=3本

lines3d(c(0,1),c(0,1),c(0,1),col=rgb(0,0,1),lwd=1)
lines3d(c(0,1),c(1,0),c(1,0),col=rgb(0,0,1),lwd=1)
lines3d(c(0,1),c(0,1),c(1,0),col=rgb(0,0,1),lwd=1)

#正四面体(1辺sqrt(2))=2個(000起点)
triangles3d(c(0,1,1),c(0,1,0),c(0,0,1),col=rgb(0,0,1),lwd=1)
triangles3d(c(0,1,0),c(0,0,1),c(0,1,1),col=rgb(0,0,1),lwd=1)
triangles3d(c(0,0,1),c(0,1,1),c(0,1,0),col=rgb(0,0,1),lwd=1)
triangles3d(c(1,1,0),c(1,0,1),c(0,1,1),col=rgb(0,0,1),lwd=1)

#正四面体(1辺sqrt(2))=2個(111起点)
triangles3d(c(1,0,0),c(1,1,0),c(1,0,1),col=rgb(1,0,0),lwd=1)
triangles3d(c(1,0,1),c(1,1,0),c(1,0,0),col=rgb(1,0,0),lwd=1)
triangles3d(c(1,1,0),c(1,0,0),c(1,0,1),col=rgb(1,0,0),lwd=1)
triangles3d(c(0,0,1),c(0,1,0),c(1,0,0),col=rgb(1,0,0),lwd=1)

#アニメーション
movie3d(spin3d(axis=c(0,0,1),rpm=5),duration=10,fps=25,movie="~/Desktop/triangles001") 

そして2つの正四面体の交点として正八面体が現れる。

library(rgl)
#頂点座標=8個
texts3d(0,0,0,texts=c("(0,0,0)"),col=rgb(0,0,0),adj=1.0)
texts3d(1,0,0,texts=c("(1,0,0)"),col=rgb(0,0,0),adj=1.0)
texts3d(0,1,0,texts=c("(0,1,0)"),col=rgb(0,0,0),adj=1.0)
texts3d(1,1,0,texts=c("(1,1,0)"),col=rgb(0,0,0),adj=1.0)
texts3d(0,0,1,texts=c("(0,0,1)"),col=rgb(0,0,0),adj=1.0)
texts3d(1,0,1,texts=c("(1,0,1)"),col=rgb(0,0,0),adj=1.0)
texts3d(0,1,1,texts=c("(0,1,1)"),col=rgb(0,0,0),adj=1.0)
texts3d(1,1,1,texts=c("(1,1,1)"),col=rgb(0,0,0),adj=1.0)
#正六面体(Square)本体=6面

lines3d(c(0,1,1,0,0),c(0,0,1,1,0),c(0,0,0,0,0),col=rgb(0,0,0),lwd=1)
lines3d(c(0,1,1,0,0),c(0,0,1,1,0),c(1,1,1,1,1),col=rgb(0,0,0),lwd=1)
lines3d(c(0,0),c(0,0),c(0,1),col=rgb(0,0,0),lwd=1)
lines3d(c(1,1),c(0,0),c(0,1),col=rgb(0,0,0),lwd=1)
lines3d(c(0,0),c(1,1),c(0,1),col=rgb(0,0,0),lwd=1)
lines3d(c(1,1),c(1,1),c(0,1),col=rgb(0,0,0),lwd=1)

#平方対角線(長さsqrt(2))=6面*2=12本
lines3d(c(0,1),c(0,1),c(0,0),col=rgb(0,1,0),lwd=1)
lines3d(c(0,1),c(1,0),c(0,0),col=rgb(0,1,0),lwd=1)
lines3d(c(0,1),c(0,1),c(1,1),col=rgb(0,1,0),lwd=1)
lines3d(c(0,0),c(0,1),c(0,1),col=rgb(0,1,0),lwd=1)
lines3d(c(0,1),c(1,0),c(1,1),col=rgb(0,1,0),lwd=1)
lines3d(c(0,0),c(0,1),c(1,0),col=rgb(0,1,0),lwd=1)
lines3d(c(0,1),c(0,0),c(0,1),col=rgb(0,1,0),lwd=1)
lines3d(c(0,1),c(0,0),c(1,0),col=rgb(0,1,0),lwd=1)
lines3d(c(1,1),c(0,1),c(1,0),col=rgb(0,1,0),lwd=1)
lines3d(c(1,1),c(0,1),c(0,1),col=rgb(0,1,0),lwd=1)
lines3d(c(0,1),c(1,1),c(1,0),col=rgb(0,1,0),lwd=1)
lines3d(c(0,1),c(1,1),c(0,1),col=rgb(0,1,0),lwd=1)

#立方対角線(長さsqrt(3))=3本

lines3d(c(0,1),c(0,1),c(0,1),col=rgb(0,0,1),lwd=1)
lines3d(c(0,1),c(1,0),c(1,0),col=rgb(0,0,1),lwd=1)
lines3d(c(0,1),c(0,1),c(1,0),col=rgb(0,0,1),lwd=1)

#正八面体(1辺sqrt(2))
triangles3d(c(1,1/2,1/2),c(1/2,1,1/2),c(1/2,1/2,0),col=rgb(0,1,0),lwd=1)
triangles3d(c(1/2,0,1/2),c(1,1/2,1/2),c(1/2,1/2,0),col=rgb(0,1,0),lwd=1)
triangles3d(c(0,1/2,1/2),c(1/2,0,1/2),c(1/2,1/2,0),col=rgb(0,1,0),lwd=1)
triangles3d(c(1/2,1,1/2),c(0,1/2,1/2),c(1/2,1/2,0),col=rgb(0,1,0),lwd=1)

triangles3d(c(1,1/2,1/2),c(1/2,1,1/2),c(1/2,1/2,1),col=rgb(0,1,0),lwd=1)
triangles3d(c(1/2,0,1/2),c(1,1/2,1/2),c(1/2,1/2,1),col=rgb(0,1,0),lwd=1)
triangles3d(c(0,1/2,1/2),c(1/2,0,1/2),c(1/2,1/2,1),col=rgb(0,1,0),lwd=1)
triangles3d(c(1/2,1,1/2),c(0,1/2,1/2),c(1/2,1/2,1),col=rgb(0,1,0),lwd=1)

#アニメーション
movie3d(spin3d(axis=c(0,0,1),rpm=5),duration=10,fps=25,movie="~/Desktop/triangles004") 

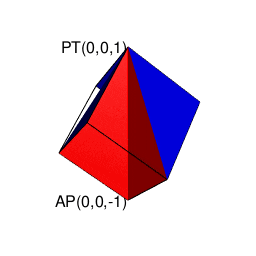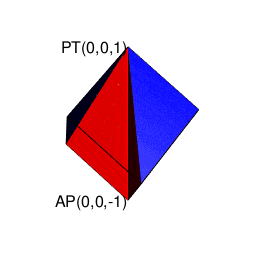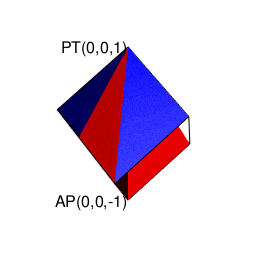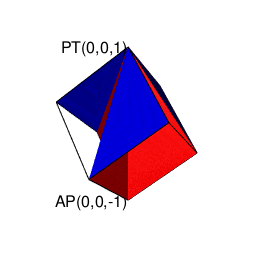
また正四面体は正六面体や正十二面体同様「頭蹠と対蹠にそれぞれ正三角形を３枚集めた奇数図形(不安定状態)」から出発して安定した偶数状態に到達した結果とも見て取れるのです。

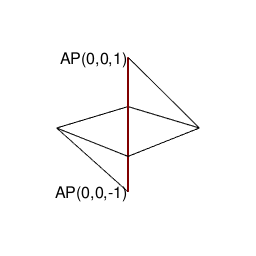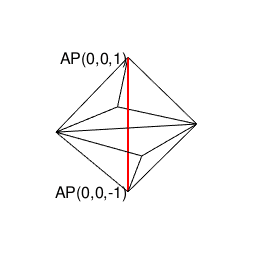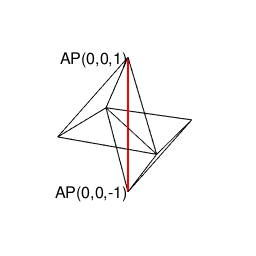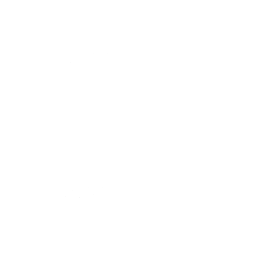
library(rgl)
#分割数Nod(Number of divide)=4
NoD<-4
#円周分割数列(Sequence of Divided Circumference)
SoDC<-seq(0,2*pi,length=NoD+1)

#原蹠(PorTal)
portal_i<-0
portal_j<-0
portal_k<-1
portal_text=paste0("AP(",portal_i,",",portal_j,",",portal_k,")")

#原蹠表示
texts3d(portal_i,portal_j,portal_k,texts=portal_text,col=rgb(0,0,0),adj=1.0)

#対蹠(AntiPordal)
antipordal_i<-0
antipordal_j<-0
antipordal_k<--1
antipordal_text=paste0("AP(",antipordal_i,",",antipordal_j,",",antipordal_k,")")

#対蹠表示
texts3d(antipordal_i,antipordal_j,antipordal_k,texts=antipordal_text,col=rgb(0,0,0),adj=1.0)

#立方対角線(Cubic Diagonal)
lines3d(c(portal_i,antipordal_i),c(portal_j,antipordal_j),c(portal_k,antipordal_k),col=rgb(1,0,0),lwd=2)

#正八面体描画
mx<-cos(SoDC)
my<-sin(SoDC)

lines3d(c(portal_i,mx[1]),c(portal_j,my[1]),c(portal_k,0),col=rgb(0,0,0),lwd=1)
lines3d(c(portal_i,mx[2]),c(portal_j,my[2]),c(portal_k,0),col=rgb(0,0,0),lwd=1)
#lines3d(c(portal_i,mx[3]),c(portal_j,my[3]),c(portal_k,0),col=rgb(0,0,0),lwd=1)
lines3d(c(portal_i,mx[4]),c(portal_j,my[4]),c(portal_k,0),col=rgb(0,0,0),lwd=1)

lines3d(c(mx[1],mx[2]),c(my[1],my[2]),c(0,0),col=rgb(0,0,0),lwd=1)
lines3d(c(mx[2],mx[3]),c(my[2],my[3]),c(0,0),col=rgb(0,0,0),lwd=1)
lines3d(c(mx[3],mx[4]),c(my[3],my[4]),c(0,0),col=rgb(0,0,0),lwd=1)
lines3d(c(mx[4],mx[1]),c(my[4],my[1]),c(0,0),col=rgb(0,0,0),lwd=1)

#lines3d(c(mx[1],antipordal_i),c(my[1],antipordal_j),c(0,antipordal_k),col=rgb(0,0,0),lwd=1)
lines3d(c(mx[2],antipordal_i),c(my[2],antipordal_j),c(0,antipordal_k),col=rgb(0,0,0),lwd=1)
lines3d(c(mx[3],antipordal_i),c(my[3],antipordal_j),c(0,antipordal_k),col=rgb(0,0,0),lwd=1)
lines3d(c(mx[4],antipordal_i),c(my[4],antipordal_j),c(0,antipordal_k),col=rgb(0,0,0),lwd=1)

#追加立方対角線(Cubic Diagonal)
#lines3d(c(mx[1],mx[3]),c(my[1],my[3]),c(0,0),col=rgb(0,0,0),lwd=1)
lines3d(c(mx[2],mx[4]),c(my[2],my[4]),c(0,0),col=rgb(0,0,0),lwd=1)

#アニメーション
movie3d(spin3d(axis=c(0,0,1),rpm=5),duration=10,fps=25,movie="~/Desktop/Preoctahedron04")

とはいえ「あと一工夫で何とかなりそう」に見えるのもまた事実。実際、やり方によってはなんとかならないでもないのです。

S：立体では中点連結の定理は成り立たないのですね。合同で縦にも横にも上にも拡げて行ける合同な四面体ってあるのかな。
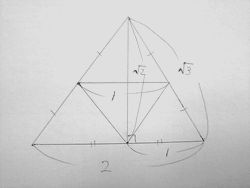
T：実は、そういう四面体があるのです。この展開図を見てください。
《２：√３：√３》の三角形で作る四面体です。

S：並べてみよう。・・・確かにすきまなく積みあげることができる。

S：ちゃんと８個で２倍の三角錐ができた。

こういう応用形もあります。

上掲は「底の3辺が2,残り3辺がsqrt(3)の三角錐」ですが、こちらは「2辺が2,残り4辺がsqrt(3)の三角錐」となります。
テトラパック(Tetra Pak) - Wikipedia

食品用紙容器の開発・製造を主たる業務とする国際企業。創業の地であるスウェーデンのルンドに本社を置く。創業者はルーベン・ラウジング。「テトラパック」及び「Tetra Pak」はこの会社の登録商標である。同社が開発して製造する四面体型紙容器の旧名称で、現在は「テトラ・クラシック (TC)」と称する。

現在は四角い「テトラ・ブリック(TB)」や屋根型の「テトラ・レックス (TR)」なども手がける、飲料用紙容器と充填包装システムで有数の企業である。主力商品の「テトラ・ブリック・アセプティック」は常温で長期保存を可能とし、日本の国外へ向けた豆腐などが採用している。

テトラ・クラシック

日本で三角パックと多く俗称される「テトラ・クラシック」は1944年3月27日に特許がおり、1952年に当社が発売した飲料用紙容器である。三角形の形状はピラミッド型の四角錐と誤解も多いが、実際は四面体の三角錐で、名称の"Tetra"も「4」の意味である。単位容積あたりの包装材が廃棄分や糊代を算入すると最小となり、一枚の長い紙で製造できる利点と、輸送に六角形の専用ケースを要する欠点がある。

現在は輸送や店頭の陳列で利点が多いブリックタイプが主流となり、採用例が減少して日本テトラパックは国内の販売を2004年6月から休止していたが、2014年7月に10年ぶりに販売を再開した。

形としてはこんな感じ。

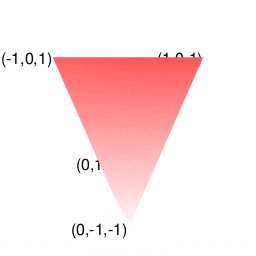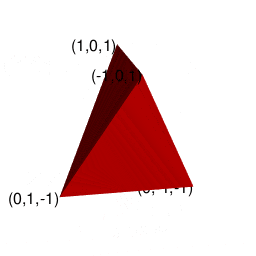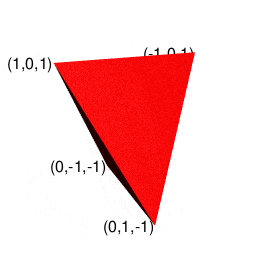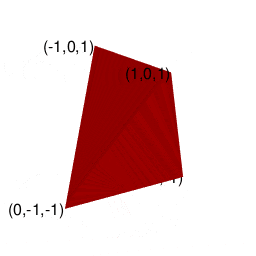
library(rgl)
#頂点座標=8個
texts3d(1,0,1,texts=c("(1,0,1)"),col=rgb(0,0,0),adj=1.0)
texts3d(-1,0,1,texts=c("(-1,0,1)"),col=rgb(0,0,0),adj=1.0)
texts3d(0,1,-1,texts=c("(0,1,-1)"),col=rgb(0,0,0),adj=1.0)
texts3d(0,-1,-1,texts=c("(0,-1,-1)"),col=rgb(0,0,0),adj=1.0)

#二等辺三角形４面
triangles3d(c(1,-1,0),c(0,0,1),c(1,1,-1),col=rgb(1,0,0),lwd=1)
triangles3d(c(-1,0,0),c(0,1,-1),c(1,-1,-1),col=rgb(1,0,0),lwd=1)
triangles3d(c(0,0,1),c(1,-1,0),c(-1,-1,1),col=rgb(1,0,0),lwd=1)
triangles3d(c(0,1,-1),c(-1,0,0),c(-1,1,1),col=rgb(1,0,0),lwd=1)

#アニメーション
movie3d(spin3d(axis=c(0,0,1),rpm=5),duration=10,fps=25,movie="~/Desktop/triangles010") 

座標格子入りVer.(各面が三辺比1:sqrt(2):sqrt(3)の直角三角形x2枚の構成である事が明瞭に見て取れる)

#mo(Minus One),cp(Center Point),po(Plus One)
grid_draw01<-function(m,c,p){
#座標(Coordinate)合成関数Cd
cd<-function(a,b,c){paste0("(",a,",",b,",",c,")")}
#頂点座標=8個
texts3d(m,m,m,texts=cd(m,m,m),col=c(200,200,200),adj=1.0,cex=0.5)
texts3d(p,m,m,texts=cd(p,m,m),col=c(200,200,200),adj=1.0,cex=0.5)
texts3d(m,p,m,texts=cd(m,p,m),col=c(200,200,200),adj=1.0,cex=0.5)
texts3d(p,p,m,texts=cd(p,p,m),col=c(200,200,200),adj=1.0,cex=0.5)
texts3d(m,m,p,texts=cd(m,m,p),col=c(200,200,200),adj=1.0,cex=0.5)
texts3d(p,m,p,texts=cd(p,m,p),col=c(200,200,200),adj=1.0,cex=0.5)
texts3d(m,p,p,texts=cd(m,p,p),col=c(200,200,200),adj=1.0,cex=0.5)
texts3d(p,p,p,texts=cd(p,p,p),col=c(200,200,200),adj=1.0,cex=0.5)
#頂点間中点=1+6+12=19個
texts3d(c,c,c,texts=cd(c,c,c),col=rgb(0,0,0),adj=1.0)
texts3d(m,c,c,texts=cd(m,c,c),col=rgb(0,0,0),adj=1.0)
texts3d(c,m,c,texts=cd(c,m,c),col=rgb(0,0,0),adj=1.0)
texts3d(c,c,m,texts=cd(c,c,m),col=rgb(0,0,0),adj=1.0)
texts3d(p,c,c,texts=cd(p,c,c),col=rgb(0,0,0),adj=1.0)
texts3d(c,p,c,texts=cd(c,p,c),col=rgb(0,0,0),adj=1.0)
texts3d(c,c,p,texts=cd(c,c,p),col=rgb(0,0,0),adj=1.0)
texts3d(c,m,m,texts=cd(c,m,m),col=rgb(0,0,0),adj=1.0)
texts3d(c,m,p,texts=cd(c,m,p),col=rgb(0,0,0),adj=1.0)
texts3d(c,p,m,texts=cd(c,p,m),col=rgb(0,0,0),adj=1.0)
texts3d(c,p,p,texts=cd(c,p,p),col=rgb(0,0,0),adj=1.0)
texts3d(m,c,m,texts=cd(m,c,m),col=rgb(0,0,0),adj=1.0)
texts3d(m,c,p,texts=cd(m,c,p),col=rgb(0,0,0),adj=1.0)
texts3d(p,c,m,texts=cd(p,c,m),col=rgb(0,0,0),adj=1.0)
texts3d(p,c,p,texts=cd(p,c,p),col=rgb(0,0,0),adj=1.0)
texts3d(m,m,c,texts=cd(m,m,c),col=rgb(0,0,0),adj=1.0)
texts3d(m,p,c,texts=cd(m,p,c),col=rgb(0,0,0),adj=1.0)
texts3d(p,m,c,texts=cd(p,m,c),col=rgb(0,0,0),adj=1.0)
texts3d(p,p,c,texts=cd(p,p,c),col=rgb(0,0,0),adj=1.0)
#正六面体(Square)本体=6面

lines3d(c(m,p,p,m,m),c(m,m,p,p,m),c(m,m,m,m,m),col=c(200,200,200),lwd=1)
lines3d(c(m,p,p,m,m),c(m,m,p,p,m),c(p,p,p,p,p),col=c(200,200,200),lwd=1)
lines3d(c(m,m),c(m,m),c(m,p),col=c(200,200,200),lwd=1)
lines3d(c(p,p),c(m,m),c(m,p),col=c(200,200,200),lwd=1)
lines3d(c(m,m),c(p,p),c(m,p),col=c(200,200,200),lwd=1)
lines3d(c(p,p),c(p,p),c(m,p),col=c(200,200,200),lwd=1)
#頂点間中線=3+12=15本
lines3d(c(p,m),c(c,c),c(c,c),col=rgb(0,0,0),lwd=1)
lines3d(c(c,c),c(p,m),c(c,c),col=rgb(0,0,0),lwd=1)
lines3d(c(c,c),c(c,c),c(p,m),col=rgb(0,0,0),lwd=1)
lines3d(c(c,c,c,c,c),c(m,p,p,m,m),c(m,m,p,p,m),col=rgb(0,0,0),lwd=1)
lines3d(c(m,p,p,m,m),c(c,c,c,c,c),c(m,m,p,p,m),col=rgb(0,0,0),lwd=1)
lines3d(c(m,p,p,m,m),c(m,m,p,p,m),c(c,c,c,c,c),col=rgb(0,0,0),lwd=1)
}
grid_draw01(-1,0,1)

#二等辺三角形４面
triangles3d(c(1,-1,0),c(0,0,1),c(1,1,-1),col=rgb(1,0,0),lwd=1)
triangles3d(c(-1,0,0),c(0,1,-1),c(1,-1,-1),col=rgb(1,0,0),lwd=1)
triangles3d(c(0,0,1),c(1,-1,0),c(-1,-1,1),col=rgb(1,0,0),lwd=1)
triangles3d(c(0,1,-1),c(-1,0,0),c(-1,1,1),col=rgb(1,0,0),lwd=1)
#アニメーション
movie3d(spin3d(axis=c(0,0,1),rpm=5),duration=10,fps=5,movie="~/Desktop/triangles018")

ところで、ここに登場する三辺比１:sqrt(2):sqrt(3)の直角三角形って、「半径１の単位球面に内接する立方体の対蹠頂点間を２回直角に曲がって結ぶ際に半径(1)と平方対角線(Square diagonal=sqrt(2))と立方対角線(Cubic diagonal=sqrt(3))が成す直角三角形」そのものだったりします。知らない間に思わぬ高度な図形が日常を侵食してたものです。
【Rで球面幾何学】正方形における平方対角線(Square diagonal)と立方体における立方対角線(Cubic diagonal)の関係について。
【Rで球面幾何学】ハミルトンの四元数(Quaternion)は何を表しているのか？

正三角形や正方形や正六角形が単独図形で平面充当性を備えているのは、それに内接あるいは外接する同心円が対数比で推移するからと考えると、オイラーの公式（Euler's formula）e^iθ=cos(θ)+sin(iθ)がどうやって指数関数と三角関数を結び付けてるかとも関係してくる話…そちらの話は以下続報という事で。