【オイラーの多面体定理と正多面体】正六面体と正十二面体の間の往復(「屋根掛け法」とは何か？)

古代ギリシャ時代から「正六面体(Regular DodecahedronCube)と正十二面体(Regular Dodecahedron)の間を往復する方法」として知られてきた「屋根掛け法(Roofing Method)」の出発点は「正五角形の三角形と四角形への分割」です。

#分割数Nod(Number of divide)=5

NoD<-5
#円周分割数列(Sequence of Divided Circumference)
SoDC<-seq(0,2*pi,length=NoD+1)
#円周上の五角形の頂点を集める。
cx_nomal=cos(SoDC)
cy_nomal=sin(SoDC)
cx_reverse=cos(SoDC+pi)
cy_reverse=sin(SoDC+pi)
#グラフ描画
plot(cx_nomal,cy_nomal,asp=1,col=rgb(0,0,1),type="l",xlim=c(-1,1),ylim=c(-1,1),main="Regular Pentagon",xlab="Cos(θ)",ylab="Sin(θ)",lwd=1.2)
par(new=T)
plot(cx_reverse,cy_reverse,asp=1,col=rgb(1,0,0),type="l",xlim=c(-1,1),ylim=c(-1,1),main="",xlab="",ylab="",lwd=1.2)
#背景円の塗り潰し
Circumference<-seq(0,2*pi,length=60)
cx_circle=cos(Circumference)
cy_circle=sin(Circumference)
polygon(cx_circle, #x
cy_circle, #y
density=c(30), #塗りつぶす濃度
angle=c(45),　 　　　#塗りつぶす斜線の角度
col=c(200,200,200)) 　#塗りつぶす色

#三角形(正方向)の塗り潰し
polygon(c(cx_nomal[1],cx_nomal[2],cx_nomal[5],cx_nomal[1]), #x
c(cy_nomal[1],cy_nomal[2],cy_nomal[5],cy_nomal[1]), #y
density=c(30), #塗りつぶす濃度
angle=c(45),　 　　　#塗りつぶす斜線の角度
col=rgb(0,0,1)) 　#塗りつぶす色

#三角形(逆方向)の塗り潰し
polygon(c(cx_reverse[1],cx_reverse[2],cx_reverse[5],cx_reverse[1]), #x
c(cy_reverse[1],cy_reverse[2],cy_reverse[5],cy_reverse[1]), #y
density=c(30), #塗りつぶす濃度
angle=c(45),　 　　　#塗りつぶす斜線の角度
col=rgb(1,0,0)) 　#塗りつぶす色

#文字追加
text(cx_nomal,cy_nomal, labels=c("a","b","c","d","e"),col=rgb(0,0,1))
text(cx_reverse,cy_reverse, labels=c("a","b","c","d","e"),col=rgb(1,0,0))
#補助線
segments(1,0,-1,0,lty=3,col=rgb(0,0,0))

とりあえずイメージ操作的には以下の様な「いない、いない、ばぁ!!」形式で思い浮かべたら良いでしょう。

• まずは上図でいうところの三角形abeと四角形bcde(正五角形の断片)がそれぞれ表面に12個ずつ現れる24面体を構成する（いない、いない…）。
• それぞれを１対ずつ水平に並べて正五角形を再現すれば、これが表面に12個並ぶ正十二面体があらためて顕現する（…ばぁ!!）。

平面上におけるイメージ展開は以下。

①まずは上掲イメージ展開に現れる「正方形」「分割三角形」「分割四角形」が全て射影(Projection)として同居する正十六角形(Regular Hexadecagon)をイメージする（あくまで射影なので、形が多少崩れてても気にしない）。

#分割数Nod(Number of divide)=16
NoD<-16
#円周分割数列(Sequence of Divided Circumference)
SoDC<-seq(0,2*pi,length=NoD+1)
#円周上の四角形の頂点を集める。
cx_nomal=cos(SoDC)
cy_nomal=sin(SoDC)

#グラフ描画
plot(cx_nomal,cy_nomal,asp=1,col=rgb(0,0,0),type="l",xlim=c(-1,1),ylim=c(-1,1),main="Regular Hexadecagon",xlab="Cos(θ)",ylab="Sin(θ)",lwd=1.2)

#背景円の塗り潰し
Circumference<-seq(0,2*pi,length=60)
cx_circle=cos(Circumference)
cy_circle=sin(Circumference)
polygon(cx_circle, #x
cy_circle, #y
density=c(30), #塗りつぶす濃度
angle=c(45),　 　　　#塗りつぶす斜線の角度
col=c(200,200,200)) 　#塗りつぶす色

#文字追加
text(cx_nomal,cy_nomal, labels=c("a","b","c","d","e","f","g","h","i","j","k","l","m","n","o","p"),col=rgb(0,0,0))

#正方形塗り潰し
polygon(c(cx_nomal[1],cx_nomal[5],cx_nomal[9],cx_nomal[13],cx_nomal[1]), #x
c(cy_nomal[1],cy_nomal[5],cy_nomal[9],cy_nomal[13],cy_nomal[1]), #y
density=c(30), #塗りつぶす濃度
angle=c(45),　 　　　#塗りつぶす斜線の角度
col=rgb(0,1,0)) 　#塗りつぶす色

#分割三角形塗り潰し
polygon(c(cx_nomal[1],(cx_nomal[3]+cx_nomal[15])/2,cx_nomal[5],cx_nomal[1]), #x
c(cy_nomal[1],cy_nomal[3],cy_nomal[5],cy_nomal[1]), #y
density=c(30), #塗りつぶす濃度
angle=c(45),　 　　　#塗りつぶす斜線の角度
col=rgb(1,0,0)) 　#塗りつぶす色

polygon(c(cx_nomal[9],cx_nomal[11],cx_nomal[13],cx_nomal[9]), #x
c(cy_nomal[9],cy_nomal[11],cy_nomal[13],cy_nomal[9]), #y
density=c(30), #塗りつぶす濃度
angle=c(45),　 　　　#塗りつぶす斜線の角度
col=rgb(1,0,0)) 　#塗りつぶす色

#分割四角形塗り潰し
polygon(c(cx_nomal[5],cx_nomal[6],cx_nomal[8],cx_nomal[9],cx_nomal[5]), #x
c(cy_nomal[5],cy_nomal[6],cy_nomal[8],cy_nomal[9],cy_nomal[5]), #y
density=c(30), #塗りつぶす濃度
angle=c(45),　 　　　#塗りつぶす斜線の角度
col=rgb(0,0,1)) 　#塗りつぶす色

polygon(c(cx_nomal[13],cx_nomal[14],cx_nomal[16],cx_nomal[1],cx_nomal[13]), #x
c(cy_nomal[13],cy_nomal[14],cy_nomal[16],cy_nomal[1],cy_nomal[13]), #y
density=c(30), #塗りつぶす濃度
angle=c(45),　 　　　#塗りつぶす斜線の角度
col=rgb(0,0,1)) 　#塗りつぶす色

②次いで「正方形」表面上に「分割三角形」と「分割四角形」のイメージを射影する。

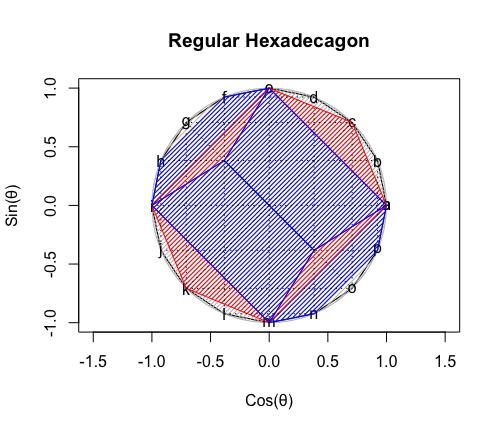
#分割数Nod(Number of divide)=16
NoD<-16
#円周分割数列(Sequence of Divided Circumference)
SoDC<-seq(0,2*pi,length=NoD+1)
#円周上の四角形の頂点を集める。
cx_nomal=cos(SoDC)
cy_nomal=sin(SoDC)

#グラフ描画
plot(cx_nomal,cy_nomal,asp=1,col=rgb(0,0,0),type="l",xlim=c(-1,1),ylim=c(-1,1),main="Regular Hexadecagon",xlab="Cos(θ)",ylab="Sin(θ)",lwd=1.2)

#背景円の塗り潰し
Circumference<-seq(0,2*pi,length=60)
cx_circle=cos(Circumference)
cy_circle=sin(Circumference)
polygon(cx_circle, #x
cy_circle, #y
density=c(30), #塗りつぶす濃度
angle=c(45),　 　　　#塗りつぶす斜線の角度
col=c(200,200,200)) 　#塗りつぶす色

#文字追加
text(cx_nomal,cy_nomal, labels=c("a","b","c","d","e","f","g","h","i","j","k","l","m","n","o","p"),col=rgb(0,0,0))

#分割三角形塗り潰し
polygon(c(cx_nomal[1],cx_nomal[3],cx_nomal[5],cx_nomal[1]), #x
c(cy_nomal[1],cy_nomal[3],cy_nomal[5],cy_nomal[1]), #y
density=c(30), #塗りつぶす濃度
angle=c(45),　 　　　#塗りつぶす斜線の角度
col=rgb(1,0,0)) 　#塗りつぶす色

polygon(c(cx_nomal[9],cx_nomal[11],cx_nomal[13],cx_nomal[9]), #x
c(cy_nomal[9],cy_nomal[11],cy_nomal[13],cy_nomal[9]), #y
density=c(30), #塗りつぶす濃度
angle=c(45),　 　　　#塗りつぶす斜線の角度
col=rgb(1,0,0)) 　#塗りつぶす色

#分割四角形塗り潰し
polygon(c(cx_nomal[5],cx_nomal[6],cx_nomal[8],cx_nomal[9],cx_nomal[5]), #x
c(cy_nomal[5],cy_nomal[6],cy_nomal[8],cy_nomal[9],cy_nomal[5]), #y
density=c(30), #塗りつぶす濃度
angle=c(45),　 　　　#塗りつぶす斜線の角度
col=rgb(0,0,1)) 　#塗りつぶす色

polygon(c(cx_nomal[13],cx_nomal[14],cx_nomal[16],cx_nomal[1],cx_nomal[13]), #x
c(cy_nomal[13],cy_nomal[14],cy_nomal[16],cy_nomal[1],cy_nomal[13]), #y
density=c(30), #塗りつぶす濃度
angle=c(45),　 　　　#塗りつぶす斜線の角度
col=rgb(0,0,1)) 　#塗りつぶす色

#「射影された」分割三角形塗り潰し
polygon(c(cx_nomal[5],cx_nomal[9],cx_nomal[6],cx_nomal[5]), #x
c(cy_nomal[5],cy_nomal[9],cy_nomal[8],cy_nomal[5]), #y
density=c(30), #塗りつぶす濃度
angle=c(45),　 　　　#塗りつぶす斜線の角度
col=rgb(1,0,0)) 　#塗りつぶす色

polygon(c(cx_nomal[13],cx_nomal[1],cx_nomal[14],cx_nomal[13]), #x
c(cy_nomal[13],cy_nomal[1],cy_nomal[16],cy_nomal[13]), #y
density=c(30), #塗りつぶす濃度
angle=c(45),　 　　　#塗りつぶす斜線の角度
col=rgb(1,0,0)) 　#塗りつぶす色

#「射影された」分割四角形塗り潰し
polygon(c(cx_nomal[1],cx_nomal[5],cx_nomal[6],cx_nomal[14],cx_nomal[1]), #x
c(cy_nomal[1],cy_nomal[5],cy_nomal[8],cy_nomal[16],cy_nomal[1]), #y
density=c(30), #塗りつぶす濃度
angle=c(45),　 　　　#塗りつぶす斜線の角度
col=rgb(0,0,1)) 　#塗りつぶす色

polygon(c(cx_nomal[9],cx_nomal[13],cx_nomal[14],cx_nomal[6],cx_nomal[9]), #x
c(cy_nomal[9],cy_nomal[13],cy_nomal[16],cy_nomal[8],cy_nomal[9]), #y
density=c(30), #塗りつぶす濃度
angle=c(45),　 　　　#塗りつぶす斜線の角度
col=rgb(0,0,1)) 　#塗りつぶす色

#補助線(X軸とY軸)
segments(-1,0,1,0,lty=3,col=rgb(0,0,0))
segments(0,-1,0,1,lty=3,col=rgb(0,0,0))

#「分割三角形」を巡る補助線と横罫線
segments(cx_nomal[3],cy_nomal[3],cx_nomal[11],cy_nomal[11],lty=3,col=rgb(0,0,0))

segments(cx_nomal[2],cy_nomal[2],cx_nomal[8],cy_nomal[8],lty=3,col=rgb(0,0,0))
segments(cx_nomal[3],cy_nomal[3],cx_nomal[7],cy_nomal[7],lty=3,col=rgb(0,0,0))
segments(cx_nomal[4],cy_nomal[4],cx_nomal[6],cy_nomal[6],lty=3,col=rgb(0,0,0))

segments(cx_nomal[10],cy_nomal[10],cx_nomal[16],cy_nomal[16],lty=3,col=rgb(0,0,0))
segments(cx_nomal[11],cy_nomal[11],cx_nomal[15],cy_nomal[15],lty=3,col=rgb(0,0,0))
segments(cx_nomal[12],cy_nomal[12],cx_nomal[14],cy_nomal[14],lty=3,col=rgb(0,0,0))

#「分割四角形」を巡る補助線と縦罫線
segments(cx_nomal[7],cy_nomal[7],cx_nomal[15],cy_nomal[15],lty=3,col=rgb(0,0,0))

segments(cx_nomal[2],cy_nomal[2],cx_nomal[16],cy_nomal[16],lty=3,col=rgb(0,0,0))
segments(cx_nomal[3],cy_nomal[3],cx_nomal[15],cy_nomal[15],lty=3,col=rgb(0,0,0))
segments(cx_nomal[4],cy_nomal[4],cx_nomal[14],cy_nomal[14],lty=3,col=rgb(0,0,0))

segments(cx_nomal[6],cy_nomal[6],cx_nomal[12],cy_nomal[12],lty=3,col=rgb(0,0,0))
segments(cx_nomal[7],cy_nomal[7],cx_nomal[11],cy_nomal[11],lty=3,col=rgb(0,0,0))
segments(cx_nomal[8],cy_nomal[8],cx_nomal[10],cy_nomal[10],lty=3,col=rgb(0,0,0))

③実際の３次元空間上での見え方はこんな感じ。正十二面体に内接する立方体の6面それぞれに「屋根掛け(Roofing)」した結果の様にも見えるので「屋根掛け法(Roofing Method)」と呼ばれる。

library(rgl)

#原蹠(PorTal)
portal_i<-0
portal_j<-0
portal_k<-1
portal_text=paste0("PT(",portal_i,",",portal_j,",",portal_k,")")

#原蹠表示
texts3d(portal_i,portal_j,portal_k,texts=portal_text,col=rgb(0,0,0),adj=1.0)

#対蹠(AntiPordal)
antipordal_i<-0
antipordal_j<-0
antipordal_k<--1
antipordal_text=paste0("AP(",antipordal_i,",",antipordal_j,",",antipordal_k,")" main="Cross section for ")

#対蹠表示
texts3d(antipordal_i,antipordal_j,antipordal_k,texts=antipordal_text,col=rgb(0,0,0),adj=1.0)

#立方対角線(Cubic Diagonal)
lines3d(c(portal_i,antipordal_i),c(portal_j,antipordal_j),c(portal_k,antipordal_k),col=rgb(1,0,0),lwd=2)

###正十二面体の描画###

#xy軸上の経度(LoNgitude)座標

#最初の頂点３個x2
LN01=sin(1/5*pi)
c0<-seq(0,2*pi,length=4)

#頭蹠側一段目３個
LNa_cos<-cos(c0)*LN01
LNa_sin<-sin(c0)*LN01

#対蹠側一段目３個
LNd_cos<-cos(c0+pi)*LN01
LNd_sin<-sin(c0+pi)*LN01

#中央の頂点6個x2
LN10=sin(2/5*pi)
c00<-seq(0,2*pi,length=4)

#頭蹠側一段目３個
bx00<-cos(c00+pi/2)
by00<-sin(c00+pi/2)
bx01<-cos(c00+pi*2/5+pi/2)
by01<-sin(c00+pi*2/5+pi/2)
bx02<-c(bx00[1],bx01[1],bx00[2],bx01[2],bx00[3],bx01[3],bx00[4])
by02<-c(by00[1],by01[1],by00[2],by01[2],by00[3],by01[3],by00[4])
LNb_cos<-bx02*LN10
LNb_sin<-by02*LN10

#対蹠側一段目３個
cx00<-cos(c00-pi/2)
cy00<-sin(c00-pi/2)
cx01<-cos(c00+pi*2/5-pi/2)
cy01<-sin(c00+pi*2/5-pi/2)
cx02<-c(cx00[1],cx01[1],cx00[2],cx01[2],cx00[3],cx01[3],cx00[4])
cy02<-c(cy00[1],cy01[1],cy00[2],cy01[2],cy00[3],cy01[3],cy00[4])
LNc_cos<-cx02*LN10
LNc_sin<-cy02*LN10

#立方体におけるz軸上の緯度(LaTitude)座標
LTa=4/5
LTb=2/5
LTc=-2/5
LTd=-4/5

#正12面体描写(原蹠から最初の隣点３個へ)
lines3d(c(portal_i,LNa_cos[1]),c(portal_j,LNa_sin[1]),c(portal_k,LTa),col=rgb(0,0,1),lwd=1)
lines3d(c(portal_i,LNa_cos[2]),c(portal_j,LNa_sin[2]),c(portal_k,LTa),col=rgb(0,0,1),lwd=1)
lines3d(c(portal_i,LNa_cos[3]),c(portal_j,LNa_sin[3]),c(portal_k,LTa),col=rgb(0,0,1),lwd=1)

#正12面体描写(対蹠から最初の隣点３個へ)
lines3d(c(antipordal_i,LNd_cos[1]),c(antipordal_j,LNd_sin[1]),c(antipordal_k,LTd),col=rgb(0,0,1),lwd=1)
lines3d(c(antipordal_i,LNd_cos[2]),c(antipordal_j,LNd_sin[2]),c(antipordal_k,LTd),col=rgb(0,0,1),lwd=1)
lines3d(c(antipordal_i,LNd_cos[3]),c(antipordal_j,LNd_sin[3]),c(antipordal_k,LTd),col=rgb(0,0,1),lwd=1)

#正12面体描写(原蹠からの最初の隣点３個から次の隣点６個へ)
lines3d(c(LNa_cos[1],LNb_cos[5]),c(LNa_sin[1],LNb_sin[5]),c(LTa,LTb),col=rgb(0,0,1),lwd=1)
lines3d(c(LNa_cos[1],LNb_cos[6]),c(LNa_sin[1],LNb_sin[6]),c(LTa,LTb),col=rgb(0,0,1),lwd=1)
lines3d(c(LNa_cos[2],LNb_cos[1]),c(LNa_sin[2],LNb_sin[1]),c(LTa,LTb),col=rgb(0,0,1),lwd=1)
lines3d(c(LNa_cos[2],LNb_cos[2]),c(LNa_sin[2],LNb_sin[2]),c(LTa,LTb),col=rgb(0,0,1),lwd=1)
lines3d(c(LNa_cos[3],LNb_cos[3]),c(LNa_sin[3],LNb_sin[3]),c(LTa,LTb),col=rgb(0,0,1),lwd=1)
lines3d(c(LNa_cos[3],LNb_cos[4]),c(LNa_sin[3],LNb_sin[4]),c(LTa,LTb),col=rgb(0,0,1),lwd=1)

#正12面体描写(原蹠からの次の隣点６個からの水平線３本)
lines3d(c(LNb_cos[2],LNb_cos[3]),c(LNb_sin[2],LNb_sin[3]),c(LTb,LTb),col=rgb(0,0,1),lwd=1)
lines3d(c(LNb_cos[4],LNb_cos[5]),c(LNb_sin[4],LNb_sin[5]),c(LTb,LTb),col=rgb(0,0,1),lwd=1)
lines3d(c(LNb_cos[6],LNb_cos[1]),c(LNb_sin[6],LNb_sin[1]),c(LTb,LTb),col=rgb(0,0,1),lwd=1)

#正12面体描写(対蹠からの最初の隣点３個から次の隣点６個へ)
lines3d(c(LNd_cos[1],LNc_cos[5]),c(LNd_sin[1],LNc_sin[5]),c(LTd,LTc),col=rgb(0,0,1),lwd=1)
lines3d(c(LNd_cos[1],LNc_cos[6]),c(LNd_sin[1],LNc_sin[6]),c(LTd,LTc),col=rgb(0,0,1),lwd=1)
lines3d(c(LNd_cos[2],LNc_cos[1]),c(LNd_sin[2],LNc_sin[1]),c(LTd,LTc),col=rgb(0,0,1),lwd=1)
lines3d(c(LNd_cos[2],LNc_cos[2]),c(LNd_sin[2],LNc_sin[2]),c(LTd,LTc),col=rgb(0,0,1),lwd=1)
lines3d(c(LNd_cos[3],LNc_cos[3]),c(LNd_sin[3],LNc_sin[3]),c(LTd,LTc),col=rgb(0,0,1),lwd=1)
lines3d(c(LNd_cos[3],LNc_cos[4]),c(LNd_sin[3],LNc_sin[4]),c(LTd,LTc),col=rgb(0,0,1),lwd=1)

#正12面体描写(対蹠からの次の隣点６個からの水平線３本)
lines3d(c(LNc_cos[2],LNc_cos[3]),c(LNc_sin[2],LNc_sin[3]),c(LTc,LTc),col=rgb(0,0,1),lwd=1)
lines3d(c(LNc_cos[4],LNc_cos[5]),c(LNc_sin[4],LNc_sin[5]),c(LTc,LTc),col=rgb(0,0,1),lwd=1)
lines3d(c(LNc_cos[6],LNc_cos[1]),c(LNc_sin[6],LNc_sin[1]),c(LTc,LTc),col=rgb(0,0,1),lwd=1)

#正12面体描写(原蹠からの経路と対蹠からの経路の結合線6本)
lines3d(c(LNb_cos[1],LNc_cos[4]),c(LNb_sin[1],LNc_sin[4]),c(LTb,LTc),col=rgb(0,0,1),lwd=1)
lines3d(c(LNb_cos[2],LNc_cos[5]),c(LNb_sin[2],LNc_sin[5]),c(LTb,LTc),col=rgb(0,0,1),lwd=1)
lines3d(c(LNb_cos[3],LNc_cos[6]),c(LNb_sin[3],LNc_sin[6]),c(LTb,LTc),col=rgb(0,0,1),lwd=1)
lines3d(c(LNb_cos[4],LNc_cos[1]),c(LNb_sin[4],LNc_sin[1]),c(LTb,LTc),col=rgb(0,0,1),lwd=1)
lines3d(c(LNb_cos[5],LNc_cos[2]),c(LNb_sin[5],LNc_sin[2]),c(LTb,LTc),col=rgb(0,0,1),lwd=1)
lines3d(c(LNb_cos[6],LNc_cos[3]),c(LNb_sin[6],LNc_sin[3]),c(LTb,LTc),col=rgb(0,0,1),lwd=1)

###この立方体に内接する正六面体の座標抽出###

#立方体描写(最初に抽出する正方形)
lines3d(c(LNa_cos[1],LNa_cos[2],LNb_cos[3],LNb_cos[4],LNa_cos[1]),c(LNa_sin[1],LNa_sin[2],LNb_sin[3],LNb_sin[4],LNa_sin[1]),c(LTa,LTa,LTb,LTb,LTa),col=rgb(0,1,0),lwd=1)

#立方体描写(最初に抽出した正方形の対面)
lines3d(c(LNd_cos[1],LNd_cos[2],LNc_cos[3],LNc_cos[4],LNd_cos[1]),c(LNd_sin[1],LNd_sin[2],LNc_sin[3],LNc_sin[4],LNd_sin[1]),c(LTd,LTd,LTc,LTc,LTd),col=rgb(0,1,0),lwd=1)

#立方体描写(２つの正方形を結ぶ辺４本)
lines3d(c(LNa_cos[1],LNc_cos[3]),c(LNa_sin[1],LNc_sin[3]),c(LTa,LTc),col=rgb(0,1,0),lwd=1)
lines3d(c(LNa_cos[2],LNc_cos[4]),c(LNa_sin[2],LNc_sin[4]),c(LTa,LTc),col=rgb(0,1,0),lwd=1)
lines3d(c(LNb_cos[3],LNd_cos[1]),c(LNb_sin[3],LNd_sin[1]),c(LTb,LTd),col=rgb(0,1,0),lwd=1)
lines3d(c(LNb_cos[4],LNd_cos[2]),c(LNb_sin[4],LNd_sin[2]),c(LTb,LTd),col=rgb(0,1,0),lwd=1)

#アニメーション
movie3d(spin3d(axis=c(0,0,1),rpm=5),duration=10,fps=25,movie="~/Desktop/cube_in_dodecahedron19")

明らかに「オイラーの多面体定理」に基づく作図法とはあくまで異質の座標の取り方ですね。

library(rgl)

#原蹠(PorTal)
portal_i<-0
portal_j<-0
portal_k<-1
portal_text=paste0("PT(",portal_i,",",portal_j,",",portal_k,")")

#原蹠表示
texts3d(portal_i,portal_j,portal_k,texts=portal_text,col=rgb(0,0,0),adj=1.0)

#対蹠(AntiPordal)
antipordal_i<-0
antipordal_j<-0
antipordal_k<--1
antipordal_text=paste0("AP(",antipordal_i,",",antipordal_j,",",antipordal_k,")" main="Cross section for ")

#対蹠表示
texts3d(antipordal_i,antipordal_j,antipordal_k,texts=antipordal_text,col=rgb(0,0,0),adj=1.0)

#立方対角線(Cubic Diagonal)
lines3d(c(portal_i,antipordal_i),c(portal_j,antipordal_j),c(portal_k,antipordal_k),col=rgb(1,0,0),lwd=2)

###内接する正六面体の描画###

#立方体におけるxy軸上の経度(LoNgitude)座標
CLN0=sin(pi/3)
Cc0<-seq(0,2*pi,length=4)
CLN01_cos<-cos(Cc0)*CLN0
CLN01_sin<-sin(Cc0)*CLN0
CLN02_cos<-cos(Cc0+pi)*CLN0
CLN02_sin<-sin(Cc0+pi)*CLN0

#立方体におけるz軸上の緯度(LaTitude)座標
CLT0=1/3
CAP01=LT0
CAP02=-LT0

#立方体におけるz軸上の緯度(LaTitude)座標
CLT0=1/3
CAP01=CLT0
CAP02=-CLT0

#立方体描写(原蹠から最初の隣点)
lines3d(c(portal_i,CLN01_cos[1]),c(portal_j,CLN01_sin[1]),c(portal_k,CAP01),col=rgb(0,1,0),lwd=1)
lines3d(c(portal_i,CLN01_cos[2]),c(portal_j,CLN01_sin[2]),c(portal_k,CAP01),col=rgb(0,1,0),lwd=1)
lines3d(c(portal_i,CLN01_cos[3]),c(portal_j,CLN01_sin[3]),c(portal_k,CAP01),col=rgb(0,1,0),lwd=1)

#立方体描写(原蹠から最初の隣点)
lines3d(c(antipordal_i,CLN02_cos[1]),c(antipordal_j,CLN02_sin[1]),c(antipordal_k,CAP02),col=rgb(0,1,0),lwd=1)
lines3d(c(antipordal_i,CLN02_cos[2]),c(antipordal_j,CLN02_sin[2]),c(antipordal_k,CAP02),col=rgb(0,1,0),lwd=1)
lines3d(c(antipordal_i,CLN02_cos[3]),c(antipordal_j,CLN02_sin[3]),c(antipordal_k,CAP02),col=rgb(0,1,0),lwd=1)

#立方体描写(中線の結合)
lines3d(c(CLN01_cos[1],CLN02_cos[3],CLN01_cos[2],CLN02_cos[1],CLN01_cos[3],CLN02_cos[2],CLN01_cos[1]),c(CLN01_sin[1],CLN02_sin[3],CLN01_sin[2],CLN02_sin[1],CLN01_sin[3],CLN02_sin[2],CLN01_sin[1]),c(CAP01,CAP02,CAP01,CAP02,CAP01,CAP02,CAP01),col=rgb(0,1,0),lwd=1)

###正十二面体の描画###

#xy軸上の経度(LoNgitude)座標

#最初の頂点３個x2
LN01=sin(1/5*pi)
c0<-seq(0,2*pi,length=4)

#頭蹠側一段目３個
LNa_cos<-cos(c0)*LN01
LNa_sin<-sin(c0)*LN01

#対蹠側一段目３個
LNd_cos<-cos(c0+pi)*LN01
LNd_sin<-sin(c0+pi)*LN01

#中央の頂点6個x2
LN10=sin(2/5*pi)
c00<-seq(0,2*pi,length=4)

#頭蹠側一段目３個
bx00<-cos(c00+pi/2)
by00<-sin(c00+pi/2)
bx01<-cos(c00+pi*2/5+pi/2)
by01<-sin(c00+pi*2/5+pi/2)
bx02<-c(bx00[1],bx01[1],bx00[2],bx01[2],bx00[3],bx01[3],bx00[4])
by02<-c(by00[1],by01[1],by00[2],by01[2],by00[3],by01[3],by00[4])
LNb_cos<-bx02*LN10
LNb_sin<-by02*LN10

#対蹠側一段目３個
cx00<-cos(c00-pi/2)
cy00<-sin(c00-pi/2)
cx01<-cos(c00+pi*2/5-pi/2)
cy01<-sin(c00+pi*2/5-pi/2)
cx02<-c(cx00[1],cx01[1],cx00[2],cx01[2],cx00[3],cx01[3],cx00[4])
cy02<-c(cy00[1],cy01[1],cy00[2],cy01[2],cy00[3],cy01[3],cy00[4])
LNc_cos<-cx02*LN10
LNc_sin<-cy02*LN10

#立方体におけるz軸上の緯度(LaTitude)座標
LTa=4/5
LTb=2/5
LTc=-2/5
LTd=-4/5

#正12面体描写(原蹠から最初の隣点３個へ)
lines3d(c(portal_i,LNa_cos[1]),c(portal_j,LNa_sin[1]),c(portal_k,LTa),col=rgb(0,0,1),lwd=1)
lines3d(c(portal_i,LNa_cos[2]),c(portal_j,LNa_sin[2]),c(portal_k,LTa),col=rgb(0,0,1),lwd=1)
lines3d(c(portal_i,LNa_cos[3]),c(portal_j,LNa_sin[3]),c(portal_k,LTa),col=rgb(0,0,1),lwd=1)

#正12面体描写(対蹠から最初の隣点３個へ)
lines3d(c(antipordal_i,LNd_cos[1]),c(antipordal_j,LNd_sin[1]),c(antipordal_k,LTd),col=rgb(0,0,1),lwd=1)
lines3d(c(antipordal_i,LNd_cos[2]),c(antipordal_j,LNd_sin[2]),c(antipordal_k,LTd),col=rgb(0,0,1),lwd=1)
lines3d(c(antipordal_i,LNd_cos[3]),c(antipordal_j,LNd_sin[3]),c(antipordal_k,LTd),col=rgb(0,0,1),lwd=1)

#正12面体描写(原蹠からの最初の隣点３個から次の隣点６個へ)
lines3d(c(LNa_cos[1],LNb_cos[5]),c(LNa_sin[1],LNb_sin[5]),c(LTa,LTb),col=rgb(0,0,1),lwd=1)
lines3d(c(LNa_cos[1],LNb_cos[6]),c(LNa_sin[1],LNb_sin[6]),c(LTa,LTb),col=rgb(0,0,1),lwd=1)
lines3d(c(LNa_cos[2],LNb_cos[1]),c(LNa_sin[2],LNb_sin[1]),c(LTa,LTb),col=rgb(0,0,1),lwd=1)
lines3d(c(LNa_cos[2],LNb_cos[2]),c(LNa_sin[2],LNb_sin[2]),c(LTa,LTb),col=rgb(0,0,1),lwd=1)
lines3d(c(LNa_cos[3],LNb_cos[3]),c(LNa_sin[3],LNb_sin[3]),c(LTa,LTb),col=rgb(0,0,1),lwd=1)
lines3d(c(LNa_cos[3],LNb_cos[4]),c(LNa_sin[3],LNb_sin[4]),c(LTa,LTb),col=rgb(0,0,1),lwd=1)

#正12面体描写(原蹠からの次の隣点６個からの水平線３本)
lines3d(c(LNb_cos[2],LNb_cos[3]),c(LNb_sin[2],LNb_sin[3]),c(LTb,LTb),col=rgb(0,0,1),lwd=1)
lines3d(c(LNb_cos[4],LNb_cos[5]),c(LNb_sin[4],LNb_sin[5]),c(LTb,LTb),col=rgb(0,0,1),lwd=1)
lines3d(c(LNb_cos[6],LNb_cos[1]),c(LNb_sin[6],LNb_sin[1]),c(LTb,LTb),col=rgb(0,0,1),lwd=1)

#正12面体描写(対蹠からの最初の隣点３個から次の隣点６個へ)
lines3d(c(LNd_cos[1],LNc_cos[5]),c(LNd_sin[1],LNc_sin[5]),c(LTd,LTc),col=rgb(0,0,1),lwd=1)
lines3d(c(LNd_cos[1],LNc_cos[6]),c(LNd_sin[1],LNc_sin[6]),c(LTd,LTc),col=rgb(0,0,1),lwd=1)
lines3d(c(LNd_cos[2],LNc_cos[1]),c(LNd_sin[2],LNc_sin[1]),c(LTd,LTc),col=rgb(0,0,1),lwd=1)
lines3d(c(LNd_cos[2],LNc_cos[2]),c(LNd_sin[2],LNc_sin[2]),c(LTd,LTc),col=rgb(0,0,1),lwd=1)
lines3d(c(LNd_cos[3],LNc_cos[3]),c(LNd_sin[3],LNc_sin[3]),c(LTd,LTc),col=rgb(0,0,1),lwd=1)
lines3d(c(LNd_cos[3],LNc_cos[4]),c(LNd_sin[3],LNc_sin[4]),c(LTd,LTc),col=rgb(0,0,1),lwd=1)

#正12面体描写(対蹠からの次の隣点６個からの水平線３本)
lines3d(c(LNc_cos[2],LNc_cos[3]),c(LNc_sin[2],LNc_sin[3]),c(LTc,LTc),col=rgb(0,0,1),lwd=1)
lines3d(c(LNc_cos[4],LNc_cos[5]),c(LNc_sin[4],LNc_sin[5]),c(LTc,LTc),col=rgb(0,0,1),lwd=1)
lines3d(c(LNc_cos[6],LNc_cos[1]),c(LNc_sin[6],LNc_sin[1]),c(LTc,LTc),col=rgb(0,0,1),lwd=1)

#正12面体描写(原蹠からの経路と対蹠からの経路の結合線6本)
lines3d(c(LNb_cos[1],LNc_cos[4]),c(LNb_sin[1],LNc_sin[4]),c(LTb,LTc),col=rgb(0,0,1),lwd=1)
lines3d(c(LNb_cos[2],LNc_cos[5]),c(LNb_sin[2],LNc_sin[5]),c(LTb,LTc),col=rgb(0,0,1),lwd=1)
lines3d(c(LNb_cos[3],LNc_cos[6]),c(LNb_sin[3],LNc_sin[6]),c(LTb,LTc),col=rgb(0,0,1),lwd=1)
lines3d(c(LNb_cos[4],LNc_cos[1]),c(LNb_sin[4],LNc_sin[1]),c(LTb,LTc),col=rgb(0,0,1),lwd=1)
lines3d(c(LNb_cos[5],LNc_cos[2]),c(LNb_sin[5],LNc_sin[2]),c(LTb,LTc),col=rgb(0,0,1),lwd=1)
lines3d(c(LNb_cos[6],LNc_cos[3]),c(LNb_sin[6],LNc_sin[3]),c(LTb,LTc),col=rgb(0,0,1),lwd=1)

#アニメーション
movie3d(spin3d(axis=c(0,0,1),rpm=5),duration=10,fps=25,movie="~/Desktop/cube_with_dodecahedron02")

ちなみに立方体表面上における「(右手法・左手法的に)左右に１回ずつ曲がって原蹠(Portal)から対蹠(Antipodal)に到達する5頂点操作」が正十二面体表面上における「左右に2回ずつ曲がって原蹠から対蹠に到達する6頂点操作」に拡張されていく様は「屋根掛け法」でも観測可能ですが、如何せんここに登場する正六面体と正十二面体は原蹠と対蹠の位置がズレているので、この操作の前後に調整操作を挟まねばなりません。やはり三次元以上の概念が絡むと途端に顕現に難が…
【Rで球面幾何学】正方形における平方対角線(Square diagonal)と立方体における立方対角線(Cubic diagonal)の関係について。

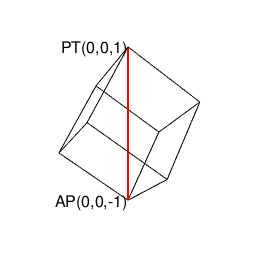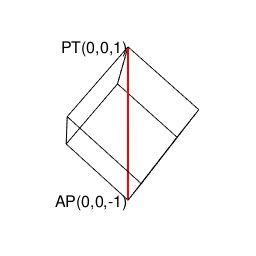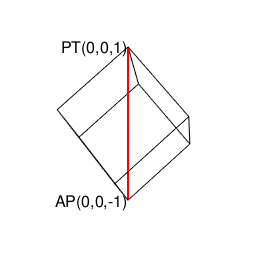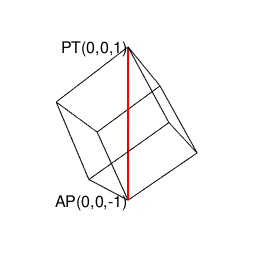
その一方で(原蹠と対蹠を結ぶ経路に注目する)球面幾何学側からのアプローチでは「正四面体を二枚張り合わせた立体」が出発点となります。
【Rで球面幾何学】正四面体(Tetrahedron)と正六面体(Cube)と正八面体(Octahedron)と正二十面体(Icosahedron)の狭間。そして正十二面体（Dodecahedron）との関係について。

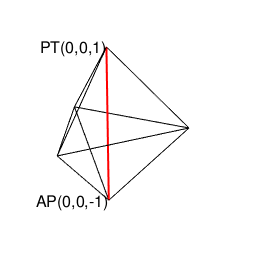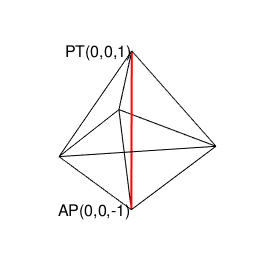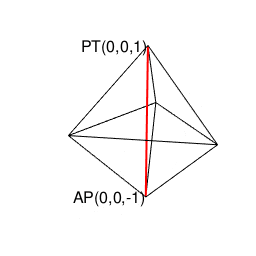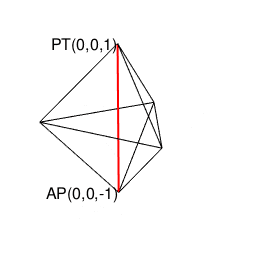
原蹠あるいは対蹠からそれぞれ３方に伸ばされた辺…その閉じてない側の頂点からさらに２辺ずつ伸ばし、三番目の六角形の断面に到達するのが以下の形。既に正十二面体の「原蹠あるいは対蹠から５角形が3面伸びる」特徴が現れてますね。

library(rgl)

#原蹠(PorTal)
portal_i<-0
portal_j<-0
portal_k<-1
portal_text=paste0("PT(",portal_i,",",portal_j,",",portal_k,")")

#原蹠表示
texts3d(portal_i,portal_j,portal_k,texts=portal_text,col=rgb(0,0,0),adj=1.0)

#対蹠(AntiPordal)
antipordal_i<-0
antipordal_j<-0
antipordal_k<--1
antipordal_text=paste0("AP(",antipordal_i,",",antipordal_j,",",antipordal_k,")")

#対蹠表示
texts3d(antipordal_i,antipordal_j,antipordal_k,texts=antipordal_text,col=rgb(0,0,0),adj=1.0)

#立方対角線(Cubic Diagonal)
lines3d(c(portal_i,antipordal_i),c(portal_j,antipordal_j),c(portal_k,antipordal_k),col=rgb(1,0,0),lwd=2)

#立方体におけるxy軸上の経度(LoNgitude)座標
LN0=sin(pi/3)
c0<-seq(0,2*pi,length=4)
c1<-seq(0,2*pi,length=7)
LN01_cos<-cos(c0)*LN0
LN01_sin<-sin(c0)*LN0
LN02_cos<-cos(c1-pi/6)*LN0
LN02_sin<-sin(c1-pi/6)*LN0

#立方体におけるz軸上の緯度(LaTitude)座標
LT0=1/3
AP01=LT0
AP02=-LT0

#多面体描写(原蹠から最初の３隣点)
lines3d(c(portal_i,LN01_cos[1]),c(portal_j,LN01_sin[1]),c(portal_k,AP01),col=rgb(0,0,0),lwd=1)
lines3d(c(portal_i,LN01_cos[2]),c(portal_j,LN01_sin[2]),c(portal_k,AP01),col=rgb(0,0,0),lwd=1)
lines3d(c(portal_i,LN01_cos[3]),c(portal_j,LN01_sin[3]),c(portal_k,AP01),col=rgb(0,0,0),lwd=1)

#多面体描写(最初の３隣点から次の6隣点へ)
lines3d(c(LN01_cos[1],LN02_cos[1]),c(LN01_sin[1],LN02_sin[1]),c(AP01,AP02),col=rgb(0,0,0),lwd=1)
lines3d(c(LN01_cos[1],LN02_cos[2]),c(LN01_sin[1],LN02_sin[2]),c(AP01,AP02),col=rgb(0,0,0),lwd=1)
lines3d(c(LN01_cos[2],LN02_cos[3]),c(LN01_sin[2],LN02_sin[3]),c(AP01,AP02),col=rgb(0,0,0),lwd=1)
lines3d(c(LN01_cos[2],LN02_cos[4]),c(LN01_sin[2],LN02_sin[4]),c(AP01,AP02),col=rgb(0,0,0),lwd=1)
lines3d(c(LN01_cos[3],LN02_cos[5]),c(LN01_sin[3],LN02_sin[5]),c(AP01,AP02),col=rgb(0,0,0),lwd=1)
lines3d(c(LN01_cos[3],LN02_cos[6]),c(LN01_sin[3],LN02_sin[6]),c(AP01,AP02),col=rgb(0,0,0),lwd=1)

#多面体描写(底面)
lines3d(c(LN02_cos[1:6],LN02_cos[1]),c(LN02_sin[1:6],LN02_sin[1]),c(AP02,AP02,AP02,AP02,AP02,AP02,AP02),col=rgb(0,0,0),lwd=1)

#アニメーション
movie3d(spin3d(axis=c(0,0,1),rpm=5),duration=10,fps=25,movie="~/Desktop/Polygon009")

ところでこの立体も、正四面体同様「原蹠と対蹠を結ぶ直線が存在しない奇数系図形」なので２つセットで現れます。

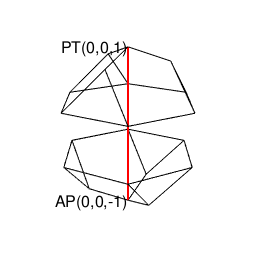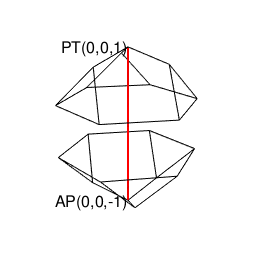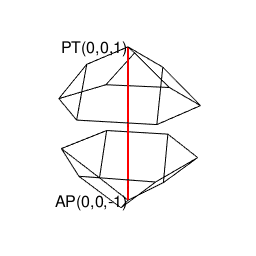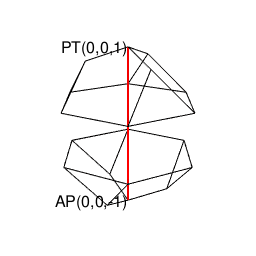
library(rgl)

#原蹠(PorTal)
portal_i<-0
portal_j<-0
portal_k<-1
portal_text=paste0("PT(",portal_i,",",portal_j,",",portal_k,")")

#原蹠表示
texts3d(portal_i,portal_j,portal_k,texts=portal_text,col=rgb(0,0,0),adj=1.0)

#対蹠(AntiPordal)
antipordal_i<-0
antipordal_j<-0
antipordal_k<--1
antipordal_text=paste0("AP(",antipordal_i,",",antipordal_j,",",antipordal_k,")")

#対蹠表示
texts3d(antipordal_i,antipordal_j,antipordal_k,texts=antipordal_text,col=rgb(0,0,0),adj=1.0)

#立方対角線(Cubic Diagonal)
lines3d(c(portal_i,antipordal_i),c(portal_j,antipordal_j),c(portal_k,antipordal_k),col=rgb(1,0,0),lwd=2)

#立方体におけるxy軸上の経度(LoNgitude)座標
LN1=sin(pi/6)
LN2=sin(pi/3)
c0<-seq(0,2*pi,length=4)
c1<-seq(0,2*pi,length=7)
LN01_cos<-cos(c0)*LN1
LN01_sin<-sin(c0)*LN1
LN02_cos<-cos(c1-pi/6)*LN2
LN02_sin<-sin(c1-pi/6)*LN2
RLN01_cos<-cos(c0+pi)*LN1
RLN01_sin<-sin(c0+pi)*LN1
RLN02_cos<-cos(c1-pi/6+pi)*LN2
RLN02_sin<-sin(c1-pi/6+pi)*LN2

#立方体におけるz軸上の緯度(LaTitude)座標
AP01=5/6
AP02=1/3

#正方向多面体描写(原蹠から最初の３隣点)
lines3d(c(portal_i,LN01_cos[1]),c(portal_j,LN01_sin[1]),c(portal_k,AP01),col=rgb(0,0,0),lwd=1)
lines3d(c(portal_i,LN01_cos[2]),c(portal_j,LN01_sin[2]),c(portal_k,AP01),col=rgb(0,0,0),lwd=1)
lines3d(c(portal_i,LN01_cos[3]),c(portal_j,LN01_sin[3]),c(portal_k,AP01),col=rgb(0,0,0),lwd=1)

#正方向多面体描写(最初の３隣点から次の6隣点へ)
lines3d(c(LN01_cos[1],LN02_cos[1]),c(LN01_sin[1],LN02_sin[1]),c(AP01,AP02),col=rgb(0,0,0),lwd=1)
lines3d(c(LN01_cos[1],LN02_cos[2]),c(LN01_sin[1],LN02_sin[2]),c(AP01,AP02),col=rgb(0,0,0),lwd=1)
lines3d(c(LN01_cos[2],LN02_cos[3]),c(LN01_sin[2],LN02_sin[3]),c(AP01,AP02),col=rgb(0,0,0),lwd=1)
lines3d(c(LN01_cos[2],LN02_cos[4]),c(LN01_sin[2],LN02_sin[4]),c(AP01,AP02),col=rgb(0,0,0),lwd=1)
lines3d(c(LN01_cos[3],LN02_cos[5]),c(LN01_sin[3],LN02_sin[5]),c(AP01,AP02),col=rgb(0,0,0),lwd=1)
lines3d(c(LN01_cos[3],LN02_cos[6]),c(LN01_sin[3],LN02_sin[6]),c(AP01,AP02),col=rgb(0,0,0),lwd=1)

#正方向多面体描写(底面)
lines3d(c(LN02_cos[1:6],LN02_cos[1]),c(LN02_sin[1:6],LN02_sin[1]),c(AP02,AP02,AP02,AP02,AP02,AP02,AP02),col=rgb(0,0,0),lwd=1)

#負方向多面体描写(対蹠から最初の３隣点)
lines3d(c(antipordal_i,RLN01_cos[1]),c(antipordal_j,RLN01_sin[1]),c(antipordal_k,-AP01),col=rgb(0,0,0),lwd=1)
lines3d(c(antipordal_i,RLN01_cos[2]),c(antipordal_j,RLN01_sin[2]),c(antipordal_k,-AP01),col=rgb(0,0,0),lwd=1)
lines3d(c(antipordal_i,RLN01_cos[3]),c(antipordal_j,RLN01_sin[3]),c(antipordal_k,-AP01),col=rgb(0,0,0),lwd=1)

#負方向多面体描写(最初の３隣点から次の6隣点へ)
lines3d(c(RLN01_cos[1],RLN02_cos[1]),c(RLN01_sin[1],RLN02_sin[1]),c(-AP01,-AP02),col=rgb(0,0,0),lwd=1)
lines3d(c(RLN01_cos[1],RLN02_cos[2]),c(RLN01_sin[1],RLN02_sin[2]),c(-AP01,-AP02),col=rgb(0,0,0),lwd=1)
lines3d(c(RLN01_cos[2],RLN02_cos[3]),c(RLN01_sin[2],RLN02_sin[3]),c(-AP01,-AP02),col=rgb(0,0,0),lwd=1)
lines3d(c(RLN01_cos[2],RLN02_cos[4]),c(RLN01_sin[2],RLN02_sin[4]),c(-AP01,-AP02),col=rgb(0,0,0),lwd=1)
lines3d(c(RLN01_cos[3],RLN02_cos[5]),c(RLN01_sin[3],RLN02_sin[5]),c(-AP01,-AP02),col=rgb(0,0,0),lwd=1)
lines3d(c(RLN01_cos[3],RLN02_cos[6]),c(RLN01_sin[3],RLN02_sin[6]),c(-AP01,-AP02),col=rgb(0,0,0),lwd=1)

#負方向多面体描写(底面)
lines3d(c(RLN02_cos[1:6],RLN02_cos[1]),c(RLN02_sin[1:6],RLN02_sin[1]),c(-AP02,-AP02,-AP02,-AP02,-AP02,-AP02,-AP02),col=rgb(0,0,0),lwd=1)

#アニメーション
movie3d(spin3d(axis=c(0,0,1),rpm=5),duration=10,fps=25,movie="~/Desktop/Twin_Polygon005")

イメージ上の操作もここまで到れば正六面体同様「境界線上での辺と面の結びつきの調整」が自然進行して正十二面体が顕現する訳です。
【Rで球面幾何学】正12面体(Regular Dodecahedron)の作図について。

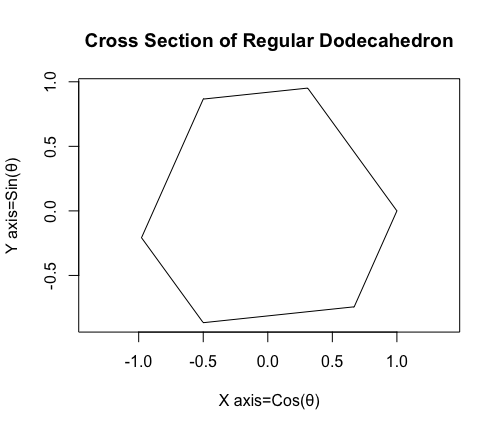
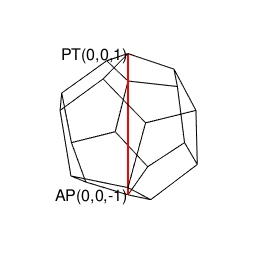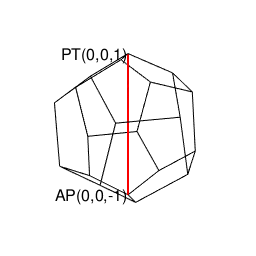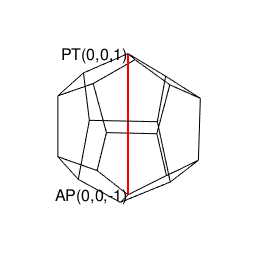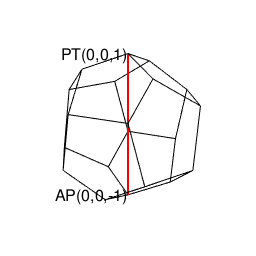
ある意味ファインマンの経路積分(Path Integral)的世界観なので「どっちがアルゴリズム的に優れてるか?」とか、そういうのはありません。
経路積分 - Wikipedia

古典力学（古典系）では、ある質点の運動の様子（運動の経路）は初期状態を決めてしまえば後は運動方程式を解くことによって一意的に定まる。一方、量子系では量子的な不確定さ（量子ゆらぎ）が存在するため、古典系のような一意的な経路の決定はできない。
量子系で素粒子などの運動の様子を求める方法はいくつか存在するが、その一つとして経路積分による方法がある。
経路積分の数式では、始点と終点を結ぶ経路は無数にかつ大域的に分布している。それら無数の経路を計算上で合成すると求める結果となる。 経路積分法によって求めた測定値の確率分布は、通常の演算子形式で求めた確率分布と一致する。よって演算子形式と経路積分法は等価な理論である。

#ここまでのまとめ（全体像の俯瞰）。

そう、まさにユークリッド幾何学と非ユークリッド幾何学、ニュートン力学と量子力学の狭間に登場してくるアレ…現代人は何でもここからの逆算で考えねばならなくなってしまったのですね。
【Rで射影幾何学】そもそも「幾何学」とは何か？

• (立体を原蹠と対蹠を結ぶ経路の広がりと規定する)オイラーの多面体定理(Euler's Polyhedron Theorem)Vertex(頂点数)-Edge(辺数)+Face(面数)=2の条件を満たさない立体は三次元上に存在し得ない(もちろん水面下では色々あり、条件さえ満たされたなら変化は突如として、ほとんど不連続的としか見えない形で訪れる)。
• 原蹠と対蹠を結ぶ経路が存在する偶数系図形と異なり、それが存在しない奇数系図形は常に2個セットで考える（そう考えた方が数理上得する事が多い）。
• 二次元上に存在する図形や三次元上に存在する立体は「可能な限り小さく単純な原理原則への集約を求める」すなわち平方充填や立体充填の条件を満たしたり正多角形や正多面体に近付こうとする指向性を有していると考える（そう考えた方が数理上得する事が多い）。

ここでいう「そう考えた方が数理上得する事が多い」は別に教条主義的押し付けではなく(ポパーの反論可能性原則に従って代替案が現れるまで)むやみやたらと疑い続ける事にまるで意味がない」というだけの話なのですが…
【対訳版】ユージン・ウィグナー『自然科学における数学の理不尽なまでの有効性(1959年)』

第一の点は、〈数学の概念は、まったく予想外のさまざまな文脈のなかに登場してくる〉ということ。
The first point is that mathematical concepts turn up in entirely unexpected connections.
しかも、予想もしなかった文脈に、予想もしなかったほどぴったりと当てはまって、正確に現象を記述してくれることが多いのだ。
Moreover, they often permit an unexpectedly close and accurate description of the phenomena in these connections.
第二の点は、予想外の文脈に現れるということと、そしてまた、数学がこれほど役立つ理由を私たちが理解していないことのせいで、〈数学の概念を駆使して、なにか一つの理論が定式化できたとしても、それが唯一の適切な理論なのかどうかがわからない〉ということ。 
〔Secondly, just because of this circumstance, and because we do not understand the reasons of their usefulness, we cannot know whether a theory formulated in terms of mathematical concepts is uniquely appropriate.
〔この二つの論点をさらに言い直すと〕第一の点は〈数学は自然科学のなかで、ほとんど神秘的なまでに、途方もなく役立っているのに、そのことには何の合理的説明もない〉ということ。
The first point is that the enormous usefulness of mathematics in the natural sciences is something bordering on the mysterious and that there is no rational explanation for it.
第二の点は〈数学の概念の、まさにこの奇怪な有用性のせいで、物理学の理論の一意性が疑わしく思えてしまう〉ということ。
Second, it is just this uncanny usefulness of mathematical concepts that raises the question of the uniqueness of our physical theories.

「それじゃカオス理論とかどうなるの？」って話ですが、そうした諸研究はあくまで「かかる大原則の例外となる特定条件とその振る舞いの範囲を明らかにする」のを目的としてるのであって別に「ユークリッド以来の幾何学やニュートン以来の物理学に何の意味もなかった事が証明されつつある」訳でもないんですね。かかる諸概念の総本山ともいうべきラスボスが「(大数学者オイラーの師匠ベルヌーイが提唱者に擬されている)大数の法則(英LLN=Law of Large Numbers, 仏Loi des grands nombres）」。ここまで疑えば統計学はおろか古代より天文学の恩恵を受けてきた諸学問が根幹から瓦解してしまう最終防衛ラインな訳ですが、19世紀末以降「文系世界(Humanities Bacground Set)」の住人が乱入してきてこれを自らの権威付けに用いたり、逆に党争の種に利用して全面否定に走ったりと「核兵器をジャックナイフやサタデーナイトスペシャル感覚で振り回そうとするチンピラ(ウィリアム・ギブスン「クローム襲撃（Burning Chrome,1982年）」初出のサイバーパンク文学慣用句)」と化して今日なお傍若無人な振る舞いに出続けている有様。そういう人達に是非認識してもらたいのが「大数学者ガウス（Johann Carl Friedrich Gauß/Carolus Fridericus Gauss、1777年~1855年）が正規分布の関数化(すなわち今日におけるパラメトリック検定概念の基礎樹立)に成功した歴史時点では、まだ分散(Variance ロナルド・フィッシャーが1918年に導入)の概念など存在していなかった」辺り。ならば代わりにあったのは？（ヒント画像を挙げ様としたらQiita Downloaderに全否定された。そんなにヤバい話だった？）
パラメトリックとノンパラメトリックの違い

とりあえず、現時点におけるここでの球面幾何学(Spherical geometry)の話題で登場してくる「数理の不思議」は、あくまで原則として「大数の法則」に絡まない以下の範囲に限定されています。

①コイントスを連想させる振動関数-1^xの2値展開…実数範囲では頭蹠と対蹠の往復に中間段階が存在しない原始状態(二項展開を図式化したパスカルの三角形における2段目「1,1」)だが、虚数(Imaginary Number)i^2=-1概念を導入すると正方向範囲(+1~0)と負方向範囲(-1~0)それぞれで円を描く(i^2x。二項展開を図式化したパスカルの三角形における「1,2,1」)。
【Rで球面幾何学】等比数列(幾何数列)③振動関数を巡る収束と拡散。

②各面の中心（面心）を頂点に取り、それらを結んだ結果構成される図形も元と同じ正多角形か正多面体となる双対(Duality)概念…途中過程が全く想像不可能で、かつ想像する事に自体に意味がない。
【Rで球面幾何学】オイラーの多面体定理(Euler's Polyhedron Theorem)と平面充填(Tiling)の連続性について。

• 平面充填性を備える(面を中心に4枚6辺集めると自己相似する)正三角形と(頂点を中心にその正三角形を6舞集めた)正六角形(その面を中心に平面充填性を備える)の相似…まさしく「オイラーの多面体定理」そのものの実装という感じがする。
• 平面充填性を備える(頂点を中心に8個集めた)正六面体と(面を中心に8個集めた)正方形の自己相似(Self Duality)…原点Self Duality0を中心に直交する半直線の積み重ねたN次元直交座標系(Cartesian Coordinate System)や直積(Direct Product)の概念とも絡んでくる分野。このシリーズで本格的に踏み込む展開となるのはまだ先？
• 正四面体の自己双対(Self Duality)…正四面体は全５種類ある正多面体のうち唯一の「不安定な」奇数系図形(頭蹠から伸びた図形も対蹠から伸びた図形も反対側まで到達しておらず、常に一対で顕現する)なので展開が飛び抜けて多い。
• 正六面体と正八面体の双対…断面数と各断面の頂点数の間に往復が存在する(正八面体が[1,2,1(パスカルの三角形3段目)]、正六面体が[1,3,3,1(パスカルの三角形4段目)])。
• 正十二面体面体と正二十面体の双対…断面数と各断面の頂点数の間に往復が存在する(正二十面体が[1,5,5,1]、正十二面体が[1,3,6,6,3,1])。

③「いないいないばぁ!!」挙動…図形変換の内容も途中過程も全く想像不可能で、かつ想像する事に意味がない。

• 平面充填性を備える正三角形三枚から正四面体へ…まさしく「オイラーの多面体定理」そのものの実装という感じがする。最後の1枚(底面)が自然に自動的に補完されたものと見做す？
• 一対の正四面体から立方体へ…まさしく「オイラーの多面体定理」そのものの実装という感じがする。他の立方体と異なりハミルトンの四元数への入口が開く。
• 一対の正四面体(あるいは3枚の正三角形から)から正十二面体へ…まさしく「オイラーの多面体定理」そのものの実装という感じがする。この投稿で扱った内容。
• 一対の正四面体(あるいは4枚の正三角形から)から八面体へ…まさしく「オイラーの多面体定理」そのものの実装という感じがする。一方、一対の正四面体からの変遷の場合「その底辺が必要に応じて三辺比1:1:sqrt(2)の二等辺三角形に変貌する可能性」を想定せざるを得なくなる。そんな場合まで想定しないといけないのか…
• 正三角形5枚から正十二面体へ…まさしく「オイラーの多面体定理」そのものの実装という感じがする。

ほとんどメモ同然で申し訳ありませんが、。大体この辺りの遷移は全貌が見えてきたので、そのうちライブラリ化するかもしれません。もちろん捉え切れてない数理も多いので一筋縄では行かないと思いますが…