今から思い返すに、私が数理世界(Mathematical Things Set)で最初に躓いたのは、まさにこの定義においてだったのです。
幾何学とは (キカガクとは) [単語記事] - ニコニコ大百科
図形について考察する数学の一分野。現代では所謂"幾何学的"な整然とした図形だけでなく、より広範な対象を扱う。
それでは(古代オリエント灌漑農業の世界においてしばしば大河の氾濫開始時期と密接に結び付けて考えられてきた)シリウス星に導かれるまま、順番にこの問題を解きほぐしていく事にしましょう。
シリウス星(Sirius) - Wikipedia

幾何学の概念の歴史的大源流
その発祥は非常に古く、古代オリエントのナイル川流域における測量に端を発すると言われている。ナイル川流域は年に一度氾濫を起こし、氾濫が終わった後には肥沃な土壌を上流から運んでいた。しかし、氾濫により一帯が全て洗い流されてしまうため、氾濫後には土地を元通りに配分しなくてはならなかったのである。このような背景の下、古代オリエントでは測量術が発達し、測量術から派生する形で幾何学は誕生した。ラテン語でGeometria、英語でGeometryと表記するのもその名残(geo-:土地の / -metry:測定法)である。
さらには(しばしば同時に農業暦を整える神殿宗教を司る神官集団を代表する立場にもあった)古代オリエントの祭政者達は、同時に毎年毎年氾濫が起こる
時期を必要にして十分なだけ正確に予測する責務も担わされていたので(数理的には円弧/球面幾何学に立脚する)天文学(Astronomy)分野も早くから発達してきたのでした。
天文学 - Wikipedia(英Astronomy, 独Astronomie,Sternkunde, 蘭Astronomie (Astronomia),Sterrenkunde (Sterrekunde),仏Astronomie)
天動説と地動説の違いを説明するアニメーションの数学的美しさ

我々人類のちっぽけな知性(Our Poor Little Intelligence)には到底直接は手を伸し得ない「辺長が無限小(1/Inf)で辺数が無限大(Inf)の辺数で構成される円そのもの(Circle / Sphere Surface)上の永劫回帰運動(独:Ewige Regression Bewegung)」を、コンピューターに扱える加算直積可能世界(Countable and Productable Sets)に持ち込むべく近似法概念(Approximation Method Concept)の開発(Development)が始まったのもまさにこの頃だったのです。例えば現代人の次空間概念を基礎付けた古代シュメール文明の60進法…
【初心者向け】「円そのもの」の近似から派生した角度と経度の概念の起源

また、どうして漢字圏ではGeometria/Geometryが「幾何学」と呼ばれるようになったのかについて、さらにこんなややこしい話がある様です。こういう話でありがちな様に、やはり背後に近世イエズス会士の暗躍があったらしい?
満洲語資料からみた「幾何」の語源について (数学史の研究)
直角三角形の「典型的角度」について。
この時代の有名な発見物として、三辺比3:4:5の直角三角形がある。この三角形により、簡単な整数比から直角を作ることが可能となった。
ここに登場する三辺比3:4:5の直角三角形の物凄いところは、概ねその値が小さい方の角度がArcsin(3/5)(36.87度/0.6435011Radian)、大きい方の角度がArcsin(4/5)(53.13度/0.9272952Radian)とされ、未だにちゃんとした角度が割り当てられてない(割り当て様がない)辺り。だからその一方で学校教育の現場などでは別の三角定規のセットが用いられてきたのです。
# 直角=90度はArcsin(1)=1.570796Radian。
asin(1)
[1] 1.570796
> asin(1)/(2*pi)*360
[1] 90
# 小角=36.87度はArcsin(3/5)=0.6435011Radian。
> asin(3/5)
[1] 0.6435011
> asin(3/5)/(2*pi)*360
[1] 36.8699
# 大角=53.13度はArcsin(4/5)=0.9272952Radian。
> asin(4/5)
[1] 0.9272952
> asin(4/5)/(2*pi)*360
[1] 53.1301
# もちろん大角+小角=直角。
> asin(3/5)+asin(4/5)
[1] 1.570796
> (asin(3/5)+asin(4/5))/(2*pi)*360
[1] 90
とりあえず、三辺比3:4:5の直角三角形のデカルト座標系(Rectangular Coordinate System / Orthogonal Coordinate System=直交座標系)における表現(Expression)はこうなります。
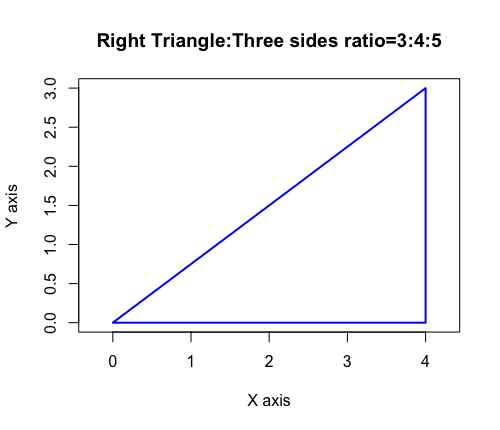
# "斜辺5"に関する記述が明示的に現れない点に注意。
cx=c(0,4,4,0)
cy=c(0,0,3,0)
plot(cx,cy,type="l",asp=1,col=rgb(0,0,1),lwd=2, main="Right Triangle:Three sides ratio=3:4:5",xlab="X axis",ylab="Y axis")
それでは、代わりに普及した三角定規は一体どんな比率で興成されていたのでしょうか。
三角定規とコンパスの歴史
①正方形(Square)を対角線で2つに分割した辺長比1:1:sqrt(2),角度比45度(π/4ラジアン):45度(π/4ラジアン):90度((π/2ラジアン)の二等辺三角形…平方眼(Square Grid)や立方眼(Cube Grid)上の平方対角線(Square Diagonal)に対応。

# "斜辺sqrt(2)"に関する記述が明示的に現れない点に注意。
cx=c(0,1,1,0)
cy=c(0,0,1,0)
plot(cx,cy,type="l",asp=1,col=rgb(0,0,1),lwd=2, main="Right Triangle:Three sides ratio=1:1:sqrt(2)",xlab="X axis",ylab="Y axis")
②正三角形(Equilateral Triangle)を垂線で2つに分割した辺長比1:2:sqrt(3),角度比30度(π/6ラジアン):60度(π/3ラジアン):90度(π/2ラジアン)の直角三角形…
【Rで球面幾何学】正四面体と正六面体と正八面体の連続性と「テトラパックの思わぬ正体」について。
デカルト座標系においては平方眼や立方眼上における2マス(X軸1マスY軸2マスか、X軸2マスY軸1マス)の平方対角線(Square diagonal)の算出に用いる。
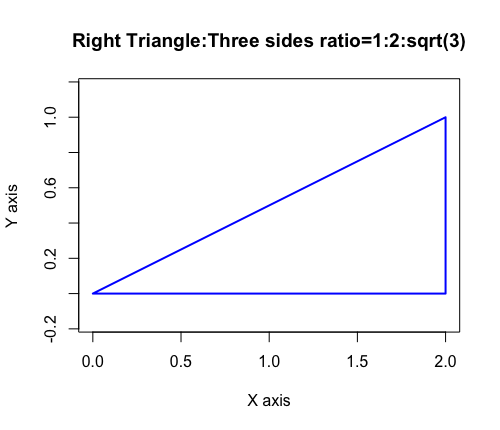
# "斜辺sqrt(3)"に関する記述が明示的に現れない点に注意。
cx=c(0,2,2,0)
cy=c(0,0,1,0)
plot(cx,cy,type="l",asp=1,col=rgb(0,0,1),lwd=2, main="Right Triangle:Three sides ratio=1:2:sqrt(3)",xlab="X axis",ylab="Y axis")
③ハミルトンの四元数(Hamilton's Quaternion)における「球面上に位置する原蹠と対蹠の間を2回直角に曲がって結ぶ3次元系空間処理」の際に現れる辺長比1:sqrt(2):sqrt(3),角度比28度(π/10ラジアン):72度(2π/5ラジアン):90度(π/2ラジアン)の直角三角形…
【Rで球面幾何学】正方形における平方対角線(Square diagonal)と立方体における立方対角線(Cubic diagonal)の関係について。
【Rで球面幾何学】ハミルトンの四元数(Quaternion)は何を表しているのか?
【Rで球面幾何学】正四面体と正六面体と正八面体の連続性と「テトラパックの思わぬ正体」について。
# 直角=90度はCos(0)=Sin(pi/2)=1
> cos(0)
[1] 1
> cos(0)*90
[1] 90
> sin(pi/2)
[1] 1
> sin(pi/2)*90
[1] 90
# 小角=28度はπ/10Radian。
>pi/10/pi*180
[1] 18
# 大角=>72度は2π/5Radian。
> 2*pi/5/pi*180
[1] 72
# cos(2π/5)/π=sin(π/10)/π=0.3027307
> cos(2*pi/5)
[1] 0.309017
> sin(pi/10)
[1] 0.309017
「えっ、そんな被率の三角定規見た事も聞いた事もないよ!!」と思う人が大半で、実際私自身も見た事も聞いた事もないが、ハミルトンの四元数(Hamilton's Quaternion)の内容を理解する上で極めて便利だし、実際テトラパックの様な形で実用化もされているので、あえて挙げてみた次第。

# "斜辺sqrt(3)"に関する記述が明示的に現れない点に注意。
cx=c(0,sqrt(2),sqrt(2),0)
cy=c(0,0,1,0)
plot(cx,cy,type="l",asp=1,col=rgb(0,0,1),lwd=2, main="Right Triangle:Three sides ratio=1:sqrt(2):sqrt(3)",xlab="X axis",ylab="Y axis")

いずれにせよ、単位円(Unit Circle)上における平方ピタゴラスの定理(Square Pythagorean theorem)Hamilton's Quaternionsqrt(x^2+y^2)=1や単位球面(Unit Sphere)上における立方ピタゴラスの定理(Cubic Pythagorean theorem)sqrt(x^2+y^2+z^2)=1の振る舞いがちゃんと脳内に導入(Introduction)済みだったなら、あくまでその特殊例に過ぎないので態々実物を携帯する必要はありません。そもそも、どうしてそういう「原則として作図にコンパスも定規も不要」時代が訪れたかというのが今回の投稿の肝だったりして…
「ユークリッド幾何学」の登場
その後古代ギリシアに於いて研究が進み、大きな発展を遂げる。特筆すべきは証明(Mathematical Proof)という手法を導入した点にある。現在から考えれば当たり前のような手法かもしれないが、僅かな前提(公理・公準)から、当然とは思えないような結論(公理)を厳密な演繹により導き出すこの手法は、当時としては画期的な手法であった。この時代の主要な人物としてはターレス、ピタゴラス、ユークリッドなどが挙げられる。中でもユークリッドは『原論』を著わし、この時代における証明の手法を完成させたと言われる。
ユークリッドの提案した公理
- 公理1: 同じものと等しいもの同士は互いに等しい(A=BならB=A, A=BかつB=CならA=C)。
- 公理2: 同じものに同じものを足した場合、その合計は等しい(A=BならA+X=B+X)。
- 公理3: 同じものから同じものを引いた場合、その残りは等しい(A=BならA-X=B-X)。
- 公理4: 互いに一致するものは、互いに等しい。
- 公理5: 全体は部分より大きい。
ユークリッドの提案した公準
- 公準1: 任意の1点から他の1点へ線を引くことができる。
- 公準2: 有限の直線は連続的にまっすぐ延長することができる。
- 公準3: 任意の点を中心に、任意の半径の円を描くことができる。
- 公準4: 全ての直角は等しい。
- 公準5: 1本の直線Aが2本の直線B,Cに交わるとする。このとき、同じ側の内角が2直角未満であれば、B,Cを無限に延長すれば何処かで交差する(平行線は交わらない)。
これまでの「円周/球面幾何学」関連投稿では、そもそもそれが極座標系(Polar Coordinate System)に立脚する非ユークリッド幾何学に分類される内容であった為、こういった部分から再建を果たす必要がありました。
①流石にピタゴラスの定理(Cubic Pythagorean theorem)や加法定理(Trigonometric Addition Formulas)などは継承せざるを得ず、独自証明を試みた上で採択。
【初心者向け】ピタゴラスの定理あるいは三平方の定理からの出発

【初心者向け】「加法定理の幾何学的証明」に挑戦。
②公準1に「任意の1点から他の1点へ線を引くことができる」とあるが、この世界(Set)においては円周/球表面上の任意の点は、対蹠発見まで事実上半直線扱いとしている。全体量が未定なので目盛りも振れない。
【Rで球面幾何学】単位円と単位球②円周角(Circumference Angle)とは何か?

「辺長が無限小(1/Inf)で辺数が無限大(Inf)の辺数で構成される円そのもの(Circle / Sphere Surface)上の永劫回帰運動(独:Ewige Regression Bewegung)」の基本概念上、円周/球表面上の任意の点は中心から伸ばされた垂線と垂直に交わる水平線上に位置するとされる。この性質はそれらが物理学上の等速円運動と結び付けられる上でも重要な役割を果たしているのだが、如何せん直接確かめる手段がないのでかかる対応とならざるを得ないのであった。
【初心者向け】物理学における「単位円筒(Unit Cylinder)」の概念について。
XY軸(円弧)

XZ軸(Cos波)

YZ軸(Sin波)

【初心者向け】「単位円筒」から「単位球面」へ

③逆をいうと対蹠発見は、そのままその円周(Circumference)/球表面(Sphere Surface)上の中心位置(Origin)や半径(Radius)/直径(Diameter)の取得につながり、正弦定理A/sin(a)=B/sin(b)=C/sin(c)=2Rの特殊形たるターレスの定理「その円の弧に対する円周角は常に直角である」を用いて直角概念も援用可能となるので「円弧上に位置する原蹠と対蹠の間を1回も曲がらず直線で結ぶ1次元処理」「円弧上に位置する原蹠と対蹠の間を1回直角に曲がって結ぶ2次元処理」「球面上に位置する原蹠と対蹠の間を2回直角に曲がって結ぶ3次元系の空間処理」なども展開可能となる(もちろんその時発見された円周/球表面が、その点が本来属する筈の円そのものである確証だけは得られない。それはそれで絶対的にそういうものと諦めざるを得ないのである。)。ある意味この世界においては、こうした諸概念こそがユークリッド公準4「全ての直角は等しい」に該当するといえよう(とどのつまり「ピタゴラスの定理は偉大」「ターレスの定理は偉大」これに尽きる。)。
【計算上の往復】半径・直径・円周長・円の面積・球の表面積・球の体積の計算上の往復

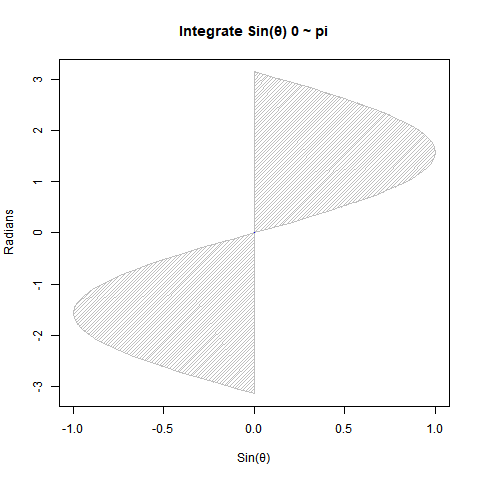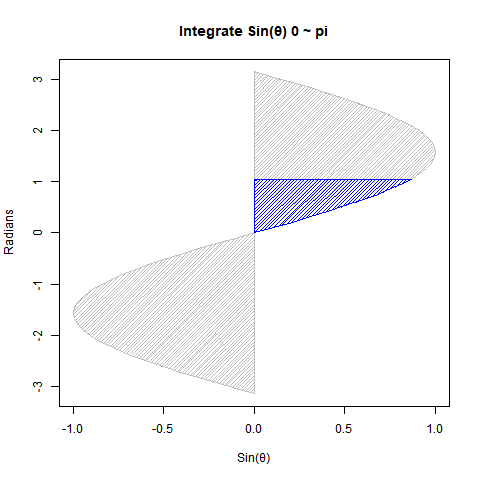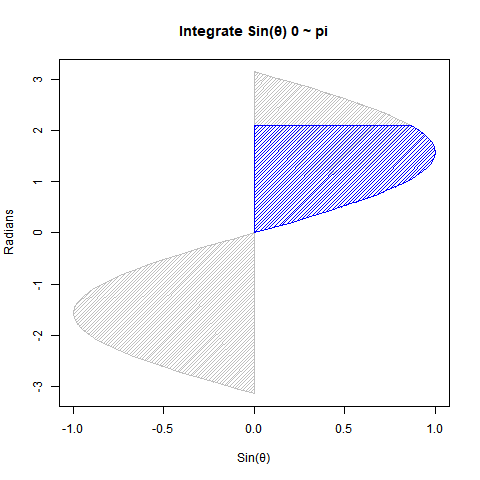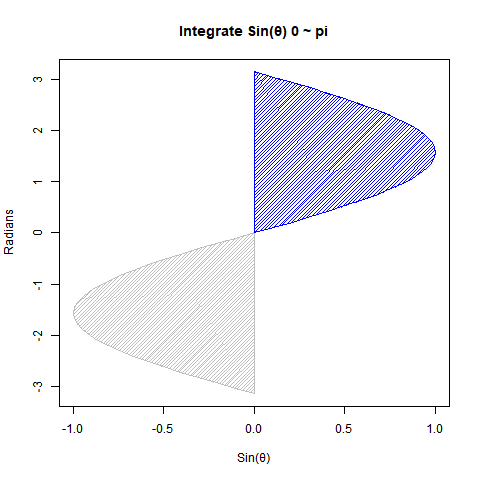
【Rで球面幾何学】単位円と単位球①「半径1」と「直径2」の関係について。
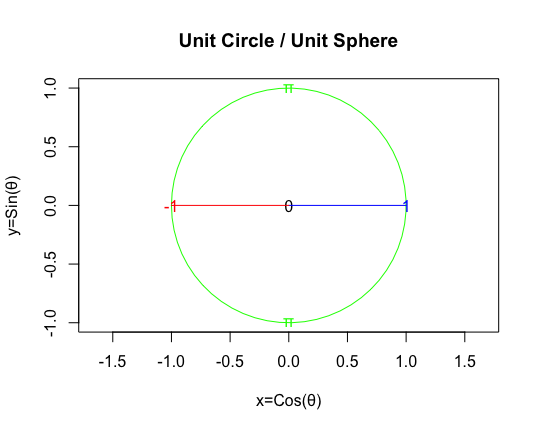
【Rで球面幾何学】ハミルトンの四元数(Quaternion)は何を表しているのか?
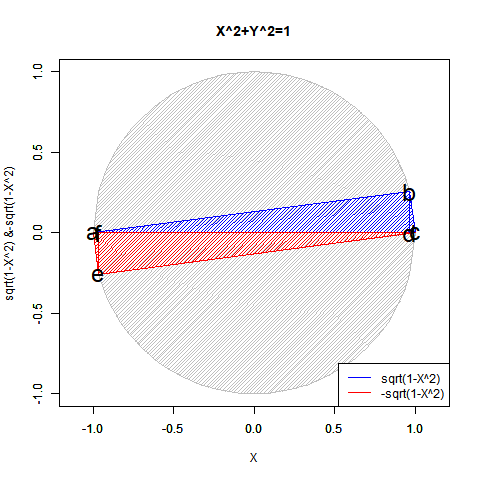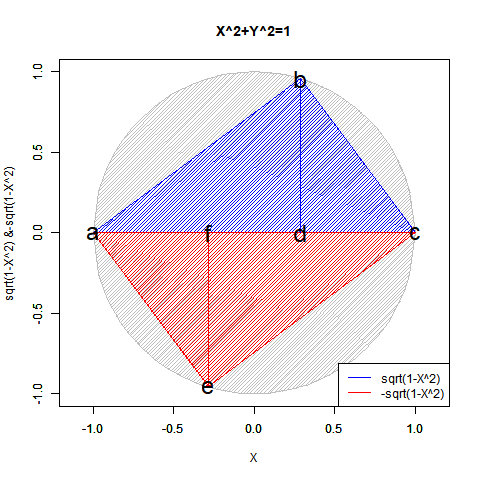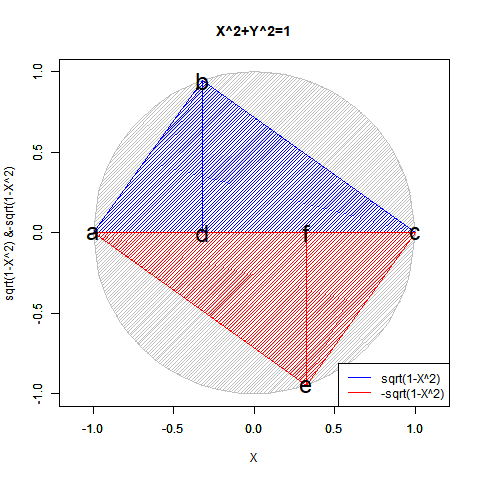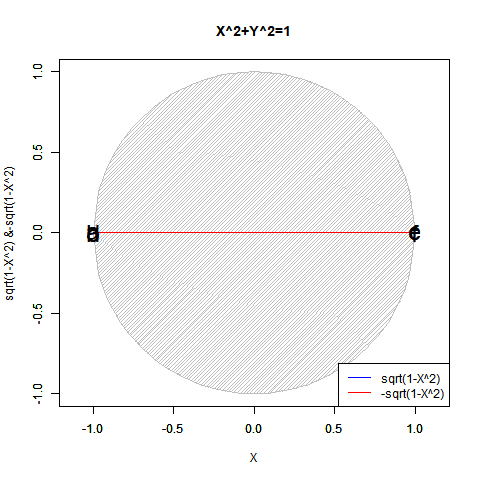

④かくしてこの世界における単位円(Unit Circle)/単位球(Unit Sphere)の概念が固まってやっと、中心0や半径1を初項とする等差数列(Arithmetic Progression/Arithmetic Sequence=算術数列)や等比数列(Geometric Progression/Geometric Sequence=幾何数列)が展開可能となり、それぞれが固有の同心円集合(Concentric set)を構成する。元よりN次元展開を含むが、ここで重要となってくるのが各次元の導入(Introduction)に際して符号概念を導入せず片側無限数列(One-Sided Infinite Sequence)を構成するか、それを導入して両側無限数列(Two-Sided Infinite Sequence)を構成するかの選択。この辺りがユークリッドの公準1「任意の1点から他の1点へ線を引くことができる。」公準2「有限の直線は連続的にまっすぐ延長することができる。」公準3「任意の点を中心に、任意の半径の円を描くことができる。」に該当してくるとはいえようが、この世界においてはどれもそれぞれ相応に厳密な演算結果として実現する点が異なってくる(「測量」を原点とする幾何学より「天体観測」から出発した物理学の影響を色濃く受けているせいとも。)。
【Rで球面幾何学】等差数列(算術数列)① 数直線(Number Line)概念の導入(Introduction)について。
【Rで球面幾何学】等比数列(幾何数列)①その基本的性質について。
【Rで球面幾何学】等差数列(算術数列)②数直線(Number Line)概念から同心円集合(Concentric Set)概念へ
片側の端点(End Point)のみが無限大Infもしくは無限小-Infに開かれた片側無限算術数列(One-Sided Infinite Arithmetic Sequence)。

無限大Infと無限小-Infに挟まれた開区間(Open Interval)で仕切られた両側無限算術数列(Two-Sided Infinite Arithmetic Sequence)。Y軸に符号による峻別を採用した場合。

X軸に符号による峻別を採用した場合。

【Rで球面幾何学】等比数列(幾何数列)②同心円集合(Concentric Set)に射影(Projection)する準備
(初項a,公差0の等差数列と完全に合致する)初項a,公比1の等差数列を目盛に採用した片側無限幾何数列(One-Sided Infinite Geometric Sequence)。

指数尺(すなわち自然指数関数e^xの値)を目盛に採用した片側無限幾何数列(One-Sided Infinite Geometric Sequence)。

「平行線公準」問題
以来、長らくユークリッドが体系化した「ユークリッド幾何学」は唯一の幾何学として研究が進められていた。というのも、直感的に納得のできる空間のあり方での幾何学だったからである。その一方で、公準5(平行線公準)については長らく妥当性に疑問が投げ掛けられていた。平行線公準の証明は、正に「世紀の難問」だったのである。
「円が半円しか描けない」問題も存在し、こちらは実際には18世紀頃、指数関数(Exponential Function)/対数関数(Log Function)や虚数(Imaginary Number)や共役複素数(Conjugate Complex)の概念の導入によってまとめて突破される展開を迎えたのである。ただし以降も幾何学の世界はこうした成果の黙殺を続けた感もある。
【Rで球面幾何学】「半円しか描けなかった」世界の思い出?
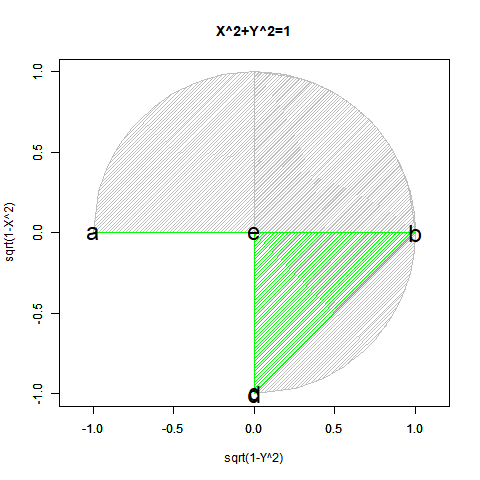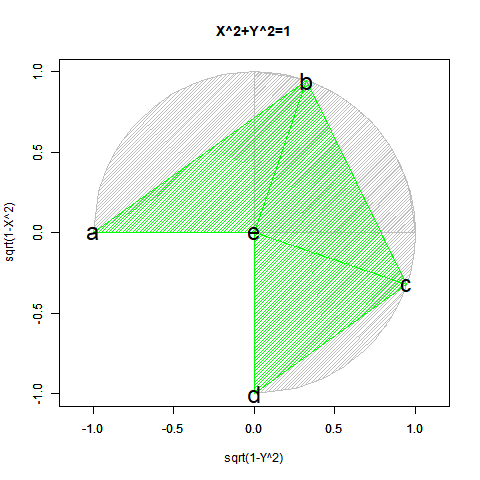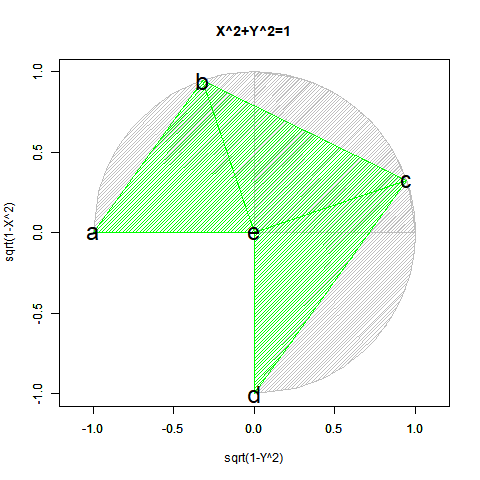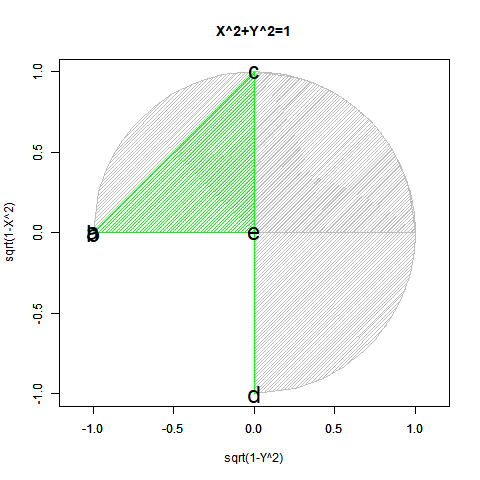
【初心者向け】三角関数と指数・対数関数の「巡回性」について。
【Rで球面幾何学】指数・対数関数の発見
【Rで球面幾何学】オイラーの公式を導出したマクローリン級数の限界?

「非ユークリッド幾何学」の登場
19世紀にフリードリヒ・ガウスは公準5(平行線公準)を「平行線は交差する」と置き換えても整合性のある幾何学が成立する可能性を示唆した。これにより、後年に非ユークリッド幾何学が生み出された。余談だが、ガウス自身は宗教紛争に巻き込まれることを嫌って非ユークリッド幾何学を提唱することはなかったのである。
これまでの投稿範囲では到底言及に及んでませんが、私の中でフリードリヒ・ガウス(Johann Carl Friedrich Gauß, 1777年〜1855年)は以下のパラダイムシフトを成し遂げた偉人という位置付けとなります。

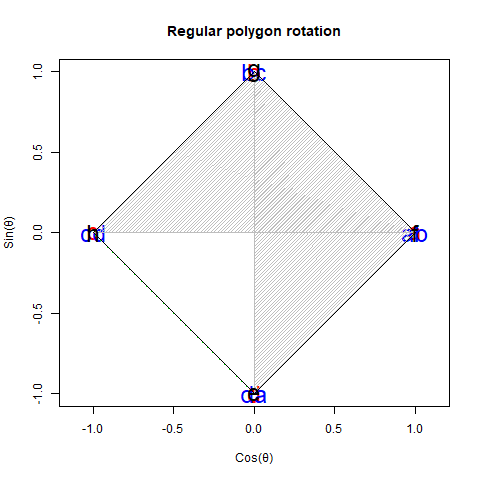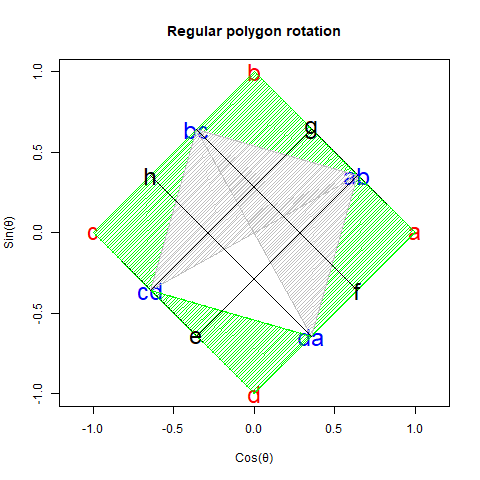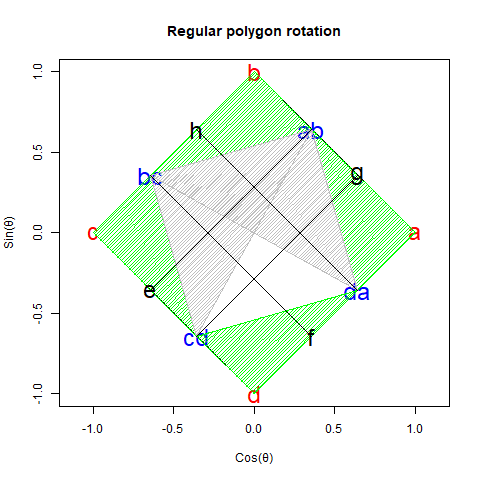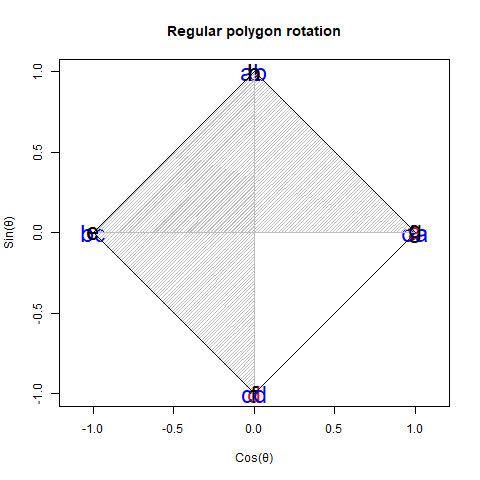
①「1の冪根の巡回性」を発見し、作図の世界から定規やコンパスを追放してコンピューター・グラフイック実現の下地を造った人物。
1の冪根(Root of Unity) - Wikipedia -
もう本当にね、ここに投稿したプログラムだけで幾度c0=seq(-pi,pi,length=NoS);cx=cos(c0);cy=sin(c0)(NoS(Number of Sides)=描く多角形の辺数+巡回を完成させる為の1)の構文を使い倒してきた事か。
【初心者向け】挟み撃ち定理(Squeeze Theorem)による円周率πの近似

②ガウス積分発表によって「広義積分、すなわち無限遠点を範囲に含む定積分ではそれまで用いてきた近似概念の間に可換性が生じる(近似さえちゃんと出来てれば、細けぇこたぁいいんだよ!)」なる概念を導入した人物。そもそも実はオイラーの公式(Euler's formula)e^θi=cos(θ)+sin(θi)もコンセプトは同じだったのかもしれない。そういう発想に至れたのも、かかるヒントがあったから。
ガウス積分の公式
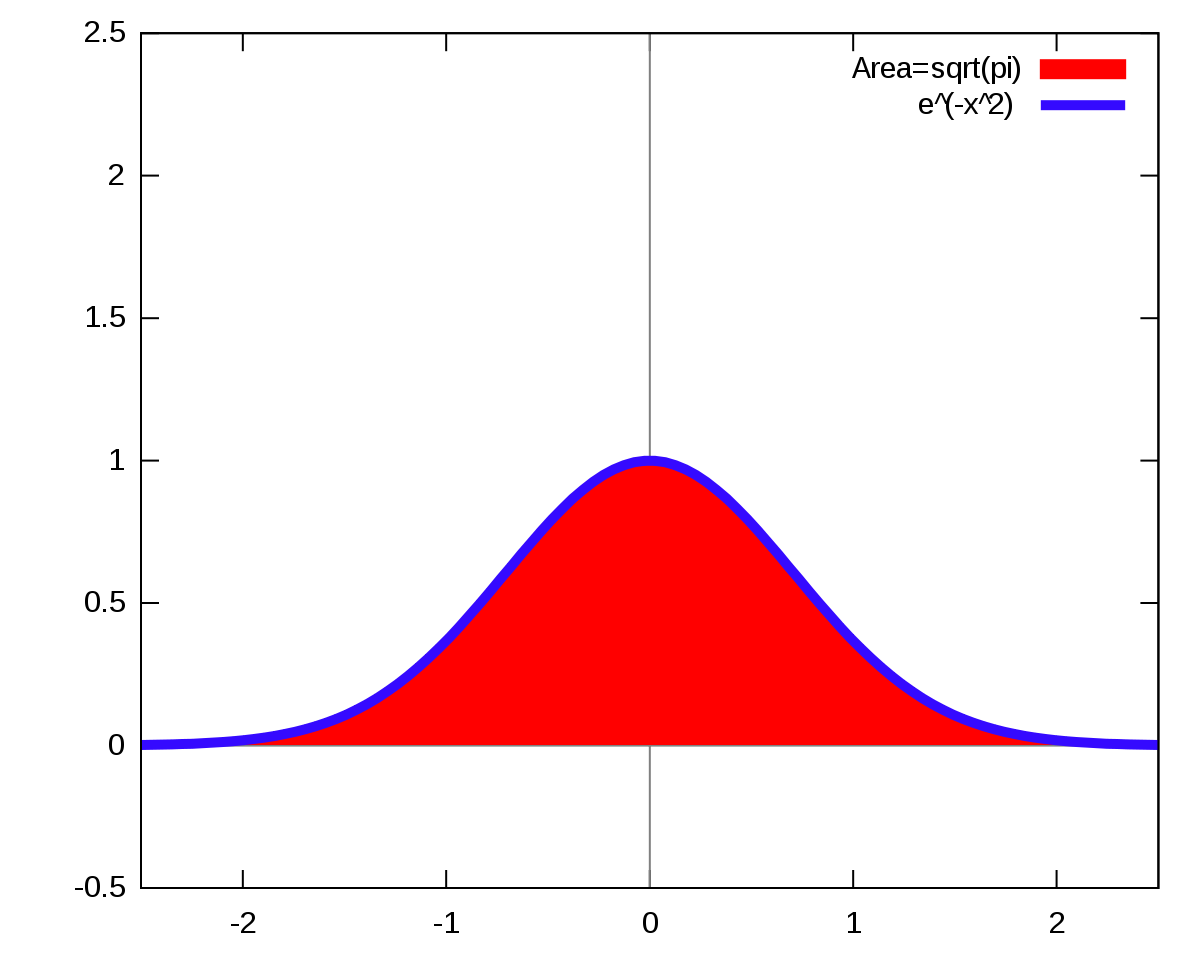
ネイピア数e^1と円周率πの算出過程(収束する数値こそ違ど、無限遠点に向かう区間設定の動かし方は同じ)
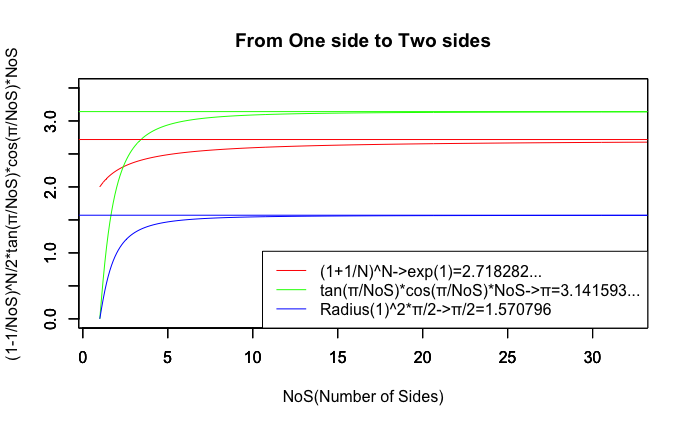
# オイラーの「ネイピアの対数表」に基づく算出方法
cx0<-seq(1,70,length=700)
f0<-function(x){(1+1/x)^x}
cy0<-f0(cx0)
# グラフ化してみる。
plot(cx0,cy0,xlim=c(1,32),ylim=c(0,3.5),type="l",col=rgb(1,0,0),main="From One side to Two sides", xlab="NoS(Number of Sides)", ylab="(1-1/NoS)^N/2*tan(π/NoS)*cos(π/NoS)*NoS")
par(new=T)#上書き指定
# 円周計算
cx1=seq(1,70,length=700)
f1=function(x) tan(pi/x)*cos(pi/x)*x
cy1<-f1(cx1)
plot(cx1,cy1,xlim=c(1,32),ylim=c(0,3.5),type="l",col=rgb(0,1,0),main="", xlab="", ylab="")
par(new=T)#上書き指定
# 面積計算
cx2=seq(1,70,length=700)
f2=function(x) tan(pi/x)*cos(pi/x)*x/2
cy2<-f2(cx2)
plot(cx2,cy2,xlim=c(1,32),ylim=c(0,3.5),type="l",col=rgb(0,0,1),main="", xlab="", ylab="")
# 自然対数1/eと比較。
abline(h=exp(1),col=rgb(1,0,0))#exp(1)=2.718282...
abline(h=pi/2,col=rgb( 0,0,1))#π/2=1.570796...
abline(h=pi,col=rgb(0,1,0))#π=3.141593...
# 凡例
legend("bottomright", legend=c("(1+1/N)^N->exp(1)=2.718282...","tan(π/NoS)*cos(π/NoS)*NoS->π=3.141593...","Radius(1)^2*π/2->π/2=1.570796"),lty=c(1,1),col=c(rgb(1,0,0),rgb(0,1,0),rgb(0,0,1)))
ネイピア数e^-1と円周率2πの算出過程(収束する数値こそ違ど、無限遠点に向かう区間設定の動かし方は同じ)
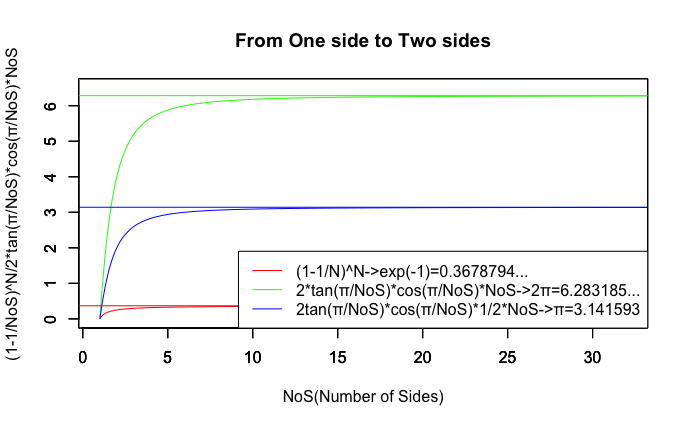
# オイラーの「ネイピアの対数表」に基づく算出方法
cx0<-seq(1,70,length=700)
f0<-function(x){(1-1/x)^x}
cy0<-f0(cx0)
# グラフ化してみる。
plot(cx0,cy0,xlim=c(1,32),ylim=c(0,6.5),type="l",col=rgb(1,0,0),main="From One side to Two sides", xlab="NoS(Number of Sides)", ylab="(1-1/NoS)^N/2*tan(π/NoS)*cos(π/NoS)*NoS")
par(new=T)#上書き指定
# 円周計算
cx1=seq(1,70,length=700)
f1=function(x) 2*tan(pi/x)*cos(pi/x)*x
cy1<-f1(cx1)
plot(cx1,cy1,xlim=c(1,32),ylim=c(0,6.5),type="l",col=rgb(0,1,0),main="", xlab="", ylab="")
par(new=T)#上書き指定
# 面積計算
cx2=seq(1,70,length=700)
f2=function(x) tan(pi/x)*cos(pi/x)*x
cy2<-f2(cx2)
plot(cx2,cy2,xlim=c(1,32),ylim=c(0,6.5),type="l",col=rgb(0,0,1),main="", xlab="", ylab="")
# 自然対数1/eと比較。
abline(h=exp(-1),col=rgb(1,0,0))#exp(-1)=0.3678794...
abline(h=pi,col=rgb( 0,0,1))#2π=6.283185...
abline(h=2*pi,col=rgb(0,1,0))#2π=6.283185...
# 凡例
legend("bottomright", legend=c("(1-1/N)^N->exp(-1)=0.3678794...","2*tan(π/NoS)*cos(π/NoS)*NoS->2π=6.283185...","2tan(π/NoS)*cos(π/NoS)*1/2*NoS->π=3.141593"),lty=c(1,1),col=c(rgb(1,0,0),rgb(0,1,0),rgb(0,0,1)))
古来、2次曲線は放物線、楕円(円を含む)、双曲線の3種類に分類されてきました。 これらは円錐曲線とも呼ばれ、円錐面を、 母線と平行な平面で切った断面は放物線、 母線より浅い角度を成す平面で切った断面は楕円、 母線より深い角度を成す平面で切った断面は双曲線となります。2次元の無限遠点を考えることによってこれらは皆同じものであるという解釈ができます。
こうして、これまでの投稿内容の全体像が相応に振り返れた時点で、以下続報…